Cluster Analysis of Cell Nuclei in H&E-Stained Histological Sections of Prostate Cancer and Classification Based on Traditional and Modern Artificial Intelligence Techniques
Abstract
1. Introduction
2. Related Work
3. Materials and Methods
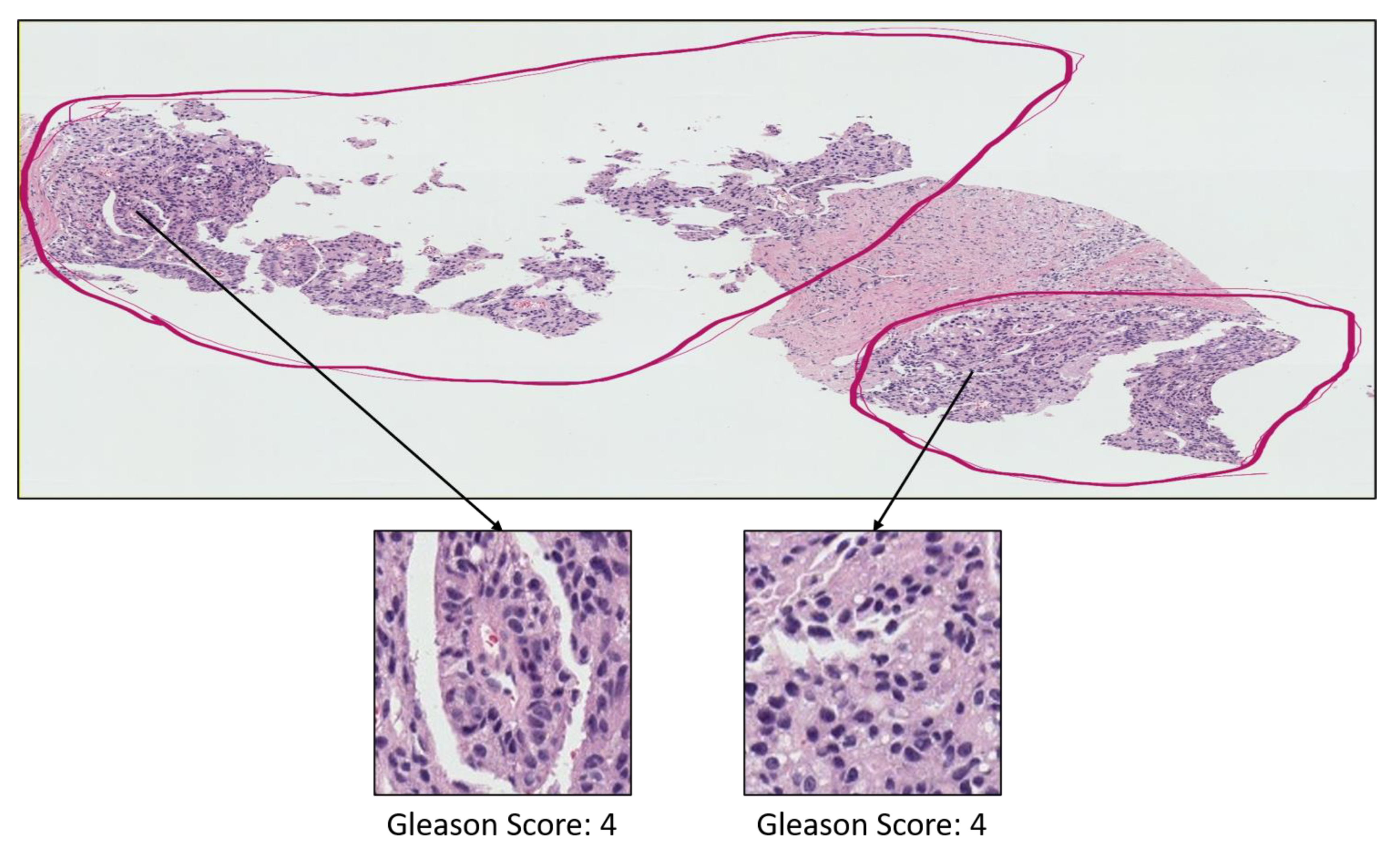
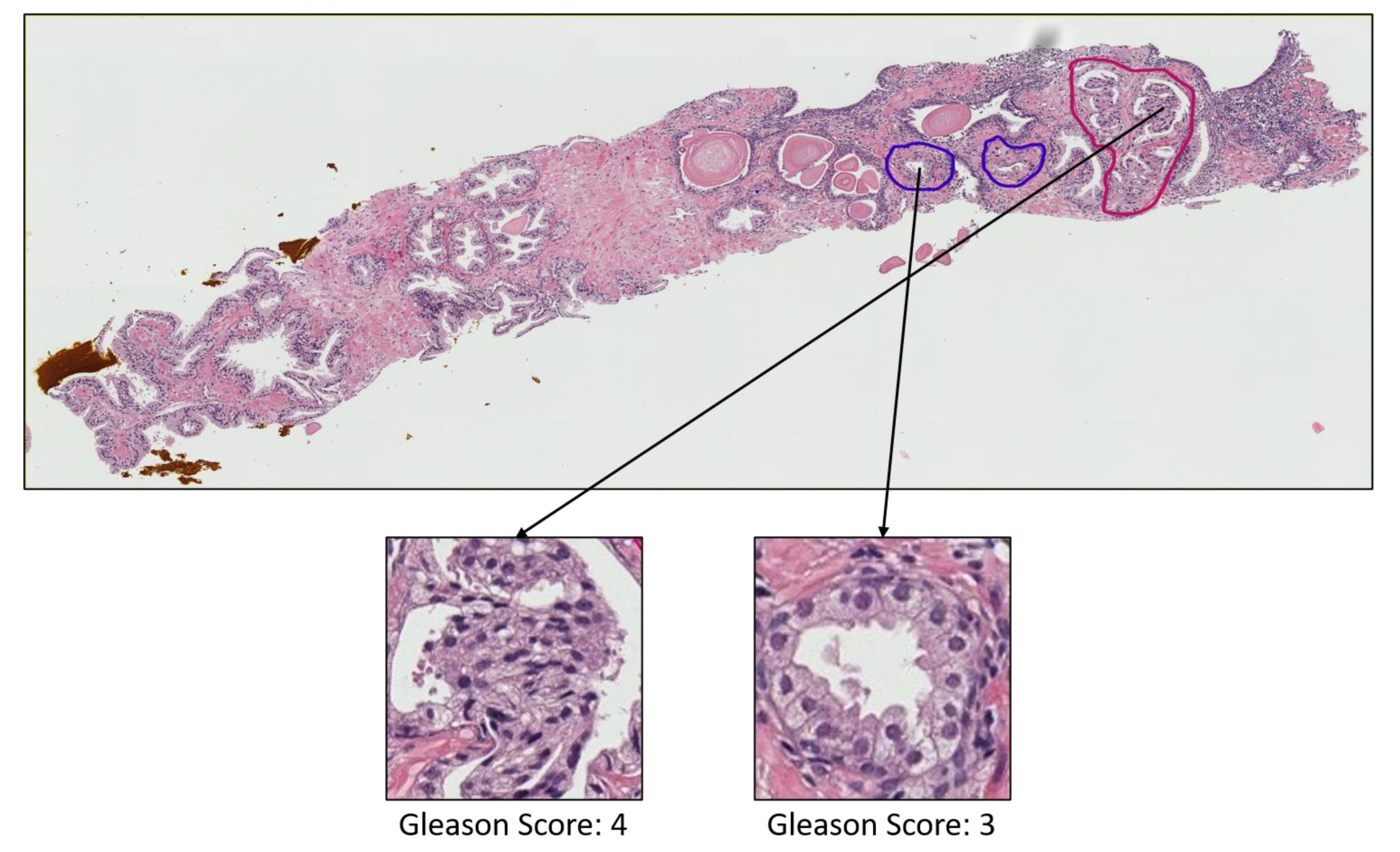
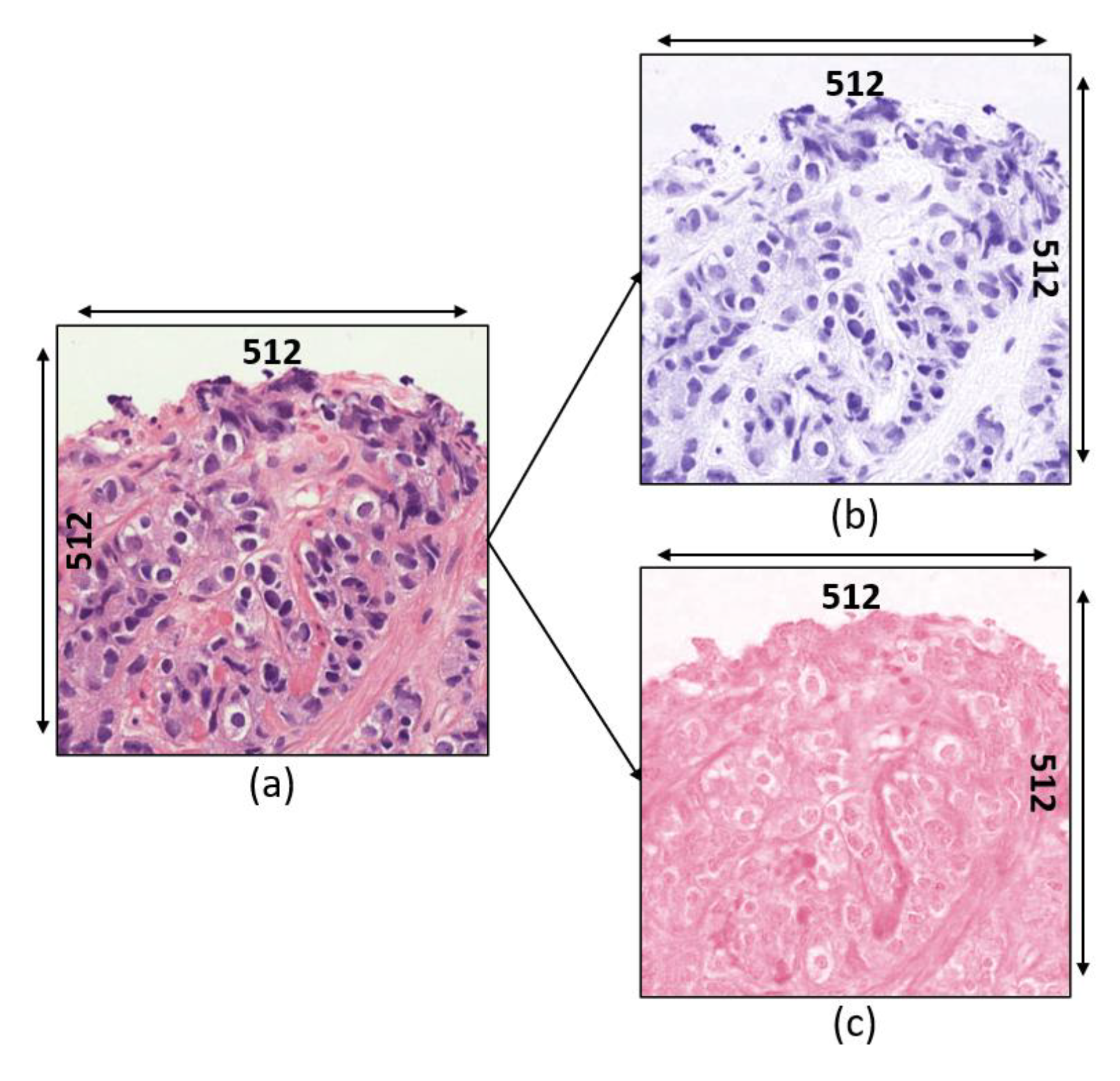
3.1. Data Acquisition
- Grade 3: Gleason score 4 + 3 = 7. Distinctly infiltrative margin.
- Grade 4: Gleason score 4 + 4 = 8. Irregular masses of neoplastic glands. Cancer cells have lost their ability to form glands.
- Grade 5: Gleason score 4 + 5, 5 + 4, or 5 + 5 = 9 or 10. Only occasional gland formation. Sheets of cancer cells throughout the tissue.
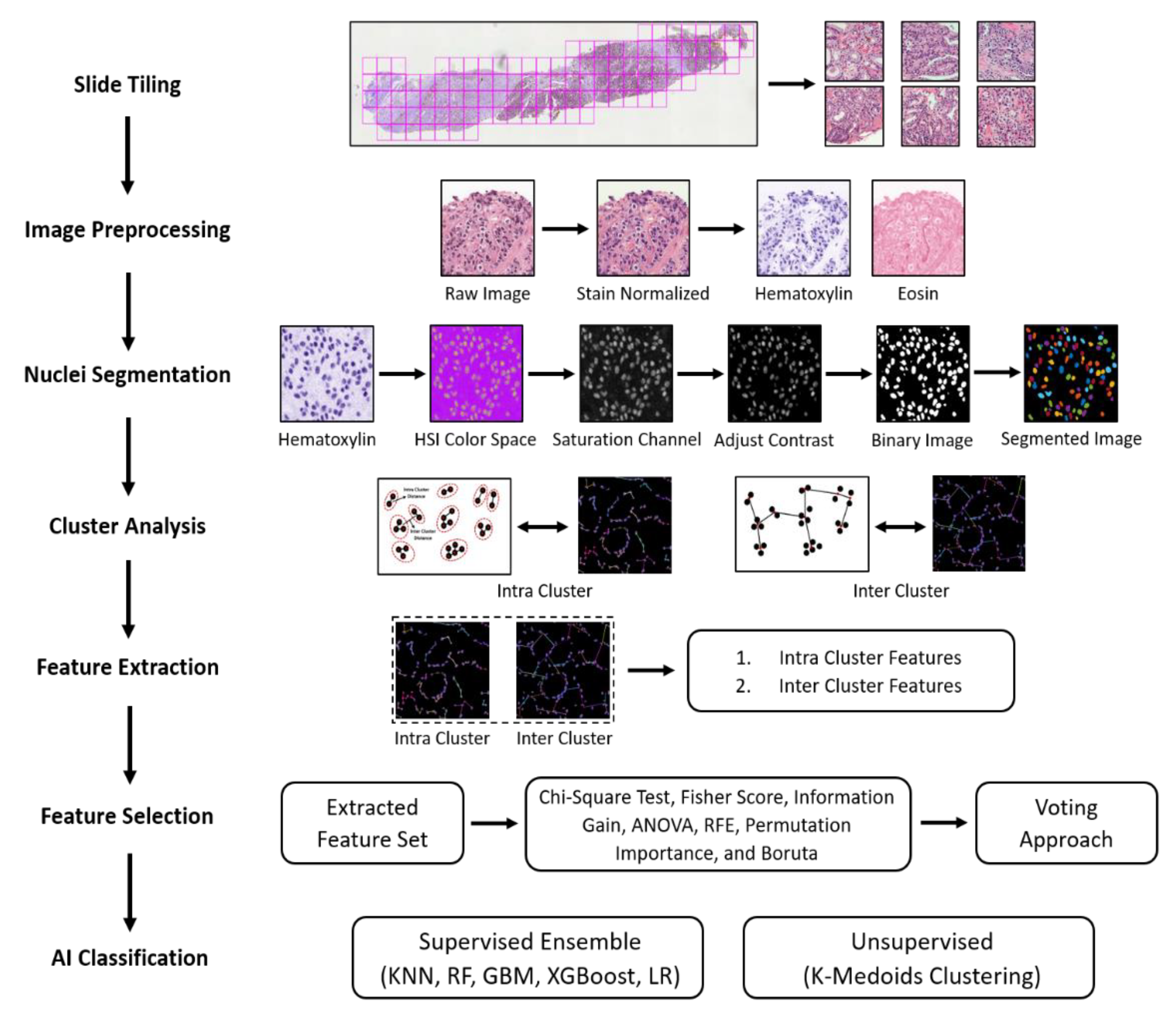
3.2. Research Pipeline
3.2.1. Image Preprocessing
3.2.2. Nuclear Segmentation of Cancer Cells
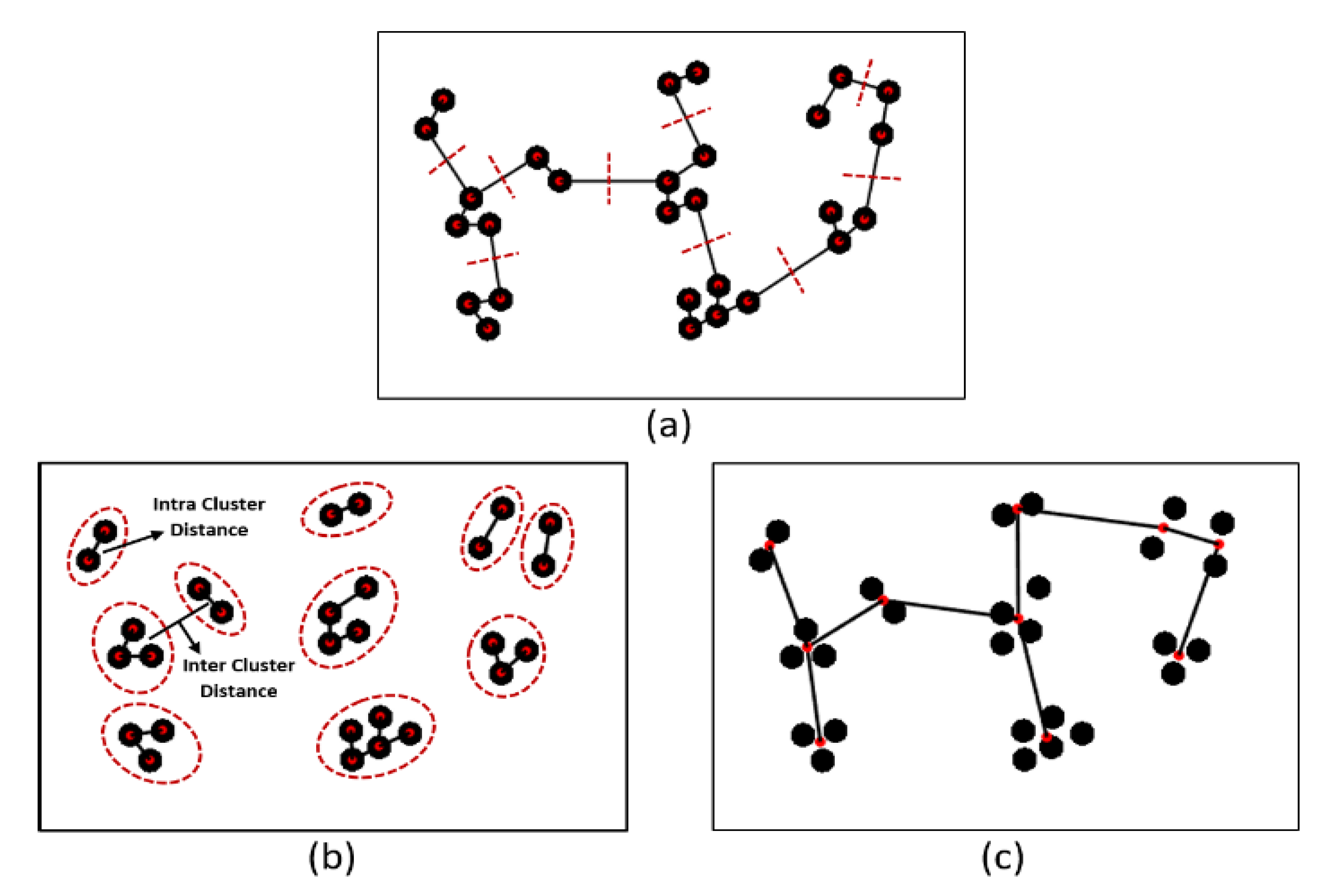
3.2.3. Cluster Analysis
- Create an adjacent grid matrix using the input image.
- Calculate the total grid numbers in the rows and columns.
- Generate a graph from an adjacent matrix, which must contain the minimum and maximum weights of all vertices.
- Create an MST-set to track all vertices.
- Find a minimum weight for all vertices in the input graph.
- Assign that weight to the first vertex.
- As the MST-set does not include all vertices:
- Select a vertex u not present in the MST-set that has the minimum weight;
- Add u to the MST-set;
- Update the minimum weights of all vertices adjacent to u by iterating through all adjacent vertices. For every adjacent vertex v, if the weight of edge u-v is less than the previous key value of v, update that minimum weight;
- Iterate step 7 until the MST is complete.
3.2.4. Feature Extraction and Selection
3.2.5. AI Classification
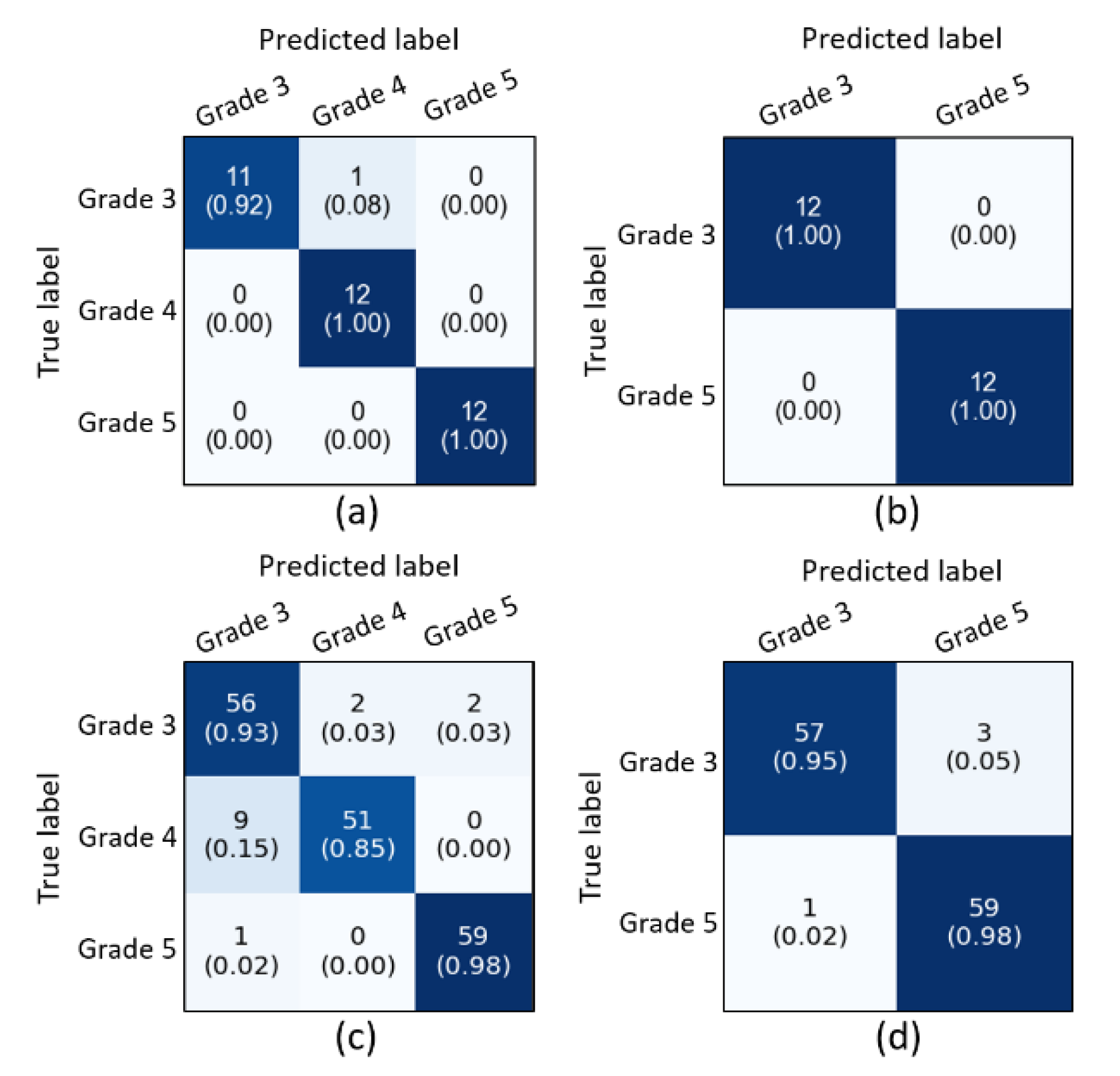
4. Experimental Results and Discussion
- The size of the image datasets was too small to perform cluster analysis and apply deep learning-based algorithms, such as graph convolution neural network (GCNN) and LSTM network, and the study could be improved by increasing the data samples.
- Cell nuclei segmentation using traditional-based algorithms is a major issue, but we can improve this problem gradually by performing cell-level analysis applying different state-of-the-art methods.
- We know that unsupervised classification is very important in the real-world environment, the classifiers used in our study performed well but did not achieve astounding results compared to supervised classification. Therefore, we can improve this problem by analyzing the feature dissimilarities between the PCa grades.
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Zhu, Y.; Williams, S.; Zwiggelaar, R. Computer Technology in Detection and Staging of Prostate Carcinoma: A Review. Med. Image Anal. 2006, 10, 179–199. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Zhao, D.; Spring, D.J.; DePinho, R.A. Genetics and Biology of Prostate Cancer. Genes Dev. 2018, 32, 1105–1140. [Google Scholar] [CrossRef]
- Shen, M.M.; Abate-Shen, C. Molecular Genetics of Prostate Cancer: New Prospects for Old Challenges. Genes Dev. 2010, 24, 1967–2000. [Google Scholar] [CrossRef]
- Barron, D.A.; Rowley, D.R. The Reactive Stroma Microenvironment and Prostate Cancer Progression. Endocr.-Relat. Cancer 2012, 19, R187–R204. [Google Scholar] [CrossRef] [PubMed]
- Gleason, D.F.; Mellinger, G.T.; Veterans Administration Cooperative Urological Research Group. Prediction of Prognosis for Prostatic Adenocarcinoma by Combined Histological Grading and Clinical Staging. J. Urol. 2017, 197, S134–S139. [Google Scholar] [CrossRef] [PubMed]
- Cintra, M.L.; Billis, A. Histologic Grading of Prostatic Adenocarcinoma: Intraobserver Reproducibility of the Mostofi, Gleason and Böcking Grading Systems. Int. Urol. Nephrol. 1991, 23, 449–454. [Google Scholar] [CrossRef]
- Özdamar, Ş.O.; Sarikaya, Ş.; Yildiz, L.; Atilla, M.K.; Kandemir, B.; Yildiz, S. Intraobserver and Interobserver Reproducibility of WHO and Gleason Histologic Grading Systems in Prostatic Adenocarcinomas. Int. Urol. Nephrol. 1996, 28, 73–77. [Google Scholar] [CrossRef] [PubMed]
- Egevad, L.; Ahmad, A.S.; Algaba, F.; Berney, D.M.; Boccon-Gibod, L.; Compérat, E.; Evans, A.J.; Griffiths, D.; Grobholz, R.; Kristiansen, G.; et al. Standardization of Gleason Grading among 337 European Pathologists. Histopathology 2013, 62, 247–256. [Google Scholar] [CrossRef]
- Xu, Y.; Olman, V.; Xu, D. Minimum Spanning Trees for Gene Expression Data Clustering. Genome Inform. 2001, 12, 24–33. [Google Scholar] [CrossRef]
- Kruskal, J.B. On the Shortest Spanning Subtree of a Graph and the Traveling Salesman Problem. Proc. Am. Math. Soc. USA 1956, 7, 48–50. [Google Scholar] [CrossRef]
- Gower, J.C.; Ross, G.J.S. Minimum Spanning Trees and Single Linkage Cluster Analysis. Appl. Stat. 1969, 18, 54–64. [Google Scholar] [CrossRef]
- Pliner, H.A.; Shendure, J.; Trapnell, C. Supervised classification enables rapid annotation of cell atlases. Nat. Methods 2019, 16, 983–986. [Google Scholar] [CrossRef]
- Poojitha, U.P.; Lal Sharma, S. Hybrid Unified Deep Learning Network for Highly Precise Gleason Grading of Prostate Cancer. In Proceedings of the 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 899–903. [Google Scholar] [CrossRef]
- Jafari-Khouzani, K.; Soltanian-Zadeh, H. Multiwavelet Grading of Pathological Images of Prostate. IEEE Trans. Biomed. Eng. 2003, 50, 697–704. [Google Scholar] [CrossRef] [PubMed]
- Kwak, J.T.; Hewitt, S.M. Nuclear Architecture Analysis of Prostate Cancer via Convolutional Neural Networks. IEEE Access 2017, 5, 18526–18533. [Google Scholar] [CrossRef]
- Linkon, A.H.M.; Labib, M.M.; Hasan, T.; Hossain, M.; Jannat, M.-E. Deep Learning in Prostate Cancer Diagnosis and Gleason Grading in Histopathology Images: An Extensive Study. Inform. Med. Unlocked 2021, 24, 100582. [Google Scholar] [CrossRef]
- Wang, J.; Chen, R.J.; Lu, M.Y.; Baras, A.; Mahmood, F. Weakly Supervised Prostate Tma Classification Via Graph Convolutional Networks. In Proceedings of the IEEE 17th International Symposium on Biomedical Imaging (ISBI), Iowa City, IA, USA, 3–7 April 2020; pp. 239–243. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Park, H.G.; Kim, C.H.; Prakash, D.; Madusanka, N.; So, J.H.; Cho, N.H.; Choi, H.K. Quantitative Analysis of Benign and Malignant Tumors in Histopathology: Predicting Prostate Cancer Grading Using SVM. Appl. Sci. 2019, 9, 2969. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Kim, C.H.; Prakash, D.; Park, H.G.; Cho, N.H.; Choi, H.K. An Efficient Lightweight Cnn and Ensemble Machine Learning Classification of Prostate Tissue Using Multilevel Feature Analysis. Appl. Sci. 2020, 10, 8013. [Google Scholar] [CrossRef]
- Nir, G.; Hor, S.; Karimi, D.; Fazli, L.; Skinnider, B.F.; Tavassoli, P.; Turbin, D.; Villamil, C.F.; Wang, G.; Wilson, R.S.; et al. Automatic grading of prostate cancer in digitized histopathology images: Learning from multiple experts. Med. Image Anal. 2018, 50, 167–180. [Google Scholar] [CrossRef] [PubMed]
- Ali, S.; Veltri, R.; Epstein, J.A.; Christudass, C.; Madabhushi, A. Cell Cluster Graph for Prediction of Biochemical Recurrence in Prostate Cancer Patients from Tissue Microarrays. In Medical Imaging 2013: Digital Pathology; Gurcan, M.N., Madabhushi, A., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2013; p. 86760H. [Google Scholar] [CrossRef]
- Kim, C.-H.; Bhattacharjee, S.; Prakash, D.; Kang, S.; Cho, N.-H.; Kim, H.-C.; Choi, H.-K. Artificial Intelligence Techniques for Prostate Cancer Detection through Dual-Channel Tissue Feature Engineering. Cancers 2021, 13, 1524. [Google Scholar] [CrossRef]
- Reinhard, E.; Ashikhmin, M.; Gooch, B.; Shirley, P. Color Transfer between Images. IEEE Comput. Graph. Appl. 2001, 21, 34–41. [Google Scholar] [CrossRef]
- Ruifrok, A.C.; Johnston, D.A. Quantification of Histochemical Staining by Color Deconvolution. Anal. Quant. Cytol. Histol. 2001, 23, 291–299. [Google Scholar]
- Tan, K.S.; Mat Isa, N.A.; Lim, W.H. Color Image Segmentation Using Adaptive Unsupervised Clustering Approach. Appl. Soft Comput. 2013, 13, 2017–2036. [Google Scholar] [CrossRef]
- Azevedo Tosta, T.A.; Neves, L.A.; do Nascimento, M.Z. Segmentation Methods of H&E-Stained Histological Images of Lymphoma: A Review. Inform. Med. Unlocked 2017, 9, 34–43. [Google Scholar] [CrossRef]
- Song, J.; Xiao, L.; Lian, Z. Contour-Seed Pairs Learning-Based Framework for Simultaneously Detecting and Segmenting Various Overlapping Cells/Nuclei in Microscopy Images. IEEE Trans. Image Process. 2018, 27, 5759–5774. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Shang, F.; Ozolek, J.; Rohde, G. Detecting and Segmenting Cell Nuclei in Two-Dimensional Microscopy Images. J. Pathol. Inform. 2016, 7, 42–50. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Lu, C.; Mandal, M. An Efficient Technique for Nuclei Segmentation Based on Ellipse Descriptor Analysis and Improved Seed Detection Algorithm. IEEE J. Biomed. Health Inform. 2014, 18, 1729–1741. [Google Scholar] [CrossRef]
- Guven, M.; Cengizler, C. Data Cluster Analysis-Based Classification of Overlapping Nuclei in Pap Smear Samples. Biomed. Eng. Online 2014, 13, 159–177. [Google Scholar] [CrossRef]
- Lv, X.; Ma, Y.; He, X.; Huang, H.; Yang, J. CciMST: A Clustering Algorithm Based on Minimum Spanning Tree and Cluster Centers. Math. Probl. Eng. 2018, 2018, 8451796. [Google Scholar] [CrossRef]
- Nithyanandam, G. Graph based image segmentation method for identification of cancer in prostate MRI image. J. Comput. Appl. 2011, 4, 104–108. [Google Scholar]
- Pike, R.; Lu, G.; Wang, D.; Chen, Z.G.; Fei, B. A Minimum Spanning Forest-Based Method for Noninvasive Cancer Detection with Hyperspectral Imaging. IEEE Trans. Biomed. Eng. 2016, 63, 653–663. [Google Scholar] [CrossRef] [PubMed]
- Ying, S.; Xu, G.; Li, C.; Mao, Z. Point Cluster Analysis Using a 3D Voronoi Diagram with Applications in Point Cloud Segmentation. ISPRS Int. J. Geo-Inf. 2015, 4, 1480–1499. [Google Scholar] [CrossRef]
- Nithya, S.; Bhuvaneswari, S.; Senthil, S. Robust Minimal Spanning Tree Using Intuitionistic Fuzzy C-Means Clustering Algorithm for Breast Cancer Detection. Am. J. Neural Netw. Appl. 2019, 5, 12–22. [Google Scholar] [CrossRef]
- Bommert, A.; Sun, X.; Bischl, B.; Rahnenführer, J.; Lang, M. Benchmark for Filter Methods for Feature Selection in High-Dimensional Classification Data. Comput. Stat. Data Anal. 2020, 143, 106839. [Google Scholar] [CrossRef]
- Karabulut, E.M.; Özel, S.A.; İbrikçi, T. A Comparative Study on the Effect of Feature Selection on Classification Accuracy. Procedia Technol. 2012, 1, 323–327. [Google Scholar] [CrossRef]
- Pirgazi, J.; Alimoradi, M.; Esmaeili Abharian, T.; Olyaee, M.H. An Efficient Hybrid Filter-Wrapper Metaheuristic-Based Gene Selection Method for High Dimensional Datasets. Sci. Rep. 2019, 9, 18580. [Google Scholar] [CrossRef] [PubMed]
- Zhao, G.; Wu, Y. Feature Subset Selection for Cancer Classification Using Weight Local Modularity. Sci. Rep. 2016, 6, 34759. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Liu, Y.; Wei, D.; Xu, M.; Chen, H.; Han, J. Selection of Interdependent Genes via Dynamic Relevance Analysis for Cancer Diagnosis. J. Biomed. Inform. 2013, 46, 252–258. [Google Scholar] [CrossRef]
- Isabelle, G.; Jason, W.; Stephen, B.; Vladimir, V. Gene Selection for Cancer Classification Using Support Vector Machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar]
- Zhang, S.; Li, X.; Zong, M.; Zhu, X.; Wang, R. Efficient KNN Classification with Different Numbers of Nearest Neighbors. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 1774–1785. [Google Scholar] [CrossRef]
- Toth, R.; Schiffmann, H.; Hube-Magg, C.; Büscheck, F.; Höflmayer, D.; Weidemann, S.; Lebok, P.; Fraune, C.; Minner, S.; Schlomm, T.; et al. Random Forest-Based Modelling to Detect Biomarkers for Prostate Cancer Progression. Clin. Epigenet. 2019, 11, 148. [Google Scholar] [CrossRef]
- Natekin, A.; Knoll, A. Gradient Boosting Machines, a Tutorial. Front. Neurorobot. 2013, 7, 21. [Google Scholar] [CrossRef] [PubMed]
- Ma, B.; Meng, F.; Yan, G.; Yan, H.; Chai, B.; Song, F. Diagnostic Classification of Cancers Using Extreme Gradient Boosting Algorithm and Multi-Omics Data. Comput. Biol. Med. 2020, 121, 103761. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Liu, K.Y.; Wong, S.T.C. Cancer Classification and Prediction Using Logistic Regression with Bayesian Gene Selection. J. Biomed. Inform. 2004, 37, 249–259. [Google Scholar] [CrossRef]
- Sahran, S.; Albashish, D.; Abdullah, A.; Shukor, N.A.; Hayati Md Pauzi, S. Absolute Cosine-Based SVM-RFE Feature Selection Method for Prostate Histopathological Grading. Artif. Intell. Med. 2018, 87, 78–90. [Google Scholar] [CrossRef] [PubMed]
- García Molina, J.F.; Zheng, L.; Sertdemir, M.; Dinter, D.J.; Schönberg, S.; Rädle, M. Incremental Learning with SVM for Multimodal Classification of Prostatic Adenocarcinoma. PLoS ONE 2014, 9, e93600. [Google Scholar] [CrossRef] [PubMed]
- Albashish, D.; Sahran, S.; Abdullah, A.; Shukor, N.A.; Pauzi, S. Ensemble Learning of Tissue Components for Prostate Histopathology Image Grading. Int. J. Adv. Sci. Eng. Inf. Technol. 2016, 6, 1134–1140. [Google Scholar] [CrossRef][Green Version]
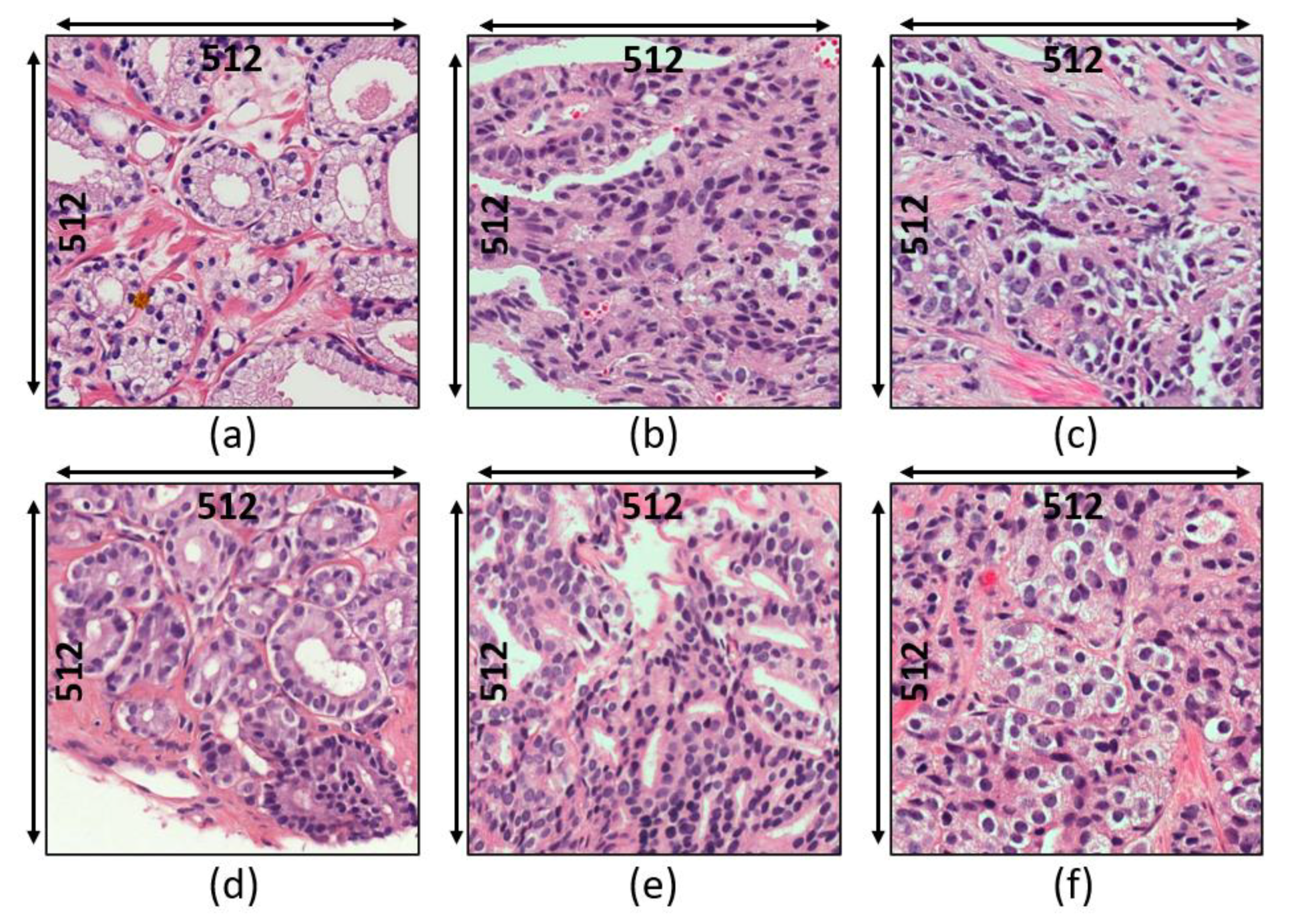
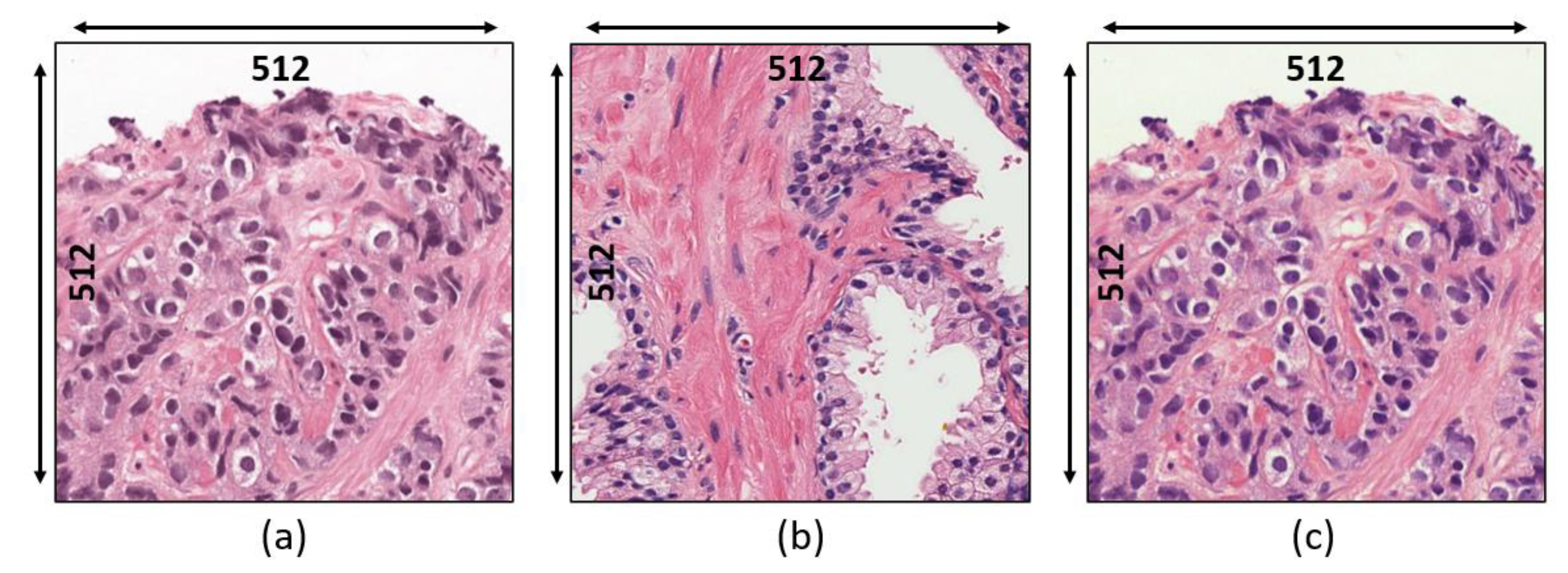






| Author | Techniques | Classification Types | Description and Performance |
|---|---|---|---|
| Uthappa et al., 2019 [13] | CNN-based texture analysis | Multiclass (grade 2, 3, 4, and 5) | Developed a hybrid unified deep learning network to grade the PCa and achieved an accuracy of 98.0% |
| Khouzani et al., 2003 [14] | Handcrafted-based texture analysis | Multiclass (grade 2, 3, 4, and 5) | Calculated energy and entropy features of multiwavelet coefficients of the image and used ML classifier to classify each image to the appropriate grade. They achieved an accuracy of 97.0% |
| Kwak et al., 2017 [15] | CNN-based texture and nuclear architectural analysis | Binary class (benign and cancer) | The author presented a CNN approach to identify PCa. In addition, they extracted handcrafted nuclear architecture features and performed ML classification. The performance of their CNNs (0.95 AUC) was significantly better than that of other ML algorithms |
| Linkon et al., 2021 [16] | Different techniques related to PCa detection and histopathology image analysis have been discussed | N/A | The author discussed recent advances in CAD systems using DL for automatic detection and recognition. In addition, they discussed the current state and existing techniques as well as unique insights in PCa detection and described research findings, current limitations, and future scope for research |
| Wang et al., 2020 [17] | Morphological, texture, and contrastive predictive coding feature analysis | Binary class (score 3 + 3 and 3 + 4) | The author proposed a weakly supervised approach for grade classification in tissue micro-arrays using graph CNN. An accuracy of 88.6% and an AUC of 0.96 were achieved using their proposed model |
| Bhattacharjee et al., 2019 [18] | Morphological analysis | Binary class (benign vs. malignant, grade 3 vs. grade 4, 5, and grade 4 vs. grade 5) Multiclass (benign, grade 3, grade 4, and grade 5) | The author used histopathology images to perform morphological analysis of cell nucleus and lumen and carried out multiclass and binary classification. The best accuracy of 92.5% was achieved for binary classification (grade 4 vs. grade 5 using support vector machine classifier |
| Bhattacharjee et al., 2020 [19] | Handcrafted and non-handcrafted feature analysis using AI techniques | Binary class (benign vs. malignant) | The author introduced two lightweight CNN models for histopathology image classification and performed a comparative analysis with other state-of-the-art models. An accuracy of 94.0% was achieved using the proposed DL model |
| Nir et al., 2018 [20] | Glandular-, nuclear-, and image-based feature analysis | Binary class (benign vs. all grades) and (grade 3 vs. grade 4, 5) | Proposed some novel features based on intra- and inter-nuclei properties for classification using ML and DL algorithms and achieved the best accuracy of 91.6% for benign vs. all grades using linear discriminant analysis |
| Ali et al., 2013 [21] | Morphological and architectural feature analysis from cell cluster graph | Binary class (no recurrence vs. recurrence) | The author defined cells clusters as a node and constructed a novel graph called Cell Cluster Graph (CCG). In addition, they extracted global and local features from the CCG that best capture the morphology of the tumor. A randomized three-fold cross-validation was applied via support vector machine classifier and achieved an accuracy of 83.1% |
| Kim et al., 2021 [22] | Texture analysis using DL and ML techniques | Binary class (benign vs. malignant) and (low- vs. high-grade) | The author used DL (long short-term memory network) and ML (logistic regression, bagging tree, boosting tree, and support vector machine) techniques to classify dual-channel tissue features extracted from hematoxylin and eosin tissue images |
| Features | FS | IG | ANOVA | RFE | PI | Boruta | Votes | Select/Reject | |
|---|---|---|---|---|---|---|---|---|---|
| total intra-cluster total MST distance | True | True | True | True | True | True | True | 7 | Select |
| total intra-cluster nucleus to nucleus maximum distance | True | True | True | True | True | True | True | 7 | Select |
| inter-cluster centroid to centroid total distance | True | False | True | True | True | True | True | 6 | Select |
| inter-cluster total MST distance | True | True | True | True | True | False | True | 6 | Select |
| number of clusters | True | True | True | True | True | False | True | 6 | Select |
| total intra-cluster maximum MST distance | True | True | True | True | True | False | True | 6 | Select |
| average intra-cluster nucleus to nucleus minimum distance | False | True | True | True | True | False | True | 5 | Select |
| average intra-cluster nucleus to nucleus maximum distance | False | True | True | True | True | False | True | 5 | Select |
| average intra-cluster maximum MST distance | False | True | True | True | True | False | True | 5 | Select |
| average cluster area | True | True | False | False | True | True | True | 5 | Select |
| total intra-cluster nucleus to nucleus total distance | True | False | False | True | True | True | True | 5 | Select |
| total intra-cluster minimum MST distance | True | True | True | True | False | False | True | 5 | Select |
| total intra-cluster nucleus to nucleus minimum distance | True | True | True | True | False | False | True | 5 | Select |
| inter-cluster maximum MST distance | True | True | False | False | True | False | True | 4 | Select |
| average intra-cluster total MST distance | False | True | True | False | True | False | True | 4 | Select |
| average intra-cluster minimum MST distance | False | True | True | True | False | False | True | 4 | Select |
| total cluster area | True | False | False | False | False | True | True | 3 | Reject |
| inter-cluster average MST distance | False | False | True | True | False | False | True | 3 | Reject |
| average intra-cluster nucleus to nucleus average distance | False | False | True | True | False | False | True | 3 | Reject |
| inter-cluster centroid to centroid average distance | False | True | False | False | True | False | False | 2 | Reject |
| minimum area of cluster | True | False | False | False | True | False | False | 2 | Reject |
| average intra-cluster nucleus to nucleus total distance | True | False | False | False | False | False | True | 2 | Reject |
| inter-cluster centroid to centroid minimum distance | False | False | False | False | False | False | True | 1 | Reject |
| inter-cluster centroid to centroid maximum distance | False | False | False | False | False | False | True | 1 | Reject |
| maximum area of cluster | True | False | False | False | False | False | False | 1 | Reject |
| inter-cluster minimum MST distance | False | False | False | False | False | False | True | 1 | Reject |
| (A) Supervised Ensemble Classification—Modern AI Techniques | ||||
|---|---|---|---|---|
| Multiclass Classification (Grade 3 vs. Grade 4 vs. Grade 5) | ||||
| Test Split | Accuracy | Precision | Recall | F1-Score |
| Split 1 | 97.2% | 97.3% | 97.3% | 97.3% |
| Split 2 | 91.7% | 92.0% | 91.7% | 91.7% |
| Split 3 | 97.2% | 97.3% | 97.3% | 97.3% |
| Split 4 | 94.4% | 94.7% | 94.7% | 94.7% |
| Split 5 | 91.7% | 91.7% | 91.7% | 91.7% |
| Average Split | 94.4% | 94.7% | 94.3% | 94.7% |
| Binary Classification (Grade 3 vs. Grade 5) | ||||
| Test Split | Accuracy | Precision | Recall | F1-Score |
| Split 1 | 91.7% | 91.6 | 0.916 | 0.916 |
| Split 2 | 100% | 100% | 100% | 100% |
| Split 3 | 95.8% | 96.2% | 95.8% | 95.9% |
| Split 4 | 95.8% | 96.2% | 95.8% | 95.9% |
| Split 5 | 91.7% | 92.8% | 91.6% | 92.2% |
| Average Split | 95.0% | 95.0% | 95.0% | 95.0% |
| (B) K-Medoids Unsupervised Classification—Traditional AI Technique | ||||
| Multiclass Classification (Grade 3 vs. Grade 4 vs. Grade 5) | ||||
| Data Split | Accuracy | Precision | Recall | F1-Score |
| Split 1 | 86.1% | 87.0% | 86.0% | 86.3% |
| Split 2 | 92.3% | 92.7% | 92.0% | 92.3% |
| Split 3 | 86.7% | 88.3% | 86.7% | 87.0% |
| Split 4 | 88.3% | 88.3% | 88.3% | 88.0% |
| Split 5 | 91.6% | 91.7% | 91.7% | 91.7% |
| Average Split | 88.5% | 89.7% | 88.3% | 88.7% |
| Binary Classification (Grade 3 vs. Grade 5) | ||||
| Data Split | Accuracy | Precision | Recall | F1-Score |
| Split 1 | 81.7% | 82.0% | 81.5% | 81.5% |
| Split 2 | 96.7% | 96.5% | 96.5% | 97.0% |
| Split 3 | 89.2% | 89.5% | 89.0% | 89.0% |
| Split 4 | 86.7% | 87.5% | 86.5% | 86.5% |
| Split 5 | 93.3% | 93.5% | 93.5% | 93.5% |
| Average Split | 88.3% | 88.5% | 88.5% | 88.5% |
| Authors | Methods | Classification Type | Performance | |
|---|---|---|---|---|
| Uthappa et al., 2019 [13] | Hybrid DL | Multiclass (grade 2, 3, 4, and 5) | 98.0% (Accuracy) | |
| Khouzani et al., 2003 [14] | ML | Multiclass (grade 2, 3, 4, and 5) | 97.0% (Accuracy) | |
| Kwak et al., 2017 [15] | CNN | Binary (benign and cancer) | 0.95 (AUC) | |
| Wang et al., 2020 [16] | Graph CNN | Binary (score 3 + 3 and 3 + 4) | 88.6% (Accuracy) | |
| Bhattacharjee et al., 2019 [18] | ML | Binary | benign vs. malignant | 88.7% (Accuracy) |
| grade 3 vs. grade 4, 5 | 85.0% (Accuracy) | |||
| grade 4 vs. grade 5 | 92.5% (Accuracy) | |||
| Bhattacharjee et al., 2020 [19] | DL | Binary (benign vs. malignant) | 94.0% (Accuracy) | |
| Nir et al., 2018 [20] | ML | Binary | benign vs. all grades | 88.5% (Accuracy) |
| grade 3 vs. grade 4, 5 | 73.8% (Accuracy) | |||
| Ali et al., 2013 [21] | ML | Binary (no recurrence vs. recurrence) | 83.1% (Accuracy) | |
| Kim et al., 2021 [22] | DL | Binary | benign vs. malignant | 98.6% (Accuracy) |
| low- vs. high-grade | 93.6% (Accuracy) | |||
| Proposed | ML | Binary (Split 2) | grade 3 vs. grade 5 | 100% (Accuracy) |
| Multiclass (Split 1) | grade 3 vs. grade 4 vs. grade 5 | 97.2% (Accuracy) | ||
| K-Medoids Clustering | Binary (Split 2) | grade 3 vs. grade 5 | 96.7% (Accuracy) | |
| Multiclass (Split 2) | grade 3 vs. grade 4 vs. grade 5 | 92.3% (Accuracy) | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhattacharjee, S.; Ikromjanov, K.; Carole, K.S.; Madusanka, N.; Cho, N.-H.; Hwang, Y.-B.; Sumon, R.I.; Kim, H.-C.; Choi, H.-K. Cluster Analysis of Cell Nuclei in H&E-Stained Histological Sections of Prostate Cancer and Classification Based on Traditional and Modern Artificial Intelligence Techniques. Diagnostics 2022, 12, 15. https://doi.org/10.3390/diagnostics12010015
Bhattacharjee S, Ikromjanov K, Carole KS, Madusanka N, Cho N-H, Hwang Y-B, Sumon RI, Kim H-C, Choi H-K. Cluster Analysis of Cell Nuclei in H&E-Stained Histological Sections of Prostate Cancer and Classification Based on Traditional and Modern Artificial Intelligence Techniques. Diagnostics. 2022; 12(1):15. https://doi.org/10.3390/diagnostics12010015
Chicago/Turabian StyleBhattacharjee, Subrata, Kobiljon Ikromjanov, Kouayep Sonia Carole, Nuwan Madusanka, Nam-Hoon Cho, Yeong-Byn Hwang, Rashadul Islam Sumon, Hee-Cheol Kim, and Heung-Kook Choi. 2022. "Cluster Analysis of Cell Nuclei in H&E-Stained Histological Sections of Prostate Cancer and Classification Based on Traditional and Modern Artificial Intelligence Techniques" Diagnostics 12, no. 1: 15. https://doi.org/10.3390/diagnostics12010015
APA StyleBhattacharjee, S., Ikromjanov, K., Carole, K. S., Madusanka, N., Cho, N.-H., Hwang, Y.-B., Sumon, R. I., Kim, H.-C., & Choi, H.-K. (2022). Cluster Analysis of Cell Nuclei in H&E-Stained Histological Sections of Prostate Cancer and Classification Based on Traditional and Modern Artificial Intelligence Techniques. Diagnostics, 12(1), 15. https://doi.org/10.3390/diagnostics12010015










