Application of the Kvaal Method in Age Estimation of the Serbian Population Based on Dental Radiographs
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Population
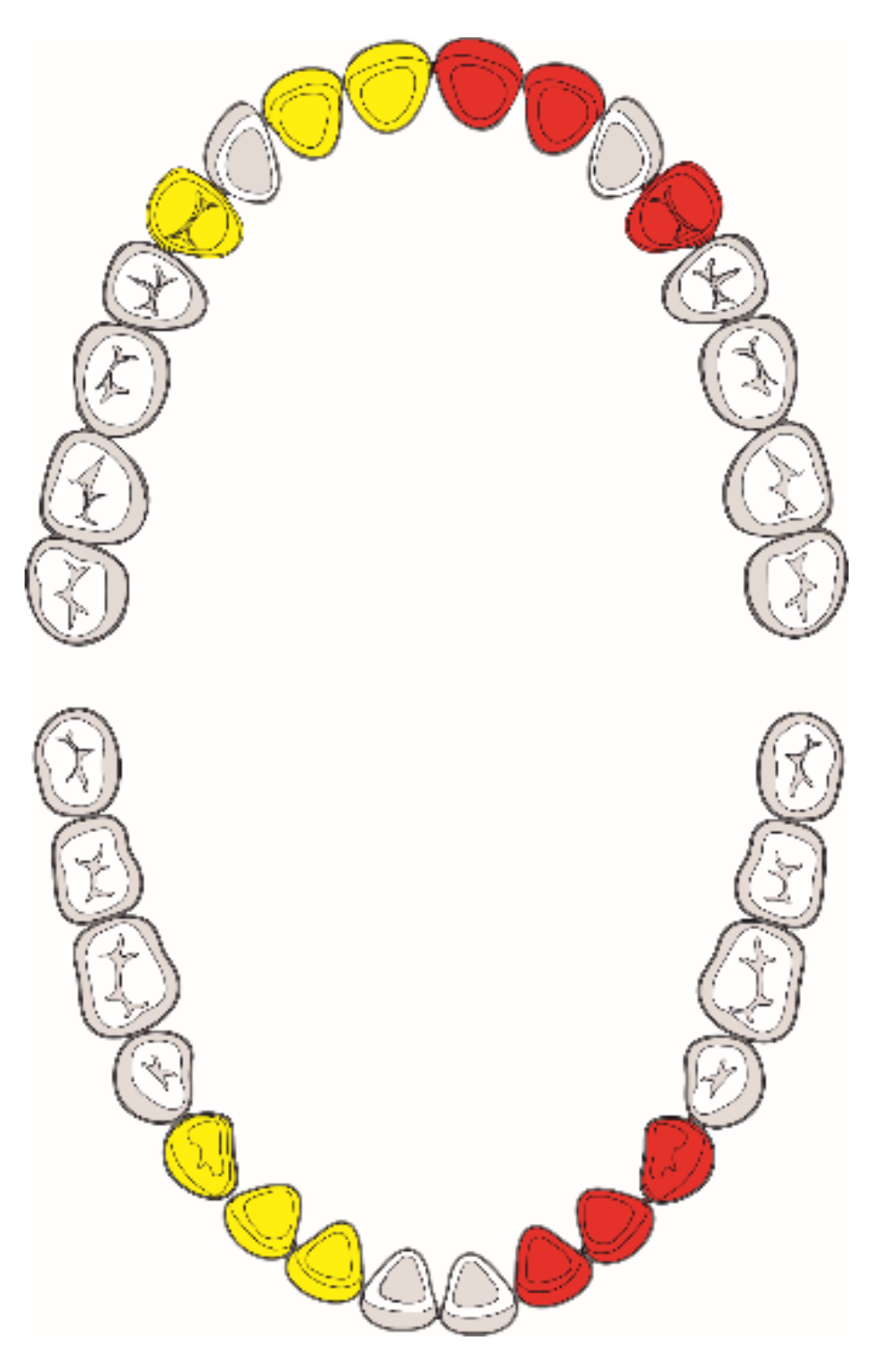
2.2. Tooth Selection
2.3. Inclusion Criteria
2.4. Measurements
2.5. Statistical Analysis
- (1)
- The three maxillary teeth with their individual M and W-L values (6 predictors), and averaged M and W-L values (2 predictors).
- (2)
- The three mandibular teeth with their individual M and W-L values (6 predictors), and averaged M and W-L values (2 predictors).
- (3)
- All six teeth with their individual M and W-L values (12 predictors), and averaged M and W-L values (2 predictors).
- (4)
- Kvaal dental coefficients with the strongest correlation with age (10 predictors reduced to 5 predictors in the backward regression model).
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kellinghaus, M.; Schulz, R.; Vieth, V.; Schmidt, S.; Schmeling, A. Forensic age estimation in living subjects based on the ossification status of the medial clavicular epiphysis as revealed by thin-slice multidetector computed tomography. Int. J. Leg. Med. 2010, 124, 149–154. [Google Scholar] [CrossRef] [PubMed]
- Gustafson, G. Age determination on teeth. J. Am. Dent. Assoc. 1950, 41, 45–54. [Google Scholar] [CrossRef] [PubMed]
- Melo, M.; Ata-Ali, J. Accuracy of the estimation of dental age in comparison with chronological age in a Spanish sample of 2641 living subjects using the Demirjian and Nolla methods. Forensic Sci. Int. 2017, 270, 276-e1. [Google Scholar] [CrossRef] [PubMed]
- Willems, G.; Moulin-Romsee, C.; Solheim, T. Non-destructive dental-age calculation methods in adults: Intra- and inter-observer effects. Forensic Sci. Int. 2002, 126, 221–226. [Google Scholar] [CrossRef]
- Shrigiriwar, M.; Jadhav, V. Age estimation from physiological changes of teeth by Gustafson’s method. Med. Sci. Law 2013, 53, 67–71. [Google Scholar] [CrossRef] [PubMed]
- Olze, A.; Hertel, J.; Schulz, R.; Wierer, T.; Schmeling, A. Radiographic evaluation of Gustafson’s criteria for the purpose of forensic age diagnostics. Int. J. Leg. Med. 2012, 126, 615–621. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Geng, K.; Chu, Y.; Xu, M.; Zha, L. Third molar mineralization in relation to chronologic age estimation of the Han in central southern China. Int. J. Leg. Med. 2018, 132, 1427–1435. [Google Scholar] [CrossRef]
- Kolltveit, K.M.; Solheim, T.; Kvaal, S.I. Methods of measuring morphological parameters in dental radiographs. Comparison between image analysis and manual measurements. Forensic Sci. Int. 1998, 94, 87–95. [Google Scholar] [CrossRef]
- Kvaal, S.I.; Kolltveit, K.M.; Thomsen, I.O.; Solheim, T. Age estimation of adults from dental radiographs. Forensic Sci. Int. 1995, 74, 175–185. [Google Scholar] [CrossRef]
- Babshet, M.; Acharya, A.B.; Naikmasur, V.G. Age estimation in Indians from pulp/tooth area ratio of mandibular canines. Forensic Sci. Int. 2010, 197, 125. [Google Scholar] [CrossRef]
- Dehghani, M.; Shadkam, E.; Ahrari, F.; Dehghani, M. Age estimation by canines’ pulp/tooth ratio in an Iranian population using digital panoramic radiography. Forensic Sci. Int. 2018, 285, 44–49. [Google Scholar] [CrossRef] [PubMed]
- Li, M.J.; Chu, G.; Han, M.Q.; Chen, T.; Zhou, H.; Guo, Y.C. Application of the Kvaal method for age estimation using digital panoramic radiography of Chinese individuals. Forensic Sci. Int. 2019, 301, 76–81. [Google Scholar] [CrossRef] [PubMed]
- Karkhanis, S.; Mack, P.; Franklin, D. Age estimation standards for a Western Australian population using the dental age estimation technique developed by Kvaal et al. Forensic Sci. Int. 2014, 235, 104. [Google Scholar] [CrossRef] [PubMed]
- Chandan, P.K.; Arora, K.S.; Das, M.; Kaur, P.; Mohaptra, S.; Pareek, S. Assessment of validity and reliability of Kvaal’s method for age estimation among a population sample—A retrospective study. Indian J. Dent. Res. 2020, 31, 186–190. [Google Scholar]
- Miranda, J.C.; Azevedo, A.; Rocha, M.; Michel-Crosato, E.; Biazevic, M. Age estimation in Brazilian adults by Kvaal’s and Cameriere’s methods. Braz. Oral Res. 2020, 34, e051. [Google Scholar] [CrossRef]
- Ramli, U.; Muhd, U.S.; Mohd Yusof, M. Accuracy of Kvaal’s radiographic and translucent dentinal root techniques of extracted teeth in Malay adults for dental age estimation. J. Forensic Odonto-Stomatol. 2021, 2, 38–44. [Google Scholar]
- Pires, A.C.; Vargas de Sousa Santos, R.F.; Pereira, C.P. Dental age assessment by the pulp/tooth area proportion in cone beam computed tomography: Is medico-legal application for age estimation reliable? J. Forensic Odonto-Stomatol. 2021, 2, 2–14. [Google Scholar]
- Vossoughi, M.; Movahhedian, N.; Ghafoori, A. The impact of age mimicry bias on the accuracy of methods for age estimation based on Kvaal’s pulp/tooth ratios: A bootstrap study. Int. J. Leg. Med. 2022, 136, 269–278. [Google Scholar] [CrossRef]
- Knivsberg, I.C.; Kopperud, S.E.; Bjørk, M.B.; Torgersen, G.; Skramstad, K.; Kvaal, S.I. Digitalised exercise material in forensic odontology. Int. J. Leg. Med. 2022, 136, 381–390. [Google Scholar] [CrossRef]
- International Commission on Missing Persons. Available online: https://www.icmp.int/wp-content/uploads/2021/08/ICMP_Global-Report_Dec12_Digital.pdf (accessed on 16 February 2022.).
- Šelo-Šabić, S. The Impact of the Refugee Crisis in the Balkans: A Drift Towards Security. J. Reg. Secur. 2017, 12, 51–74. [Google Scholar] [CrossRef]
- Patil, S.K.; Mohankumar, K.P.; Donoghue, M. Estimation of age by Kvaal’s technique in sample Indian population to establish the need for local Indian-based formulae. J. Forensic Dent. Sci. 2014, 6, 166–170. [Google Scholar] [PubMed]
- Erbudak, H.Ö.; Ozbek, M.; Uysal, S.; Karabulut, E. Application of Kvaal et al.’s age estimation method to panoramic radiographs from Turkish individuals. Forensic Sci. Int. 2012, 219, 141–146. [Google Scholar] [CrossRef] [PubMed]
- Roh, B.Y.; Lee, W.J.; Ryu, J.W.; Ahn, J.M.; Yoon, C.L.; Lee, S.S. The application of the Kvaal method to estimate the age of live Korean subjects using digital panoramic radiographs. Int. J. Leg. Med. 2018, 132, 1161–1166. [Google Scholar] [CrossRef] [PubMed]
- Kanchan-Talreja, P.; Acharya, A.B.; Naikmasur, V.G. An assessment of the versatility of Kvaal’s method of adult dental age estimation in Indians. Arch. Oral Biol. 2012, 57, 277–284. [Google Scholar] [CrossRef]
- Bosmans, N.; Ann, P.; Aly, M.; Willems, G. The application of Kvaal’s dental age calculation technique on panoramic dental radiographs. Forensic Sci. Int. 2005, 153, 208–212. [Google Scholar] [CrossRef]
- Meinl, A.; Tangl, S.; Pernicka, S.; Fenes, C.; Watzek, G. On the applicability of secondary dentin formation to radiological age estimation in young adults. J. Forensic Sci. 2007, 52, 438–441. [Google Scholar] [CrossRef]
- Marroquin Penaloza, T.Y.; Karkhanis, S.; Kvaal, S.I.; Nurul, F.; Kanagasingam, S.; Franklin, D.; Vasudavan, S.; Kruger, E.; Tennant, M. Application of the Kvaal method for adult dental age estimation using Cone Beam Computed Tomography (CBCT). J. Forensic Leg. Med. 2016, 44, 178–182. [Google Scholar] [CrossRef]
- Thurzo, A.; Kosnáčová, H.S.; Kurilová, V.; Kosmeľ, S.; Beňuš, R.; Moravanský, N.; Kováč, P.; Kuracinová, K.M.; Palkovič, M.; Varga, I. Use of Advanced Artificial Intelligence in Forensic Medicine, Forensic Anthropology and Clinical Anatomy. Healthcare 2021, 9, 1545. [Google Scholar] [CrossRef]
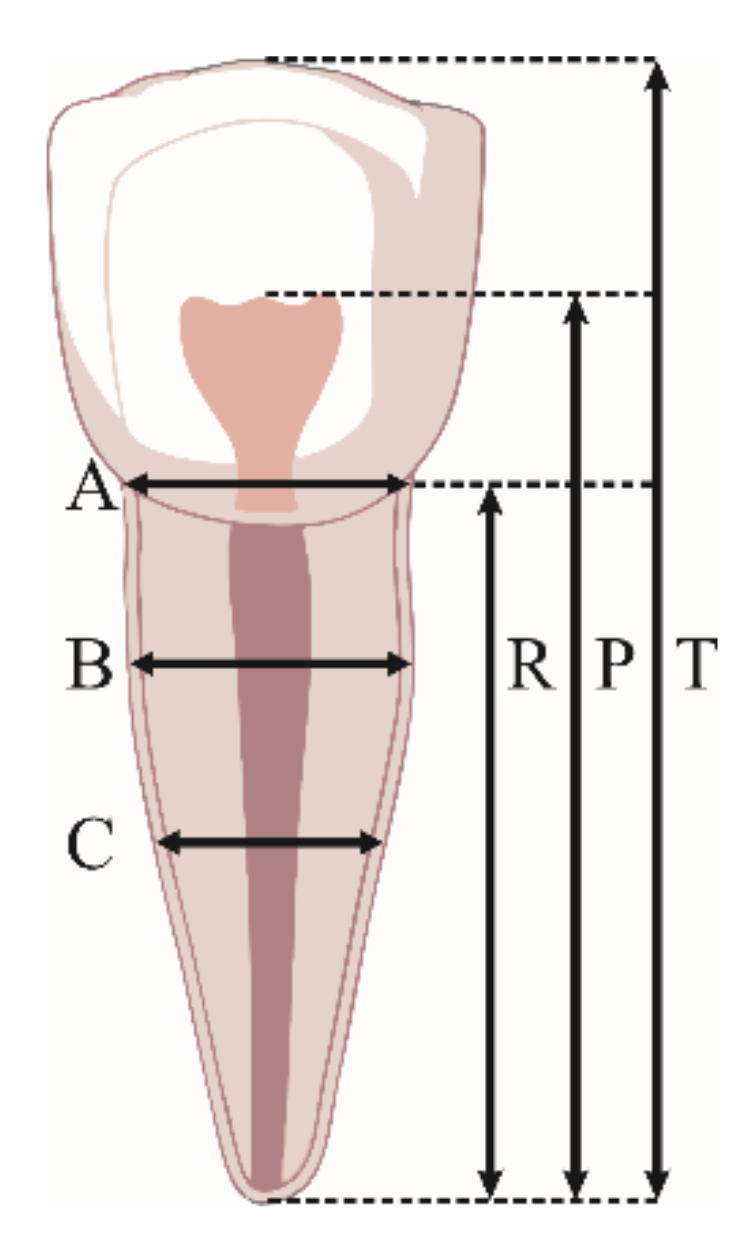
| Tooth Measurements Performed in This Study | |
|---|---|
| T | maximum tooth length (distance from the most occlusal aspect of the tooth to the root apex) |
| P | length of the pulp cavity (distance from the most occlusal aspect of the radiolucent pulp cavity to the root apex) |
| R | root length (distance from the mesial enamel–cementum junction to the root apex) |
| A | mesiodistal width of the pulp/root measured at the enamel–cementum junction level |
| B | mesiodistal width of the pulp/root measured at half the distance between enamel–cementum junction and half of the root length |
| C | mesiodistal width of pulp/root measured at half of the root length |
| M | mean of all measured values |
| W | mean value of tooth widths measured at points B and C |
| L | mean value of lengths measured at points P and R |
| W-L | difference in mean values obtained for parameters W and L |
| Ratio | Tooth (FDI) | |||||
|---|---|---|---|---|---|---|
| 11/21 | 12/22 | 15/25 | 32/42 | 33/43 | 34/44 | |
| T | −0.162 | −0.126 | 0.059 | −0.020 | 0.079 | −0.042 |
| P | −0.293 ** | −0.240 ** | 0.035 | −0.040 | −0.002 | −0.115 |
| R | −0.069 | −0.113 | 0.107 | −0.008 | 0.062 | −0.081 |
| A | −0.060 | 0.028 | 0.016 | −0.084 | −0.163 | −0.270 ** |
| B | 0.038 | 0.097 | 0.034 | −0.006 | −0.181 * | −0.139 |
| C | 0.050 | 0.037 | 0.070 | −0.010 | −0.190 * | −0.111 |
| M | −0.167 | −0.133 | 0.084 | −0.047 | −0.058 | −0.160 |
| W | 0.046 | 0.069 | 0.054 | −0.023 | −0.189 * | −0.130 |
| L | −0.198 * | −0.186 * | 0.075 | −0.025 | 0.029 | −0.101 |
| W-L | −0.206 * | −0.216 * | 0.052 | −0.017 | 0.108 | −0.054 |
| Tooth (FDI) | R | R2 | Equation | SEE (±Years) |
|---|---|---|---|---|
| 11/21 | 0.208 | 0.043 | Age = 48.242 − 0.429(M) − 0.882(W-L) | 12.443 |
| 12/22 | 0.226 | 0.051 | Age = 42.867 + 1.207(M) − 1.698(W-L) | 12.393 |
| 15/25 | 0.087 | 0.007 | Age = 20.751 + 1.066(M) − 0.039(W-L) | 12.676 |
| 32/42 | 0.058 | 0.003 | Age = 39.148 − 1.202(M) + 0.280(W-L) | 12.700 |
| 33/43 | 0.210 | 0.044 | Age = 38.923 − 2.505(M) + 1.521(W-L) | 12.437 |
| 34/44 | 0.178 | 0.032 | Age = 54.865 − 3.017(M) + 0.704(W-L) | 12.518 |
| Tooth (FDI) | Mean | SD | S.E.M. | t-Test |
|---|---|---|---|---|
| 11/21 | 0.0075 | 12.9794 | 1.1428 | ns |
| 12/22 | 0.0032 | 12.9152 | 1.1371 | ns |
| 15/25 | 0.0084 | 12.5787 | 1.1075 | ns |
| 32/42 | −0.0024 | 12.7406 | 1.1218 | ns |
| 33/43 | −0.0124 | 13.1383 | 1.1568 | ns |
| 34/44 | −0.0009 | 13.0175 | 1.1461 | ns |
| 3 Maxillary teeth (2 predictors) | −0.0017 | 13.1132 | 1.1546 | ns |
| 3 Maxillary teeth (6 predictors) | 0.0067 | 13.3327 | 1.1739 | ns |
| 3 Mandibular teeth (2 predictors) | 0.0022 | 12.9366 | 1.1390 | ns |
| 3 Mandibular teeth (6 predictors) | 0.0015 | 13.1566 | 1.1584 | ns |
| 6 Teeth (2 predictors) | 0.0075 | 12.9794 | 1.1428 | ns |
| 6 Teeth (12 predictors) | 0.0120 | 13.5849 | 1.1961 | ns |
| Tooth (FDI) | R | R2 | Equation | SEE (±Years) |
|---|---|---|---|---|
| 3 Maxillary teeth (2 predictors) | 0.171 | 0.029 | Age = 49.998 − 2.079(M) + 0.537(W-L) | 12.534 |
| 3 Maxillary teeth (6 predictors) | 0.315 | 0.099 | Age = 36.303 − 2.198(11/21M) + 0.150(11/21W-L) + 1.326(12/22M) − 1.648(12/22W-L) +2.723(15/25M) + 0.045(15/25W-L) | 12.269 |
| 3 Mandibular teeth (2 predictors) | 0.213 | 0.045 | Age = 42.606 − 1.114(M) + 0.300(W-L) | 12.429 |
| 3 Mandibular teeth (6 predictors) | 0.276 | 0.076 | Age = 56.132 − 1.033(32/42M) − 0.329(32/42W-L) − 1.589(33/43M) + 1.985(33/43W-L) − 1.803(34/44M) − 0.076(34/44W-L) | 12.428 |
| 6 Teeth (2 predictors) | 0.208 | 0.043 | Age = 48.242 − 0.429(M) − 0.882(W-L) | 12.443 |
| 6 Teeth (12 predictors) | 0.405 | 0.164 | Age = 46.980 − 1.662(11/21M) − 0.108(11/21W-L) + 1.824(12/22M) − 1.553(12/22W-L) + 3.454(15/25M) − 0.197(15/25W-L) − 0.697(32/42M) − 0.083(32/42W-L) − 1.676(33/43M) + 1.787(33/43W-L) − 2.102(34/44M) − 0.134(34/44W-L) | 12.120 |
| Variables | R | R2 | Equation | SEE (±Years) |
|---|---|---|---|---|
| UWLAVG, 33/44B, gender, 33/44A, 12/22P, 11/21P, 33/43C, 11/21L, 12/22W-L, 12/22L | 0.541 | 0.292 | Age = 88.603 − 7.967(gender) − 2.109(11/21P) − 4.187(12/22P) − 4.394(34/44A) − 0.901(33/43B) − 0.034(33/43C) + 1.796(11/21L) + 5.750(12/22L) − 1.584(12/22W-L) − 0.407(UWLAVG) | 11.057 |
| UWLAVG, 33/44B, gender, 33/44A, 12/22P, 11/21P, 11/21L, 12/22W-L, 12/22L | 0.541 | 0.292 | Age = 89.639 − 7.968(gender) − 2.108(11/21P) − 4.188(12/22P) − 4.392(34/44A) − 0.935(33/43B) + 1.794(11/21L) + 5.754(12/22L) − 1.587(12/22W-L) − 0.406(UWLAVG) | 11.011 |
| 33/44B, gender, 33/44A, 12/22P, 11/21P, 11/21L, 12/22W-L, 12/22L | 0.540 | 0.292 | Age = 90.444 − 7.936(gender) − 2.150(11/21P) − 4.197(12/22P) − 4.301(34/44A) − 0.914(33/43B) + 1.438(11/21L) + 5.989(12/22L) − 1.843(12/22W-L) | 10.968 |
| gender, 33/44A, 12/22P, 11/21P, 11/21L, 12/22W-L, 12/22L | 0.537 | 0.289 | Age = 88.464 − 7.795(gender) − 2.240(11/21P) − 4.039(12/22P) − 4.875(34/44A) + 1.577(11/21L) + 5.818(12/22L) − 1.919(12/22W-L) | 10.947 |
| gender, 33/44A, 12/22P, 11/21P, 11/21L, 12/22L | 0.530 | 0.281 | Age = 92.121 − 7.910(gender) − 2.482(11/21P) − 4.491(12/22P) − 4.191(34/44A) + 1.715(11/21L) + 4.562(12/22L) | 10.962 |
| gender, 33/44A, 12/22P, 11/21P, 12/22L | 0.515 | 0.265 | Age = 92.577 − 7.565(gender) − 1.219(11/21P) − 5.405(12/22P) − 4.106(34/44A) + 5.829(12/22L) b | 11.037 |
| Tooth (FDI) | Mean Estimated Age (Years) | Min. Error of Estimate (Years) | Max. Error of Estimate (Years) | Standard Error of Estimate (±Years) |
|---|---|---|---|---|
| 11/21 | 30.071 | 0.139 | 13.141 | 11.657 |
| 12/22 | 30.369 | 0.266 | 15.881 | 11.704 |
| 15/25 | 31.524 | 1.838 | 14.009 | 11.670 |
| 32/42 | 31.543 | 0.442 | 13.684 | 11.696 |
| 33/43 | 32.472 | 0.008 | 16.208 | 12.052 |
| 34/44 | 31.464 | 1.353 | 15.286 | 11.930 |
| 3 Maxillary teeth (2 predictors) | 33.754 | 1.308 | 16.475 | 12.294 |
| 3 Maxillary teeth (6 predictors) | 31.788 | 1.443 | 14.229 | 11.520 |
| 3 Mandibular teeth (2 predictors) | 36.118 | 0.032 | 18.156 | 13.288 |
| 3 Mandibular teeth (6 predictors) | 32.511 | 0.156 | 16.476 | 12.594 |
| 6 Teeth (2 predictors) | 30.071 | 0.139 | 13.141 | 11.657 |
| 6 Teeth (12 predictors) | 30.852 | 0.664 | 15.537 | 11.985 |
| Study | Sample Size | Age Range (Years) | Population | Standard Deviation (Years) |
|---|---|---|---|---|
| Bosman et al. [26] | 197 | 19–75 | Belgian | 5.41 (SD) |
| Meinl et al. [27] | 44 | 13–24 | Austrian | 5.84 (SD) |
| Li et al. [13] | 360 | 20–65 | Chinese | 11.8 (SD) |
| Kanchan-Talreja et al. [25] | 100 | 25–77 | Indian | 14.7 (SD) |
| Erbudak et al. [23] | 123 | 14–57 | Turkish | 11.82 (SD) |
| Roh et al. [24] | 266 | 20–29 | Korean | 11.58 (SD) |
| Present study | 170 | 17–77 | Serbian | 13.58 (SD) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zdravkovic, D.; Jovanovic, M.; Papic, M.; Ristic, V.; Milojevic Samanovic, A.; Kocovic, A.; Sovrlic, M.; Vuletic, M.; Misic, A.; Mladenovic, R.; et al. Application of the Kvaal Method in Age Estimation of the Serbian Population Based on Dental Radiographs. Diagnostics 2022, 12, 911. https://doi.org/10.3390/diagnostics12040911
Zdravkovic D, Jovanovic M, Papic M, Ristic V, Milojevic Samanovic A, Kocovic A, Sovrlic M, Vuletic M, Misic A, Mladenovic R, et al. Application of the Kvaal Method in Age Estimation of the Serbian Population Based on Dental Radiographs. Diagnostics. 2022; 12(4):911. https://doi.org/10.3390/diagnostics12040911
Chicago/Turabian StyleZdravkovic, Dejan, Milica Jovanovic, Milos Papic, Vladimir Ristic, Andjela Milojevic Samanovic, Aleksandar Kocovic, Miroslav Sovrlic, Miona Vuletic, Aleksandra Misic, Rasa Mladenovic, and et al. 2022. "Application of the Kvaal Method in Age Estimation of the Serbian Population Based on Dental Radiographs" Diagnostics 12, no. 4: 911. https://doi.org/10.3390/diagnostics12040911
APA StyleZdravkovic, D., Jovanovic, M., Papic, M., Ristic, V., Milojevic Samanovic, A., Kocovic, A., Sovrlic, M., Vuletic, M., Misic, A., Mladenovic, R., Milosavljevic, M., & Todic, J. (2022). Application of the Kvaal Method in Age Estimation of the Serbian Population Based on Dental Radiographs. Diagnostics, 12(4), 911. https://doi.org/10.3390/diagnostics12040911








