A Novel Fuzzy Parameterized Fuzzy Hypersoft Set and Riesz Summability Approach Based Decision Support System for Diagnosis of Heart Diseases
Abstract
:1. Introduction
1.1. Research Gap and Motivation
- The hypersoft setting, which demands the categorization of parameters into their relevant subclasses containing their subparametric values; such kind of classification can only be managed by employing maa-function, which takes the Cartesian product (C-product) of subparametric-valued classes as its domain and then approximates them for universal set.
- Riesz Summability setting, which is capable of tackling the sequential nature of data.
1.2. Significant Contributions
- An innovative model fuzzy parameterized fuzzy hypersoft set (-set) is characterized and some of its axiomatic cum algebraic properties are investigated. This model employs maa-function with fuzzy parametric tuples as its domain and collection of fuzzy subsets as its codomain;
- The classical concept of Riesz mean is reviewed and modified for -settings;
- The real attributes of CD-set are analyzed for heart-based ailments analysis and only those of them are opted that have a pertinent role for the adopted model;
- In order to have their respective attribute values, the operational roles of all opted attributes are discussed along with description on their measuring units;
- The opted traits and their subvalues are changed to fuzzy values by employing a suitable algebraic technique;
- Two algorithms (one for aggregations of -set and other for Riesz mean) are proposed and implemented in real-world scenario of medical diagnosis for heart diseases based on fuzzy-valued attributes of CD-set.
2. Preliminaries
3. Fuzzy Parameterized Fuzzy Hypersoft Set (-Set)
- It transforms to -set if -setting is replaced with s-setting.
- It takes the form of -set if fuzzy parameterization is omitted.
- It converts to -set if fuzzy parameterization is ignored and -setting is replaced with s-setting.
- It becomes s-set if fuzzy parameterization is ignored, -setting is replaced with s-setting and fuzzy grades are omitted.
- It converts to f-set if fuzzy parameterization is ignored, -setting is replaced with s-setting, and fuzzy approximations are ignored.
4. Methodology and Algorithms
4.1. Aggregations of -Set
- Only select those parametric tuples that contain in their approximations, i.e., the value of will be equal to their corresponding fuzzy grades .
- Compute the product of fuzzy parameterized value and the obtained value of ; then, determine the sum of these products.
- Lastly, divide the computed sum with cardinality of .
- Divide the computed sum with the value that is explained in Definition 12 and Example 1.
4.2. Cleveland Dataset
4.3. Salient Features of Opted Attributes
- Age. Aging is a self-determining menace aspect for heart ailments. Although this factor is reported higher in aged persons (more than 60 years), with the involvement of various supplementary reasons, adults can also be in danger. The cardiologists have classified the aging factor into four groups: (i) 20 years or less, (ii) 40 years or less, (iii) 60 years or less, (iv) more than 60 years.
- Chest Pain Type. Chest pain is a significant factor that leads to the suffering of cardiac disorder. It may vary due to quality, span, area, and force. Its intensity may be sharp, distressing feeling, and deadly upset. The chest pain attached with heart diseases can be sorted as Typical Angina (TA), Atypical Angina (ATA), Non-Anginal pain, and Asymptomatic (AM) (see [58]). The first two types are considered significant factors towards the suffering of heart diseases; the others are of less significance but cannot be ignored.
- Resting Blood Pressure. This pressure is produced due to blood flow in blood vessels on its walls. The narrowness of the blood vessels is reported due to this pressure. The medical experts have sorted it as systolic and diastolic. These are produced during active blood flow and relaxing state, respectively. Its measuring unit is mm Hg, in accordance with dataset. The standard values for systolic and diastolic are 120 and 80 mm Hg, respectively. More than 120 mm Hg and less than 80 mm Hg (see [59]) are considered abnormal values for systolic and diastolic, respectively.
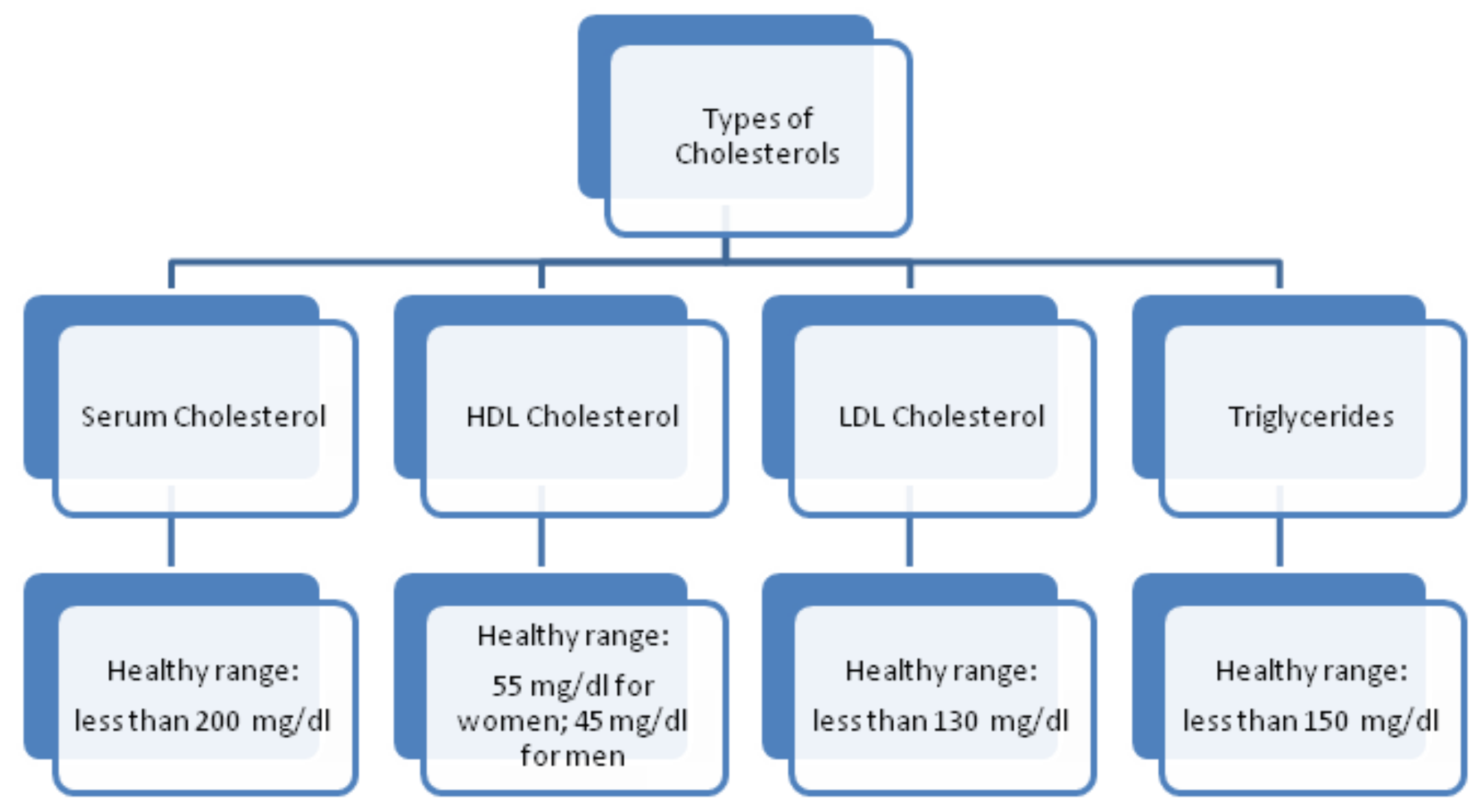
- Serum Cholesterol. Cholesterol is a variety of fat, recognized as lipid, which is encapsulated in proteins bundles (lipoproteins) and flows in blood vessels and capillaries. The common types of cholesterol are LDL, HDL, and triglycerides. These cholesterols cause the narrowness of the blood vessels, which may lead to severe heart issue. The LDL and HDL are also regarded as bad cholesterol and good cholesterol, respectively. A particular lab test ”Lipid Profile Test (LPT)“ is used to assess the values of these cholesterols. Its measuring unit is mg/dL, which is used in the adopted dataset. The serum cholesterol depends upon these cholesterol collectively and its level is determined by summing up the values of HDL and LDL along with 20% of triglycerides. Its values lie in the interval [126, 564] (see [60]). The types of cholesterol and their ranges are provided in Figure 2.
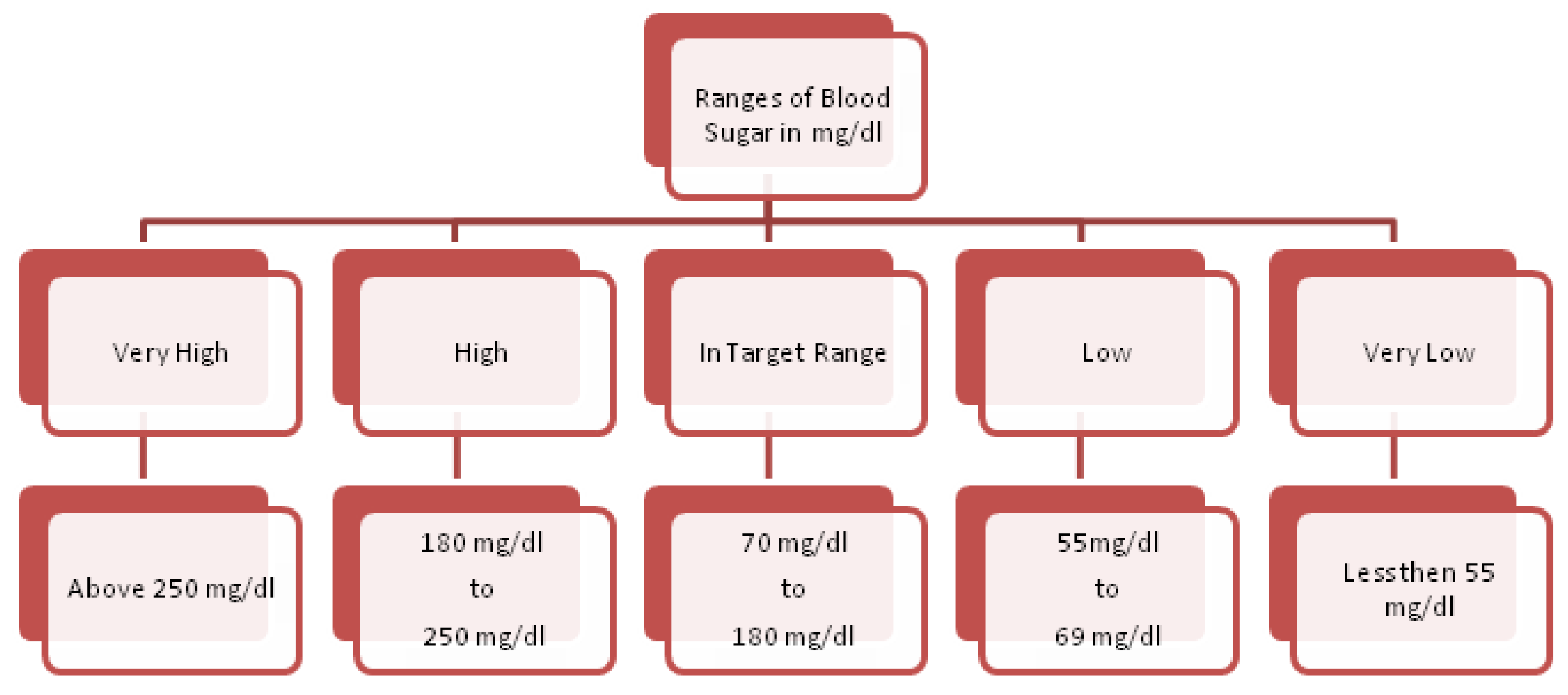
- Fasting Blood Sugar. This is regarded as another authentic factor for the analysis of heart diseases. It is usually observed that heart patients have high glucose due to the ”tension reaction“. In other words, nondiabetic patients may also have its high ratio. The ranges for its usual observed values are presented in Figure 3. Its measuring unit is mg/dL, which is used in the adopted dataset. A value of 120 mg/dL (see [58]) is regarded as a typical value for healthy individual.
- Maximum Heart Rate Achieved. Heart rate is the number of hearts beats per minute (bpm) and is regarded as a reliable source to determine the oxygen utilization in heart patients. Its values lies in the interval of 71 bpm, 195 bpm (see [61]).
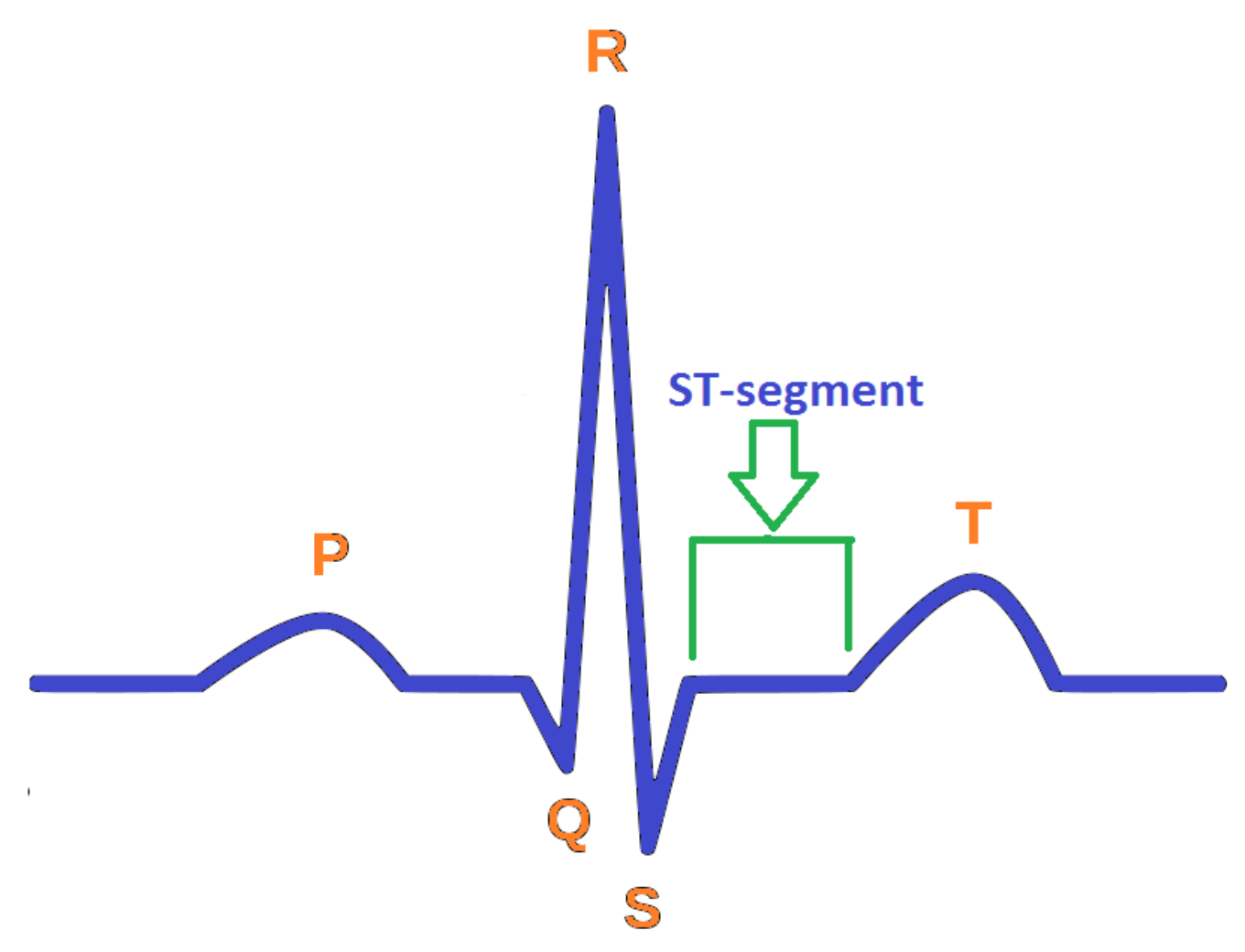
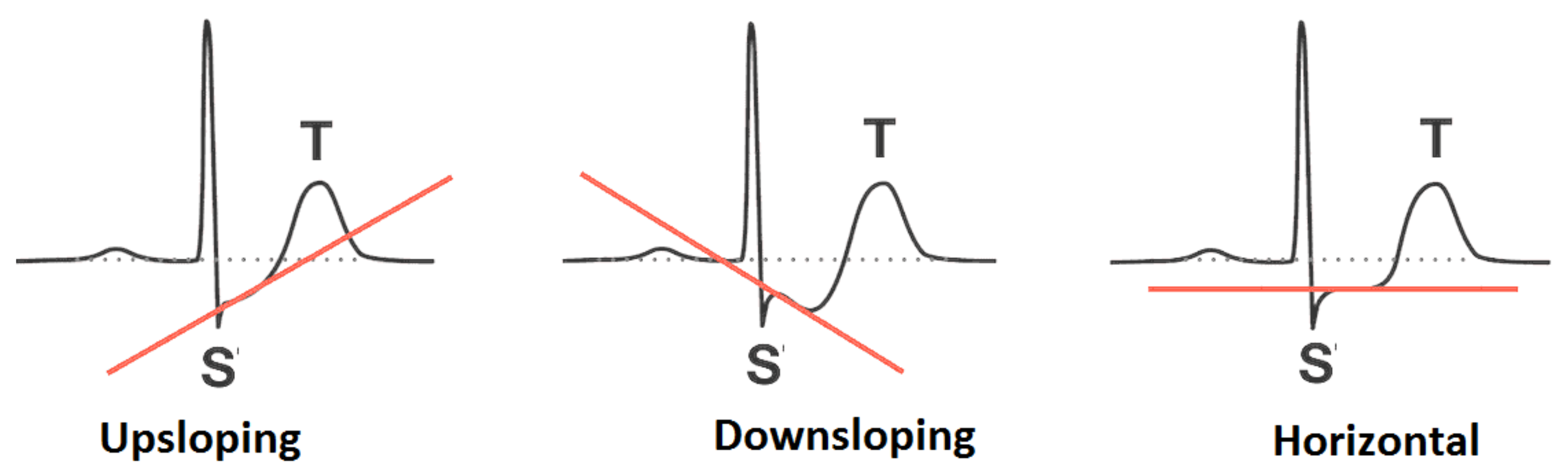
- Oldpeak and Slope. Oldpeak is usually meant for Shock-Toxicity depression (also known as ST-depression), which is provoked by rest-base work out. It is regarded as a trustworthy ECG (electrocardiogram) result for the analysis of disruptive coronary issues. Its measuring unit is mm, which can take values from the interval [0.0, 0.5]. Figure 4 presents its pictographic view. Its slope can be sorted into three types (see [58]): (i) Upsloping, (ii) Flat (Horizontal), (iii) Downsloping. The pictorial display of these categories is presented in Figure 5.
- Thal. This is a familiar turmoil of blood recognized as thalassemia, which can be sorted into four categories: (i) Null (i.e., no flow of blood at all) (ii) Fixed Defect (i.e., partial flow of blood in some sections of the heart), (iii) Normal Blood Flow, and (iv) Reversible Defect (i.e., observation of blood flow without normality). The corresponding values assigned by medical experts to these categories are 0, 3, 6, and 7, respectively (see [58]). In case of heart disease diagnosis, the category (i) is usually disregarded.
4.4. Determination of Fuzzy-Values-Based Ranges for Opted Parameters
4.5. Declaration of Problem
4.6. Proposed Algorithm Based on -set and Its Implementation
| Algorithm 1: Steps for the analysis of heart-related diseases based on -set. |
|
4.7. Proposed Algorithm Based on Riesz Summability
| Algorithm 2: Analysis of Heart-related Diseases through the concept of Riesz Summability. |
|
5. Discussion and Comparison Analysis
- 1.
- The setting when parameters and their subparametric-values-based tuples are ambiguous, i.e., decision makers are not sure about their preference-based selection. In other words, the parameters and their subparametric-values-based tuples are uncertain for decision-makers.
- 2.
- The setting where it is necessary to categorize the parameters into their related disjoint subclasses having their subparametric values. This setting demands the entitlement of multiargument approximate function, which has the capability to cope with such subparametric-valued disjoint classes. Its domain is the C-product of these classes and range is the subsets of initial universe.
Merits of Proposed Study
- The presented approach took the importance of inspiration of fuzzy-parameterization associated by -set to manage modern-day DM issues. The assignment of parameterized fuzzy grade imitates the possibility of recognition level; in this way, it has incredible prospective in the real description within the scope of computational scenarios.
- Real attributes of CD-set are converted to fuzzy membership by using algebraic technique.
- The sequential nature of approximate values of -set is managed by employing classical concept of Riesz Summability and analogous results have been achieved.
- Since the presented model put emphasis on comprehensive study of parameters (i.e., additional classification of parameters) more willingly than focusing on parameters merely, consequently, it enables decision-makers to have better and more reliable decisions.
- The two proposed algorithms have ranked the patients with analogous and consistent results by considering a smaller number of attributes.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zadeh, L. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Molodtsov, D. Soft set theory—First results. Comput. Math. Appl. 1999, 37, 19–31. [Google Scholar] [CrossRef] [Green Version]
- Maji, P.K.; Biswas, R.; Roy, A.R. Fuzzy soft sets. J. Fuzzy Math. 2001, 9, 589–602. [Google Scholar]
- Çağman, N.; Enginoğlu, S.; Çitak, F. Fuzzy soft set theory and its applications. Iran. J. Fuzzy Syst. 2011, 8, 137–147. [Google Scholar]
- Ali, M.I.; Feng, F.; Liu, X.; Min, W.K.; Sabir, M. On some new operations in soft set theory. Comput. Math. Appl. 2009, 57, 1547–1553. [Google Scholar] [CrossRef] [Green Version]
- Li, F. Notes on soft set operations. ARPN J. Syst. Softw. 2011, 1, 205–208. [Google Scholar]
- Maji, P.K.; Biswas, R.; Roy, A.R. Soft set theory. Comput. Math. Appl. 2003, 45, 555–562. [Google Scholar] [CrossRef] [Green Version]
- Pei, D.; Miao, D. From soft set to information system. In Proceedings of the International Conference of Granular Computing IEEE, Beijing, China, 25–27 July 2005; Volume 2, pp. 617–621. [Google Scholar] [CrossRef]
- Sezgin, A.; Atagun, A.O. On operations of soft sets. Comput. Math. Appl. 2011, 61, 1457–1467. [Google Scholar] [CrossRef] [Green Version]
- Babitha, K.V.; Sunil, J.J. Soft set relations and functions. Comput. Math. Appl. 2010, 60, 1840–1849. [Google Scholar] [CrossRef] [Green Version]
- Babitha, K.V.; Sunil, J.J. Transitive closure and ordering in soft set. Comput. Math. Appl. 2011, 61, 2235–2239. [Google Scholar] [CrossRef] [Green Version]
- Feng, F.; Fujita, H.; Ali, M.I.; Yager, R.R.; Liu, X. Another view on generalized intuitionistic fuzzy soft sets and related multiattribute decision making methods. IEEE Trans. Fuzzy Syst. 2018, 27, 474–488. [Google Scholar] [CrossRef]
- Tian, Y.; Liu, L.; Mi, X.; Kang, B. ZSLF: A new soft likelihood function based on Z-numbers and its application in expert decision system. IEEE Trans. Fuzzy Syst. 2020, 29, 2283–2295. [Google Scholar] [CrossRef]
- Smarandache, F. Extension of soft set of hypersoft set, and then to plithogenic hypersoft set. Neutrosophic Sets Syst. 2018, 22, 168–170. [Google Scholar] [CrossRef]
- Saeed, M.; Rahman, A.U.; Ahsan, M.; Smarandache, F. An Inclusive Study on Fundamentals of Hypersoft Set. In Theory and Application of Hypersoft Set; Pons Publication House: Brussel, Belgium, 2021; pp. 1–23. [Google Scholar]
- Ihsan, M.; Rahman, A.U.; Saeed, M. Hypersoft expert set with application in decision making for recruitment process. Neutrosophic Sets Syst. 2021, 42, 191–207. [Google Scholar] [CrossRef]
- Rahman, A.U.; Saeed, M.; Smarandache, F.; Ahmad, M.R. Development of hybrids of hypersoft set with complex fuzzy set, complex intuitionistic fuzzy set and complex neutrosophic set. Neutrosophic Sets Syst. 2020, 38, 335–354. [Google Scholar] [CrossRef]
- Rahman, A.U.; Saeed, M.; Smarandache, F. Convex and concave hypersoft sets with some properties. Neutrosophic Sets Syst. 2020, 38, 497–508. [Google Scholar] [CrossRef]
- Rahman, A.U.; Saeed, M.; Dhital, A. Decision making application based on neutrosophic parameterized hypersoft set theory. Neutrosophic Sets Syst. 2021, 41, 1–14. [Google Scholar] [CrossRef]
- Rahman, A.U.; Saeed, M.; Zahid, S. Application in decision making based on fuzzy parameterized hypersoft set theory. Asia Math. 2021, 5, 19–27. [Google Scholar] [CrossRef]
- Rahman, A.U.; Hafeez, A.; Saeed, M.; Ahmad, M.R.; Farwa, U. Development of Rough Hypersoft Set With Application in Decision Making for the Best Choice of Chemical Material. In Theory and Application of Hypersoft Set; Pons Publication House: Brussel, Belgium, 2021; pp. 192–202. [Google Scholar] [CrossRef]
- Rahman, A.U.; Saeed, M.; Hafeez, A. Theory of bijective hypersoft set with application in decision making. Punjab Univ. J. Math. 2021, 53, 511–526. [Google Scholar] [CrossRef]
- Rahman, A.U.; Saeed, M.; Alodhaibi, S.S.; Khalifa, H.A.W. Decision making algorithmic approaches based on parameterization of neutrosophic set under hypersoft set environment with fuzzy, intuitionistic fuzzy and neutrosophic settings. CMES Comput. Model. Eng. Sci. 2021, 128, 743–777. [Google Scholar] [CrossRef]
- Saeed, M.; Ahsan, M.; Saeed, M.H.; Mehmood, A.; Abdeljawad, T. An application of neutrosophic hypersoft mapping to diagnose hepatitis and propose appropriate treatment. IEEE Access 2021, 9, 70455–70471. [Google Scholar] [CrossRef]
- Saeed, M.; Ahsan, M.; Abdeljawad, T. A development of complex multi-fuzzy hypersoft set with application in mcdm based on entropy and similarity measure. IEEE Access 2021, 9, 60026–60042. [Google Scholar] [CrossRef]
- Saeed, M.; Rahman, A.U.; Arshad, M. A study on some operations and product of neutrosophic hypersoft graphs. J. Appl. Math. Comput. 2021, 1–28. [Google Scholar] [CrossRef]
- Saeed, M.; Ahsan, M.; Rahman, A.U.; Saeed, M.H.; Mehmood, A. An application of neutrosophic hypersoft mapping to diagnose brain tumor and propose appropriate treatment. J. Intell. Fuzzy Syst. 2021, 41, 1677–1699. [Google Scholar] [CrossRef]
- Saeed, M.; Ahsan, M.; Rahman, A.U. A Novel Approach to Mappings on Hypersoft Classes with Application. In Theory and Application of Hypersoft Set; Pons Publication House: Brussel, Belgium, 2021; pp. 175–191. [Google Scholar] [CrossRef]
- Saeed, M.; Siddique, M.K.; Ahsan, M.; Ahmad, M.R.; Rahman, A.U. A Novel Approach to the Rudiments of Hypersoft Graphs. In Theory and Application of Hypersoft Set; Pons Publication House: Brussel, Belgium, 2021; pp. 203–214. [Google Scholar] [CrossRef]
- Saqlain, M.; Jafar, N.; Moin, S.; Saeed, M.; Broumi, S. Single and multi-valued neutrosophic hypersoft set and tangent similarity measure of single valued neutrosophic hypersoft sets. Neutrosophic Sets Syst. 2020, 32, 317–329. [Google Scholar] [CrossRef]
- Saqlain, M.; Moin, S.; Jafar, N.; Saeed, M.; Smarandache, F. Aggregate operators of neutrosophic hypersoft sets. Neutrosophic Sets Syst. 2020, 32, 294–306. [Google Scholar] [CrossRef]
- Saqlain, M.; Saeed, M.; Ahmad, M.R.; Smarandache, F. Generalization of topsis for neutrosophic hypersoft sets using accuracy function and its application. Neutrosophic Sets Syst. 2020, 27, 131–137. [Google Scholar] [CrossRef]
- Rahman, A.U.; Saeed, M.; Mohammed, M.A.; Krishnamoorthy, S.; Kadry, S. An Integrated Algorithmic MADM Approach for Heart Diseases’ Diagnosis Based on Neutrosophic Hypersoft Set with Possibility Degree-Based Setting. Life 2022, 12, 729. [Google Scholar] [CrossRef]
- Rahman, A.U.; Saeed, M.; Alburaikan, A.; Khalifa, H.A.E.W. An Intelligent Multiattribute Decision-Support Framework Based on Parameterization of Neutrosophic Hypersoft Set. Comput. Intell. Neurosci. 2022, 2022, 6229947. [Google Scholar] [CrossRef]
- Alyasseri, Z.A.A.; Alomari, O.A.; Papa, J.P.; Al-Betar, M.A.; Abdulkareem, K.H.; Mohammed, M.A.; Kadry, S.; Thinnukool, O.; Khuwuthyakorn, P. EEG Channel Selection Based User Identification via Improved Flower Pollination Algorithm. Sensors 2022, 22, 2092. [Google Scholar] [CrossRef]
- Subathra, M.S.P.; Mohammed, M.A.; Maashi, M.S.; Garcia-Zapirain, B.; Sairamya, N.J.; George, S.T. Detection of focal and non-focal electroencephalogram signals using fast walsh-hadamard transform and artificial neural network. Sensors 2020, 20, 4952. [Google Scholar]
- Alyasseri, Z.A.A.; Alomari, O.A.; Al-Betar, M.A.; Awadallah, M.A.; Abdulkareem, K.H.; Mohammed, M.A.; Kadry, S.; Rajinikanth, V.; Rho, S. EEG Channel Selection Using Multiobjective Cuckoo Search for Person Identification as Protection System in Healthcare Applications. Comput. Intell. Neurosci. 2022, 2022, 5974634. [Google Scholar]
- Elhoseny, M.; Mohammed, M.A.; Mostafa, S.A.; Abdulkareem, K.H.; Maashi, M.S.; Garcia-Zapirain, B.; Mutlag, A.A.; Maashi, M.S. A new multi-agent feature wrapper machine learning approach for heart disease diagnosis. Comput. Mater. Contin. 2021, 67, 51–71. [Google Scholar] [CrossRef]
- Çağman, N.; Çitak, F.; Enginoğlu, S. Fuzzy parameterized fuzzy soft set theory and its applications. Turk. J. Fuzzy Syst. 2010, 1, 21–35. [Google Scholar]
- Yılmaz, Ş.; Eraslan, S. Fuzzy parametrized fuzzy soft set and Riesz summability applying to a decision making problem. Gaziosmanpaşa Bilimsel Araştrma Dergisi 2012, 1, 27–34. (In Turkish) [Google Scholar]
- Kirişci, M. A case study for medical decision making with the fuzzy soft sets. Afr. Mat. 2020, 31, 557–564. [Google Scholar] [CrossRef]
- Kirişci, M. Medical decision making with respect to the fuzzy soft sets. J. Interdiscip. Math. 2020, 23, 767–776. [Google Scholar] [CrossRef]
- Riaz, M.; Hashmi, M.R. Certain applications of fuzzy parameterized fuzzy soft sets in decision-making problems. Int. J. Algebra Stat. 2016, 5, 135–146. [Google Scholar] [CrossRef] [Green Version]
- Zhu, K.; Zhan, J. Fuzzy parameterized fuzzy soft sets and decision making. Int. J. Mach. Learn. Cybern. 2016, 7, 1207–1212. [Google Scholar] [CrossRef]
- Alkhazaleh, S.; Salleh, A.R.; Hassan, N. Fuzzy parameterized interval-valued fuzzy soft set. Appl. Math. Sci. 2011, 5, 3335–3346. [Google Scholar]
- Hassan, N.; Al-Qudah, Y. Fuzzy parameterized complex multi-fuzzy soft set. J. Phys. Conf. Ser. 2019, 1212, 012016. [Google Scholar] [CrossRef]
- Hazaymeh, A.; Abdullah, I.B.; Balkhi, Z.; Ibrahim, R. Fuzzy parameterized fuzzy soft expert set. Appl. Math. Sci. 2012, 6, 5547–5564. [Google Scholar]
- Rahman, A.U.; Saeed, M.; Khalifa, H.A.W. Decision making application based on parameterization of fuzzy hypersoft set with fuzzy setting. Ital. J. Pure Appl. Math. 2022, in press. [Google Scholar]
- Enginoğlu, S.; Çağman, N. Fuzzy parameterized fuzzy soft matrices and their application in decision-making. TWMS J. Appl. Eng. Math. 2020, 10, 1105–1115. [Google Scholar]
- Riaz, M.; Hashmi, M.R. Fuzzy parameterized fuzzy soft compact spaces with decision-making. Punjab Univ. J. Math. 2020, 50, 131–145. [Google Scholar]
- Memiş, S.; Enginoğlu, S.; Erkan, U. Numerical data classification via distance-based similarity measures of fuzzy parameterized fuzzy soft matrices. IEEE Access 2021, 9, 88583–88601. [Google Scholar] [CrossRef]
- Memiş, S.; Enginoğlu, S.; Erkan, U. A classification method in machine learning based on soft decision-making via fuzzy parameterized fuzzy soft matrices. Soft Comput. 2022, 26, 1165–1180. [Google Scholar] [CrossRef]
- Memiş, S.; Enginoğlu, S.; Erkan, U. A new classification method using soft decision-making based on an aggregationoperator of fuzzy parameterized fuzzy soft matrices. Turk. J. Electr. Eng. Comput. Sci. 2022, 30, 871–890. [Google Scholar] [CrossRef]
- Enginoğlu, S.; Öngel, T. Configurations of several soft decision-making methods to operate in fuzzy parameterized fuzzy soft matrices space. Eskişehir Tech. Univ. J. Sci. Technol. A Appl. Sci. Eng. 2020, 21, 58–71. [Google Scholar] [CrossRef] [Green Version]
- Altay, B.; Başar, F. On the paranormed Riesz sequence spaces of non-absolute type. Southeast Asian Bull. Math. 2002, 26, 701–715. [Google Scholar]
- Kirişci, M. Riesz type integrated and differentiated sequence spaces. Bull. Math. Anal. Appl. 2015, 7, 14–27. [Google Scholar]
- Petersen, G.M. Regular Matrix Transformations; McGraw-Hill Publ.: London, UK; New York, NY, USA; Toronto, ON, Canada; Sydney, Australia, 1969. [Google Scholar]
- UC Irvine Machine Learning Repository, Cleveland Heart Disease Data Details. Dataset. 2010. Available online: https://archive.ics.uci.edu/ml/datasets/heart+Disease (accessed on 3 October 2021).
- National Institute on Aging: High Blood Pressure and Older Adults. Available online: https://www.nia.nih.gov/health/high-blood-pressure-and-older-adults#:~:text=Normal (accessed on 6 June 2022).
- MedicalNewsToday: What Is Serum Cholesterol? Available online: https://www.medicalnewstoday.com/articles/321519#optimal-ranges (accessed on 6 June 2022).
- MedicalNewsToday: What Should My Heart Rate Be? Available online: https://www.medicalnewstoday.com/articles/can-overwork-kill-you#How-overwork-and-stress-impact-health (accessed on 6 June 2022).






| Ordering by Scrutiny | Ordering by CD-Set | Parameters (Short Names) | Parameters (Full Names) |
|---|---|---|---|
| 1 | 3 | age | Age in years |
| 2 | 4 | sex | Sex (male/female) |
| 3 | 9 | cp | Chest pain type) |
| 4 | 10 | trestpbs | Resting blood pressure (mm Hg) |
| 5 | 12 | chol | Serum cholesterol (mg/dL) |
| 6 | 16 | fbs | Fasting blood sugar (120 mg/dL) |
| 7 | 19 | restecg | Resting electrocardiographic results |
| 8 | 32 | Thalach | Maximum heart rate achieved |
| 9 | 38 | Exang | Exercise-induced angina |
| 10 | 40 | Oldpeak | ST depression induced by exercise relative to rest |
| 11 | 41 | slope | The slope of the peak exercise ST segment |
| 12 | 44 | ca | Number of major vessels (0–3) colored by fluoroscopy |
| 13 | 51 | thal | 3 = normal; 6 = fixed defect; 7 = reversible defect |
| 14 | 58 | num | Diagnosis of heart disease (angiographic disease status) |
| Ordering by Scrutiny | Ordering by CD-Set | Parameters (Short Names) | Parameters (Full Names) | Values related to Parameters in CD-Set |
|---|---|---|---|---|
| 1 | 3 | age | Age in years | 0–20, 21–40, 41–60, Above 60 |
| 3 | 9 | cp | Chest pain type | 1. Typical angina, 2. atypical angina, 3. non-anginal pain, 4. asymptomatic |
| 4 | 10 | trestpbs | Resting blood pressure (mm Hg) | 90–200 mm Hg |
| 5 | 12 | chol | Serum cholesterol (mg/dL) | 126–564 mg/dL |
| 6 | 16 | fbs | Fasting blood sugar (120 mg/dL) | 120 mg/dL |
| 8 | 32 | Thalach | Maximum heart rate achieved | 71–195 |
| 10 | 40 | Oldpeak | ST depression induced by exercise relative to rest | 0.0–5.6 |
| 11 | 41 | slope | The slope of the peak exercise ST segment | 1. upsloping, 2. flat, 3. downsloping |
| 13 | 51 | thal | 3 = normal; 6 = fixed defect; 7 = reversible defect | 1. normal, 2. fixed defect, 3. reversible defect |
| Selected Parameters | Relevant Values in CD-Set | Transformed Fuzzy Membership Grades |
|---|---|---|
| Age | 0–20, 21–40, 41–60, 61–80 | 0–0.25, 0.2625–0.50, 0.5125–0.75, 0.7625–1.00 |
| Chest pain type) | 1, 2, 3, 4 | 0.25, 0.50, 0.75, 1.00 |
| Resting blood pressure | 90–200 | 0.45–1.00 |
| Serum cholesterol | 126–564 | 0.2234–1.0000 |
| Fasting blood sugar | 0, 120 | 0,1 |
| Maximum heart rate achieved | 71–195 | 0.3641–1.0000 |
| Oldpeak | 0.0–5.6 | 0–1 |
| Slope | 1, 2, 3 | 0.33, 0.66, 1.00 |
| Thal | 3, 6, 7 | 0.43, 0.86, 1.00 |
| 0.5 | 0.7 | ||
| 0.25 | 0.50 | ||
| 0.75 | 0.57 | ||
| 1.00 | 0.42 | ||
| 0.72 | 0.66 | ||
| 1.00 | 0.86 |
| 0.5 | 0.5 | 0.5 | 0.5 | |||||
| 0.7 | 0.7 | 0.7 | 0.7 | |||||
| 0.25 | 0.25 | 0.25 | 0.25 | |||||
| 0.5 | 0.5 | 0.5 | 0.5 | |||||
| 0.75 | 0.75 | 0.75 | 0.75 | 0.75 | 0.75 | 0.75 | 0.75 | |
| 0.57 | 0.57 | 0.57 | 0.57 | 0.57 | 0.57 | 0.57 | 0.57 | |
| 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| 0.42 | 0.42 | 0.42 | 0.42 | |||||
| 0.72 | 0.72 | 0.72 | 0.72 | |||||
| 0.66 | 0.66 | 0.66 | 0.66 | 0.66 | 0.66 | 0.66 | 0.66 | |
| 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| 0.86 | 0.86 | 0.86 | 0.86 | 0.86 | 0.86 | 0.86 | 0.86 | |
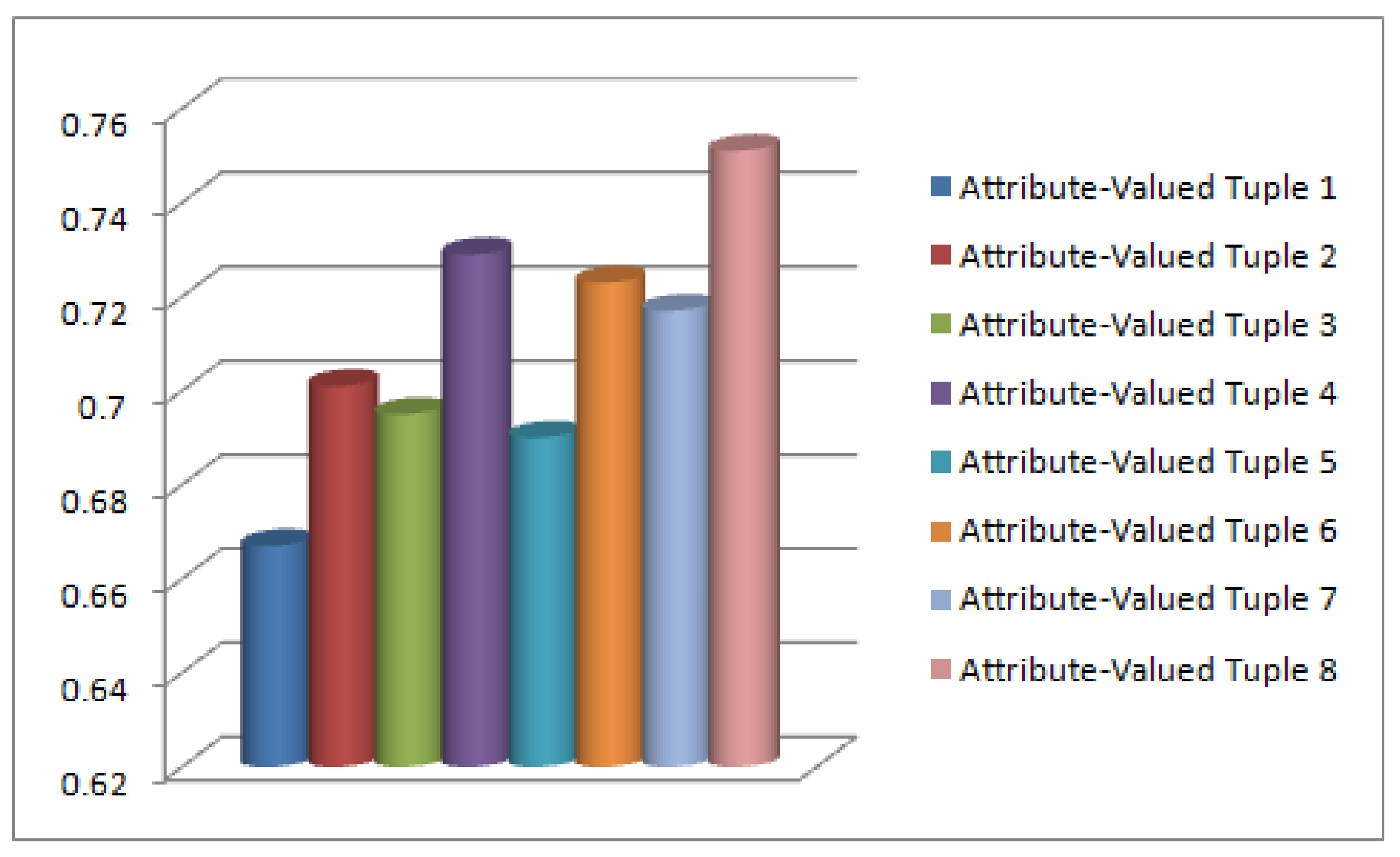
| 0.667 | 0.701 | 0.695 | 0.729 | 0.690 | 0.723 | 0.717 | 0.751 |
| 0.2 | 0.3 | 0.0 | 0.4 | 0.6 | 0.7 | |
| 0.0 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | |
| 0.3 | 0.5 | 0.3 | 0.0 | 0.4 | 0.5 | |
| 0.5 | 0.4 | 0.3 | 0.2 | 0.0 | 0.1 | |
| 0.0 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | |
| 0.4 | 0.4 | 0.5 | 0.6 | 0.8 | 0.0 | |
| 0.3 | 0.6 | 0.4 | 0.4 | 0.5 | 0.2 | |
| 0.7 | 0.5 | 0.3 | 0.5 | 0.4 | 0.3 |
| , , , , , | |
| , , , , , , , | |
| , , , , , , | |
| , , , , , , | |
| , , , , , , | |
| , , , , , , |
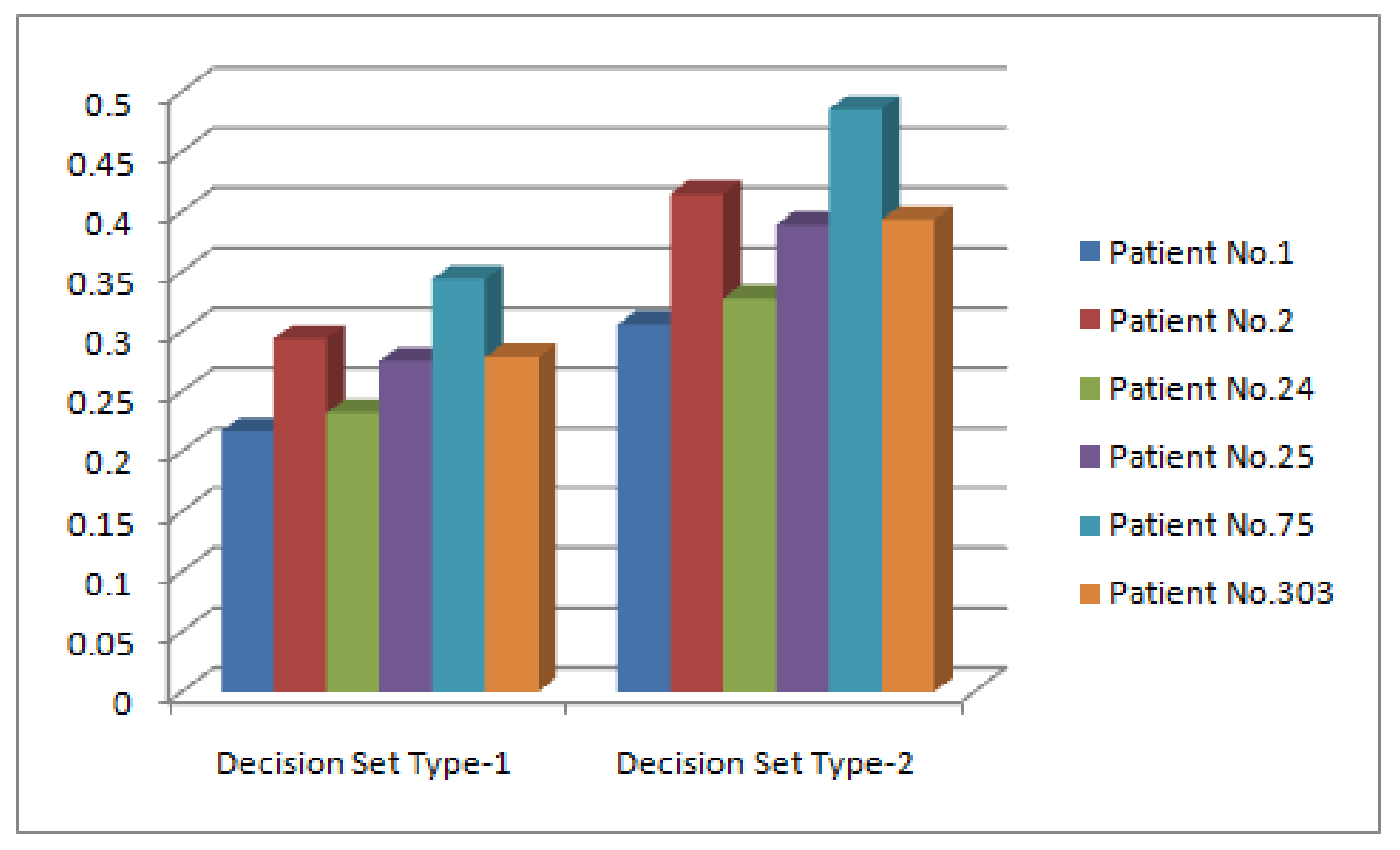
| 0.217050 | |
| 0.294063 | |
| 0.232288 | |
| 0.275663 | |
| 0.343900 | |
| 0.278850 |
| 0.306081 | |
| 0.414684 | |
| 0.327569 | |
| 0.388736 | |
| 0.484964 | |
| 0.393231 |
| Authors | Structures | Focus on Attributes | Focus on Subattributive Values | Data Set | Proper Criteria for Fuzzification of Fuzzy Parameters | Riesz Summability |
|---|---|---|---|---|---|---|
| Ça man et al. [39] | -set | Yes | Ignored | Hypothetical | N/A | N/A |
| Yılmaz et al. [40] | -set | Yes | Ignored | Hypothetical | N/A | Yes |
| Kirişci [41,42] | -set | Yes | Ignored | CD-set | N/A | N/A |
| Riaz et al. [43] | -set | Yes | Ignored | Hypothetical | N/A | N/A |
| Zhu et al. [44] | -set | Yes | Ignored | Hypothetical | N/A | N/A |
| Rahman et al. [48] | -set | Yes | Yes | Hypothetical | N/A | N/A |
| Proposed Study | -set | Yes | Yes | CD-set | Adopted | Yes |
| Authors | Structures | NOA | NOP | Ranking Based on Riesz Summability Method | Ranking Based on Other Adopted Method | Remarks |
|---|---|---|---|---|---|---|
| Kirişci [41] | -set | 11 | 06 | N/A | subattributive values are ignored. | |
| Kirişci [42] | -set | 11 | 06 | N/A | subattributive values are ignored. | |
| Proposed Study | -set | 09 | 06 | Although values of both methods are different but they both proved analogous with similar ranking of patients. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, A.U.; Saeed, M.; Mohammed, M.A.; Jaber, M.M.; Garcia-Zapirain, B. A Novel Fuzzy Parameterized Fuzzy Hypersoft Set and Riesz Summability Approach Based Decision Support System for Diagnosis of Heart Diseases. Diagnostics 2022, 12, 1546. https://doi.org/10.3390/diagnostics12071546
Rahman AU, Saeed M, Mohammed MA, Jaber MM, Garcia-Zapirain B. A Novel Fuzzy Parameterized Fuzzy Hypersoft Set and Riesz Summability Approach Based Decision Support System for Diagnosis of Heart Diseases. Diagnostics. 2022; 12(7):1546. https://doi.org/10.3390/diagnostics12071546
Chicago/Turabian StyleRahman, Atiqe Ur, Muhammad Saeed, Mazin Abed Mohammed, Mustafa Musa Jaber, and Begonya Garcia-Zapirain. 2022. "A Novel Fuzzy Parameterized Fuzzy Hypersoft Set and Riesz Summability Approach Based Decision Support System for Diagnosis of Heart Diseases" Diagnostics 12, no. 7: 1546. https://doi.org/10.3390/diagnostics12071546
APA StyleRahman, A. U., Saeed, M., Mohammed, M. A., Jaber, M. M., & Garcia-Zapirain, B. (2022). A Novel Fuzzy Parameterized Fuzzy Hypersoft Set and Riesz Summability Approach Based Decision Support System for Diagnosis of Heart Diseases. Diagnostics, 12(7), 1546. https://doi.org/10.3390/diagnostics12071546










