Proposing Intelligent Approach to Predicting Air Kerma within Radiation Beams of Medical X-ray Imaging Systems
Abstract
1. Introduction
- 1-.
- The determination of the air kerma by considering the heel effect;
- 2-.
- The determination of the air kerma using an artificial neural network, and the training of it with limited data at different angles, distances, and tube voltages;
- 3-.
- The calculation of the air kerma at a very high speed in comparison with previous works, and with a very high accuracy, using an artificial neural network;
- 4-.
- The determination of the air kerma for the tube voltages used in medical applications.
2. Methodology
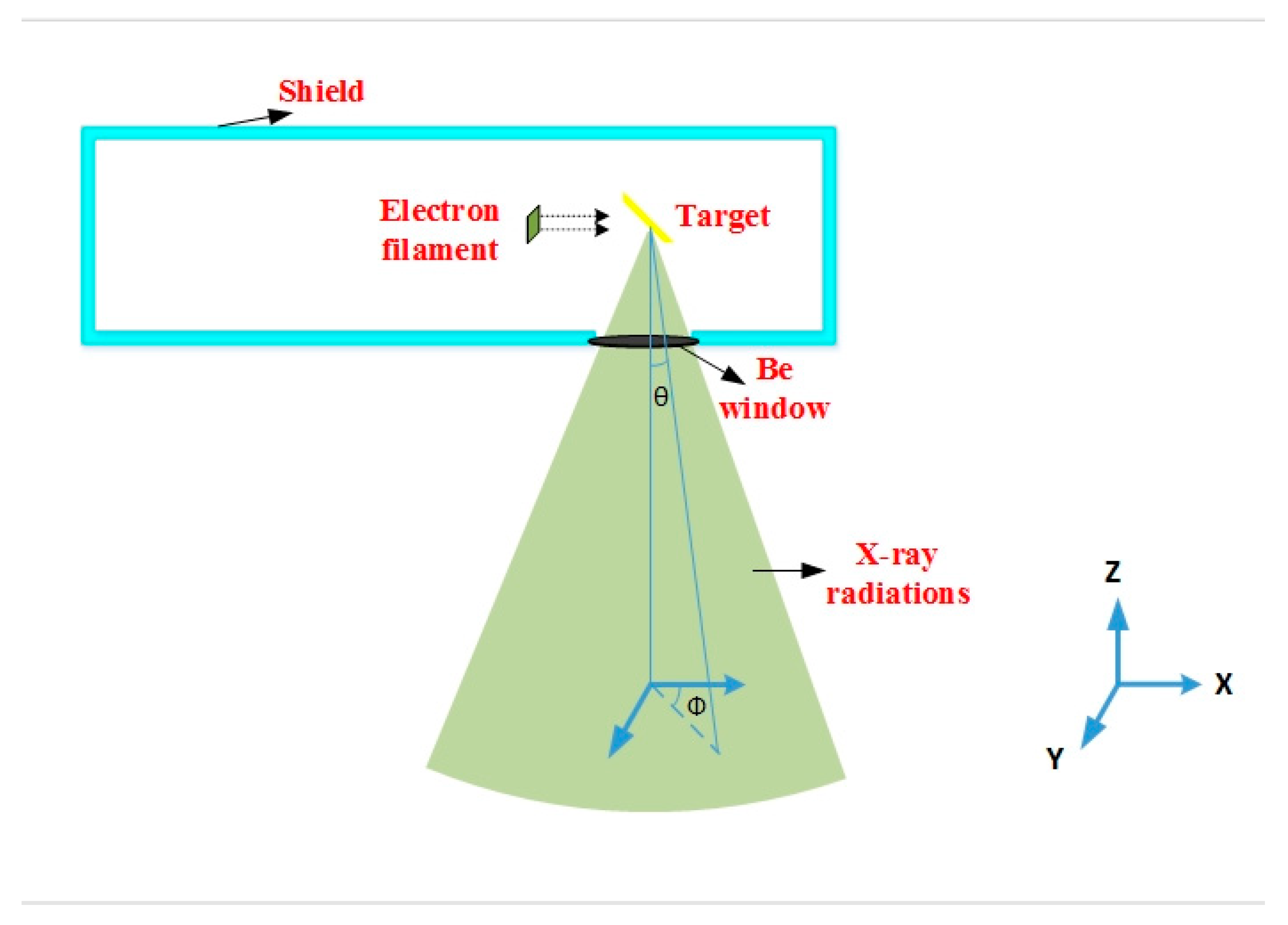
2.1. Modeling Tube of Medical X-ray Imaging System
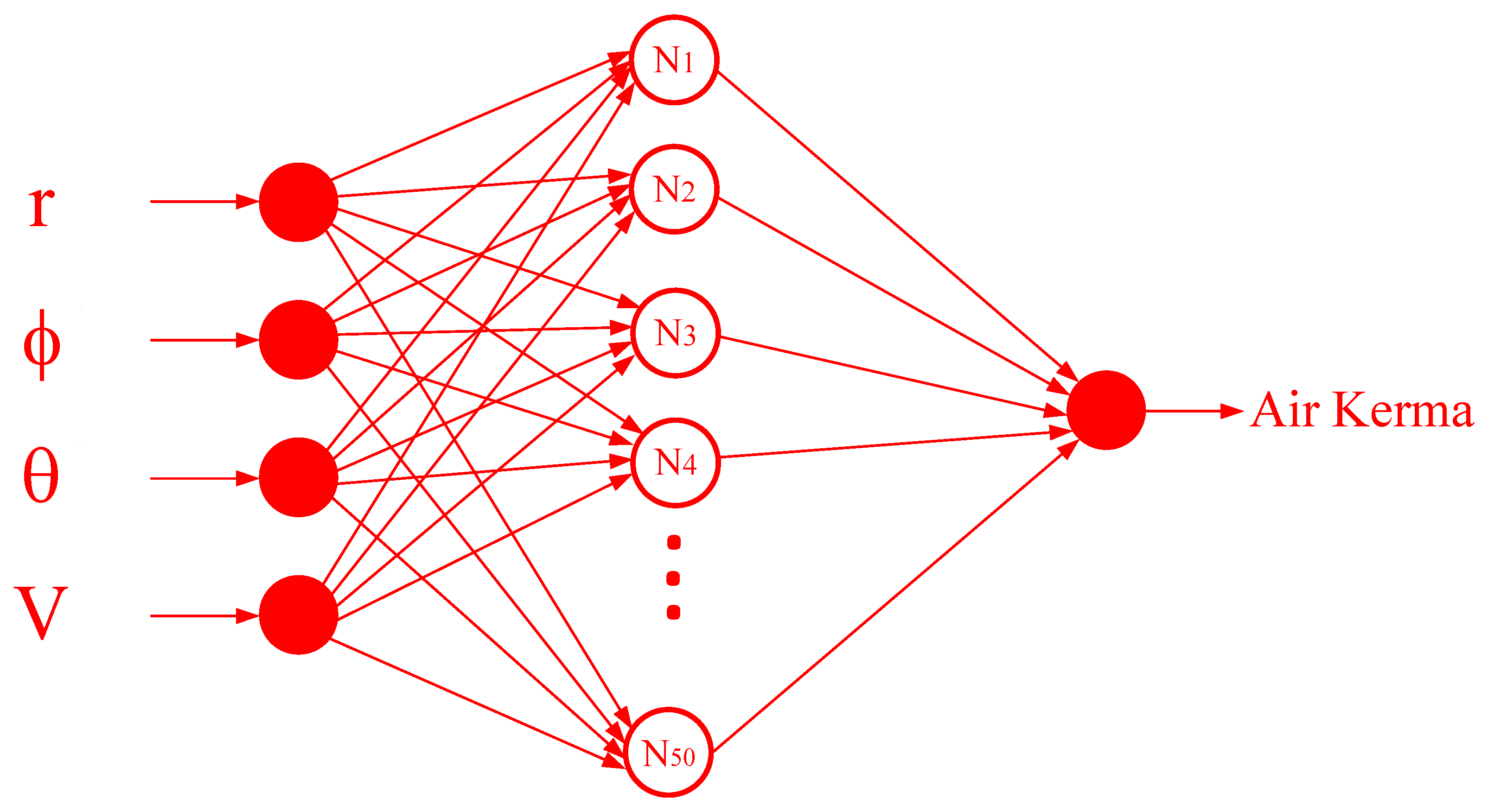
2.2. Artificial Neural Network
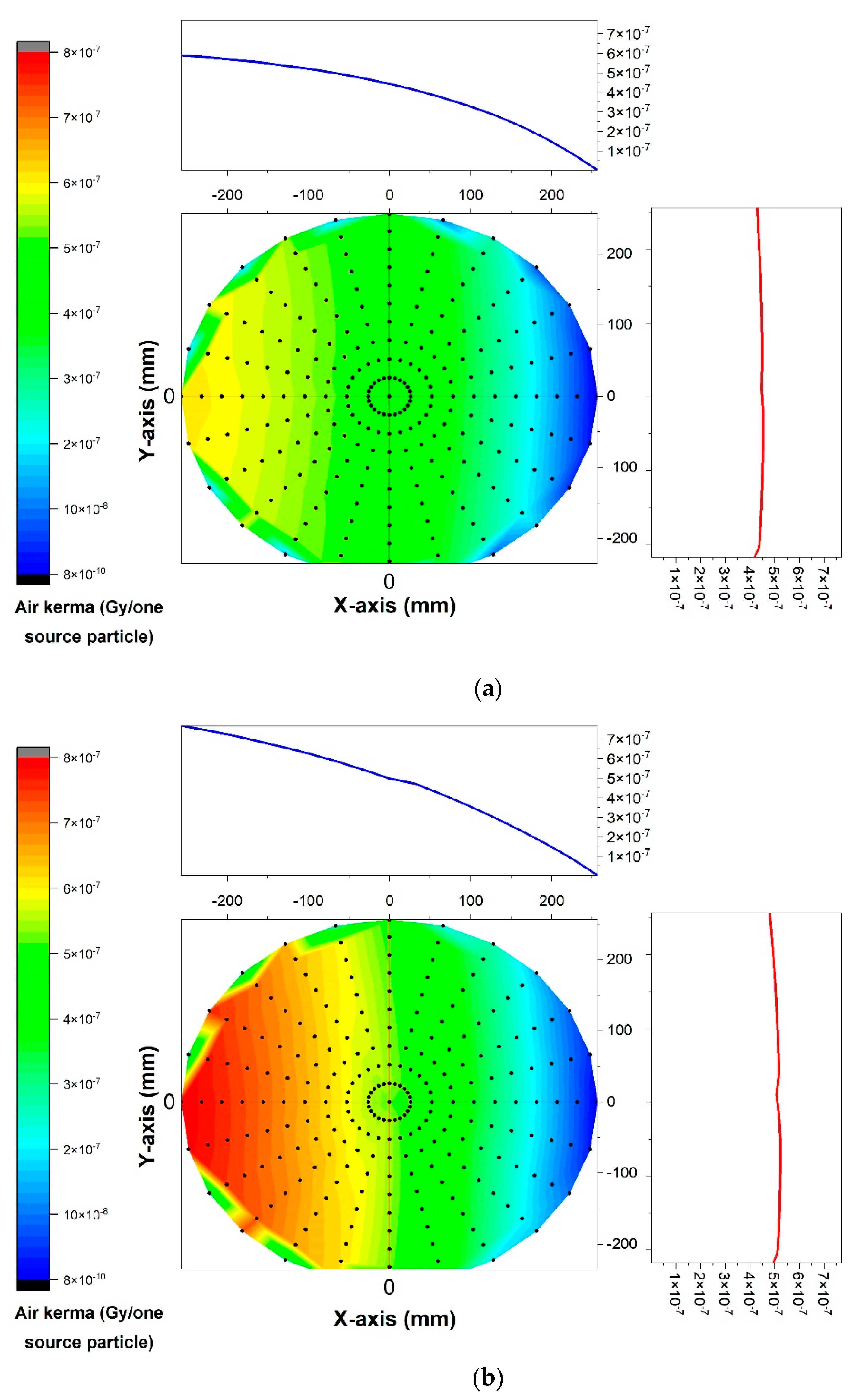
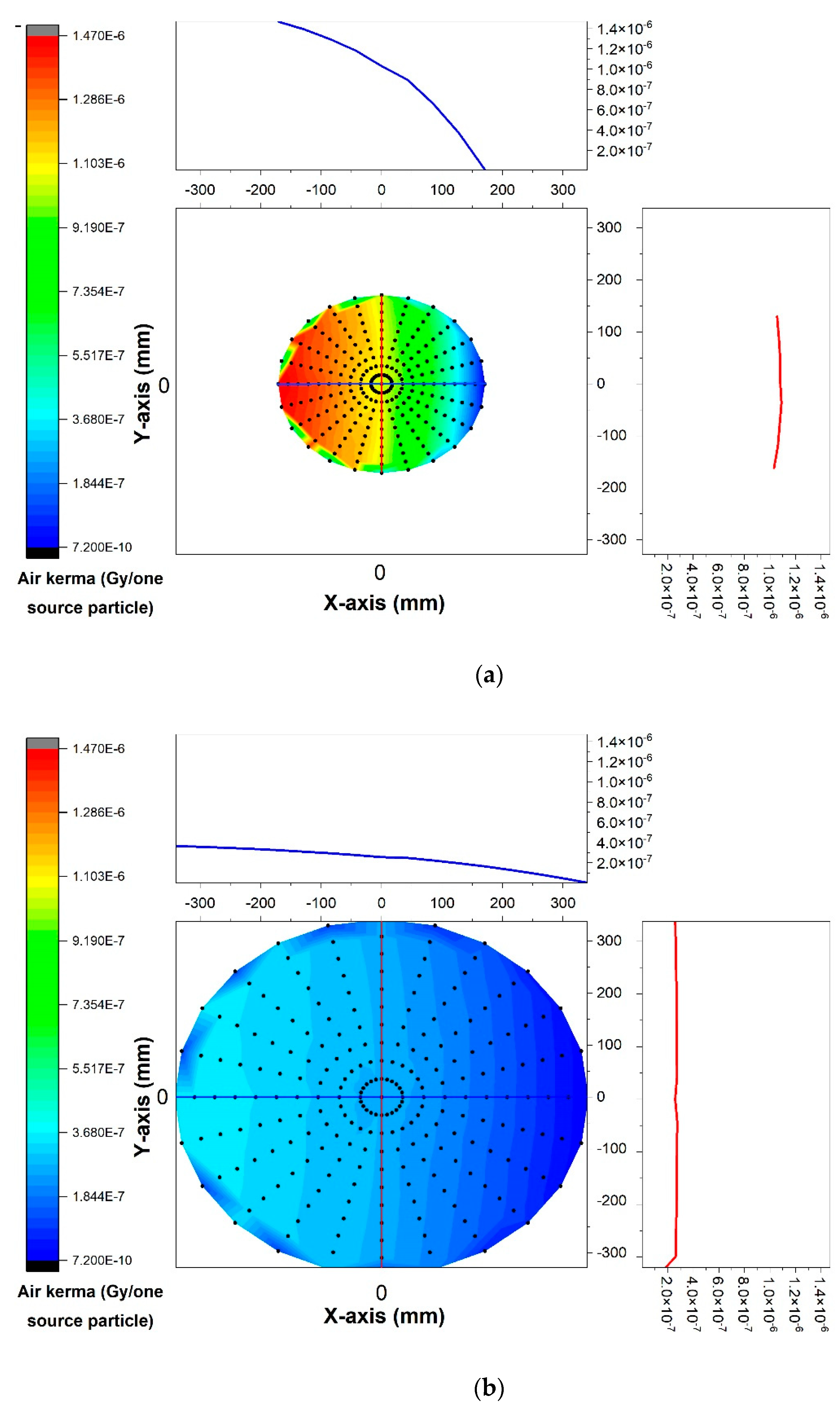
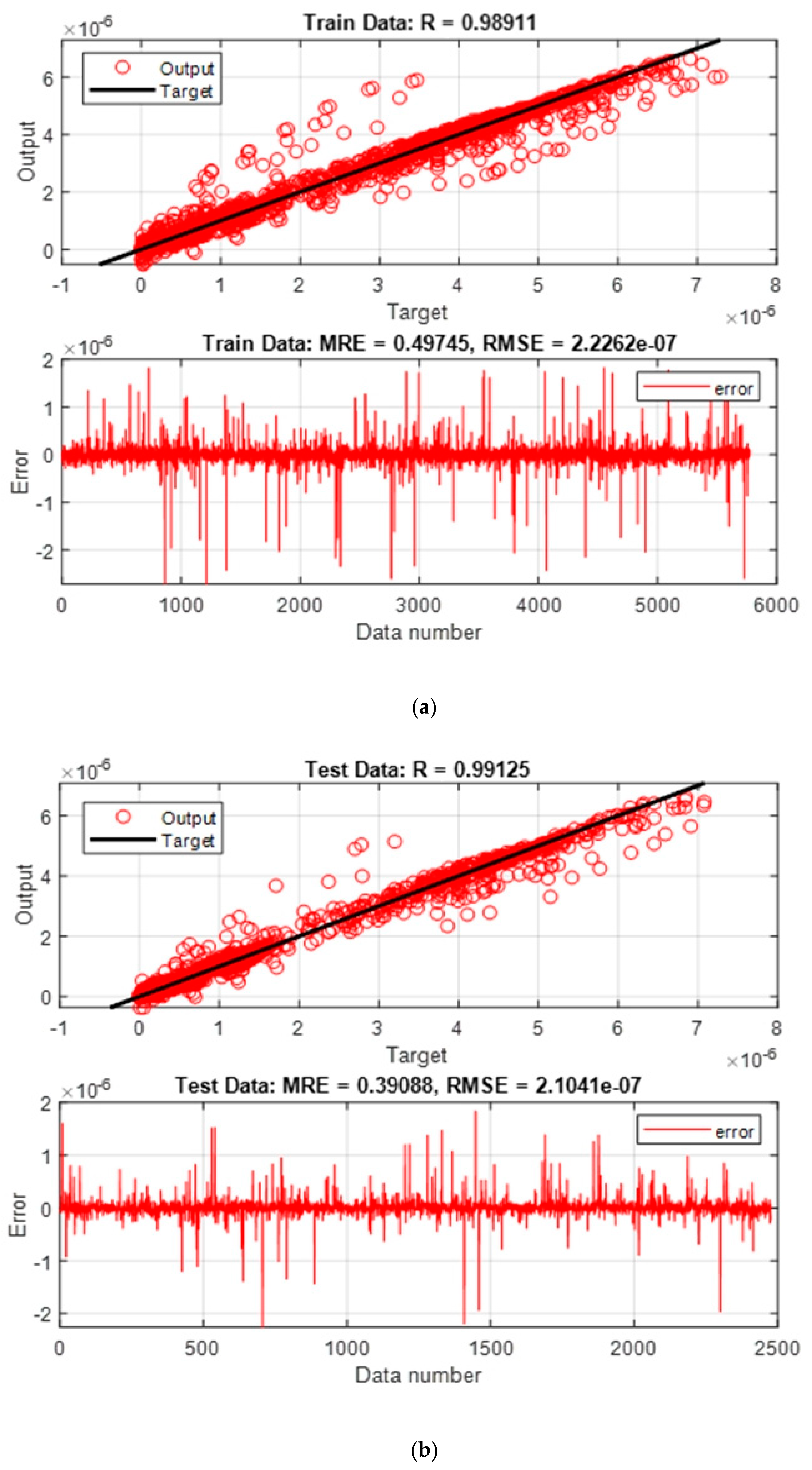
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cember, H.; Johnson, T.E. Introduction to Health Physics; McGraw-Hill Inc.: New York, NY, USA, 2009. [Google Scholar]
- IAEA. Calibration of Radiation Protection. Monitoring Instruments; IAEA Safety Report No. 16; IAEA: Vienna, Austria, 2000. [Google Scholar]
- Miller, D.L.; Balter, S.; Schueler, B.A.; Wagner, L.K.; Strauss, K.J.; Vano, E. Clinical radiation management for fluoroscopically guided interventional procedures. Radiology 2010, 257, 321–332. [Google Scholar] [CrossRef]
- Katoh, Y.; Mita, S.; Fukushi, M.; Nyui, Y.; Abe, S.; Kimura, J. Calculation of airkerma rate of diagnostic X-ray generators. Radiol. Phys. Technol. 2011, 4, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, L.S.R.; Conti, C.C.; Amorim, A.S.; Balthar, M.C.V. NaI (Tl) scintillator detectors stripping procedure for air kerma measurements of diagnostic X-ray beams. Nucl. Instrum. Methods Phys. Res. 2013, 705, 106–110. [Google Scholar] [CrossRef][Green Version]
- Porto, L.; Lunelli, N.; Paschuk, S.; Oliveira, A.; Ferreira, J.L.; Schelin, H.; Miguel, C.; Denyak, V.; Kmiecik, C.; Tilly, J.; et al. Evaluation of entrance surface air kerma in pediatric chest radiography. Radiat. Phys. Chem. 2014, 104, 252–259. [Google Scholar] [CrossRef]
- Alonso, T.C.; Mourão Filho, A.P.; Da Silva, T.A. Measurements of air kerma index in computed tomography: A comparison among methodologies. Appl. Radiat. Isot. 2018, 138, 10–13. [Google Scholar] [CrossRef] [PubMed]
- Haba, T.; Koyama, S.; Aoyama, T.; Kinomura, Y.; Ida, Y.; Kobayashi, M.; Kameyama, H.; Tsutsumi, Y. Pin-photodiode array for the measurement of fan-beam energy and air kerma distributions of X-ray CT scanners. Phys. Med. 2016, 32, 905–913. [Google Scholar] [CrossRef] [PubMed]
- Kwon, D.; Little, M.P.; Miller, D.L. Reference air kerma and kerma-area product as estimators of peak skin dose for fluoroscopically guided interventions. Med. Phys. 2011, 38, 4196–4204. [Google Scholar] [CrossRef] [PubMed]
- Bushberg, J.T.; Seibert, J.A.; Leidholdt, E.M., Jr.; Boone, J.M. The Essential Physics of Medical Imaging, 3rd ed.; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2012. [Google Scholar]
- Perera, H.; Williamson, J.F.; Li, Z.; Mishra, V.; Meigooni, A.S. Dosimetric Characteristics, Air-Kerma Strength Calibration and Verification of Monte Carlo Simulation for a New Ytterbium-169 Brachytherapy Source. Int. J. Radiat. Oncol. Biol. Phys. 1994, 28, 953–970. [Google Scholar] [CrossRef]
- Oliveira, C.; Salgado, J.; de Carvalho, A.F. Dose rate determinations in the Portuguese Gamma Irradiation Facility: Monte Carlo simulations and measurements. Radiat. Phys. Chem. 2000, 58, 279–285. [Google Scholar] [CrossRef]
- Liu, Y.; Wei, B.; Zhuoa, R.; Wena, D.; Ding, D.; Xu, Y.; Mao, B. Determination of the Conventional True Value of Gamma-Ray Air Kerma in a Mini-type Reference Radiation. Appl. Radiat. Isot. 2016, 118, 238–245. [Google Scholar] [CrossRef]
- Ounoughi, N.; Mavon, C.; Belafrites, A.; Fromm, M. Spatial distribution of air kerma rate and impact of accelerating voltage on the quality of an ultra-soft X-ray beam generated by a cold cathode tube in air. Radiat. Meas. 2015, 80, 23–28. [Google Scholar] [CrossRef]
- Nazemi, E.; Roshani, G.H.; Feghhi, S.A.H.; Setayeshi, S.; Zadeh, E.E.; Fatehi, A. Optimization of a method for identifying the flow regime and measuring void fraction in a broad beam gamma-ray attenuation technique. Int. J. Hydrogen Energy 2016, 41, 7438–7444. [Google Scholar] [CrossRef]
- Roshani, G.H.; Hanus, R.; Khazaei, A.; Zych, M.; Nazemi, E.; Mosorov, V. Density and velocity determination for single-phase flow based on radiotracer technique and neural networks. Flow Meas. Instrum. 2018, 61, 9–14. [Google Scholar] [CrossRef]
- Roshani, G.H.; Nazemi, E.; Roshani, M.M. Intelligent recognition of gas-oil-water three-phase flow regime and determination of volume fraction using radial basis function. Flow Meas. Instrum. 2017, 54, 39–45. [Google Scholar] [CrossRef]
- Roshani, G.H.; Roshani, S.; Nazemi, E.; Roshani, S. Online measuring density of oil products in annular regime of gas-liquid two phase flows. Measurement 2018, 129, 296–301. [Google Scholar] [CrossRef]
- Nazemi, E.; Feghhi, S.A.H.; Roshani, G.H.; Peyvandi, R.G.; Setayeshi, S. Precise void fraction measurement in two-phase flows independent of the flow regime using gamma-ray attenuation. Nucl. Eng. Technol. 2016, 48, 64–71. [Google Scholar] [CrossRef]
- Hosseini, S.; Taylan, O.; Abusurrah, M.; Akilan, T.; Nazemi, E.; Eftekhari-Zadeh, E.; Bano, F.; Roshani, G.H. Application of Wavelet Feature Extraction and Artificial Neural Networks for Improving the Performance of Gas–Liquid Two-Phase Flow Meters Used in Oil and Petrochemical Industries. Polymers 2021, 13, 3647. [Google Scholar] [CrossRef]
- Nazemi, E.; Movafeghi, A.; Rokrok, B.; Dastjerdi, M.C. A novel method for predicting pixel value distribution non-uniformity due to heel effect of X-ray tube in industrial digital radiography using artificial neural network. J. Nondestruct. Eval. 2019, 38, 3. [Google Scholar] [CrossRef]
- Sattari, M.A.; Roshani, G.H.; Hanus, R.; Nazemi, E. Applicability of time-domain feature extraction methods and artificial intelligence in two-phase flow meters based on gamma-ray absorption technique. Measurement 2021, 168, 108474. [Google Scholar] [CrossRef]
- Sattari, M.A.; Roshani, G.H.; Hanus, R. Improving the structure of two-phase flow meter using feature extraction and GMDH neural network. Radiat. Phys. Chem. 2020, 171, 108725. [Google Scholar] [CrossRef]
- Mayet, A.M.; Alizadeh, S.M.; Nurgalieva, K.S.; Hanus, R.; Nazemi, E.; Narozhnyy, I.M. Extraction of Time-Domain Characteristics and Selection of Effective Features Using Correlation Analysis to Increase the Accuracy of Petroleum Fluid Monitoring Systems. Energies 2022, 15, 1986. [Google Scholar] [CrossRef]
- Roshani, G.H.; Nazemi, E.; Feghhi, S.A.H.; Setayeshi, S. Flow regime identification and void fraction prediction in two-phase flows based on gamma ray attenuation. Measurement 2015, 62, 25–32. [Google Scholar] [CrossRef]
- Mayet, A.M.; Salama, A.S.; Alizadeh, S.M.; Nesic, S.; Guerrero, J.W.G.; Eftekhari-Zadeh, E.; Nazemi, E.; Iliyasu, A.M. Applying Data Mining and Artificial Intelligence Techniques for High Precision Measuring of the Two-Phase Flow’s Characteristics Independent of the Pipe’s Scale Layer. Electronics 2022, 11, 459. [Google Scholar] [CrossRef]
- Roshani, M.; Sattari, M.A.; Ali, P.J.M.; Roshani, G.H.; Nazemi, B.; Corniani, E.; Nazemi, E. Application of GMDH neural network technique to improve measuring precision of a simplified photon attenuation based two-phase flowmeter. Flow Meas. Instrum. 2020, 75, 101804. [Google Scholar] [CrossRef]
- Roshani, G.H.; Feghhi, S.A.H.; Mahmoudi-Aznaveh, A.; Nazemi, E.; Adineh-Vand, A. Precise volume fraction prediction in oil–water–gas multiphase flows by means of gamma-ray attenuation and artificial neural networks using one detector. Measurement 2014, 51, 34–41. [Google Scholar] [CrossRef]
- Karami, A.; Roshani, G.H.; Khazaei, A.; Nazemi, E.; Fallahi, M. Investigation of different sources in order to optimize the nuclear metering system of gas–oil–water annular flows. Neural Comput. Appl. 2020, 32, 3619–3631. [Google Scholar] [CrossRef]
- Alanazi, A.K.; Alizadeh, S.M.; Nurgalieva, K.S.; Nesic, S.; Grimaldo Guerrero, J.W.; Abo-Dief, H.M.; Eftekhari-Zadeh, E.; Nazemi, E.; Narozhnyy, I.M. Application of Neural Network and Time-Domain Feature Extraction Techniques for Determining Volumetric Percentages and the Type of Two Phase Flow Regimes Independent of Scale Layer Thickness. Appl. Sci. 2022, 12, 1336. [Google Scholar] [CrossRef]
- Hartman, E.J.; Keeler, J.D.; Kowalski, J.M. Layered neural networks with Gaussian hidden units as universal approxima-tors. Neural Comput. 1990, 2, 210–215. [Google Scholar] [CrossRef]
- Ralambondrainy, H. A conceptual version of the k-means algorithm. Pattern Recognit. Lett. 1995, 16, 1147–1157. [Google Scholar] [CrossRef]
- Cottrell, M.; Rousset, P. The Kohonen algorithm: A powerful tool for analysing and representing multidimensional quantitative and qualitative data. In International Work-Conference on Artificial Neural Networks; Springer: Berlin/Heidelberg, Germany, 1997; pp. 861–871. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Zheng, N.; Ye, M.; Zhu, Y.; Zhang, G.; Nazemi, E.; He, J. Proposing Intelligent Approach to Predicting Air Kerma within Radiation Beams of Medical X-ray Imaging Systems. Diagnostics 2023, 13, 190. https://doi.org/10.3390/diagnostics13020190
Lu Y, Zheng N, Ye M, Zhu Y, Zhang G, Nazemi E, He J. Proposing Intelligent Approach to Predicting Air Kerma within Radiation Beams of Medical X-ray Imaging Systems. Diagnostics. 2023; 13(2):190. https://doi.org/10.3390/diagnostics13020190
Chicago/Turabian StyleLu, Yanjie, Nan Zheng, Mingtao Ye, Yihao Zhu, Guodao Zhang, Ehsan Nazemi, and Jie He. 2023. "Proposing Intelligent Approach to Predicting Air Kerma within Radiation Beams of Medical X-ray Imaging Systems" Diagnostics 13, no. 2: 190. https://doi.org/10.3390/diagnostics13020190
APA StyleLu, Y., Zheng, N., Ye, M., Zhu, Y., Zhang, G., Nazemi, E., & He, J. (2023). Proposing Intelligent Approach to Predicting Air Kerma within Radiation Beams of Medical X-ray Imaging Systems. Diagnostics, 13(2), 190. https://doi.org/10.3390/diagnostics13020190






