Using A-Mode Ultrasound to Assess the Body Composition of Soccer Players: A Comparative Study of Prediction Formulas
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Population
2.2. A-Mode Ultrasound Measurements
2.3. Statistical Analyses
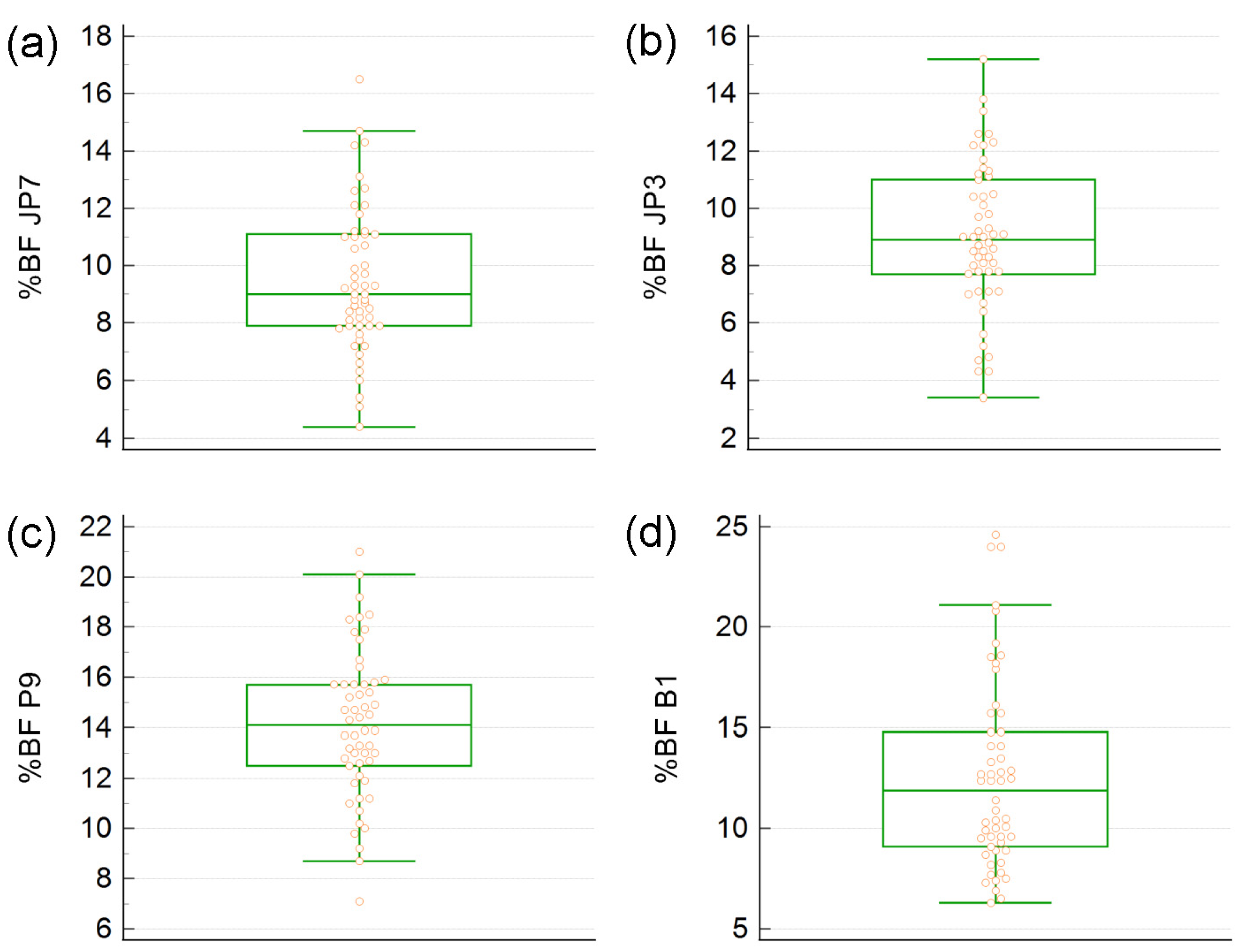
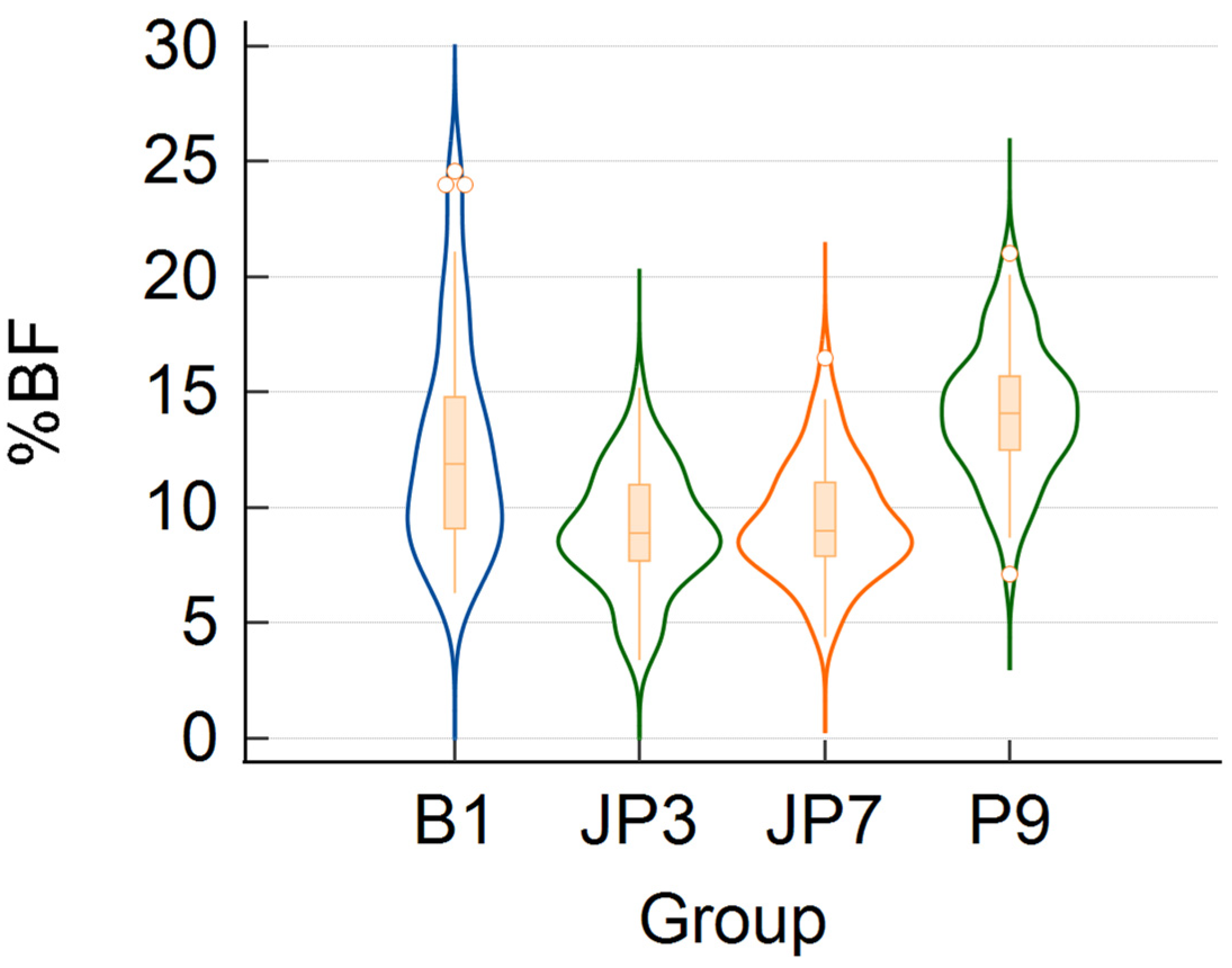
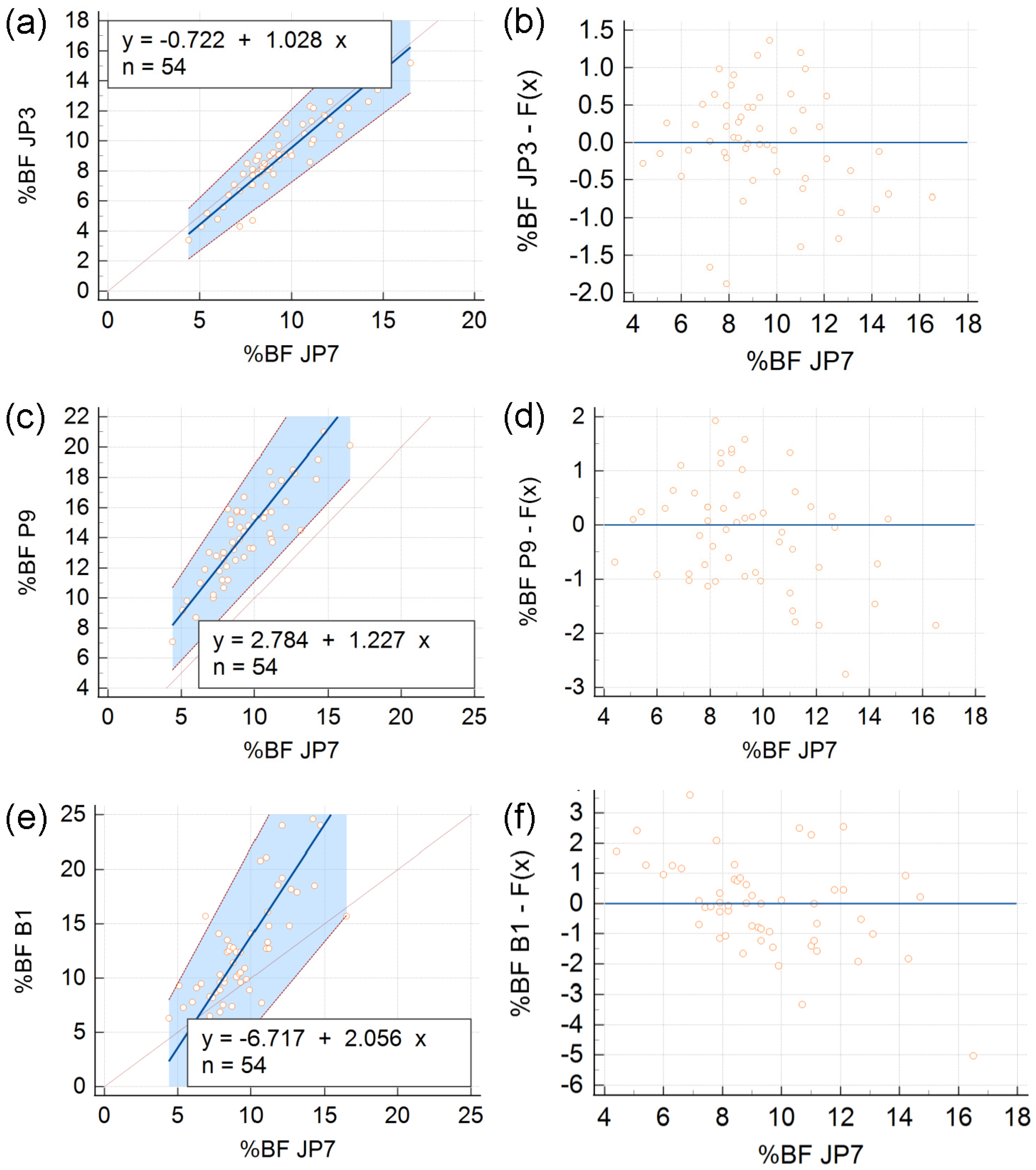
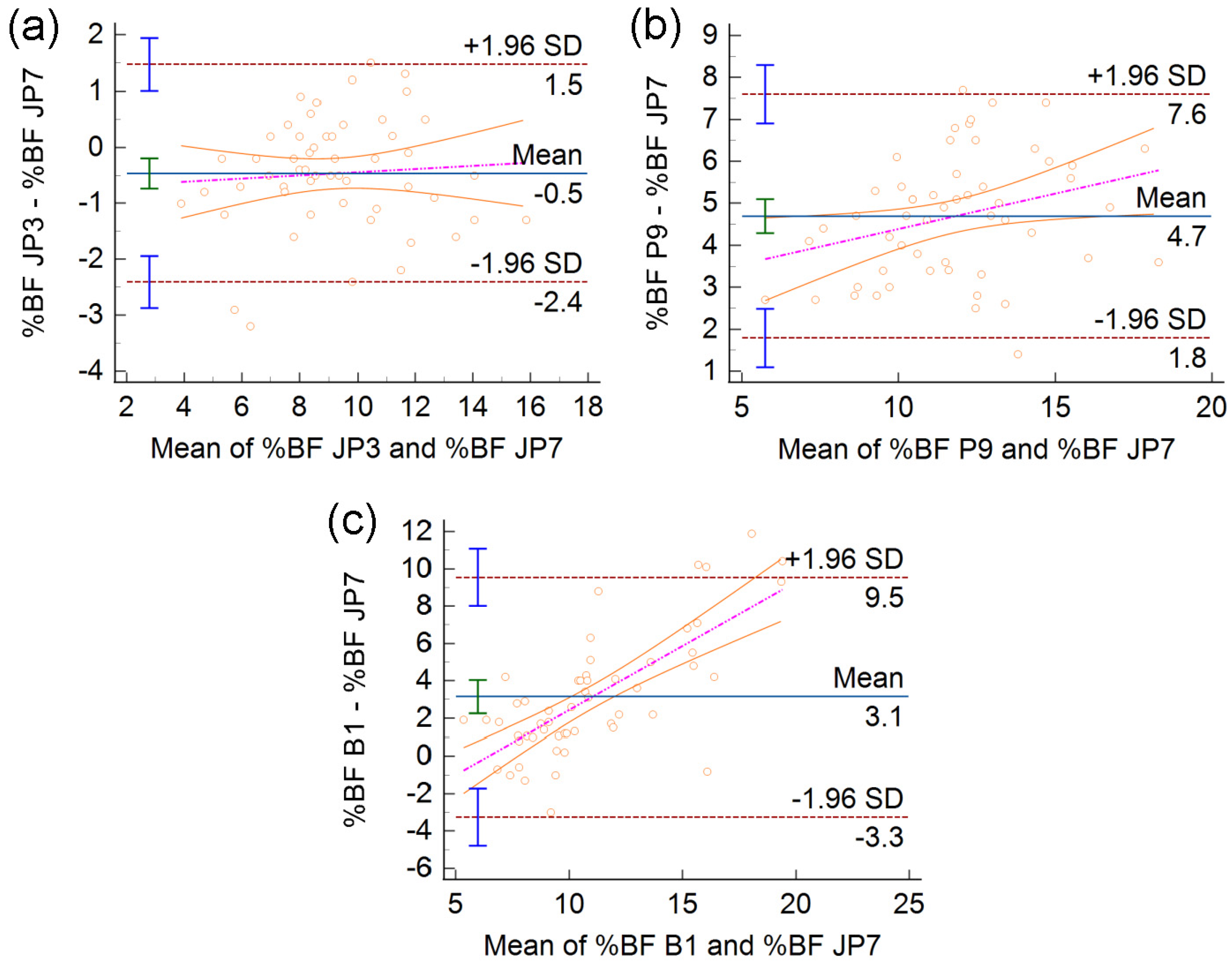
3. Results
3.1. Descriptive Statistics and One-Way Analysis of Variance
3.2. Passing–Bablok Regression
3.3. Bland-Altman Analysis
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ackland, T.R.; Lohman, T.G.; Sundgot-Borgen, J.; Maughan, R.J.; Meyer, N.L.; Stewart, A.D.; Müller, W. Current status of body composition assessment in sport. Sport. Med. 2012, 42, 227–249. [Google Scholar] [CrossRef] [PubMed]
- Müller, M.J.; Braun, W.; Pourhassan, M.; Geisler, C.; Bosy-Westphal, A. Application of standards and models in body composition analysis. Proc. Nutr. Soc. 2015, 75, 181–187. [Google Scholar] [CrossRef] [PubMed]
- Sundgot-Borgen, J.; Meyer, N.L.; Lohman, T.G.; Ackland, T.R.; Maughan, R.J.; Stewart, A.D.; Müller, W. How to minimise the health risks to athletes who compete in weight-sensitive sports review and position statement on behalf of the Ad Hoc Research Working Group on Body Composition, Health and Performance, under the auspices of the IOC Medical Commission. Br. J. Sport. Med. 2013, 47, 1012–1022. [Google Scholar] [CrossRef] [PubMed]
- Leão, C.; Silva, A.F.; Badicu, G.; Clemente, F.M.; Carvutto, R.; Greco, G.; Cataldi, S.; Fischetti, F. Body Composition Interactions with Physical Fitness: A Cross-Sectional Study in Youth Soccer Players. Int. J. Environ. Res. Public Health 2022, 19, 3598. [Google Scholar] [CrossRef] [PubMed]
- Kasper, A.M.; Langan-Evans, C. Come Back Skinfolds, All Is Forgiven: A Narrative Review of the Efficacy of Common Body Composition Methods in Applied Sports Practice. Nutrients 2021, 13, 1075. [Google Scholar] [CrossRef] [PubMed]
- Kobel, S.; Kirsten, J.; Kelso, A. Anthropometry—Assessment of Body Composition. Dtsch. Z. Für Sportmed. 2022, 73, 106–111. [Google Scholar] [CrossRef]
- Stewart, A.; Marfell-Jones, M.; Olds, T.; De Ridder, J. International Standards for Anthropometric Assessment, 3rd ed.; International Society for the Advancement of Kinanthropometry: Lower Hutt, New Zealand, 2011. [Google Scholar]
- Wagner, D.R. Ultrasound as a Tool to Assess Body Fat. J. Obes. 2013, 280713, 9. [Google Scholar] [CrossRef] [PubMed]
- Wagner, D.R.; Cotter, J.D. Ultrasound Measurements of Subcutaneous Fat Thickness Are Robust Against Hydration Changes. Int. J. Sport Nutr. Exerc. Metab. 2021, 31, 244–249. [Google Scholar] [CrossRef]
- Wagner, D.R.; Teramoto, M. Interrater reliability of novice examiners using A-mode ultrasound and skinfolds to measure subcutaneous body fat. PLoS ONE 2020, 15, e0244019. [Google Scholar] [CrossRef]
- Wagner, D.R.; Cain, D.L.; Clark, N.W. Validity and Reliability of A-Mode Ultrasound for Body Composition Assessment of NCAA Division I Athletes. PLoS ONE 2016, 11, e0153146. [Google Scholar] [CrossRef] [PubMed]
- Miclos-Balica, M.; Muntean, P.; Schick, F.; Haragus, H.G.; Glisici, B.; Pupazan, V.; Neagu, A.; Neagu, M. Reliability of body composition assessment using A-mode ultrasound in a heterogeneous sample. Eur. J. Clin. Nutr. 2021, 75, 438–445. [Google Scholar] [CrossRef]
- Johnson, K.E.; Naccarato, I.A.; Corder, M.A.; Repovich, W. Validation of Three Body Composition Techniques with a Comparison of Ultrasound Abdominal Fat Depths against an Octopolar Bioelectrical Impedance Device. Int. J. Exerc. Sci. 2012, 5, 205–213. [Google Scholar] [PubMed]
- Smith-Ryan, A.E.; Fultz, S.N.; Melvin, M.N.; Wingfield, H.L.; Woessner, M.N. Reproducibility and Validity of A-Mode Ultrasound for Body Composition Measurement and Classification in Overweight and Obese Men and Women. PLoS ONE 2014, 9, e91750. [Google Scholar] [CrossRef] [PubMed]
- Totosy de Zepetnek, J.O.; Lee, J.J.; Boateng, T.; Plastina, S.E.; Cleary, S.; Huang, L.; Kucab, M.; Paterakis, S.; Brett, N.R.; Bellissimo, N. Test–retest reliability and validity of body composition methods in adults. Clin. Physiol. Funct. Imaging 2021, 41, 417–425. [Google Scholar] [CrossRef] [PubMed]
- Lowry, R.S.; Wagner, D.R.; Bigler, M. Evaluation of Body Fat Prediction Equations from a Portable A-Mode Ultrasound Compared to Air Displacement Plethysmography. Meas. Phys. Educ. Exerc. Sci. 2021, 25, 314–321. [Google Scholar] [CrossRef]
- Parrillo, J.; Greenwood-Robinson, M. High-Performance Bodybuilding; Perigee Trade: New York, NY, USA, 1993. [Google Scholar]
- Loenneke, J.P.; Barnes, J.T.; Wagganer, J.D.; Wilson, J.M.; Lowery, R.P.; Green, C.E.; Pujol, T.J. Validity and reliability of an ultrasound system for estimating adipose tissue. Clin. Physiol. Funct. Imaging 2014, 34, 159–162. [Google Scholar] [CrossRef] [PubMed]
- Association, W.M. Declaration of Helsinki. Available online: https://www.wma.net/what-we-do/medical-ethics/declaration-of-helsinki/doh-oct2008/ (accessed on 17 December 2022).
- Jackson, A.S.; Pollock, M.L. Generalized equations for predicting body density of men. Br. J. Nutr. 1978, 40, 497–504. [Google Scholar] [CrossRef] [PubMed]
- Conover, W.J. Practical Nonparametric Statistics, 3rd ed.; Jony Wiley and Sons: New York, NY, USA, 1999. [Google Scholar]
- Passing, H.; Bablok, W. A New Biometrical Procedure for Testing the Equality of Measurements from Two Different Analytical Methods. Application of linear regression procedures for method comparison studies in Clinical Chemistry, Part I. J. Clin. Chem. Clin. Biochem. 1983, 21, 709–720. [Google Scholar] [CrossRef] [PubMed]
- Passing, H.; Bablok, W. Comparison of Several Regression Procedures for Method Comparison Studies and Determination of Sample Sizes Application of linear regression procedures for method comparison studies in Clinical Chemistry, Part II. J. Clin. Chem. Clin. Biochem. 1984, 22, 431–445. [Google Scholar] [CrossRef]
- Bland, M.J.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 327, 307–310. [Google Scholar] [CrossRef]
- Giavarina, D. Understanding Bland Altman analysis. Biochem. Med. 2015, 25, 141–151. [Google Scholar] [CrossRef] [PubMed]
- Bland, J.M.; Altman, D.G. Measuring agreement in method comparison studies. Stat. Methods Med. Res. 1999, 8, 135–160. [Google Scholar] [CrossRef] [PubMed]
- Ludbrook, J. Linear regression analysis for comparing two measurers or methods of measurement: But which regression? Clin. Exp. Pharmacol. Physiol. 2010, 37, 692–699. [Google Scholar] [CrossRef] [PubMed]
- Lin, L.I. A concordance correlation coefficient to evaluate reproducibility. Biometrics 1989, 45, 255–268. [Google Scholar] [CrossRef] [PubMed]
- Blue, M.N.M.; Hirsch, K.R.; Brewer, G.J.; Cabre, H.E.; Gould, L.M.; Tinsley, G.M.; Ng, B.K.; Ryan, E.D.; Padua, D.; Smith-Ryan, A.E. The validation of contemporary body composition methods in various races and ethnicities. Br. J. Nutr. 2022, 128, 2387–2397. [Google Scholar] [CrossRef] [PubMed]
- Nickerson, B.S.; Tinsley, G.M.; Esco, M.R. Validity of Field and Laboratory Three-Compartment Models in Healthy Adults. Med. Sci. Sport. Exerc. 2019, 51, 1032–1039. [Google Scholar] [CrossRef]
- Müller, W.; Fürhapter-Rieger, A.; Ahammer, H.; Lohman, T.G.; Meyer, N.L.; Sardinha, L.B.; Stewart, A.D.; Maughan, R.J.; Sundgot-Borgen, J.; Müller, T.; et al. Relative Body Weight and Standardised Brightness-Mode Ultrasound Measurement of Subcutaneous Fat in Athletes: An International Multicentre Reliability Study, Under the Auspices of the IOC Medical Commission. Sport. Med. 2020, 50, 597–614. [Google Scholar] [CrossRef] [PubMed]
- Müller, W.; Lohman, T.G.; Stewart, A.D.; Maughan, R.J.; Meyer, N.L.; Sardinha, L.B.; Kirihennedige, N.; Reguant-Closa, A.; Risoul-Salas, V.; Sundgot-Borgen, J.; et al. Subcutaneous fat patterning in athletes: Selection of appropriate sites and standardisation of a novel ultrasound measurement technique: Ad hoc working group on body composition, health and performance, under the auspices of the IOC Medical Commission. Br. J. Sport. Med. 2016, 50, 45–54. [Google Scholar] [CrossRef] [PubMed]
- Störchle, P.; Müller, W.; Sengeis, M.; Ahammer, H.; Fürhapter-Rieger, A.; Bachl, N.; Lackner, S.; Mörkl, S.; Holasek, S. Standardized Ultrasound Measurement of Subcutaneous Fat Patterning: High Reliability and Accuracy in Groups Ranging from Lean to Obese. Ultrasound Med. Biol. 2017, 43, 427–438. [Google Scholar] [CrossRef]
- Müller, W.; Horn, M.; Fürhapter-Rieger, A.; Kainz, P.; Kröpfl, J.M.; Ackland, T.R.; Lohman, T.G.; Maughan, R.J.; Meyer, N.L.; Sundgot-Borgen, J.; et al. Body composition in sport: Interobserver reliability of a novel ultrasound measure of subcutaneous fat tissue. Br. J. Sport. Med. 2013, 47, 1036–1043. [Google Scholar] [CrossRef] [PubMed]
| Mean ± SD 1 | Min | Max | Q1 | Q2 | Q3 | |
|---|---|---|---|---|---|---|
| Age (y) | 22.9 ± 3.83 | 18 | 32 | 20 | 22 | 25 |
| Height (m) | 1.82 ± 6.01 | 1.73 | 1.95 | 1.77 | 1.82 | 1.86 |
| BM (kg) | 75.5 ± 6.04 | 65 | 90 | 71 | 74.5 | 80 |
| BMI (kg/m2) | 22.8 ± 1.39 | 19.5 | 26.1 | 21.7 | 22.7 | 23.8 |
| Site | Description | Formulas 1 |
|---|---|---|
| Biceps | midway between the tip of the shoulder and the elbow along the anterior midline | B1, P9 |
| Triceps | midway between the tip of the shoulder and the elbow along the posterior midline | JP7, P9 |
| Chest | midway between the axillary line of the underarm and the nipple | JP7, JP3, P9 |
| Scapula | just below the bottom tip of the shoulder blade at the inferior angle | JP7, P9 |
| Axilla | on the midaxillary line and level with the lower tip of the breastbone (Xiphoid Process) | JP7 |
| Waist | one inch (2.54 cm) to the right of the umbilicus | JP7, JP3, P9 |
| Hip | just above the iliac crest (front tip of the top of the hip bone) | JP7, P9 |
| Thigh | midway between the proximal border of the kneecap and the crease of the hip | JP7, JP3, P9 |
| Lower Back | over the kidney and two inches to the right of the spine | P9 |
| Calf | at the maximum circumference of the calf, midline of its medial inside border | P9 |
| Formula | Mean ± SD | Median | Min | Max | Skewness | Kurtosis | p1 |
|---|---|---|---|---|---|---|---|
| JP7 | 9.45 ± 2.51 | 9.0 | 4.4 | 16.5 | 0.556 | 0.321 | 0.290 |
| JP3 | 8.99 ± 2.58 | 8.9 | 3.4 | 15.2 | 0.031 | −0.167 | 0.846 |
| P9 | 14.1 ± 2.94 | 14.1 | 7.1 | 21.0 | 0.050 | −0.065 | 0.994 |
| B1 | 12.6 ± 4.72 | 11.9 | 6.3 | 24.6 | 0.950 | 0.237 | 8 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muntean, P.; Neagu, M.; Amaricai, E.; Haragus, H.G.; Onofrei, R.R.; Neagu, A. Using A-Mode Ultrasound to Assess the Body Composition of Soccer Players: A Comparative Study of Prediction Formulas. Diagnostics 2023, 13, 690. https://doi.org/10.3390/diagnostics13040690
Muntean P, Neagu M, Amaricai E, Haragus HG, Onofrei RR, Neagu A. Using A-Mode Ultrasound to Assess the Body Composition of Soccer Players: A Comparative Study of Prediction Formulas. Diagnostics. 2023; 13(4):690. https://doi.org/10.3390/diagnostics13040690
Chicago/Turabian StyleMuntean, Paul, Monica Neagu, Elena Amaricai, Horia G. Haragus, Roxana Ramona Onofrei, and Adrian Neagu. 2023. "Using A-Mode Ultrasound to Assess the Body Composition of Soccer Players: A Comparative Study of Prediction Formulas" Diagnostics 13, no. 4: 690. https://doi.org/10.3390/diagnostics13040690
APA StyleMuntean, P., Neagu, M., Amaricai, E., Haragus, H. G., Onofrei, R. R., & Neagu, A. (2023). Using A-Mode Ultrasound to Assess the Body Composition of Soccer Players: A Comparative Study of Prediction Formulas. Diagnostics, 13(4), 690. https://doi.org/10.3390/diagnostics13040690









