Microwave Near-Field Dynamical Tomography of Thorax at Pulmonary and Cardiovascular Activity
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dynamical Pulse 1D Tomography (Profiling)
2.1.1. Theory
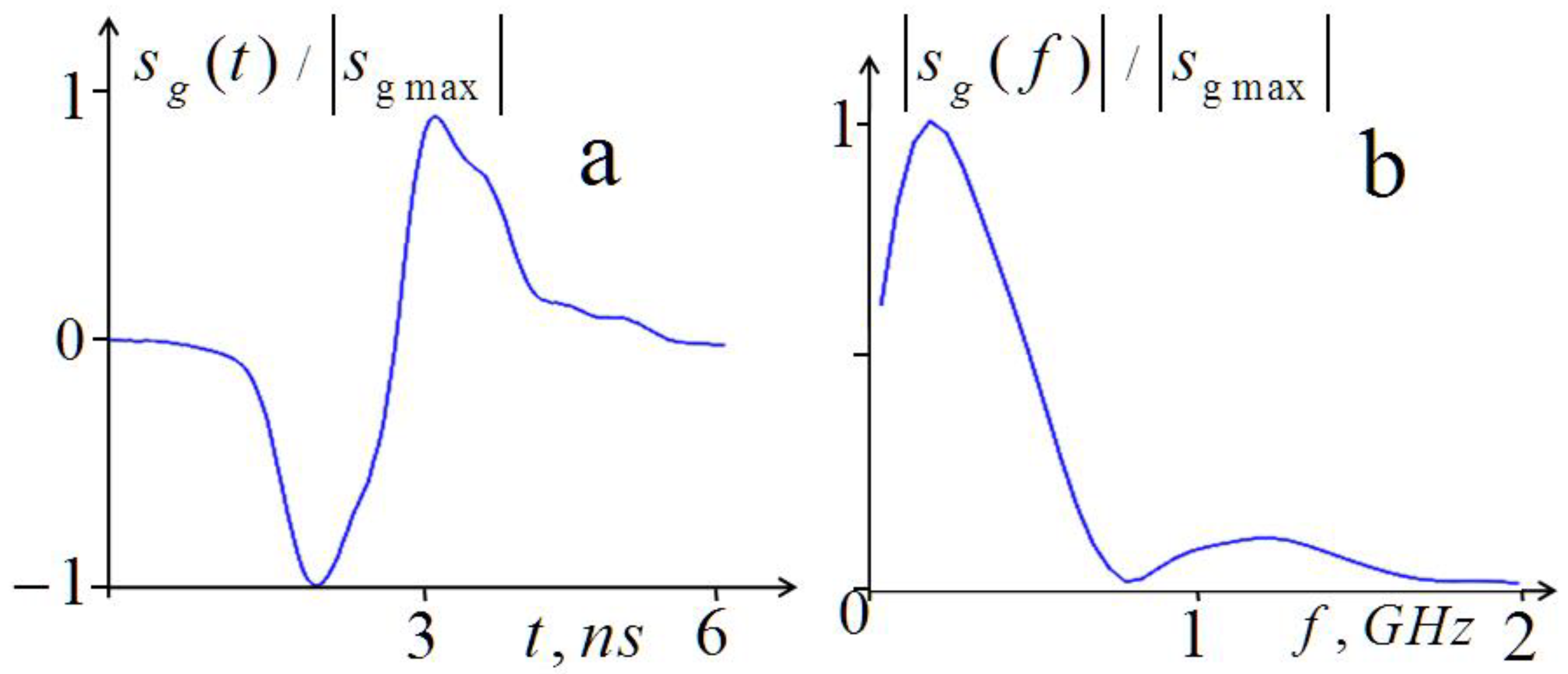
2.1.2. Numerical Simulation
- (a)
- Calculation of the received signal spectrum for the simulated five-layer structure in the exhalation phase;
- (b)
- Calculation of the corresponding scattered pulse ;
- (c)
- Adding simulated uncorrelated normally distributed random errors with rms that corresponded to that in the measured data;
- (d)
- Recalculating the pulse spectrum with errors;
- (e)
- Allocation of the informative analysis band outside the band of the more high-frequency spectrum of random errors;
- (f)
- Solving the inverse scattering problem (4) and comparison of the results with the preset structure .
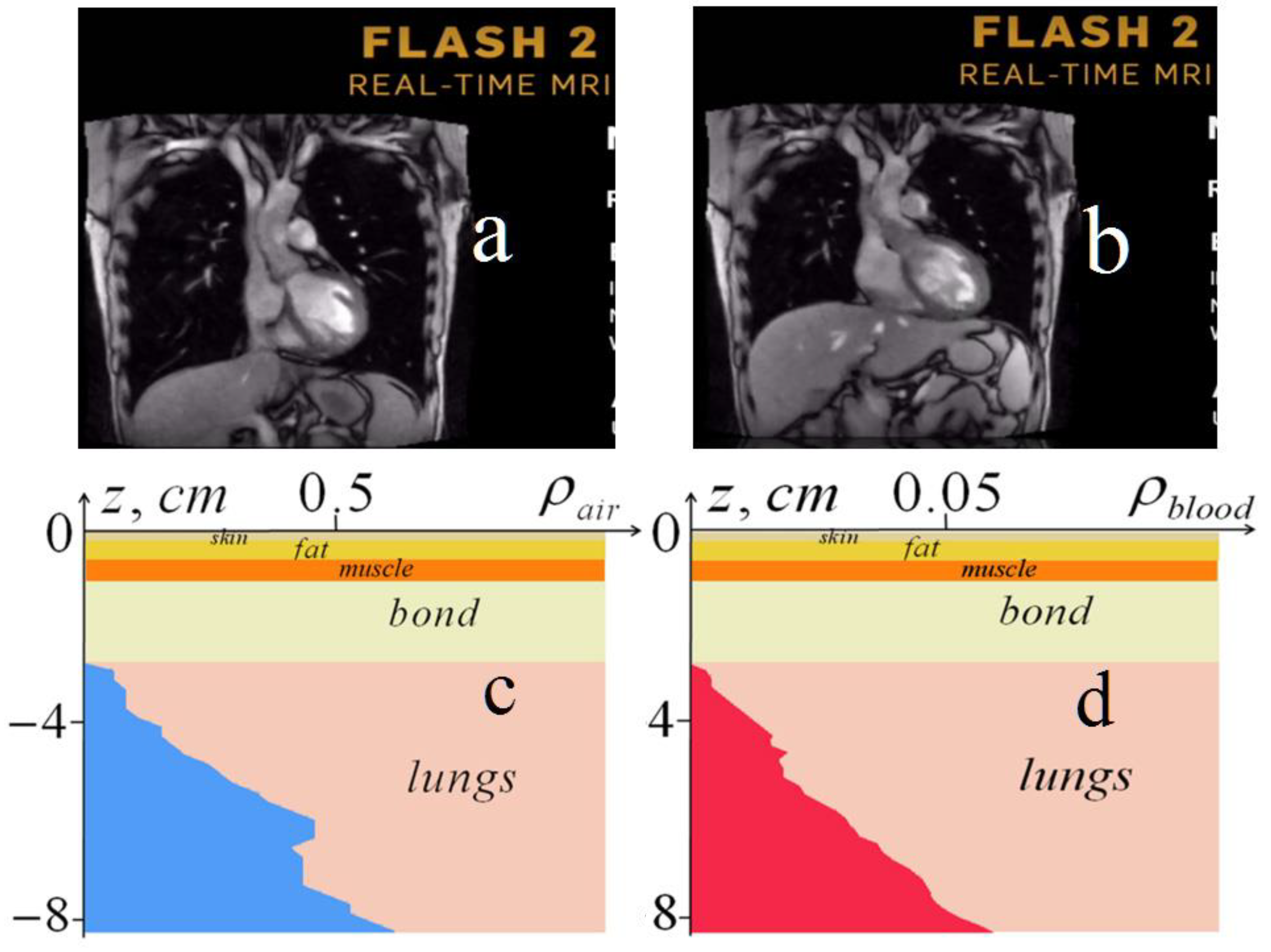
2.2. Methods of 3D Tomography
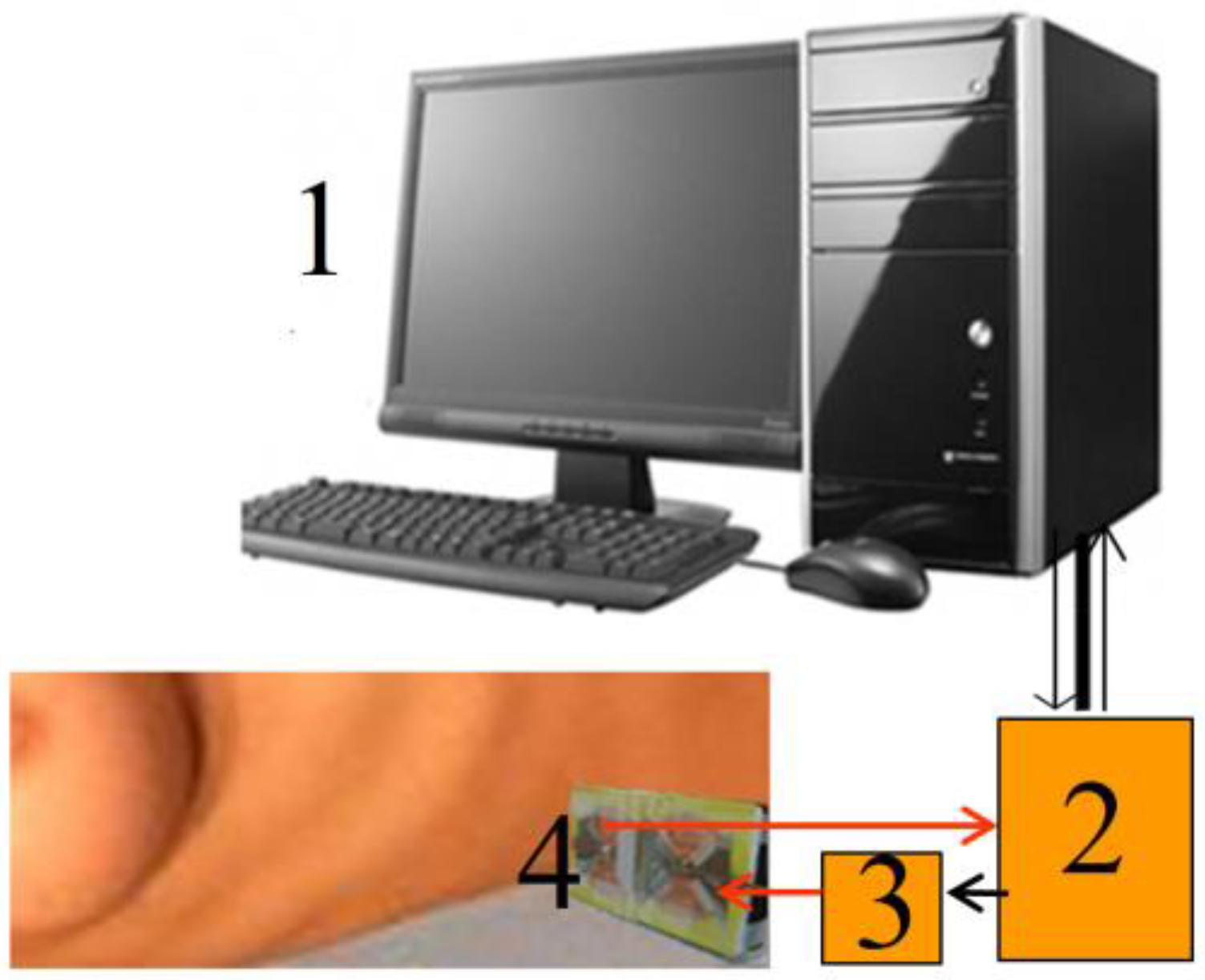
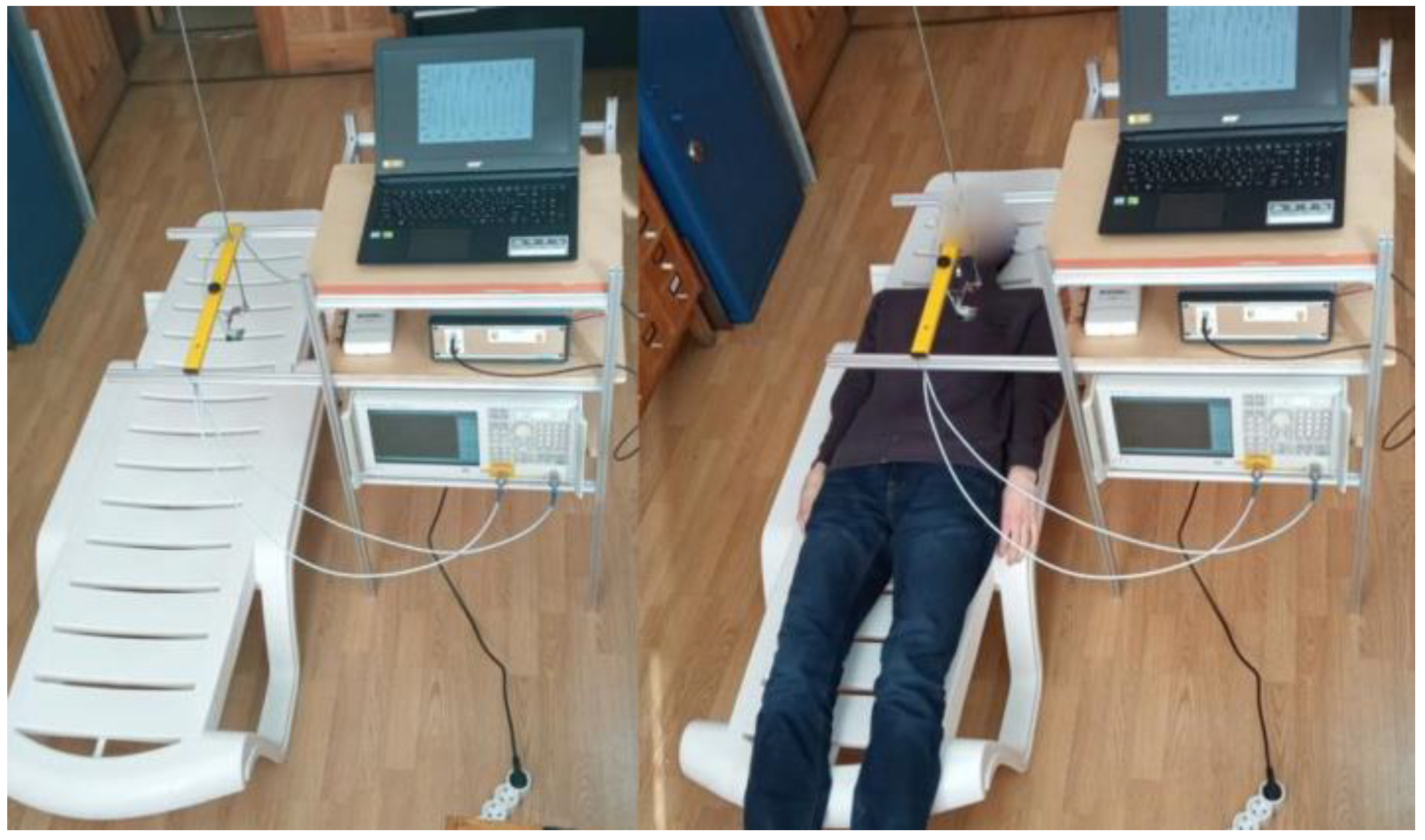
3. Experiment
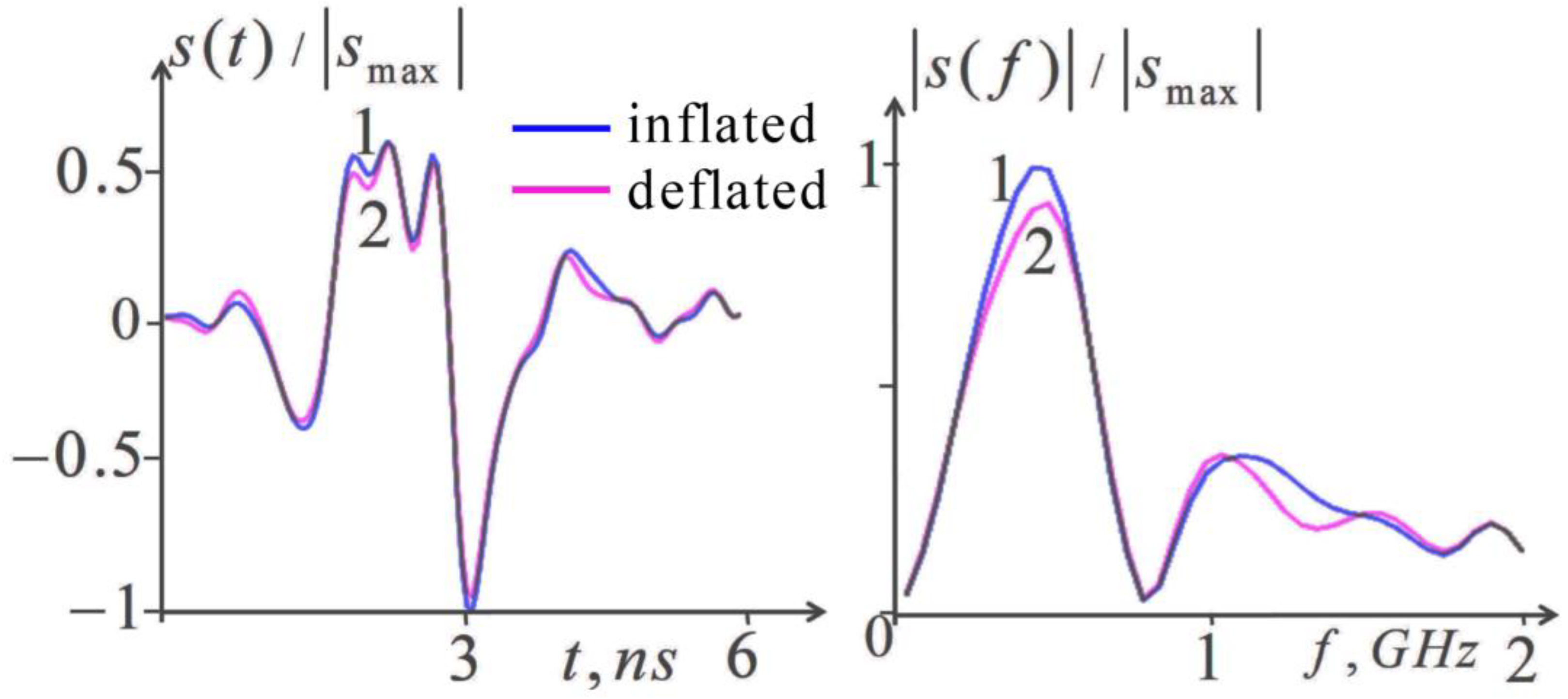
3.1. Dynamical Pulse 1D Tomography (Profiling)
3.2. Tomography Based on Multi-Position Profiling
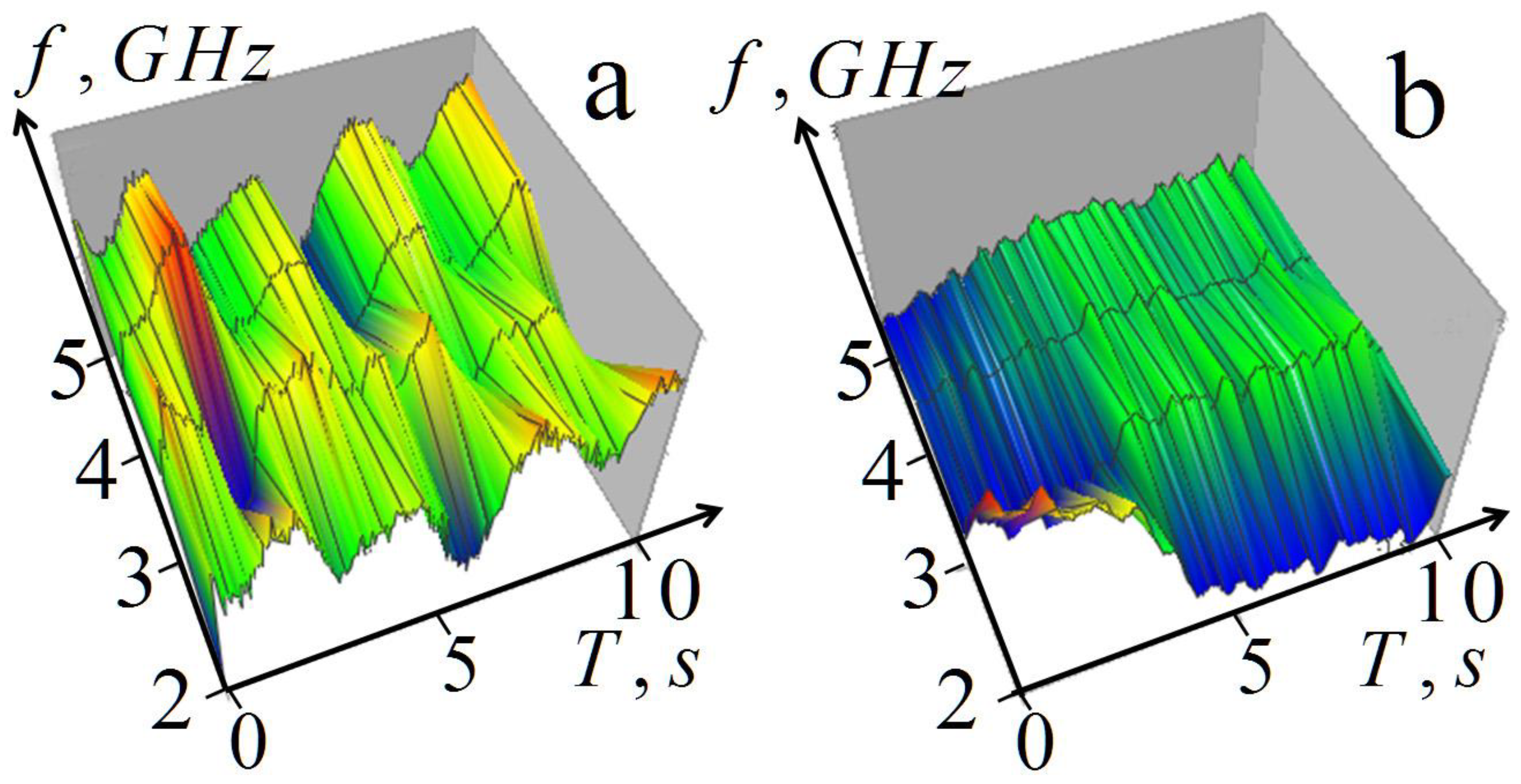
3.3. Multifrequency Observations of Breathing
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. One-Dimensional Diagnostics

Appendix A.2. Three-Dimensional Diagnostics
References
- Hagness, S.C.; Taflove, A.; Bridges, J.E. Two-dimensional FDTD analysis of a pulsed microwave confocal system for breast cancer detection: Fixed-focus and antenna-array sensors. IEEE Trans. Biomed. Eng. 1998, 45, 1470–1479. [Google Scholar] [CrossRef] [Green Version]
- Fear, E.C.; Li, X.; Hagness, S.C.; Stuchly, M.A. Confocal microwave imaging for breast cancer detection: Localization of tumors in three dimensions. IEEE Trans. Biomed. Eng. 2002, 49, 812–822. [Google Scholar] [CrossRef] [Green Version]
- Lim, H.B.; Nhung, N.T.; Li, E.; Thang, N.D. Confocal microwave imaging for breast cancer detection: Delay-multiply-and-sum image reconstruction algorithm. IEEE Trans. Biomed. Eng. 2008, 55, 1697–1704. [Google Scholar]
- Bucci, O.M.; Bellizzi, G.; Catapano, I.; Crocco, L.; Scapaticci, R. MNP enhanced microwave breast cancer imaging: Measurement constraints and achievable performances. IEEE Antennas Wirel. Propagat. Lett. 2012, 11, 1630–1633. [Google Scholar] [CrossRef]
- Azghani, M.; Kosmas, P.; Marvasti, F. Microwave Medical Imaging Based on Sparsity and an Iterative Method with Adaptive Thresholding. IEEE Trans. Med. Imaging 2015, 34, 357–365. [Google Scholar] [CrossRef] [Green Version]
- Ambrosanio, M.; Kosmas, P.; Pascazio, V. A Multithreshold Iterative DBIM-Based Algorithm for the Imaging of Heterogeneous Breast Tissues. IEEE Trans. Biomed. Eng. 2018, 66, 509–520. [Google Scholar] [CrossRef] [Green Version]
- Aldhaeebi, M.A.; Alzoubi, K.; Almoneef, T.S.; Bamatraf, S.M.; Attia, H.; Ramahi, O.M. Review of Microwaves Techniques for Breast Cancer Detection. Sensors 2020, 20, 2390. [Google Scholar] [CrossRef] [Green Version]
- AlSawaftah, N.; El-Abed, S.; Dhou, S.; Zakaria, A. Microwave Imaging for Early Breast Cancer Detection: Current State, Challenges, and Future Directions. J. Imaging 2022, 8, 123. [Google Scholar] [CrossRef]
- Greneker, E.F. Radar Sensing of Heartbeat and Respiration at a Distance with Security Applications. Proc. SPIE Radar Sens. Technol. II 1997, 3066, 22–27. [Google Scholar]
- Staderini, E.M. UWB radars in medicine. IEEE Aerosp. Electron. Syst. Mag. 2002, 17, 13–18. [Google Scholar] [CrossRef]
- Jelen, M.; Biebl, E.M. Multi-frequency sensor for remote measurement of breath and heartbeat. Adv. Radio Sci. 2006, 4, 79–83. [Google Scholar] [CrossRef]
- Soldovieri, F.; Catapano, I.; Crocco, L.; Anishchenko, L.N.; Ivashov, S.I. A Feasibility Study for Life Signs Monitoring via a Continuous-Wave Radar. Int. J. Antennas Propag. 2012, 2012, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Mostov, K.; Liptsen, E.; Boutchko, R. Medical applications of shortwave FM radar: Remote monitoring of cardiac and respiratory motion. Med. Phys. 2010, 37, 1332–1338. [Google Scholar] [CrossRef] [Green Version]
- Lv, H.; Lu, G.H.; Jing, X.J.; Wang, J.Q. A new ultra-wideband radar for detecting survivors buried under earthquake rubbles. Microw. Opt. Technol. Lett. 2010, 52, 2621–2634. [Google Scholar] [CrossRef]
- Anishchenko, L.; Gennarelli, G.; Tataraidze, A.; Gaysina, E.; Soldovieri, F.; Ivashov, S. Evaluation of rodents’ respiratory activity using a bioradar. IET Radar Sonar Navig. 2015, 9, 1296–1302. [Google Scholar] [CrossRef]
- Purnomo, A.T.; Lin, D.-B.; Adiprabowo, T.; Fitra Hendria, W.F. Non-Contact Monitoring and Classification of Breathing Pattern for the Supervision of People Infected by COVID-19. Sensors 2021, 21, 3172. [Google Scholar] [CrossRef]
- Yu, H.; Huang, W.; Du, B. SSA-VMD for UWB Radar Sensor Vital Sign Extraction. Sensors 2023, 23, 756. [Google Scholar] [CrossRef]
- Iskander, M.F.; Durney, C.H.; Shoff, D.J.; Bragg, D.G. Diagnosis of pulmonary edema by a surgically noninvasive microwave technique. Radio Sci. 1979, 14, 265–269. [Google Scholar] [CrossRef]
- Celik, N.; Gagarin, R.; Youn, H.S.; Iskander, M.F. A Non-Invasive microwave sensor and signal processing technique for continuous monitoring of vital signs. IEEE Antenn. Wirel. Propag. Lett. 2011, 10, 286–289. [Google Scholar] [CrossRef]
- Celik, N.; Gagarin, R.; Huang, G.C. Microwave stethoscope: Development and Benchmarking of a vital signs sensor using computer-controlled Phantoms and human studies. IEEE Trans. Biomed. Eng. 2014, 61, 2341–2349. [Google Scholar] [CrossRef]
- Perron, R.R.G.; Iskander, M.F.; Seto, T.B.; Huang, G.C.; Bibb, D.A. Electromagnetics in Medical Applications: The Cardiopulmonary Stethoscope Journey. In The World of Applied Electromagnetics; Lakhtakia, A., Furse, C., Eds.; Springer: Cham, Switzerland, 2018; Chapter 18; pp. 443–479. [Google Scholar]
- Pohl, D.W.; Denk, W.; Lanz, M. Optical stethoscopy: Image recording with resolution λ/20. Appl. Phys. Lett. 1984, 44, 651–653. [Google Scholar] [CrossRef]
- Gaikovich, K.P.; Sumin, M.I.; Troitskii, R.V. Determination of internal temperature profiles by multifrequency radiothermography in medical applications. Radiophys. Quantum Electron. 1988, 31, 786–793. [Google Scholar] [CrossRef]
- Gaikovich, K.P.; Reznik, A.N.; Vaks, V.L.; Yurasova, N.V. New effect in near-field thermal emission. Phys. Rev. Lett. 2002, 88, 104302. [Google Scholar] [CrossRef]
- Gaikovich, K.P. Inverse Problems in Physical Diagnostics; Nova Science Publishers Inc.: New York, NY, USA, 2004. [Google Scholar]
- Gaikovich, K.P. Subsurface near-field scanning tomography. Phys. Rev. Lett. 2007, 98, 183902. [Google Scholar] [CrossRef]
- Gaikovich, K.P.; Gaikovich, P.K. Inverse problem of near-field scattering in multilayer media. Inverse Probl. 2010, 26, 125013. [Google Scholar] [CrossRef] [Green Version]
- Gaikovich, K.P.; Gaikovich, P.K.; Maksimovitch, Y.S.; Badeev, V.A. Pseudopulse near-field subsurface tomography. Phys. Rev. Lett. 2012, 108, 163902. [Google Scholar] [CrossRef]
- Gaikovich, K.P.; Gaikovich, P.K.; Maksimovitch, Y.S.; Badeev, V.A. Subsurface near-field microwave holography. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 74–82. [Google Scholar] [CrossRef]
- Gaikovich, K.P.; Gaikovich, P.K.; Maksimovitch, Y.S.; Smirnov, A.I.; Sumin, M.I. Dual regularization in non-linear inverse scattering problems. Inv. Probl. Sci. Eng. 2016, 24, 1215–1239. [Google Scholar] [CrossRef]
- Gaikovich, K.P.; Maksimovitch, Y.S.; Sumin, M.I. Inverse scattering problems of near-field subsurface pulse diagnostics. Inverse Probl. Sci. Eng. 2018, 26, 1590–1611. [Google Scholar] [CrossRef]
- Gaikovich, K.P. Left-handed lens tomography and holography. Inverse Probl. Sci. Eng. 2020, 28, 296–313. [Google Scholar] [CrossRef]
- Gaikovich, K.P.; Maksimovitch, Y.S.; Badeev, V.A. Near-field subsurface tomography and holography based on bistatic measurements with variable base. Inverse Probl. Sci. Eng. 2021, 29, 663–680. [Google Scholar] [CrossRef]
- Gabriel, C. Report N.AL/OE-TR-1996-0037; Occupational and Environmental Health Directorate, Radiofrequency Radiation Division; Brooks Air Force Base: San Antonio, TX, USA, 1996. [Google Scholar]
- Sihvola, A. Mixing Rules with Complex Dielectric Coefficients. Subsurf. Sens. Technol. Appl. 2000, 1, 393–415. [Google Scholar] [CrossRef]
- Kin, K.M.; Hwee, M.C. Learning and Teaching Tools for Basic and Clinical Respiratory Physiology (Springer Briefs in Physiology), 2015th ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Hirsch, F.W.; Frahm, J.; Sorge, I. Real-time magnetic resonance imaging in pediatric radiology—New approach to movement and moving children. Pediatr. Radiol. 2021, 51, 840–846. [Google Scholar] [CrossRef]
- Frahm, J. Our Body in Motion—MRI Movies in Real Time. Available online: https://www.youtube.com/watch?v=iS4VPB5IVD8Science (accessed on 19 January 2023).
- Weissman, C. Pulmonary complications after cardiac surgery. Semin. Cardiothorac. Vasc. Anesth. 2004, 8, 185–211. [Google Scholar] [CrossRef]
- Samir, A.; Elabd, A.M.; Mohamed, W.; Baess, A.I.; Sweed, R.A.; Abdelgawad, M.S. COVID-19 in Egypt after a year: The first and second pandemic waves from the radiological point of view; multi-center comparative study on 2000 patients Egyptian. J. Radiol. Nucl. Med. 2021, 52, 168. [Google Scholar] [CrossRef]
- Huang, Y.; Tan, C.; Wang, Z. Impact of coronavirus disease 2019 on pulmonary function in early convalescence phase. Respir. Res. 2020, 21, 163. [Google Scholar] [CrossRef]
- Ibrani, M.; Alma, L.; Hamiti, E. The Age-Dependence of Microwave Parameters of Biological Tissues. In Microwave Materials Characterization; Costanzo, S., Ed.; IntechOpen: London, UK, 2012; Chapter 9. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaikovich, K.P.; Maksimovitch, Y.S.; Badeev, V.A.; Bockeria, L.A.; Djitava, T.G.; Kakuchaya, T.T.; Kuular, A.M. Microwave Near-Field Dynamical Tomography of Thorax at Pulmonary and Cardiovascular Activity. Diagnostics 2023, 13, 1051. https://doi.org/10.3390/diagnostics13061051
Gaikovich KP, Maksimovitch YS, Badeev VA, Bockeria LA, Djitava TG, Kakuchaya TT, Kuular AM. Microwave Near-Field Dynamical Tomography of Thorax at Pulmonary and Cardiovascular Activity. Diagnostics. 2023; 13(6):1051. https://doi.org/10.3390/diagnostics13061051
Chicago/Turabian StyleGaikovich, Konstantin P., Yelena S. Maksimovitch, Vitaly A. Badeev, Leo A. Bockeria, Tamara G. Djitava, Tea T. Kakuchaya, and Arzhana M. Kuular. 2023. "Microwave Near-Field Dynamical Tomography of Thorax at Pulmonary and Cardiovascular Activity" Diagnostics 13, no. 6: 1051. https://doi.org/10.3390/diagnostics13061051
APA StyleGaikovich, K. P., Maksimovitch, Y. S., Badeev, V. A., Bockeria, L. A., Djitava, T. G., Kakuchaya, T. T., & Kuular, A. M. (2023). Microwave Near-Field Dynamical Tomography of Thorax at Pulmonary and Cardiovascular Activity. Diagnostics, 13(6), 1051. https://doi.org/10.3390/diagnostics13061051






