Advancing Kidney Transplantation: A Machine Learning Approach to Enhance Donor–Recipient Matching
Abstract
:1. Introduction
- The development of a ML-based approach for kidney donor–recipient matching as an alternative to traditional points-based allocation systems.
- The incorporation of a custom ranking algorithm to identify the most suitable recipient for each donor, potentially improving matching efficiency and outcomes.
- Nephron is a web-based platform integrating the ML model. Nephron facilitates efficient patient selection and prioritisation, potentially providing wider applications for solid organ allocation beyond the kidneys.
- The successful implementation of the ML-based approach demonstrates its potential to enhance kidney allocation efficiency and fairness, which are crucial factors given the global shortage of kidney donors.
2. Materials and Methods
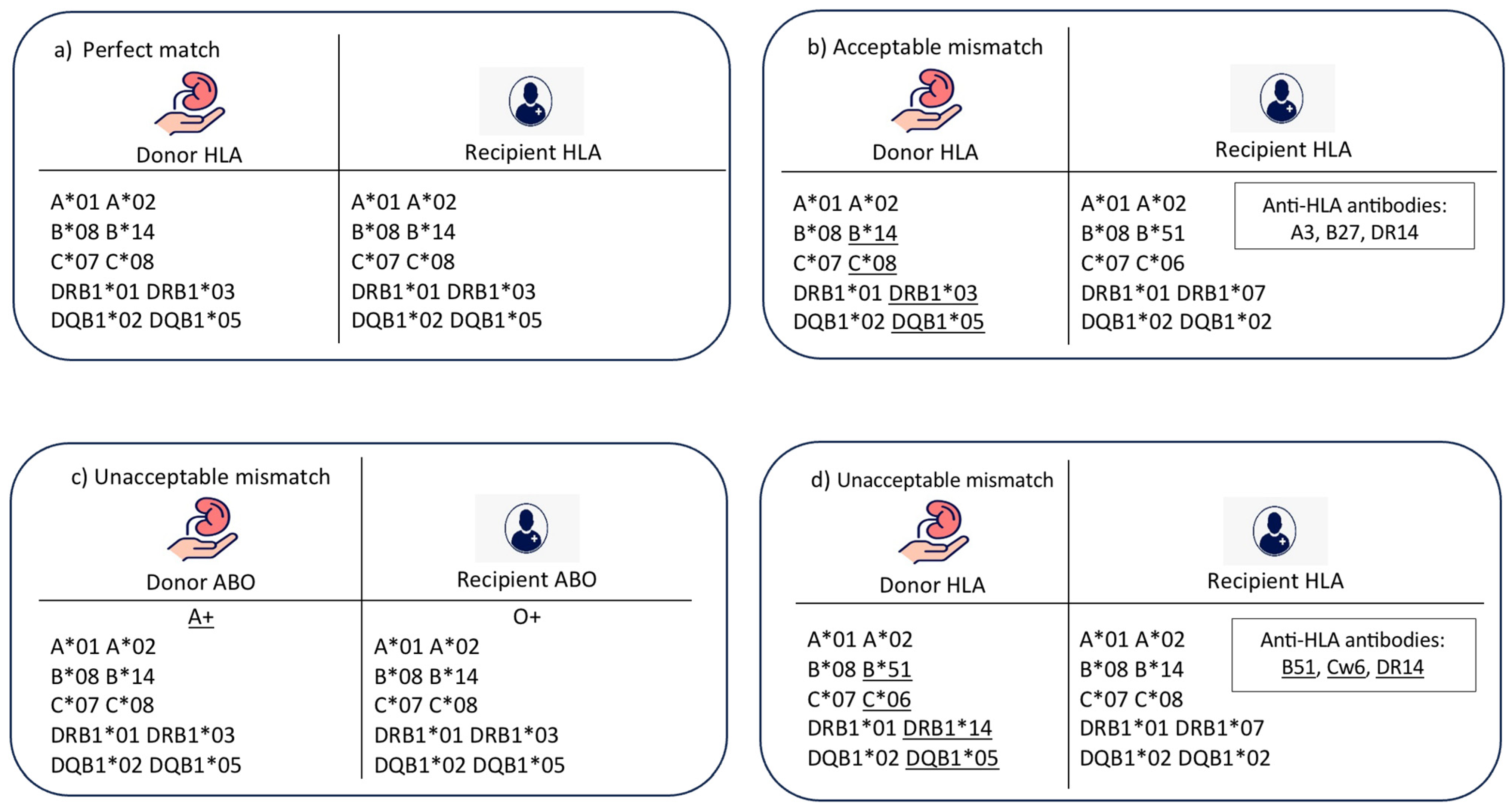
2.1. Dataset Description
- (1)
- (2)
- Acceptable mismatch (Figure 1b): In this case, there is an HLA mismatch between donor and recipient in the absence of donor-specific HLA antibodies. There is a compatibility in ABO blood group, and the age difference between donor and recipient is less than 20 years.
- (3)
- Unacceptable mismatch due to ABO blood group mismatch (Figure 1c): In this case, there is a mismatch between donor and recipient ABO blood groups, which is a contradiction to transplantation. No further matching assessment is required.
- (4)
- Unacceptable mismatch due to donor-specific HLA antibodies (Figure 1d): In this category, there are HLA antibodies against donor HLA-A, B, C, DR, or DQ antigens. This assessment is performed for a compatible pair in terms of ABO blood group and age difference.
- (5)
- Unacceptable mismatch due to donor–recipient age mismatch: This category was included to resemble the longevity matching criteria between donor and recipient. The acceptable age difference can be adjusted according to the transplant centre’s preference; however, in this model, the acceptable age difference was adjusted to 20 years as an example.
2.2. Data Preprocessing
- (1)
- Dealing with duplicated and null values:To ensure the reliability and high performance of matching models, the dataset was examined for any duplicated or null values. Duplicate values were resolved by keeping only one instance, and any null values were replaced with the average of observed features related to a corresponding case. Thoroughly selecting suitable replacements guaranteed dataset consistency and suitability for training models.
- (2)
- Encoding of categorical values:All features, except for recipient and donor age, consisted of categorical values that necessitated transformation to numerical representations. A one-hot encoder was used to encode blood groups, with a value of one being assigned, and all other categories were assigned zero. The remaining categorical features were converted by parsing their values and extracting numerical values from their categorical representations. An HLA value was typically represented using a combination of letters and digits. In this research, the value was converted to a numerical representation equal to its digit part. For example, A*04 was transformed to the numerical value 4. Likewise, an anti-HLA value was represented by a letter followed by digits and was converted to a numerical value equal to its digit part. For instance, B12 was converted to the numerical value 12.
2.3. Development of Matching Models
- (1)
- Logistic regression (LR) classifier: This linear model assumes a linear relationship between features and the log-odds of a target variable. Its performance was tuned using a grid search technique [38]. Evaluated hyperparameters include the choice of the solver (‘lbfgs’), the number of classes (‘multinomial’), regularisation types (‘l1’ and ‘l2’), and regularisation strength C (0.1, 1, 10). The option to include an intercept term was also explored using ‘True’ and ‘False’ values for the ‘fit_intercept’ parameter.
- (2)
- Decision tree (DT) classifier: This tree-like structure makes decisions based on features by recursively partitioning the data based on different attributes and creates a set of rules for classification [39]. It was tuned with the following hyperparameters: maximum depth (10, 20, 30), maximum features (None, ‘sqrt’, ‘log2’), minimum samples per leaf (1, 2, 4), and minimum samples per split (2, 5, 10).
- (3)
- Random forest (RF) classifier: This ensemble learning algorithm combines multiple decision trees to improve classification accuracy [40]. The following hyperparameters were tuned using grid search: number of trees in the forest (100, 500, 1000), minimum samples required to split an internal node (2, 5, 10), minimum samples required at each leaf node (1, 2, 4), maximum number of features considered for splitting (‘auto’, ‘sqrt’), maximum depth of the tree (None, 10, 20, 30), and bootstrapping option (True, False).
- (4)
- Support vector machine (SVM) classifier: This classifier finds an optimal hyperplane to separate data points into different classes by maximising the distance between the hyperplane and the nearest data points of each class [41]. It can handle both linear and non-linear data using different kernel functions. It was tuned with the following hyperparameters: regularisation parameter C (1, 10, 15) and kernel coefficient gamma (‘scale’, ‘auto’, 0.1, 1).
- (5)
- Gradient boosting (GB) classifier: This classifier combines multiple weak prediction models, typically decision trees, to create a strong predictive model. It works by sequentially adding new models that correct the errors made by the previous models [42]. The optimised hyperparameters included the number of estimators (100, 200, 300), learning rate (0.1, 0.2, 0.3), and maximum depth (4, 6, 8).
- (6)
- eXtreme gradient boosting (XGBoost) classifier: Similar to GB, XGBoost is a gradient boosting algorithm that iteratively adds weak prediction models and combines their predictions. However, XGBoost leverages parallel processing for significantly faster training on large datasets compared to GB, whose sequential training leads to slower execution times [43]. The following hyperparameters were tuned using grid search: gamma (0.1, 0.2, 0.3), learning rate (0.01, 0.1, 0.2), max depth (4, 6, 8), and number of estimators (100, 200, 300).
- (7)
- The CatBoost (CB) classifier: This gradient boosting algorithm excels in handling categorical features. It automatically encodes categorical variables and incorporates advanced techniques for improved performance and efficiency [44]. Grid search was used to tune its hyperparameters for optimal performance: depth (3, 4, 5), iterations (1000, 2000, 3000), and learning rate (0.01, 0.1, 0.2).
- (8)
- LightGBM (LGBM) classifier: This gradient boosting framework is known for its high speed and efficiency in handling large datasets [45]. It employs a unique decision tree growth approach that focuses on leafs rather than entire levels. Grid search was used to tune the following hyperparameters: learning rate: (0.01, 0.1, 0.2) and number of estimators (100, 200, 300).
- (9)
- The naive Bayes (NB) classifier: This algorithm is based on Bayes’ theorem and operates under the assumption of independence between features [46]. It calculates the probability of a data point belonging to a class based on the probabilities of its individual features. Unlike the previous models discussed, naive Bayes was trained without any hyperparameter tuning.
- (10)
- Neural network (NN) classifier: This classifier is inspired by the structure and function of the human brain. It consists of interconnected neurons organised into layers. Each neuron performs a simple computation (weighted sum of its inputs) and passes the result to the next layer using a non-linear activation function [47]. The performance of the neural network was optimised by exploring different hyperparameters: dropout values (0.5, 0.3, 0.35, 0.2), hidden neuron combinations, learning rates (0.001, 0.01, 0.1), and the number of epochs (1000, 1100, 1200, 1500, 2000).
2.4. Performance Evaluation
- (1)
- Accuracy: This is the percentage of instances successfully predicted out of all instances. It evaluates the overall performance of the model’s predictions [48]:
- True Positive (TP) is the number of instances in which the model correctly predicted a positive class;
- False Positive (FP) is the number of instances in which the model incorrectly predicted a positive class (Type I error);
- True Negative (TN) is the number of instances in which the model correctly predicted a negative class;
- False Negative (FN) is the number of instances in which the model incorrectly predicted a negative class (Type II error).
- (2)
- Precision: This is the percentage of accurate positive predictions, or true positive cases, out of all positive predictions made by the model. It assesses the accuracy of the model in correctly identifying positive outcomes [48]:
- (3)
- Recall: This is the proportion of genuine positive predictions (positive instances that were accurately predicted) to all actual positive instances, also known as the sensitivity or true positive rate. It evaluates how well the model can identify each good occurrence [48]:
- (4)
- F1-score: This is the harmonic mean of recall and precision. When both false positives and false negatives are considered, it offers a balance between precision and recall. It measures the compromise between recall and precision [48]:
3. Experiments and Results Discussion
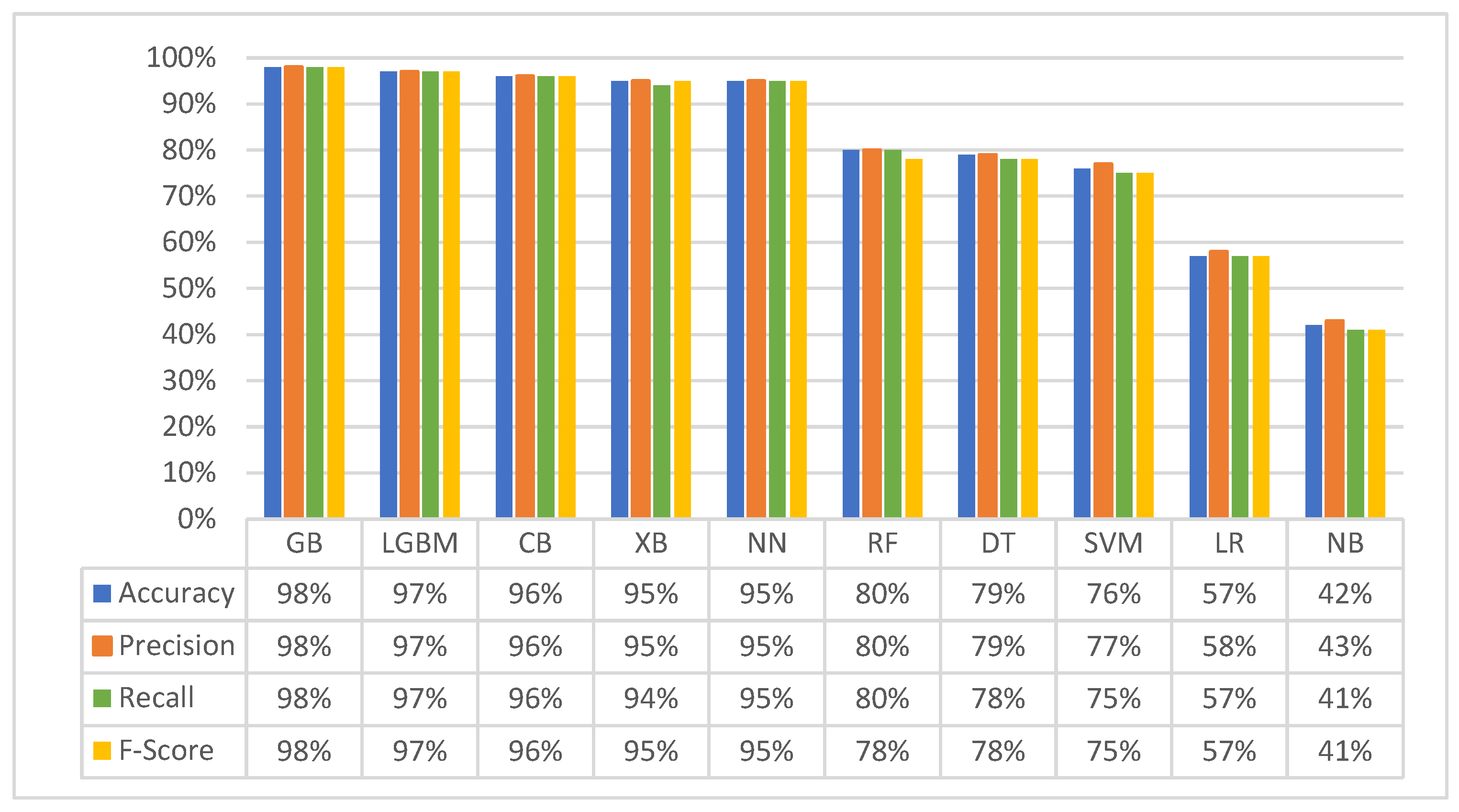
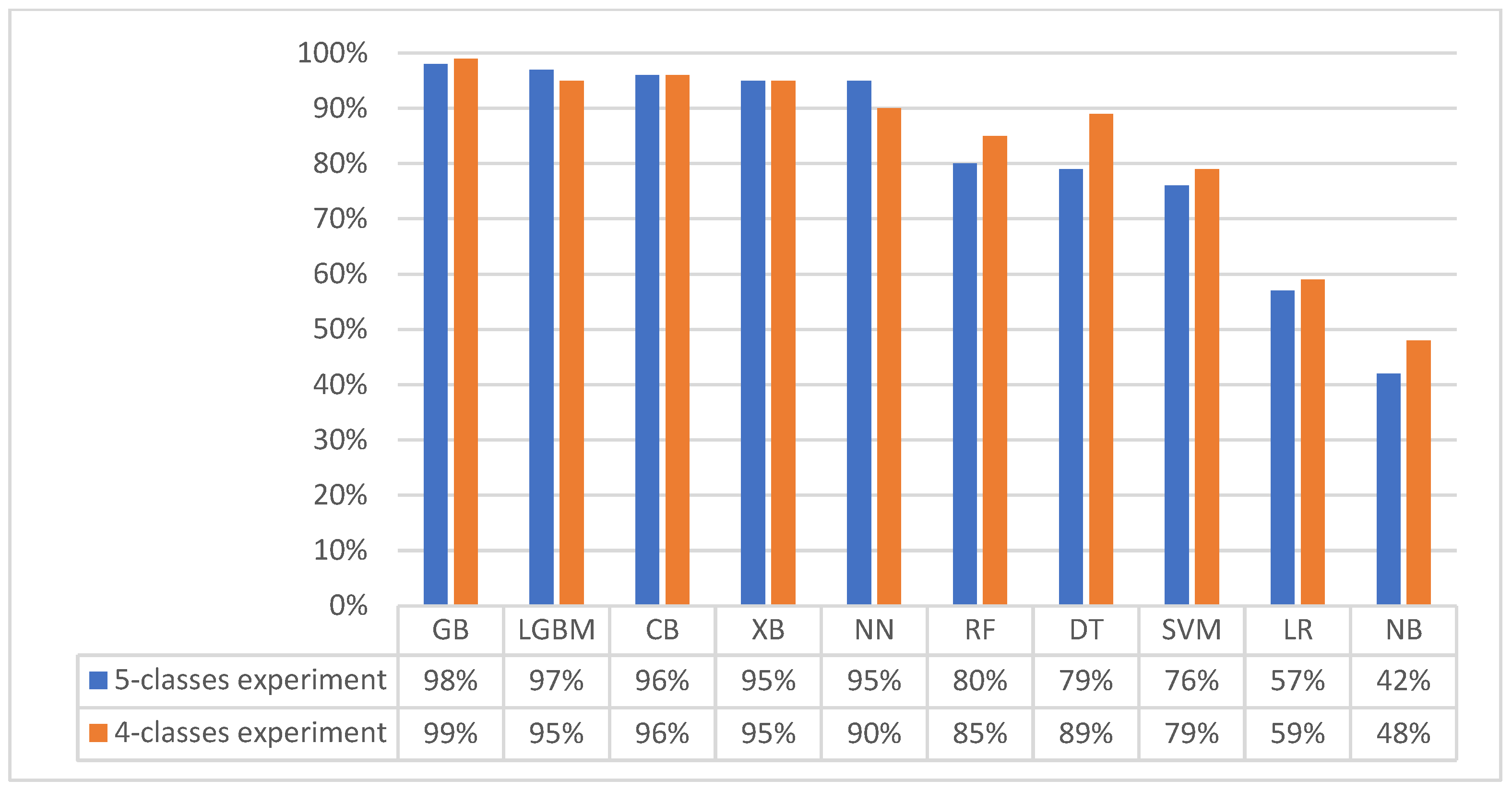
3.1. First Experiment (Baseline Original Dataset): Classification with Five Matching Classes
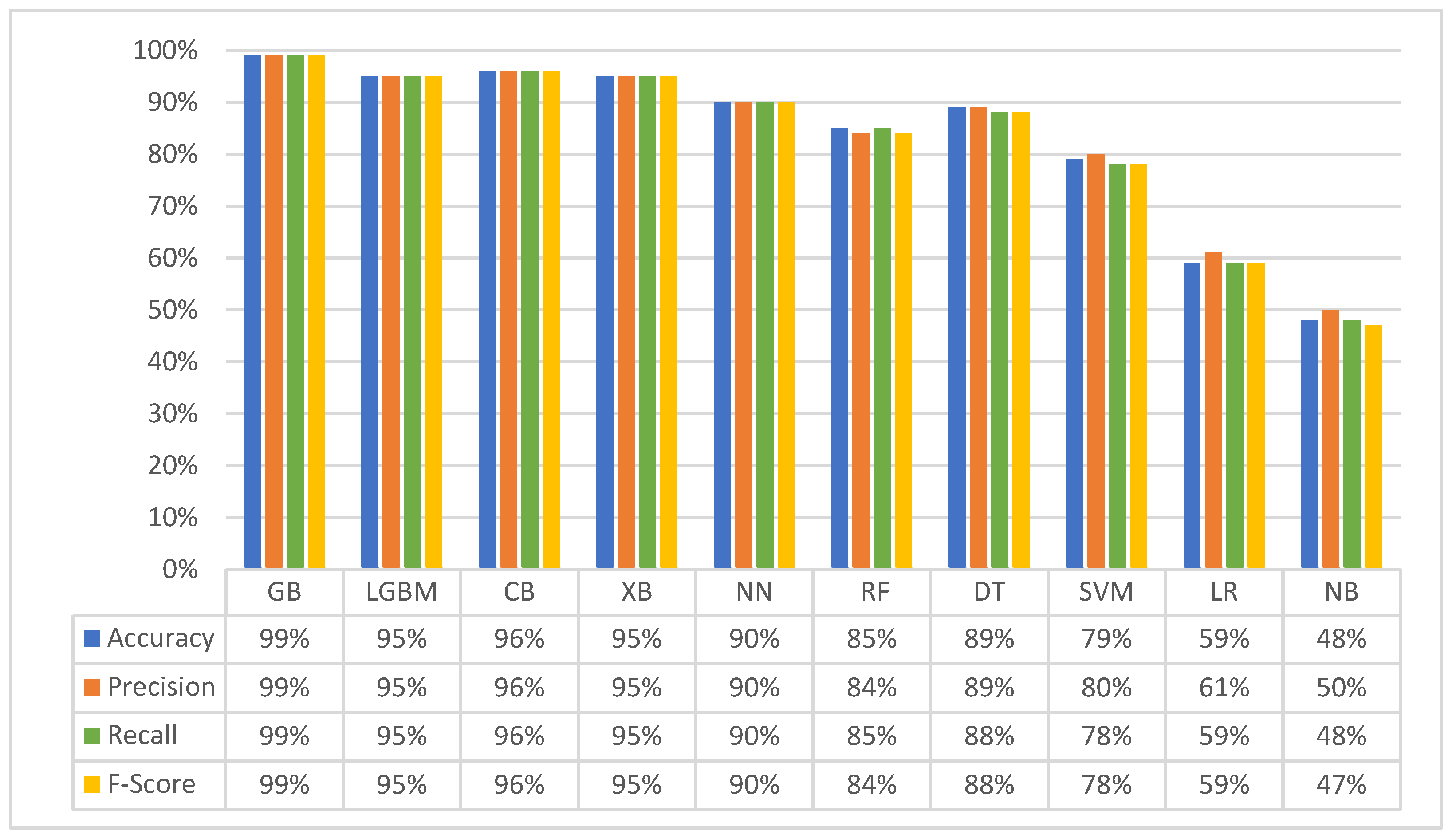
3.2. Second Experiment (Merged Dataset): Classification with Four Matching Classes
3.3. Third Experiment: Hierarchical Model
- Component one: blood compatibilityThis component evaluates blood compatibility. If blood groups are incompatible, the result is classified as a mismatch due to incompatible blood group, and the process exits. If blood groups are compatible, the process proceeds to component two.
- Component two: age compatibilityThis component evaluates donor–recipient age compatibility. If the age difference falls outside the acceptable range (20 years), the data are classified as a “mismatch due to large age gap”, and the process exits. Otherwise, the process proceeds to component three.
- Component three: HLA compatibilityThis component assesses HLA compatibility. If the recipient possesses HLA antibodies that render the donor incompatible, the data are classified as a “mismatch due to antibodies”, and the process exits. Conversely, if the recipient lacks such antibodies, and the HLA match is suitable, the data are classified as an “acceptable match”, and the process exits.
4. Automated Ranking for Efficient Donor–Recipient Matching
4.1. Cosine Similarity
4.2. Jaccard Similarity
4.3. Custom Similarity Ranking Algorithm
| Require: Donor HLAs, Patient HLAs | |
|---|---|
| Ensure: Percentage of HLA similarity | |
| 1: | Initialize SimilarityPercentage to 0 |
| 2: | for each hla in Donor HLAs do |
| 3: | if hla in Patient_HLAs then |
| 4: | Increment SimilarityPercentage by 1 |
| 5: | end if |
| 6: | end for |
| 7: | Calculate Percentage as |
| 8: | Output Percentage |
5. Introducing Nephron: A Web-Based Platform for Expert Evaluation of the Intelligent Donor–Recipient Matching System
6. Assessment of Nephron Platform Functionality
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Strohmaier, S.; Wallisch, C.; Kammer, M.; Geroldinger, A.; Heinze, G.; Oberbauer, R.; Haller, M.C. Survival Benefit of First Single-Organ Deceased Donor Kidney Transplantation Compared with Long-term Dialysis Across Ages in Transplant-Eligible Patients with Kidney Failure. JAMA Netw. Open 2022, 5, e2234971. [Google Scholar] [CrossRef]
- Yang, F.; Liao, M.; Wang, P.; Yang, Z.; Liu, Y. The Cost-Effectiveness of Kidney Replacement Therapy Modalities: A Systematic Review of Full Economic Evaluations. Appl. Health Econ. Health Policy 2021, 19, 163–180. [Google Scholar] [CrossRef]
- Howard, K.; Salkeld, G.; White, S.; McDonald, S.; Chadban, S.; Craig, J.C.; Cass, A. The cost-effectiveness of increasing kidney transplantation and home-based dialysis. Nephrology 2009, 14, 123–132. [Google Scholar] [CrossRef]
- Liyanage, T.; Ninomiya, T.; Jha, V.; Neal, B.; Patrice, H.M.; Okpechi, I.; Zhao, M.-H.; Lv, J.; Garg, A.X.; Knight, J.; et al. Worldwide access to treatment for end-stage kidney disease: A systematic review. Lancet 2015, 385, 1975–1982. [Google Scholar] [CrossRef]
- Attar, B. Renal Replacement Therapy in the Kingdom of Saudi Arabia. Saudi J. Kidney Dis. Transplant. 2021, 32, 1188. [Google Scholar] [CrossRef]
- Gutmann, T.; Land, W. The ethics of organ allocation: The state of debate. Transplant. Rev. 1997, 11, 191–207. [Google Scholar] [CrossRef]
- Israni, A.K.; Salkowski, N.; Gustafson, S.; Snyder, J.J.; Friedewald, J.J.; Formica, R.N.; Wang, X.; Shteyn, E.; Cherikh, W.; Stewart, D.; et al. New national allocation policy for deceased donor kidneys in the United States and possible effect on patient outcomes. J. Am. Soc. Nephrol. 2014, 25, 1842–1848. [Google Scholar] [CrossRef]
- Watson, C.J.E.; Johnson, R.J.; Mumford, L. Overview of the Evolution of the UK Kidney Allocation Schemes. Curr. Transplant. Rep. 2020, 7, 140–144. [Google Scholar] [CrossRef]
- Persijn, G.G. Allocation of Organs, Particularly Kidneys, Within Eurotransplant. Human Immunol. 2006, 67, 419–423. [Google Scholar] [CrossRef]
- Lee, D.; Kanellis, J.; Mulley, W.R. Allocation of deceased donor kidneys: A review of international practices. Nephrology 2019, 24, 591–598. [Google Scholar] [CrossRef]
- Friedewald, J.J.; Turgeon, N. Early Experience with the New Kidney Allocation System: A Perspective from a Transplant Center. Clin. J. Am. Soc. Nephrol. 2017, 12, 2060–2062. [Google Scholar] [CrossRef]
- Lim, W.H.; Chang, S.; Chadban, S.; Campbell, S.; Dent, H.; Russ, G.R.; McDonald, S.P. Donor-recipient age matching improves years of graft function in deceased-donor kidney transplantation. Nephrol. Dial. Transplant. 2010, 25, 3082–3089. [Google Scholar] [CrossRef] [PubMed]
- Peters-Sengers, H.; Berger, S.P.; Heemskerk, M.B.A.; Al Arashi, D.; van der Heide, J.J.H.; Hemke, A.C.; Berge, I.J.M.T.; Idu, M.M.; Betjes, M.G.H.; van Zuilen, A.D.; et al. Stretching the Limits of Renal Transplantation in Elderly Recipients of Grafts from Elderly Deceased Donors. J. Am. Soc. Nephrol. 2017, 28, 621–631. [Google Scholar] [CrossRef] [PubMed]
- Jay, C.L.; Washburn, K.; Dean, P.G.; Helmick, R.A.; Pugh, J.A.; Stegall, M.D. Survival Benefit in Older Patients Associated With Earlier Transplant With High KDPI Kidneys. Transplantation 2017, 101, 867–872. [Google Scholar] [CrossRef] [PubMed]
- Rose, C.; Sun, Y.; Ferre, E.; Gill, J.; Landsberg, D.; Gill, J. An Examination of the Application of the Kidney Donor Risk Index in British Columbia. Can. J. Kidney Health Dis. 2018, 5, 2054358118761052. [Google Scholar] [CrossRef] [PubMed]
- Chamsi-Pasha, H.; Albar, M.A. Kidney transplantation: Ethical challenges in the Arab world. Saudi J. Kidney Dis. Transpl. 2014, 25, 489–495. [Google Scholar] [CrossRef]
- Gramlick, M.E.; Trevillian, P.; Palazzi, K.L.; Heer, M.K. Time to Move on: HLA Matching Should Be Reconsidered in Modern Deceased Donor Kidney Allocation. Transpl. Direct 2022, 8, e1295. [Google Scholar] [CrossRef]
- Barker, D.J.; Maccari, G.; Georgiou, X.; Cooper, M.A.; Flicek, P.; Robinson, J.; Marsh, S.G.E. The IPD-IMGT/HLA Database. Nucleic Acids Res. 2023, 51, D1053–D1060. [Google Scholar] [CrossRef] [PubMed]
- Erlich, H.A.; Opelz, G.; Hansen, J. HLA DNA Typing and Transplantation. Immunity 2001, 14, 347–356. [Google Scholar] [CrossRef]
- Takemoto, S.; Port, F.K.; Claas, F.H.J.; Duquesnoy, R.J. HLA matching for kidney transplantation. Human Immunol. 2004, 65, 1489–1505. [Google Scholar] [CrossRef]
- Hafeez, M.S.; Awais, S.B.; Razvi, M.; Bangash, M.H.; Hsiou, D.A.; Malik, T.H.; Haq, M.U.; Awan, A.A.Y.; Rana, A.A. HLA mismatch is important for 20-year graft survival in kidney transplant patients. Transpl. Immunol. 2023, 80, 101861. [Google Scholar] [CrossRef] [PubMed]
- Williams, R.C.; Opelz, G.; McGarvey, C.J.; Weil, E.J.; Chakkera, H.A. The Risk of Transplant Failure With HLA Mismatch in First Adult Kidney Allografts From Deceased Donors. Transplantation 2016, 100, 1094–1102. [Google Scholar] [CrossRef] [PubMed]
- Nieto-Ríos, J.F.; Ochoa-García, C.L.; Serna-Campuzano, A.; Benavides-Hermosa, B.; Calderón-Puentes, L.L.; Aristizabal-Alzate, A.; Ocampo-Kohn, C.; Zuluaga-Valencia, G.; Serna-Higuita, L.M. Time of Cold Ischemia and Delayed Graft Function in a Cohort of Renal Transplant Patients in a Reference Center. Indian J. Nephrol. 2019, 29, 8–14. [Google Scholar] [PubMed]
- Rajkomar, A.; Dean, J.; Kohane, I. Machine Learning in Medicine. N. Engl. J. Med. 2019, 380, 1347–1358. [Google Scholar] [CrossRef] [PubMed]
- Amisha; Malik, P.; Pathania, M.; Rathaur, V.K. Overview of artificial intelligence in medicine. J. Family Med. Prim. Care 2019, 8, 2328–2331. [Google Scholar] [CrossRef]
- Naruka, V.; Rad, A.A.; Ponniah, H.S.; Francis, J.; Vardanyan, R.; Tasoudis, P.; Magouliotis, D.E.; Lazopoulos, G.L.; Salmasi, M.Y.; Athanasiou, T. Machine learning and artificial intelligence in cardiac transplantation: A systematic review. Artif. Organs 2022, 46, 1741–1753. [Google Scholar] [CrossRef]
- Bertsimas, D.; Kung, J.; Trichakis, N.; Wang, Y.; Hirose, R.; Vagefi, P.A. Development and validation of an optimized prediction of mortality for candidates awaiting liver transplantation. Am. J. Transplant. 2019, 19, 1109–1118. [Google Scholar] [CrossRef]
- Gholamzadeh, M.; Abtahi, H.; Safdari, R. Machine learning-based techniques to improve lung transplantation outcomes and complications: A systematic review. BMC Med. Res. Methodol. 2022, 22, 331. [Google Scholar] [CrossRef]
- Ravindhran, B.; Chandak, P.; Schafer, N.; Kundalia, K.; Hwang, W.; Antoniadis, S.; Haroon, U.; Zakri, R.H. Machine learning models in predicting graft survival in kidney transplantation: Meta-analysis. BJS Open 2023, 7, zrad011. [Google Scholar] [CrossRef]
- Seyahi, N.; Ozcan, S.G. Artificial intelligence and kidney transplantation. World J. Transplant. 2021, 11, 277–289. [Google Scholar] [CrossRef]
- Bae, S.; Massie, A.B.; Thomas, A.G.; Bahn, G.; Luo, X.; Jackson, K.R.; Ottmann, S.E.; Brennan, D.C.; Desai, N.M.; Coresh, J. Who can tolerate a marginal kidney? Predicting survival after deceased donor kidney transplant by donor-recipient combination. Am. J. Transplant. 2019, 19, 425–433. [Google Scholar] [CrossRef] [PubMed]
- Divard, G.; Raynaud, M.; Tatapudi, V.S.; Abdalla, B.; Bailly, E.; Assayag, M.; Binois, Y.; Cohen, R.; Zhang, H.; Ulloa, C.; et al. Comparison of artificial intelligence and human-based prediction and stratification of the risk of long-term kidney allograft failure. Commun. Med. 2022, 2, 150. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Tang, Z.; Hu, X.; Lu, S.; Miao, B.; Hong, S.; Bai, H.; Sun, C.; Qiu, J.; Liang, H.; et al. Machine learning for the prediction of severe pneumonia during posttransplant hospitalization in recipients of a deceased-donor kidney transplant. Ann. Transl. Med. 2020, 8, 82. [Google Scholar] [CrossRef] [PubMed]
- Kawakita, S.; Beaumont, J.L.; Jucaud, V.; Everly, M.J. Personalized prediction of delayed graft function for recipients of deceased donor kidney transplants with machine learning. Sci. Rep. 2020, 10, 18409. [Google Scholar] [CrossRef]
- Yoo, D.; Divard, G.; Raynaud, M.; Cohen, A.; Mone, T.D.; Rosenthal, J.T.; Bentall, A.J.; Stegall, M.D.; Naesens, M.; Zhang, H.; et al. A Machine Learning-Driven Virtual Biopsy System For Kidney Transplant Patients. Nat. Commun. 2024, 15, 554. [Google Scholar] [CrossRef]
- Tang, J.; Liu, R.; Zhang, Y.-L.; Liu, M.-Z.; Hu, Y.-F.; Shao, M.-J.; Zhu, L.-J.; Xin, H.-W.; Feng, G.-W.; Shang, W.-J.; et al. Application of Machine-Learning Models to Predict Tacrolimus Stable Dose in Renal Transplant Recipients. Sci. Rep. 2017, 7, 42192. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Porta-Oltra, B.; Soria-Olivas, E.; Martín-Guerrero, J.D.; Serrano-López, A.J.; Pérez-Ruixo, J.J.; Jiménez-Torres, N.V. Prediction of cyclosporine dosage in patients after kidney transplantation using neural networks. IEEE Trans. Biomed. Eng. 2003, 50, 442–448. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Kotsiantis, S.B. Decision trees: A recent overview. Artif. Intell. Rev. 2013, 39, 261–283. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Suthaharan, S. Support Vector Machine. In Machine Learning Models and Algorithms for Big Data Classification: Thinking with Examples for Effective Learning; Suthaharan, S., Ed.; Springer: Boston, MA, USA, 2016; pp. 207–235. [Google Scholar]
- Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobot. 2013, 7, 21. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; Curran Associates Inc.: New York, NY, USA, 2018; pp. 6639–6649. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Rish, I. An Empirical Study of the Naïve Bayes Classifier. In Proceedings of the IJCAI 2001 Workshop on Empirical Methods in Artificial Intelligence, Seattle, WA, USA, 4–10 August 2001; Volume 3. [Google Scholar]
- Wu, Y.-C.; Feng, J.-W. Development and Application of Artificial Neural Network. Wirel. Pers. Commun. 2018, 102, 1645–1656. [Google Scholar] [CrossRef]
- Sokolova, M.; Japkowicz, N.; Szpakowicz, S. Beyond Accuracy, F-Score and ROC: A Family of Discriminant Measures for Performance Evaluation. In Proceedings of the 19th Australian Joint Conference on Artificial Intelligence, Hobart, Australia, 4–8 December 2006; Volume 4304, pp. 1015–1021. [Google Scholar]
- Rahutomo, F.; Kitasuka, T.; Aritsugi, M. Semantic Cosine Similarity. In Proceedings of the 7th International Student Conference on Advanced Science and Technology ICAST 2012, Seoul, Republic of Korea, 29–30 October 2012. [Google Scholar]
- Bag, S.; Kumar, S.K.; Tiwari, M.K. An efficient recommendation generation using relevant Jaccard similarity. Inf. Sci. 2019, 483, 53–64. [Google Scholar] [CrossRef]



| Characteristic | Value | |
|---|---|---|
| HLA-A | A*01 | A*02 |
| HLA-B | B*07 | B*27 |
| HLA-C | C*03 | C*05 |
| HLA-DRB1 | DRB1*03 | DRB1*11 |
| HLA-DQB1 | DQB1*02 | DQB1*06 |
| Age | 35 | |
| ABO blood group | B+ | |
| HLA antibody specificities (for recipients only) | A3, B38, DQ2, DQ7 | |
| D | A | B | O | AB | |
|---|---|---|---|---|---|
| R | |||||
| A | √ | √ | |||
| B | √ | √ | |||
| O | √ | √ | √ | √ | |
| AB | √ | ||||
| Classifiers | Optimal Hyper-Parameters |
|---|---|
| GB | n_estimators: 200, learning_rate: 0.3, max_depth: 6 |
| LGBM | learning_rate: 0.1, n_estimators: 100 |
| CB | depth: 3, iterations: 2000, learning_rate: 0.01 |
| XB | gamma: 0.2, learning_rate: 0.1, max_depth: 8, n_estimators: 200 |
| NN | hidden layer: (25, 5), learning rate: 0.001, epochs: 15,000, active function: ReLU |
| RF | n_estimators: 1000, min_samples_split: 10, min_samples_leaf: 1, max_features: ‘sqrt’, max_depth: 10, bootstrap: False |
| DT | max_depth: 30, max_features: none, min_samples_leaf: 2, min_samples_split: 10 |
| SVM | C: 15, gamma: ‘scale’, kernel: ‘linear’ |
| LR | C: 0.1, penalty: ‘l2’, fit_intercept: true |
| Classifiers | Optimal Hyper-Parameters |
|---|---|
| GB | n_estimators: 200, learning_rate: 0.2, max_depth: 6 |
| LGBM | learning_rate: 0.1, n_estimators: 100 |
| CB | depth: 4, iterations: 3000, learning_rate: 0.01 |
| XB | gamma: 0.2, learning_rate: 0.1, max_depth: 6, n_estimators: 200 |
| NN | hidden layer: (25, 5), learning rate: 0.001, epochs: 15,000, active function: ReLU |
| RF | n_estimators: 1000, min_samples_split: 10, min_samples_leaf: 1, max_features: ‘sqrt’, max_depth: 30, bootstrap: False |
| DT | max_depth: 30, max_features: none, min_samples_leaf: 2, min_samples_split: 10 |
| SVM | C: 10, gamma: ‘scale’, Kernel: ‘linear’ |
| LR | C: 0.1, penalty: ‘l2’, fit_intercept: true |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alowidi, N.; Ali, R.; Sadaqah, M.; Naemi, F.M.A. Advancing Kidney Transplantation: A Machine Learning Approach to Enhance Donor–Recipient Matching. Diagnostics 2024, 14, 2119. https://doi.org/10.3390/diagnostics14192119
Alowidi N, Ali R, Sadaqah M, Naemi FMA. Advancing Kidney Transplantation: A Machine Learning Approach to Enhance Donor–Recipient Matching. Diagnostics. 2024; 14(19):2119. https://doi.org/10.3390/diagnostics14192119
Chicago/Turabian StyleAlowidi, Nahed, Razan Ali, Munera Sadaqah, and Fatmah M. A. Naemi. 2024. "Advancing Kidney Transplantation: A Machine Learning Approach to Enhance Donor–Recipient Matching" Diagnostics 14, no. 19: 2119. https://doi.org/10.3390/diagnostics14192119
APA StyleAlowidi, N., Ali, R., Sadaqah, M., & Naemi, F. M. A. (2024). Advancing Kidney Transplantation: A Machine Learning Approach to Enhance Donor–Recipient Matching. Diagnostics, 14(19), 2119. https://doi.org/10.3390/diagnostics14192119






