Automated Age Estimation from OPG Images and Patient Records Using Deep Feature Extraction and Modified Genetic–Random Forest
Abstract
:1. Introduction
- To extract pertinent features from OPG images and patient records, employing innovative approach that combines Deep 2D CNN with a Deep 1D CNN. The extracted features were then concatenated to improve the accuracy of age estimation;
- To achieve the highest coefficient of determination (R2) for age estimation by leveraging an MG-RF regressor;
- To evaluate the efficiency of the proposed methodology with respect to standard deviation (SD), mean absolute error (MAE), mean square error (MSE), root mean square error (RMSE), and R2.
2. Related Work
3. Materials and Methods
3.1. Dataset Description
3.2. Preprocessing
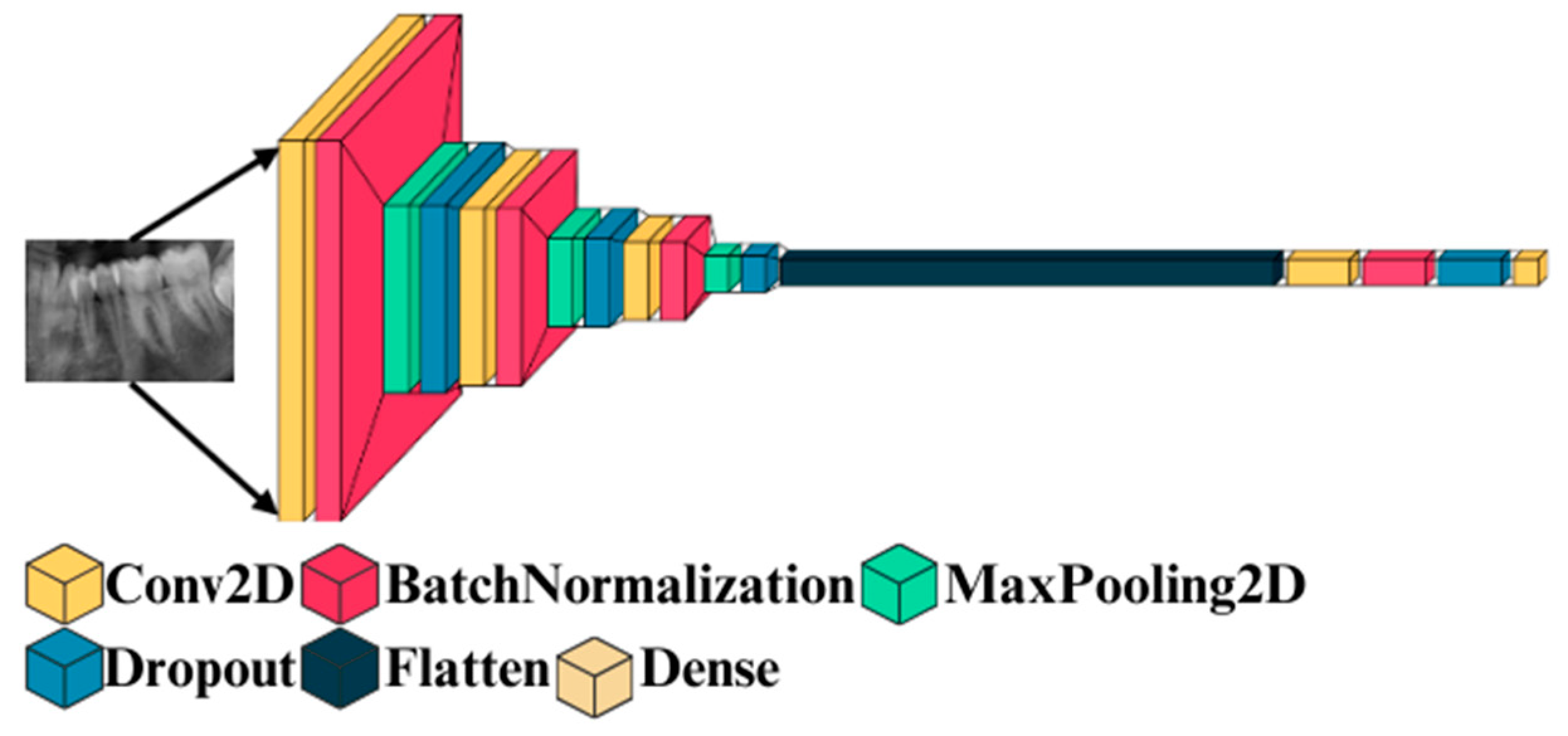
3.3. Feature Extraction: Deep Two-Dimensional Convolution Neural Network and Deep One-Dimensional Convolution Neural Network
3.3.1. Deep 2D CNN: Deep Two-Dimensional Convolutional Neural Network
- Input Layer
- 2.
- Convolution layer
- 3.
- Maxpooling layer
- 4.
- Training the model
| Algorithm 1: Deep 2D CNN | |
| 1 | Input: OPG Images |
| 2 | Output: Features |
| 3 | STEP 1: Sliding Window Process |
| 4 | STEP 2: sef ← Extract Shadow Features |
| 5 | STEP 3: Normalize sef using equation (2) |
| 6 | regularization feature data, size = 64 Units–128 Units |
| 7 | repeat: |
| 8 | STEP 4: Forward Propagation |
| 9 | cdf ← Convolution2D(sef); |
| 10 | mp ← Max_pooling(cdf); |
| 11 | fc ← Fully_connected(mp); |
| 12 | class label ← relu(fc); |
| 13 | STEP 5: Backward Propagation |
| 14 | conduct backward propagation with Adam; |
| 15 | Until wi convergences;// wi: weight |
| 16 | STEP 6: Use the trained network to predict the features |
3.3.2. Deep 1D CNN: Deep One-Dimensional Convolutional Neural Network
3.3.3. Feature Concatenation
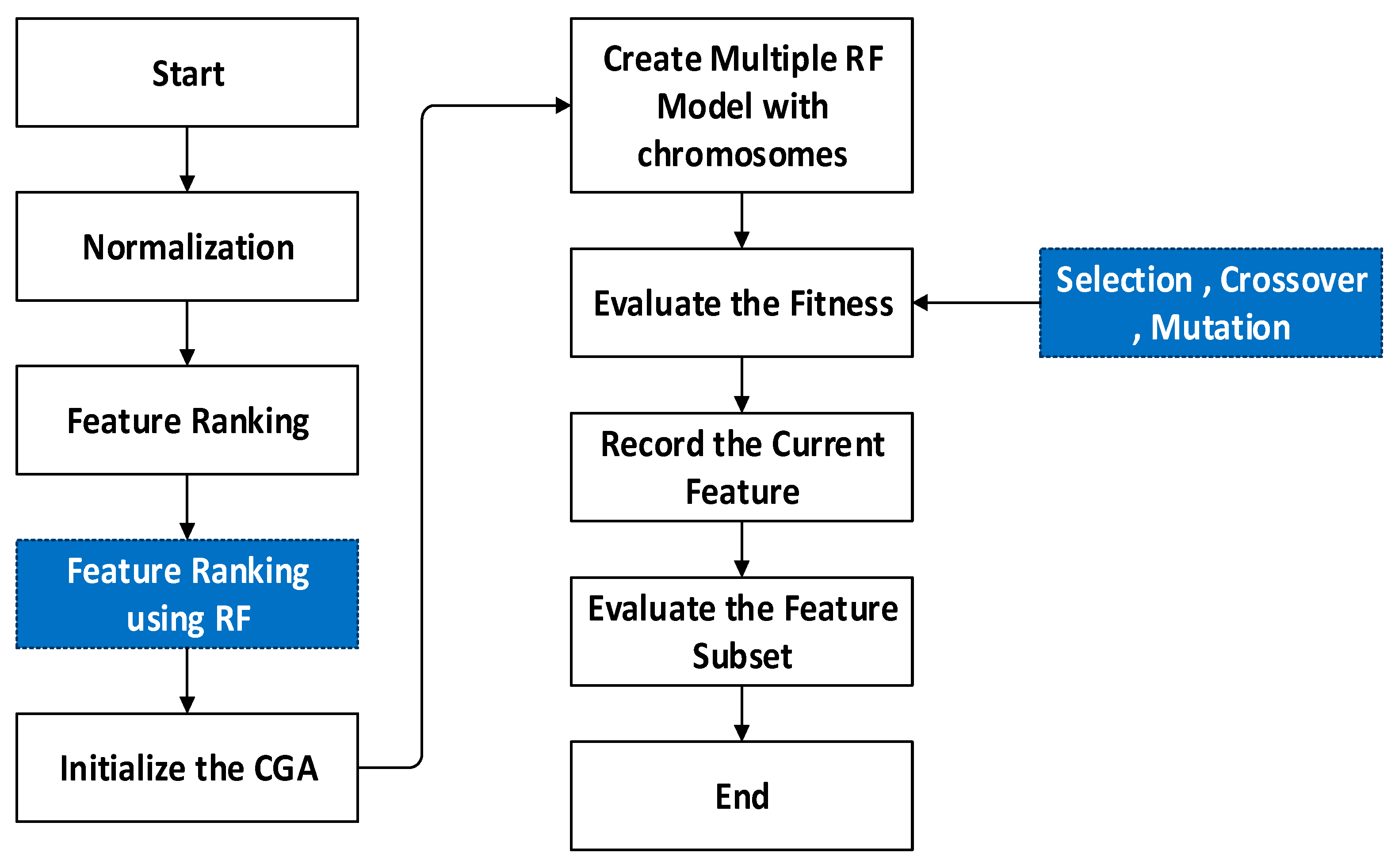
3.4. Regression-MG-RF (Modified Genetic–Random Forest)
| Algorithm 2: Genetic algorithm | |
| 1 | Input: (it, n, GA Parameters) |
| 2 | STEP 1: begin |
| 3 | STEP 2: Initialize c = 0 and i = 0, |
| 4 | STEP 3: Generation: generate random n solutions; |
| 5 | STEP 4: Compute Fitness(s) and Generation c; |
| 6 | STEP 5: While fitness not reached compute for i iterations do |
| 7 | Generation c + 1 evolve(Generation c); |
| 8 | STEP 6: fitness computeFitness (s) and Generation c; |
| 9 10 11 12 | i = i + 1; end return (solution fitness) end |
| Algorithm 3: Modified fitness computation | |
| 1 | Input: Dataset(D), Chromosome |
| 2 | Output: MAE of the Random Forests |
| 3 | STEP 1: begin |
| 4 | STEP 2: Ds—Dataset; |
| 5 | STEP 3: Compute kvalues, num_trees, mtry by decoding (Chromosome); |
| 6 | Dc—decompose the set as (Ds, kvalues); |
| 7 | STEP 4: Fitnessmodel—RF fit(Dc,num_trees,mtry); |
| 8 | STEP 5: Rank the feature using RF Regressor |
| 9 10 11 | STEP 6: MAE—evaluate(model) STEP 7: return (MAE); end |
| Algorithm 4: Optimized Random Forest | ||
| 1 | Input: minK, maxK, minNTree, maxNTree, treeIncrement, RF best, RF fit | |
| 2 | Output: Optimized RF | |
| 3 | STEP 1: begin | |
| 4 | STEP 2: Compute computeFitness(s) and Generation c; | |
| 5 | STEP 3: Evaluate fitness and return fitness, | |
| 6 | STEP 4: MAE (Fit RF best) | |
| 7 | STEP 5: Fit RF best = Optimized RF | |
| 8 | STEP 6: Optimized RF(D) = solution | |
| 9 | end | |
4. Results
4.1. Performance Metrics
4.1.1. SD (Standard Deviation)
4.1.2. MAE (Mean Absolute Error)
4.1.3. MSE (Mean Square Error)
4.1.4. R2 (Coefficient of Determination)
4.1.5. RMSE (Root Mean Square Error)
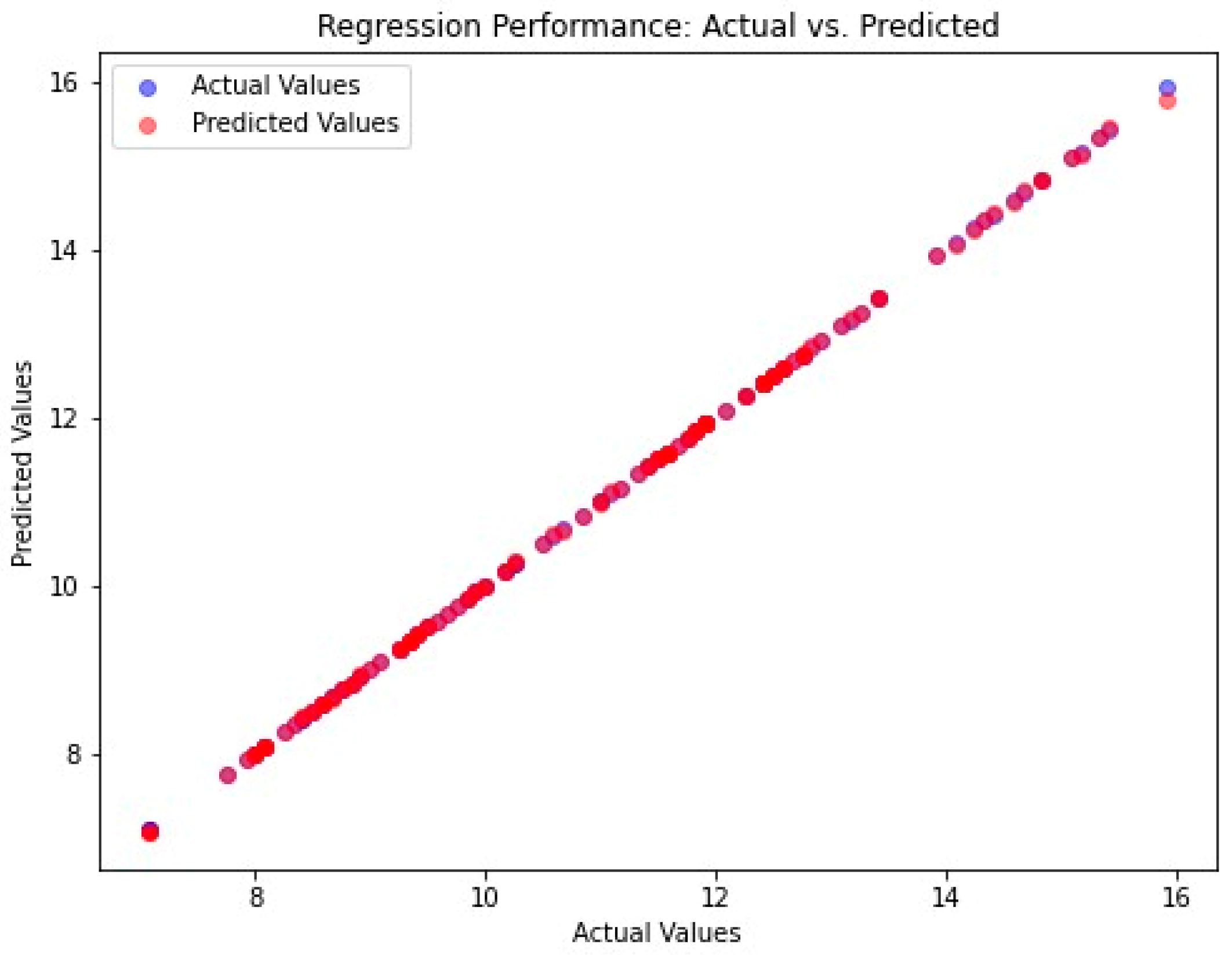
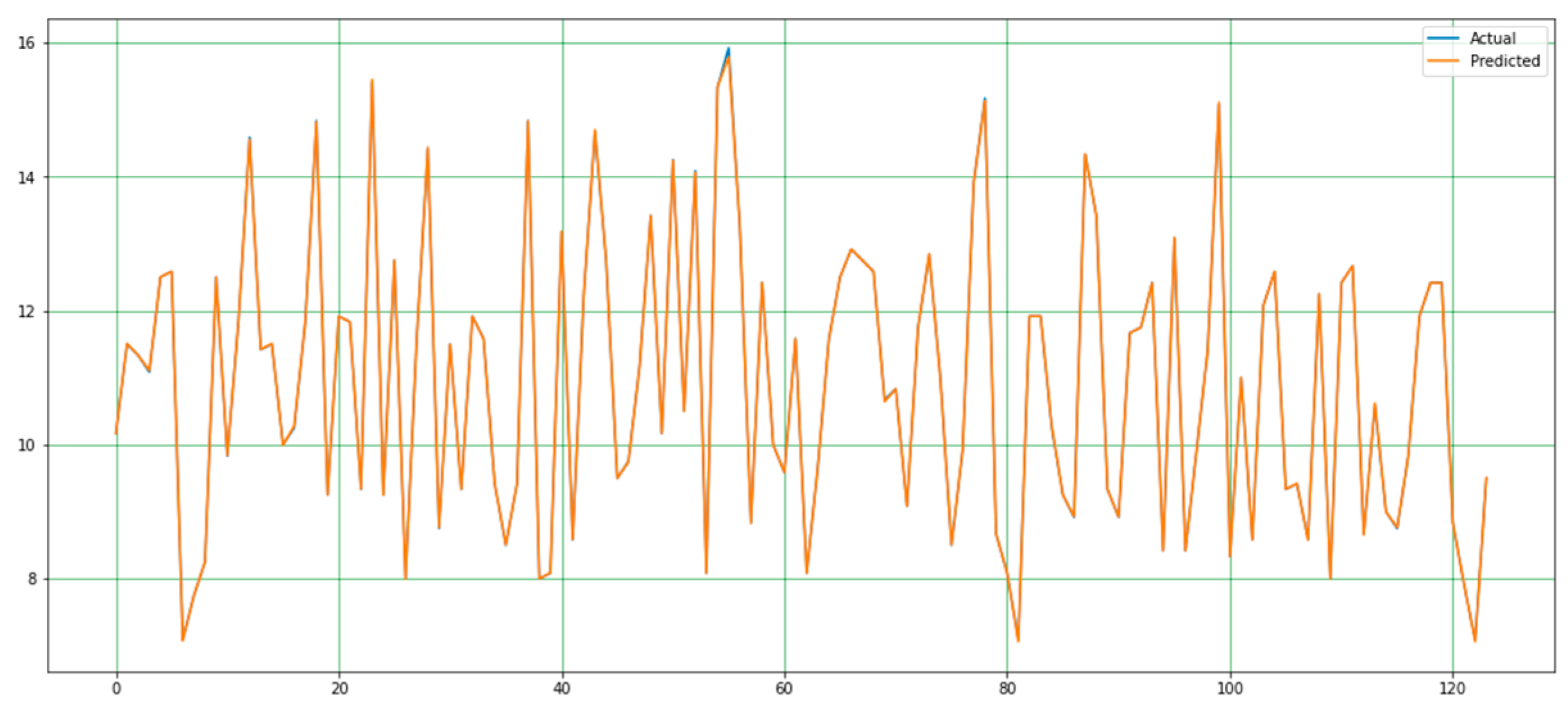
4.2. Performance Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Senn, D.R.; Stimson, P.G. Forensic Dentistry; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Apaydin, B.; Yasar, F. Accuracy of the demirjian, willems and cameriere methods of estimating dental age on turkish children. Niger. J. Clin. Pract. 2018, 21, 257. [Google Scholar] [CrossRef] [PubMed]
- Limdiwala, P.; Shah, J. Age estimation by using dental radiographs. J. Forensic Dent. Sci. 2013, 5, 118. [Google Scholar] [CrossRef] [PubMed]
- Khanagar, S.B.; Albalawi, F.; Alshehri, A.; Awawdeh, M.; Iyer, K.; Alsomaie, B.; Aldhebaib, A.; Singh, O.G.; Alfadley, A. Performance of Artificial Intelligence Models Designed for Automated Estimation of Age Using Dento-Maxillofacial Radiographs—A Systematic Review. Diagnostics 2024, 14, 1079. [Google Scholar] [CrossRef] [PubMed]
- Han, M.; Du, S.; Ge, Y.; Zhang, D.; Chi, Y.; Long, H.; Yang, J.; Yang, Y.; Xin, J.; Chen, T.; et al. With or without human interference for precise age estimation based on machine learning? Int. J. Legal. Med. 2022, 136, 821–831. [Google Scholar] [CrossRef] [PubMed]
- Garn, S.M.; Lewis, A.B.; Kerewsky, R.S. Genetic, Nutritional, and Maturational Correlates of Dental Development. J. Dent. Res. 1965, 44, 228–242. [Google Scholar] [CrossRef] [PubMed]
- Noble, H.W. The Estimation of Age from the Dentition. J. Forensic Sci. Soc. 1974, 14, 215–221. [Google Scholar] [CrossRef]
- Huda, T.F.J.; Bowman, J.E. Age determination from dental microstructure in juveniles. Am. J. Phys. Anthropol. 1995, 97, 135–150. [Google Scholar] [CrossRef]
- Graham, E.A. Economic, Racial, and Cultural Influences on the Growth and Maturation of Children. Pediatr. Rev. 2005, 26, 290–294. [Google Scholar] [CrossRef] [PubMed]
- Schmeling, A.; Grundmann, C.; Fuhrmann, A.; Kaatsch, H.J.; Knell, B.; Ramsthaler, F.; Reisinger, W.; Riepert, T.; Ritz-Timme, S.; Rösing, F.W.; et al. Criteria for age estimation in living individuals. Int. J. Legal Med. 2008, 122, 457–460. [Google Scholar] [CrossRef]
- Willems, G. A review of the most commonly used dental age estimation techniques. J. Forensic Odontostomatol. 2001, 19, 9–17. [Google Scholar] [PubMed]
- Celik, S.; Zeren, C.; Çelikel, A.; Yengil, E.; Altan, A. Applicability of the Demirjian method for dental assessment of southern Turkish children. J. Forensic Leg. Med. 2014, 25, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Uzuner, F.D.; Kaygısız, E.; Darendeliler, N. Defining Dental Age for Chronological Age Determination. In Post Mortem Examination and Autopsy—Current Issues From Death to Laboratory Analysis; InTech: Nappanee, IN, USA, 2018. [Google Scholar] [CrossRef]
- Sakuma, A.; Saitoh, H.; Suzuki, Y.; Makino, Y.; Inokuchi, G.; Hayakawa, M.; Yajima, D.; Iwase, H. Age Estimation Based on Pulp Cavity to Tooth Volume Ratio Using Postmortem Computed Tomography Images. J. Forensic Sci. 2013, 58, 1531–1535. [Google Scholar] [CrossRef] [PubMed]
- Ge, Z.-P.; Ma, R.-H.; Li, G.; Zhang, J.-Z.; Ma, X.-C. Age estimation based on pulp chamber volume of first molars from cone-beam computed tomography images. Forensic Sci. Int. 2015, 253, 133.e1–133.e7. [Google Scholar] [CrossRef]
- Vila-Blanco, N.; Carreira, M.J.; Varas-Quintana, P.; Balsa-Castro, C.; Tomas, I. Deep Neural Networks for Chronological Age Estimation from OPG Images. IEEE Trans. Med. Imaging 2020, 39, 2374–2384. [Google Scholar] [CrossRef] [PubMed]
- Milošević, D.; Vodanović, M.; Galić, I.; Subašić, M. Automated estimation of chronological age from panoramic dental X-ray images using deep learning. Expert. Syst. Appl. 2022, 189, 116038. [Google Scholar] [CrossRef]
- Putra, R.H.; Doi, C.; Yoda, N.; Astuti, E.R.; Sasaki, K. Current applications and development of artificial intelligence for digital dental radiography. Dentomaxillofacial Radiol. 2022, 51, 20210197. [Google Scholar] [CrossRef] [PubMed]
- Devito, K.L.; de Souza Barbosa, F.; Filho, W.N.F. An artificial multilayer perceptron neural network for diagnosis of proximal dental caries. Oral. Surg. Oral. Med. Oral. Pathol. Oral. Radiol. Endodontol. 2008, 106, 879–884. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.; Eun, H.; Kim, C. Boosting Proximal Dental Caries Detection via Combination of Variational Methods and Convolutional Neural Network. J. Signal Process Syst. 2018, 90, 87–97. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, D.H.; Jeong, S.N.; Choi, S.H. Detection and diagnosis of dental caries using a deep learning-based convolutional neural network algorithm. J. Dent. 2018, 77, 106–111. [Google Scholar] [CrossRef]
- Geetha, V.; Aprameya, K.S.; Hinduja, D.M. Dental caries diagnosis in digital radiographs using back-propagation neural network. Health Inf. Sci. Syst. 2020, 8, 8. [Google Scholar] [CrossRef]
- Yu, Y.; Li, Y.-J.; Wang, J.-M.; Lin, D.-H.; Ye, W.-P. Tooth Decay Diagnosis using Back Propagation Neural Network. In Proceedings of the 2006 International Conference on Machine Learning and Cybernetics, Dalian, China, 13–16 August 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 3956–3959. [Google Scholar] [CrossRef]
- Li, W.; Kuang, W.; Li, Y.; Li, Y.J.; Ye, W.P. Clinical X-Ray Image Based Tooth Decay Diagnosis using SVM. In Proceedings of the 2007 International Conference on Machine Learning and Cybernetics, Hong Kong, China, 19–22 August 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1616–1619. [Google Scholar] [CrossRef]
- Ali, R.B.; Ejbali, R.; Zaied, M. Detection and Classification of Dental Caries in X-ray Images Using Deep Neural Networks. In Proceedings of the Eleventh International Conference on Software Engineering Advances (ICSEA), Rome, Italy, 21–25 August 2016. [Google Scholar]
- Singh, P.; Sehgal, P. Automated caries detection based on Radon transformation and DCT. In Proceedings of the 2017 8th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Delhi, India, 3–5 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Szabó, V.; Szabó, B.T.; Orhan, K.; Veres, D.S.; Manulis, D.; Ezhov, M.; Sanders, A. Validation of artificial intelligence application for dental caries diagnosis on intraoral bitewing and periapical radiographs. J. Dent. 2024, 147, 105105. [Google Scholar] [CrossRef]
- El-Gayar, M.M. Hybrid Transfer Learning for Diagnosing Teeth Using Panoramic X-rays. Int. J. Adv. Comput. Sci. Appl. 2024, 15, 228–232. [Google Scholar] [CrossRef]
- Orhan, K.; Belgin, C.A.; Manulis, D.; Golitsyna, M.; Bayrak, S.; Aksoy, S.; Sanders, A.; Önder, M.; Ezhov, M.; Shamshiev, M.; et al. Determining the reliability of diagnosis and treatment using artificial intelligence software with panoramic radiographs. Imaging Sci. Dent. 2023, 53, 199. [Google Scholar] [CrossRef] [PubMed]
- Ari, T.; Sağlam, H.; Öksüzoğlu, H.; Kazan, O.; Bayrakdar, I.Ş.; Duman, S.B.; Çelik, Ö.; Jagtap, R.; Futyma-Gąbka, K.; Różyło-Kalinowska, I.; et al. Automatic Feature Segmentation in Dental Periapical Radiographs. Diagnostics 2022, 12, 3081. [Google Scholar] [CrossRef] [PubMed]
- Lin, P.L.; Huang, P.Y.; Huang, P.W. Automatic methods for alveolar bone loss degree measurement in periodontitis periapical radiographs. Comput. Methods Programs Biomed. 2017, 148, 1–11. [Google Scholar] [CrossRef]
- Lin, P.L.; Huang, P.W.; Huang, P.Y.; Hsu, H.C. Alveolar bone-loss area localization in periodontitis radiographs based on threshold segmentation with a hybrid feature fused of intensity and the H-value of fractional Brownian motion model. Comput. Methods Programs Biomed. 2015, 121, 117–126. [Google Scholar] [CrossRef] [PubMed]
- Kurt Bayrakdar, S.; Orhan, K.; Bayrakdar, I.S.; Bilgir, E.; Ezhov, M.; Gusarev, M.; Shumilov, E. A deep learning approach for dental implant planning in cone-beam computed tomography images. BMC Med. Imaging 2021, 21, 86. [Google Scholar] [CrossRef]
- Orhan, K.; Bayrakdar, I.S.; Ezhov, M.; Kravtsov, A.; Özyürek, T. Evaluation of artificial intelligence for detecting periapical pathosis on cone-beam computed tomography scans. Int. Endod. J. 2020, 53, 680–689. [Google Scholar] [CrossRef]
- Gupta, A.; Kharbanda, O.P.; Sardana, V.; Balachandran, R.; Sardana, H.K. Accuracy of 3D cephalometric measurements based on an automatic knowledge-based landmark detection algorithm. Int. J. Comput. Assist. Radiol. Surg. 2016, 11, 1297–1309. [Google Scholar] [CrossRef] [PubMed]
- Gupta, A.; Kharbanda, O.P.; Sardana, V.; Balachandran, R.; Sardana, H.K. A knowledge-based algorithm for automatic detection of cephalometric landmarks on CBCT images. Int. J. Comput. Assist. Radiol. Surg. 2015, 10, 1737–1752. [Google Scholar] [CrossRef]
- Orhan, K.; Bilgir, E.; Bayrakdar, I.S.; Ezhov, M.; Gusarev, M.; Shumilov, E. Evaluation of artificial intelligence for detecting impacted third molars on cone-beam computed tomography scans. J. Stomatol. Oral Maxillofac. Surg. 2021, 122, 333–337. [Google Scholar] [CrossRef] [PubMed]
- Vinayahalingam, S.; Xi, T.; Bergé, S.; Maal, T.; de Jong, G. Automated detection of third molars and mandibular nerve by deep learning. Sci Rep. 2019, 9, 9007. [Google Scholar] [CrossRef] [PubMed]
- Fukuda, M.; Ariji, Y.; Kise, Y.; Nozawa, M.; Kuwada, C.; Funakoshi, T.; Muramatsu, C.; Fujita, H.; Katsumata, A.; Ariji, E. Comparison of 3 deep learning neural networks for classifying the relationship between the mandibular third molar and the mandibular canal on panoramic radiographs. Oral Surg Oral Med. Oral Pathol. Oral Radiol. 2020, 130, 336–343. [Google Scholar] [CrossRef] [PubMed]
- Jaskari, J.; Sahlsten, J.; Järnstedt, J.; Mehtonen, H.; Karhu, K.; Sundqvist, O.; Hietanen, A.; Varjonen, V.; Mattila, V.; Kaski, K. Deep Learning Method for Mandibular Canal Segmentation in Dental Cone Beam Computed Tomography Volumes. Sci. Rep. 2020, 10, 5842. [Google Scholar] [CrossRef] [PubMed]
- Kwak, G.H.; Kwak, E.-J.; Song, J.M.; Park, H.R.; Jung, Y.-H.; Cho, B.-H.; Hui, P.; Hwang, J.J. Automatic mandibular canal detection using a deep convolutional neural network. Sci. Rep. 2020, 10, 5711. [Google Scholar] [CrossRef] [PubMed]
- Kuwada, C.; Ariji, Y.; Fukuda, M.; Kise, Y.; Fujita, H.; Katsumata, A.; Ariji, E. Deep learning systems for detecting and classifying the presence of impacted supernumerary teeth in the maxillary incisor region on panoramic radiographs. Oral Surg. Oral Med. Oral Pathol. Oral Radiol. 2020, 130, 464–469. [Google Scholar] [CrossRef] [PubMed]
- Johari, M.; Esmaeili, F.; Andalib, A.; Garjani, S.; Saberkari, H. Detection of vertical root fractures in intact and endodontically treated premolar teeth by designing a probabilistic neural network: An ex vivo study. Dentomaxillofac. Radiol. 2017, 46, 20160107. [Google Scholar] [CrossRef]
- Fukuda, M.; Inamoto, K.; Shibata, N.; Ariji, Y.; Yanashita, Y.; Kutsuna, S.; Nakata, K.; Katsumata, A.; Fujita, H.; Ariji, E. Evaluation of an artificial intelligence system for detecting vertical root fracture on panoramic radiography. Oral Radiol. 2020, 36, 337–343. [Google Scholar] [CrossRef] [PubMed]
- Chu, P.; Bo, C.; Liang, X.; Yang, J.; Megalooikonomou, V.; Yang, F.; Huang, B.; Li, X.; Ling, H. Using Octuplet Siamese Network for Osteoporosis Analysis on Dental Panoramic Radiographs. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; IEEE: Piscataway, NJ, USA; pp. 2579–2582. [Google Scholar] [CrossRef]
- Lee, K.S.; Jung, S.K.; Ryu, J.J.; Shin, S.W.; Choi, J. Evaluation of Transfer Learning with Deep Convolutional Neural Networks for Screening Osteoporosis in Dental Panoramic Radiographs. J. Clin. Med. 2020, 9, 392. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.S.; Adhikari, S.; Liu, L.; Jeong, H.G.; Kim, H.; Yoon, S.J. Osteoporosis detection in panoramic radiographs using a deep convolutional neural network-based computer-assisted diagnosis system: A preliminary study. Dentomaxillofac. Radiol. 2019, 48, 20170344. [Google Scholar] [CrossRef] [PubMed]
- Liang, K.; Zhang, L.; Yang, H.; Yang, Y.; Chen, Z.; Xing, Y. Metal artifact reduction for practical dental computed tomography by improving interpolation-based reconstruction with deep learning. Med. Phys. 2019, 46, pp.823–834. [Google Scholar] [CrossRef] [PubMed]
- Minnema, J.; Minnema, J.; van Eijnatten, M.; van Eijnatten, M.; Hendriksen, A.A.; Hendriksen, A.A.; Liberton, N.; Liberton, N.; Pelt, D.M.; Pelt, D.M.; et al. Segmentation of dental cone-beam CT scans affected by metal artifacts using a mixed-scale dense convolutional neural network. Med. Phys. 2019, 46, 5027–5035. [Google Scholar] [CrossRef] [PubMed]
- Hegazy, M.A.A.; Cho, M.H.; Cho, M.H.; Lee, S.Y. U-net based metal segmentation on projection domain for metal artifact reduction in dental CT. Biomed. Eng. Lett. 2019, 9, 375–385. [Google Scholar] [CrossRef]
- Flores, A.; Rysavy, S.; Enciso, R.; Okada, K. Non-invasive differential diagnosis of dental periapical lesions in cone-beam CT. In Proceedings of the 2009 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Boston, MA, USA, 28 June–1 July 2009; IEEE: Piscataway, NJ, USA; pp. 566–569. [Google Scholar] [CrossRef]
- Okada, K.; Rysavy, S.; Flores, A.; Linguraru, M.G. Noninvasive differential diagnosis of dental periapical lesions in cone-beam CT scans. Med. Phys. 2015, 42, 1653–1665. [Google Scholar] [CrossRef] [PubMed]
- Murata, M.; Ariji, Y.; Ohashi, Y.; Kawai, T.; Fukuda, M.; Funakoshi, T.; Kise, Y.; Nozawa, M.; Katsumata, A.; Fujita, H.; et al. Deep-learning classification using convolutional neural network for evaluation of maxillary sinusitis on panoramic radiography. Oral Radiol. 2019, 35, 301–307. [Google Scholar] [CrossRef]
- Kuwana, R.; Ariji, Y.; Fukuda, M.; Kise, Y.; Nozawa, M.; Kuwada, C.; Muramatsu, C.; Katsumata, A.; Fujita, H.; Ariji, E. Performance of deep learning object detection technology in the detection and diagnosis of maxillary sinus lesions on panoramic radiographs. Dentomaxillofac. Radiol. 2021, 50, 20200171. [Google Scholar] [CrossRef]
- Kim, Y.; Lee, K.J.; Sunwoo, L.; Choi, D.; Nam, C.-M.; Cho, J.; Kim, J.; Bae, Y.J.; Yoo, R.-E.; Choi, B.S.; et al. Deep Learning in Diagnosis of Maxillary Sinusitis Using Conventional Radiography. Investig. Radiol. 2019, 54, 7–15. [Google Scholar] [CrossRef] [PubMed]
- Kann, B.H.; Aneja, S.; Loganadane, G.V.; Kelly, J.R.; Smith, S.M.; Decker, R.H.; Yu, J.B.; Park, H.S.; Yarbrough, W.G.; Malhotra, A.; et al. Pretreatment Identification of Head and Neck Cancer Nodal Metastasis and Extranodal Extension Using Deep Learning Neural Networks. Sci. Rep. 2018, 8, 14036. [Google Scholar] [CrossRef]
- Ariji, Y.; Fukuda, M.; Kise, Y.; Nozawa, M.; Yanashita, Y.; Fujita, H.; Katsumata, A.; Ariji, E. Contrast-enhanced computed tomography image assessment of cervical lymph node metastasis in patients with oral cancer by using a deep learning system of artificial intelligence. Oral Surg. Oral Med. Oral Pathol. Oral Radiol. 2019, 127, 458–463. [Google Scholar] [CrossRef]
- Kise, Y.; Ikeda, H.; Fujii, T.; Fukuda, M.; Ariji, Y.; Fujita, H.; Katsumata, A.; Ariji, E. Preliminary study on the application of deep learning system to diagnosis of Sjögren’s syndrome on CT images. Dentomaxillofac. Radiol. 2019, 48, 20190019. [Google Scholar] [CrossRef]
- Keser, G.; Pekiner, F.N.; Bayrakdar, İ.Ş.; Çelik, Ö.; Orhan, K. A deep learning approach to detection of oral cancer lesions from intra oral patient images: A preliminary retrospective study. J. Stomatol. Oral Maxillofac. Surg. 2024, 125, 101975. [Google Scholar] [CrossRef] [PubMed]
- Chinnikatti, S.K. Artificial Intelligence in Forensic Science. Forensic. Sci. Addict. Res. 2018, 2. [Google Scholar] [CrossRef]
- Khanagar, S.B.; Vishwanathaiah, S.; Naik, S.; Al-Kheraif, A.A.; Divakar, D.D.; Sarode, S.C.; Bhandi, S.; Patil, S. Application and performance of artificial intelligence technology in forensic odontology—A systematic review. Leg. Med. 2021, 48, 101826. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Kahm, S.H.; Kim, J.Y.; Yoo, S.; Bae, S.M.; Kang, J.E.; Lee, S.H. Application of entire dental panorama image data in artificial intelligence model for age estimation. BMC Oral Health 2023, 23, 1007. [Google Scholar] [CrossRef]
- Kazimierczak, W.; Wajer, R.; Wajer, A.; Kiian, V.; Kloska, A.; Kazimierczak, N.; Janiszewska-Olszowska, J.; Serafin, Z. Periapical Lesions in Panoramic Radiography and CBCT Imaging—Assessment of AI’s Diagnostic Accuracy. J. Clin. Med. 2024, 13, 2709. [Google Scholar] [CrossRef] [PubMed]
- Vila-Blanco, N.; Varas-Quintana, P.; Aneiros-Ardao, Á.; Tomás, I.; Carreira, M.J. XAS: Automatic yet eXplainable Age and Sex determination by combining imprecise per-tooth predictions. Comput. Biol. Med. 2022, 149, 106072. [Google Scholar] [CrossRef]
- Galibourg, A.; Cussat-Blanc, S.; Dumoncel, J.; Telmon, N.; Monsarrat, P.; Maret, D. Comparison of different machine learning approaches to predict dental age using Demirjian’s staging approach. Int. J. Legal. Med. 2021, 135, 665–675. [Google Scholar] [CrossRef]
- Tao, J.; Wang, J.; Wang, A.; Xie, Z.; Wang, Z.; Wu, S.; Hassanien, A.E.; Xiao, K. Dental Age Estimation: A Machine Learning Perspective. In Advances in Intelligent Systems and Computing; Springer: Berlin/Heidelberg, Germany, 2020; Volume 921, pp. 722–733. [Google Scholar] [CrossRef]
- Shen, S.; Liu, Z.; Wang, J.; Fan, L.; Ji, F.; Tao, J. Machine learning assisted Cameriere method for dental age estimation. BMC Oral Health 2021, 21, 641. [Google Scholar] [CrossRef] [PubMed]
- Cular, L.; Tomaic, M.; Subasic, M.; Saric, T.; Sajkovic, V.; Vodanovic, M. Dental age estimation from panoramic X-ray images using statistical models. In International Symposium on Image and Signal Processing and Analysis, ISPA; IEEE Computer Society: Washington, DC, USA, 2017; pp. 25–30. [Google Scholar] [CrossRef]
- De Back, W.; Seurig, S.; Wagner, S.; Marré, B.; Roeder, I.; Scherf, N. Forensic Age Estimation with Bayesian Convolutional Neural Networks Based on Panoramic Dental X-Ray Imaging. Proc. Mach. Learn. Res. 2019, 1–4. [Google Scholar]
- Wallraff, S.; Vesal, S.; Syben, C.; Lutz, R.; Maier, A. Age Estimation on Panoramic Dental X-ray Images using Deep Learning. In Informatik Aktuell; Springer Science and Business Media Deutschland GmbH: Berlin, Germany, 2021; pp. 186–191. [Google Scholar] [CrossRef]
- De Tobel, J.; Radesh, P.; Vandermeulen, D.; Thevissen, P.W. An automated technique to stage lower third molar development on panoramic radiographs for age estimation: A pilot study. J. Forensic Odontostomatol. 2017, 35, 42–54. [Google Scholar]
- Merdietio Boedi, R.; Banar, N.; De Tobel, J.; Bertels, J.; Vandermeulen, D.; Thevissen, P.W. Effect of Lower Third Molar Segmentations on Automated Tooth Development Staging using a Convolutional Neural Network. J. Forensic Sci. 2020, 65, 481–486. [Google Scholar] [CrossRef]
- Banar, N.; Bertels, J.; Laurent, F.; Boedi, R.M.; De Tobel, J.; Thevissen, P.; Vandermeulen, D. Towards fully automated third molar development staging in panoramic radiographs. Int. J. Legal. Med. 2020, 134, 1831–1841. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Lee, Y.H.; Noh, Y.K.; Park, F.C.; Auh, Q.S. Age-group determination of living individuals using first molar images based on artificial intelligence. Sci. Rep. 2021, 11, 1073. [Google Scholar] [CrossRef]
- Dong, W.; You, M.; He, T.; Dai, J.; Tang, Y.; Shi, Y.; Guo, J. An automatic methodology for full dentition maturity staging from OPG images using deep learning. Appl. Intell. 2023, 53, 29514–29536. [Google Scholar] [CrossRef]
- Guo, Y.-C.; Han, M.; Chi, Y.; Long, H.; Zhang, D.; Yang, J.; Yang, Y.; Chen, T.; Du, S. Accurate age classification using manual method and deep convolutional neural network based on orthopantomogram images. Int. J. Legal. Med. 2021, 135, 1589–1597. [Google Scholar] [CrossRef]
- Kokomoto, K.; Kariya, R.; Muranaka, A.; Okawa, R.; Nakano, K.; Nozaki, K. Automatic dental age calculation from panoramic radiographs using deep learning: A two-stage approach with object detection and image classification. BMC Oral Health 2024, 24, 143. [Google Scholar] [CrossRef] [PubMed]
- Bizjak, Ž.; Robič, T. DentAge: Deep learning for automated age prediction using panoramic dental X-ray images. J. Forensic Sci. 2024, 69, 2069–2074. [Google Scholar] [CrossRef]
- Shi, Y.; Ye, Z.; Guo, J.; Tang, Y.; Dong, W.; Dai, J.; Miao, Y.; You, M. Deep learning methods for fully automated dental age estimation on orthopantomograms. Clin. Oral Investig. 2024, 28, 198. [Google Scholar] [CrossRef]
- Oliveira, W.; Albuquerque Santos, M.; Burgardt, C.A.P.; Anjos Pontual, M.L.; Zanchettin, C. Estimation of human age using machine learning on panoramic radiographs for Brazilian patients. Sci. Rep. 2024, 14, 19689. [Google Scholar] [CrossRef] [PubMed]
- Schour, I.; Massler, M. The development of the Human Dentition. J. Am. Dent. Assoc. 1941, 28, 1153–1160. [Google Scholar]
- Nolla, C.M. The development of the permanent teeth. J. Dent. Child. 1960, 27, 254–266. [Google Scholar]
- Demirjian, A.; Goldstein, H.; Tanner, J.M. A new system of dental age assessment. Hum. Biol. 1973, 45, 211–227. [Google Scholar] [PubMed]
- Demirjian, A.; Goldstein, H. New Systems for Dental Maturity Based on Seven and Four Teeth. Ann. Hum. Biol. 1976, 3, 411–421. [Google Scholar] [CrossRef]
- Kapoor, P.; Jain, V. Comprehensive Chart for Dental Age Estimation (DAEcc8) based on Demirjian 8-teeth method: Simplified for operator ease. J. Forensic Leg. Med. 2018, 59, 45–49. [Google Scholar] [CrossRef] [PubMed]



| Best Parameters from Genetic Algorithm | |
| max_depth’ | [10] |
| max_features’ | [sqrt] |
| min_samples_leaf’ | [4] |
| min_samples_split’ | [10] |
| n_estimators’ | [600] |
| Hyperparameters For RF | |
| ‘max_depth’ | [10, 20, 30, 40, 50, 60, 70, 80, 90, 100, None] |
| ‘max_features’ | [‘auto’, ‘sqrt’] |
| ‘min_samples_leaf’ | [1, 2, 4] |
| ‘min_samples_split’ | [2, 5, 10] |
| ‘n_estimators’ | [200, 400, 600, 800, 1000, 1200, 1400, 1600, 1800, 2000] |
| Model | Component | Details |
|---|---|---|
| Deep 2D CNN | Input Layer | Input size: (224, 224, 3) (Resized OPG Images) |
| Convolutional Layers | Conv1: 32 filters, kernel size (3 × 3), ReLU Conv2: 64 filters, kernel size (3 × 3), ReLU Conv3: 128 filters, kernel size (3 × 3), ReLU Conv4: 256 filters, kernel size (3 × 3), ReLU | |
| Pooling Layers | Maxpooling after each convolutional block, pool size (2 × 2) | |
| Fully Connected Layer | Dense layer: 512 units, ReLU activation | |
| Output Layer | Dense layer: 128 units (feature vector), Linear activation | |
| Deep 1D CNN | Input Layer | Input size: Variable (Patient Records) |
| Convolutional Layers | Conv1: 16 filters, kernel size (5), ReLU Conv2: 32 filters, kernel size (3), ReLU Conv3: 64 filters, kernel size (3), ReLU | |
| Pooling Layers | Global Maxpooling layer after final convolutional layer | |
| Fully Connected Layer | Dense layer: 256 units, ReLU activation | |
| Output Layer | Dense layer: 128 units (feature vector), Linear activation | |
| Feature Fusion | Concatenation Layer | Combines 128-unit outputs from both Deep 2D CNN and Deep 1D CNN |
| Modified Genetic-RF | Feature Input | 256 features (128 from Deep 2D CNN + 128 from Deep 1D CNN) |
| Regressor | Random Forest with Genetic Algorithm optimization: - Number of Trees: 100 Maximum Depth: Optimized by Genetic Algorithm- Split Criterion: Mean Squared Error |
| Methods | SD | MAE | MSE | RMSE | R2 |
|---|---|---|---|---|---|
| Demirjian | −0.705 | 1.108 | 1.981 | 1.406 | 0.816 |
| Willems | −0.220 | 0.928 | 1.418 | 1.190 | 0.868 |
| BRR | −0.002 | 0.812 | 1.030 | 1.014 | 0.904 |
| SVM | 0.016 | 0.729 | 0.901 | 0.949 | 0.916 |
| DT | −0.012 | 0.758 | 0.973 | 0.985 | 0.910 |
| RF | −0.007 | 0.731 | 0.885 | 0.940 | 0.918 |
| KNN | 0.009 | 0.738 | 0.921 | 0.959 | 0.915 |
| MLP | −0.041 | 0.742 | 0.907 | 0.952 | 0.916 |
| POLYREG | −0.008 | 0.735 | 0.913 | 0.955 | 0.915 |
| ADAB | −0.025 | 0.796 | 1.001 | 1.000 | 0.907 |
| STACK | −0.013 | 0.733 | 0.904 | 0.950 | 0.916 |
| VOTE | 0.068 | 0.770 | 0.995 | 0.984 | 0.908 |
| The proposed method | 0.0004 | 0.0079 | 0.00027 | 0.0888 | 0.9999 |
| Male | RMSE | MSE | MAE | Female | RMSE | MSE | MAE |
|---|---|---|---|---|---|---|---|
| Demirjian | 1.596 | 2.548 | 1.307 | Demirjian | 1.677 | 2.812 | 1.364 |
| Willems | 1.602 | 2.556 | 1.291 | Willems | 1.788 | 3.196 | 1.407 |
| MLP | 1.332 | 1.775 | 0.990 | MLP | 1.617 | 2.616 | 1.261 |
| The proposed method | 0.8888 | 0.00027 | 0.0079 | The proposed method | 0.8888 | 0.00027 | 0.0079 |
| Methods | MAE | MSE | RMSE | R2 |
|---|---|---|---|---|
| LR | 0.553 | 0.488 | 0.698 | 0.909 |
| SVM | 0.489 | 0.392 | 0.625 | 0.925 |
| RF | 0.495 | 0.389 | 0.623 | 0.928 |
| Cameriere Method (European Formula) | 0.846 | 0.755 | 0.869 | - |
| Cameriere Method (Chinese Formula) | 0.812 | 0.89 | 0.943 | - |
| The proposed method | 0.0079 | 0.0002 | 0.0888 | 0.9999 |
| MAE | SD | |
|---|---|---|
| AAM | 2.481 | 2.148 |
| AGM | 2.283 | 2.168 |
| The proposed method | 0.0079 | 0.0004 |
| Experiment Configuration | MAE | MSE | RMSE | R² |
|---|---|---|---|---|
| Proposed Method (Full) | 0.0079 | 0.0002 | 0.0888 | 0.9999 |
| Without Deep 2D CNN | 0.0125 | 0.0008 | 0.1414 | 0.9985 |
| Without Deep 1D CNN | 0.0113 | 0.0006 | 0.1225 | 0.9989 |
| Without Feature Concatenation | 0.0150 | 0.0012 | 0.1732 | 0.9978 |
| Using Only Deep 2D CNN | 0.0132 | 0.0009 | 0.1500 | 0.9982 |
| Using Only Deep 1D CNN | 0.0148 | 0.0011 | 0.1667 | 0.9979 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ozlu Ucan, G.; Gwassi, O.A.H.; Apaydin, B.K.; Ucan, B. Automated Age Estimation from OPG Images and Patient Records Using Deep Feature Extraction and Modified Genetic–Random Forest. Diagnostics 2025, 15, 314. https://doi.org/10.3390/diagnostics15030314
Ozlu Ucan G, Gwassi OAH, Apaydin BK, Ucan B. Automated Age Estimation from OPG Images and Patient Records Using Deep Feature Extraction and Modified Genetic–Random Forest. Diagnostics. 2025; 15(3):314. https://doi.org/10.3390/diagnostics15030314
Chicago/Turabian StyleOzlu Ucan, Gulfem, Omar Abboosh Hussein Gwassi, Burak Kerem Apaydin, and Bahadir Ucan. 2025. "Automated Age Estimation from OPG Images and Patient Records Using Deep Feature Extraction and Modified Genetic–Random Forest" Diagnostics 15, no. 3: 314. https://doi.org/10.3390/diagnostics15030314
APA StyleOzlu Ucan, G., Gwassi, O. A. H., Apaydin, B. K., & Ucan, B. (2025). Automated Age Estimation from OPG Images and Patient Records Using Deep Feature Extraction and Modified Genetic–Random Forest. Diagnostics, 15(3), 314. https://doi.org/10.3390/diagnostics15030314







