Global Mean-Motion Resonances: Part II—Laplace-like Phase Angles to Facilitate Libration Searches in Multiplanetary N-body Simulations
Abstract
1. Introduction and Motivation
1.1. Mean-Motion Resonances and Phase Angles
1.2. The Librating Phase Angle of Kepler-60
1.3. Outline
2. Method for Phase Angles in Triple Subsystems
3. Applications and Discussion
3.1. Table 1
3.2. Table 2
3.3. General Properties
- (i)
- (ii)
- (iii)
- This scenario also signifies that the same global MMR may or may not be librating in individual systems, as the incorporated -difference may or may not be locked in local resonance. The location of the most massive planet (i.e., the 1:1 orbit) in the MMR chain, as well as perturbations from neighboring planets outside of the resonance, may play an important role in determining the outcome of early dynamical evolution;
- (iv)
- The angles of five mostly mixed-order MMRs at the bottom half of Table 1 (HD 40307, PSR B1257+12, Kepler-90, VET, RTH) combine even multiples of with either or . If the terms could possibly be set aside for a moment, then the librations of angles would be determined solely by the single local -pair present in the phase angle. If the presumption in item (ii) holds for mixed/high-order MMRs as well, then the (5:3 and 8:5) MMR in Kepler-90 f-g-h and the (8:5 and 8:5) VET MMR that depend on should show circulating phases. Some local MMRs of mixed order (but not quite those listed in Table 1) have been studied numerically in the recent past (see, e.g., Refs. [5,6,17,30,42]);
- (v)
4. Summary and Conclusions
- :
- :
- :2: HD 110067 e-f-g(6), [35];
- :
- ::1 Kepler-444 d-e-f(5), [43].
- (a)
- We call principal resonant orbits those in the MMR set with . The principal MMRs are available for orbiting bodies to settle in safely, although the 2:1 MMR appears to be vacant (except in LRs and Laplace-like chains). High-order MMRs of this type provide shelter to orbiting bodies, especially to small distant planets, dwarf planets, and minor moons. For instance, Mercury and Pluto occupy the 1:50 and 21:1 MMRs of Jupiter, respectively, and Pan and Kiviuq occupy the 1:28 and 28:1 MMRs of Titan, respectively, in the Saturnian system;
- (b)
- Besides principal MMRs, very few rational outer MMRs :p and their reciprocal inner MMRs are common in multibody (sub)systems, and even fewer MMRs with appear scarcely. Our survey of 73 exosystems and solar subsystems is mapped out in Table 3. The scarce MMRs (, ) are enclosed in parentheses. An intriguing feature in this chart is that the MMRs commonly appear in reciprocal pairs. The three exceptional cases (4:5, 2:7, and 8:3) are also interesting in their own right;
- (c)
- Extending Table 3 out to and , we find only the 9:2 MMR in exosystems. Surprisingly, this MMR is common in systems that contain complete LRs (HIP 41378 d, HR 8799 b) or uncompleted (would-be) LRs (Kepler-48 d, Kepler-332 d). In the former case, two overlapping LRs are avoided (see also item 8 above); in the latter case, classical LRs are not assembled, and the global 2:1 MMR (that would have formed the LR) remains vacant.
| q | ||||||
| 1 | 2 | 3 | 4 | 5 | ||
| p | 1 | 1:2, 2:1 | 1:3, 3:1 | 1:4, 4:1 | 1:5, 5:1 | 1:6, 6:1 |
| 2 | 2:3, 3:2 | — | 2:5, 5:2 | — | 2:7 | |
| 3 | 3:4, 4:3 | 3:5, 5:3 | — | 3:7, 7:3 | 8:3 | |
| 4 | 4:5 | — | (4:7, 7:4) | — | (4:9, 9:4) | |
| 5 | — | (5:7) | (5:8) | — | — | |
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EGC | Europa-Ganymede-Callisto |
| IEG | Io-Europa-Ganymede |
| LR | Laplace Resonance |
| MMR | Mean-Motion Resonance |
| MVE | Mercury-Venus-Earth |
| RTH | Rhea-Titan-Hyperion |
| SF21 | Siegel and Fabrycky (2021), Ref. [8] |
| TR-1 | TRAPPIST-1 |
| UTO | Umbriel-Titania-Oberon |
| VET | Venus-Earth-Toro |
Appendix A. Four-Planet Laplace-like Phase Angles in HD 110067

Appendix B. Overlapping First-Order Four-Body MMRs
Appendix B.1. Four-Body Phase Angles
Appendix B.2. The Classical Double LR with rj = 1
Appendix B.3. Application to Kepler-223

| 1 | We use the term ‘local’ for MMRs between pairs of adjacent planets, such as those studied in the past. We also use the term ‘global’ for MMRs between three or more planets, such as those studied in this work. In the longest global MMR chains that include all closely packed planets (and may not include too distant planets), the most massive planet is thought to occupy the 1:1 resonant orbit because its inertia against radial excursions is the largest one. |
| 2 | As in Celletti et al. [17], we use the term ‘Laplace-like’ for some phase angles that are particular linear combinations of the mean orbital longitudes of adjacent planets. In Ref. [18], we identified three such three-body global MMRs: 1::2 (seen in HD 110067); ::1 (seen in Kepler-90, TOI-1136, and TRAPPIST-1); and :1: (seen in Kepler-223 and TOI-178). |
| 3 | Item (f) in Section 3.3: The paired MMRs are 5:4 and 7:6 and 2:1 and 7:3; the preconditions are and ; and the reduced 2 × 3 Diophantine system is with roots and . The sought-after solution is obtained by choosing . The only other solution of potential interest is obtained for , leading to the paired MMRs 3:2 and 5:4 (unrealized) and 2:1 and 5:3 (HD 40307 [46,47] in Table 1), both with the same phase . |
References
- Papaloizou, J.C.B. Three body resonances in close orbiting planetary systems: Tidal dissipation and orbital evolution. Int. J. Astrobiol. 2015, 14, 291. [Google Scholar] [CrossRef]
- Goździewski, K.; Migaszewski, C.; Panichi, F.; Szuszkiewicz, E. The Laplace resonance in the Kepler-60 planetary system. Mon. Not. R. Astron. Soc. Lett. 2016, 455, L104. [Google Scholar] [CrossRef]
- Mills, S.M.; Fabrycky, D.C.; Migaszewski, C.; Ford, E.B.; Petigura, E.; Isaacson, H. A resonant chain of four transiting, sub-Neptune planets. Nature 2016, 533, 509. [Google Scholar] [CrossRef] [PubMed]
- Delisle, J.B. Analytical model of multi-planetary resonant chains and constraints on migration scenarios. Astron. Astrophys. 2017, 605, A96. [Google Scholar] [CrossRef]
- Charalambous, C.; Martí, J.G.; Beaugé, C.; Ramos, X.S. Resonance capture and dynamics of three-planet systems. Mon. Not. R. Astron. Soc. Lett. 2018, 477, 1414. [Google Scholar] [CrossRef]
- Morrison, S.J.; Dawson, R.I.; MacDonald, M. Chains of planets in mean motion resonances arising from oligarchic growth. Astrophys. J. 2020, 904, 157. [Google Scholar] [CrossRef]
- Jontof-Hutter, D.; Ford, E.B.; Rowe, J.F.; Lissauer, J.J.; Fabrycky, D.C.; Van Laerhoven, C.; Agol, E.; Deck, K.M.; Holczer, T.; Mazeh, T. Erratum: “Secure TTV mass measurements: Ten Kepler exoplanets between 3 and 8 M⊕ with diverse densities and incident fluxes”. Astron. J. 2021, 911, 154. [Google Scholar] [CrossRef]
- Siegel, J.C.; Fabrycky, D. Resonant chains of exoplanets: Libration centers for three-body angles. Astron. J. 2021, 161, 290. [Google Scholar] [CrossRef]
- MacDonald, M.G.; Feil, L.; Quinn, T.; Rice, D. Confirming the 3:2 resonance chain of K2-138. Astron. J. 2022, 163, 162. [Google Scholar] [CrossRef]
- MacDonald, M.G.; Vivas, M.S.P.; D’Angiolillo, S.; Fernandez, A.N.; Quinn, T. exoMMR: A new python package to confirm and characterize mean motion resonances. Astron. J. 2023, 166, 94. [Google Scholar] [CrossRef]
- Quinn, T.; MacDonald, M.G. Confirming resonance in three transiting systems. Astron. J. 2023, 166, 58. [Google Scholar] [CrossRef]
- Luger, R.; Sestovic, M.; Kruse, E.; Grimm, S.L.; Demory, B.O.; Agol, E.; Bolmont, E.; Fabrycky, D.; Fernandes, C.S.; Grootel, V.V.; et al. A seven-planet resonant chain in TRAPPIST-1. Nat. Astron. 2017, 1, 0129. [Google Scholar] [CrossRef]
- Mah, J. Formation and Dynamics of the Resonant Chain in the TRAPPIST-1 Exoplanet System. Master’s Thesis, University of Hong Kong, Hong Kong, China, 2018. [Google Scholar]
- Brasser, R.; Barr, A.C.; Dobos, V. The tidal parameters of TRAPPIST-1b and c. Mon. Not. R. Astron. Soc. Lett. 2019, 487, 34. [Google Scholar] [CrossRef]
- Agol, E.; Dorn, C.; Grimm, S.L.; Turbet, M.; Ducrot, E.; Delrez, L.; Gillon, M.; Demory, B.; Burdanov, A.; Barkaoui, K.; et al. Refining the transit-timing and photometric analysis of TRAPPIST-1: Masses, radii, densities, dynamics, and ephemerides. Planet. Sci. J. 2021, 2, 1. [Google Scholar] [CrossRef]
- Lari, G.; Saillenfest, M.; Fenucci, M. The Galilean satellites’ evolution toward a 4-body mean motion resonance. In Proceedings of the EPSC-DPS Joint Meeting 2019, Geneva, Switzerland, 15–20 September 2019; Volume 13. [Google Scholar]
- Celletti, A.; Karampotsiou, E.; Lhotka, C.; Pucacco, G.; Volpi, M. Laplace-like resonances with tidal effects. Astron. Astrophys. 2021, 655, A94. [Google Scholar] [CrossRef]
- Christodoulou, D.M.; Sorabella, N.M.; Bhattacharya, S.; Laycock, S.G.T.; Kazanas, D.I. An Exceptional Multiplanetary Resonant Chain in TOI-270 and an Exact Laplace-like Resonance in HD 110067. Preprints 2024. Available online: https://www.preprints.org/manuscript/202410.1806/v1 (accessed on 24 February 2025). [CrossRef]
- Murray, C.D.; Dermott, S.F. Solar System Dynamics; Cambridge University Press: Cambridge, UK, 1999; pp. 364–371+396–399. [Google Scholar]
- Lieske, J.H. Galilean satellite ephemerides E5. Astron. Astrophys. Supl. Ser. 1998, 129, 205. [Google Scholar] [CrossRef]
- Musotto, S.; Varadi, F.; Moore, W.; Schubert, G. Numerical simulations of the orbits of the Galilean satellites. Astron. Astrophys. 2002, 159, 500. [Google Scholar] [CrossRef]
- Wolszczan, A.; Frail, D.A. A planetary system around the millisecond pulsar PSR1257+12. Nature 1992, 355, 145. [Google Scholar] [CrossRef]
- Konacki, M.; Wolszczan, A. Masses and orbital inclinations of planets in the PSR B1257+12 system. Astrophys. J. Lett. 2003, 591, L147. [Google Scholar] [CrossRef]
- Wolszczan, A. Discovery of pulsar planets. New Astron. Rev. 2012, 56, 2. [Google Scholar] [CrossRef]
- Goździewski, K.; Konacki, M.; Wolszczan, A. Long-term stability and dynamical environment of the PSR 1257+12 planetary system. Astrophys. J. 2005, 619, 1084. [Google Scholar] [CrossRef]
- Günther, M.N.; Pozuelos, F.J.; Dittmann, J.A.; Dragomir, D.; Kane, S.R.; Daylan, T.; Feinstein, A.D.; Huang, C.X.; Morton, T.D.; Bonfanti, A.; et al. A super-Earth and two sub-Neptunes transiting the nearby and quiet M dwarf TOI-270. Nat. Astron. 2019, 3, 1099. [Google Scholar] [CrossRef]
- Kaye, L.; Vissapragada, S.; Günther, M.N.; Aigrain, S.; Mikal-Evans, T.; Jensen, E.L.N.; Parviainen, H.; Pozuelos, F.J.; Abe, L.; Acton, J.S.; et al. Transit timings variations in the three-planet system: TOI-270. Mon. Not. R. Astron. Soc. Lett. 2022, 510, 5464. [Google Scholar] [CrossRef]
- Mikal-Evans, T.; Madhusudhan, N.; Dittmann, J.; Günther, M.N.; Welbanks, L.; Eylen, V.V.; Crossfield, I.J.M.; Daylan, T.; Kreidberg, L. Hubble Space Telescope transmission spectroscopy for the temperate sub-Neptune TOI-270 d: A possible hydrogen-rich atmosphere containing water vapor. Astron. J. 2023, 165, 84. [Google Scholar] [CrossRef]
- Danielsson, L. The orbital resonances between the asteroid Toro and the Earth and Venus. Moon Planets 1978, 18, 265. [Google Scholar] [CrossRef]
- MacDonald, M.G.; Ragozzine, D.; Fabrycky, D.C.; Ford, E.B.; Holman, M.J.; Isaacson, H.T.; Lissauer, J.J.; Lopez, E.D.; Mazeh, T.; Rogers, L.; et al. A dyamical analysis of the Kepler-80 system of five transiting planets. Astron. J. 2016, 152, 105. [Google Scholar] [CrossRef]
- Ćuk, M.; El Moutamid, M.; Tiscareno, M.S. Dynamical history of the Uranian system. Planet. Sci. J. 2020, 1, 22. [Google Scholar] [CrossRef]
- Jacobson, R.A. The orbits of the Uranian satellites and rings, the gravity field of the Uranian system, and the orientation of the pole of Uranus. Astron. J. 2014, 148, 76. [Google Scholar] [CrossRef]
- Christodoulou, D.M.; Laycock, S.G.T.; Kazanas, D. A library of 77 multibody solar and extrasolar subsystems. Preprints 2025. [Google Scholar] [CrossRef]
- Jacobson, R.A. The orbits of the main Saturnian satellites, the Saturnian system gravity field, and the orientation of Saturn’s pole. Astron. J. 2022, 164, 199. [Google Scholar] [CrossRef]
- Luque, R.; Osborn, H.P.; Leleu, A.; Pallé, E.; Bonfanti, A.; Barragán, O.; Wilson, T.G.; Broeg, C.; Cameron, A.C.; Lendl, M.; et al. A resonant sextuplet of sub-Neptunes transiting the bright star HD 110067. Nature 2023, 623, 932. [Google Scholar] [CrossRef] [PubMed]
- Gillon, M.; Triaud, A.H.; Demory, B.O.; Jehin, E.; Agol, E.; Deck, K.M.; Lederer, S.M.; de Wit, J.; Burdanov, A.; Ingalls, J.G.; et al. Seven temperate terrestrial planets around the nearby ultracool dwarf star TRAPPIST-1. Nature 2017, 542, 456. [Google Scholar] [CrossRef]
- Forgács-Dajka, E.; Sándor, Z.; Érdi, B. A fast method to identify mean motion resonances. Mon. Not. R. Astron. Soc. Lett. 2018, 477, 3383. [Google Scholar] [CrossRef]
- Lainey, V.; Duriez, L.; Vienne, A. Synthetic representation of the Galilean satellites’ orbital motions from L1 ephemerides. Astron. Astrophys. 2006, 456, 783. [Google Scholar] [CrossRef]
- Lari, G.; Saillenfest, M. The nature of the Laplace resonance between the Galilean moons. Celest. Mech. Dyn. Astron. 2024, 136, 19. [Google Scholar] [CrossRef]
- Batygin, K.; Morbidelli, A. Analytical treatment of planetary resonances. Astron. Astrophys. 2013, 556, A28. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, L.-Y.; Beaugé, C. Resonant chains in triple-planet systems. Astron. Astrophys. 2024, 687, A266. [Google Scholar] [CrossRef]
- Rivera, E.J.; Laughlin, G.; Butler, R.P.; Vogt, S.S.; Haghighipour, N.; Meschiari, S. The Lick-Carnegie exoplanet survey: A Uranus-mass fourth planet for GJ 876 in an extrasolar Laplace configuration. Astrophys. J. 2010, 719, 890. [Google Scholar] [CrossRef]
- Mills, S.M.; Fabrycky, D.C. Mass, density, and formation constraints in the compact, sub-Earth Kepler-444 system including two Mars-mass planets. Astrophys. J. Lett. 2017, 838, L11. [Google Scholar] [CrossRef]
- Weiss, L.M.; Isaacson, H.; Howard, A.W.; Fulton, B.J.; Petigura, E.A.; Fabrycky, D.; Jontof-Hutter, D.; Steffen, J.H.; Schlichting, H.E.; Wright, J.T.; et al. The Kepler Giant Planet Search. I. A decade of Kepler planet-host radial velocities from W. M. Keck Observatory. Astrophys. J. Suppl. Ser. 2024, 270, 8. [Google Scholar] [CrossRef]
- Barros, S.C.C.; Demangeon, O.D.S.; Alibert, Y.; Leleu, A.; Adibekyan, V.; Lovis, C.; Bossini, D.; Sousa, S.G.; Hara, N.; Bouchy, F.; et al. HD 23472: A multi-planetary system with three super-Earths and two potential super-Mercuries. Astron. Astrophys. 2022, 665, A154. [Google Scholar] [CrossRef]
- Díaz, R.F.; Ségransan, D.; Udry, S.; Lovis, C.; Pepe, F.; Dumusque, X.; Marmier, M.; Alonso, R.; Benz, W.; Bouchy, F.; et al. The HARPS search for southern extra-solar planets. XXXVIII. Bayesian re-analysis of three systems. New super-Earths, unconfirmed signals, and magnetic cycles. Astron. Astrophys. 2016, 585, A134. [Google Scholar] [CrossRef]
- Tuomi, M.; Anglada-Escudé, G.; Gerlach, E.; Jones, H.R.A.; Reiners, A.; Rivera, E.J.; Vogt, S.S.; Butler, P.R. Habitable-zone super-Earth candidate in a six-planet system around the K2.5V star HD 40307. Astron. Astrophys. 2013, 549, A48. [Google Scholar] [CrossRef]
- Rambaux, N.; Van Hoolst, T.; Karatekin, Ö. Librational response of Europa, Ganymede, and Callisto with an ocean for a non-Keplerian orbit. Astron. Astrophys. 2011, 527, A118. [Google Scholar] [CrossRef]
- Lari, G.; Saillenfest, M.; Fenucci, M. Long-term evolution of the Galilean satellites: The capture of Callisto into resonance. Astron. Astrophys. 2020, 639, A40. [Google Scholar] [CrossRef]
- Downey, B.G.; Nimmo, F.; Matsuyama, I. Inclination damping on Callisto. Mon. Not. R. Astron. Soc. Lett. 2020, 499, 40. [Google Scholar] [CrossRef]
- Goldreich, P. An explanation of the frequent occurrence of commensurable mean motions in the solar system. Mon. Not. R. Astron. Soc. Lett. 1965, 130, 159. [Google Scholar] [CrossRef]
- Hamilton, D.P.; Burns, J.A. Orbital stability zones about asteroids: II. The destabilizing effects of eccentric orbits and of solar radiation. Astron. Astrophys. 1992, 96, 43. [Google Scholar]
- Bonomo, A.S.; Dumusque, X.; Massa, A.; Mortier, A.; Bongiolatti, R.; Malavolta, L.; Sozzetti, A.; Buchhave, L.A.; Damasso, M.; Haywood, R.D.; et al. Cold Jupiters and improved masses in 38 Kepler and K2 small planet systems from 3661 HARPS-N radial velocities. Astron. Astrophys. 2023, 677, A33. [Google Scholar] [CrossRef]
- Lissauer, J.J.; Jontof-Hutter, D.; Rowe, J.F.; Fabrycky, D.C.; Lopez, E.D.; Agol, E.; Marcy, G.W.; Deck, K.M.; Fischer, D.A.; Fortney, J.J.; et al. All six planets known to orbit Kepler-11 have low densities. Astrophys. J. 2013, 770, 131. [Google Scholar] [CrossRef]
- Bedell, M.; Bean, J.L.; Meléndez, J.; Mills, S.M.; Fabrycky, D.C.; Freitas, F.C.; Ramírez, I.; Asplund, M.; Liu, F.; Yong, D. Kepler-11 is a solar twin: Revising the masses and radii of benchmark planets via precise stellar characterization. Astrophys. J. 2017, 839, 94. [Google Scholar] [CrossRef]
- Hara, N.C.; Bouchy, F.; Stalport, M.; Boisse, I.; Rodrigues, J.; Delisle, J.B.; Santerne, A.; Henry, G.W.; Arnold, L.; Astudillo-Defru, N.; et al. The SOPHIE search for northern extrasolar planets. XVI. HD 158259: A compact planetary system in a near-3:2 mean motion resonance chain. Astron. Astrophys. 2020, 636, L6. [Google Scholar] [CrossRef]
- Christiansen, J.L.; Bhure, S.; Zink, J.K.; Hardegree-Ullman, K.K.; Adkins, B.D.; Hedges, C.; Morton, T.D.; Bieryla, A.; Ciardi, D.R.; Cochran, W.D.; et al. Scaling K2. V. Statistical validation of 60 new exoplanets from K2 campaigns 2–18. Astron. J. 2022, 163, 244. [Google Scholar] [CrossRef]
- Judkovsky, Y.; Ofir, A.; Aharonson, O. Kepler multitransiting system physical properties and impact parameter variations. Astron. J. 2024, 167, 103. [Google Scholar] [CrossRef]
- Goździewski, K.; Migaszewski, C. An exact, generalized Laplace resonance in the HR 8799 planetary system. Astrophys. J. Lett. 2020, 902, L40. [Google Scholar] [CrossRef]
- Zurlo, A.; Goździewski, K.; Lazzoni, C.; Mesa, D.; Nogueira, P.; Desidera, S.; Gratton, R.; Marzari, F.; Langlois, M.; Pinna, E.; et al. Orbital and dynamical analysis of the system around HR8799. New astrometric epochs from VLT/SPHERE and LBT/LUCI. Astron. Astrophys. 2022, 666, A133. [Google Scholar] [CrossRef]
| Global MMRs (1) | Local MMR Pairs (2) | Pair Order a (3) | Phase b Angle φ (4) | Multibody System (5) |
|---|---|---|---|---|
| 1 : 3/2 : 2 | 3:2 & 4:3 | 1 | HD 110067 (most recently found LR multiple; Paper I) | |
| 2/3 : 1 : 4/3 | 3:2 & 4:3 | 1 | Kepler-223, TOI-178 | |
| 1/2 : 3/4 : 1 | 3:2 & 4:3 | 1 | Kepler-90, TOI-1136,TRAPPIST-1 (TR-1) | |
| 2/3 : 1 : 3/2 | 3:2 & 3:2 | 1 | Kepler-11, K2-138, HD 110067, TR-1(TR-1) | |
| 2/3 : 1 : 5/3 | 3:2 & 5:3 | M | HD 23472 (Section 3.3 (d) in relation to Kepler-444) | |
| 2/3 : 1 : 2/1 | 3:2 & 2:1 | 1 | TOI-1136, c Kepler-20 (::); no librations (∦) | |
| 2/3 : 1 : 5/1 | 3:2 & 5:1 | M | HD 34445 | |
| 3/4 : 1 : 3/2 | 4:3 & 3:2 | 1 | TOI-1136, HIP 41378, d Kepler-223, e HD 23472, e TR-1 | |
| 3/4 : 1 : 5/3 | 4:3 & 5:3 | M | Kepler-90 | |
| (3/4 : 1 : 5/4) | (4:3 & 5:4) | (1) | (Not observed; discussed in Section 3.3 (d) and in Table 2) | |
| 1/3 : 1 : 4/3 | 3:1 & 4:3 | M | HD 10180 | |
| 1/3 : 1 : 3/2 | 3:1 & 3:2 | M | Kepler-80 | |
| 1/2 : 1 : 3/2 | 2:1 & 3:2 | 1 | Kepler-32, Kepler-82 (::1), Umbriel-Titania-Oberon (U) | |
| 1/2 : 1 : 5/3 | 2:1 & 5:3 | M | HD 40307 | |
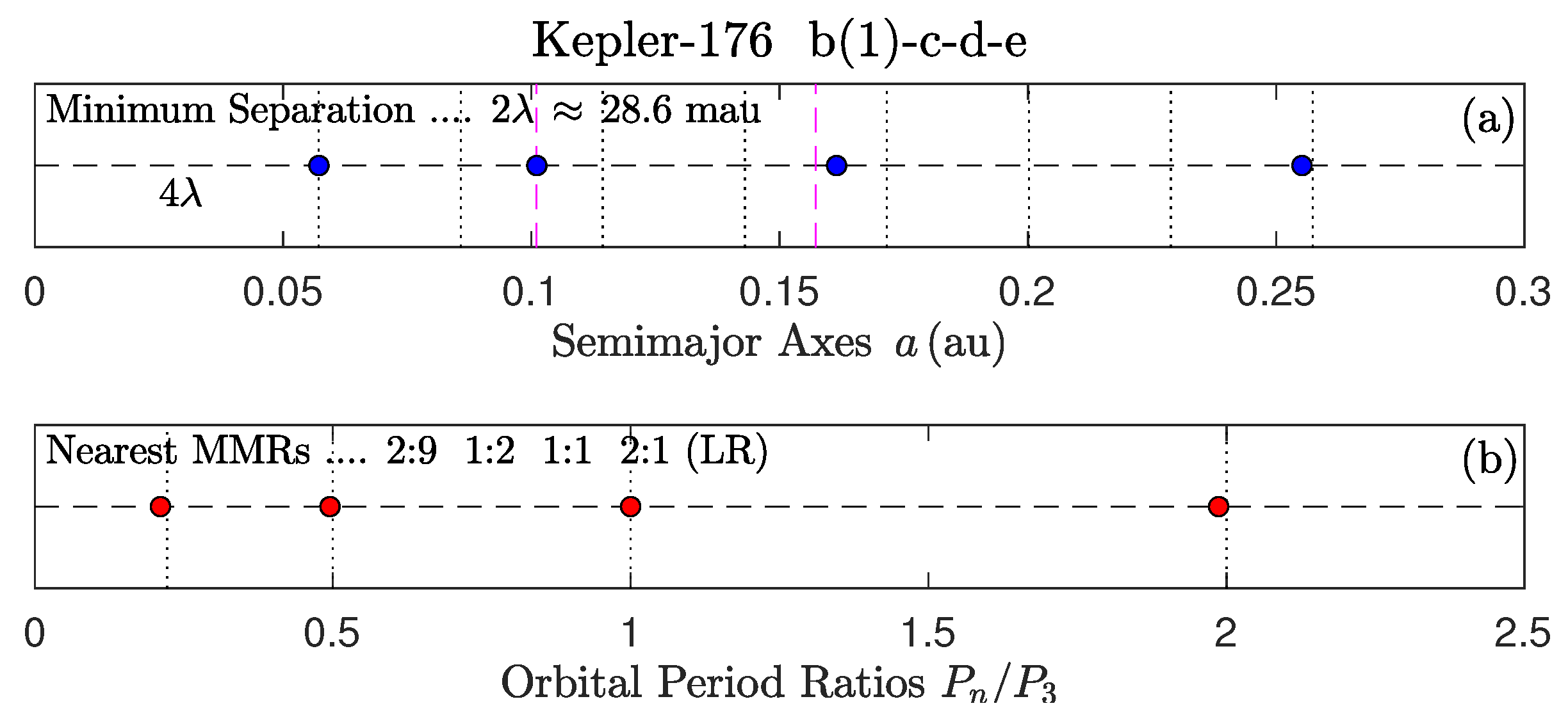
| 1/2 : 1 : 2/1 | 2:1 & 2:1 | 1 | GJ 876, HR 8799, HR 8832, Kepler-176 (Paper I) | |
| 1/4 : 1/2 : 1 | 2:1 & 2:1 | 1 | HIP 41378, Io-Europa-Ganymede (Galilean LR) (Paper I) | |
| 1/4 : 5/8 : 1 | 5:2 & 8:5 | 3 | Mercury-Venus-Earth (MVE) secondary MMR | |
| 1/2 : 1 : 7/3 | 2:1 & 7:3 | M | Europa-Ganymede-Callisto (EGC) MMR, no librations | |
| 1/5 : 1/2 : 1 | 5:2 & 2:1 | M | HD 40307 | |
| 2/5 : 1 : 3/2 | 5:2 & 3:2 | M | PSR B1257+12 f (although :1: is a strong alternative) | |
| 3/5 : 1 : 8/5 | 5:3 & 8:5 | M | Kepler-90 g | |
| 3/5 : 1 : 2/1 | 5:3 & 2:1 | M | TOI-270 h (and Ariel-Umbriel-Titania ::1 MMR) (U) | |
| 3/5 : 1 : 9/4 | 5:3 & 9:4 | M | HD 108236 | |
| 4/5 : 1 : 4/3 | 5:4 & 4:3 | 1 | Kepler-60 | |
| 5/8 : 1 : 7/4 | 8:5 & 7:4 | 3 | TOI-700 | |
| 5/8 : 1 : 8/5 | 8:5 & 8:5 | 3 | Venus-Earth-Toro (VET) secondary MMR i | |
| 2/7 : 1 : 4/3 | 7:2 & 4/3 | M | Rhea-Titan-Hyperion (RTH) (S) (Section 3.3 (g), Paper I) | |
| 4/7 : 1 : 9/4 | 7:4 & 9/4 | M | Kepler-20 |
| Row Index | Global MMRs (1) | Local MMR Pairs (2) | Phase Angle φ (3) | Equivalent Form of φ (4) | Libration Centers (°) (5) | Multibody System (6) |
|---|---|---|---|---|---|---|
| 1 | 1/2 : 1 : 2/1 | 2:1 & 2:1 | 0 | GJ 876, HR 8799, HR 8832, Kepler-176 (Paper I) | ||
| 2 | 1/4 : 1/2 : 1 | 2:1 & 2:1 | 180 | HIP 41378, IEG (Galilean LR) | ||
| 3 | 1 : 3/2 : 2/1 | 3:2 & 4:3 | HD 110067 | |||
| 4 | 2/3 : 1 : 4/3 | 3:2 & 4:3 | Kepler-223, TOI-178 | |||
| 5 | 1/2 : 3/4 : 1 | 3:2 & 4:3 | Kepler-90, TOI-1136, TR-1 | |||
| 6 | 2/3 : 1 : 2/1 | 3:2 & 2:1 | None | TOI-1136, Kepler-20 (::); no librations | ||
| 7 | 3/4 : 1 : 3/2 | 4:3 & 3:2 | TOI-1136, HIP 41378, Kepler-223, HD 23472, TR-1 | |||
| 8 | 4/5 : 1 : 4/3 | 5:4 & 4:3 | , | Kepler-60 | ||
| 9 | 2/3 : 1 : 3/2 | 3:2 & 3:2 | Kepler-11, K2-138, HD 110067, TR-1 | |||
| 10 | 1/2 : 1 : 3/2 | 2:1 & 3:2 | Kepler-32, Kepler-82, UTO | |||
| 11 | 3/4 : 1 : 5/4 | 4:3 & 5:4 | 180 | Not yet observed | ||
| 12 | 3/4 : 1 : 2/1 | 4:3 & 2:1 | None | Not observed (no librations) | ||
| 13 | 4/5 : 1 : 2/1 | 5:4 & 2:1 | None | Not observed (no librations) | ||
| 14 | 1 : 5/3 : 5/2 | 5:3 & 3:2 | TR-1 (::), Kepler-11 (::1), HD 40307 | |||
| 15 | 5/8 : 1 : 5/3 | 8:5 & 5:3 | TR-1 (::) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Christodoulou, D.M.; Sorabella, N.M.; Bhattacharya, S.; Laycock, S.G.T.; Kazanas, D. Global Mean-Motion Resonances: Part II—Laplace-like Phase Angles to Facilitate Libration Searches in Multiplanetary N-body Simulations. Galaxies 2025, 13, 41. https://doi.org/10.3390/galaxies13020041
Christodoulou DM, Sorabella NM, Bhattacharya S, Laycock SGT, Kazanas D. Global Mean-Motion Resonances: Part II—Laplace-like Phase Angles to Facilitate Libration Searches in Multiplanetary N-body Simulations. Galaxies. 2025; 13(2):41. https://doi.org/10.3390/galaxies13020041
Chicago/Turabian StyleChristodoulou, Dimitris M., Nicholas M. Sorabella, Sayantan Bhattacharya, Silas G. T. Laycock, and Demosthenes Kazanas. 2025. "Global Mean-Motion Resonances: Part II—Laplace-like Phase Angles to Facilitate Libration Searches in Multiplanetary N-body Simulations" Galaxies 13, no. 2: 41. https://doi.org/10.3390/galaxies13020041
APA StyleChristodoulou, D. M., Sorabella, N. M., Bhattacharya, S., Laycock, S. G. T., & Kazanas, D. (2025). Global Mean-Motion Resonances: Part II—Laplace-like Phase Angles to Facilitate Libration Searches in Multiplanetary N-body Simulations. Galaxies, 13(2), 41. https://doi.org/10.3390/galaxies13020041







