Analysis of the Thermo-Mechanical Behavior of a Multi-Plate Clutch during Transient Operating Conditions Using the FE Method
Abstract
:1. Introduction
1.1. Motivation and State of the Art
1.2. Research Objectives
2. Mathematical Model
2.1. Thermal Principles
2.2. Mechanical Principles
3. Finite Element Formulation
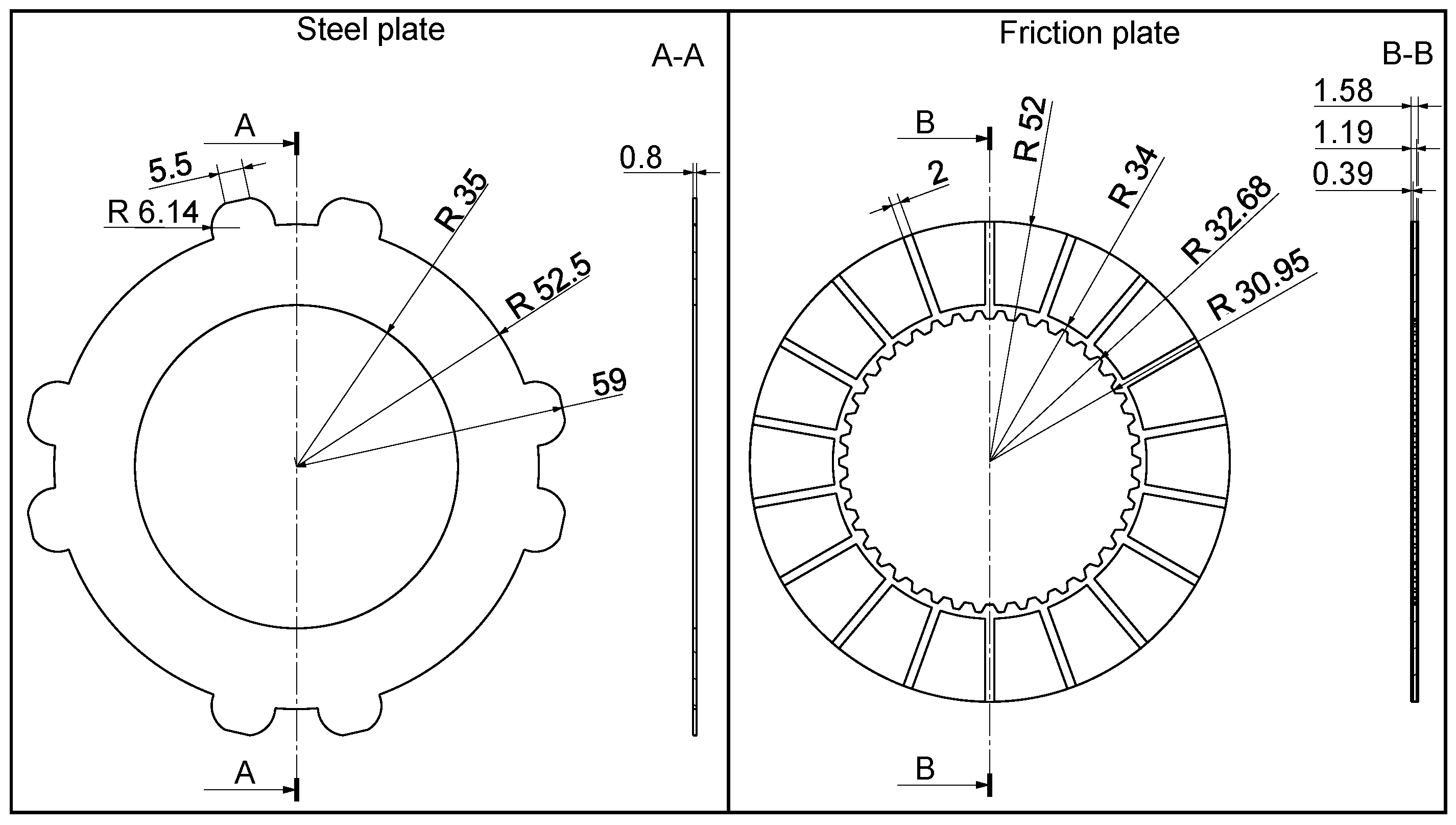
3.1. Geometry
3.2. Finite Element Method Settings
3.3. Operating Conditions
3.4. Material Properties
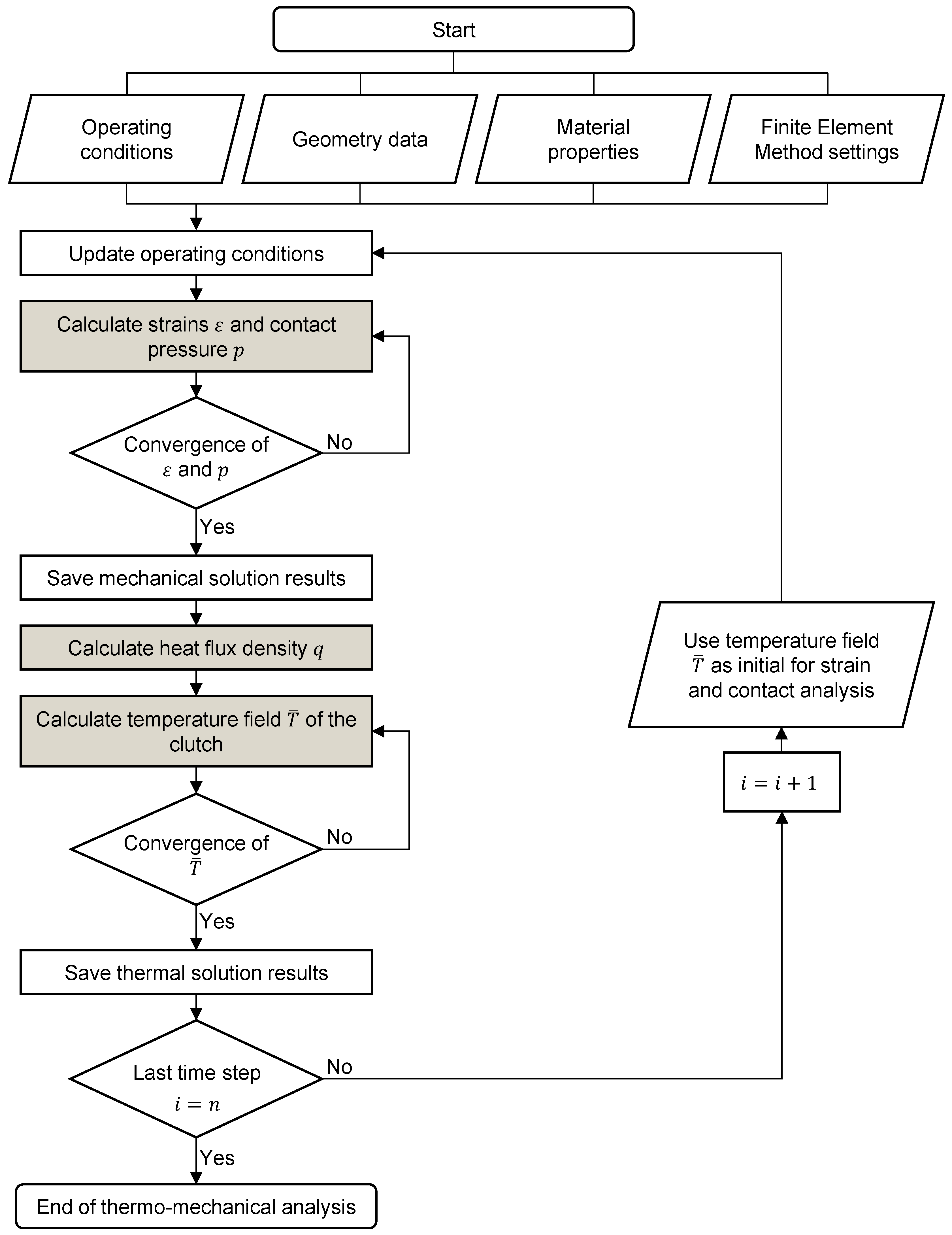
3.5. Simulation Process
4. Results
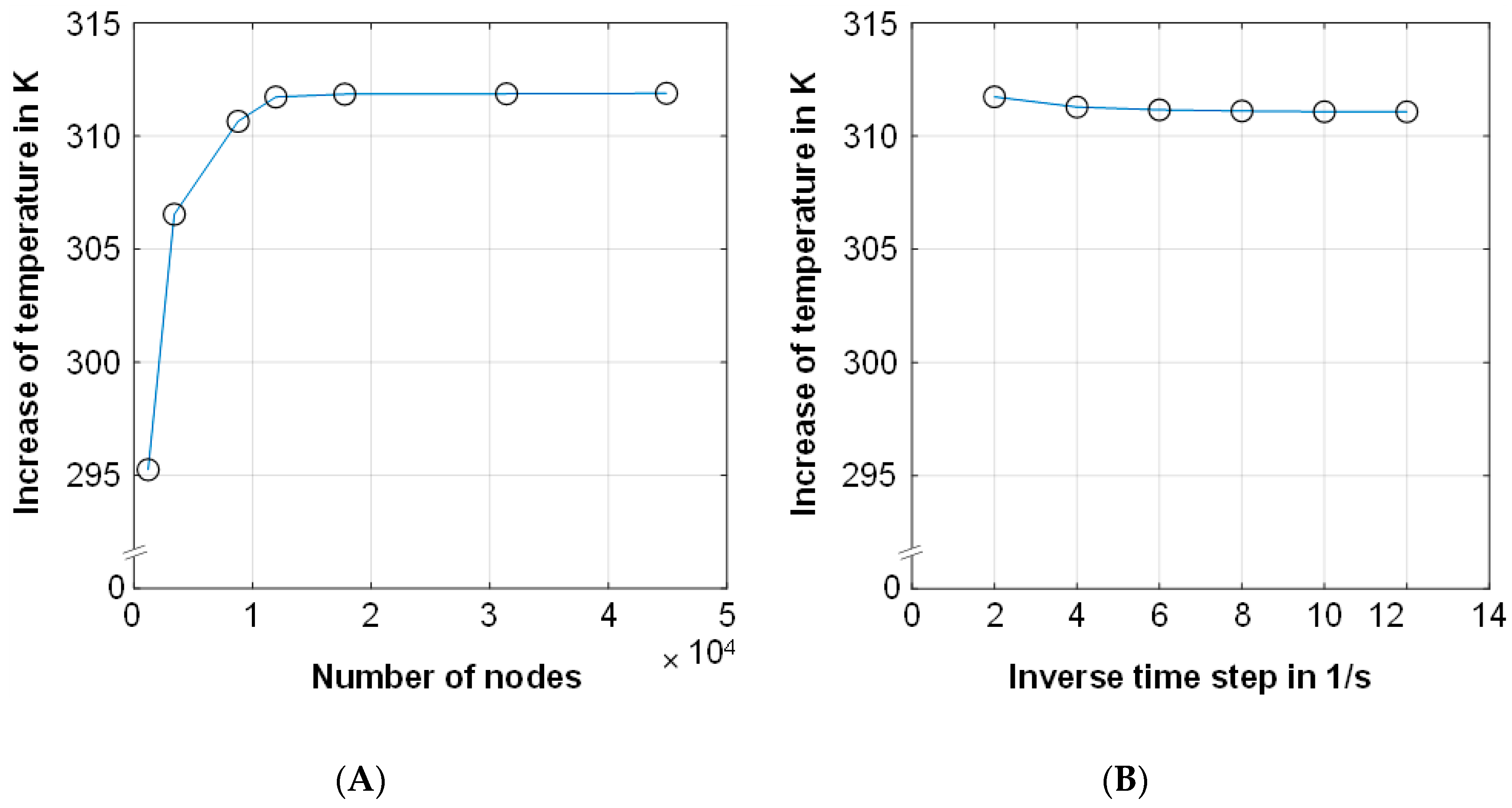
4.1. Mesh and Time-Step Sensitivity Analysis
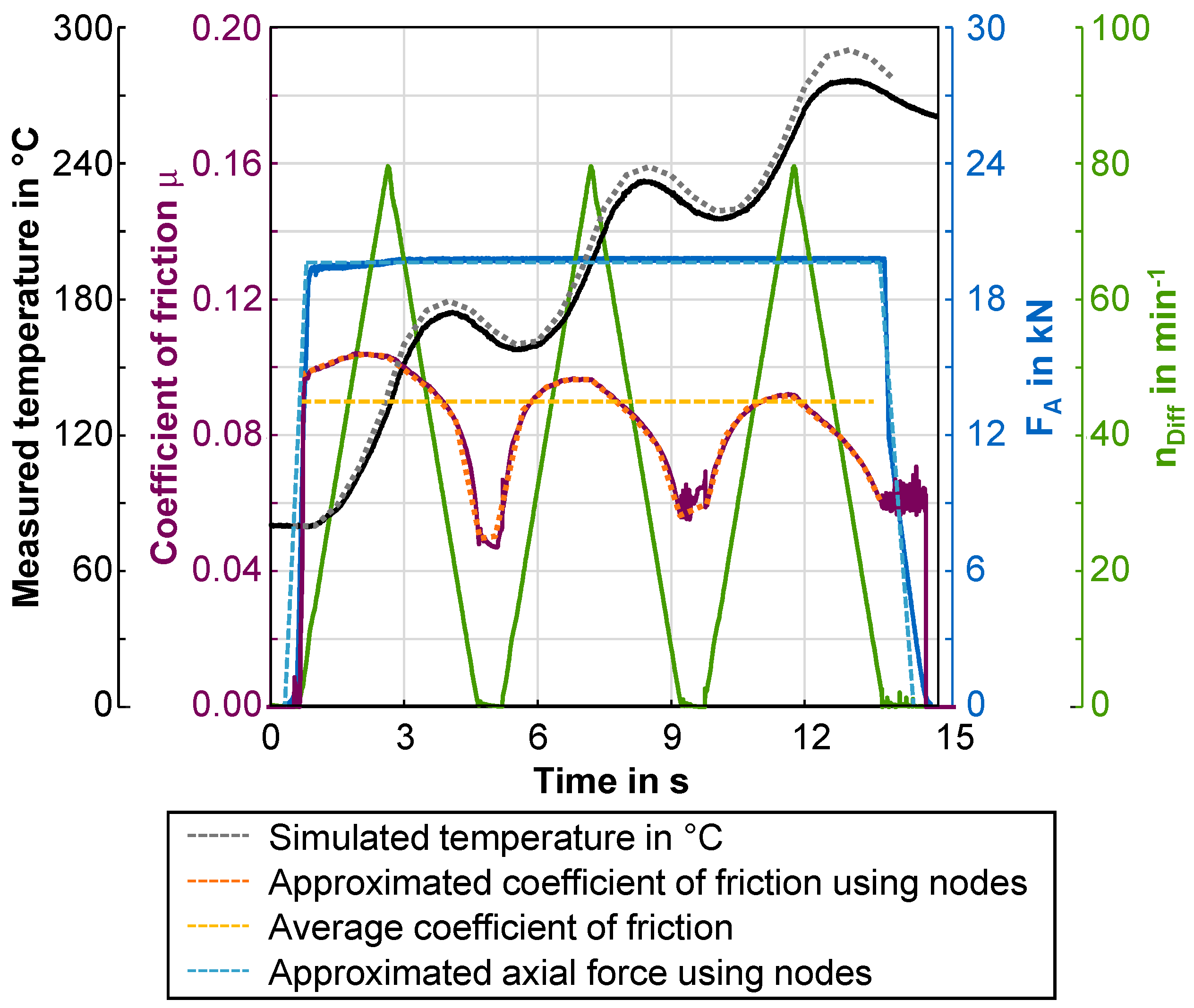
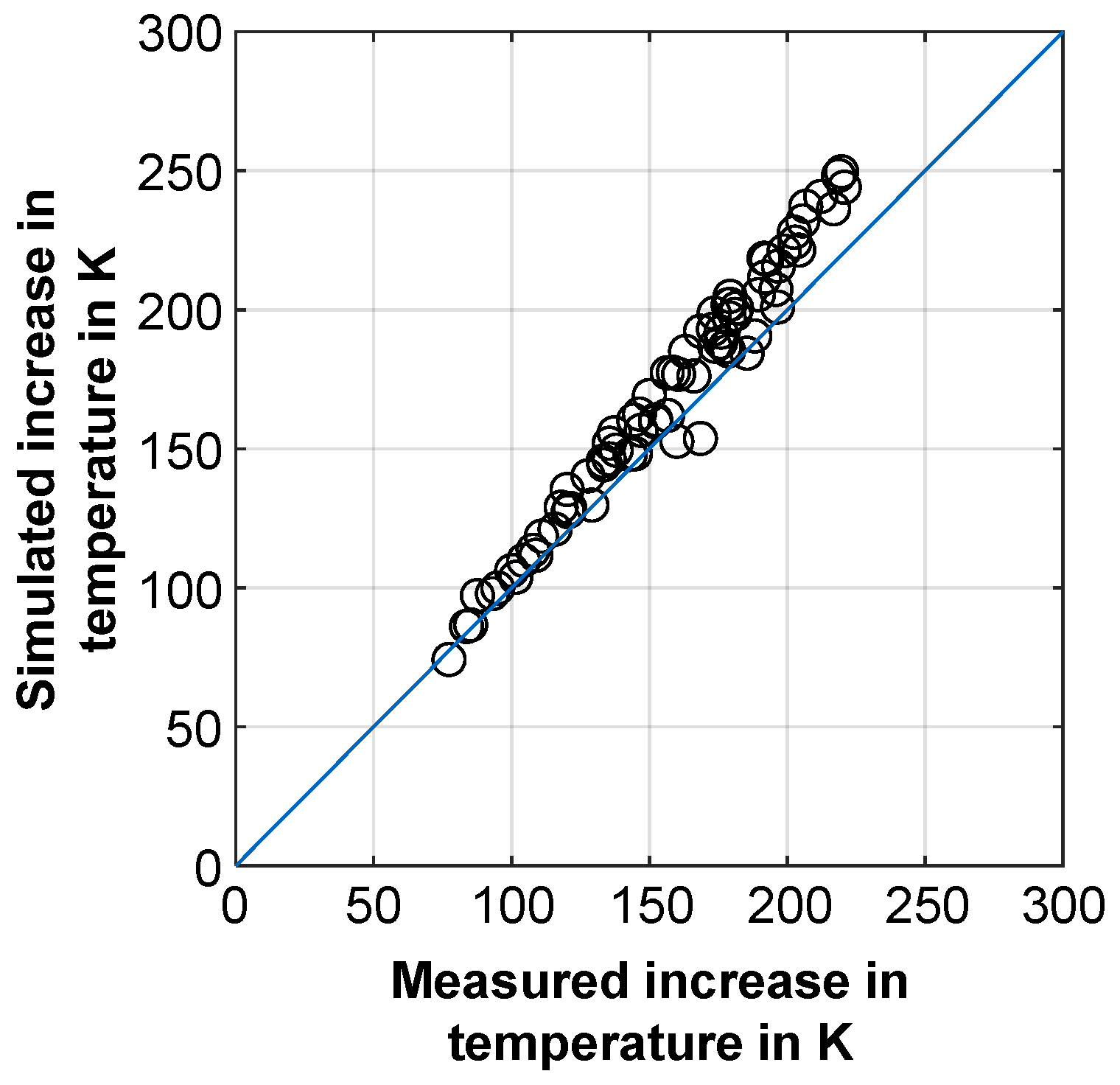
4.2. Validation with Experimental Data
- Number of slip phases
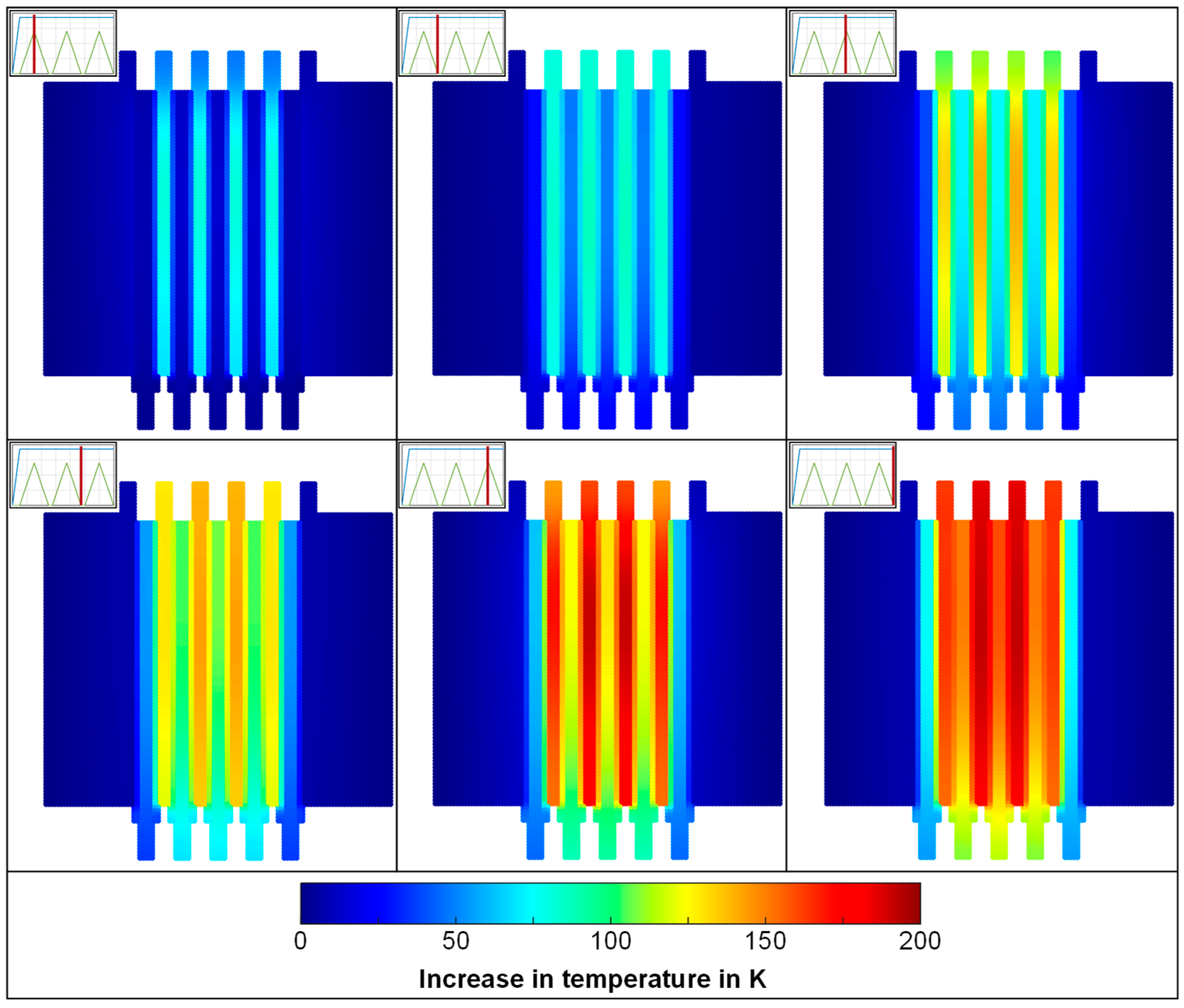
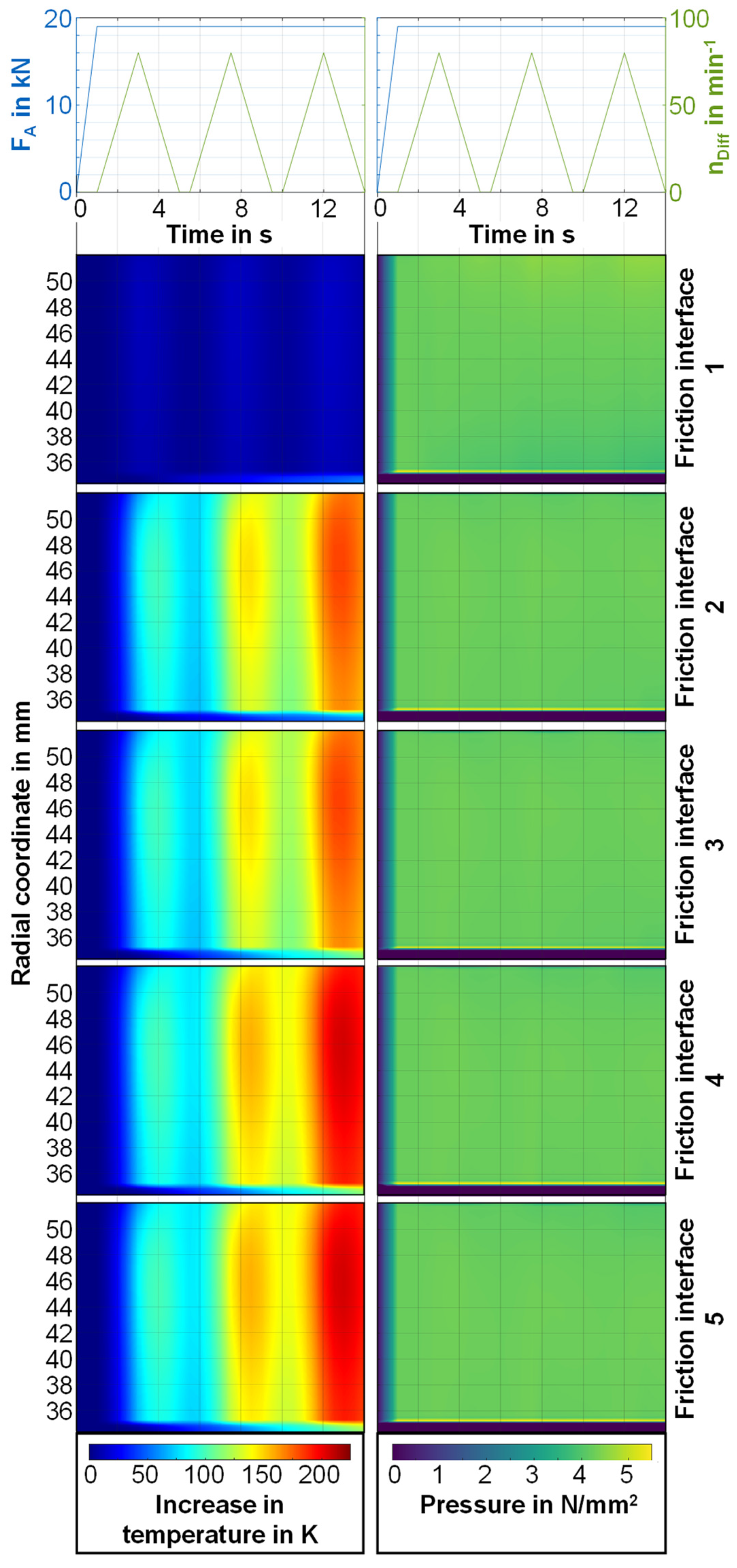
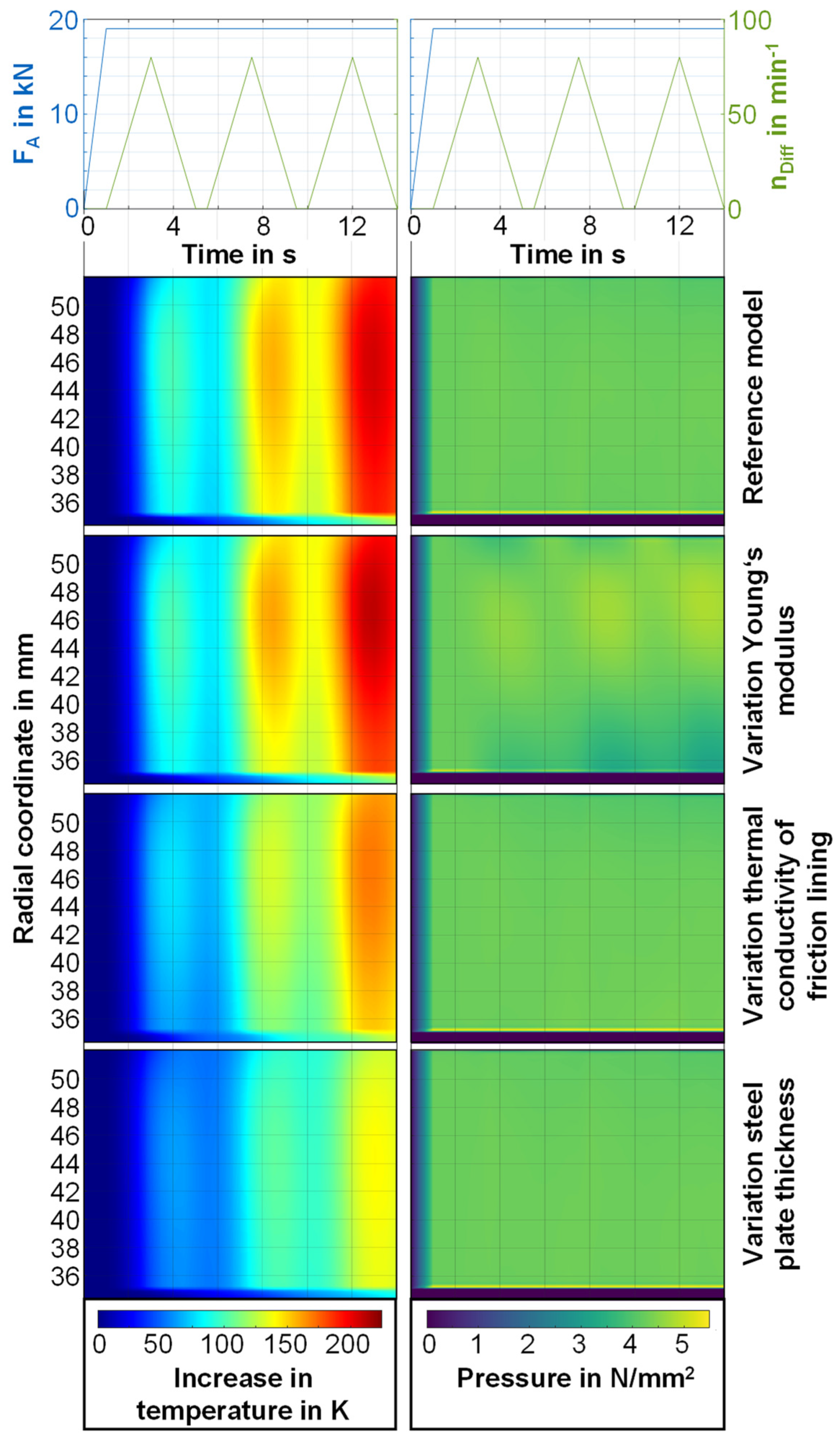
4.3. Temperature and Pressure Distribution
5. Discussion
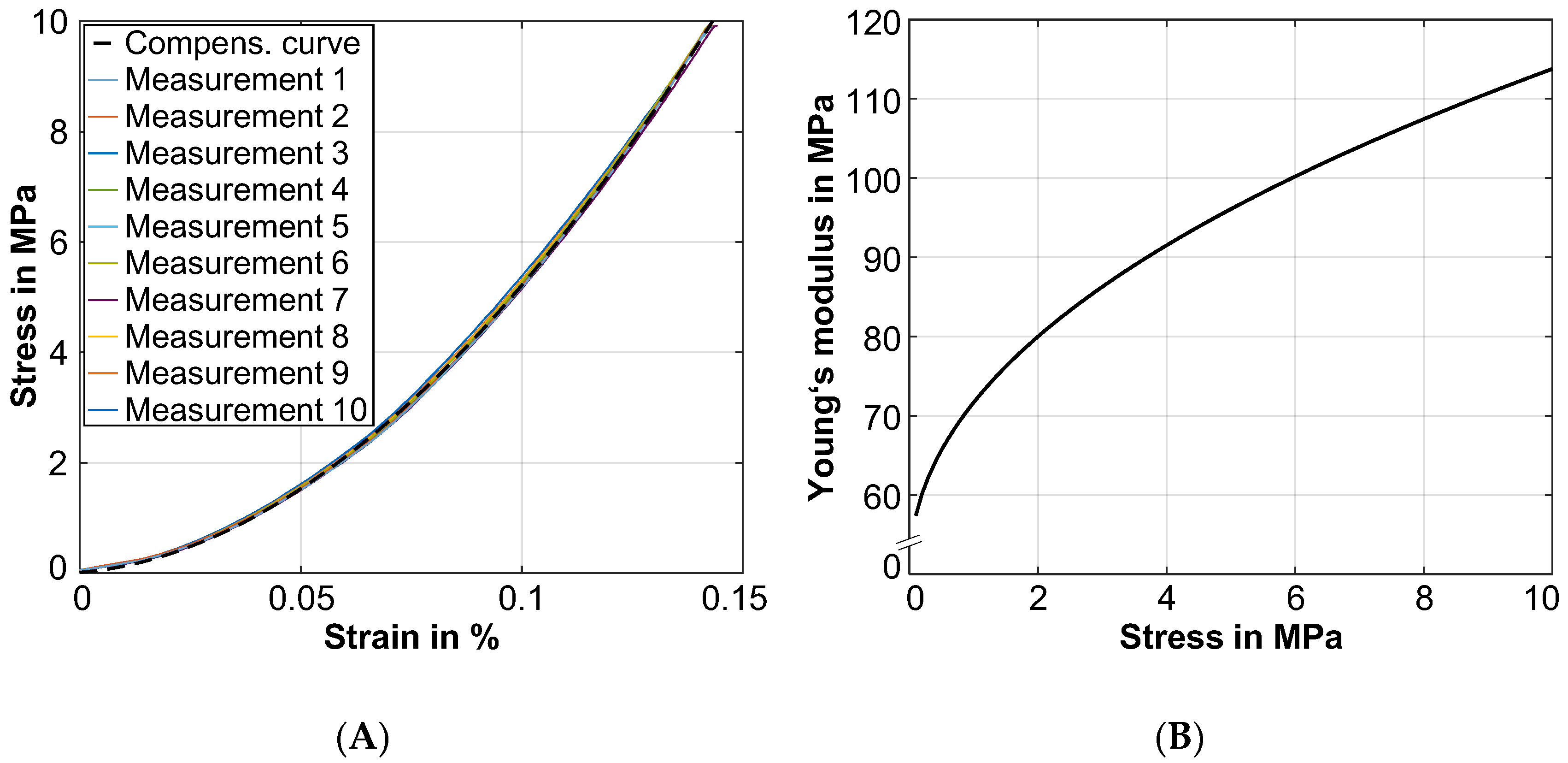
- Young’s modulus
- Thermal conductivity of the friction lining
- Steel plate thickness
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Unit | Description |
| Apparent contact area | ||
| a | Regression coefficient = | |
| Contact area in model | ||
| Tooth flank area | ||
| Area ratio of model to real part | ||
| Regression coefficient = | ||
| Regression coefficient = | ||
| Factor 1 for different interface roughness | ||
| Factor 2 for different interface roughness | ||
| Factor 3 for different interface roughness | ||
| Specific heat capacity of solid i | ||
| Elastic matrix | ||
| Diameter of the force application point on the carrier | ||
| Young’s modulus | ||
| Axial force to actuate the clutch | ||
| Hardness of contact material at temperature | ||
| Thermal contact conductance | ||
| Thermal conductivity of contact material at temperature | ||
| Stretched length | ||
| Initial length | ||
| Surface pressure | ||
| Pressure between carrier and plate toothing | ||
| Heat flux density | ||
| W | Heat flow rate | |
| Radius | ||
| Mean friction diameter | ||
| μm | Surface roughness | |
| Time | ||
| °C | Reference temperature 20 °C | |
| °C | Interface temperature | |
| Temperature field carrier plate | ||
| Temperature field friction lining | ||
| Temperature field of solid body i | ||
| Temperature field steel plate | ||
| Sliding speed | ||
| Strain | ||
| Axial coordinate | ||
| Number of teeth | ||
| Linear thermal expansion | ||
| Proportional coefficient | ||
| Effective arithmetic average slope | ||
| Length change | ||
| Temperature change | ||
| Mechanical strain | ||
| Thermal strain | ||
| Thermal conductivity friction lining | ||
| Thermal conductivity of solid i | ||
| Thermal conductivity steel plate | ||
| Effective coefficient of friction between lining and steel plate | ||
| Density of solid i | ||
| Stress | ||
| ° | Angular coordinate | |
| Relative angular velocity |
Appendix A

References
- Schneider, T.; Strebel, M.; Pflaum, H.; Stahl, K. Spontaneous damage to wet-running multi-plate clutches with organic and metallic friction linings [Spontanschädigungsverhalten von nasslaufenden Lamellenkupplungen mit organischen und metallischen Reibbelägen]. Eng. Res. 2019, 83, 199–207. [Google Scholar] [CrossRef]
- Schneider, T.; Völkel, K.; Pflaum, H.; Stahl, K. Influence of Pre-damage on the Friction Behaviour of Wet-running Multi-plate Clutches in an Endurance Test [Einfluss von Vorschädigung auf das Reibungsverhalten nasslaufender Lamellenkupplungen im Dauerschaltbetrieb]. Eng. Res. 2021, 85, 859–870. [Google Scholar] [CrossRef]
- Schneider, T.; Voelkel, K.; Pflaum, H.; Stahl, K. Friction Behavior of Pre-Damaged Wet-Running Multi-Plate Clutches in an Endurance Test. Lubricants 2020, 8, 68. [Google Scholar] [CrossRef]
- Yevtushenko, A.A.; Grzes, P.; Adamowicz, A. Numerical Analysis of Thermal Stresses in Disk Brakes and Clutches (A Review). Numer. Heat Transf. Part A Appl. 2015, 67, 170–188. [Google Scholar] [CrossRef]
- Abdullah, O.I.; Schlattmann, J.; Senatore, A.; Sabri, L.A.; Al-Sahb, W.S.A. Effect of Sliding Speed on the Thermal Stresses of Single-Disk Friction Clutches. J. Fail. Anal. Prevent. 2020, 20, 1534–1540. [Google Scholar] [CrossRef]
- Kennedy, F.E.; Ling, F.F. A Thermal, Thermoelastic, and Wear Simulation of a High-Energy Sliding Contact Problem. J. Lub. Tech. 1974, 96, 497–505. [Google Scholar] [CrossRef]
- Zagrodzki, P. Numerical analysis of temperature fields and thermal stresses in the friction discs of a multidisc wet clutch. Wear 1985, 101, 255–271. [Google Scholar] [CrossRef]
- Zagrodzki, P. Analysis of thermomechanical phenomena in multidisc clutches and brakes. Wear 1990, 140, 291–308. [Google Scholar] [CrossRef]
- Tirovic, M.; Day, A.J. Disc Brake Interface Pressure Distributions. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 1991, 205, 137–146. [Google Scholar] [CrossRef]
- Hwang, P.; Wu, X. Investigation of temperature and thermal stress in ventilated disc brake based on 3D thermo-mechanical coupling model. J. Mech. Sci. Technol. 2010, 24, 81–84. [Google Scholar] [CrossRef]
- Rouhi Moghanlou, M.; Saeidi Googarchin, H. Three-dimensional coupled thermo-mechanical analysis for fatigue failure of a heavy vehicle brake disk: Simulation of braking and cooling phases. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 3145–3163. [Google Scholar] [CrossRef]
- Belhocine, A.; Abdullah, O.I. Design and Thermomechanical Finite Element Analysis of Frictional Contact Mechanism on Automotive Disc Brake Assembly. J Fail. Anal. Prevent. 2020, 20, 270–301. [Google Scholar] [CrossRef]
- Stojanovic, N.; Glisovic, J.; Abdullah, O.; Grujic, I.; Vasiljevic, S. Pressure influence on heating of ventilating disc brakes for passenger cars. Therm. Sci. 2020, 24, 203–214. [Google Scholar] [CrossRef]
- Afzal, A.; Abdul Mujeebu, M. Thermo-Mechanical and Structural Performances of Automobile Disc Brakes: A Review of Numerical and Experimental Studies. Arch. Comput. Methods Eng. 2019, 26, 1489–1513. [Google Scholar] [CrossRef]
- Zhao, S.; Hilmas, G.E.; Dharani, L.R. Behavior of a composite multidisk clutch subjected to mechanical and frictionally excited thermal load. Wear 2008, 264, 1059–1068. [Google Scholar] [CrossRef]
- Abdullah, O.I.; Majeed, M.H.; Hussain, I.Y. Effects of Frictional Facing Thickness on the Heat Generated in Dry Friction Clutches. IOP Conf. Ser. Mater. Sci. Eng. 2018, 433, 12044. [Google Scholar] [CrossRef] [Green Version]
- Abdullah, O.I.; Schlattmann, J. Thermal behavior of friction clutch disc based on uniform pressure and uniform wear assumptions. Friction 2016, 4, 228–237. [Google Scholar] [CrossRef] [Green Version]
- Abdullah, O.I.; Schlattmann, J.; Majeed, M.H.; Sabri, L.A. The temperatures distributions of a single-disc clutches using heat partitioning and total heat generated approaches. Case Stud. Therm. Eng. 2018, 11, 43–54. [Google Scholar] [CrossRef]
- Abdullah, O.I.; Schlattmann, J.; Majeed, M.H.; Sabri, L.A. The distribution of frictional heat generated between the contacting surfaces of the friction clutch system. Int. J. Interact. Des. Manuf. 2019, 13, 487–498. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, J. Thermomechanical Coupling Simulation and Analysis of Wet Multi-Disc Brakes During Emergency Braking. J. Phys. Conf. Ser. 2021, 1875, 12005. [Google Scholar] [CrossRef]
- Cooper, M.G.; Mikic, B.B.; Yovanovich, M.M. Thermal contact conductance. Int. J. Heat Mass Transf. 1969, 12, 279–300. [Google Scholar] [CrossRef]
- Mikić, B.B. Thermal contact conductance; theoretical considerations. Int. J. Heat Mass Transf. 1974, 17, 205–214. [Google Scholar] [CrossRef]
- Asif, M.; Tariq, A. Correlations of Thermal Contact Conductance for Nominally Flat Metallic Contact in Vacuum. Exp. Heat Transf. 2016, 29, 456–484. [Google Scholar] [CrossRef]
- Tariq, A.; Asif, M. Experimental investigation of thermal contact conductance for nominally flat metallic contact. Heat Mass Transf. 2016, 52, 291–307. [Google Scholar] [CrossRef]
- Dou, R.; Ge, T.; Liu, X.; Wen, Z. Effects of contact pressure, interface temperature, and surface roughness on thermal contact conductance between stainless steel surfaces under atmosphere condition. Int. J. Heat Mass Transf. 2016, 94, 156–163. [Google Scholar] [CrossRef]
- Madhusudana, C.V.; Madhusudana, C.V. Thermal Contact Conductance; Springer: Berlin/Heidelberg, Germany, 1996; ISBN 0387945342. [Google Scholar]
- Acuner, R. Synchronisierungen Mit Carbon-Reibwerkstoffen unter Hohen und Extremen Beanspruchungen. Ph.D. Thesis, Technische Universität München, München, Germany, 2016. [Google Scholar]
- Mileti, M.; Pflaum, H.; Stahl, K. TorqueLINE Cone Clutch: Thermo-Mechanical Stability of Cone Clutches for ATs. In Proceedings of the Dritev: International VDI Congress Dritev—Drivetrain for Vehicles, EDrive, Transmissions in Mobile Machines, Bonn, Germany, 27–28 June 2018; VDI Verlag GmbH: Düsseldorf, Germany, 2018; pp. 357–368, ISBN 9783180923284. [Google Scholar]
- Abdullah, O.I.; Schlattmann, J. Temperature analysis of a pin-on-disc tribology test using experimental and numerical approaches. Friction 2016, 4, 135–143. [Google Scholar] [CrossRef] [Green Version]
- Wohlleber, F.; Pflaum, H.; Höhn, B.-R. FVA-Nr. 150 VI—Heft 899—KUPSIM 2.2: Programmerweiterung zur Thermischen Nachrechnung von Lamellenkupplungen und Integration des Programms in die FVA-Workbench; Forschungsvereinigung Antriebstechnik e.V.: Frankfurt am Main, Germany, 2009. [Google Scholar]
- Spreckels, M. Einfluss der Temperaturverteilung auf das tribologische Verhalten von Synchronisierungen. Ph.D. Thesis, Leibniz Universität Hannover, Hannover, Germany, 2001. [Google Scholar]
- Sabri, L.A.; Stojanović, N.; Senatore, A.; Jweeg, M.J.; Abed, A.M.; Abdullah, O.I. Three-Dimensional Finite Element Analysis of Contact Problem in Dry Friction Clutches. Lubricants 2021, 9, 115. [Google Scholar] [CrossRef]
- Zagrodzki, P.; Truncone, S.A. Generation of hot spots in a wet multidisk clutch during short-term engagement. Wear 2003, 254, 474–491. [Google Scholar] [CrossRef]
- Schneider, T.; Bedrikow, A.B.; Völkel, K.; Pflaum, H.; Stahl, K. Comparison of Various Wet-Running Multi-Plate Clutches with Paper Friction Lining with Regard to Spontaneous Damage Behavior. Tribol. Ind. 2021, 43, 40–56. [Google Scholar] [CrossRef]
- Groetsch, D.; Stockinger, U.; Schneider, T.; Reiner, F.; Voelkel, K.; Pflaum, H.; Stahl, K. Experimental investigations of spontaneous damage to wet multi-plate clutches with carbon friction linings. Eng. Res. 2021, 117, 2480. [Google Scholar] [CrossRef]
- Ciavarella, M.; Papangelo, A.; Barber, J.R. Effect of Wear on the Evolution of Contact Pressure at a Bimaterial Sliding Interface. Tribol. Lett. 2020, 68, 27. [Google Scholar] [CrossRef]
- Humphrey, E.; Gkinis, T.; Morris, N.J.; Leighton, M.; Rahmani, R.; Rahnejat, H. Clutch lining frictional characteristics under thermal tribodynamic conditions. In Proceedings of the 3rd Biennial International Conference on Powertrain Modelling and Control, Loughborough, UK, 7–9 September 2016. [Google Scholar]
- Gkinis, T.; Rahmani, R.; Rahnejat, H.; O’Mahony, M. Heat generation and transfer in automotive dry clutch engagement. J. Zhejiang Univ. Sci. A 2018, 19, 175–188. [Google Scholar] [CrossRef]
- Qiao, Y.; Ciavarella, M.; Yi, Y.-B.; Wang, T. Effect of wear on frictionally excited thermoelastic instability: A finite element approach. J. Therm. Stress. 2020, 43, 1564–1576. [Google Scholar] [CrossRef]
- Papangelo, A.; Ciavarella, M. Can Wear Completely Suppress Thermoelastic Instabilities? J. Tribol 2020, 142, 051501. [Google Scholar] [CrossRef]



| Parameter | Unit | Value |
|---|---|---|
| Thermal conductivity of contact material at temperature | 52 | |
| Surface roughness | μm | 0.44 |
| Effective arithmetic average slope | 0.107 | |
| Vickers hardness (HV1) | 522 | |
| Factor for different interface roughness according to Dou et al. [25] | 3.28 × 10−5 | |
| Factor for different interface roughness according to Dou et al. [25] | 0.888 | |
| Factor for different interface roughness according to Dou et al. [25] | 0.291 |
| Parameter | Unit | Steel | Friction Lining |
|---|---|---|---|
| Young’s modulus | 2.1 × 1011 | Regression function | |
| Poisson’s ratio | 0.3 | 0.2 | |
| Coefficient of thermal expansion | 13.3 × 10−6 | 70 × 10−6 | |
| Density | 7850 | 900 | |
| Specific heat capacity | 520 | 2890 | |
| Thermal conductivity | 52 | 0.25 |
| Parameter | Unit | Value |
|---|---|---|
| Pressure | 5.0 | |
| Max. differential speed | 110 |
| Parameter | Unit | Value |
|---|---|---|
| Pressure | N/mm2 | 4.0 |
| Max. differential speed | 80 | |
| Approximated coefficient of friction using nodes | 0.0977, 0.1, 0.1026, 0.1038, 0.1033, 0.0982, 0.0933, 0.0847, 0.0596, 0.0603, 0.0874, 0.0942, 0.0964, 0.0963, 0.090, 0.0597, 0.0795, 0.0878, 0.0909, 0.0917, 0.0848, 0.0794, 0.0714, 0.06066, 0.0846, 0.0768, 0.0564 | |
| Average coefficient of friction | 0.0849 |
| Pressure in N/mm2 | Max. Differential Speed in min−1 | Young’s Modulus of Friction Lining in MPa | Thermal Conductivity of Friction Lining in W/mK | Steel Plate Thickness in mm | |
|---|---|---|---|---|---|
| Reference model | 0.25 | 0.8 | |||
| Variation Young’s modulus | 0.25 | 0.8 | |||
| Variation thermal conductivity of friction lining | 0.8 | ||||
| Variation steel plate thickness | 0.25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schneider, T.; Dietsch, M.; Voelkel, K.; Pflaum, H.; Stahl, K. Analysis of the Thermo-Mechanical Behavior of a Multi-Plate Clutch during Transient Operating Conditions Using the FE Method. Lubricants 2022, 10, 76. https://doi.org/10.3390/lubricants10050076
Schneider T, Dietsch M, Voelkel K, Pflaum H, Stahl K. Analysis of the Thermo-Mechanical Behavior of a Multi-Plate Clutch during Transient Operating Conditions Using the FE Method. Lubricants. 2022; 10(5):76. https://doi.org/10.3390/lubricants10050076
Chicago/Turabian StyleSchneider, Thomas, Maximilian Dietsch, Katharina Voelkel, Hermann Pflaum, and Karsten Stahl. 2022. "Analysis of the Thermo-Mechanical Behavior of a Multi-Plate Clutch during Transient Operating Conditions Using the FE Method" Lubricants 10, no. 5: 76. https://doi.org/10.3390/lubricants10050076
APA StyleSchneider, T., Dietsch, M., Voelkel, K., Pflaum, H., & Stahl, K. (2022). Analysis of the Thermo-Mechanical Behavior of a Multi-Plate Clutch during Transient Operating Conditions Using the FE Method. Lubricants, 10(5), 76. https://doi.org/10.3390/lubricants10050076







