Static Performance Measurements and Model Predictions of Gas Foil Thrust Bearing with Curved Incline Geometry
Abstract
:1. Introduction
2. Materials and Methods
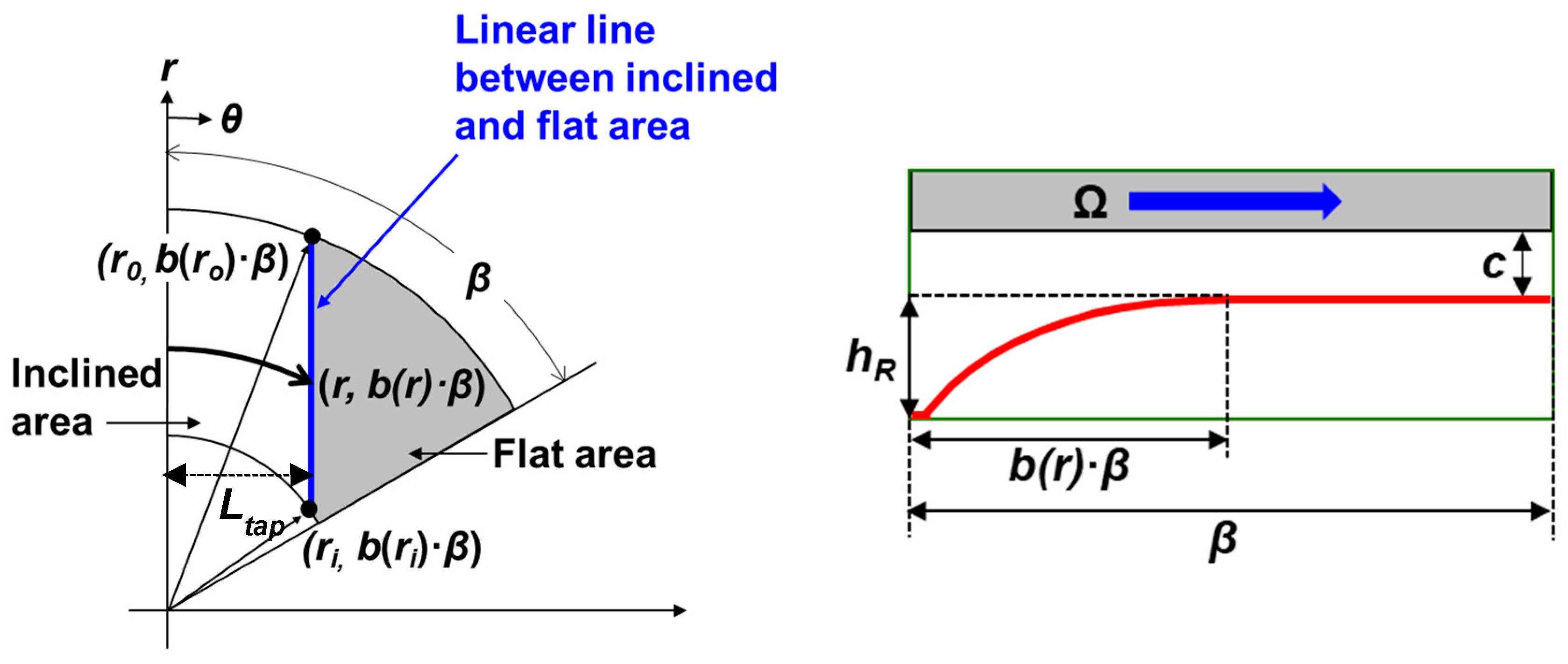
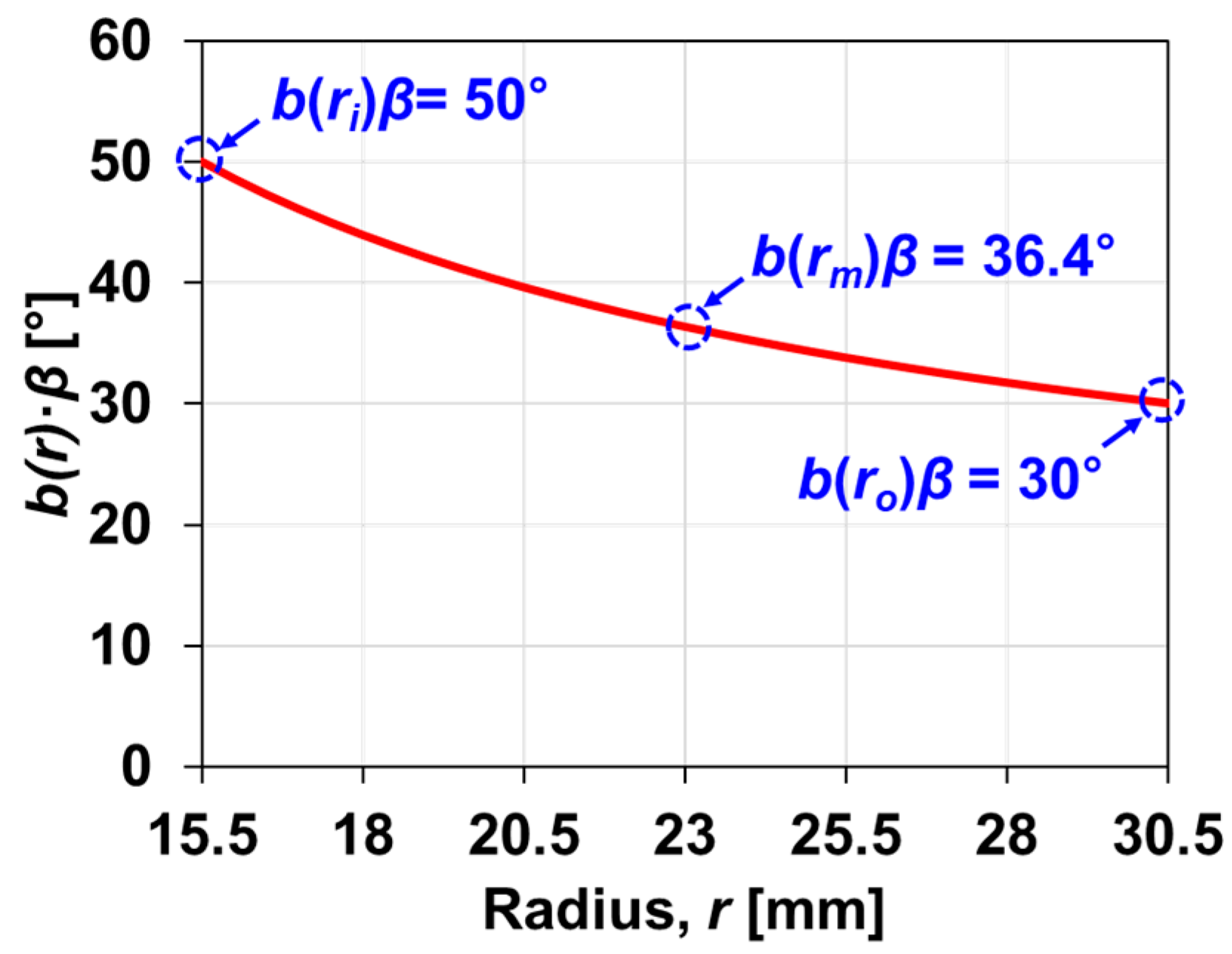
2.1. Gas Foil Thrust Bearing
2.2. Measurement of Gas Foil Thrust Bearing Height
2.3. Measurement of Static Performances
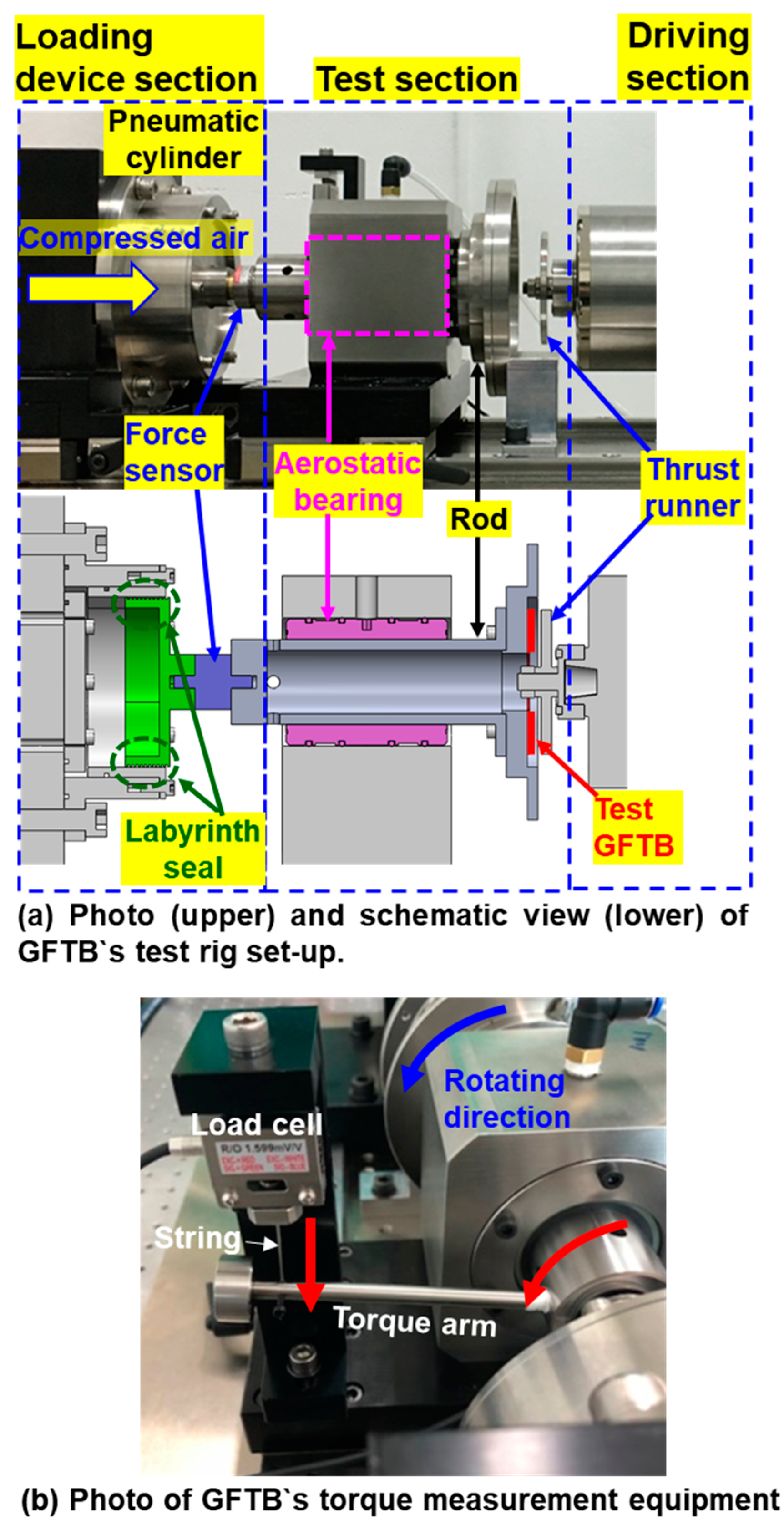
2.3.1. Description of the Test Rig
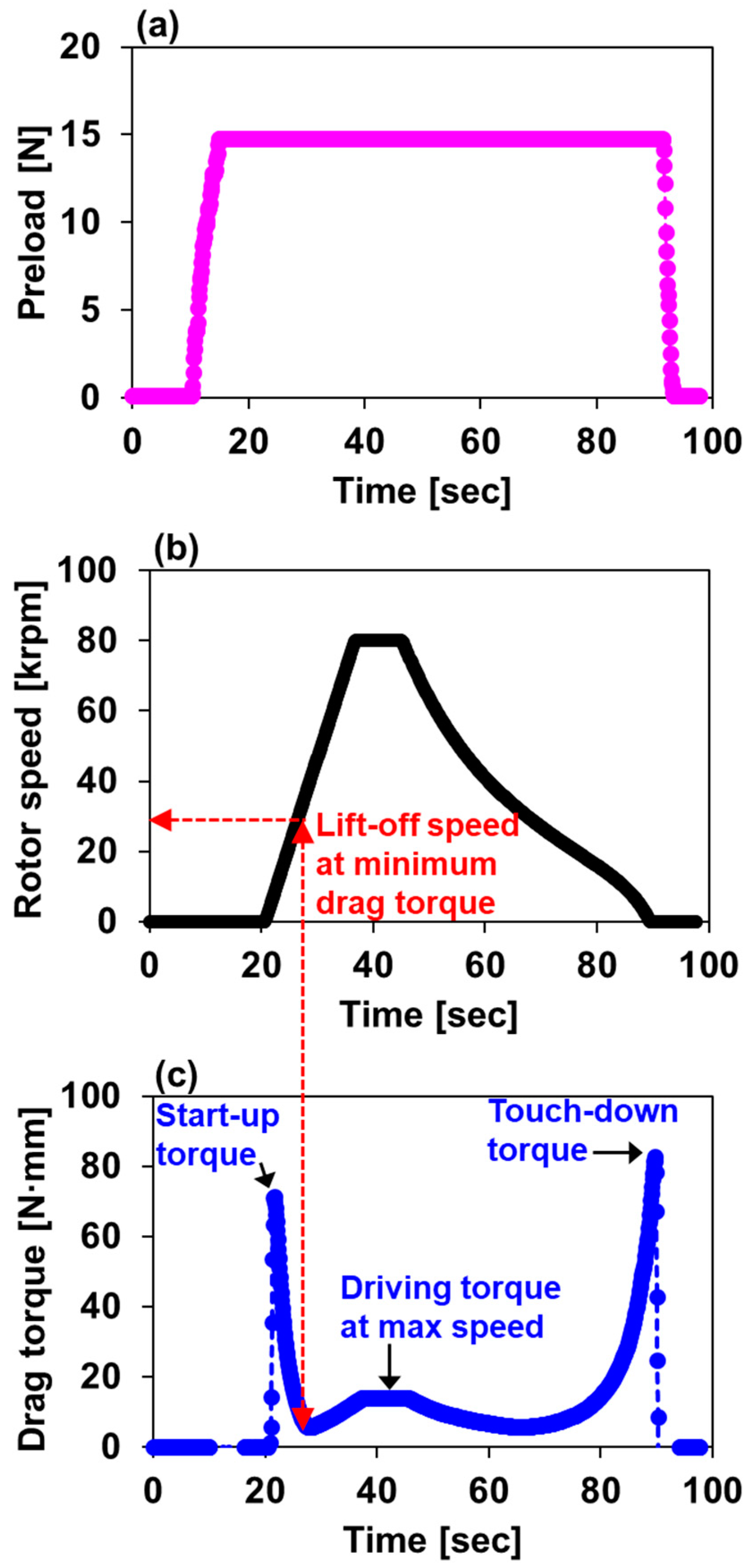
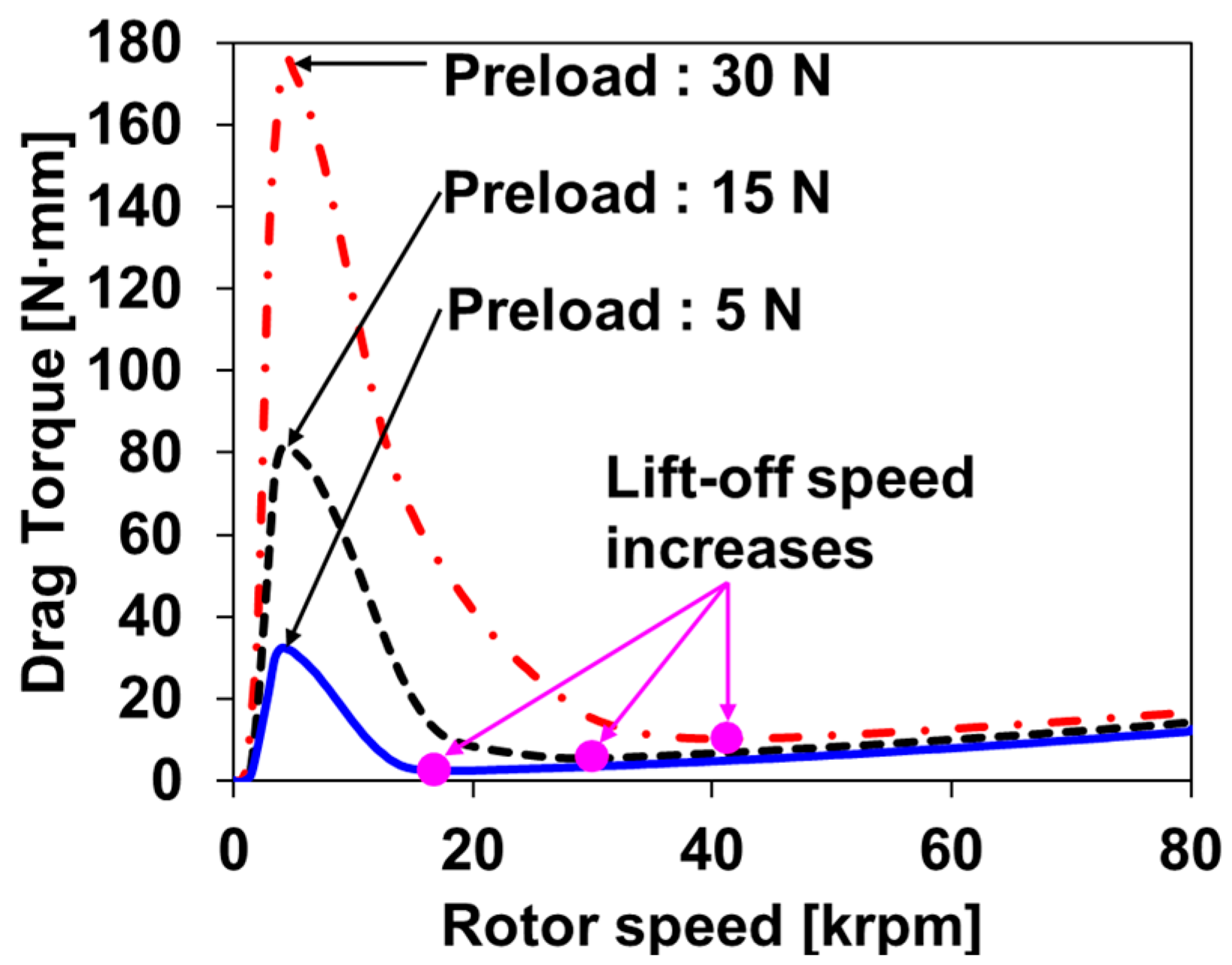
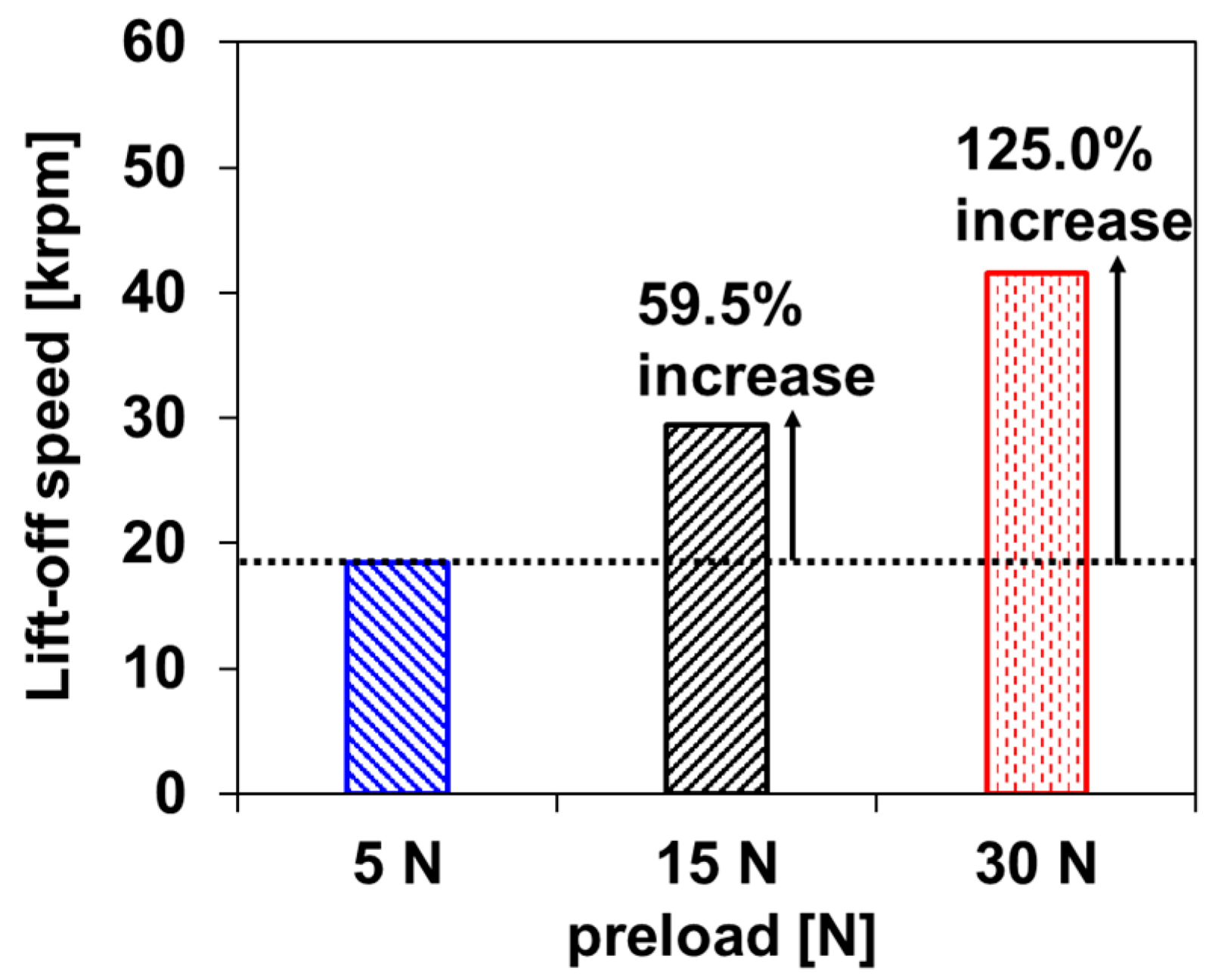
2.3.2. Lift-Off Speed Measurements
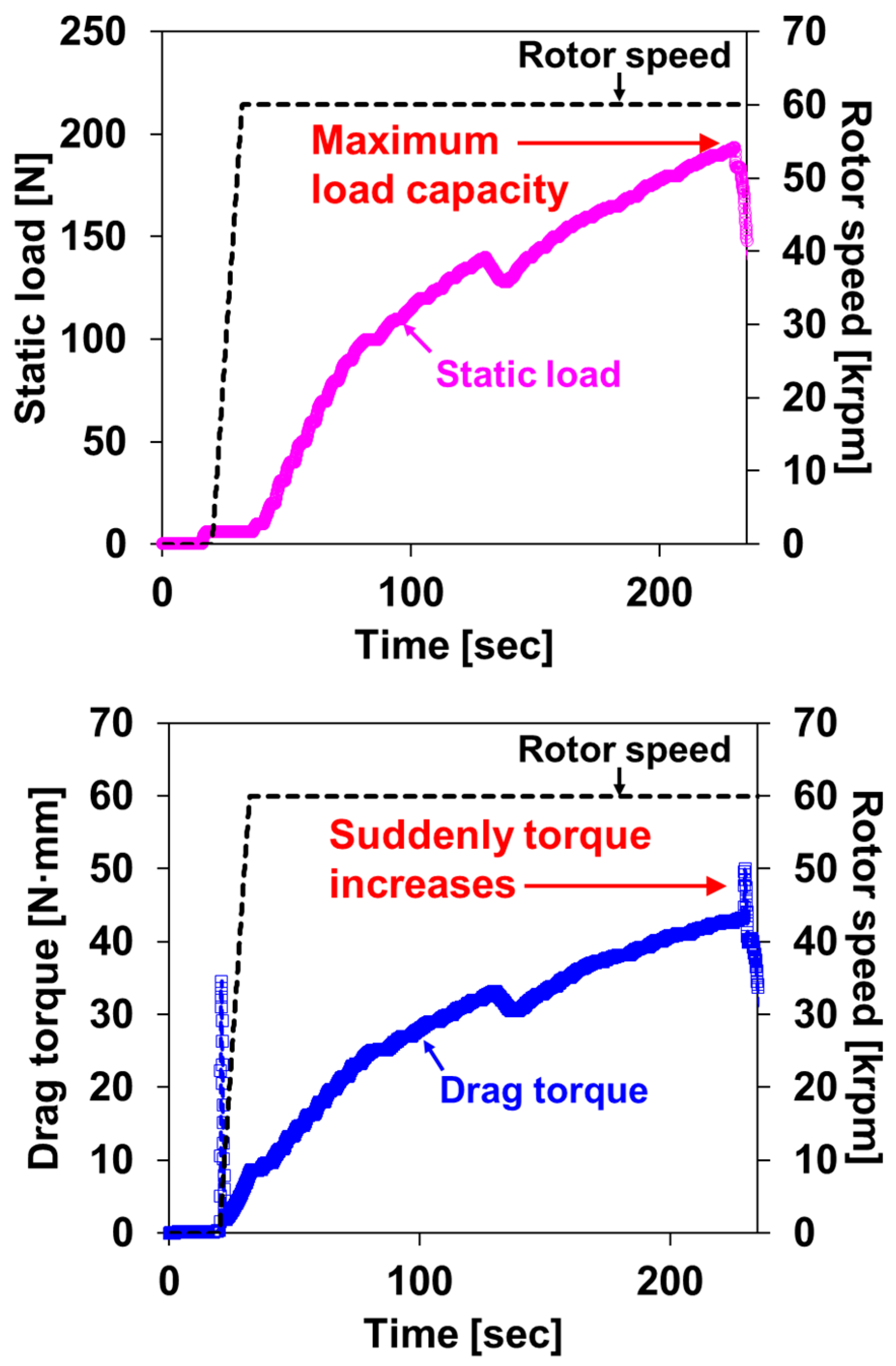
2.3.3. Load Capacity Measurement
2.4. Numerical Model
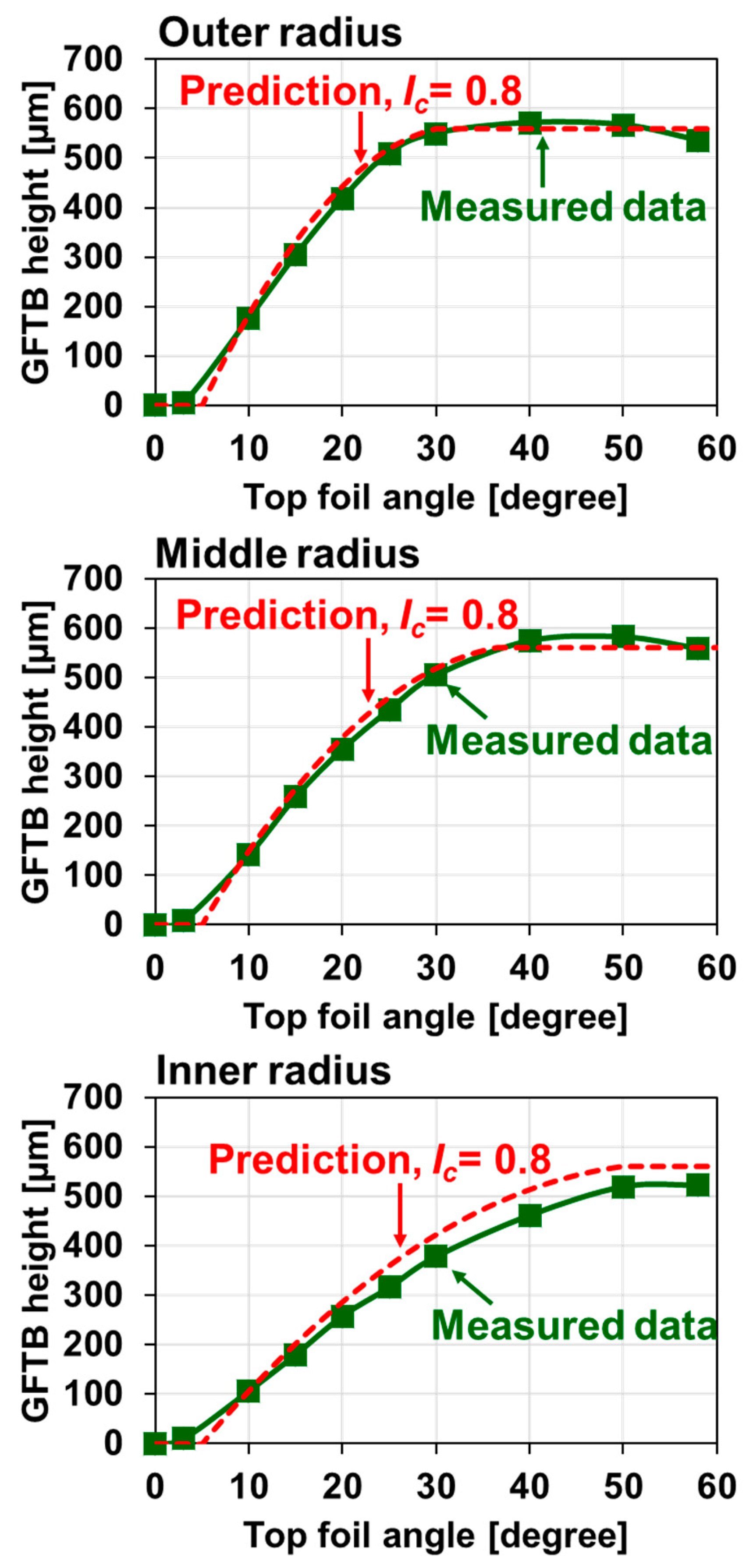
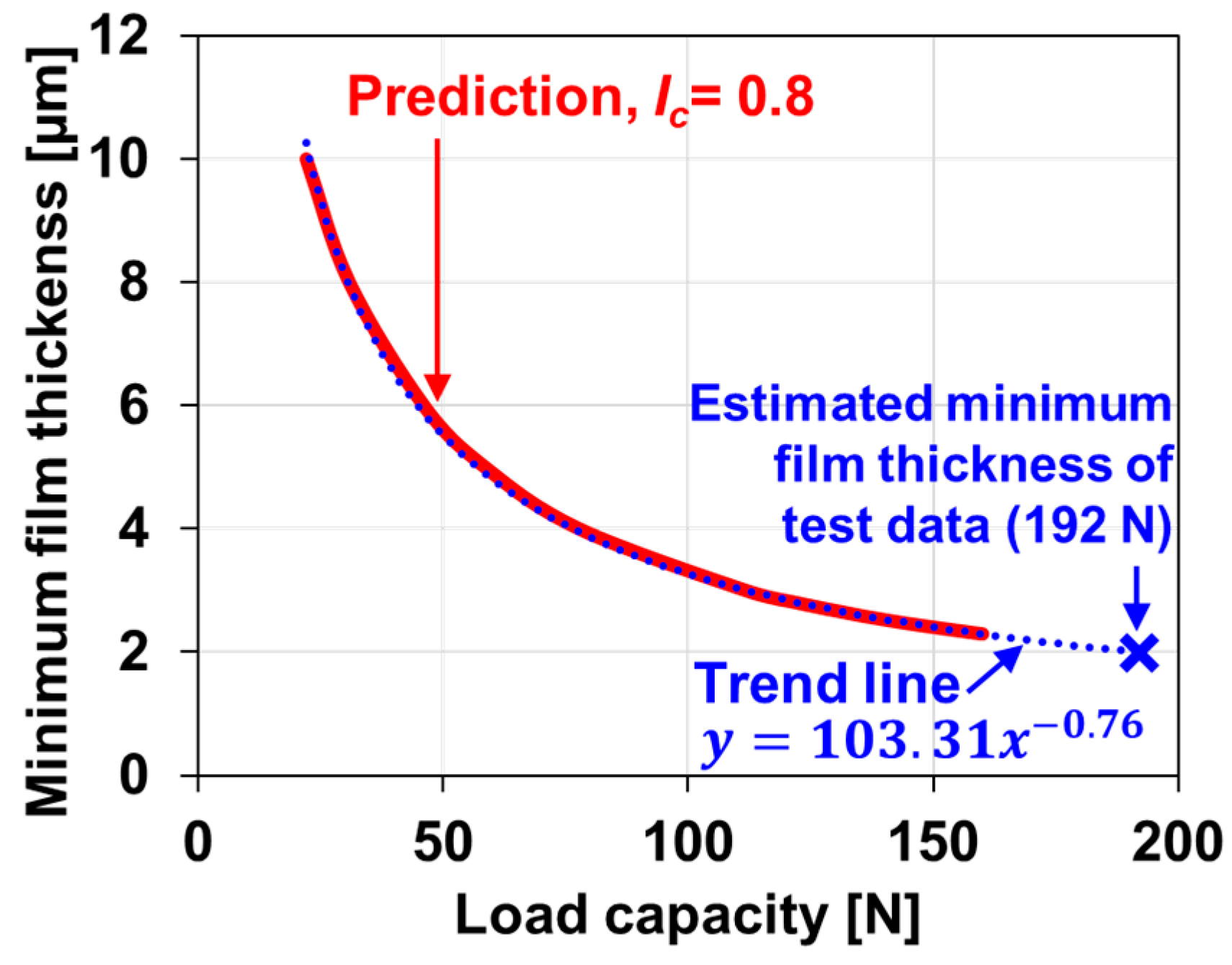
2.5. Model Validations
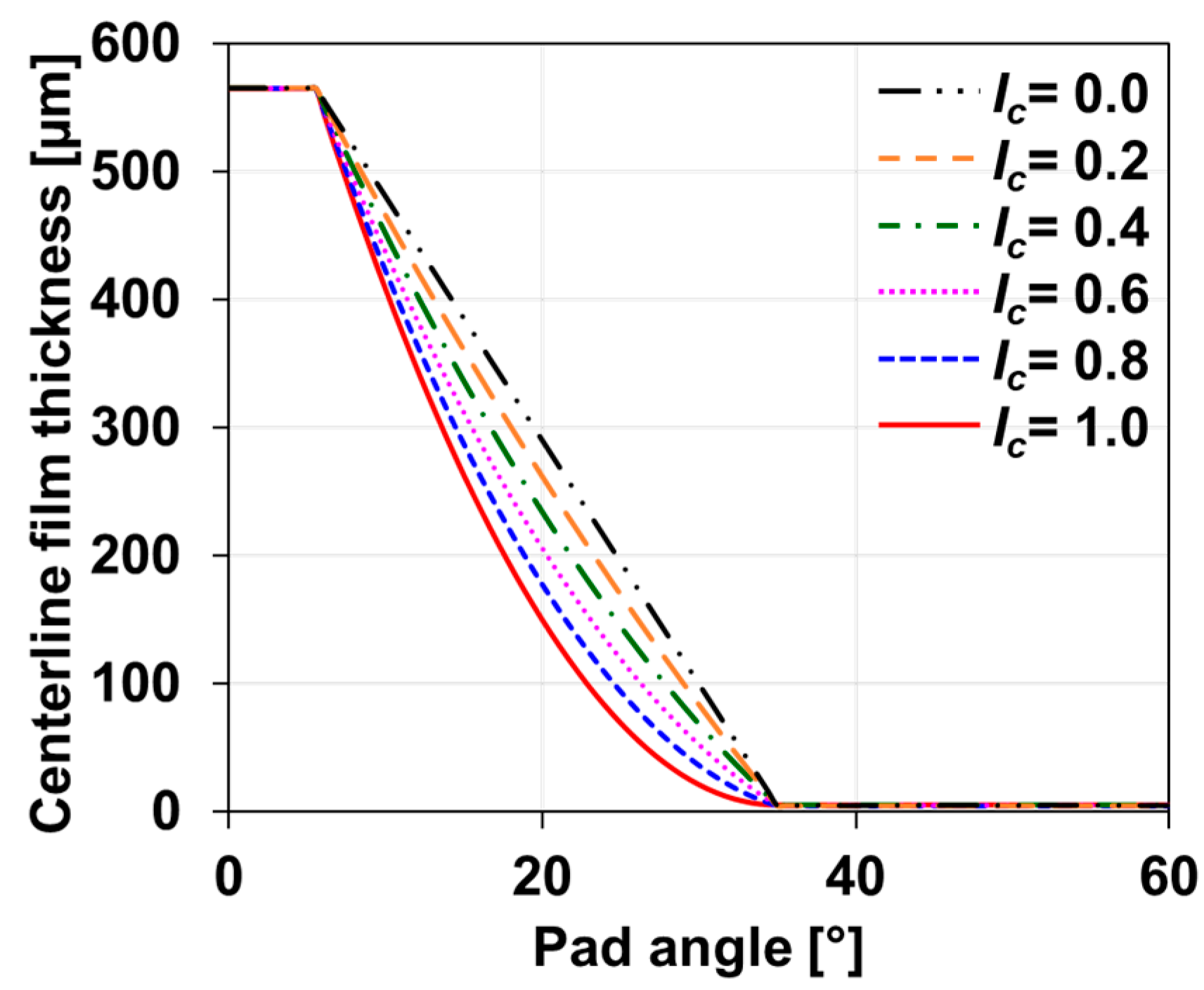
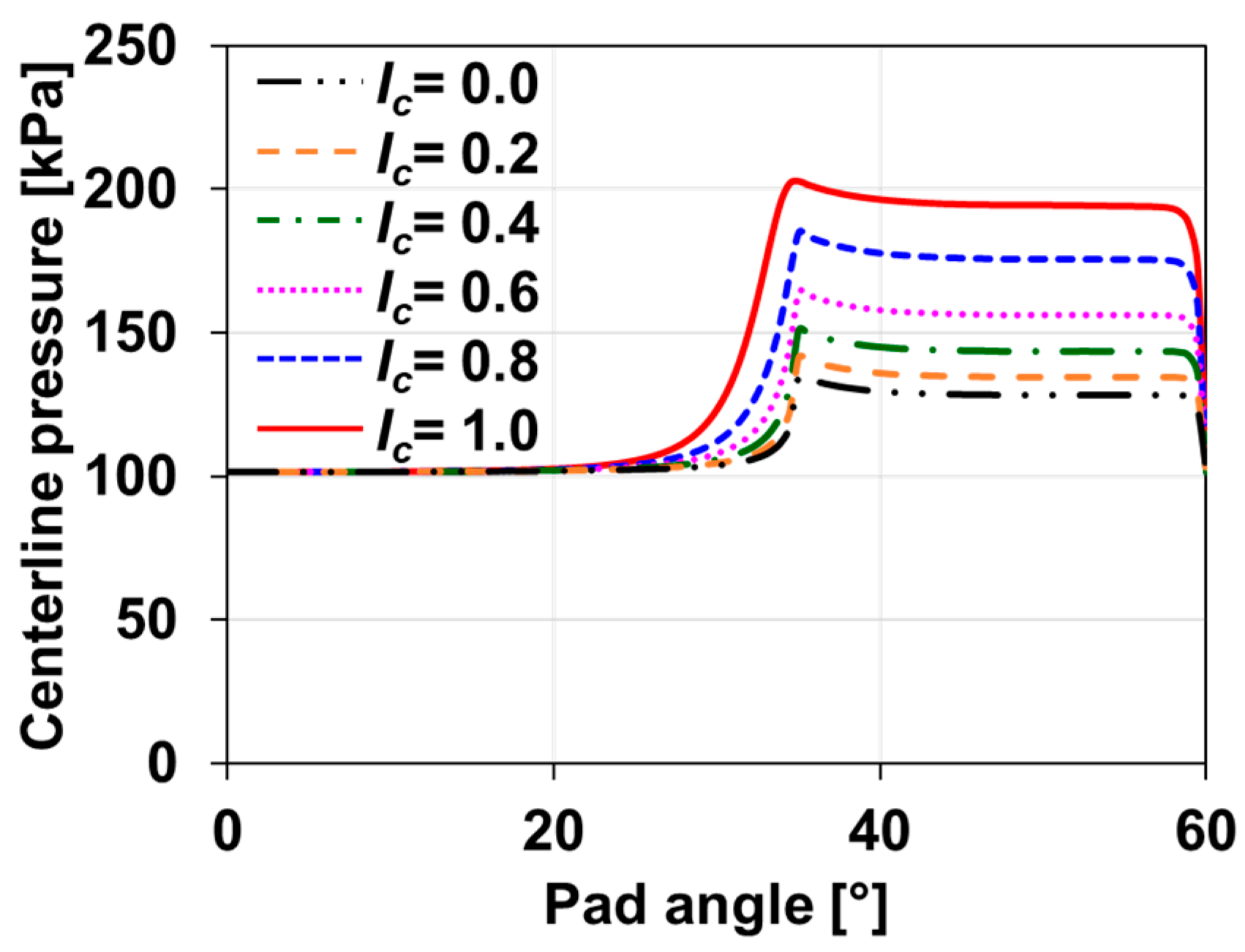
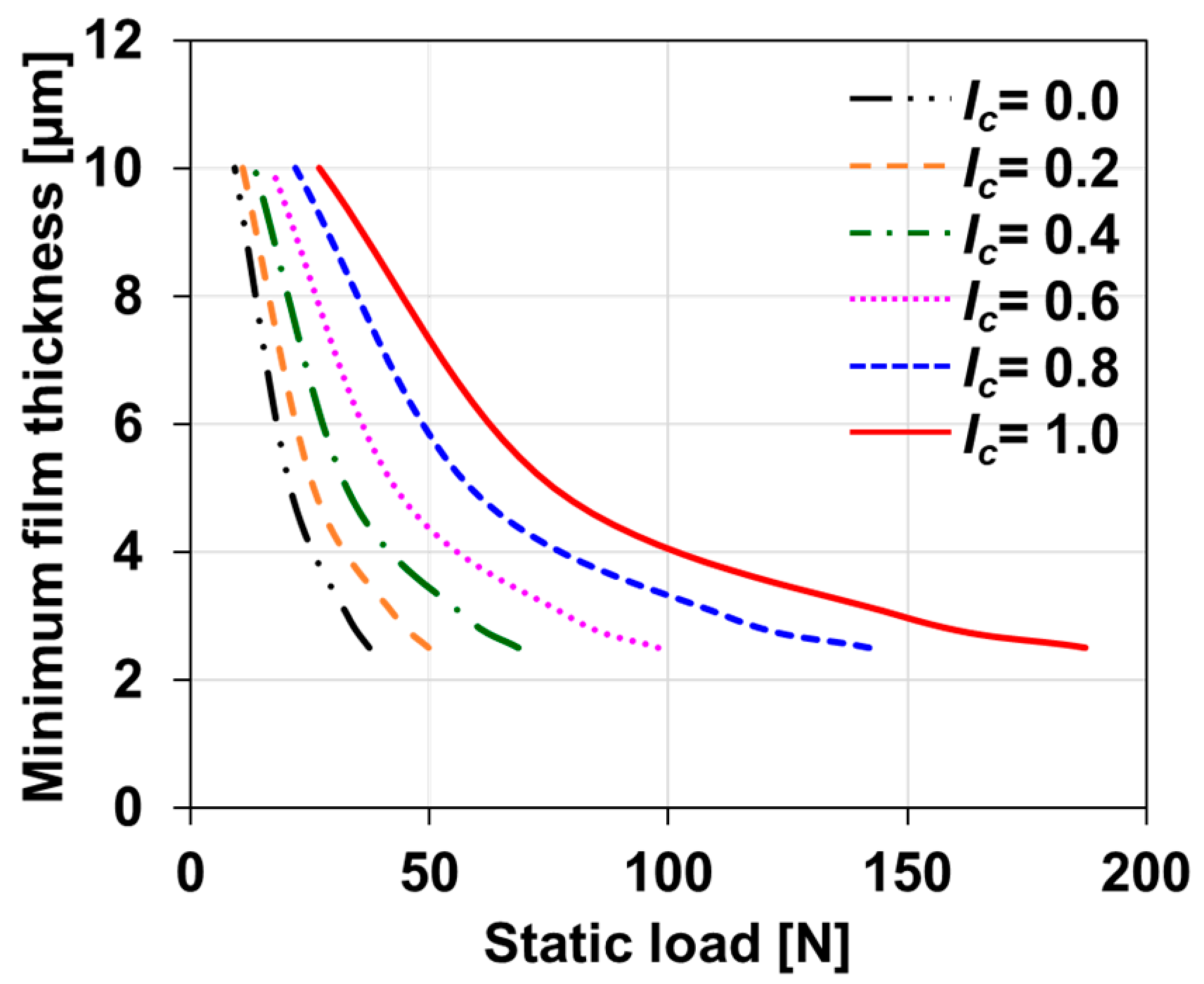
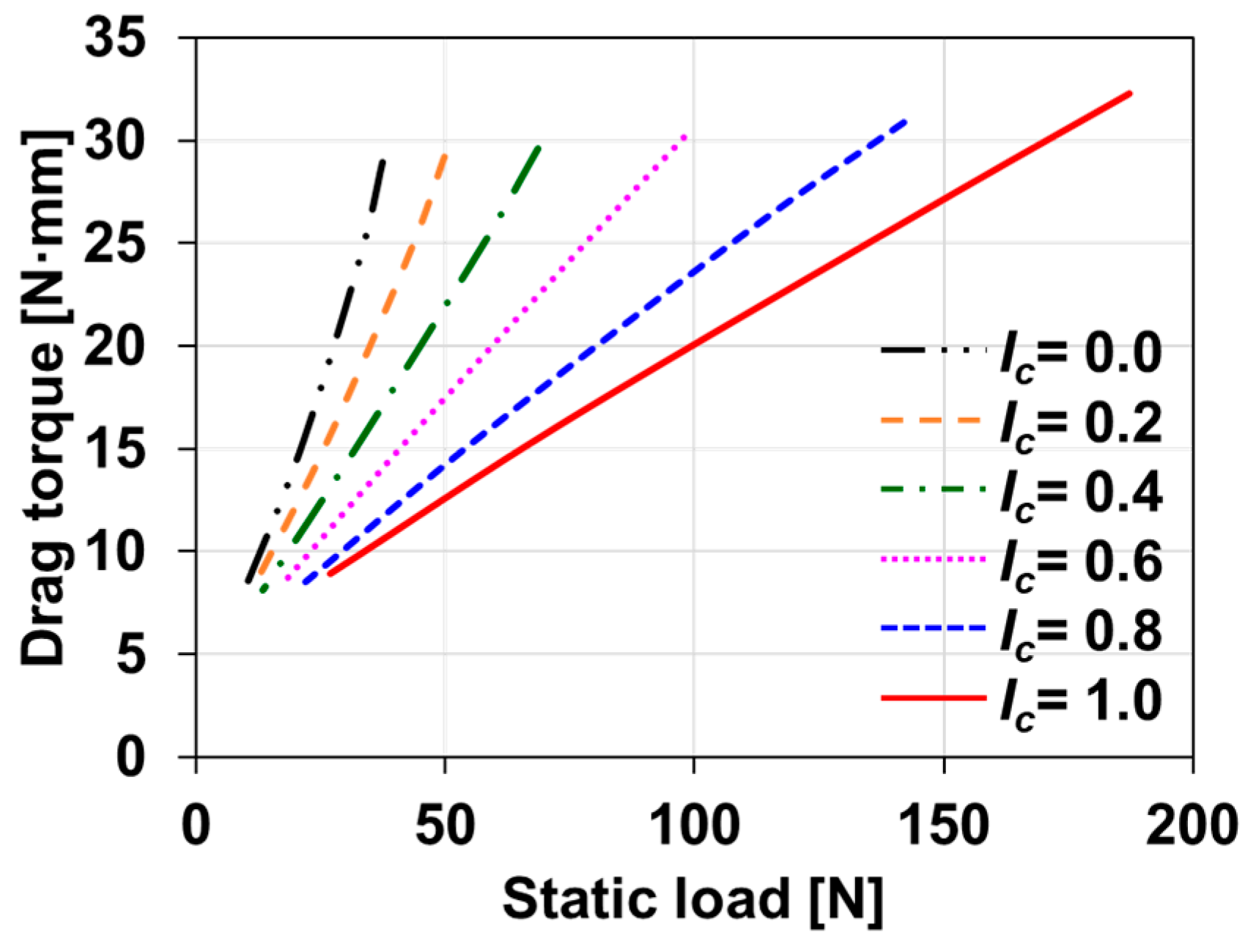
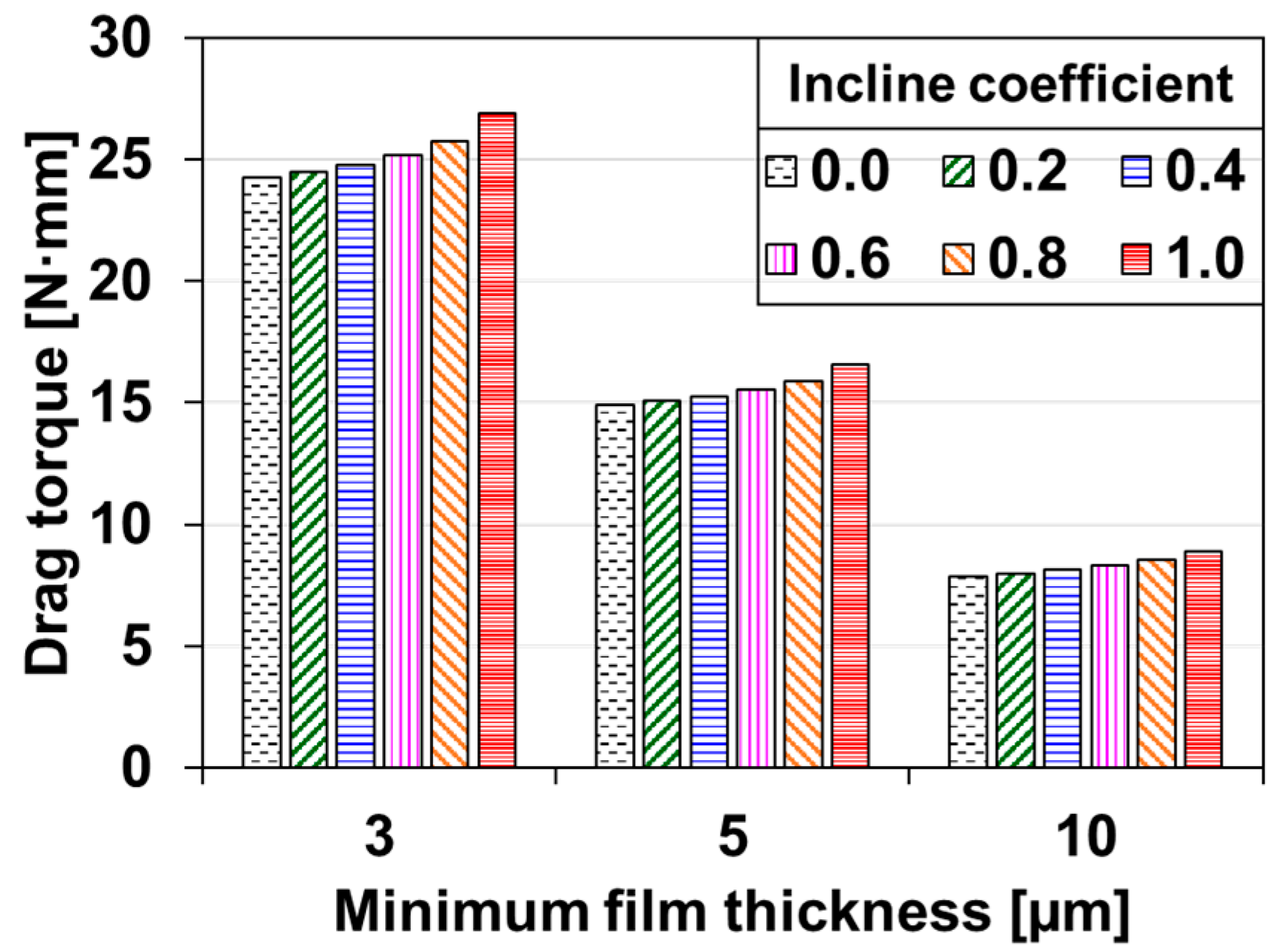
2.6. Effect of the Curved Shape for the Incline Geometry on the Performance of GFTBs
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Agrawal, G.L. Foil Air/Gas Bearing Technology—An Overview. Turbo Expo Power Land Sea Air 1997, 78682, V001T04A006. [Google Scholar]
- Agrawal, G.L. Foil Air Bearings Cleared to Land. Mech. Eng. 1998, 120, 78–80. [Google Scholar] [CrossRef]
- DellaCorte, C. Oil-Free Shaft Support System Rotordynamics: Past, Present and Future Challenges and Opportunities. Mech. Syst. Signal Process. 2012, 29, 67–76. [Google Scholar] [CrossRef]
- Heshmat, H.; Walowit, J.A.; Pinkus, O. Analysis of Gas Lubricated Compliant Thrust Bearings. J. Lubr. Technol. 1983, 105, 638–646. [Google Scholar] [CrossRef]
- Iordanoff, I. Analysis of an Aerodynamic Compliant Foil Thrust Bearing: Method for a Rapid Design. J. Tribol. 1999, 121, 816–822. [Google Scholar] [CrossRef]
- Dellacorte, C.; Valco, M. Load Capacity Estimation of Foil Air Journal Bearings for Oil-Free Turbomachinery Applications. STLE Tribol. Trans. 2000, 43, 795–801. [Google Scholar] [CrossRef]
- Dickman, J.R. An Investigation of Gas Foil Thrust Bearing Performance and Its Influencing Factors. Master’s Thesis, Case Western Reserve University, Cleveland, OH, USA, 2010. [Google Scholar]
- Dykas, B.D.; Tellier, D.W. A Foil Thrust Bearing Test Rig for Evaluation of High Temperature Performance and Durability; Report No. ARL-MR-0692; Army Research Laboratory: Adelphi, MD, USA, 2008. [Google Scholar]
- Dykas, B.D.; Prahl, J.; DellaCorte, C.; Bruckner, R. Thermal Management Phenomena in Foil Gas Thrust Bearings. Turbo Expo. Power Land Sea Air 2006, 42401, 1417–1423. [Google Scholar]
- Dykas, B.D. Factors Influencing the Performance of Foil Gas Thrust Bearings for Oil-Free Turbomachinery Applications. Ph.D. Thesis, Case Western Reserve University, Cleveland, OH, USA, 2006. [Google Scholar]
- Park, D.J.; Kim, C.H.; Jang, G.H.; Lee, Y.B. Theoretical Considerations of Static and Dynamic Characteristics of Air Foil Thrust Bearing with Tilt and Slip Flow. Tribol. Int. 2008, 41, 282–295. [Google Scholar] [CrossRef]
- Lee, Y.-B.; Kim, T.Y.; Kim, C.H. Thrust Bump Air Foil Bearings with Variable Axial Load: Theoretical Predictions and Experiments. Tribol. Trans. 2011, 54, 902–910. [Google Scholar] [CrossRef]
- Balducchi, F.; Arghir, M.; Gauthier, R.; Renard, E. Experimental Analysis of The Start-Up Torque of a Mildly Loaded Foil Tthrust Bearing. ASME J. Tribol. 2013, 135, 031702-1. [Google Scholar] [CrossRef]
- Lee, D.; Kim, D. Design and Performance Prediction of Hybrid Air Foil Thrust Bearings. J. Eng. Gas Turbines Power 2010, 133, 042501. [Google Scholar] [CrossRef]
- San Andrés, L.; Ryu, K.; Diemer, P. Prediction of Gas Thrust Foil Bearing Performance for Oil-Free Automotive Turbochargers. J. Eng. Gas Turbines Power 2014, 137, 032502. [Google Scholar] [CrossRef]
- Feng, K.; Liu, L.-J.; Guo, Z.-Y.; Zhao, X.-Y. Parametric study on static and dynamic characteristics of bump-type gas foil thrust bearing for oil-free turbomachinery. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2015, 229, 1247–1263. [Google Scholar] [CrossRef]
- Gad, A.M.; Kaneko, S. Tailoring of the bearing stiffness to enhance the performance of gas-lubricated bump-type foil thrust bearing. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2016, 230, 541–560. [Google Scholar] [CrossRef]
- Kim, T.H.; Park, M.; Lee, T.W. Design Optimization of Gas Foil Thrust Bearings for Maximum Load Capacity. ASME J. Tribol. 2017, 139, 031705. [Google Scholar] [CrossRef]
- Lehn, A.; Mahner, M.; Schweizer, B. Characterization of Static Air Foil Thrust Bearing Performance: An Elasto-Gasdynamic Analysis for Aligned, Distorted and Misaligned Operating Conditions. Arch. Appl. Mech. 2018, 88, 705–728. [Google Scholar] [CrossRef]
- Lehn, A.; Mahner, M.; Schweizer, B. A thermo-elasto-hydrodynamic model for air foil thrust bearings including self-induced convective cooling of the rotor disk and thermal runaway. Tribol. Int. 2018, 119, 281–298. [Google Scholar] [CrossRef]
- Kim, C.H.; Park, J.S. Testing of Load Capacity of a Foil Thrust Bearing. Tribol. Lubr. 2018, 34, 300–306. [Google Scholar]
- Fu, G.; Untaroiu, A.; Swanson, E.E. Effect of Foil Geometry on the Static Performance of Thrust Foil Bearings. J. Eng. Gas Turbines Power 2018, 140, V02CT47A016. [Google Scholar] [CrossRef]
- LaTray, N.T. Foil Thrust Bearing with Pocket Grooves and Tailored Bump Stiffness Distribution for Improved Static Performance. Ph.D. Thesis, The University of Texas at Arlington, Arlington, TX, USA, 2018. [Google Scholar]
- LaTray, N.; Kim, D. Design of Novel Gas Foil Thrust Bearings and Test Validation in a High-Speed Test Rig. J. Tribol. 2020, 142, 071803. [Google Scholar] [CrossRef]
- LaTray, N.; Kim, D. Novel Thrust Foil Bearing with Pocket Grooves for Enhanced Static Performance. J. Tribol. 2021, 143, 1–20. [Google Scholar] [CrossRef]
- Guenat, E.; Schiffmann, J. Performance potential of gas foil thrust bearings enhanced with spiral grooves. Tribol. Int. 2018, 131, 438–445. [Google Scholar] [CrossRef]
- Samanta, P.; Khonsari, M. The limiting load-carrying capacity of foil thrust bearings. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2017, 232, 1046–1052. [Google Scholar] [CrossRef]
- Rieken, M.; Mahner, M.; Schweizer, B. Thermal Optimization of Air Foil Thrust Bearings Using Different Foil Materials. Turbo Expo Power Land Sea Air 2019, 58691, V07BT34A031. [Google Scholar]
- Kim, T.H.; Andrés, L.S. Heavily Loaded Gas Foil Bearings: A Model Anchored to Test Data. J. Eng. Gas Turbines Power 2008, 130, 012504. [Google Scholar] [CrossRef]
- Eickhoff, M.; Theile, A.; Mayer, M.; Schweizer, B. Analysis of Air Foil Thrust Bearings with annular top foil including wear prediction, Part I: Modeling and simulation. Tribol. Int. 2023, 181, 108174. [Google Scholar] [CrossRef]
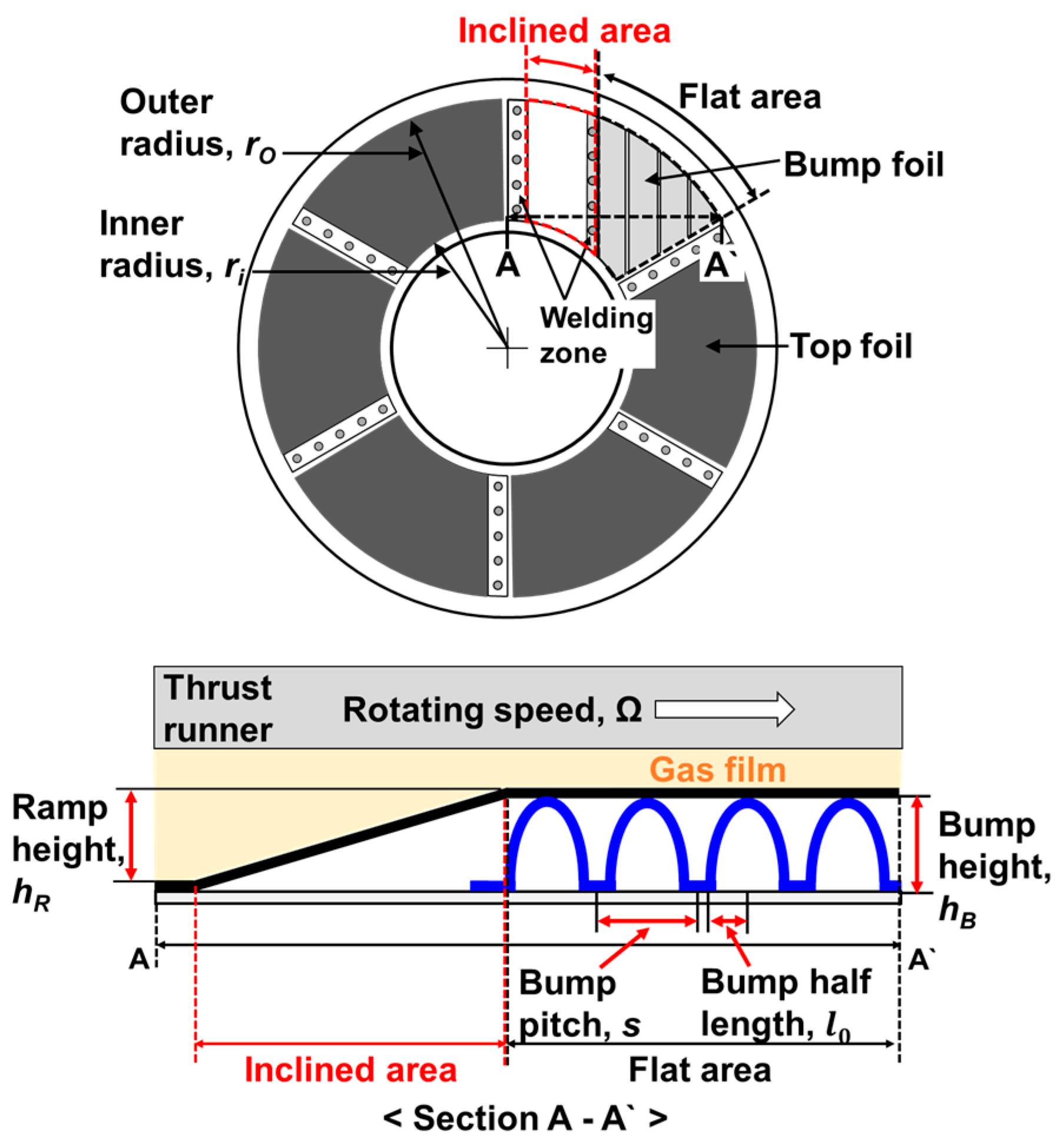
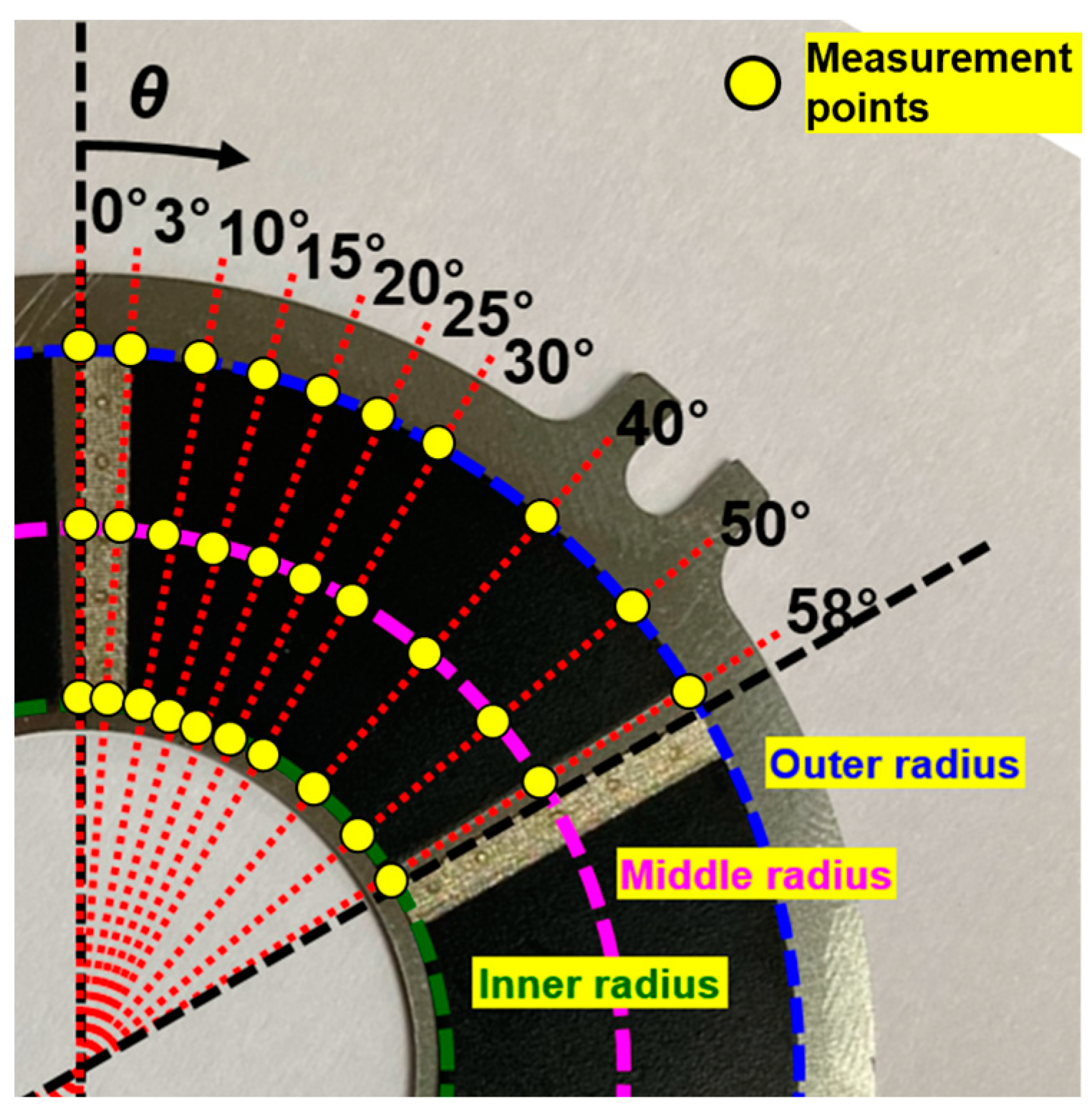
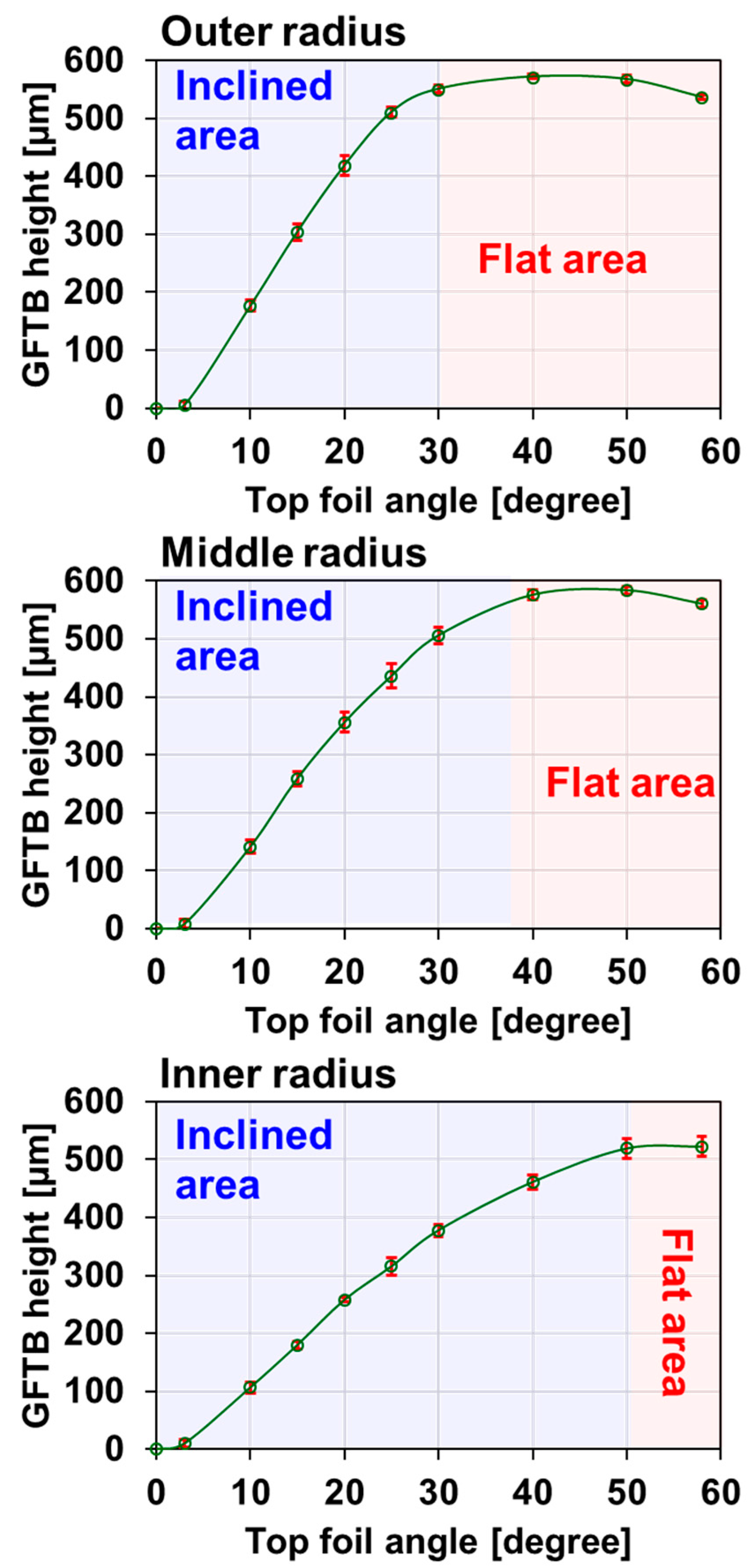
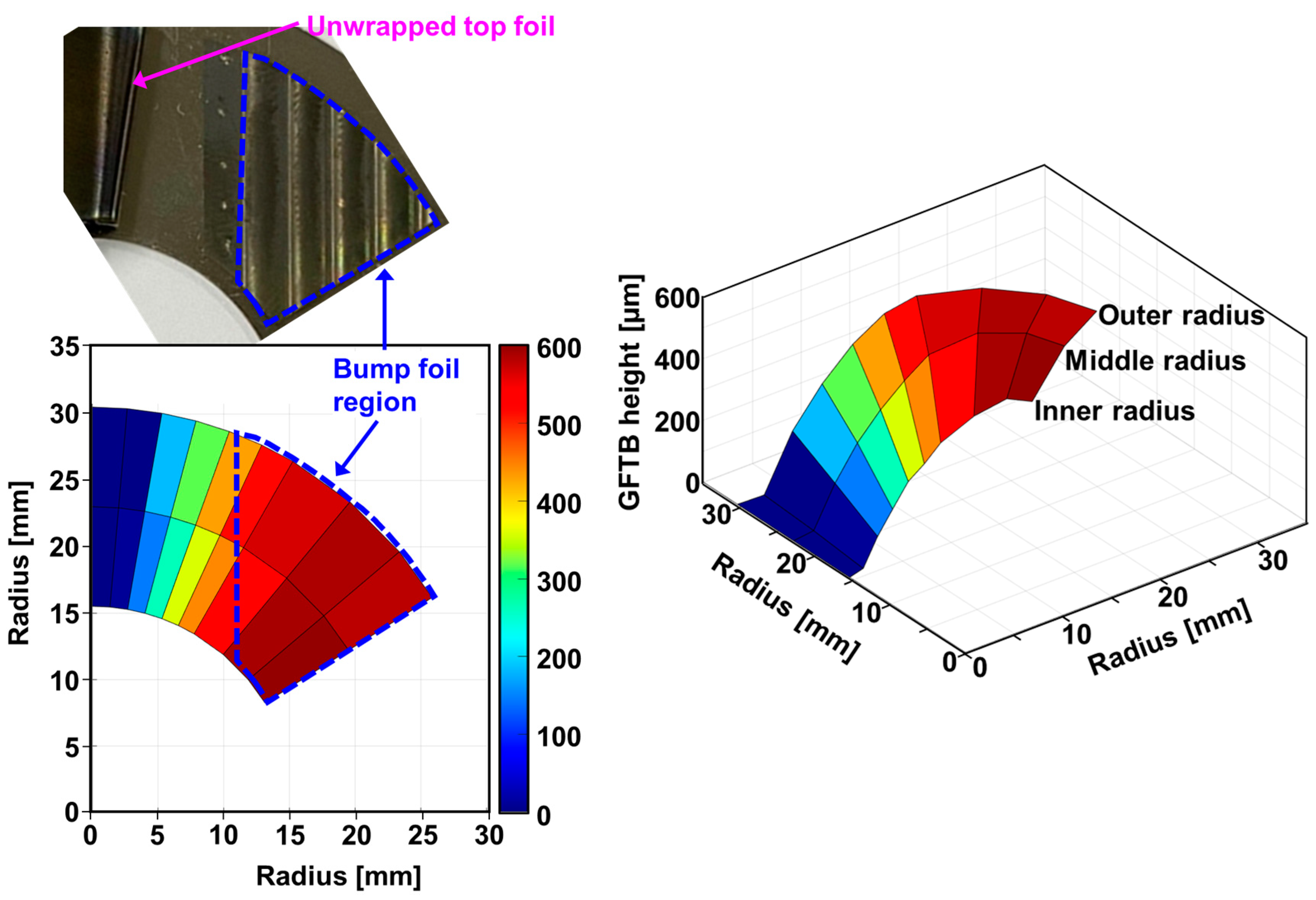


| Parameters | Values |
|---|---|
| Number of top foils | 6 |
| Top foil outer radius (r0) | 30.5 mm |
| Top foil inner radius (ri) | 15.5 mm |
| Pad arc angle (β) | 60° |
| Top Foil thickness (tT) | 200 μm |
| Bump Foil thickness (tB) | 90 μm |
| Incline(ramp) height (hR) | 500 μm |
| Bump height (hB) | 500 μm |
| Bump pitch (s) | 3.2 mm |
| Bump half-length (l0) | 1.4 mm |
| Foil modulus of elasticity (E) | 200 GPa |
| Foil Poisson’s ratio (ν) | 0.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwang, S.H.; Mehdi, S.M.; Kim, T.H. Static Performance Measurements and Model Predictions of Gas Foil Thrust Bearing with Curved Incline Geometry. Lubricants 2023, 11, 480. https://doi.org/10.3390/lubricants11110480
Hwang SH, Mehdi SM, Kim TH. Static Performance Measurements and Model Predictions of Gas Foil Thrust Bearing with Curved Incline Geometry. Lubricants. 2023; 11(11):480. https://doi.org/10.3390/lubricants11110480
Chicago/Turabian StyleHwang, Sung Ho, Syed Muntazir Mehdi, and Tae Ho Kim. 2023. "Static Performance Measurements and Model Predictions of Gas Foil Thrust Bearing with Curved Incline Geometry" Lubricants 11, no. 11: 480. https://doi.org/10.3390/lubricants11110480
APA StyleHwang, S. H., Mehdi, S. M., & Kim, T. H. (2023). Static Performance Measurements and Model Predictions of Gas Foil Thrust Bearing with Curved Incline Geometry. Lubricants, 11(11), 480. https://doi.org/10.3390/lubricants11110480






