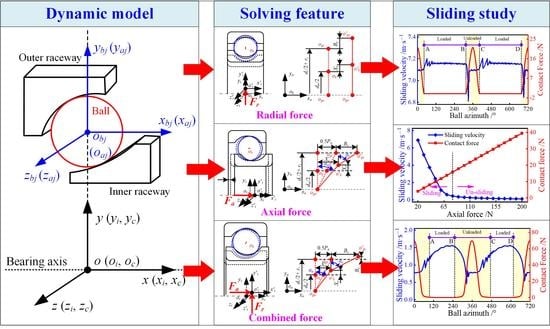
A Generalized Bearing Dynamic with Adaptive Variation of Equation Numbers and Sliding Behavior Investigation
Abstract
:1. Introduction
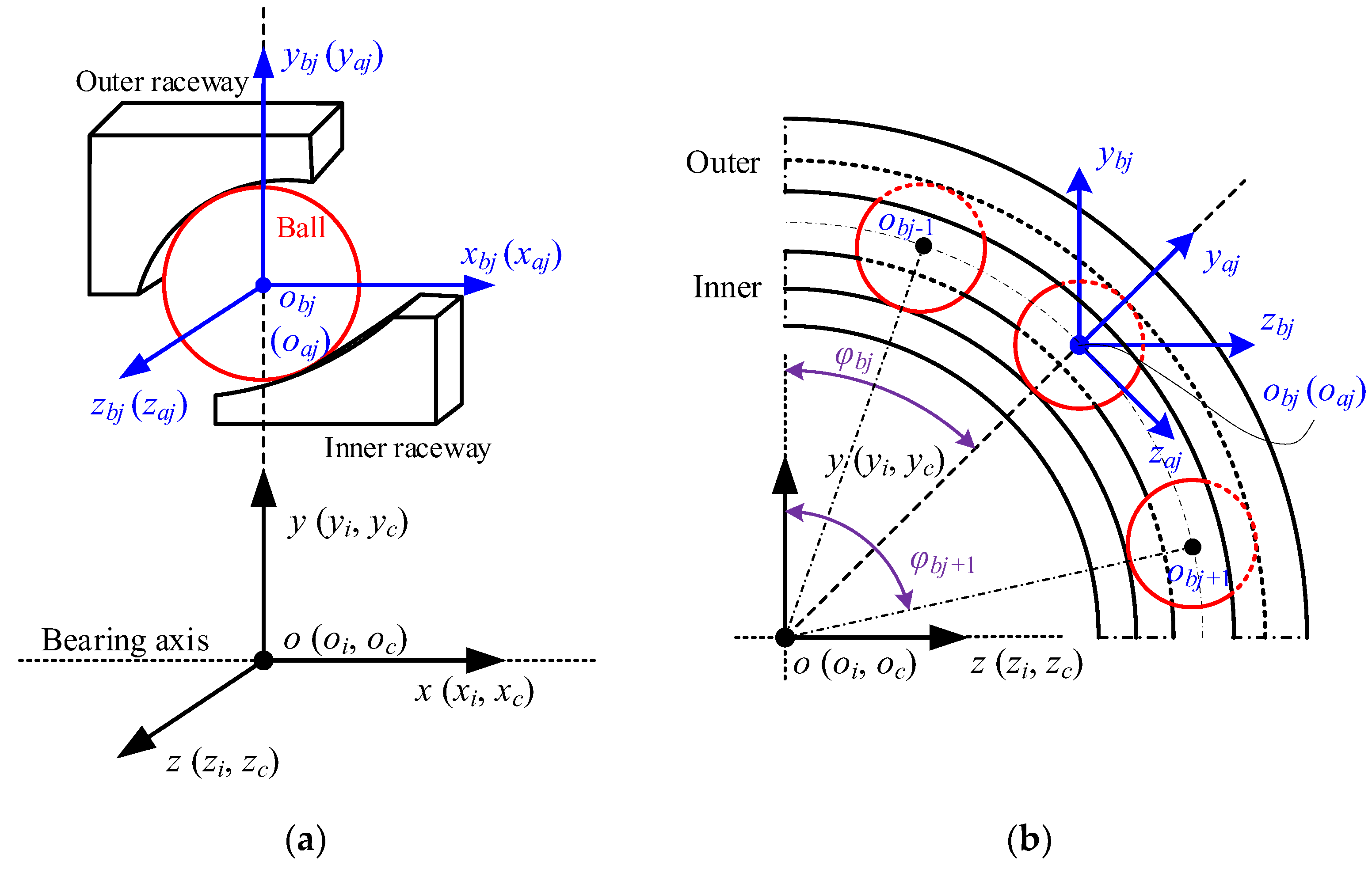
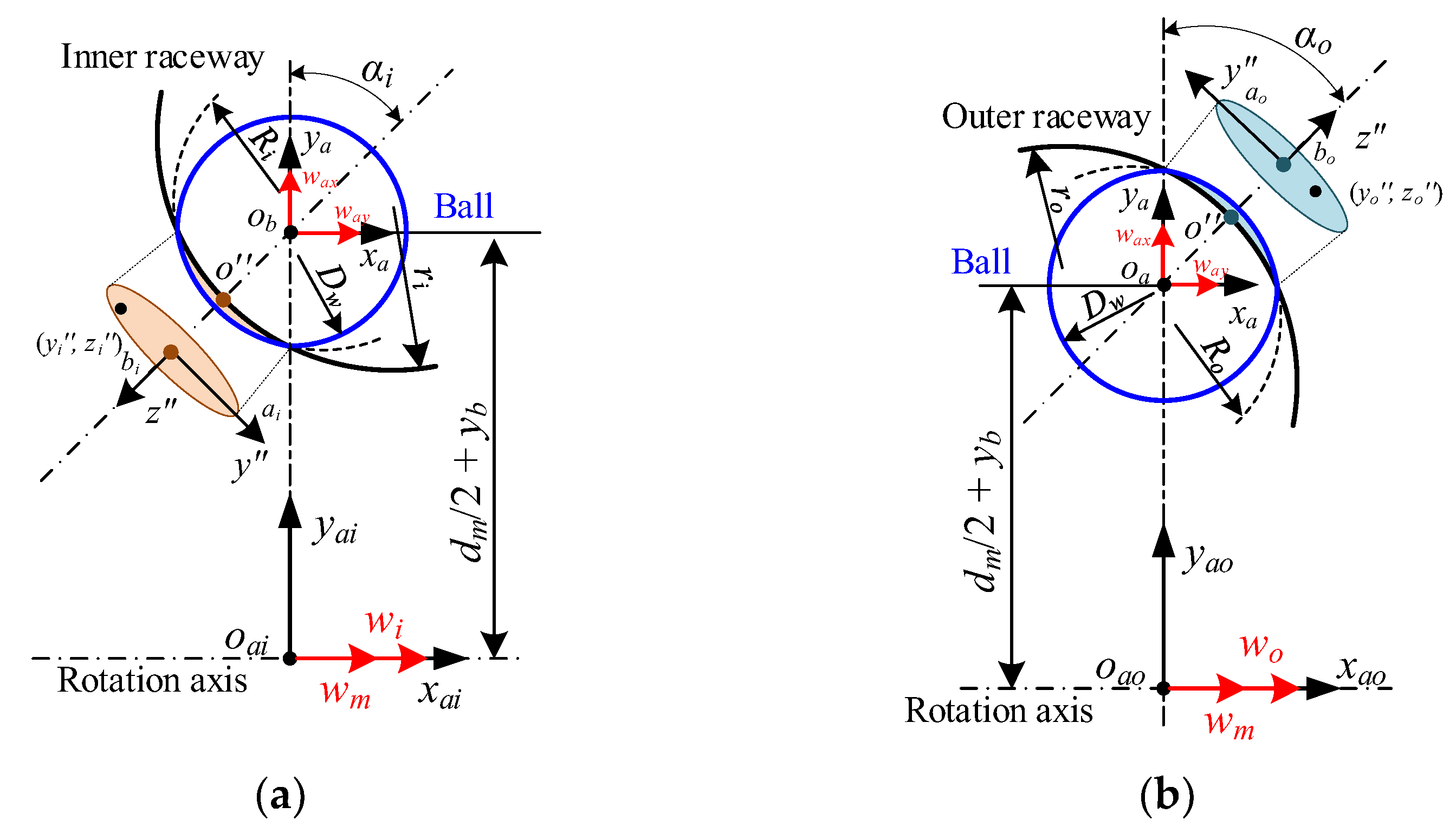
2. Ball/Raceway Interaction Modeling
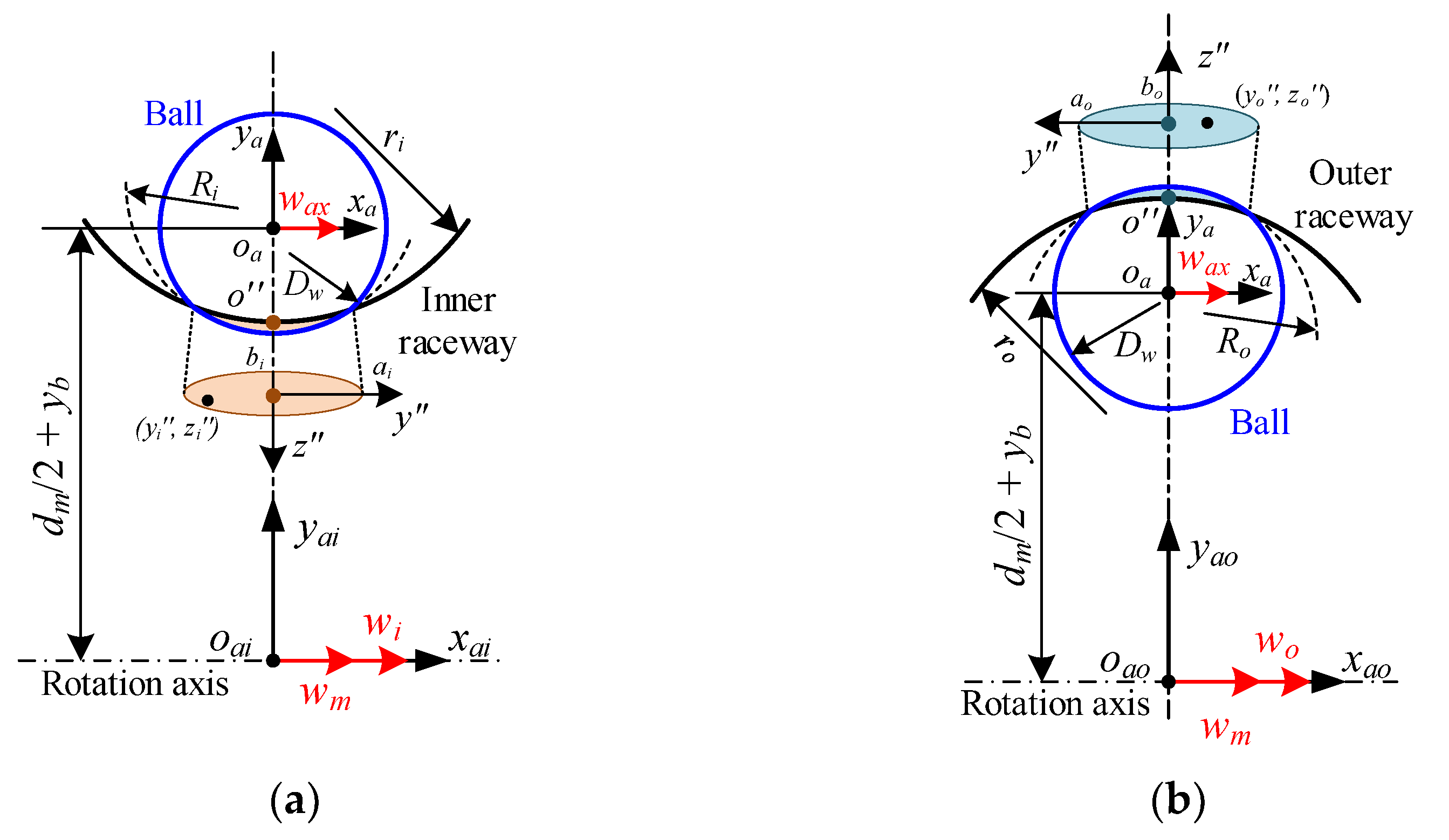
2.1. Pure Radial Force
- (1)
- Normal load
- (2)
- Traction force
- (3)
- Differential equations
2.2. Pure Axial Force
- (1)
- Normal load
- (2)
- Traction force
- (3)
- Differential equations
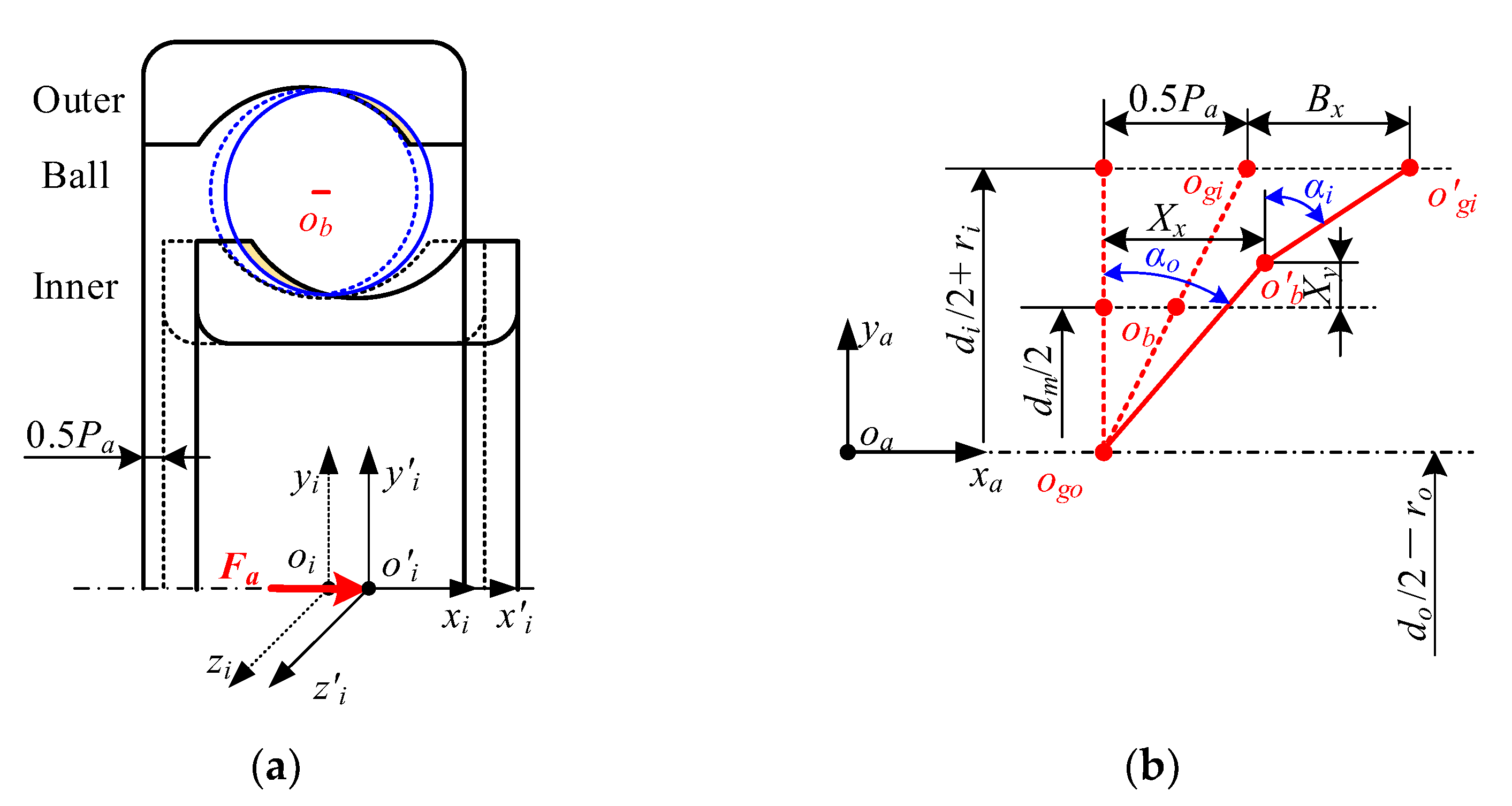
2.3. Combined Axial and Radial Load
- (1)
- Normal load
- (2)
- Differential equations
3. Theoretical Model Solving and Validation
3.1. Model Solving
3.2. Model Validation
4. Results and Discussion
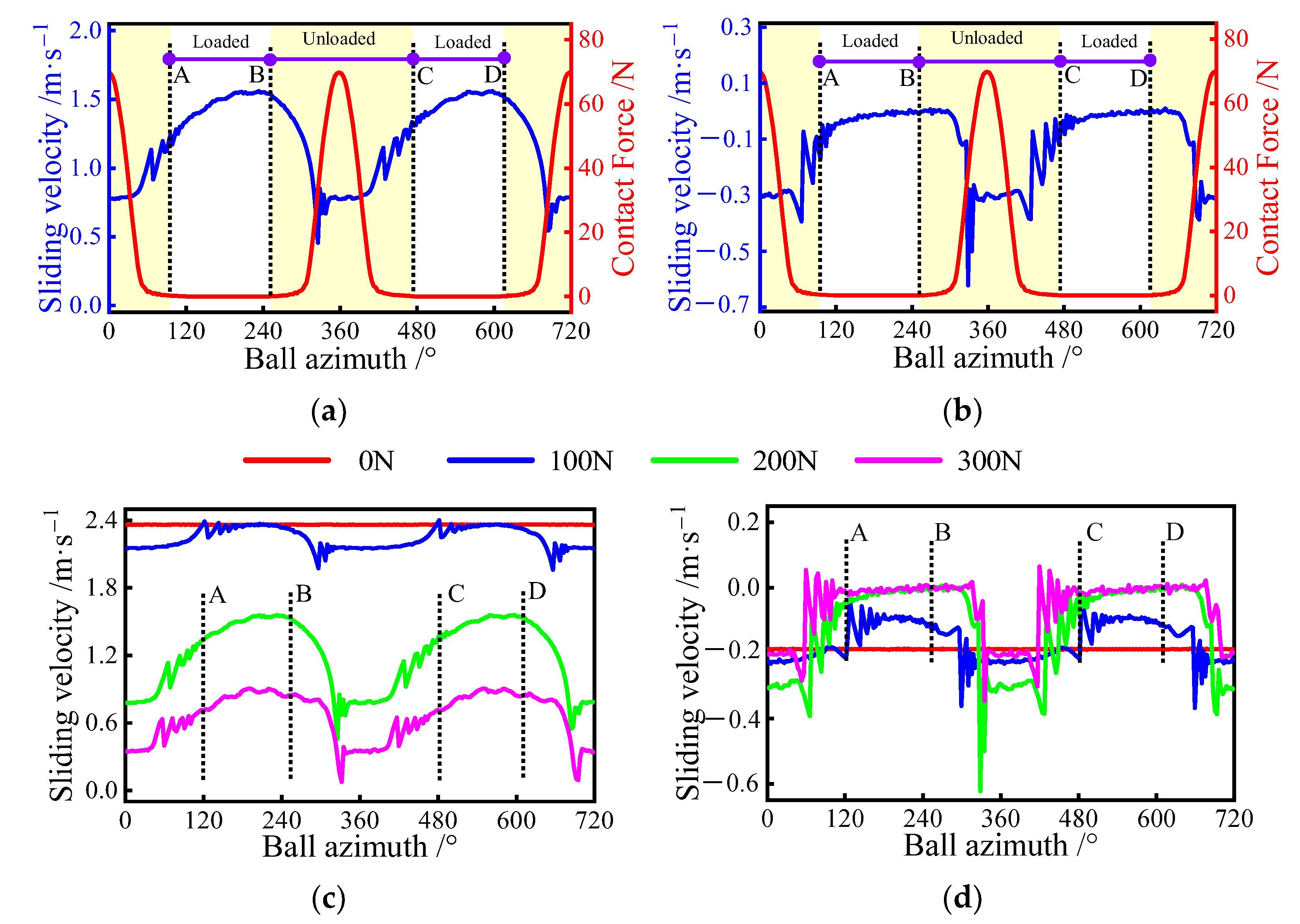
4.1. Case 1: Pure Radial Force
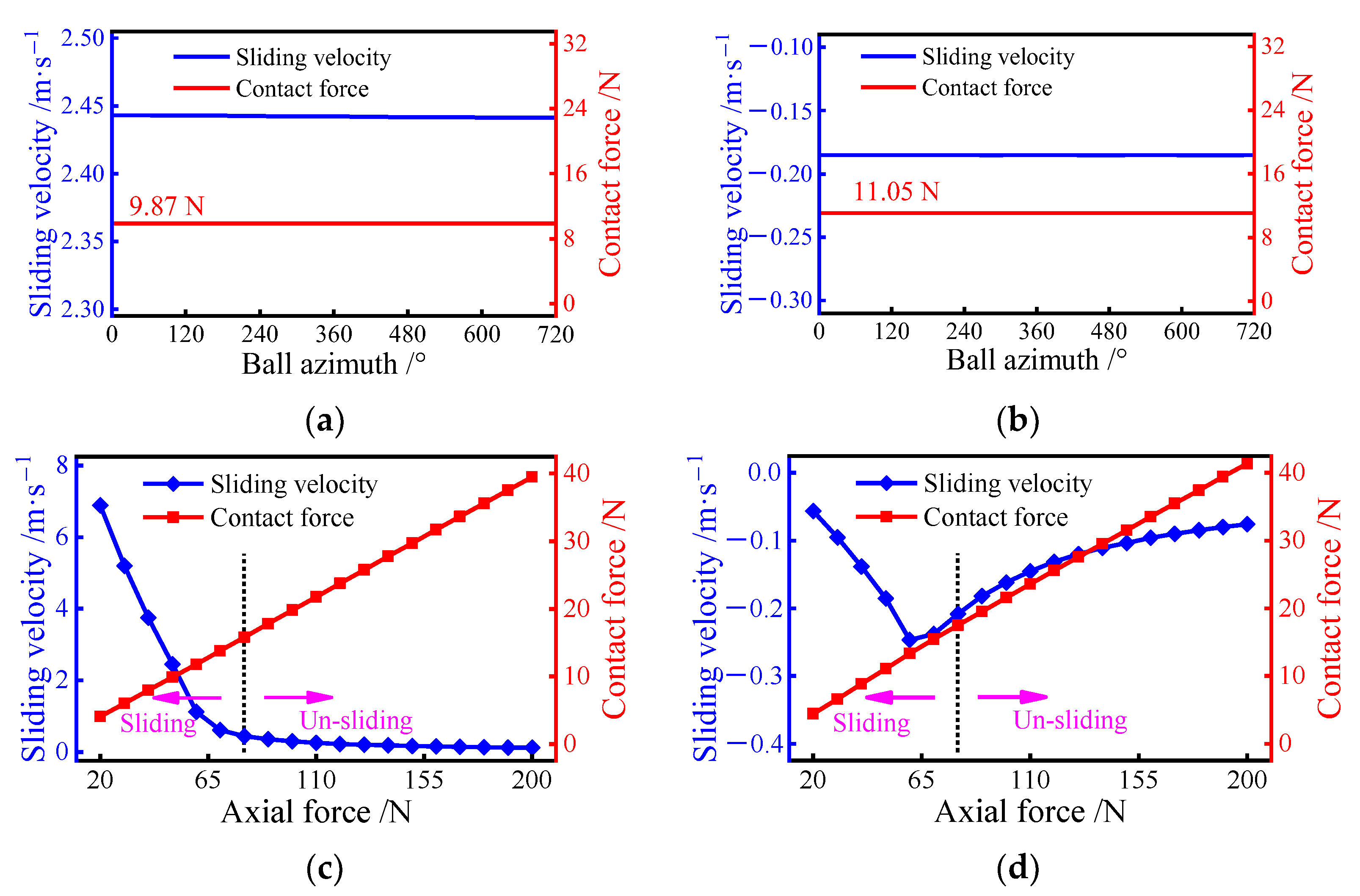
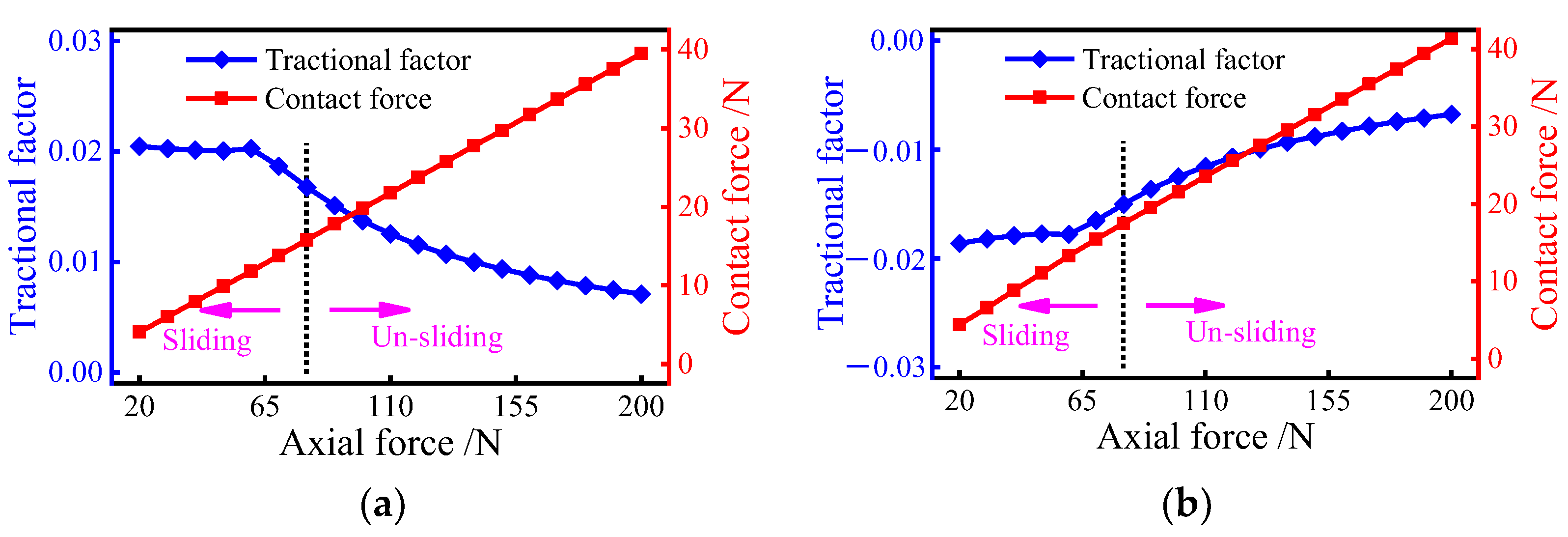
4.2. Case 2: Pure Axial Force
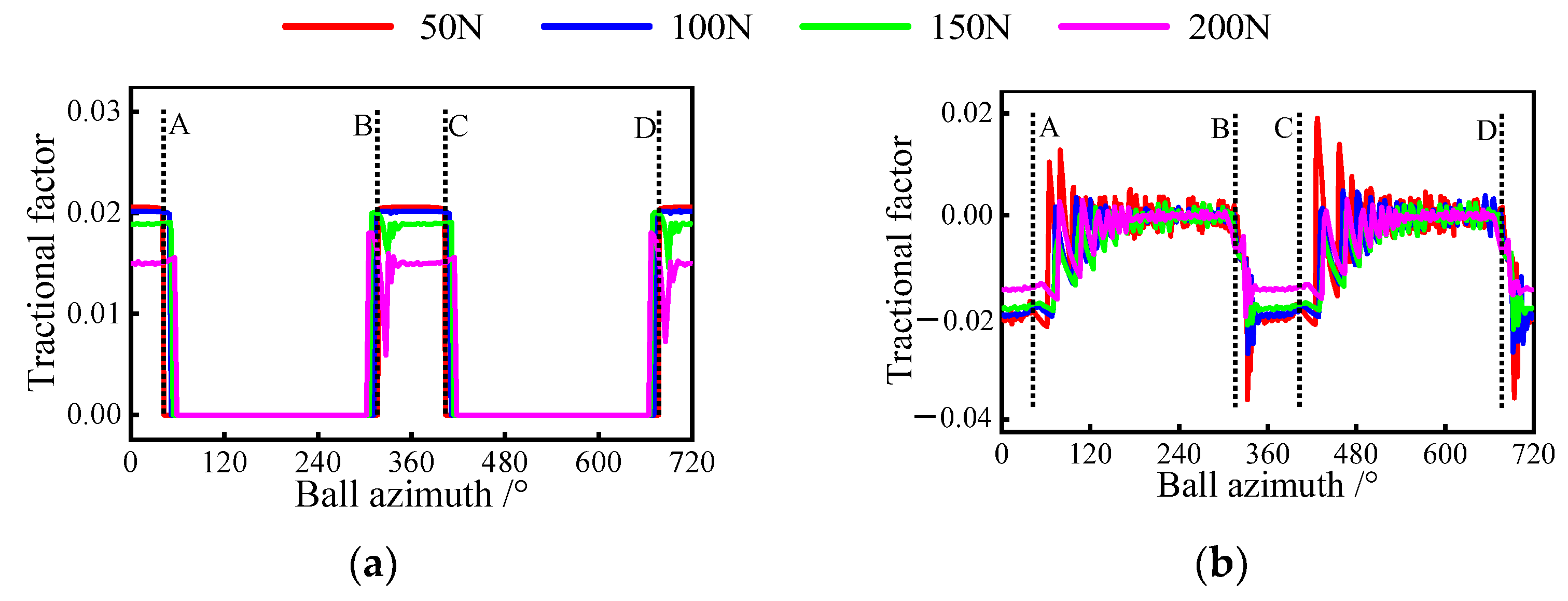
4.3. Case 3: Combined Axial and Radial Force
5. Conclusions
- (1)
- When the bearing is subjected to pure axial force, the sliding velocity in the outer raceway first increases and then decreases as the load increases;
- (2)
- Under combined load conditions, the heavy radial forces inhibit the bearing sliding while exacerbating the non-uniformity of the sliding distribution;
- (3)
- Once the unloaded zone occurs, the sliding velocity between the ball and the inner raceway is less in the loaded zone than in the unloaded zone. While the velocity on the outer raceway has the opposite trend;
- (4)
- The increased load helps to suppress severe sliding behavior inside the bearing but shortens the bearing fatigue life.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbols | Meaning |
| δ | Contact deformation |
| Bx/y | Inner groove curvature center’s displacement |
| Xx/y | Ball center’s displacement |
| Qi/o | Inner/outer normal load |
| Qc | Ball/pocket interaction force |
| Mx | Spin moment |
| p | Contact stress |
| τ | Shear stress |
| μ | Traction coefficient |
| Ti/o | Inner/outer traction load |
| αi/o | Working contact angle |
| m | Mass |
| I | Rotational inertia |
| Fc | Ball centrifugal force |
| Fdj | Oil and gas mixture mixing resistance |
| di/o | Groove bottom circle diameter of inner/outer ring |
| ri/o | Groove curvature radius of inner/outer ring |
| Dw | Ball diameter |
| dm | Bearing pitch diameter |
| Ri | Curvature radius of the contact surface |
| Z | Ball number |
| Pa | Axial clearance |
| φbj | Ball azimuth |
| Ki/o | Contact deflection coefficient |
| v | Sliding velocity |
| u | Rolling velocity |
| wm | Ball orbital angular velocity |
| wbx | Ball rotation angular velocity |
| ws | Spin velocity |
| pmax | Maximum contact stress |
| S | Micrometeoroid’s area |
| A, B, C, D | Lubricant parameters |
| s | Slide-roll ratio |
| Fa | Axial load |
| Fr | Radial load |
| o-xyz | Inertial coordinate frame |
| oi-xiyizi | Inner-fixed coordinate frame |
| oc-xcyczc | Cage-fixed coordinate frame |
| ob-xbybzb | Ball-fixed coordinate frame |
| oa-xayaza | Azimuthal coordinate frame |
References
- Cocks, M.; Tallian, T.E. Sliding Contacts in Rolling Bearings. ASLE Trans. 1971, 14, 32–40. [Google Scholar] [CrossRef]
- Qian, D.; Xu, X.; Deng, S.; Jiang, S.; Hua, L. Sliding behavior of high speed ball bearings based on improved nonlinear dynamic model. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2021, 235, 627–640. [Google Scholar] [CrossRef]
- Gupta, P.K. Minimum Energy Hypothesis in Quasi-Static Equilibrium Solutions for Angular Contact Ball Bearings. Tribol. Trans. 2020, 63, 1051–1066. [Google Scholar] [CrossRef]
- Zhang, P.; Pan, A.; Yan, K.; Sun, J. High stability temperature sensors by CdTe quantum dots encapsulated in SiO2/PVA hybrids for bearing rotating elements. Mater. Today Commun. 2023, 34, 105456. [Google Scholar] [CrossRef]
- Jorgensen, B.R.; Shin, Y. Dynamics of Machine Tool Spindle/Bearing Systems Under Thermal Growth. J. Tribol. 1997, 119, 875–882. [Google Scholar] [CrossRef]
- Aramaki, H.; Shoda, Y.; Morishita, Y.; Sawamoto, T. The Performance of Ball Bearings With Silicon Nitride Ceramic Balls in High Speed Spindles for Machine Tools. J. Tribol. 1988, 110, 693–698. [Google Scholar] [CrossRef]
- Harris, T. Rolling Bearing Analysis, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1984. [Google Scholar]
- Xu, T.; Xu, G.; Zhang, Q.; Hua, C.; Tan, H.; Zhang, S.; Luo, A. A preload analytical method for ball bearings utilising bearing skidding criterion. Tribol. Int. 2013, 67, 44–50. [Google Scholar] [CrossRef]
- Liao, N.T.; Lin, J.F. Ball bearing skidding under radial and axial loads. Mech. Mach. Theory 2002, 37, 91–113. [Google Scholar] [CrossRef]
- Liao, N.-T.; Lin, J.F. Rolling-Sliding Analysis in Ball Bearing Considering Thermal Effect. Tribol. Trans. 2006, 49, 1–16. [Google Scholar] [CrossRef]
- Hirano, F. Motion of a Ball in Angular-Contact Ball Bearing. ASLE Trans. 1965, 8, 425–434. [Google Scholar] [CrossRef]
- Oktaviana, L.; Tong, V.-C.; Hong, S.-W. Skidding analysis of angular contact ball bearing subjected to radial load and angular misalignment. J. Mech. Sci. Technol. 2019, 33, 837–845. [Google Scholar] [CrossRef]
- Nelias, D.; Bercea, I.; Paleu, V. Prediction of Roller Skewing in Tapered Roller Bearings. Tribol. Trans. 2008, 51, 128–139. [Google Scholar] [CrossRef]
- Cao, H.; Niu, L.; Xi, S.; Chen, X. Mechanical model development of rolling bearing-rotor systems: A review. Mech. Syst. Signal Process. 2018, 102, 37–58. [Google Scholar] [CrossRef]
- Meeks, C.R.; Ng, K.O. The Dynamics of Ball Separators in Ball Bearings—Part I: Analysis. ASLE Trans. 1985, 28, 277–287. [Google Scholar] [CrossRef]
- Meeks, C.R.; Tran, L. Ball Bearing Dynamic Analysis Using Computer Methods—Part I: Analysis. J. Tribol. 1996, 118, 52–58. [Google Scholar] [CrossRef]
- Jones, A.B. Ball Motion and Sliding Friction in Ball Bearings. Trans. ASME J. Basic Eng. 1959, 81, 1–12. [Google Scholar] [CrossRef]
- Jones, A.B. A General Theory for Elastically Constrained Ball and Radial Roller Bearings Under Arbitrary Load and Speed Conditions. J. Basic Eng. 1960, 82, 309–320. [Google Scholar] [CrossRef]
- Jain, S.; Hunt, H. A dynamic model to predict the occurrence of skidding in wind-turbine bearings. J. Phys. Conf. Ser. 2011, 305, 012027. [Google Scholar] [CrossRef]
- Han, Q.; Chu, F. Nonlinear dynamic model for skidding behavior of angular contact ball bearings. J. Sound Vib. 2015, 354, 219–235. [Google Scholar] [CrossRef]
- Gao, S.; Chatterton, S.; Naldi, L.; Pennacchi, P. Ball bearing skidding and over-skidding in large-scale angular contact ball bearings: Nonlinear dynamic model with thermal effects and experimental results. Mech. Syst. Signal Process. 2020, 147, 107120. [Google Scholar] [CrossRef]
- Gupta, P. Advanced Dynamics of Rolling Bearings; Springer: Boston, MA, USA, 2013. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Zhang, S.; Zhao, Z. Investigation of skidding in angular contact ball bearings under high speed. Tribol. Int. 2015, 92, 404–417. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Zhao, Z. Effect of race conformities in angular contact ball bearing. Tribol. Int. 2016, 104, 109–120. [Google Scholar] [CrossRef]
- Yunlong, W.; Wenzhong, W.; Shengguang, Z.; Ziqiang, Z. Effects of raceway surface roughness in an angular contact ball bearing. Mech. Mach. Theory 2018, 121, 198–212. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, W.; Qing, T.; Zhang, Y.; Liang, H.; Zhang, S. The effect of lubricant temperature on dynamic behavior in angular contact ball bearings. Mech. Mach. Theory 2020, 149, 103832. [Google Scholar] [CrossRef]
- Ma, S.; Li, W.; Yan, K.; Li, Y.; Zhu, Y.; Hong, J. A study on the dynamic contact feature of four-contact-point ball bearing. Mech. Syst. Signal Process. 2022, 174, 109111. [Google Scholar] [CrossRef]
- Xu, H.; Wang, P.; Ma, H.; He, D.; Zhao, X.; Yang, Y. Analysis of axial and overturning ultimate load-bearing capacities of deep groove ball bearings under combined loads and arbitrary rotation speed. Mech. Mach. Theory 2021, 169, 104665. [Google Scholar] [CrossRef]
- Li, B.L.; Zeng, L. Fractional Calculus Control of Road Vehicle Lateral Stability after a Tire Blowout. Mechanika 2021, 27, 475–482. [Google Scholar] [CrossRef]
- Walczak, M.; Caban, J. Tribological characteristics of polymer materials used for slide bearings. Open Eng. 2021, 11, 624–629. [Google Scholar] [CrossRef]
- Gil, L.; Przystupa, K.; Pieniak, D.; Kozłowski, E.; Antosz, K.; Gauda, K.; Izdebski, P. Influence of Contamination of Gear Oils in Relation to Time of Operation on Their Lubricity. Appl. Sci. 2021, 11, 11835. [Google Scholar] [CrossRef]
- Fang, B.; Zhang, J.; Hong, J.; Yan, K. Research on the Nonlinear Stiffness Characteristics of Double-Row Angular Contact Ball Bearings under Different Working Conditions. Lubricants 2023, 11, 44. [Google Scholar] [CrossRef]
- Wang, M.; Yan, K.; Zhang, X.; Zhu, Y.; Hong, J. A comprehensive study on dynamic performance of ball bearing considering bearing de-formations and ball-inner raceway separation. Mech. Syst. Signal Process. 2023, 185, 109826. [Google Scholar] [CrossRef]
- Ma, S.; Yin, Y.; Chao, B.; Yan, K.; Fang, B.; Hong, J. A real-time coupling model of bearing-rotor system based on semi-flexible body element. Int. J. Mech. Sci. 2023, 245, 108098. [Google Scholar] [CrossRef]
- Han, Q.; Li, X.; Chu, F. Skidding behavior of cylindrical roller bearings under time-variable load conditions. Int. J. Mech. Sci. 2018, 135, 203–214. [Google Scholar] [CrossRef]
- Pasdari, M.; Gentle, C.R. Effect of Lubricant Starvation on the Minimum Load Condition in a Thrust-Loaded Ball Bearing. ASLE Trans. 1987, 30, 355–359. [Google Scholar] [CrossRef]








| Static Model | Quasi-Static Model | Dynamic Model | |
|---|---|---|---|
| Nonlinear Equations | Nonlinear Equations | Differential Equations | |
| Case: 1 | 1 | 1 + N | 1 + 1 + 3 N |
| Case: 2 | 1 | 1 + 2 | 1 + 1 + 6 N |
| Case: 3 | 2 | 2 + 2 N | 2 + 1 + 6 N |
| General model | 2 | 2 + 2 N | 2 + 1 + 6 N |
| Name | Value |
|---|---|
| Pitch circle diameter dm/mm | 54 |
| Inner curvature radius ri/mm | 3.990 |
| Outer curvature radius ro/mm | 3.780 |
| Ball diameter Dw/mm | 7.000 |
| Number of balls Z | 18 |
| Initial contact angle α0/° | 15 |
| Cage pocket clearness Cb/mm | 0.200 |
| Ring material | Bearing Steel |
| Ball material | Bearing Steel |
| Cage material | Nylon |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, S.; Yin, Y.; Chen, F.; Fang, B.; Yan, K.; Hong, J. A Generalized Bearing Dynamic with Adaptive Variation of Equation Numbers and Sliding Behavior Investigation. Lubricants 2023, 11, 96. https://doi.org/10.3390/lubricants11030096
Ma S, Yin Y, Chen F, Fang B, Yan K, Hong J. A Generalized Bearing Dynamic with Adaptive Variation of Equation Numbers and Sliding Behavior Investigation. Lubricants. 2023; 11(3):96. https://doi.org/10.3390/lubricants11030096
Chicago/Turabian StyleMa, Shuaijun, Yanjing Yin, Fei Chen, Bin Fang, Ke Yan, and Jun Hong. 2023. "A Generalized Bearing Dynamic with Adaptive Variation of Equation Numbers and Sliding Behavior Investigation" Lubricants 11, no. 3: 96. https://doi.org/10.3390/lubricants11030096