Pin-on-Plate vs. Pin-on-Disk Wear Tests: Theoretical and Numerical Observations on the Initial Transient Phase
Abstract
:1. Introduction
2. Materials and Methods
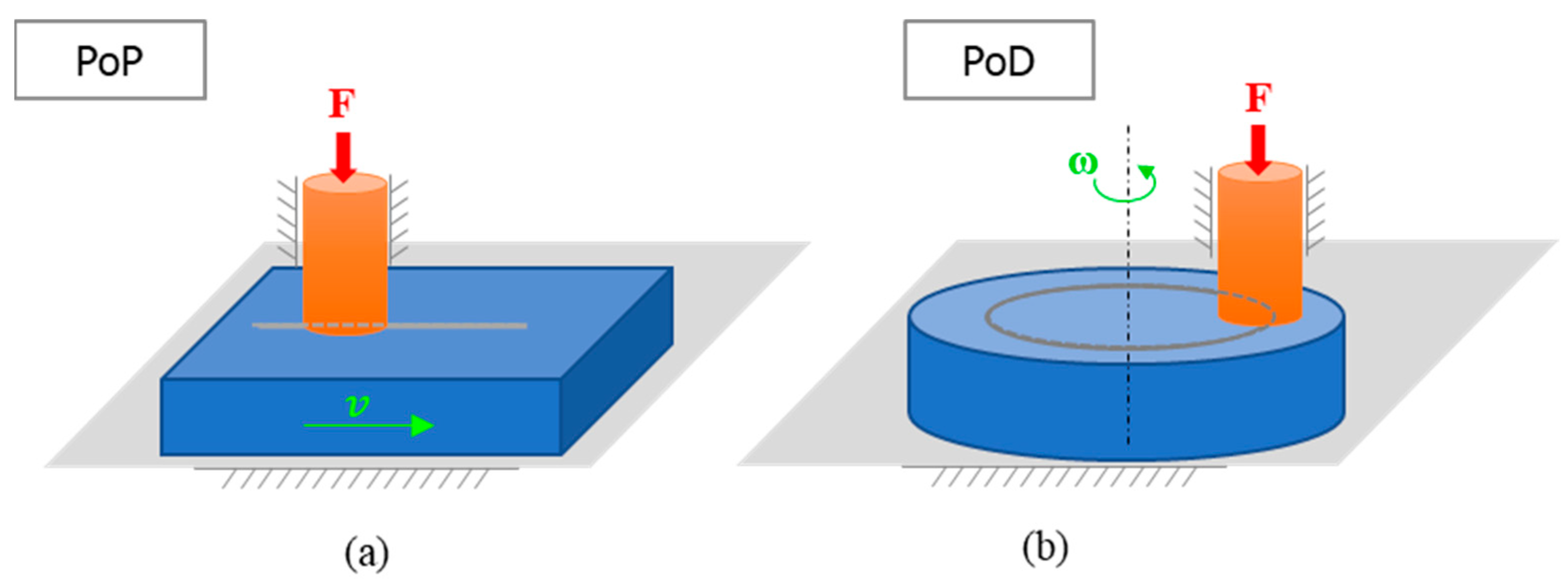
2.1. Test Cases
2.2. Finite Element Models
2.2.1. Geometry and Materials
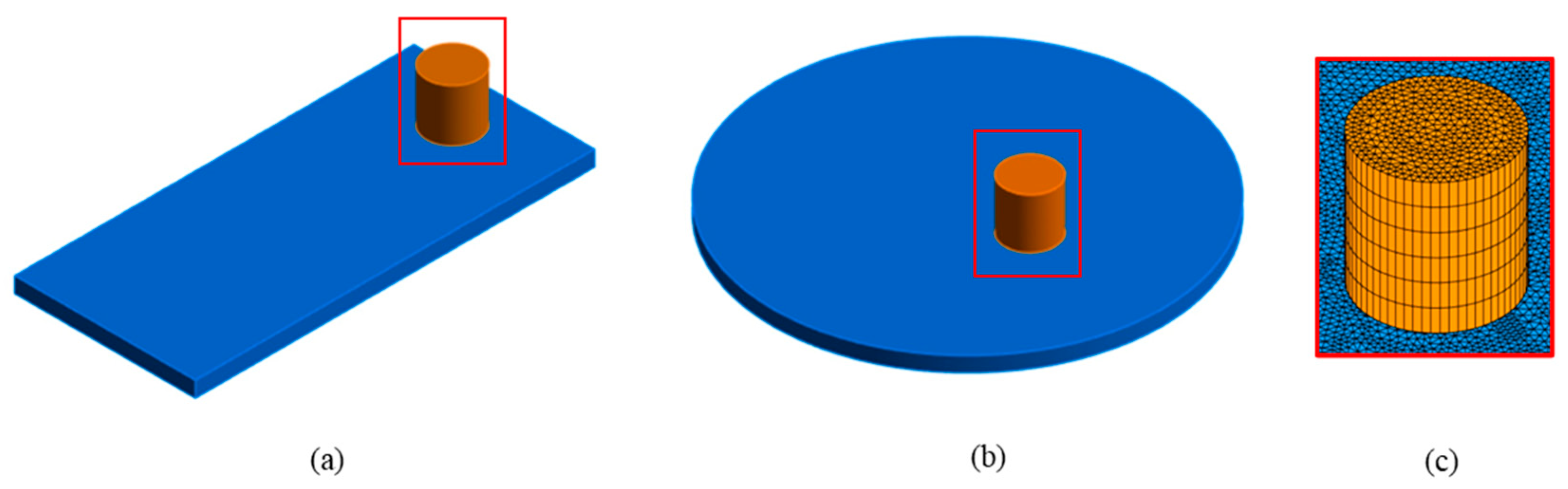
2.2.2. Mesh
2.2.3. Contact and Wear Conditions
2.2.4. Boundary Conditions
2.2.5. Analysis Settings
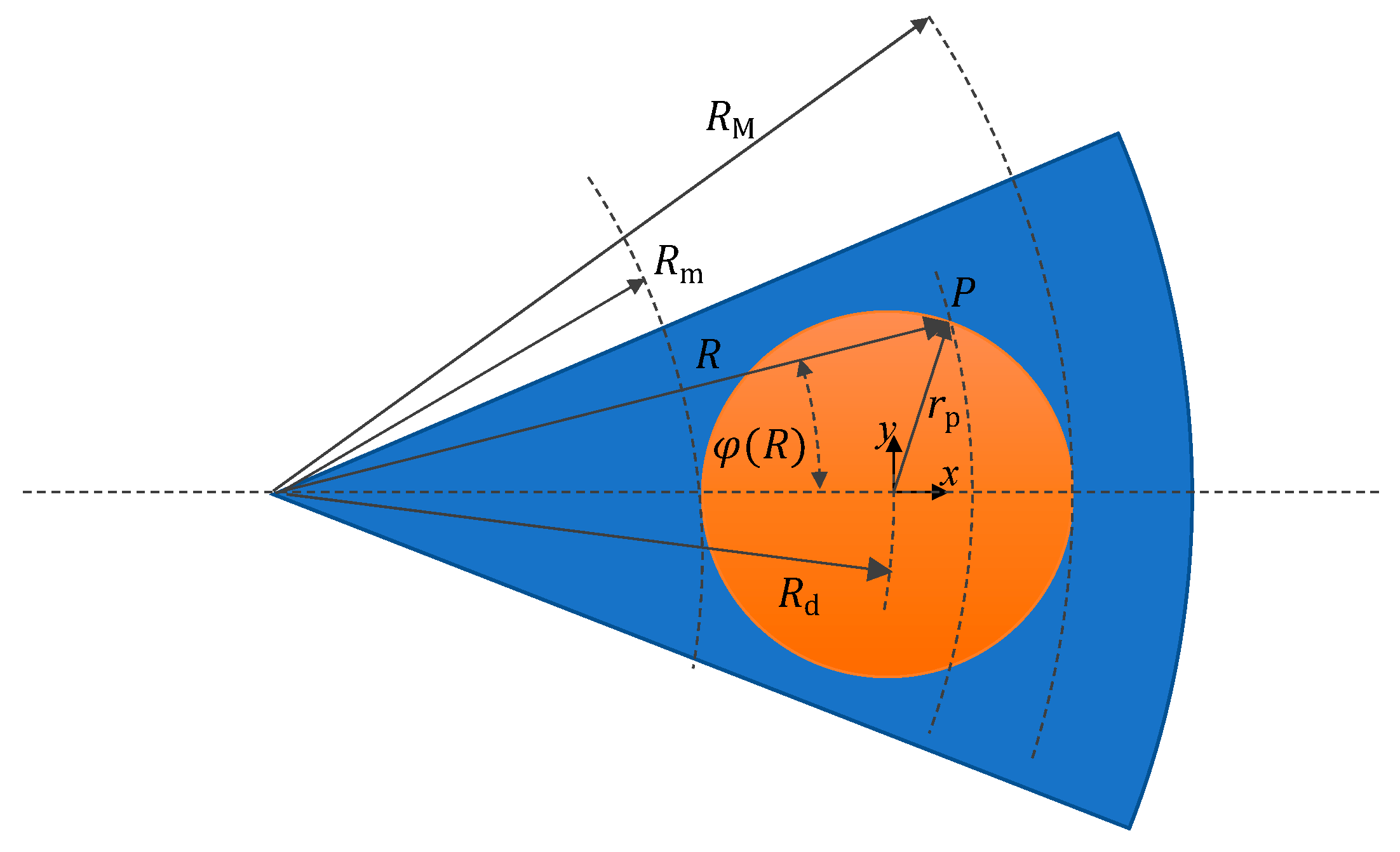
2.3. Analytical Approach
3. Result and Discussion
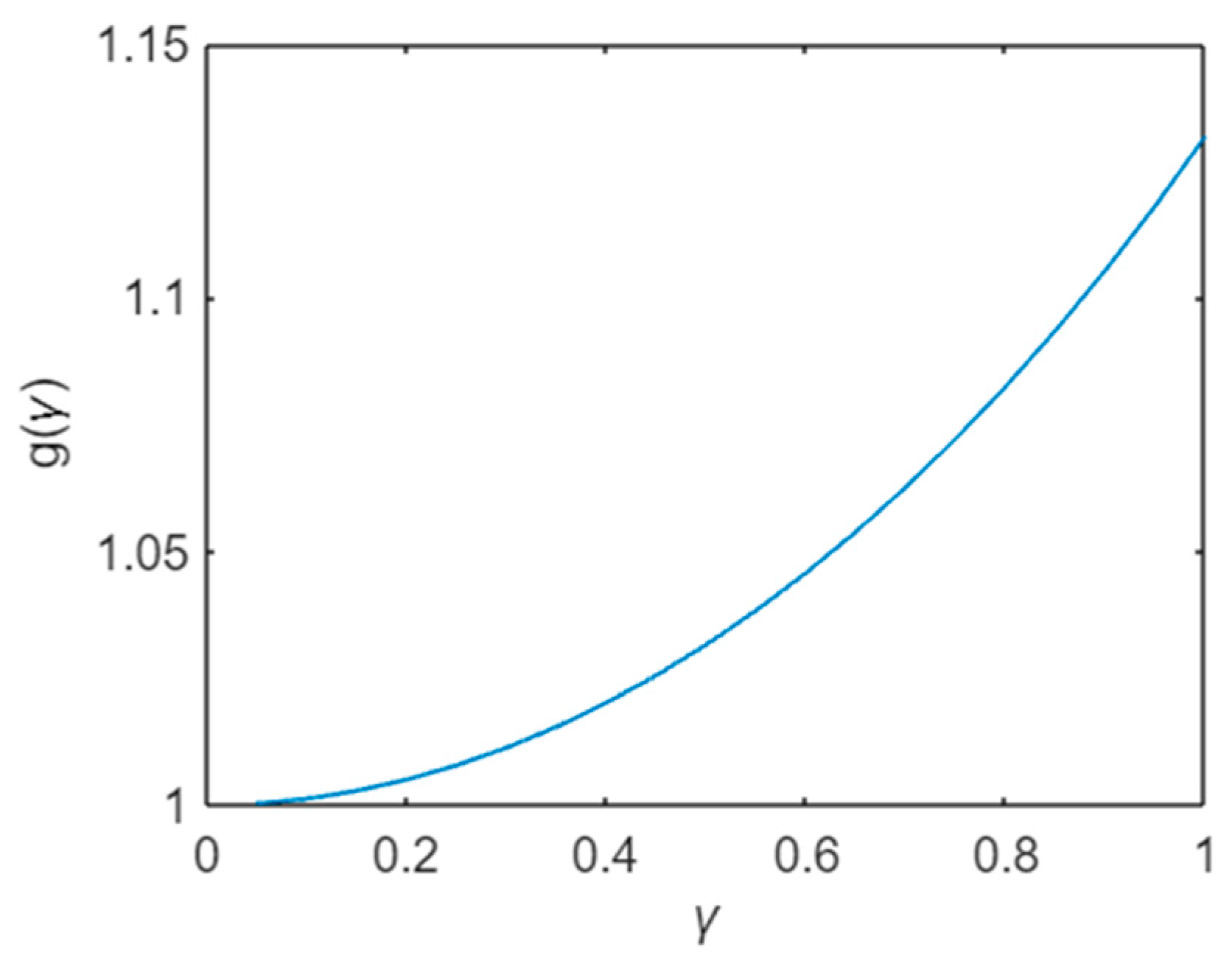
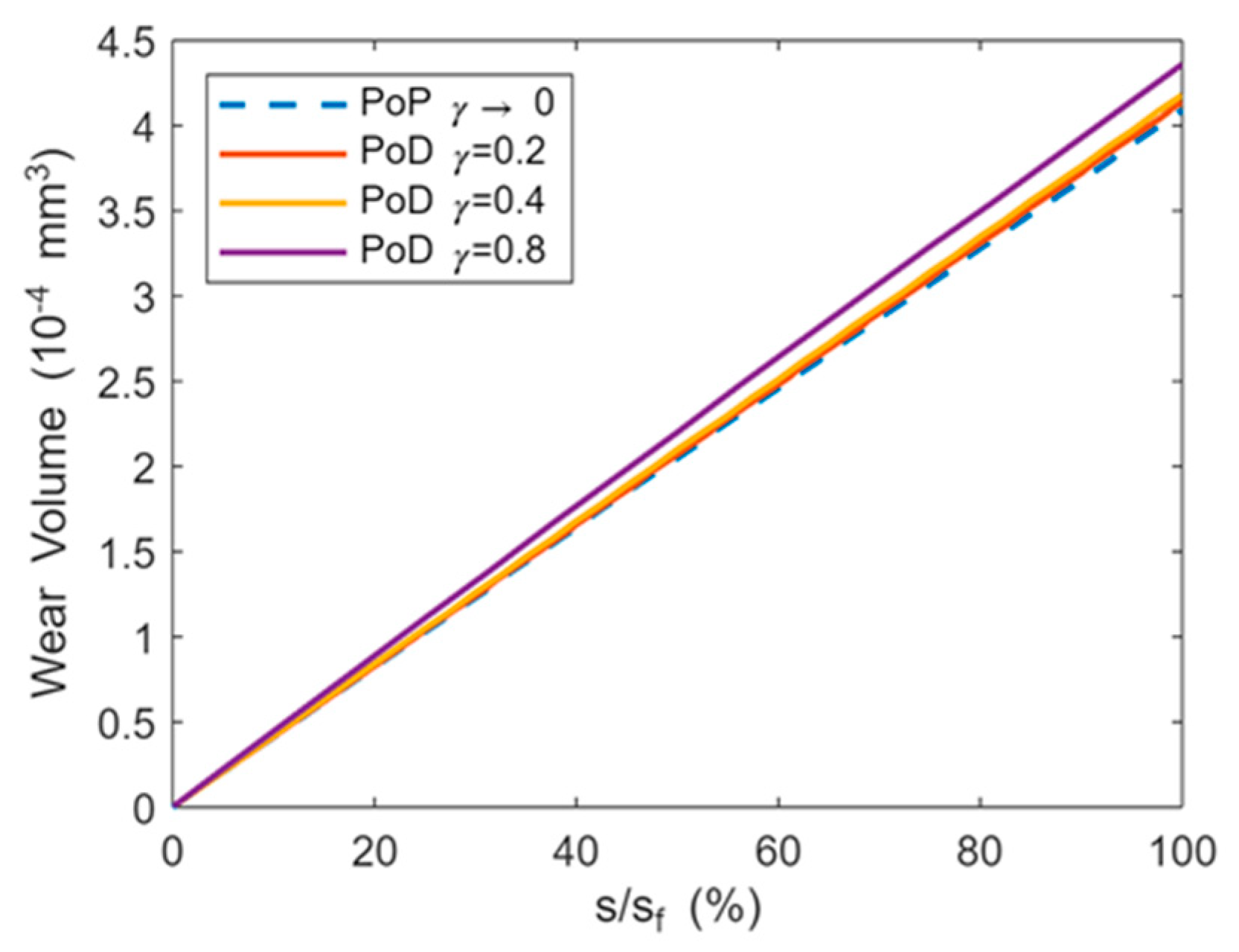
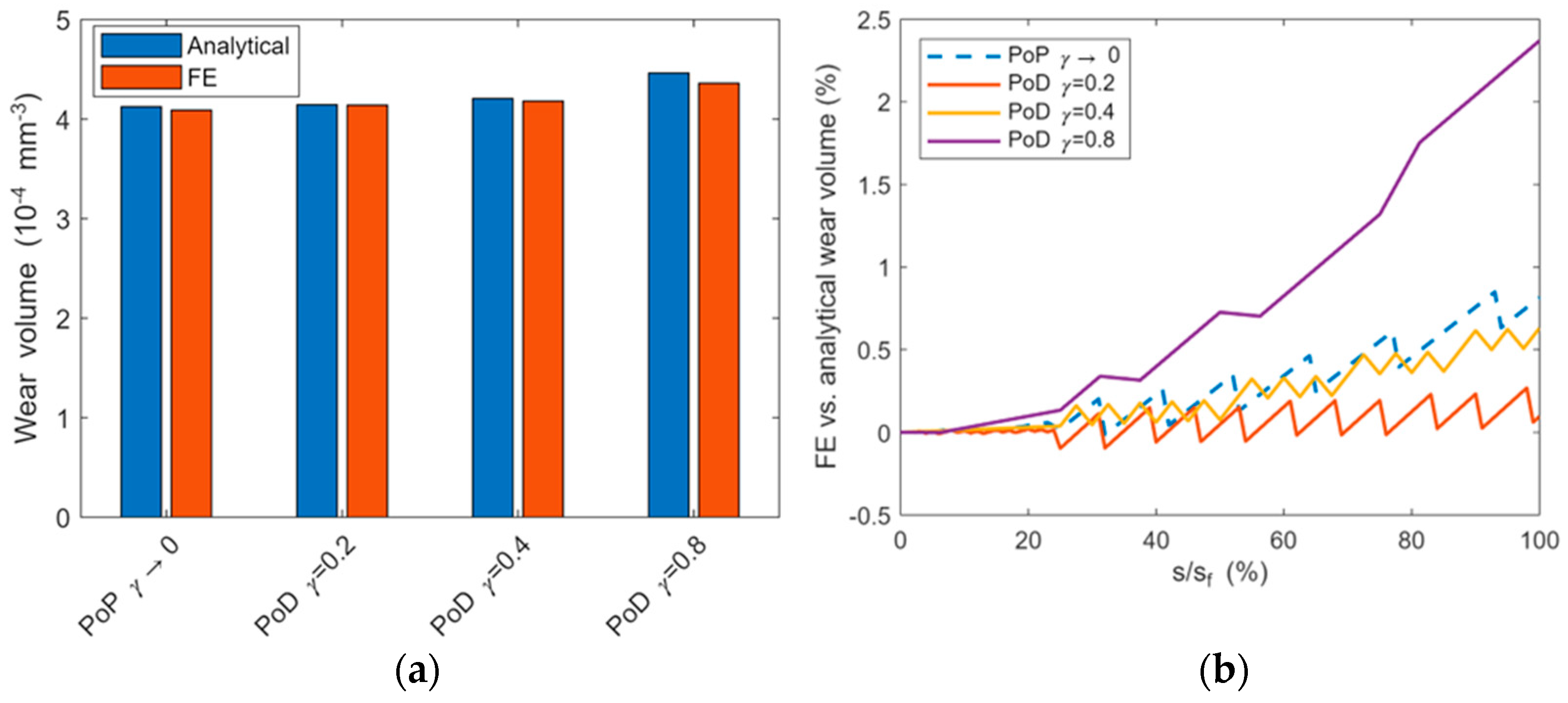
3.1. Corrective Fucntion for Wear Volume in PoD Tests
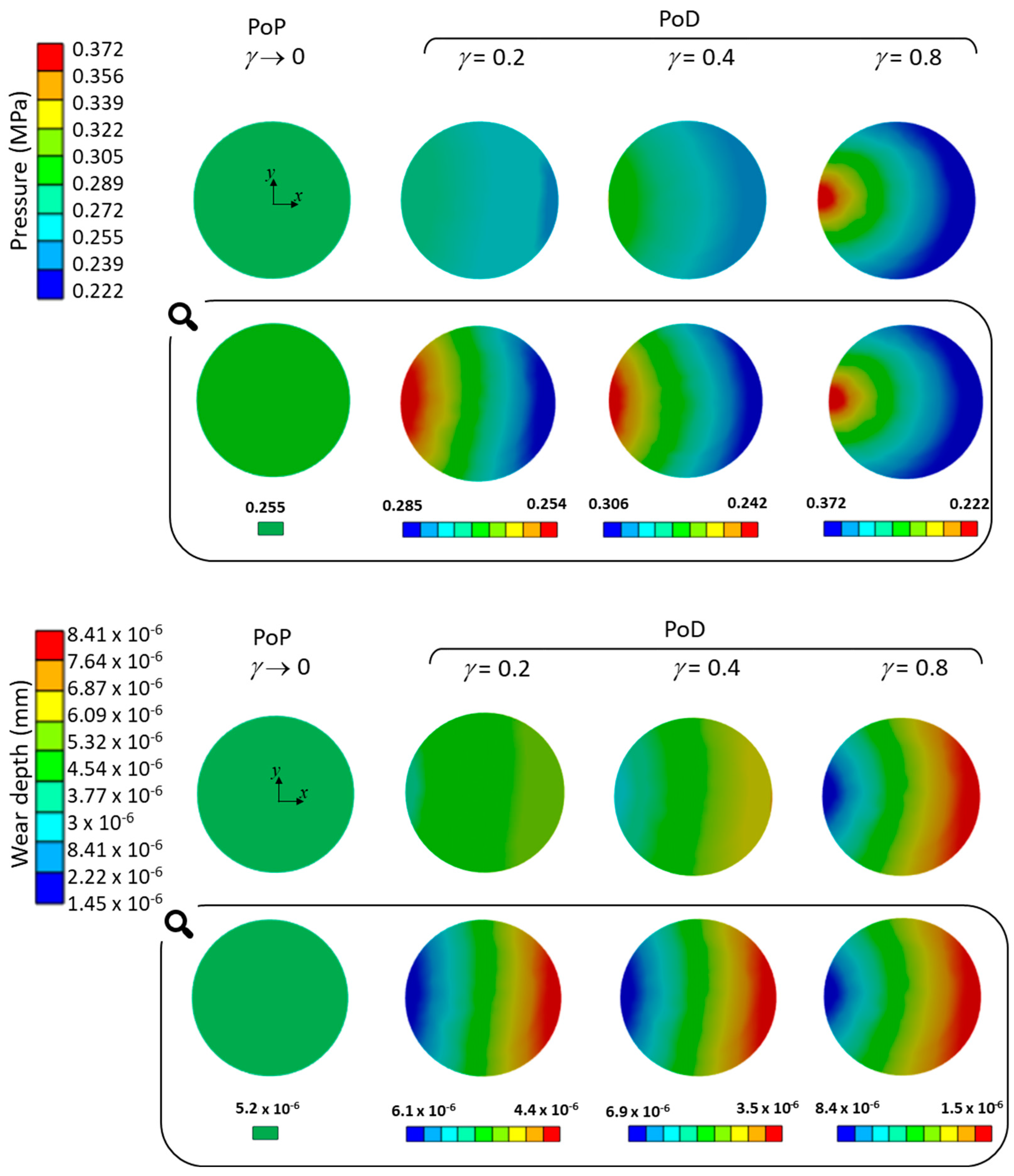
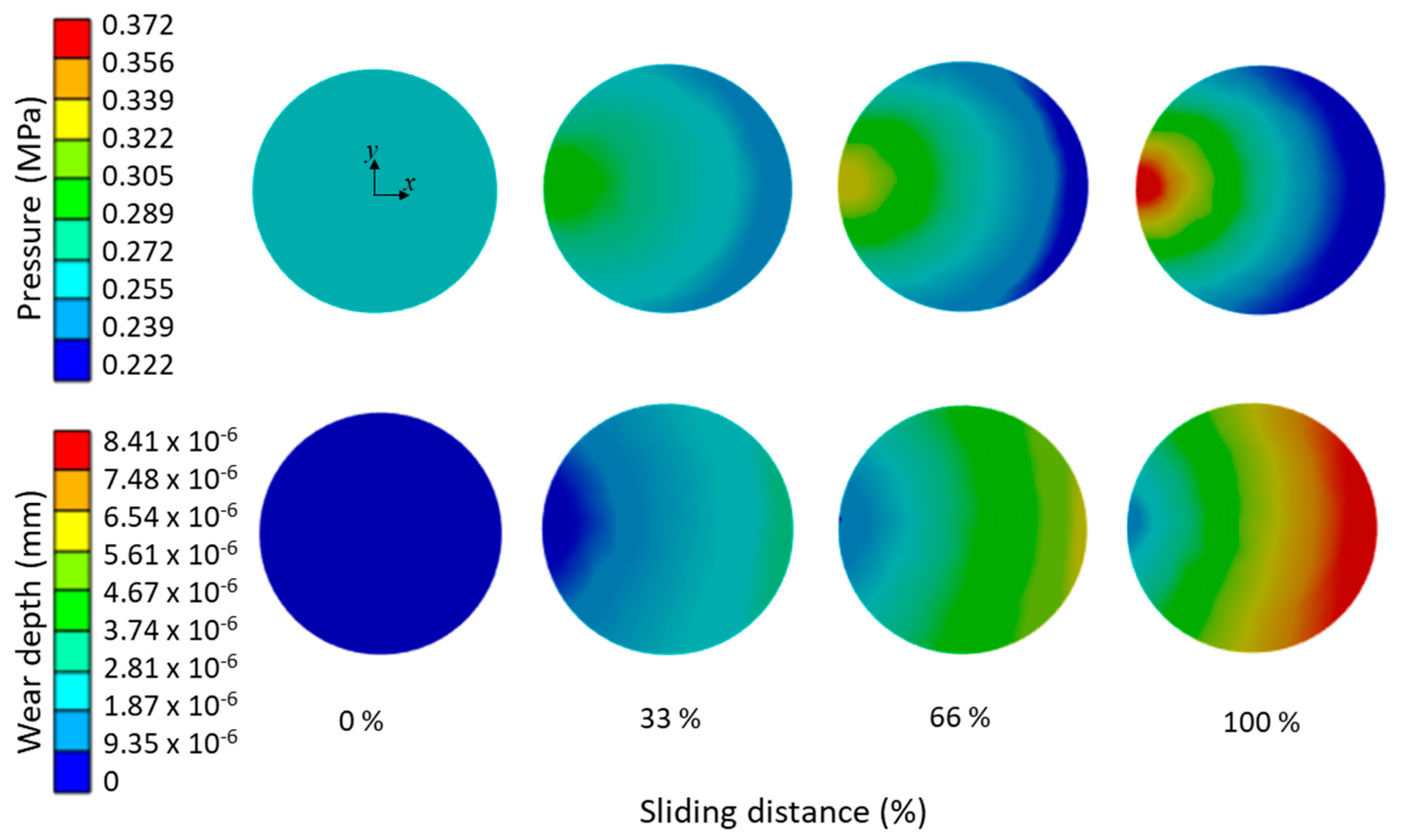
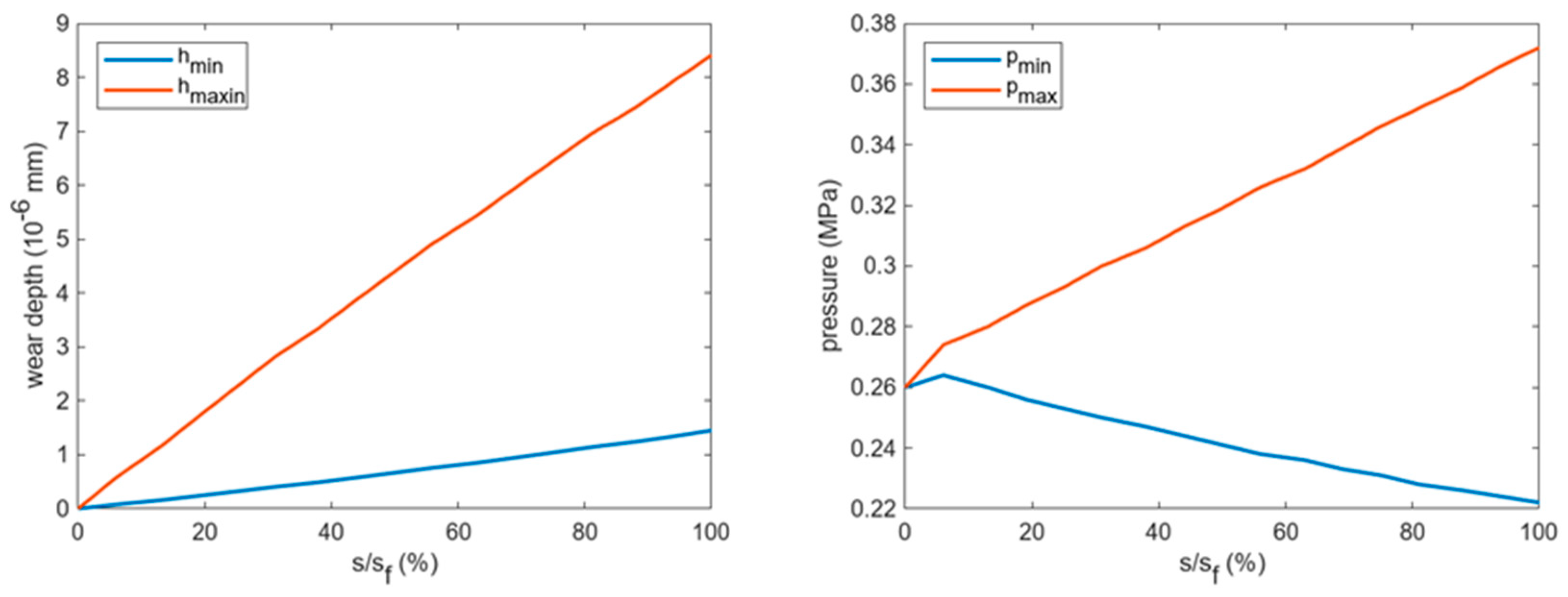
3.2. Effect of the Sliding Distance on Wear and Contact Pressure Distribution
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- ASTM G99; Test Method for Wear Testing with a Pin-on-Disk Apparatus. ASTM: West Conshohocken, PA, USA, 2017.
- ASTM D4170-16; Standard Test Method for Fretting Wear Protection by Lubricating Greases. ASTM: West Conshohocken, PA, USA, 2017.
- ASTM G133; Standard Test Method for Linearly Reciprocating Ball-on-Flat Sliding Wear. ASTM: West Conshohocken, PA, USA, 2016.
- Liu, H.; Chen, Y.; Wang, X.; Guo, Y.; Xue, W.; Li, D.; Chen, X.-Q. Correlating Numerical Modelling with Experimental Studies to Quantify the Wear Resistance of High-Carbon Chromium Bearing Steel in Mixed Lubrication. Tribol. Int. 2023, 188, 108819. [Google Scholar] [CrossRef]
- Bastola, A.; McCarron, R.; Shipway, P.; Stewart, D.; Dini, D. Experimental and Numerical Investigations of Sliding Wear Behaviour of an Fe-Based Alloy for PWR Wear Resistance Applications. Wear 2024, 540–541, 205186. [Google Scholar] [CrossRef]
- Bastola, A.; Stewart, D.; Dini, D. Three-Dimensional Finite Element Simulation and Experimental Validation of Sliding Wear. Wear 2022, 504–505, 204402. [Google Scholar] [CrossRef]
- Mattei, L.; Di Puccio, F. How Accurate Is the Archard Law to Predict Wear of UHMWPE in Hard-on-Soft Hip Implants? A Numerical and Experimental Investigation. Tribol. Int. 2023, 187, 108768. [Google Scholar] [CrossRef]
- Archard, J.F. Contact and Rubbing of Flat Surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Lancaster, J.K. The Influence of Substrate Hardness on the Formation and Endurance of Molybdenum Disulphide Films. Wear 1967, 10, 103–117. [Google Scholar] [CrossRef]
- Matkovič, S.; Pogačnik, A.; Kalin, M. Wear-Coefficient Analyses for Polymer-Gear Life-Time Predictions: A Critical Appraisal of Methodologies. Wear 2021, 480–481, 203944. [Google Scholar] [CrossRef]
- Borawski, A. Testing Passenger Car Brake Pad Exploitation Time’s Impact on the Values of the Coefficient of Friction and Abrasive Wear Rate Using a Pin-on-Disc Method. Materials 2022, 15, 1991. [Google Scholar] [CrossRef] [PubMed]
- Hatam, A.; Khalkhali, A. Simulation and Sensitivity Analysis of Wear on the Automotive Brake Pad. Simul. Model. Pract. Theory 2018, 84, 106–123. [Google Scholar] [CrossRef]
- Reichelt, M.; Cappella, B. Large Scale Multi-Parameter Analysis of Wear of Self-Mated 100Cr6 Steel—A Study of the Validity of Archard’s Law. Tribol. Int. 2021, 159, 106945. [Google Scholar] [CrossRef]
- Põdra, P.; Andersson, S. Simulating Sliding Wear with Finite Element Method. Tribol. Int. 1999, 32, 71–81. [Google Scholar] [CrossRef]
- Mattei, L.; Di Puccio, F. Frictionless vs. Frictional Contact in Numerical Wear Predictions of Conformal and Non-Conformal Sliding Couplings. Tribol. Lett. 2022, 70, 115. [Google Scholar] [CrossRef]
- Di Puccio, F.; Mattei, L. Simple Analytical Description of Contact Pressure and Wear Evolution in Non-Conformal Contacts. Tribol. Int. 2023, 178, 108084. [Google Scholar] [CrossRef]
- Liu, F.; Galvin, A.; Jin, Z.; Fisher, J. A New Formulation for the Prediction of Polyethylene Wear in Artificial Hip Joints. Proc. Inst. Mech. Eng. H 2011, 225, 16–24. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; He, Y.; Gao, Z.; Jiao, D. Enhanced Computational Modelling of UHMWPE Wear in Total Hip Joint Replacements: The Role of Frictional Work and Contact Pressure. Wear 2021, 482–483, 203985. [Google Scholar] [CrossRef]
- Joshi, V.; Ramkumar, P. Transient Wear FEA Modelling Using Extrapolation Technique for Steel-on-Steel Dry Sliding Contact. Tribol. Online 2022, 17, 162–174. [Google Scholar] [CrossRef]
- Yan, L.; Guan, L.; Wang, D.; Xiang, D. Application and Prospect of Wear Simulation Based on ABAQUS: A Review. Lubricants 2024, 12, 57. [Google Scholar] [CrossRef]
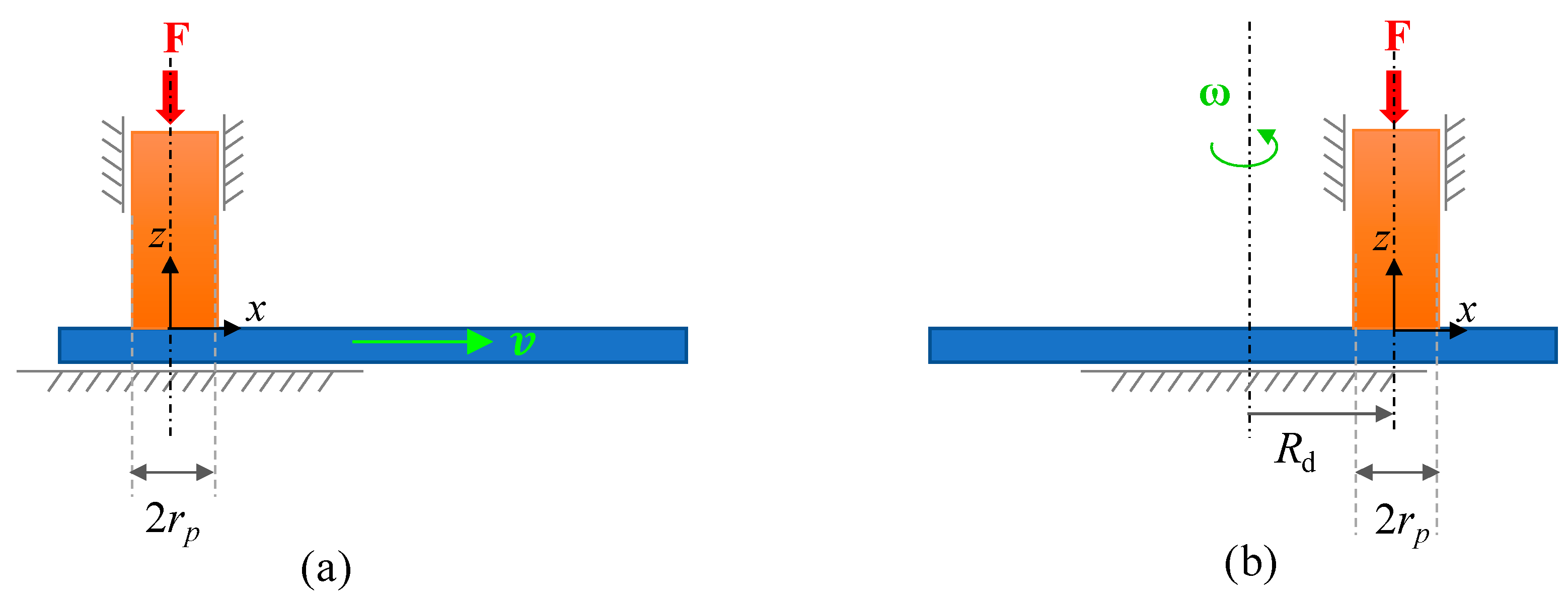
| γ | 100 | 100 |
|---|---|---|
| 0.2 | 12.1% | 32.5% |
| 0.4 | 25% | 66.4% |
| 0.8 | 57.6% | 141% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Puccio, F.; Di Pietro, A.; Mattei, L. Pin-on-Plate vs. Pin-on-Disk Wear Tests: Theoretical and Numerical Observations on the Initial Transient Phase. Lubricants 2024, 12, 134. https://doi.org/10.3390/lubricants12040134
Di Puccio F, Di Pietro A, Mattei L. Pin-on-Plate vs. Pin-on-Disk Wear Tests: Theoretical and Numerical Observations on the Initial Transient Phase. Lubricants. 2024; 12(4):134. https://doi.org/10.3390/lubricants12040134
Chicago/Turabian StyleDi Puccio, Francesca, Andrea Di Pietro, and Lorenza Mattei. 2024. "Pin-on-Plate vs. Pin-on-Disk Wear Tests: Theoretical and Numerical Observations on the Initial Transient Phase" Lubricants 12, no. 4: 134. https://doi.org/10.3390/lubricants12040134
APA StyleDi Puccio, F., Di Pietro, A., & Mattei, L. (2024). Pin-on-Plate vs. Pin-on-Disk Wear Tests: Theoretical and Numerical Observations on the Initial Transient Phase. Lubricants, 12(4), 134. https://doi.org/10.3390/lubricants12040134






