Vibration Analysis of the Double Row Planetary Gear System for an Electromechanical Energy Conversion System
Abstract
:1. Introduction
2. A Dynamic Modeling Method of the DRPGS for an EECS
2.1. Kinematic Modeling of the DRPGS
2.2. Motion Equations of the DRPGS
3. Results and Discussion
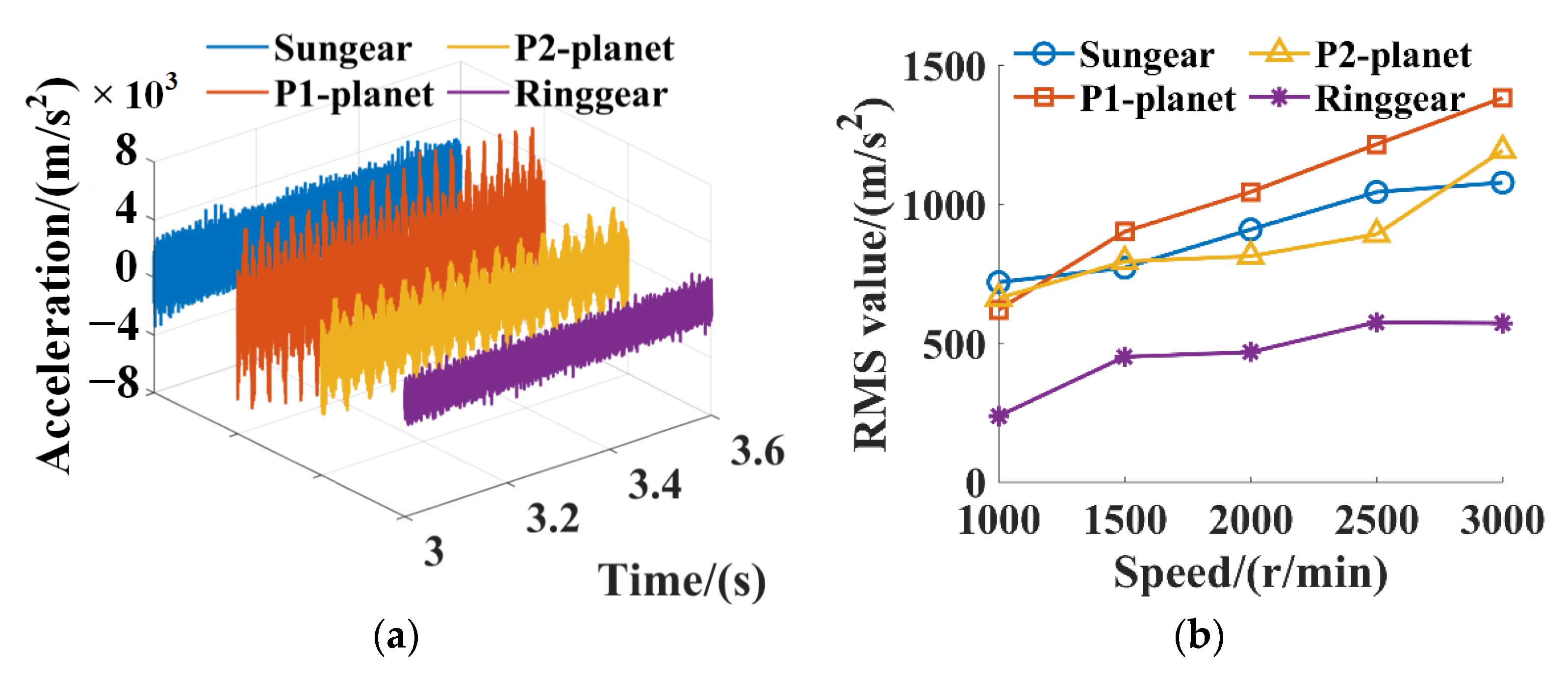
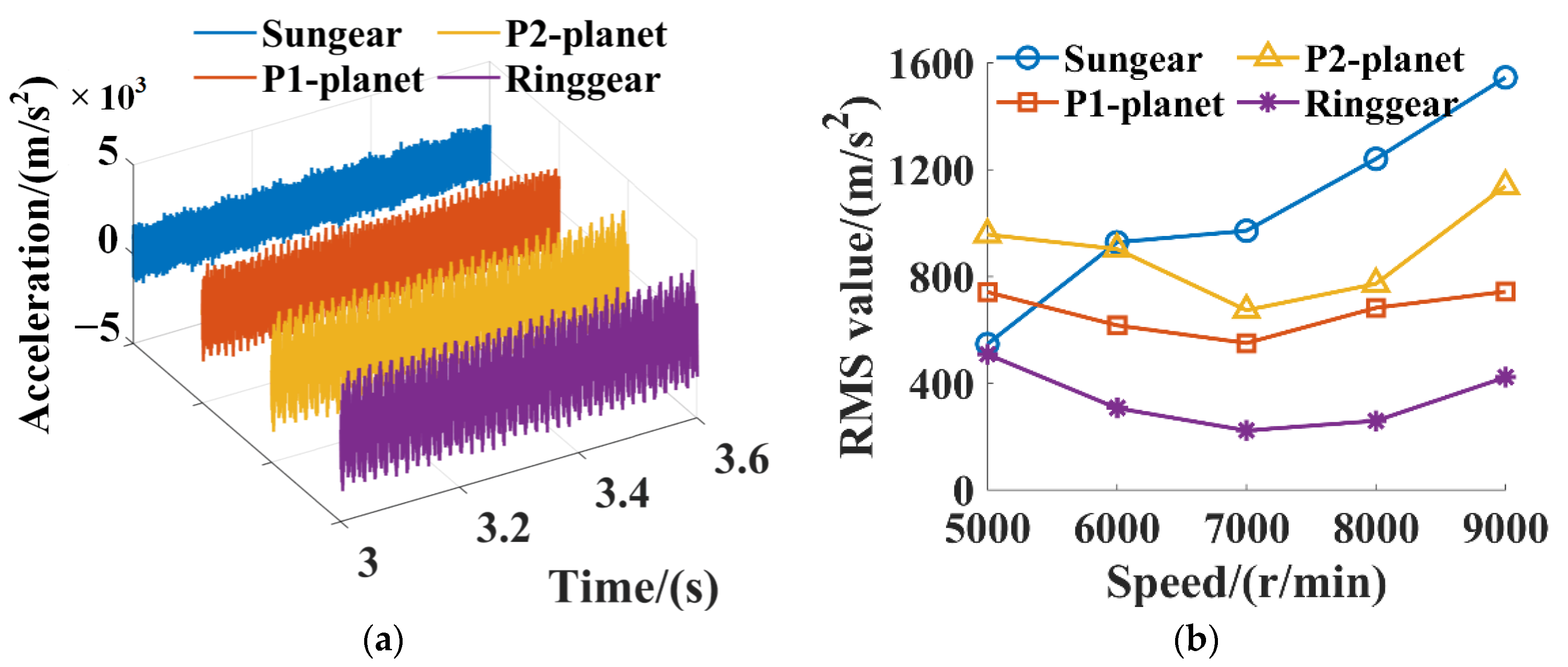
3.1. Effects of Operating Conditions on the Vibration Characteristics of the DRPGS
3.1.1. Constant Torque Condition
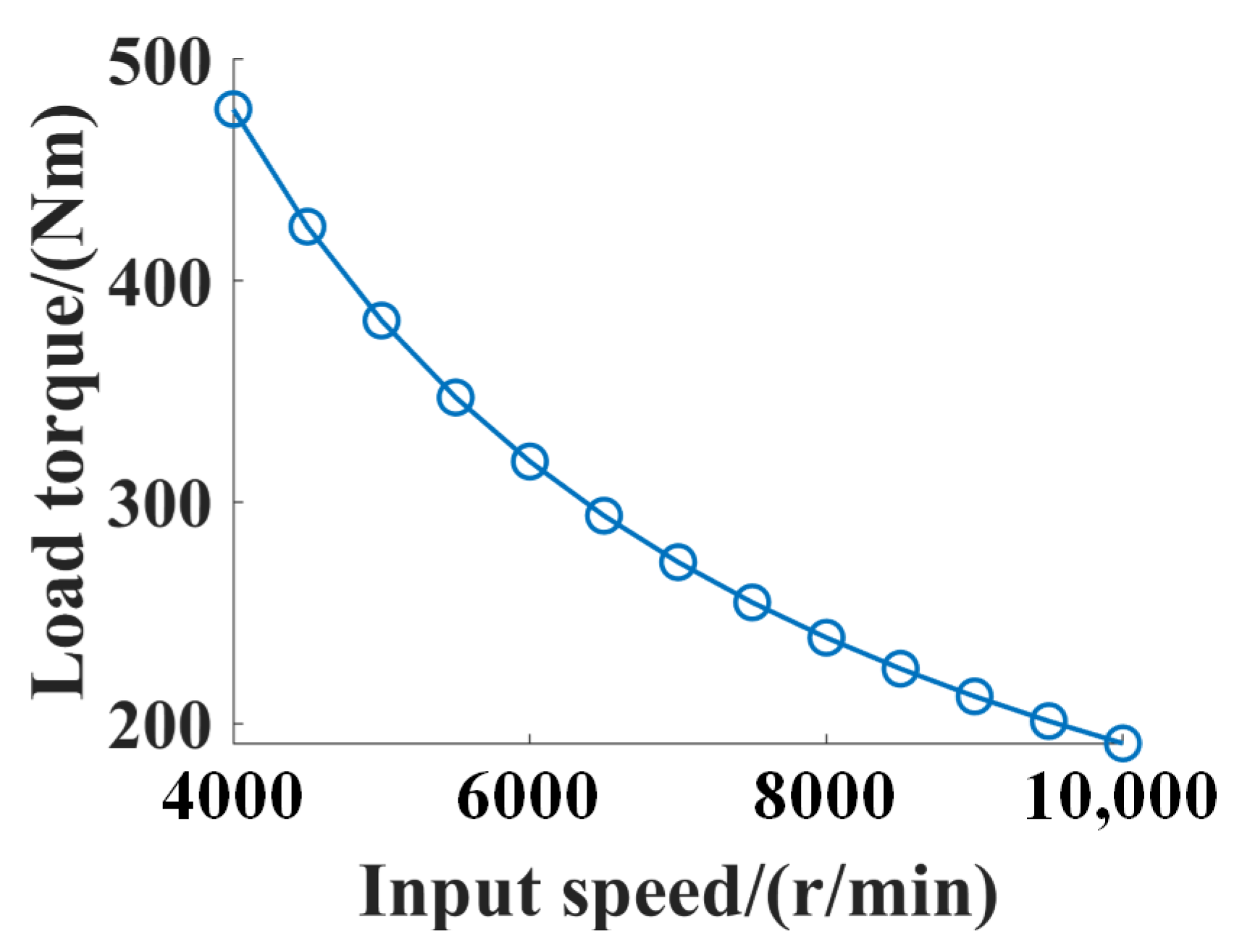
3.1.2. Constant Power Condition
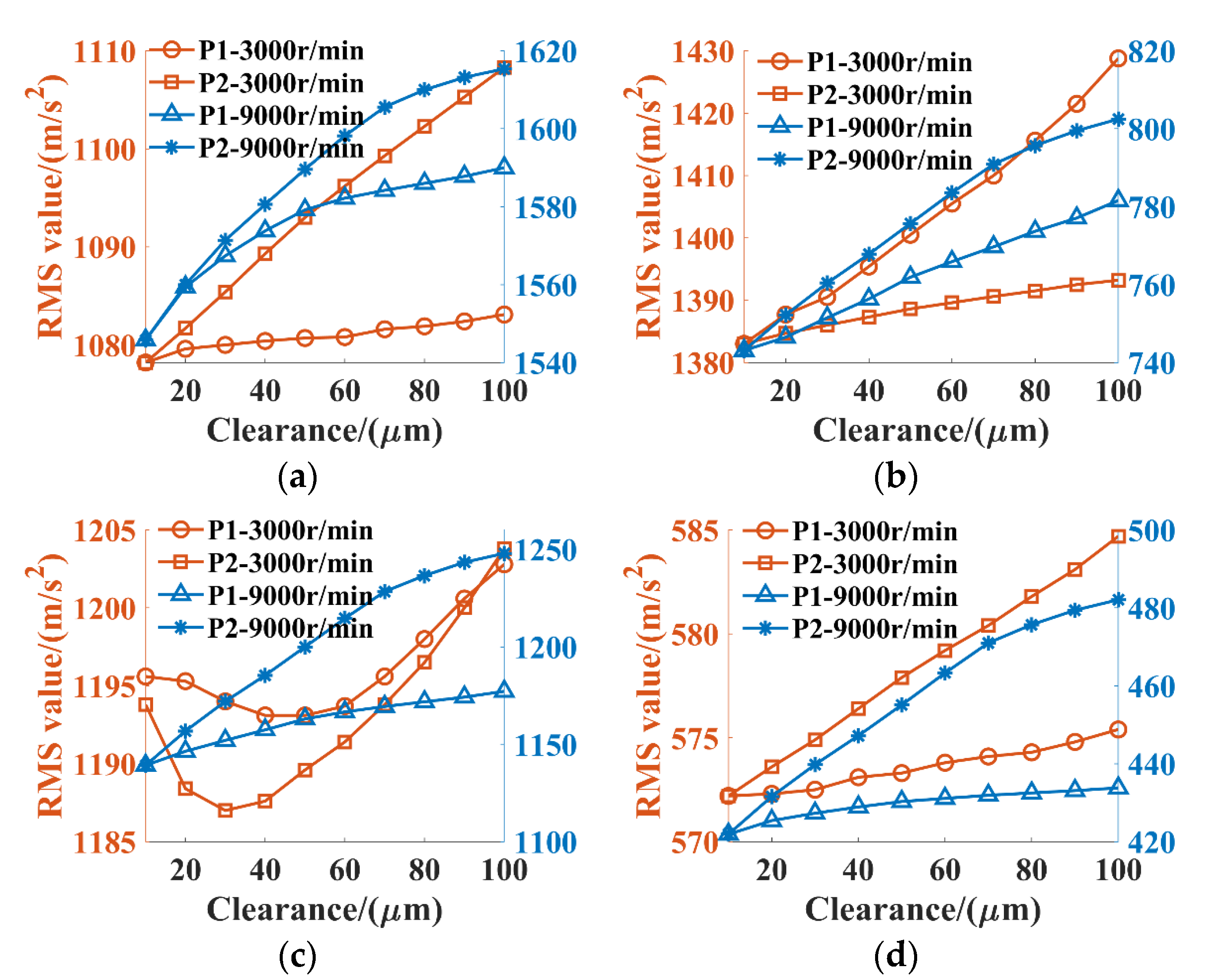
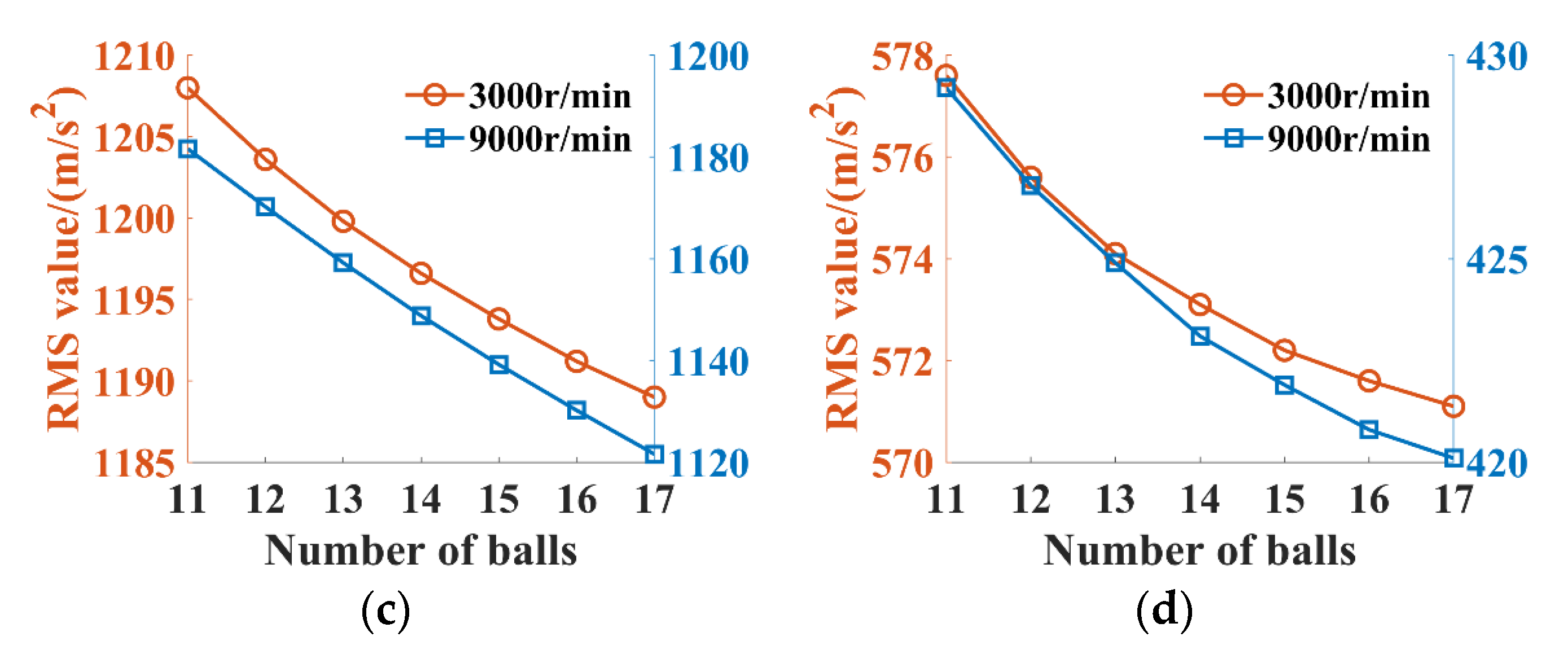
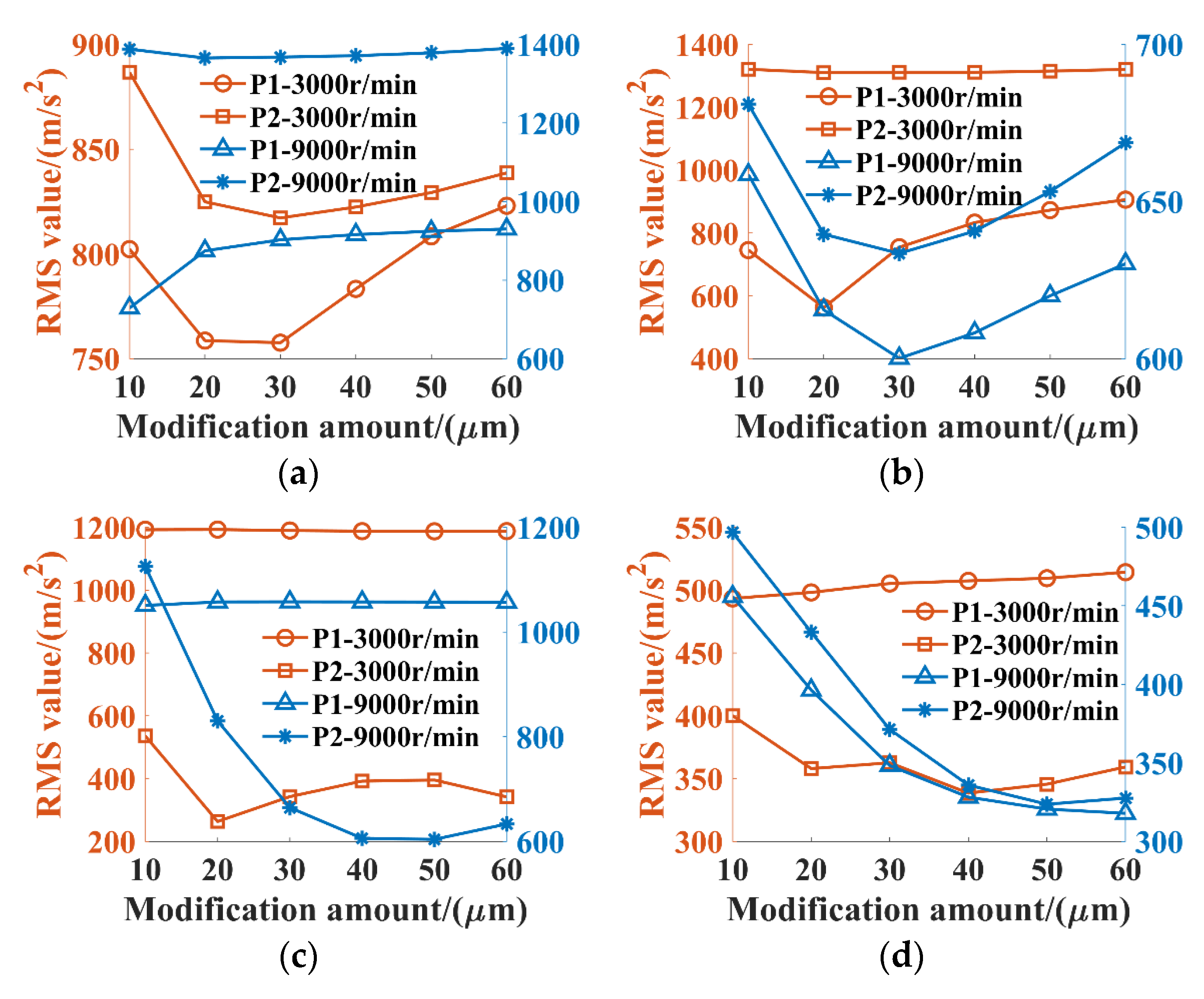
3.2. Effects of Structural Parameters on the Vibration Characteristics of the DRPGS
3.2.1. Effects of Bearing Clearances
3.2.2. Effects of Bearing Ball Numbers
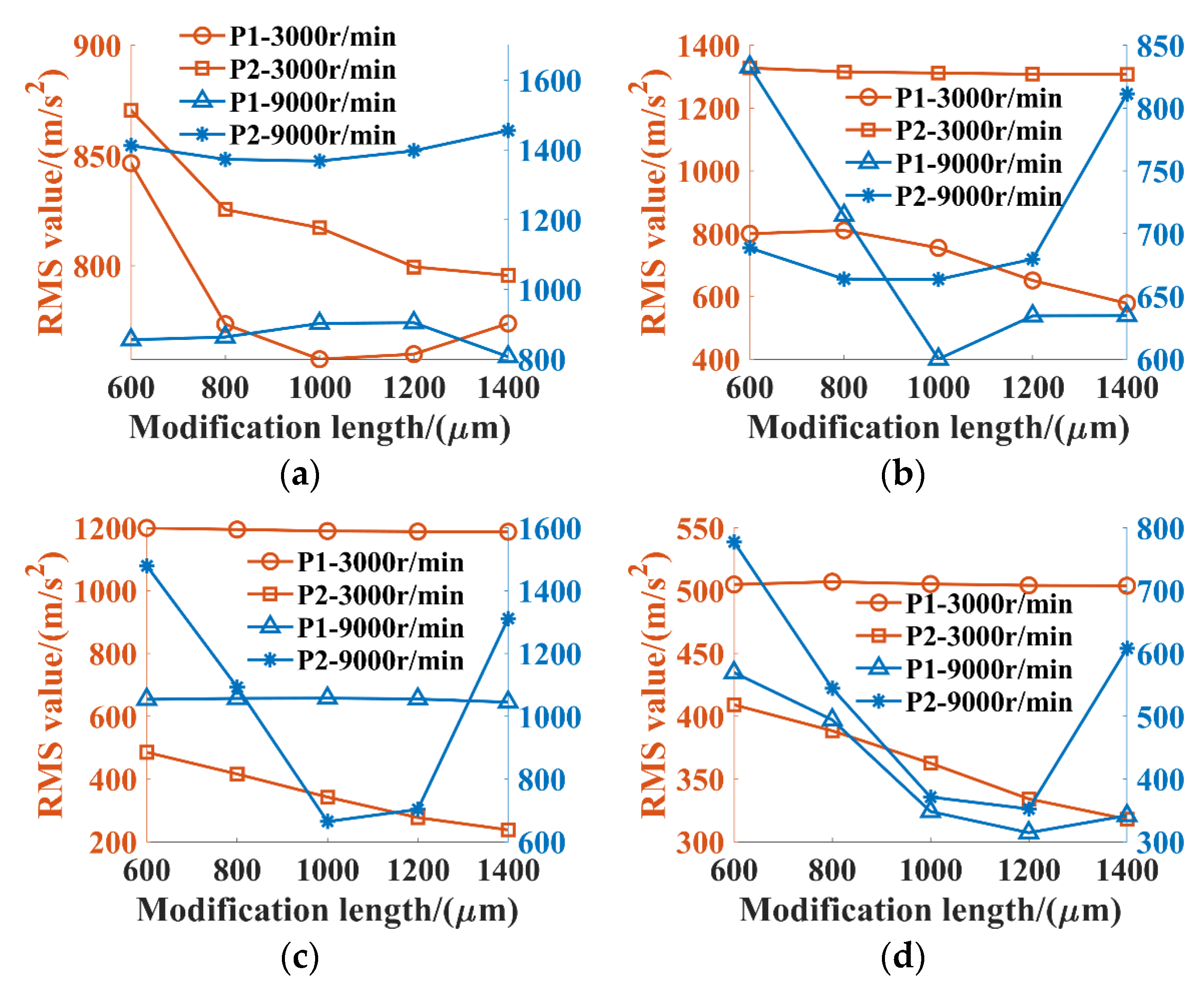
3.2.3. Effects of Gear Tooth Modification
4. Conclusions
- (1)
- The vibrations of the components in the DRPGS increase with the input speed at constant torque conditions. The levels of vibrations for the DRPGS components decrease firstly, then increase with the input speed at constant power conditions. It indicates that the vibrations of the DRPGS are more sensitive to the load torque at low-speed conditions.
- (2)
- The bearing clearance indeed has influences on the system vibration. Improving the manufacturing precision and matching quality can be beneficial to controlling the system vibration.
- (3)
- An increase in the number of balls of the planet gear bearings can be effective in reducing the system vibration and changing the number of balls for the P2 planet gear bearings is more effective.
- (4)
- Both the modification amounts and lengths have more significant influences on the system vibration at 9000 r/min than those at 3000 r/min. The appropriate modification amounts and lengths can indeed suppress the system vibrations, the modification amount for this DRPGS should be within the range of 20 μm to 40 μm; the modification amount for this DRPGS was chosen in the range of 1000 μm to 1200 μm.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bai, Z.; Ning, Z. Dynamic responses of the planetary gear mechanism considering Dynamic wear effects. Lubricants 2023, 11, 255. [Google Scholar] [CrossRef]
- He, G.; Ding, K.; Wu, X.; Yang, X. Dynamics modeling and vibration modulation signal analysis of wind turbine planetary gearbox with a floating sun gear. Renew. Energy 2019, 139, 718–729. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Xia, M. A dynamic model for the planetary bearings in a double planetary gear set. Mech. Syst. Signal. Process. 2023, 194, 110257. [Google Scholar] [CrossRef]
- Xu, X.; Fan, X.; Diao, P.; Liu, H. An investigation on the influence of modification parameters on transmission characteristics of planetary gear system. J. Mech. Sci. Technol. 2019, 33, 3105–3114. [Google Scholar] [CrossRef]
- Chen, X.; Hu, Q.; Xu, Z.; Zhu, C. Numerical modeling and dynamic characteristics study of coupling vibration of multistage face gearsplanetary transmission. Mech. Sci. 2019, 10, 475–495. [Google Scholar] [CrossRef]
- Qiu, W.; Yang, F.; Wang, D.; Jiang, X. Design and free vibration characteristics of linkage planetary gear trains. J. Braz. Soc. Mech. Sci. 2022, 44, 58. [Google Scholar] [CrossRef]
- Wang, C.; Parker, R. Nonlinear dynamics of lumped-parameter planetary gears with general mesh phasing. J. Sound Vib. 2022, 523, 116682. [Google Scholar] [CrossRef]
- Dai, H.; Wang, Y.; Luo, S.; Li, Y.; Zi, B. Dynamic modeling and vibration analysis of planetary gear sets concerning mesh phasing modulation. Mech. Syst. Signal. Process. 2023, 200, 110557. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, H.; Yu, H.; Zhang, T. Numerical and experimental investigation on nonlinear dynamic characteristics of planetary gear train. J. Theor. App. Mech. 2020, 58, 1009–1022. [Google Scholar] [CrossRef]
- Mo, S.; Huang, X.; Liu, W.; Zhang, W. Study on nonlinear vibration and primary resonance characteristics of helicopter face gear-planetary gear coupling transmission system. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2023, 237, 534–554. [Google Scholar] [CrossRef]
- Sun, Z.; Chen, S.; Hu, Z.; Lei, D. Vibration response analysis of a gear-rotor-bearing system considering steady-state temperature. Nonlinear Dynam. 2022, 107, 477–493. [Google Scholar] [CrossRef]
- Lai, J.; Liu, Y.; Xu, X.; Li, H.; Xu, J.; Wang, S.; Guo, W. Dynamic modeling and analysis of Ravigneaux planetary gear set with unloaded floating ring gear. Mech. Mach. Theory 2022, 170, 104696. [Google Scholar] [CrossRef]
- Tatar, A.; Schwingshackl, C.; Friswell, M. Modal sensitivity of three-dimensional planetary geared rotor systems to planet gear parameters. Appl. Math. Model. 2023, 113, 309–332. [Google Scholar] [CrossRef]
- Fan, Z.; Zhu, C.; Song, C. Dynamic analysis of planetary gear transmission system considering the flexibility of internal ring gear. Iran. J. Sci. Technol. Trans. Mech. Eng. 2020, 44, 695–706. [Google Scholar] [CrossRef]
- Hu, A.; Liu, S.; Xiang, L.; Zhang, Y. Dynamic modeling and analysis of multistage planetary gear system considering tooth crack fault. Eng. Fail. Anal. 2022, 137, 106408. [Google Scholar] [CrossRef]
- Li, X.; Liu, J.; Xu, J.; Chen, Y.; Hu, Z.; Pan, G. A vibration model of a planetary bearing system considering the time-varying wear. Nonlinear Dynam. 2023, 111, 19817–19840. [Google Scholar] [CrossRef]
- Li, X.; Liu, J.; Ding, S.; Xu, Y.; Zhang, Y.; Xia, M. Dynamic modeling and vibration analysis of double row cylindrical roller bearings with irregular-shaped defects. Nonlinear Dynam. 2024, 112, 2501–2521. [Google Scholar] [CrossRef]
- Yang, H.; Li, X.; Xu, J.; Yang, Z.; Chen, R. Dynamic characteristics analysis of planetary gear system with internal and external excitation under turbulent wind load. Sci. Prog. 2021, 104, 00368504211035604. [Google Scholar] [CrossRef] [PubMed]
- Cheng, G.; Ma, J.; Li, J.; Sun, K.; Wang, K.; Wang, Y. Study on the Dynamic Characteristics of Gears Considering Surface Topography in a Mixed Lubrication State. Lubricants 2023, 12, 7. [Google Scholar] [CrossRef]
- Xu, H.; Ren, H.; Qin, D. Dynamic characteristics of the planetary gear system with rolling bearing. Multibody Syst. Dyn. 2023, 59, 171–191. [Google Scholar] [CrossRef]
- Geng, Z.; Li, J.; Xiao, K.; Wang, J. Analysis on the vibration reduction for a new rigid–flexible gear transmission system. J. Vib Control 2022, 28, 2212–2225. [Google Scholar] [CrossRef]
- Wang, P.; Xu, H.; Ma, H.; Han, Z.; Yang, Y. Effects of three types of bearing misalignments on dynamic characteristics of planetary gear set-rotor system. Mech. Syst. Signal. Process. 2022, 169, 108736. [Google Scholar] [CrossRef]
- Xin, W.; Zhang, Y.; Fu, Y.; Yang, W.; Zheng, H. A multi-objective optimization design approach of large mining planetary gear reducer. Sci. Rep. 2023, 13, 18640. [Google Scholar] [CrossRef] [PubMed]
- Öztürk, V.; Cigeroglu, E.; Özgüven, H. Ideal tooth profile modifications for improving nonlinear dynamic response of planetary gear trains. J. Sound Vib. 2021, 500, 116007. [Google Scholar] [CrossRef]
- Zhang, K.; Shao, Y.; Galar, D. The dynamic response of a planetary gear train in the presence of a spalling fault. In Proceedings of the Intelligent Technologies for Equipment and Human Performance Monitoring (MFPT 2018), Virginia Beach, VA, USA, 15–17 May 2018; Society for Machinery Failure Prevention Technology: Dresher, PA, USA, 2018; pp. 252–266. [Google Scholar]
- Zhang, C.; Yu, W.; Zhang, Y.; Xu, J.; Zeng, Q.; Li, L.; Wang, L.; Huang, W. Dynamics modeling and analysis of the multistage planetary gear set-bearing-rotor-clutch coupling system considering the tooth impacts of clutches. Mech. Syst. Signal. Process. 2024, 214, 111365. [Google Scholar] [CrossRef]
- Liu, J.; Ni, H.; Zhou, R.; Li, X.; Xing, Q.; Pan, G. A simulation analysis of ball bearing lubrication characteristics considering the cage clearance. J. Tribol. 2023, 145, 044301. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, Y.; Gu, Y.; Dong, H. Assembly accuracy prediction method of planetary gear train considering bolt-bearing-shaft-gear coupling effects. Appl. Math. Model. 2024, 131, 403–422. [Google Scholar] [CrossRef]
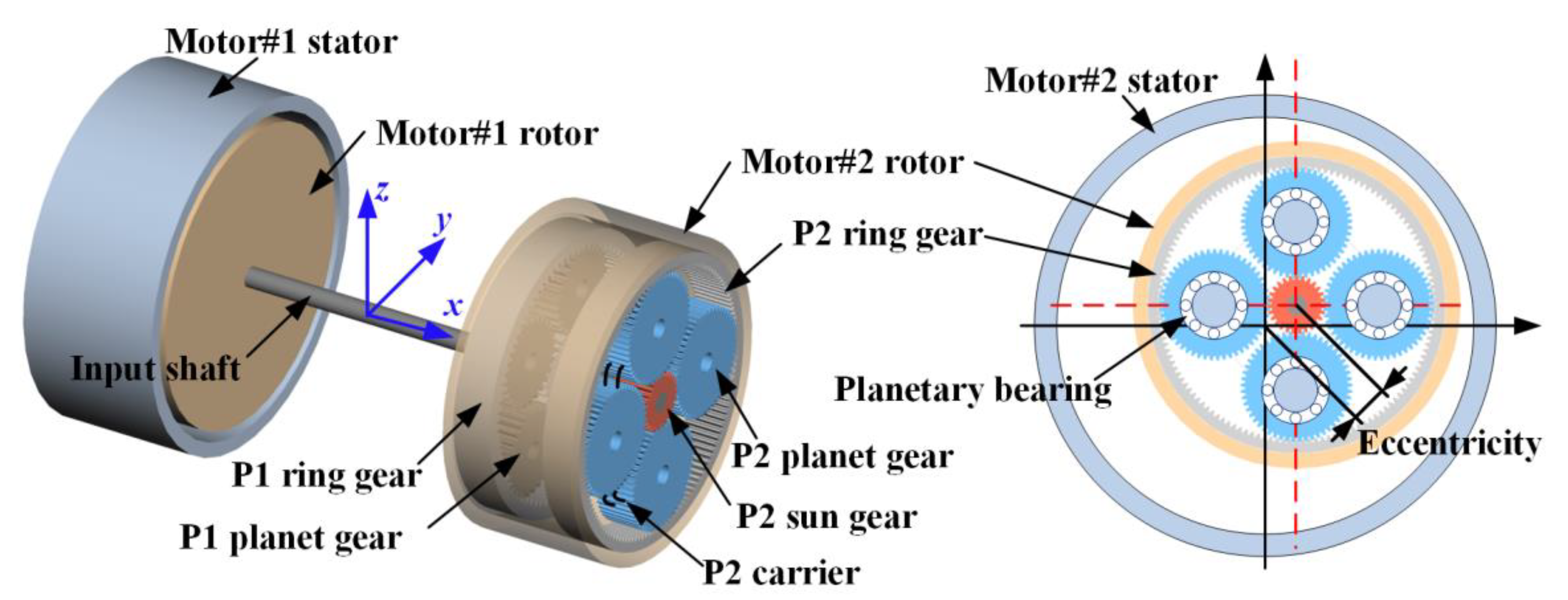
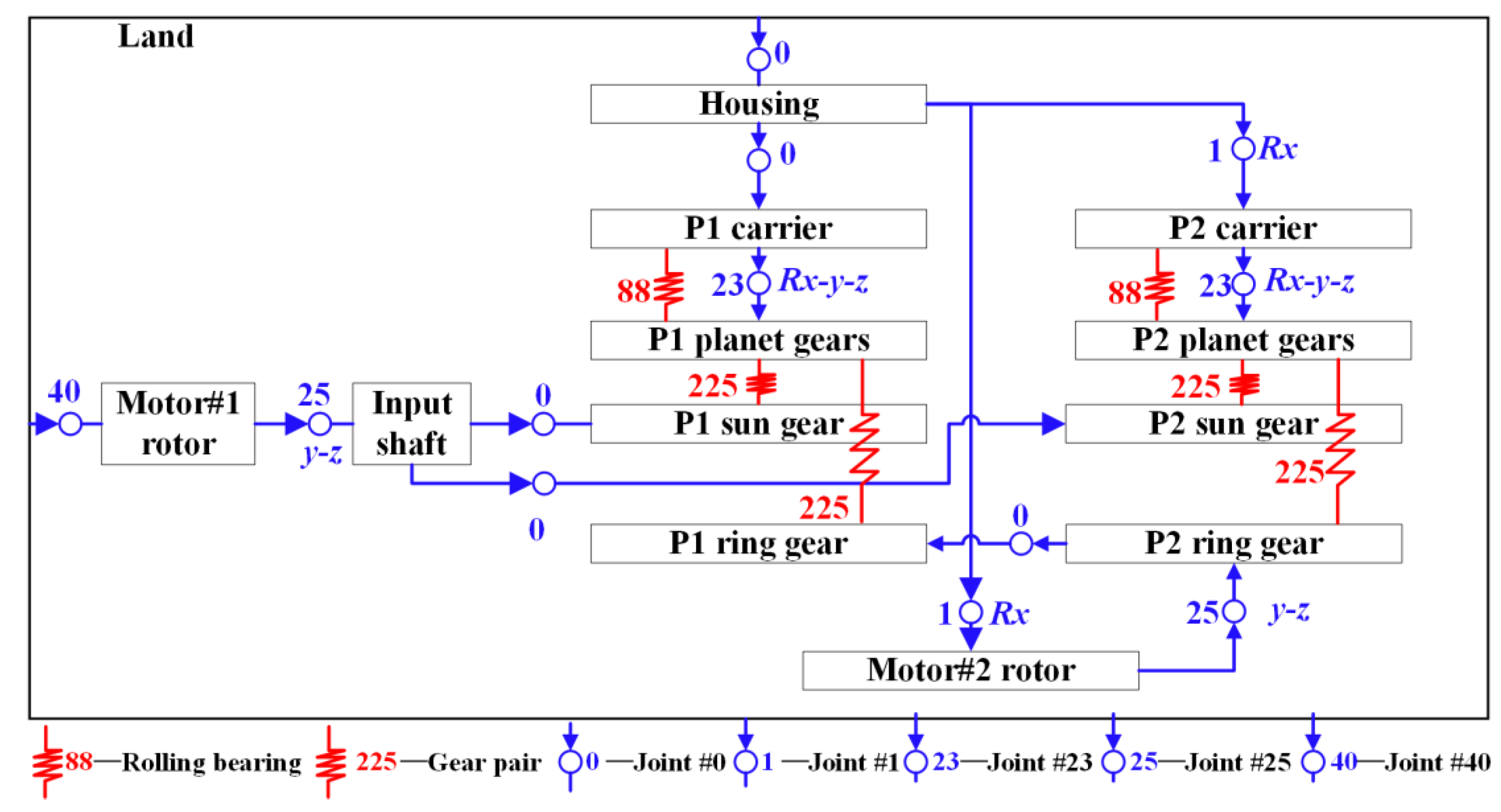




| From Component | To Component | Joint Type |
|---|---|---|
| Land | Housing | Joint #0 (0 degrees of freedom) |
| Land | Motor #1 rotor | Joint #40 (single-axis u(t)) |
| Motor #1 rotor | Input shaft | Joint #25 (user-defined: y-z) |
| Input shaft | P1 sun gear | Joint #0 |
| Input shaft | P2 sun gear | Joint #0 |
| Housing | P1 carrier | Joint #0 |
| P1 carrier | P1 planet gears | Joint #23 (planar Rx-y-z) |
| Housing | Motor #2 rotor | Joint #1 (revolute Rx) |
| P2 ring gear | P1 ring gear | Joint #0 |
| Motor #2 rotor | P2 ring gear | Joint #25 (user-defined: y-z) |
| Housing | P2 carrier | Joint #1 (revolute Rx) |
| P2 carrier | P2 planet gears | Joint #23 (planar Rx-y-z) |
| Parameters | P1 Sun Gear | P1 Planet Gear | P1 Ring Gear | P2 Sun Gear | P2 Planet Gear | P2 Ring Gear |
|---|---|---|---|---|---|---|
| Number of teeth | 27 | 28 | 83 | 27 | 53 | 133 |
| Modulus | 3 | 3 | 3 | 2 | 2 | 2 |
| Width/mm | 40 | |||||
| Pressure angle/° | 20 | |||||
| Modification coefficient | 0.0138 | −0.0138 | 0.0138 | 0.1893 | −0.1893 | 0.1893 |
| Material | 40Cr | |||||
| Parameters | NJ 1005ECJ | FG 42205 |
|---|---|---|
| Bore diameter/mm | 25 | 25 |
| Outside diameter/mm | 47 | 52 |
| Width/mm | 11.9 | 14.88 |
| Inner raceway diameter/mm | 30.4 | 31.42 |
| Outer raceway diameter/mm | 40.88 | 46.06 |
| Number of rolling elements | 15 | 12 |
| Roller diameter/mm | 5.24 | 7.32 |
| Roller effective length/mm | 5.7 | 8.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Xu, Y.; Liu, J.; Wu, W. Vibration Analysis of the Double Row Planetary Gear System for an Electromechanical Energy Conversion System. Lubricants 2024, 12, 211. https://doi.org/10.3390/lubricants12060211
Li X, Xu Y, Liu J, Wu W. Vibration Analysis of the Double Row Planetary Gear System for an Electromechanical Energy Conversion System. Lubricants. 2024; 12(6):211. https://doi.org/10.3390/lubricants12060211
Chicago/Turabian StyleLi, Xinyong, Yajun Xu, Jing Liu, and Wei Wu. 2024. "Vibration Analysis of the Double Row Planetary Gear System for an Electromechanical Energy Conversion System" Lubricants 12, no. 6: 211. https://doi.org/10.3390/lubricants12060211
APA StyleLi, X., Xu, Y., Liu, J., & Wu, W. (2024). Vibration Analysis of the Double Row Planetary Gear System for an Electromechanical Energy Conversion System. Lubricants, 12(6), 211. https://doi.org/10.3390/lubricants12060211






