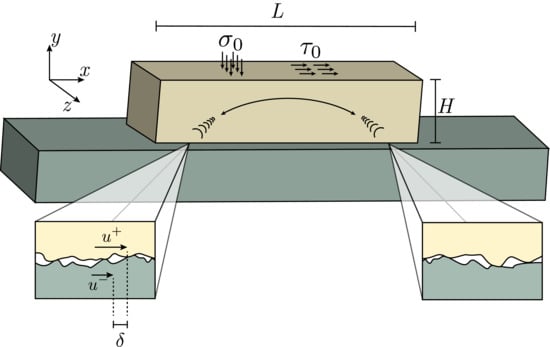
Spatiotemporal Dynamics of Frictional Systems: The Interplay of Interfacial Friction and Bulk Elasticity
Abstract
:1. Introduction
2. Generic Properties of Interfacial Constitutive Laws
2.1. Conventional RSF Models
2.2. Limitations of Conventional RSF Models and Proposed Modifications
2.2.1. Linear Reversible Response and an Extended RSF Model
2.2.2. Short Time Cutoff and the Steady-State Friction Curve
3. Bulk Elasticity in Frictional Systems
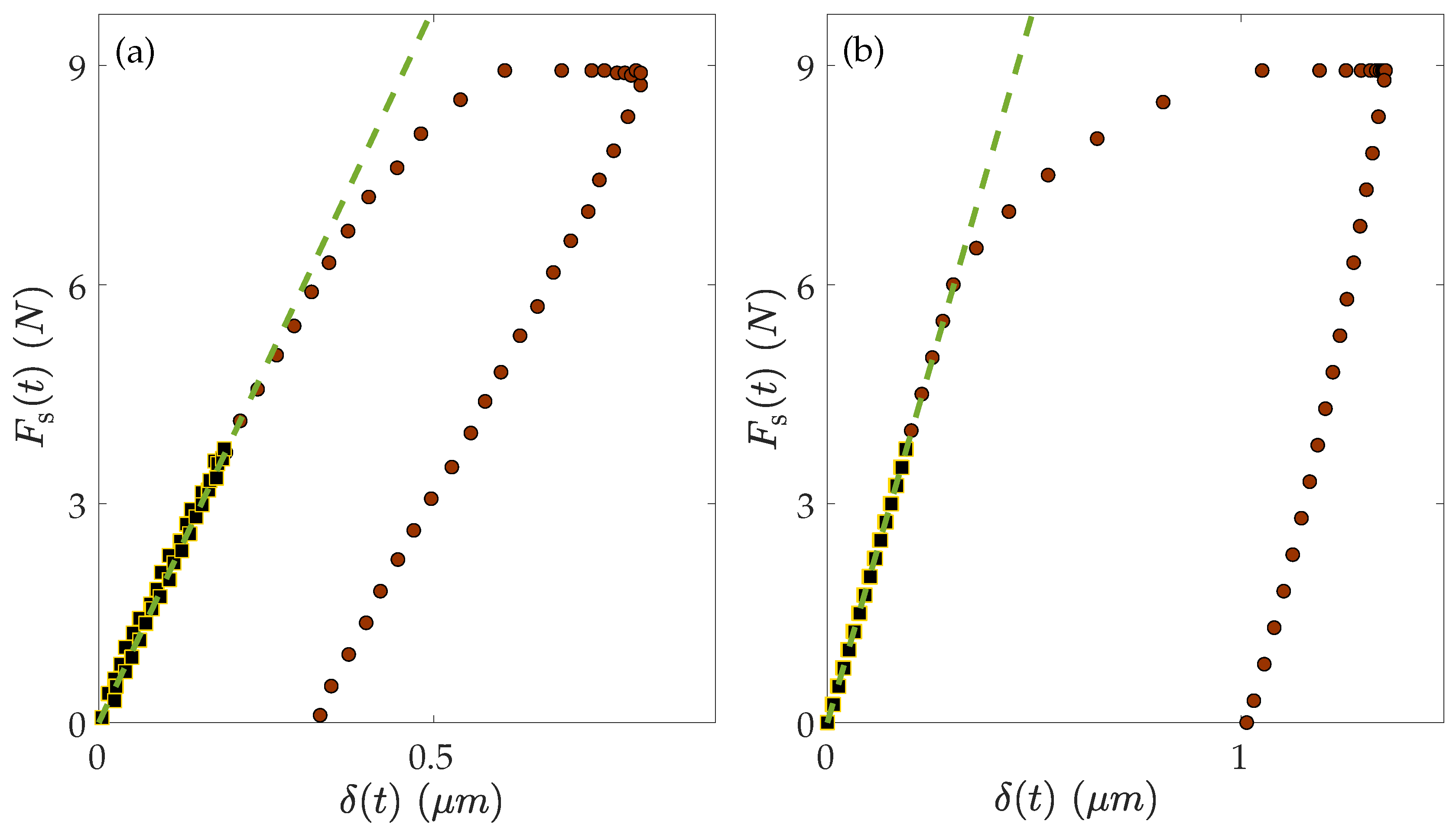
4. Basic Phenomena in Spatially Extended Frictional Systems
4.1. The Stability of Homogeneous Sliding
4.2. The Onset of Sliding Motion: Creep Patches and Their Stability
4.3. Propagating Frictional Modes
5. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Summary of the Mathematical Formulation of the Extended Friction Law
Appendix A.2. Theoretical Predictions for Frictional Dynamics under Small Stresses
Appendix A.3. A Treadmill FEM Routine for Obtaining Steady-State Frictional Modes
| Parameter | Value |
|---|---|
| 3.1 GPa | |
| 1/3 | |
| 60 kg/m | |
| b | 0.075 |
| s | |
| m/s | |
| D | m |
| Pa |
References
- Bowden, F.P.; Tabor, D. The Friction and Lubrication of Solids; Oxford University Press: New York, NY, USA, 1950. [Google Scholar]
- Persson, B.N.J. Sliding Friction: Physical Principles and Applications; Springer Sciense & Business Media: Berlin, Germany, 1998. [Google Scholar]
- Svetlizky, I.; Bayart, E.; Fineberg, J. Brittle Fracture Theory Describes the Onset of Frictional Motion. Annu. Rev. Condens. Matter Phys. 2019, 10, 253–273. [Google Scholar] [CrossRef]
- Sørensen, M.; Jacobsen, K.; Stoltze, P. Simulations of atomic-scale sliding friction. Phys. Rev. B 1996, 53, 2101–2113. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Q.; Tullis, T.E.; Goldsby, D.L.; Carpick, R.W. Frictional ageing from interfacial bonding and the origins of rate and state friction. Nature 2011, 480, 233–236. [Google Scholar] [CrossRef] [PubMed]
- Vanossi, A.; Manini, N.; Urbakh, M.; Zapperi, S.; Tosatti, E. Colloquium: Modeling friction: From nanoscale to mesoscale. Rev. Mod. Phys. 2013, 85, 529–552. [Google Scholar] [CrossRef]
- Armstrong-Hélouvry, B.; Dupont, P.; Canudas de Wit, C. A Survey of Models, Analysis Tools and Compensations Methods for the Control of Machines with Friction. Automatica 1994, 30, 1083–1138. [Google Scholar] [CrossRef]
- Wojewoda, J.; Stefański, A.; Wiercigroch, M.; Kapitaniak, T. Hysteretic effects of dry friction: modelling and experimental studies. Philos. Trans. A Math. Phys. Eng. Sci. 2008, 366, 747–765. [Google Scholar] [CrossRef]
- Marone, C. Laboratoty-derived friction laws and their application to seismic faulting. Annu. Rev. Earth Planet. Sci. 1998, 26, 643–696. [Google Scholar] [CrossRef]
- Ben-Zion, Y. Dynamic ruptures in recent models of earthquake faults. J. Mech. Phys. Solids 2001, 49, 2209–2244. [Google Scholar] [CrossRef]
- Scholz, C.H. The Mechanics of Earthquakes and Faulting; Cambridge University Press: New York, NY, USA, 2002. [Google Scholar]
- Ohnaka, M. The Physics of Rock Failure and Earthquakes; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Gnecco, E.; Bennewitz, R.; Gyalog, T.; Meyer, E. Friction experiments on the nanometre scale. J. Phys. Condens. Matter 2001, 13, 202. [Google Scholar] [CrossRef]
- Baumberger, T.; Caroli, C. Solid friction from stick–slip down to pinning and aging. Adv. Phys. 2006, 55, 279–348. [Google Scholar] [CrossRef]
- Ben-Zion, Y. Collective behavior of earthquakes and faults: Continuum-discrete transitions, progressive evolutionary changes, and different dynamic regimes. Rev. Geophys. 2008, 46, RG4006. [Google Scholar] [CrossRef]
- Vakis, A.; Yastrebov, V.; Scheibert, J.; Nicola, L.; Dini, D.; Minfray, C.; Almqvist, A.; Paggi, M.; Lee, S.; Limbert, G.; et al. Modeling and simulation in tribology across scales: An overview. Tribol. Int. 2018, 125, 169–199. [Google Scholar] [CrossRef]
- Dieterich, J.H. Time-dependent friction and the mechanics of stick-slip. Pure Appl. Geophys. 1978, 116, 790–806. [Google Scholar] [CrossRef]
- Dieterich, J.H. Modeling of rock friction: 1. Experimental results and constitutive equations. J. Geophys. Res. Solid Earth 1979, 84, 2161. [Google Scholar] [CrossRef]
- Rice, J.R.; Ruina, A.L. Stability of Steady Frictional Slipping. J. Appl. Mech. 1983, 50, 343–349. [Google Scholar] [CrossRef] [Green Version]
- Ruina, A.L. Slip instability and state variable friction laws. J. Geophys. Res. 1983, 88, 10359–10370. [Google Scholar] [CrossRef]
- Heslot, F.; Baumberger, T.; Perrin, B.; Caroli, B.; Caroli, C. Creep, stick-slip, and dry-friction dynamics: Experiments and a heuristic model. Phys. Rev. E 1994, 49, 4973–4988. [Google Scholar] [CrossRef]
- Popov, V.L.; Grzemba, B.; Starcevic, J.; Fabry, C. Accelerated creep as a precursor of friction instability and earthquake prediction. Phys. Mesomech. 2010, 13, 283–291. [Google Scholar] [CrossRef]
- Dieterich, J.H. A model for the nucleation of earthquake slip. In Earthquake Source Mechanics; Wiley Online Library: Washington, DC, USA, 1986; pp. 37–47. [Google Scholar] [CrossRef]
- Rice, J.R. The mechanics of earthquake rupture. In Physics of the Earth’s Interior; Academic Press: New York, NY, USA, 1980; pp. 555–649. [Google Scholar]
- Rabinowicz, E. The Nature of the Static and Kinetic Coefficients of Friction. J. Appl. Phys. 1951, 22, 1373–1379. [Google Scholar] [CrossRef]
- Dieterich, J.H.; Kilgore, B.D. Direct observation of frictional contacts: New insights for state-dependent properties. Pure Appl. Geophys. 1994, 143, 283–302. [Google Scholar] [CrossRef]
- Rubinstein, S.M.; Cohen, G.; Fineberg, J. Detachment fronts and the onset of dynamic friction. Nature 2004, 430, 1005–1009. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, S.M.; Cohen, G.; Fineberg, J. Dynamics of Precursors to Frictional Sliding. Phys. Rev. Lett. 2007, 98, 226103. [Google Scholar] [CrossRef] [PubMed]
- Nagata, K.; Nakatani, M.; Yoshida, S. Monitoring frictional strength with acoustic wave transmission. Geophys. Res. Lett. 2008, 35, L06310. [Google Scholar] [CrossRef]
- Estrin, Y.; Bréchet, Y. On a model of frictional sliding. Pure Appl. Geophys. 1996, 147, 745–762. [Google Scholar] [CrossRef]
- Dieterich, J.H. Time-dependent friction in rocks. J. Geophys. Res. 1972, 77, 3690–3697. [Google Scholar] [CrossRef]
- Beeler, N.M.; Tullis, T.E.; Weeks, J.D. The roles of time and displacement in the evolution effect in rock friction. Geophys. Res. Lett. 1994, 21, 1987–1990. [Google Scholar] [CrossRef]
- Berthoud, P.; Baumberger, T.; G’Sell, C.; Hiver, J.M. Physical analysis of the state- and rate-dependent friction law: Static friction. Phys. Rev. B 1999, 59, 14313. [Google Scholar] [CrossRef]
- Bureau, L.; Baumberger, T.; Caroli, C.; Ronsin, O. Low-velocity friction between macroscopic solids. Comptes Rendus l’Académie des Sci. Ser. IV Phys. 2001, 2, 699–707. [Google Scholar] [CrossRef]
- Ben-David, O.; Rubinstein, S.M.; Fineberg, J. Slip-stick and the evolution of frictional strength. Nature 2010, 463, 76–79. [Google Scholar] [CrossRef]
- Tullis, T.E.; Weeks, J.D. Constitutive behavior and stability of frictional sliding of granite. Pure Appl. Geophys. 1986, 124, 383–414. [Google Scholar] [CrossRef]
- Kilgore, B.D.; Blanpied, M.L.; Dieterich, J.H. Velocity dependent friction of granite over a wide range of conditions. Geophys. Res. Lett. 1993, 20, 903–906. [Google Scholar] [CrossRef]
- Baumberger, T.; Berthoud, P. Physical analysis of the state- and rate-dependent friction law. II. Dynamic friction. Phys. Rev. B 1999, 60, 3928–3939. [Google Scholar] [CrossRef]
- Reches, Z.; Lockner, D.A. Fault weakening and earthquake instability by powder lubrication. Nature 2010, 467, 452–455. [Google Scholar] [CrossRef] [PubMed]
- Rice, J.R.; Lapusta, N.; Ranjith, K. Rate and state dependent friction and the stability of sliding between elastically deformable solids. J. Mech. Phys. Solids 2001, 49, 1865–1898. [Google Scholar] [CrossRef] [Green Version]
- Nakatani, M. Conceptual and physical clarification of rate and state friction: Frictional sliding as a thermally activated rheology. J. Geophys. Res. Solid Earth 2001, 106, 13347–13380. [Google Scholar] [CrossRef]
- Beeler, N.M.; Tullis, T.E.; Kronenberg, A.K.; Reinen, L.A. The instantaneous rate dependence in low temperature laboratory rock friction and rock deformation experiments. J. Geophys. Res. 2007, 112, B07310. [Google Scholar] [CrossRef]
- Bar-Sinai, Y.; Spatschek, R.; Brener, E.A.; Bouchbinder, E. On the velocity-strengthening behavior of dry friction. J. Geophys. Res. Solid Earth 2014, 119, 1738–1748. [Google Scholar] [CrossRef]
- Chester, F.M.; Higgs, N.G. Multimechanism friction constitutive model for ultrafine quartz gouge at hypocentral conditions. J. Geophys. Res. 1992, 97, 1859–1870. [Google Scholar] [CrossRef]
- Perrin, G.; Rice, J.R.; Zheng, G. Self-healing slip pulse on a frictional surface. J. Mech. Phys. Solids 1995, 43, 1461–1495. [Google Scholar] [CrossRef] [Green Version]
- Putelat, T.; Dawes, J.H. Steady and transient sliding under rate-and-state friction. J. Mech. Phys. Solids 2015, 78, 70–93. [Google Scholar] [CrossRef]
- Zheng, G.; Rice, J.R. Conditions under which velocity-weakening friction allows a self-healing versus a cracklike mode of rupture. Bull. Seismol. Soc. Am. 1998, 88, 1466–1483. [Google Scholar]
- Courtney-Pratt, J.S.; Eisner, E. The effect of a tangential force on the contact of metallic bodies. Proc. R. Soc. Lond. A 1957, 238, 529–550. [Google Scholar] [CrossRef]
- Archard, J.F. Elastic Deformation and the Laws of Friction. Proc. R. Soc. A Math. Phys. Eng. Sci. 1957, 243, 190–205. [Google Scholar] [CrossRef]
- Berthoud, P.; Baumberger, T. Shear stiffness of a solid-solid multicontact interface. Proc. R. Soc. A Math. Phys. Eng. Sci. 1998, 454, 1615–1634. [Google Scholar] [CrossRef]
- Bureau, L.; Baumberger, T.; Caroli, C. Shear response of a frictional interface to a normal load modulation. Phys. Rev. E 2000, 62, 6810–6820. [Google Scholar] [CrossRef] [Green Version]
- Campañá, C.; Persson, B.N.J.; Müser, M.H. Transverse and normal interfacial stiffness of solids with randomly rough surfaces. J. Phys. Condens. Matter 2011, 23, 085001. [Google Scholar] [CrossRef] [Green Version]
- Povirk, G.L.; Needleman, A. Finite Element Simulations of Fiber Pull-Out. J. Eng. Mater. Technol. 1993, 115, 286. [Google Scholar] [CrossRef]
- Coker, D.; Lykotrafitis, G.; Needleman, A.; Rosakis, A.J. Frictional sliding modes along an interface between identical elastic plates subject to shear impact loading. J. Mech. Phys. Solids 2005, 53, 884–922. [Google Scholar] [CrossRef] [Green Version]
- Shi, Z.; Ben-Zion, Y.; Needleman, A. Properties of dynamic rupture and energy partition in a solid with a frictional interface. J. Mech. Phys. Solids 2008, 56, 5–24. [Google Scholar] [CrossRef]
- Braun, O.M.; Barel, I.; Urbakh, M. Dynamics of Transition from Static to Kinetic Friction. Phys. Rev. Lett. 2009, 103, 194301. [Google Scholar] [CrossRef] [Green Version]
- Shi, Z.; Needleman, A.; Ben-Zion, Y. Slip modes and partitioning of energy during dynamic frictional sliding between identical elastic–viscoplastic solids. Int. J. Fract. 2010, 162, 51–67. [Google Scholar] [CrossRef]
- Bouchbinder, E.; Brener, E.A.; Barel, I.; Urbakh, M. Slow Cracklike Dynamics at the Onset of Frictional Sliding. Phys. Rev. Lett. 2011, 107, 235501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rubinstein, S.M.; Barel, I.; Reches, Z.; Braun, O.M.; Urbakh, M.; Fineberg, J. Slip Sequences in Laboratory Experiments Resulting from Inhomogeneous Shear as Analogs of Earthquakes Associated with a Fault Edge. Pure Appl. Geophys. 2011, 168, 2151–2166. [Google Scholar] [CrossRef]
- Bar Sinai, Y.; Brener, E.A.; Bouchbinder, E. Slow rupture of frictional interfaces. Geophys. Res. Lett. 2012, 39, L03308. [Google Scholar] [CrossRef]
- Bar-Sinai, Y.; Spatschek, R.; Brener, E.A.; Bouchbinder, E. Instabilities at frictional interfaces: Creep patches, nucleation, and rupture fronts. Phys. Rev. E 2013, 88, 060403. [Google Scholar] [CrossRef] [Green Version]
- Ferry, J. Viscoelastic Properties of Polymers, 3rd ed.; Wiley: New York, NY, USA, 1980. [Google Scholar]
- Thomson, W. On the Elasticity and Viscosity of Metals. Proc. R. Soc. Lond. 1865, 14, 289–297. [Google Scholar] [CrossRef]
- Bureau, L.; Caroli, C.; Baumberger, T. Elasticity and onset of frictional dissipation at a non-sliding multi-contact interface. Proc. R. Soc. A Math. Phys. Eng. Sci. 2003, 459, 2787–2805. [Google Scholar] [CrossRef]
- Nakatani, M.; Scholz, C.H. Intrinsic and apparent short-time limits for fault healing: Theory, observations, and implications for velocity-dependent friction. J. Geophys. Res. Solid Earth 2006, 111, 1–19. [Google Scholar] [CrossRef]
- Nagata, K.; Nakatani, M.; Yoshida, S. A revised rate- and state-dependent friction law obtained by constraining constitutive and evolution laws separately with laboratory data. J. Geophys. Res. Solid Earth 2012, 117, B02314. [Google Scholar] [CrossRef]
- Marone, C. The effect of loading rate on static friction and the rate of fault healing during the earthquake cycle. Nature 1998, 391, 69–72. [Google Scholar] [CrossRef]
- Shimamoto, T. Transition Between Frictional Slip and Ductile Flow for Halite Shear Zones at Room Temperature. Science 1986, 231, 711–714. [Google Scholar] [CrossRef] [PubMed]
- Bar-Sinai, Y.; Spatschek, R.; Brener, E.A.; Bouchbinder, E. Velocity-strengthening friction significantly affects interfacial dynamics, strength and dissipation. Sci. Rep. 2015, 5, 7841. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Di Toro, G.; Goldsby, D.L.; Tullis, T.E. Friction falls towards zero in quartz rock as slip velocity approaches seismic rates. Nature 2004, 427, 436–439. [Google Scholar] [CrossRef]
- Goldsby, D.L.; Tullis, T.E. Flash Heating Leads to Low Frictional Strength of Crustal Rocks at Earthquake Slip Rates. Science 2011, 334, 216–218. [Google Scholar] [CrossRef]
- Weertman, J. Unstable slippage across a fault that separates elastic media of different elastic constants. J. Geophys. Res. Solid Earth 1980, 85, 1455–1461. [Google Scholar] [CrossRef]
- Aldam, M.; Bar-Sinai, Y.; Svetlizky, I.; Brener, E.A.; Fineberg, J.; Bouchbinder, E. Frictional Sliding without Geometrical Reflection Symmetry. Phys. Rev. X 2016, 6, 041023. [Google Scholar] [CrossRef] [Green Version]
- Heimisson, E.R.; Dunham, E.M.; Almquist, M. Poroelastic effects destabilize mildly rate-strengthening friction to generate stable slow slip pulses. J. Mech. Phys. Solids 2019, 130, 262–279. [Google Scholar] [CrossRef] [Green Version]
- Geubelle, P.; Rice, J.R. A spectral method for three-dimensional elastodynamic fracture problems. J. Mech. Phys. Solids 1995, 43, 1791–1824. [Google Scholar] [CrossRef]
- Morrissey, J.W.; Geubelle, P.H. A numerical scheme for mode III dynamic fracture problems. Int. J. Numer. Methods Eng. 1997, 40, 1181–1196. [Google Scholar] [CrossRef]
- Breitenfeld, M.S.; Geubelle, P.H. Numerical analysis of dynamic debonding under 2D in-plane and 3D loading. Int. J. Fract. 1998, 93, 13–38. [Google Scholar] [CrossRef]
- Ben-Zion, Y.; Rice, J.R. Slip patterns and earthquake populations along different classes of faults in elastic solids. J. Geophys. Res. Solid Earth 1995, 100, 12959–12983. [Google Scholar] [CrossRef]
- Crupi, P.; Bizzarri, A. The role of radiation damping in the modeling of repeated earthquake events. Ann. Geophys. 2013, 56, R0111. [Google Scholar] [CrossRef]
- Weertman, J. Relationship between displacements on a free surface and the stress on a fault. Bull. Seismol. Soc. Am. 1965, 55, 945–953. [Google Scholar]
- Acheson, D.J. Elementary Fluid Dynamics; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Viesca, R.C. Self-similar slip instability on interfaces with rate- and state-dependent friction. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20160254. [Google Scholar] [CrossRef]
- Thomsen, J. Using fast vibrations to quench friction-induced oscillations. J. Sound Vib. 1999, 228, 1079–1102. [Google Scholar] [CrossRef]
- Rhee, S.; Jacko, M.; Tsang, P. The role of friction film in friction, wear and noise of automotive brakes. Wear 1991, 146, 89–97. [Google Scholar] [CrossRef]
- Brace, W.F.; Byerlee, J.D. Stick-Slip as a Mechanism for Earthquakes. Science 1966, 153, 990–992. [Google Scholar] [CrossRef] [Green Version]
- Dieterich, J.H. Model for earthquake precursers based on premonitory fault slip. Trans. Geophys. Union 1975, 56, 1059–1060. [Google Scholar]
- Aldam, M.; Weikamp, M.; Spatschek, R.; Brener, E.A.; Bouchbinder, E. Critical Nucleation Length for Accelerating Frictional Slip. Geophys. Res. Lett. 2017, 44, 11390–11398. [Google Scholar] [CrossRef]
- Dieterich, J.H. Earthquake nucleation on faults with rate-and state-dependent strength. Tectonophysics 1992, 211, 115–134. [Google Scholar] [CrossRef] [Green Version]
- Brener, E.A.; Weikamp, M.; Spatschek, R.; Bar-Sinai, Y.; Bouchbinder, E. Dynamic instabilities of frictional sliding at a bimaterial interface. J. Mech. Phys. Solids 2016, 89, 149–173. [Google Scholar] [CrossRef] [Green Version]
- Lapusta, N.; Rice, J.R. Nucleation and early seismic propagation of small and large events in a crustal earthquake model. J. Geophys. Res. Solid Earth 2003, 108, 2205. [Google Scholar] [CrossRef]
- Rubin, A.M.; Ampuero, J.P. Earthquake nucleation on (aging) rate and state faults. J. Geophys. Res. Solid Earth 2005, 110, B11312. [Google Scholar] [CrossRef]
- Ampuero, J.P.; Rubin, A.M. Earthquake nucleation on rate and state faults—Aging and slip laws. J. Geophys. Res. Solid Earth 2008, 113, B01302. [Google Scholar] [CrossRef]
- Kammer, D.S.; Yastrebov, V.A.; Spijker, P.; Molinari, J.F. On the Propagation of Slip Fronts at Frictional Interfaces. Tribol. Lett. 2012, 48, 27–32. [Google Scholar] [CrossRef] [Green Version]
- Svetlizky, I.; Fineberg, J. Classical shear cracks drive the onset of dry frictional motion. Nature 2014, 509, 205–208. [Google Scholar] [CrossRef] [PubMed]
- Brener, E.A.; Malinin, S.V.; Marchenko, V.I. Fracture and friction: Stick-slip motion. Eur. Phys. J. E 2005, 17, 101–113. [Google Scholar] [CrossRef]
- Cocco, M.; Bizzarri, A. On the slip-weakening behavior of rate- and state dependent constitutive laws. Geophys. Res. Lett. 2002, 29, 1516. [Google Scholar] [CrossRef]
- Freund, L.B. Dynamic Fracture Mechanics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Ben-David, O.; Cohen, G.; Fineberg, J. The Dynamics of the Onset of Frictional Slip. Science 2010, 330, 211–214. [Google Scholar] [CrossRef]
- Kaproth, B.M.; Marone, C. Slow Earthquakes, Preseismic Velocity Changes, and the Origin of Slow Frictional Stick-Slip. Science 2013, 341, 1229–1232. [Google Scholar] [CrossRef]
- Bürgmann, R. The geophysics, geology and mechanics of slow fault slip. Earth Planet. Sci. Lett. 2018, 495, 112–134. [Google Scholar] [CrossRef] [Green Version]
- Putelat, T.; Dawes, J.H.; Champneys, A.R. A phase-plane analysis of localized frictional waves. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20160606. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brener, E.A.; Aldam, M.; Barras, F.; Molinari, J.F.; Bouchbinder, E. Unstable Slip Pulses and Earthquake Nucleation as a Nonequilibrium First-Order Phase Transition. Phys. Rev. Lett. 2018, 121, 234302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heaton, T.H. Evidence for and implications of self-healing pulses of slip in earthquake rupture. Phys. Earth Planet. Inter. 1990, 64, 1–20. [Google Scholar] [CrossRef]
- Noda, H.; Dunham, E.M.; Rice, J.R. Earthquake ruptures with thermal weakening and the operation of major faults at low overall stress levels. J. Geophys. Res. Solid Earth 2009, 114, B07302. [Google Scholar] [CrossRef]
- Uenishi, K.; Rice, J.R. Universal nucleation length for slip-weakening rupture instability under nonuniform fault loading. J. Geophys. Res. Solid Earth 2003, 108, 2042. [Google Scholar] [CrossRef]
- Barras, F.; Aldam, M.; Roch, T.; Brener, E.A.; Bouchbinder, E.; Molinari, J.F. The emergence of crack-like behavior of frictional rupture: The origin of stress drops. arXiv 2019, arXiv:1906.11533. [Google Scholar]
- Barras, F.; Aldam, M.; Roch, T.; Brener, E.A.; Bouchbinder, E.; Molinari, J.F. The emergence of crack-like behavior of frictional rupture: Edge singularity and energy balance. arXiv 2019, arXiv:1907.04376. [Google Scholar]
- Lu, X.; Rosakis, A.J.; Lapusta, N. Rupture modes in laboratory earthquakes: Effect of fault prestress and nucleation conditions. J. Geophys. Res. Solid Earth 2010, 115, 1–25. [Google Scholar] [CrossRef]
- Ida, Y. Cohesive force across the tip of a longitudinal-shear crack and Griffith’s specific surface energy. J. Geophys. Res. 1972, 77, 3796–3805. [Google Scholar] [CrossRef]
- Palmer, A.C.; Rice, J.R. The growth of slip surfaces in the progressive failure of over-consolidated clay. Proc. R. Soc. A Math. Phys. Eng. Sci. 1973, 332, 527–548. [Google Scholar] [CrossRef]
- Woodhouse, J.; Putelat, T.; McKay, A. Are there reliable constitutive laws for dynamic friction? Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Radiguet, M.; Kammer, D.S.; Gillet, P.; Molinari, J.F. Survival of Heterogeneous Stress Distributions Created by Precursory Slip at Frictional Interfaces. Phys. Rev. Lett. 2013, 111, 164302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Radiguet, M.; Kammer, D.S.; Molinari, J.F. The role of viscoelasticity on heterogeneous stress fields at frictional interfaces. Mech. Mater. 2015, 80, 276–287. [Google Scholar] [CrossRef]
- Allison, K.L.; Dunham, E.M. Earthquake cycle simulations with rate-and-state friction and power-law viscoelasticity. Tectonophysics 2017. [Google Scholar] [CrossRef]
- Dunham, E.M.; Rice, J.R. Earthquake slip between dissimilar poroelastic materials. J. Geophys. Res. Solid Earth 2008, 113, B09304. [Google Scholar] [CrossRef]
- Hecht, F. New development in freefem++. J. Numer. Math. 2012, 20. [Google Scholar] [CrossRef]







© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bar-Sinai, Y.; Aldam, M.; Spatschek, R.; Brener, E.A.; Bouchbinder, E. Spatiotemporal Dynamics of Frictional Systems: The Interplay of Interfacial Friction and Bulk Elasticity. Lubricants 2019, 7, 91. https://doi.org/10.3390/lubricants7100091
Bar-Sinai Y, Aldam M, Spatschek R, Brener EA, Bouchbinder E. Spatiotemporal Dynamics of Frictional Systems: The Interplay of Interfacial Friction and Bulk Elasticity. Lubricants. 2019; 7(10):91. https://doi.org/10.3390/lubricants7100091
Chicago/Turabian StyleBar-Sinai, Yohai, Michael Aldam, Robert Spatschek, Efim A. Brener, and Eran Bouchbinder. 2019. "Spatiotemporal Dynamics of Frictional Systems: The Interplay of Interfacial Friction and Bulk Elasticity" Lubricants 7, no. 10: 91. https://doi.org/10.3390/lubricants7100091
APA StyleBar-Sinai, Y., Aldam, M., Spatschek, R., Brener, E. A., & Bouchbinder, E. (2019). Spatiotemporal Dynamics of Frictional Systems: The Interplay of Interfacial Friction and Bulk Elasticity. Lubricants, 7(10), 91. https://doi.org/10.3390/lubricants7100091