Study of Break-In Process and its Effects on Piston Skirt Lubrication in Internal Combustion Engines
Abstract
:1. Introduction
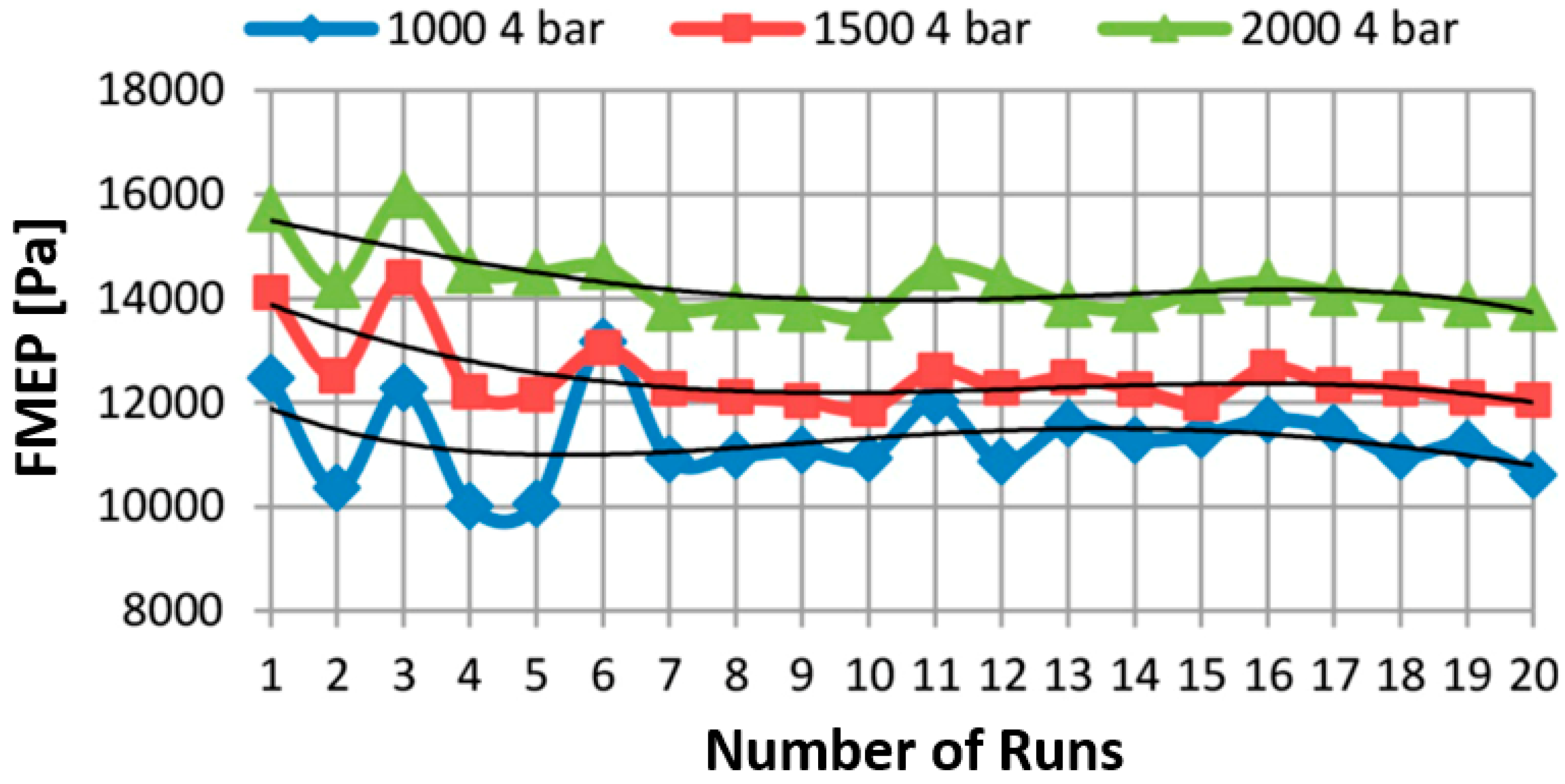
1.1. Floating Liner Engine Testing
1.2. Piston Skirt Lubrication Model
2. Model Development
2.1. Update on the Average Flow Model
2.2. Contact Pressure
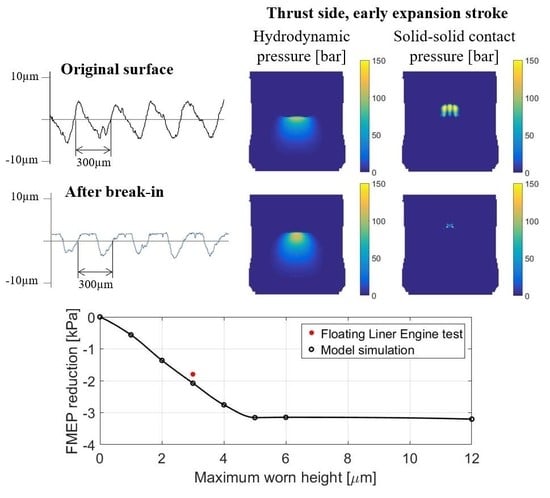
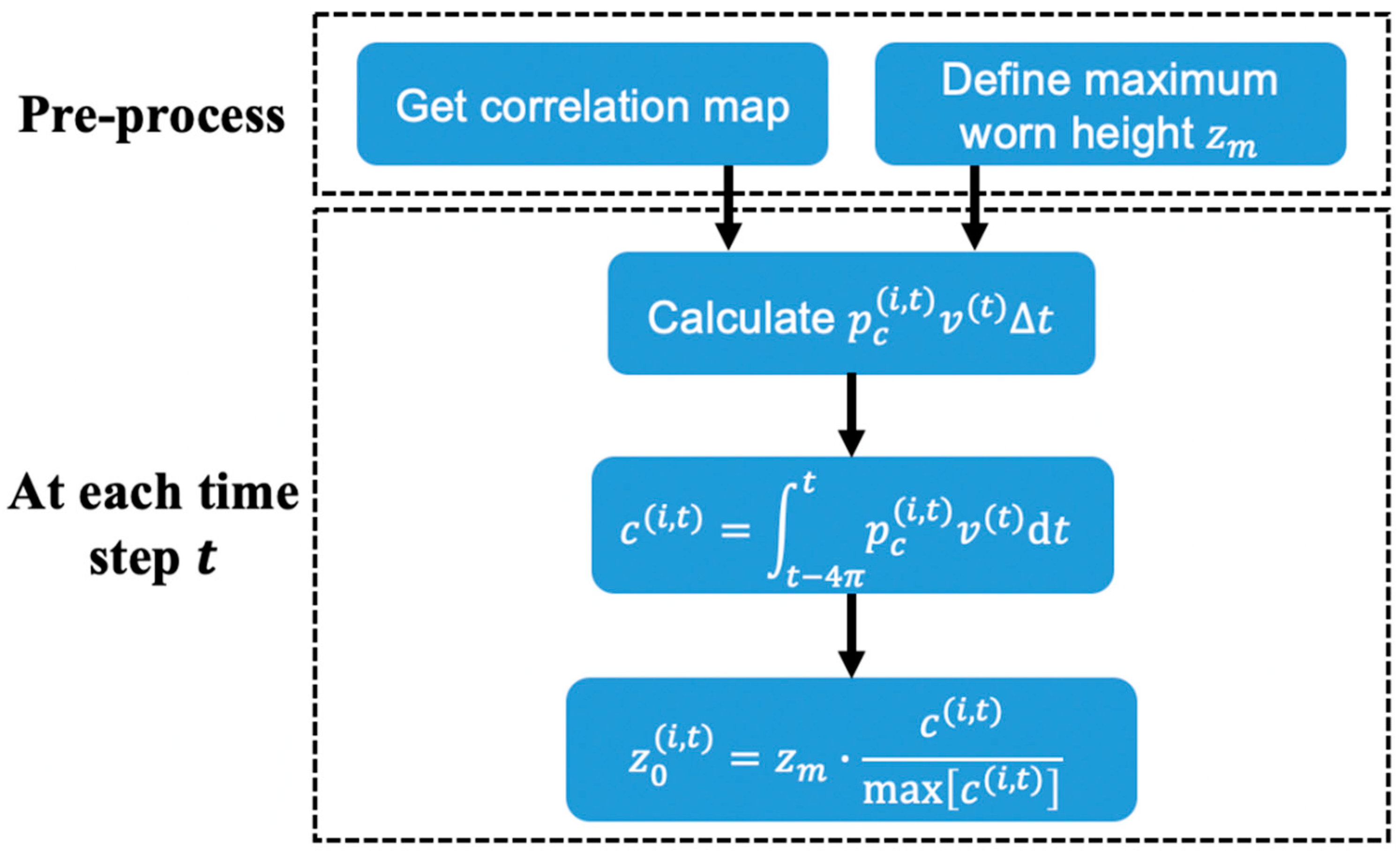
2.3. Worn Height of Waviness
3. Results
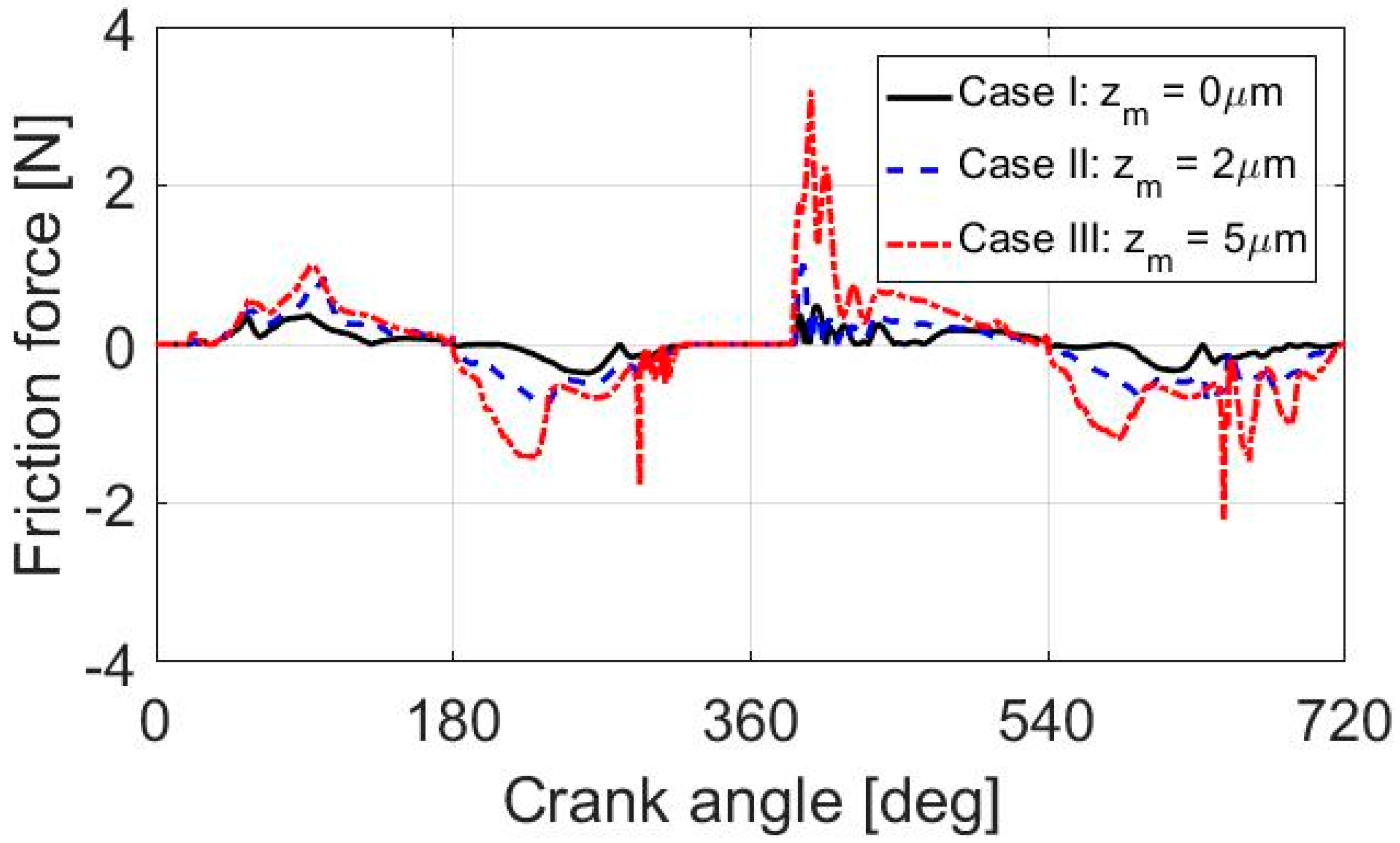
3.1. Effects of Break-In
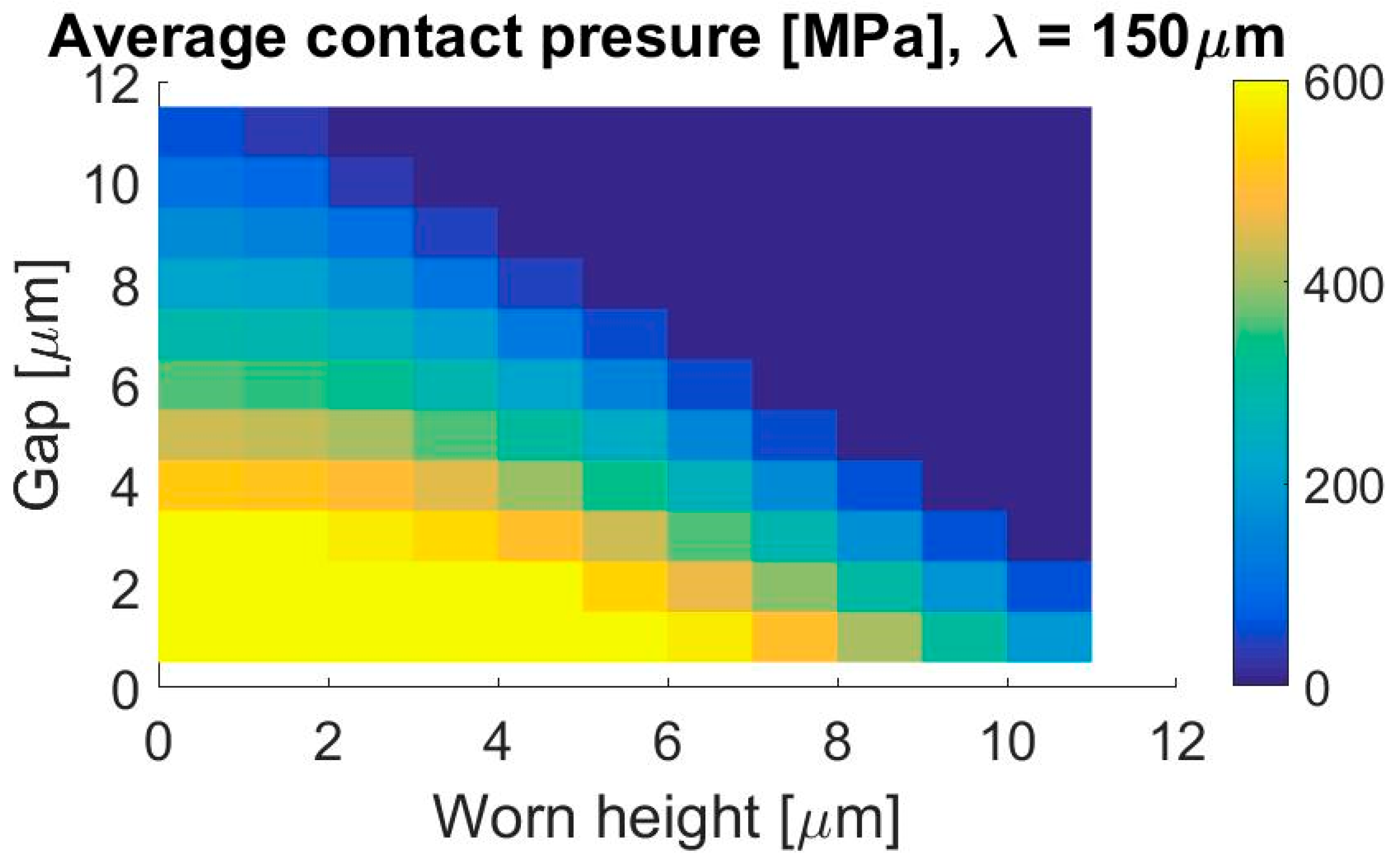
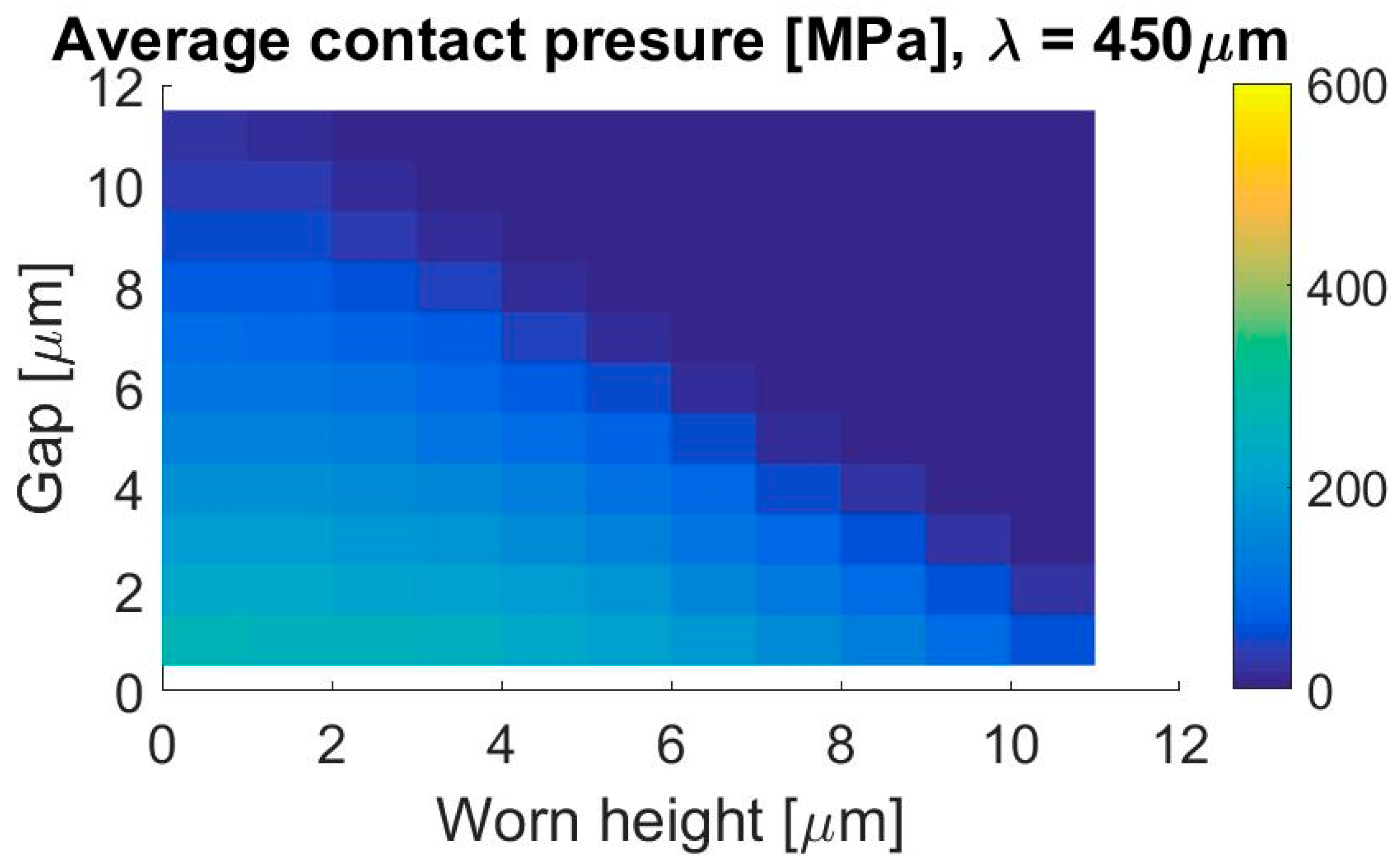
3.2. Effects of Wavelength
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| angle between the central axis of the piston and the connecting rod | |
| wavelength of the tooling marks on the piston skirt | |
| half of the peak-to-valley distance of the waves on the skirt without break-in | |
| hydrodynamic shear stress | |
| , | flow factors for the Poiseuille term in the average Reynolds equation |
| flow factor for the Couette term in the average Reynolds equation | |
| , , | flow factors for the shear stress |
| gauge pressure in full film region and opposite value of the void ratio in partial film region | |
| local distance between the liner and the skirt | |
| distance between the liner and the peak of the wave on the skirt without break-in | |
| distance between the liner and the valley of the wave on the skirt | |
| average value of over the wavelength of the skirt profile | |
| average value of over the wavelength of the skirt profile | |
| contact pressure | |
| worn height of the wave on the skirt | |
| maximum worn height allowed | |
| effective Young’s modulus between the skirt coating and the liner | |
| indicator of full film and partial film regions | |
| dimensionless sliding velocity of the piston |
References
- Meng, Z. Numerical Investigation of the Piston Skirt Lubrication in Heavy Duty Diesel Engines. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2017. [Google Scholar]
- Meng, Z.; Ahling, S.; Tian, T. Modeling of Oil Transport between Piston Skirt and Cylinder Liner in Internal Combustion Engines (No. 2019-01-0590); SAE Technical Paper; SAE: Warrendale, PA, USA; Troy, MI, USA, 2019. [Google Scholar]
- Meng, Z.; Ahling, S.; Tian, T. Study of the Effects of Oil Supply and Piston Skirt Profile on Lubrication Performance in Power Cylinder Systems (No. 2019-01-2364); SAE Technical Paper: Warrendale, PA, USA; Troy, MI, USA, 2019. [Google Scholar]
- Wang, Y.; Tung, S.C. Scuffing and wear behavior of aluminum piston skirt coatings against aluminum cylinder bore. Wear 1999, 225, 1100–1108. [Google Scholar] [CrossRef]
- Wang, Y.; Brogan, K.; Tung, S.C. Wear and scuffing characteristics of composite polymer and nickel/ceramic composite coated piston skirts against aluminum and cast iron cylinder bores. Wear 2001, 250, 706–717. [Google Scholar] [CrossRef]
- Zhang, G.; Li, W.Y.; Cherigui, M.; Zhang, C.; Liao, H.; Bordes, J.M.; Coddet, C. Structures and tribological performances of PEEK (poly-ether-ether-ketone)-based coatings designed for tribological application. Prog. Org. Coat. 2007, 60, 39–44. [Google Scholar] [CrossRef]
- Deuß, T.; Ehnis, H.; Rose, R.; Künzel, R. Friction power measurements of a fired diesel engine–influence of piston skirt coatings. MTZ Worldw. Emag. 2011, 72, 18–23. [Google Scholar] [CrossRef]
- Moosavian, A.; Najafi, G.; Ghobadian, B.; Mirsalim, M.; Jafari, S.M.; Sharghi, P. Piston scuffing fault and its identification in an IC engine by vibration analysis. Appl. Acoust. 2016, 102, 40–48. [Google Scholar] [CrossRef]
- Demas, N.G.; Erck, R.A.; Ajayi, O.O.; Fenske, G.R. Tribological studies of coated pistons sliding against cylinder liners under laboratory test conditions. Lubr. Sci. 2012, 24, 216–227. [Google Scholar] [CrossRef]
- Moosavian, A.; Najafi, G.; Ghobadian, B.; Mirsalim, M. The effect of piston scratching fault on the vibration behavior of an IC engine. Appl. Acoust. 2007, 126, 91–100. [Google Scholar] [CrossRef]
- Ogihara, H. Research into surface improvement for low friction pistons. In SAE Transactions; SAE Technical Paper; SAE: Warrendale, PA, USA; Troy, MI, USA, 2005; pp. 1182–1190. [Google Scholar]
- Sugimura, K. Development of Piston Surface Treatment for Internal Combustion Engine. SAE Int. J. Mater. Manuf. 2009, 1, 824–831. [Google Scholar] [CrossRef]
- Cho, D.H.; Lee, S.A.; Lee, Y.Z. The effects of surface roughness and coatings on the tribological behavior of the surfaces of a piston skirt. Tribol. Trans. 2009, 53, 137–144. [Google Scholar] [CrossRef]
- Westerfield, Z.; Totaro, P.; Kim, D.; Tian, T. An Experimental Study of Piston Skirt Roughness and Profiles on piston Friction Using the Floating Liner Engine (No. 2016-01-1043); SAE Technical Paper; SAE: Warrendale, PA, USA; Troy, MI, USA, 2016. [Google Scholar]
- Dursunkaya, Z.; Keribar, R.; Ganapathy, V. A model of piston secondary motion and elastohydrodynamic skirt lubrication. J. Tribol. 1994, 116, 777–785. [Google Scholar] [CrossRef]
- Liu, K.; Xie, Y.B.; Gui, C.L. A comprehensive study of the friction and dynamic motion of the piston assembly. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 1998, 212, 221–226. [Google Scholar] [CrossRef]
- Malik, M.A.; Rashid, B.; Qasim, S.A.; Khushnood, S. Modeling and simulation of elastohydrodynamic lubrication of piston skirts considering elastic deformation in the initial engine start-up. In ASME/STLE 2004 International Joint Tribology Conference; American Society of Mechanical Engineers: New York, NY, USA, 2004; pp. 859–867. [Google Scholar]
- Duyar, M.; Bell, D.; Perchanok, M. A Comprehensive Piston Skirt Lubrication Model Using a Mass Conserving EHL Algorithm (No. 2005-01-1640); SAE Technical Paper; SAE: Warrendale, PA, USA; Troy, MI, USA, 2005. [Google Scholar]
- Greenwood, J.A.; Williamson, J.P. Contact of nominally flat surfaces. In Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences; Royal Society: London, UK, 1966; Volume 295, pp. 300–319. [Google Scholar]
- Kobayashi, T. Prediction of Piston Skirt Scuffing Via 3D Piston Motion Simulation (No. 2016-01-1044); SAE Technical Paper; SAE: Warrendale, PA, USA; Troy, MI, USA, 2016. [Google Scholar]
- MAHLE GmbH. Pistons and Engine Testing, Stuttgart: AZ Druck and Datentechnik; MAHLE GmbH: Stuttgart, Germany, 2012. [Google Scholar]
- McClure, F. Numerical Modeling of Piston Secondary Motion and Skirt Lubrication in Internal Combustion Engines. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2007. [Google Scholar]
- Bai, D. Modeling Piston Skirt Lubrication in Internal Combustion Engines. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2012. [Google Scholar]
- Totaro, P. Modeling Piston Secondary Motion and Skirt Lubrication with Applications. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2014. [Google Scholar]
- Patir, N.; Cheng, H.S. An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Elrod, H.G. A cavitation algorithm. J. Lubr. Technol. 1981, 103, 350–354. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Application of average flow model to lubrication between rough sliding surfaces. J. Lubr. Technol. 1979, 101, 220–229. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Sato, O.; Takiguchi, M.; Takayuki, A.; Seki, Y.; Fujimura, K.; Tateishi, Y. Improvement of Piston Lubrication in a Diesel Engine by Means of Cylinder Surface Roughness (No. 2004-01-0604); SAE Technical Paper; SAE: Warrendale, PA, USA; Troy, MI, USA, 2004. [Google Scholar]


















| Parameter | Value | Unit |
|---|---|---|
| Displaced volume | 0.496 | L |
| Stroke | 92.8 | Mm |
| Bore | 82.51 | Mm |
| Compression ratio | 10:1 | - |
| Maximum BMEP | 0.7 | MPa |
| Maximum engine speed | 3000 | rpm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, Z.; Zhang, L.; Tian, T. Study of Break-In Process and its Effects on Piston Skirt Lubrication in Internal Combustion Engines. Lubricants 2019, 7, 98. https://doi.org/10.3390/lubricants7110098
Meng Z, Zhang L, Tian T. Study of Break-In Process and its Effects on Piston Skirt Lubrication in Internal Combustion Engines. Lubricants. 2019; 7(11):98. https://doi.org/10.3390/lubricants7110098
Chicago/Turabian StyleMeng, Zhen, Linfeng Zhang, and Tian Tian. 2019. "Study of Break-In Process and its Effects on Piston Skirt Lubrication in Internal Combustion Engines" Lubricants 7, no. 11: 98. https://doi.org/10.3390/lubricants7110098
APA StyleMeng, Z., Zhang, L., & Tian, T. (2019). Study of Break-In Process and its Effects on Piston Skirt Lubrication in Internal Combustion Engines. Lubricants, 7(11), 98. https://doi.org/10.3390/lubricants7110098