The Multivariate Regression Models Suggested as Standardising Tools for Categorising Solitarious and Gregarious Groups of the Main Pest Locust, Schistocerca gregaria, Produce Reproducible Results
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
3. Results
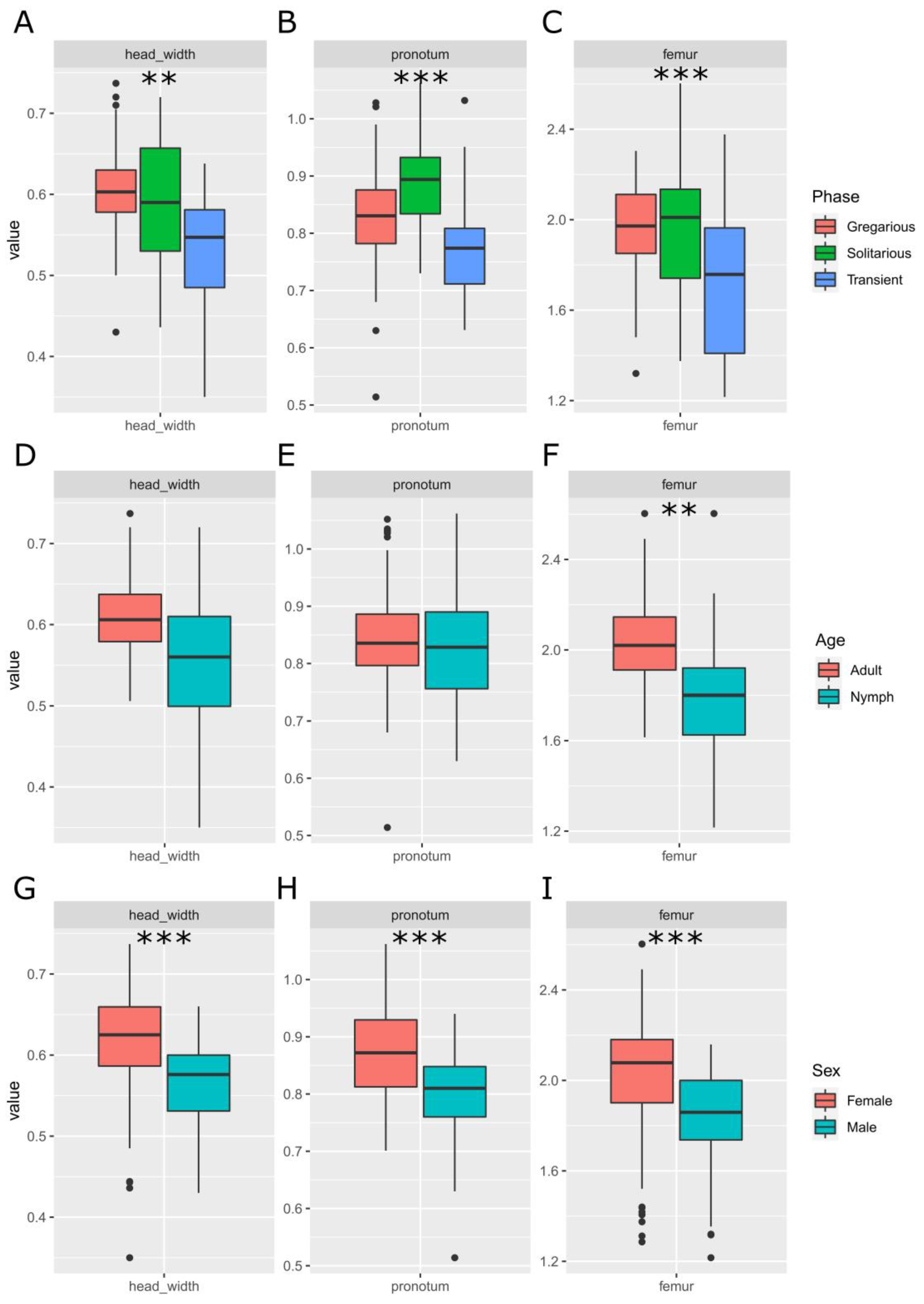
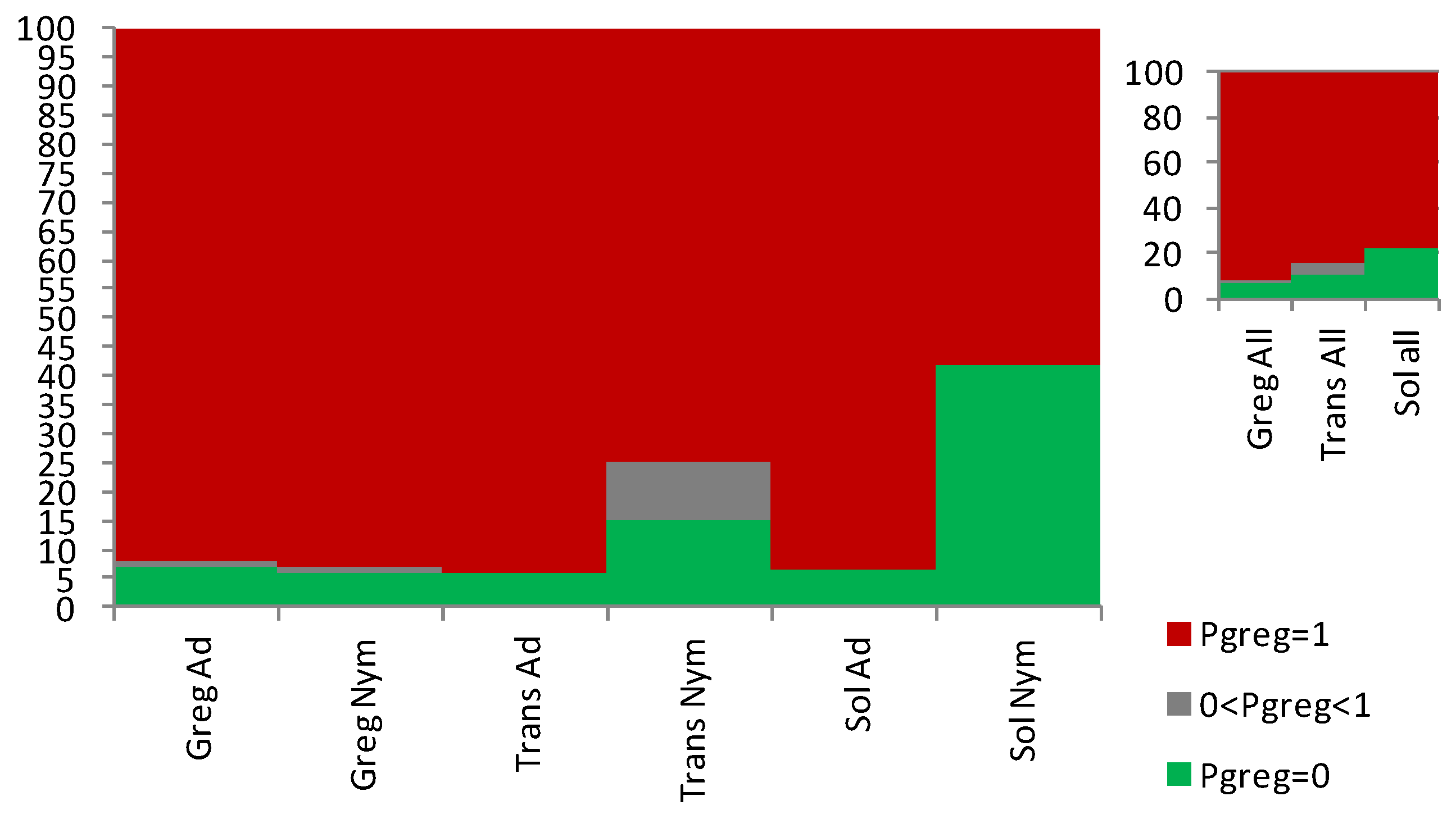
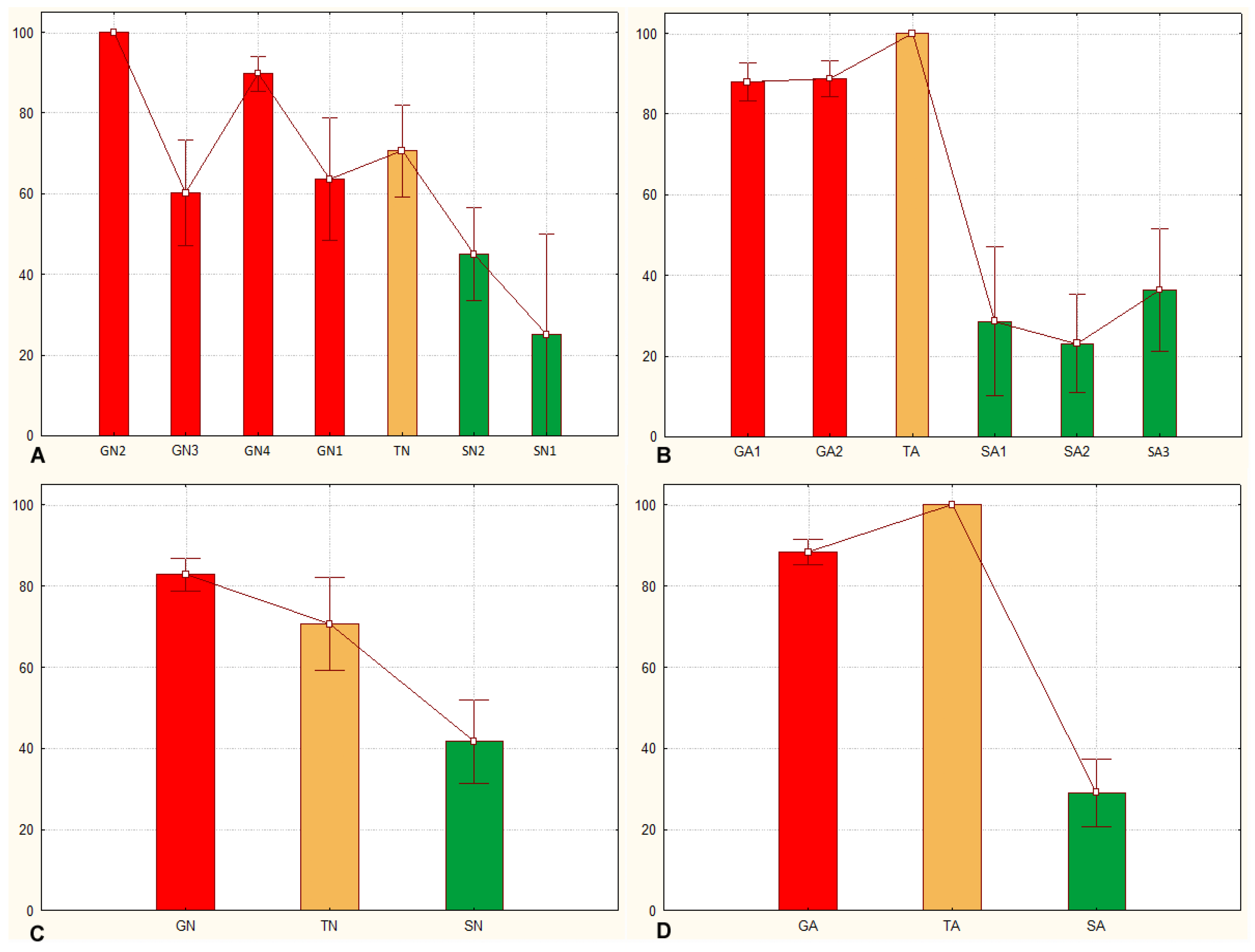
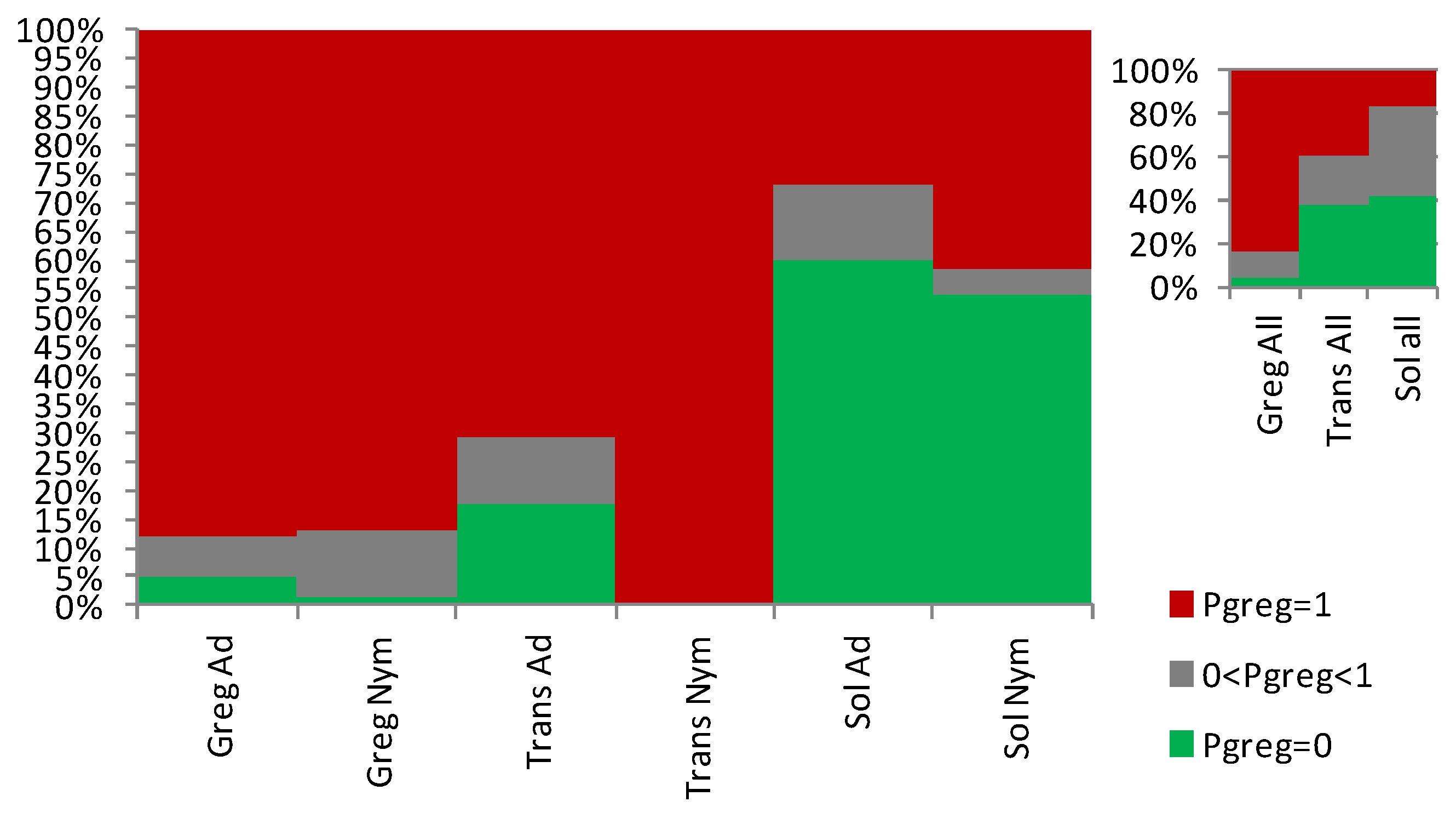
3.1. Sets of Locusts Used Are Significantly Different from Each Other
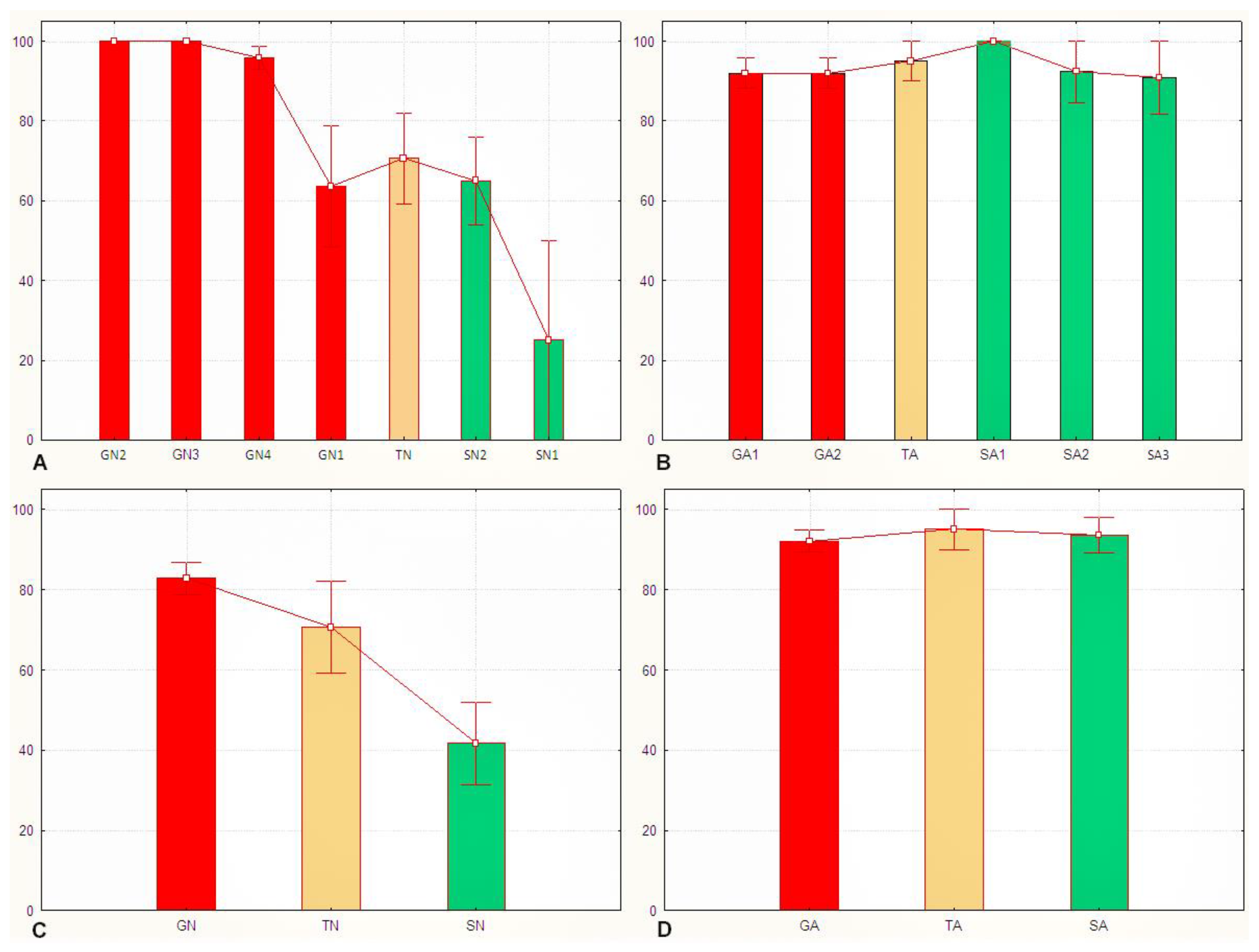
3.2. The Sg_extended_corrected Model Is Not Accurate, although It Does Distinguish between Solitarious and Gregarious Nymphs
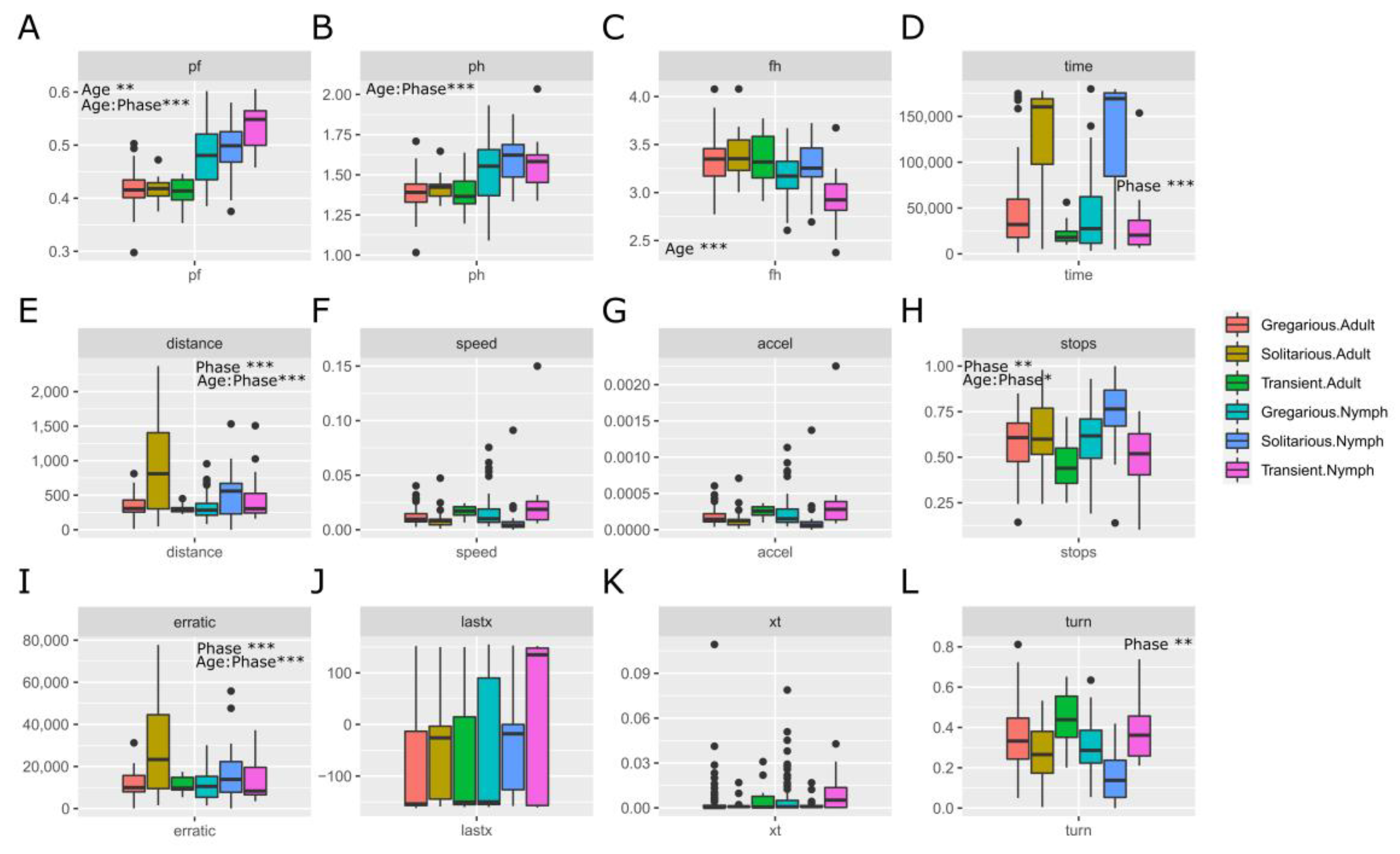
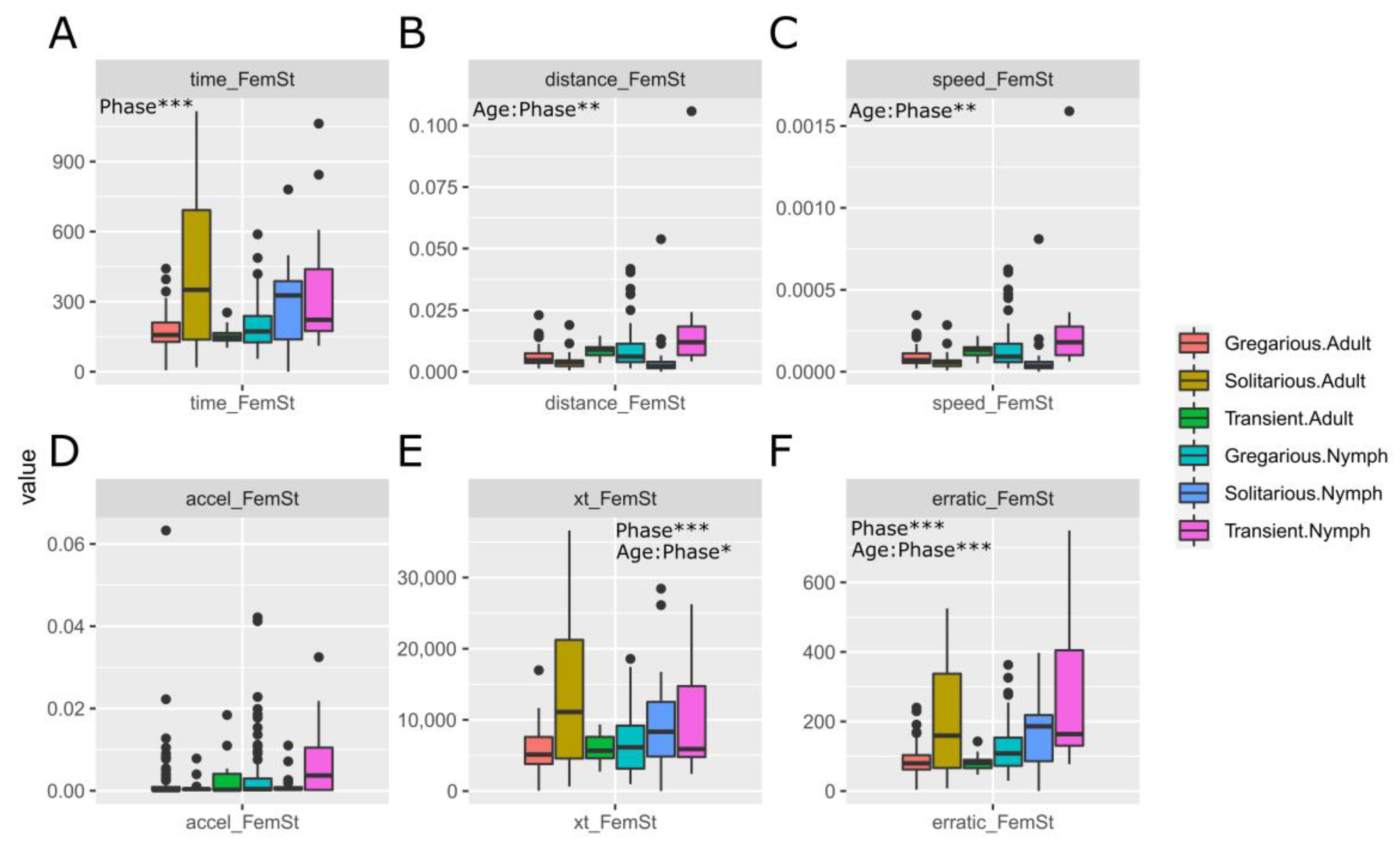
3.3. The Sg_non-morphometric Model Does Distinguish between Solitarious and Gregarious Locusts
4. Discussion
4.1. Should We Normalise by Locust Size?
4.2. Can Morphometry and Behaviour Be in the Same Model?
4.3. Do the Models Do What We Want Them to Do?
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Uvarov, B. Grasshoppers and Locusts; Cambridge University Press: Cambridge, UK, 1966. [Google Scholar]
- Dingle, H.; Mousseau, T.A.; Scott, S.M. Altitudinal variation in life cycle syndromes of california populations of the grasshopper, Melanoplus sanguinipes (f.). Oecologia 1990, 84, 199–206. [Google Scholar] [CrossRef] [PubMed]
- Waloff, Z.; Green, S.M. Regularities in duration of regional desert locust plagues. Nature 1975, 256, 484–485. [Google Scholar] [CrossRef] [PubMed]
- Poot-Pech, M.A.; Ruiz-Sanchez, E.; Ballina-Gomez, H.S.; Gamboa-Angulo, M.M.; Reyes-Ramirez, A. Olfactory response and host plant feeding of the central american locust schistocerca piceifrons piceifrons walker to common plants in a gregarious zone. Neotrop. Entomol. 2016, 45, 382–388. [Google Scholar] [CrossRef]
- Latchininsky, A.V. Moroccan locust dociostaurus maroccanus (thunberg, 1815): A faunistic rarity or an important economic pest? J. Insect Conserv. 1998, 2, 167–178. [Google Scholar] [CrossRef]
- Key, K. The regional and seasonal incidence of grasshopper plagues in Australia. Coun. Sci. Industr. Res. Aust. 1938, 117, 87. [Google Scholar]
- Waloff, Z. Upsurges and Recessions of the Desert Locust Plague: An Historical Survey; Anti-Locust Research Centre: London, UK, 1966. [Google Scholar]
- Pedgley, D. Desert Locust Forecasting Manual; Centre for Overseas Pest Research: London, UK, 1981; Volumes I and II. [Google Scholar]
- Showler, A.T.; Lecoq, M. Incidence and ramifications of armed conflict in countries with major desert locust breeding areas. Agronomy 2021, 11, 114. [Google Scholar] [CrossRef]
- Applebaum, S.; Heifetz, Y. Density-dependent physiological phase in insects. Annu. Rev. Entomol. 1999, 44, 317–341. [Google Scholar] [CrossRef]
- Nishide, Y.; Tanaka, S. Yellowing, morphology and behaviour in sexually mature gynandromorphs of the desert locust Schistocerca gregaria. Physiol. Entomol. 2012, 37, 379–383. [Google Scholar] [CrossRef]
- Stower, W.; Davies, D.; Jones, I. Morphometric studies of the desert locust, Schistocerca gregaria (forsk.). J. Anim. Ecol. 1960, 29, 309–339. [Google Scholar] [CrossRef]
- Symmons, P. A morphometric measure of phase in the desert locust, Schistocerca gregaria (forsk.). Bull. Entomol. Res. 1969, 58, 803–809. [Google Scholar] [CrossRef]
- Bouaichi, A.; Roessingh, P.; Simpson, S.J. An analysis of the behavioural effects of crowding and re-isolation on solitary-reared adult desert locusts (Schistocerca gregaria) and their offspring. Physiol. Entomol. 1995, 20, 199–208. [Google Scholar] [CrossRef]
- Bouaïchi, A.; Simpson, S. Density-dependent accumulation of phase characteristics in a natural population of the desert locust Schistocerca gregaria. Physiol. Entomol. 2003, 28, 25–31. [Google Scholar] [CrossRef]
- Simpson, S.J.; McCaffery, A.; Hägele, B.F. A behavioural analysis of phase change in the desert locust. Biol. Rev. 1999, 74, 461–480. [Google Scholar] [CrossRef]
- Tanaka, S.; Nishide, Y. Behavioral phase shift in nymphs of the desert locust, Schistocerca gregaria: Special attention to attraction/avoidance behaviors and the role of serotonin. J. Insect Physiol. 2013, 59, 101–112. [Google Scholar] [CrossRef] [PubMed]
- Gunn, D.; Hunter-Jones, P. Laboratory experiments on phase differences in locusts. Anti-Locust Bull. 1952, 12, 1–29. [Google Scholar]
- Stower, W. The colour pattern of hoppers of the desert locust (Schistocerca gregaria forskal). Anti-Locust Bull. 1959, 32, 75. [Google Scholar]
- Bouaichi, A.; Simpson, S.J.; Roessingh, P. The influence of environmental microstructure on the behavioural phase state and distribution of the desert locust Schistocerca gregaria. Physiol. Entomol. 1996, 21, 247–256. [Google Scholar] [CrossRef]
- Bakkali, M.; Martín-Blázquez, R. RNA-seq reveals large quantitative differences between the transcriptomes of outbreak and non-outbreak locusts. Sci. Rep. 2018, 8, 9207. [Google Scholar] [CrossRef] [PubMed]
- Martin-Blazquez, R.; Chen, B.; Kang, L.; Bakkali, M. Evolution, expression and association of the chemosensory protein genes with the outbreak phase of the two main pest locusts. Sci. Rep. 2017, 7, 6653. [Google Scholar] [CrossRef]
- Sugahara, R.; Saeki, S.; Jouraku, A.; Shiotsuki, T.; Tanaka, S. Knockdown of the corazonin gene reveals its critical role in the control of gregarious characteristics in the desert locust. J. Insect Physiol. 2015, 79, 80–87. [Google Scholar] [CrossRef]
- Bakkali, M. A bird’s-eye view on the modern genetics workflow and its potential applicability to the locust problem. Comptes Rendus Biol. 2013, 336, 375–383. [Google Scholar] [CrossRef] [PubMed]
- Rogers, S.M.; Cullen, D.A.; Anstey, M.L.; Burrows, M.; Despland, E.; Dodgson, T.; Matheson, T.; Ott, S.R.; Stettin, K.; Sword, G.A.; et al. Rapid behavioural gregarization in the desert locust, Schistocerca gregaria entails synchronous changes in both activity and attraction to conspecifics. J. Insect Physiol. 2014, 65, 9–26. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Guo, X.; Lei, H.; Li, T.; Hao, S.; Kang, L. Octopamine and tyramine respectively regulate attractive and repulsive behavior in locust phase changes. Sci. Rep. 2015, 5, 8036. [Google Scholar] [CrossRef]
- Martín-Blázquez, R.; Bakkali, M. Standardization of multivariate regression models for estimation of the gregariousness level of the main pest locust. Entomol. Exp. Et Appl. 2017, 163, 9–25. [Google Scholar] [CrossRef]
- Ott, S.R. Regressions fit for purpose: Models of locust phase state must not conflate morphology with behavior. Front. Behav. Neurosci. 2018, 12, 137. [Google Scholar] [CrossRef]
- Piou, C.; Zagaglia, G.; Medina, H.E.; Trumper, E.; Rojo Brizuela, X.; Maeno, K.O. Band movement and thermoregulation in schistocerca cancellata. J. Insect Physiol. 2022, 136, 104328. [Google Scholar] [CrossRef]
- Hamouda, A.B.; Tanaka, S.; Hamouda, M.H.B.; Bouain, A. Density-dependent phenotypic plasticity in body coloration and morphometry and its transgenerational changes in the migratory locust, locusta migratoria. J. Entomol. Nematol. 2011, 3, 105–116. [Google Scholar]
- Chen, S.; Yang, P.; Jiang, F.; Wei, Y.; Ma, Z.; Kang, L. De novo analysis of transcriptome dynamics in the migratory locust during the development of phase traits. PLoS ONE 2010, 5, e15633. [Google Scholar] [CrossRef]
- Chapuis, M.P.; Lecoq, M.; Michalakis, Y.; Loiseau, A.; Sword, G.A.; Piry, S.; Estoup, A. Do outbreaks affect genetic population structure? A worldwide survey in locusta migratoria, a pest plagued by microsatellite null alleles. Mol. Ecol. 2008, 17, 3640–3653. [Google Scholar] [CrossRef] [PubMed]
- Hägele, B.F.; Simpson, S.J. The influence of mechanical, visual and contact chemical stimulation on the behavioural phase state of solitarious desert locusts (Schistocerca gregaria). J. Insect Physiol. 2000, 46, 1295–1301. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.S.; Roessingh, P.; Simpson, S.J.; McCaffery, A.R. Parental effects on the behaviour and colouration of nymphs of the desert locust Schistocerca gregaria. J. Insect Physiol. 1994, 40, 173–181. [Google Scholar] [CrossRef]
- Islam, M.S.; Roessingh, P.; Simpson, S.J.; Mccaffery, A.R. Effects of population density experienced by parents during mating and oviposition on the phase of hatchling desert locusts, Schistocerca gregaria. Proc. R. Soc. Lond. B Biol. Sci. 1994, 257, 93–98. [Google Scholar] [CrossRef]
- Roessingh, P.; Simpson, S.J.; James, S. Analysis of phase-related changes in behaviour of desert locust nymphs. Proc. R. Soc. Lond. B Biol. Sci. 1993, 252, 43–49. [Google Scholar]
- Gillett, S.D. Social determinants of aggregation behaviour in adults of the desert locust. Anim. Behav. 1973, 21, 599–606. [Google Scholar] [CrossRef]
- Dingle, H.; Haskell, J.B. Phase polymorphism in the grasshopper melanoplus differentialis. Science 1967, 155, 590–592. [Google Scholar] [CrossRef]
- Ellis, P.E. Changes in the social aggregation of locust hoppers with changes in rearing conditions. Anim. Behav. 1963, 11, 152–160. [Google Scholar] [CrossRef]
| Correction Factor and Variables of the Model’s Logistic Regression Formulae | Constants and Coefficients of the Model: | ||
|---|---|---|---|
| I | II | ||
| C | 1/104 | 1 | |
| Intercept (β0) | −2.83 × 107 | 1.12 × 104 | |
| Pronotum-femur index | Pronotum-femur index (PF = pronotum dorsal length divided by hind femur length) | 5.11 × 107 | 0 |
| Pronotum-head index | Pronotum-head index (PH = pronotum dorsal length divided by head width) | −1.69 × 107 | 0 |
| Femur-head index | Femur-head index (FH = hind femur length divided by head width) | 9.39 × 106 | 0 |
| Choice | CH = a binary variable describing the side of the arena where the experimental animal was positioned at the end of the recording, with 0 being the blank side and 1 being the stimulus side | 1.03 × 106 | 8.45 × 103 |
| Elapsed time | ET = total time of the recording, maximum 3 min if the animal does not reach one side of the observation arena earlier | −3.53 | 5.30 × 10−3 |
| Total distance | TD = total distance travelled by the experimental animal during the recording time | −6.68 × 102 | −21.3 |
| Average speed | AS = average of dividing the distance increments by the time increments at each time frame | 7.91 × 108 | −3.41 × 105 |
| Average acceleration | AA = average of dividing the speed increments by the time increments at each time frame | −2.53 × 105 | −1.47 × 104 |
| Last coordinate | LC = value of the observation arena’s X-axis coordinate where the animal was positioned at the end of the recording, ranging between 150 at the blank side and +150 at the stimulus side | −3.68 × 103 | −18.3 |
| Choice by time | CT or XT = last coordinate divided by the elapsed time | 1.90 × 107 | −6.46 × 104 |
| Stop ratio | SR = number of 67-ms time frames with no distance increment divided by the total number of time frames of the recording | −9.04 × 105 | −7.53 × 103 |
| Turn ratio | TR = number of time frames when the animal turned divided by total number of time frames of the recording. A deviation from the path is considered as turn if the angle increment between two consecutive time frames exceeds 9°, i.e., 5% of a full, 180° turn | −5.33 × 1010 | 2.04 × 107 |
| Erratic movement | EM = the summed product of the turn angle and the distance per time frame | 29.1 | 0.435 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saadi, S.; Bakkali, N.; Martín-Blázquez, R.; Badih, A.; Bakkali, M. The Multivariate Regression Models Suggested as Standardising Tools for Categorising Solitarious and Gregarious Groups of the Main Pest Locust, Schistocerca gregaria, Produce Reproducible Results. Insects 2024, 15, 102. https://doi.org/10.3390/insects15020102
Saadi S, Bakkali N, Martín-Blázquez R, Badih A, Bakkali M. The Multivariate Regression Models Suggested as Standardising Tools for Categorising Solitarious and Gregarious Groups of the Main Pest Locust, Schistocerca gregaria, Produce Reproducible Results. Insects. 2024; 15(2):102. https://doi.org/10.3390/insects15020102
Chicago/Turabian StyleSaadi, Somia, Noureddine Bakkali, Rubén Martín-Blázquez, Abdelmounim Badih, and Mohammed Bakkali. 2024. "The Multivariate Regression Models Suggested as Standardising Tools for Categorising Solitarious and Gregarious Groups of the Main Pest Locust, Schistocerca gregaria, Produce Reproducible Results" Insects 15, no. 2: 102. https://doi.org/10.3390/insects15020102
APA StyleSaadi, S., Bakkali, N., Martín-Blázquez, R., Badih, A., & Bakkali, M. (2024). The Multivariate Regression Models Suggested as Standardising Tools for Categorising Solitarious and Gregarious Groups of the Main Pest Locust, Schistocerca gregaria, Produce Reproducible Results. Insects, 15(2), 102. https://doi.org/10.3390/insects15020102






