Biomechanical Insights in Ancient Greek Combat Sports: A Static Analysis of Selected Pottery Depictions
Abstract
1. Introduction
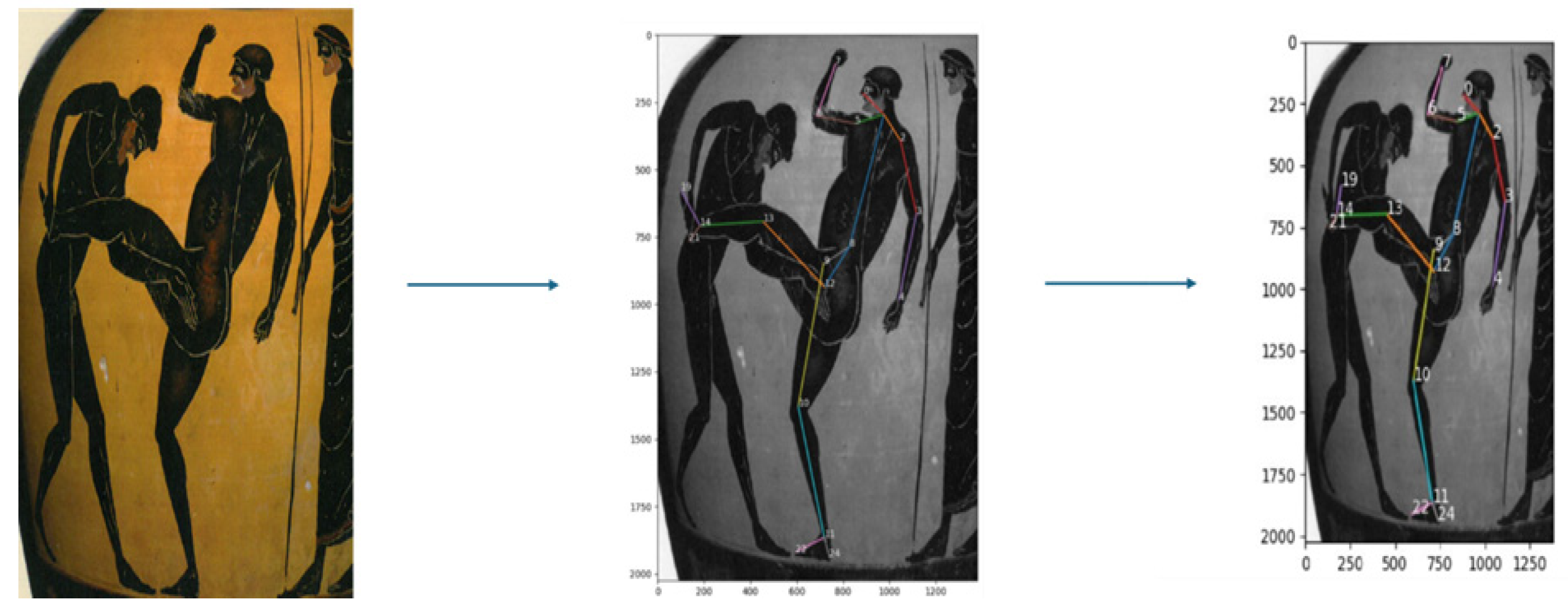
2. Methods
2.1. Segmental and Total CoM
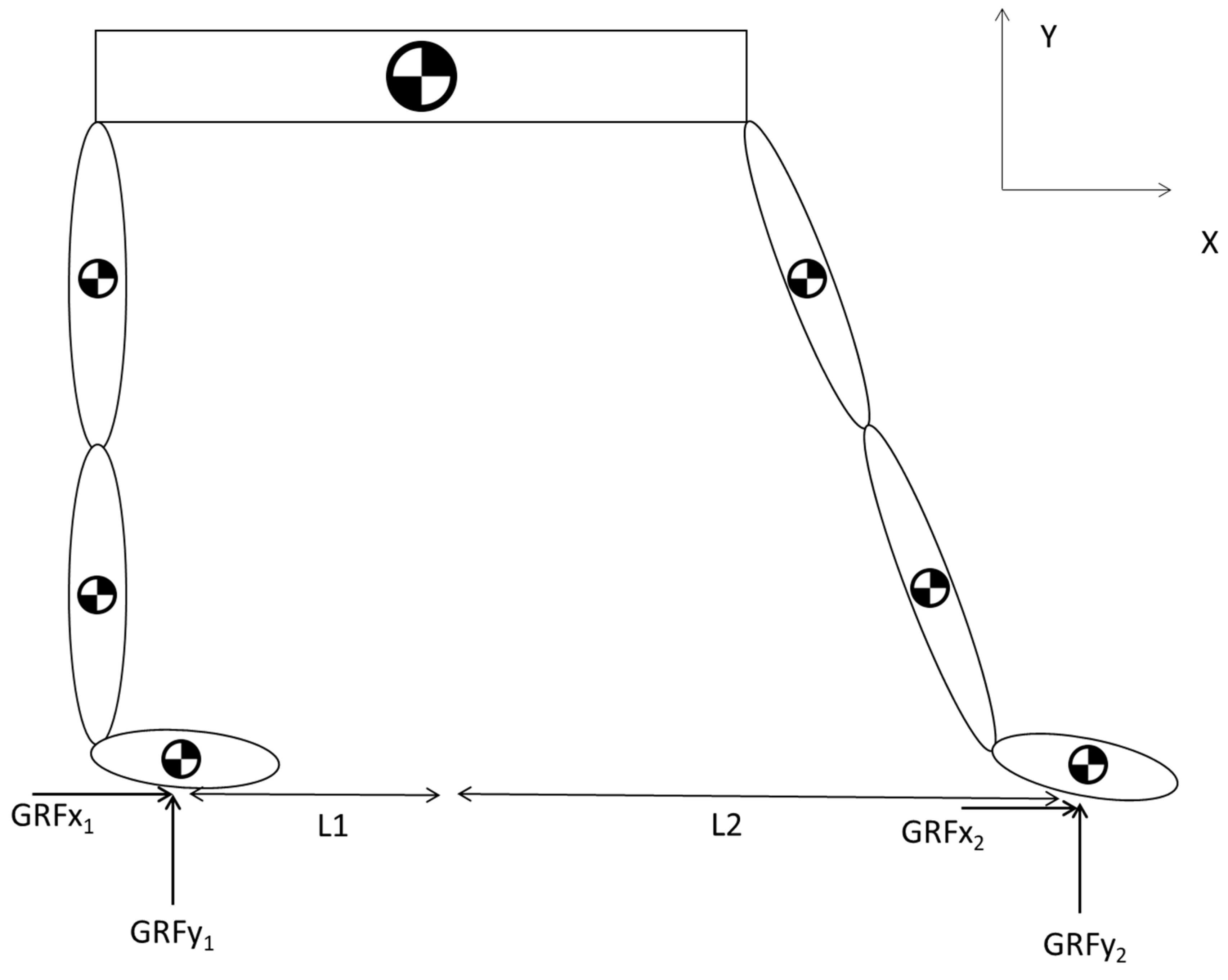
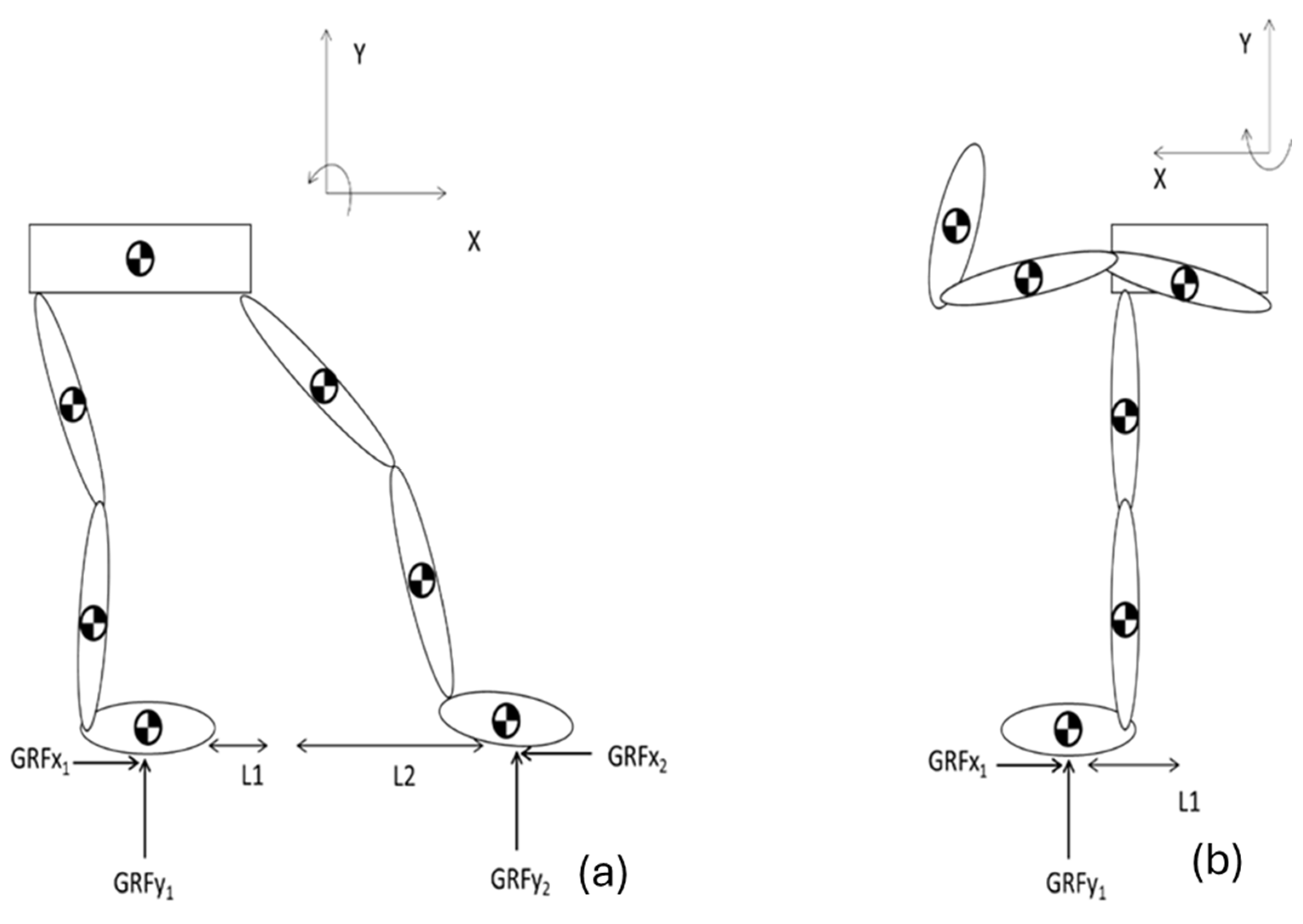
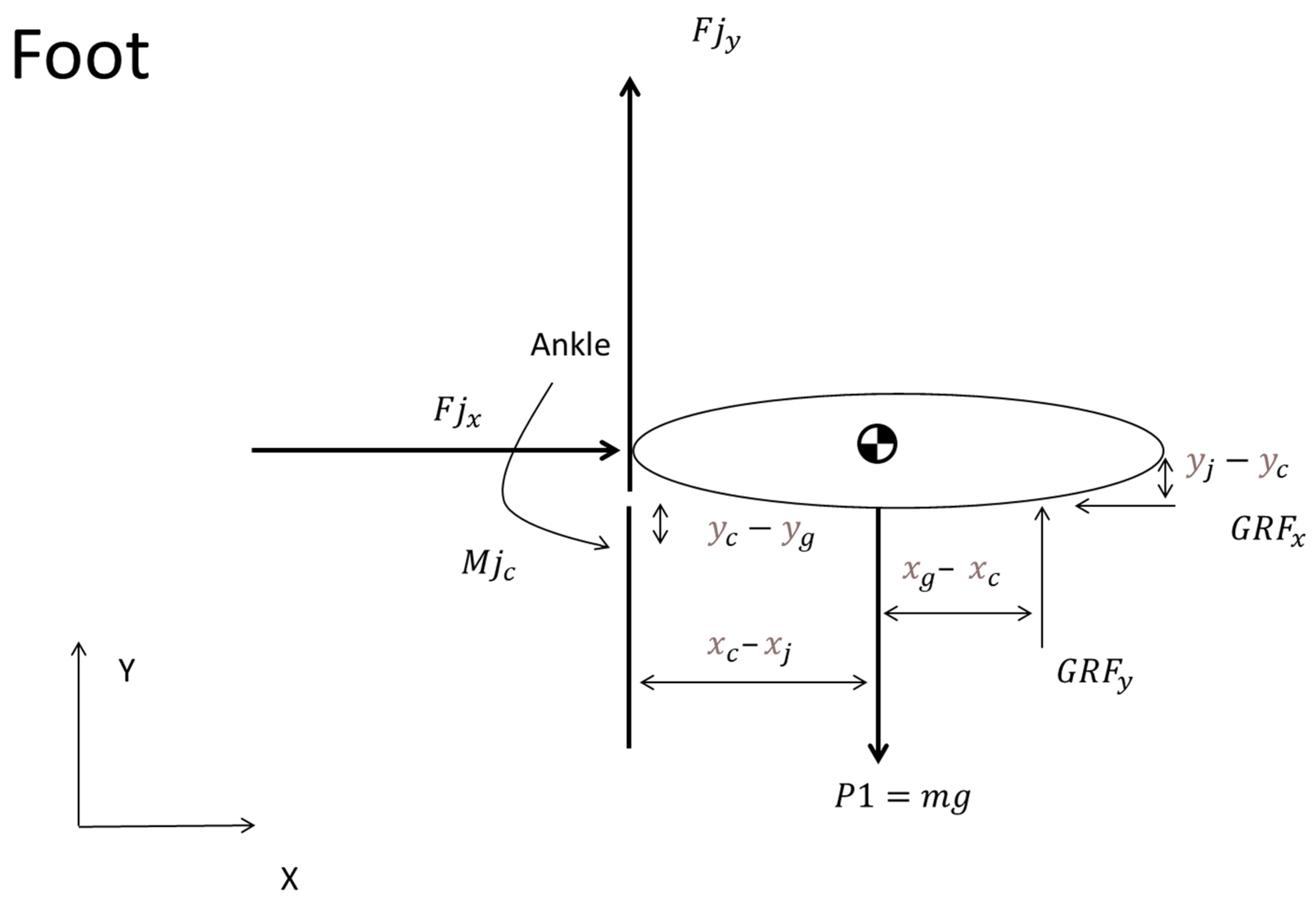
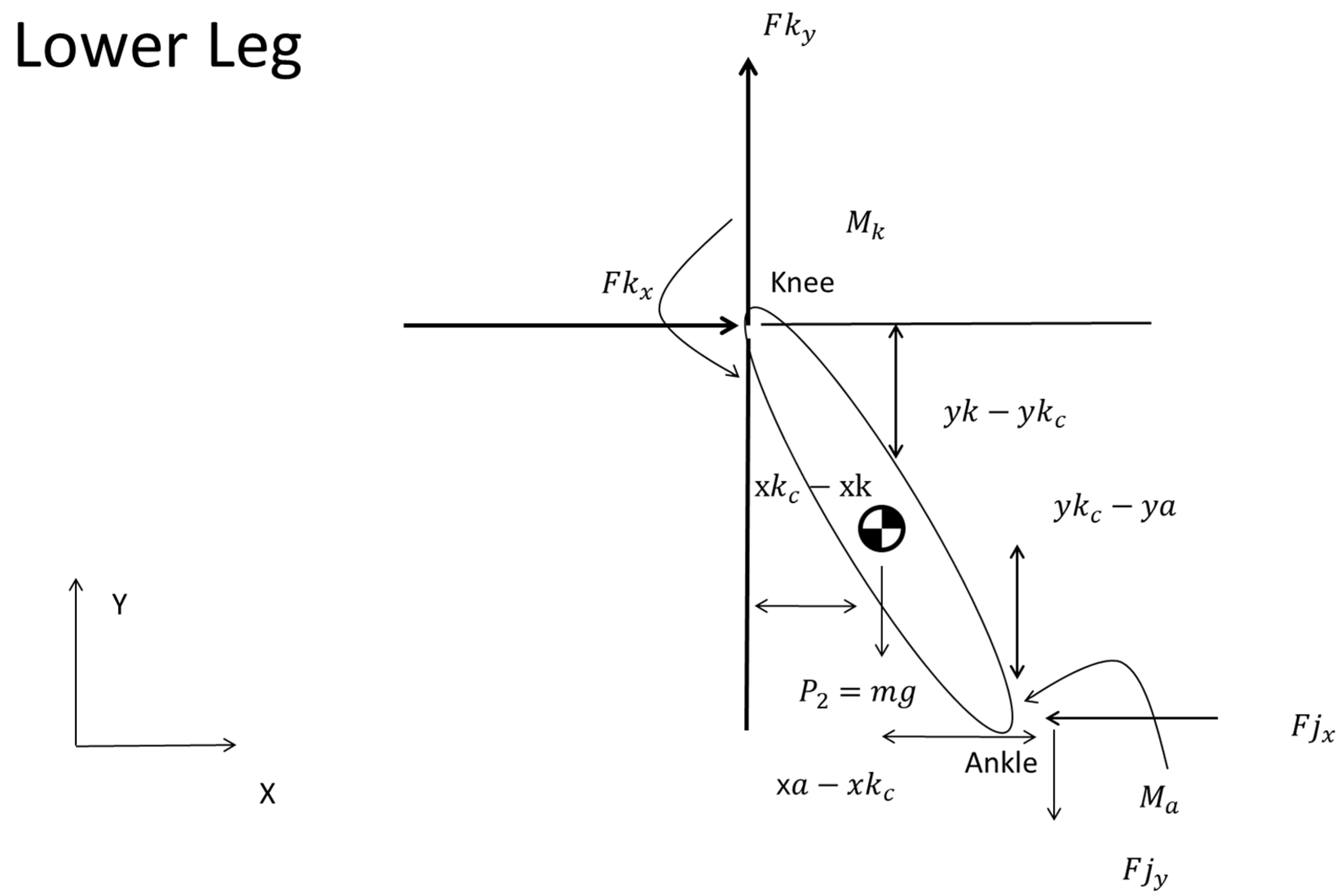
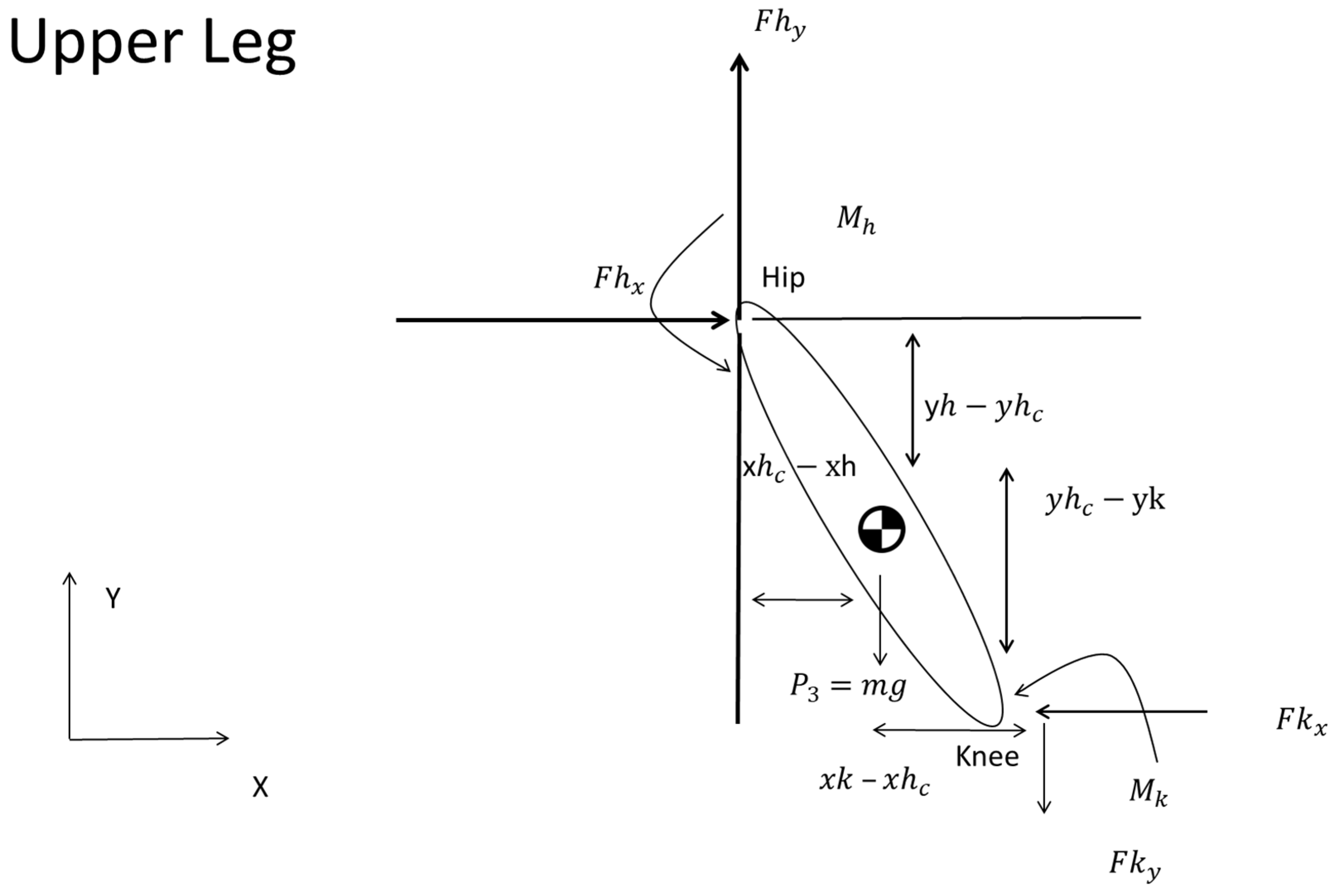
2.2. Static Multi-Segmental Model of the Lower Extremity
2.3. Anthropometric Parameters of a Hypothetical Male Athlete Model
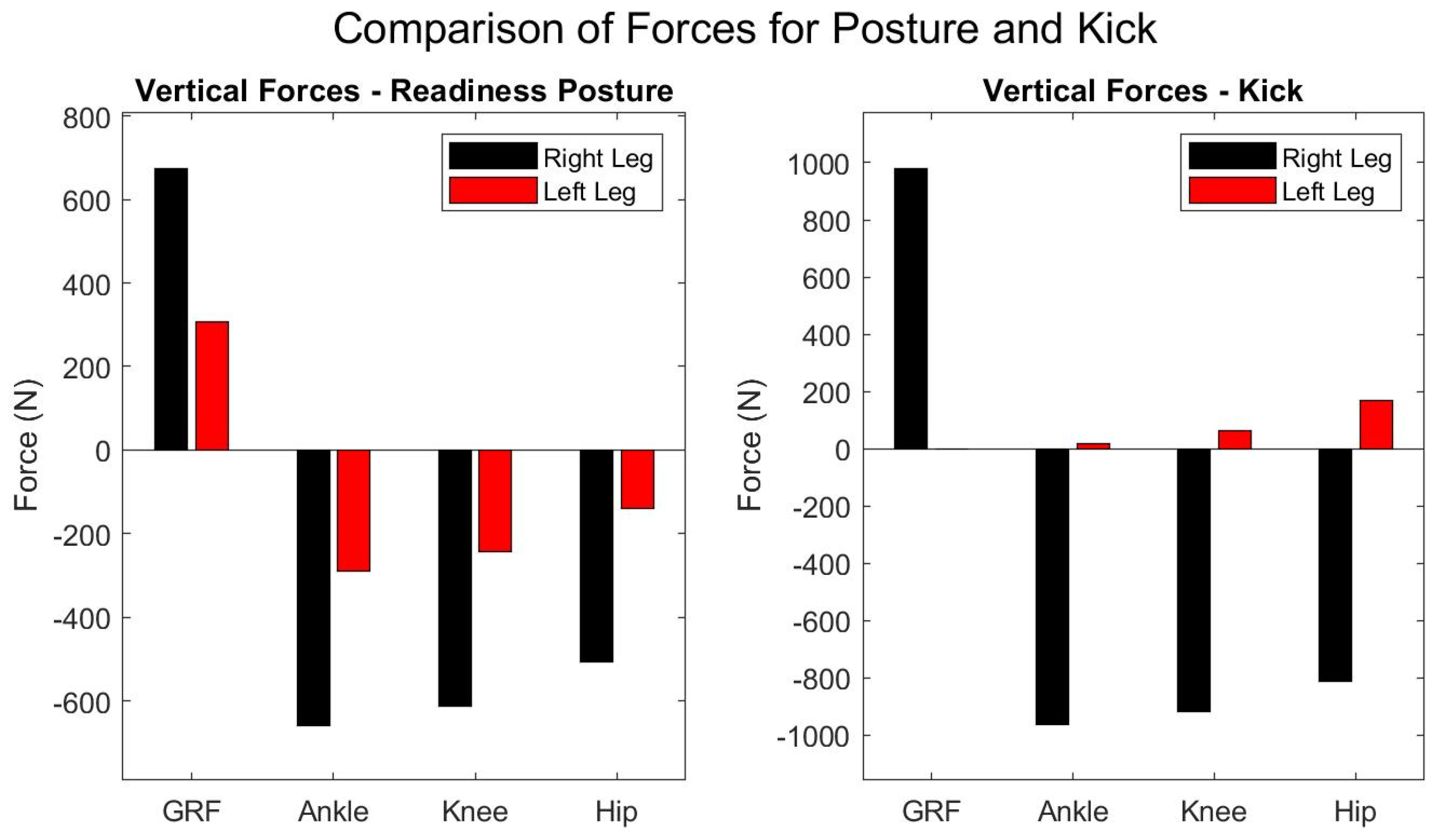
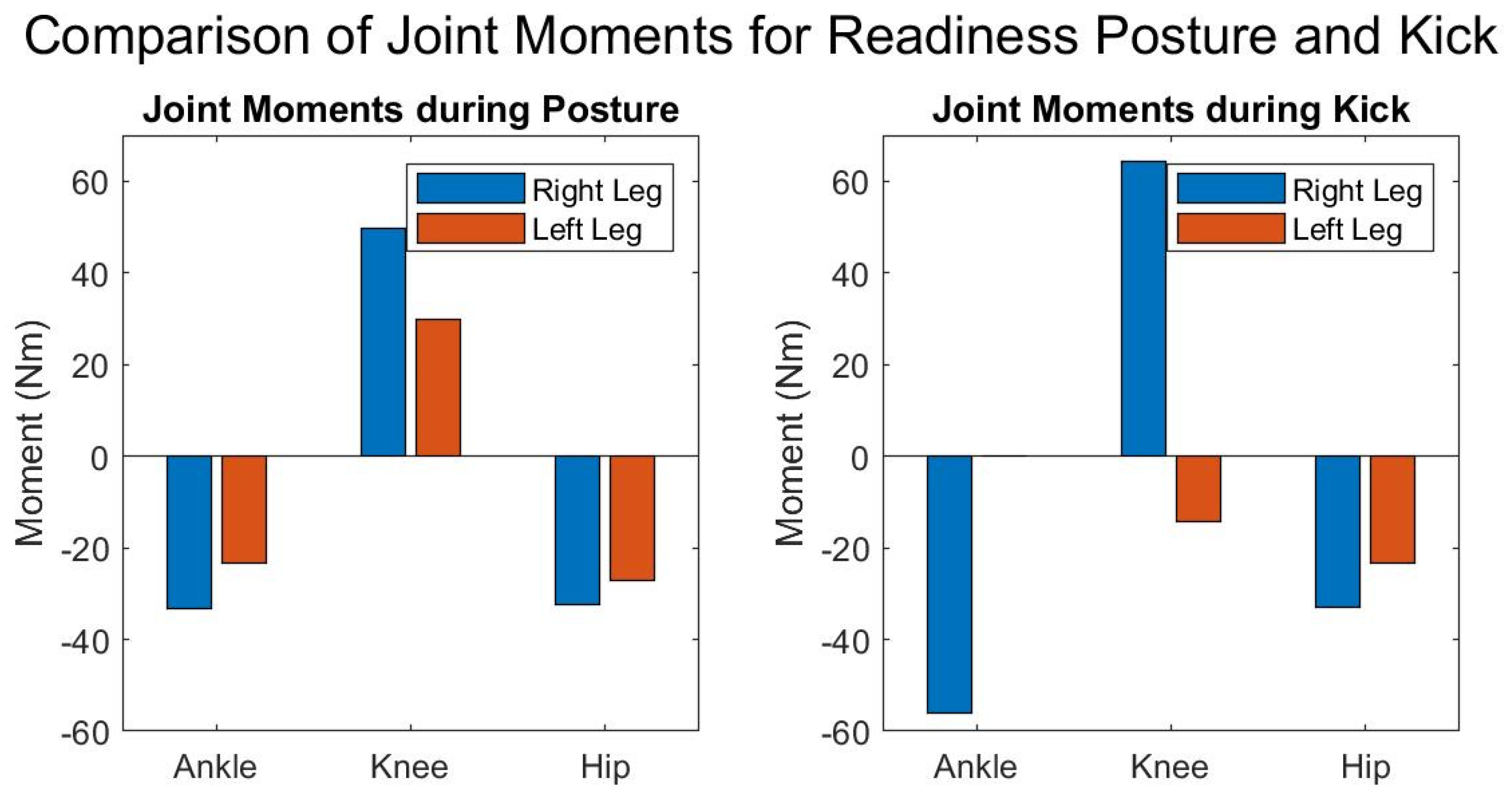
3. Results
Kick Posture
4. Discussion
4.1. Considerations of the Examined Postures Weight Distribution and Ground Reaction Forces
4.2. Strategic and Training Implications of the Analysis in Athletic Performance
4.3. Limitations
5. Conclusions
6. Practical Applications
Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- van Middendorp, J.J.; Sanchez, G.M.; Burridge, A.L. The Edwin Smith papyrus: A clinical reappraisal of the oldest known document on spinal injuries. Eur. Spine J. 2010, 19, 1815–1823. [Google Scholar] [CrossRef] [PubMed]
- Jacques, J. Greek Medicine from Hippocrates to Galen: Selected Papers; van der Eijk, P., Ed.; Translated by Allies, N.; Brill: Leiden, The Netherlands, 2012; Volume 40, pp. 4–9. [Google Scholar]
- Nussbaum, M.C. Aristotle’s De Motu Animalium; Princeton University Press: Princeton, NJ, USA, 1979; pp. 48–50. [Google Scholar]
- Friedman, H.; Miller, P.J. Reconstruction of the Ancient Greek Long Jump—An Opportunity for Multidisciplinary Collaboration. EXARC J. 2017, 3. Available online: https://exarc.net/ark:/88735/10300 (accessed on 25 November 2024).
- Bourantanis, A.G.; Nomikos, N.N.; Trompoukis, C.C.; Wang, W.W. Estimating Athletes’ Centre of Mass as Presented on Ancient Greek Pottery Depictions. Am. J. Sports Sci. Med. 2022, 10, 12–16. [Google Scholar] [CrossRef]
- Kiers, K.; Ellenberger, L.; Jermann, J.; Oberle, F.; Frey, W.O.; Spörri, J. Prospective Study on Dynamic Postural Stability in Youth Competitive Alpine Skiers: Test-Retest Reliability and Reference Values as a Function of Sex, Age and Biological Maturation. Front. Physiol. 2022, 13, 804165. [Google Scholar] [CrossRef] [PubMed]
- Hrysomallis, C. Balance Ability and Athletic Performance. Sports Med. 2011, 41, 221–232. [Google Scholar] [CrossRef]
- Hrysomallis, C. Relationship Between Balance Ability, Training and Sports Injury Risk. Sports Med. 2007, 37, 547–556. [Google Scholar] [CrossRef]
- Sacripanti, A. Judo: Biomechanical Science for Ijf Academy; ISBN: 978-99957-1-518-2. 2022. Available online: https://78884ca60822a34fb0e6-082b8fd5551e97bc65e327988b444396.ssl.cf3.rackcdn.com/up/2022/01/Science_of_teaching_and_coachi-1641301820.pdf (accessed on 27 October 2024).
- Clancy, C.E.; Gatti, A.A.; Ong, C.F.; Maly, M.R.; Delp, S.L. Muscle-driven simulations and experimental data of cycling. Sci. Rep. 2023, 13, 21534. [Google Scholar] [CrossRef]
- Prilutsky, B.I.; Zatsiorsky, V.M. Optimization-Based Models of Muscle Coordination. Exerc. Sport Sci. Rev. 2002, 30, 32–38. [Google Scholar] [CrossRef]
- Dembia, C.L.; Bianco, N.A.; Falisse, A.; Hicks, J.L.; Delp, S.L. OpenSim Moco: Musculoskeletal optimal control. PLoS Comput. Biol. 2019, 16, e1008493. [Google Scholar] [CrossRef]
- Uhlrich, S.D.; Jackson, R.W.; Seth, A.; Kolesar, J.A.; Delp, S.L. Muscle coordination retraining inspired by musculoskeletal simulations reduces knee contact force. Sci. Rep. 2022, 12, 9842. [Google Scholar] [CrossRef]
- Bourantanis, A. A Static Analysis of Emblazonments Depicting Ancient Greek Pankration; University of Dundee: Dundee, UK, 2021. [Google Scholar]
- Bourantanis, A. Biomechanical Analysis of the Movement of the Ancient Greek Combat Sports’ Athletes in Classical Antiquity. Master’s Thesis, University of Dundee, Dundee, UK, 2024. [Google Scholar]
- Swaddling, J. The Ancient Olympic Games, 2nd ed.; British Museum: London, UK, 1999. [Google Scholar]
- Wren, T.A.L.; Isakov, P.; Rethlefsen, S.A. Comparison of kinematics between Theia markerless and conventional marker-based gait analysis in clinical patients. Gait Posture 2023, 104, 9–14. [Google Scholar] [CrossRef] [PubMed]
- Lam, W.W.T.; Tang, Y.-M.; Fong, K.N.K. A systematic review of the applications of markerless motion capture (MMC) technology for clinical measurement in rehabilitation. J. Neuroeng. Rehabil. 2023, 20, 57. [Google Scholar] [CrossRef] [PubMed]
- Wade, L.; Needham, L.; McGuigan, P.M.; Bilzon, J.L.J. Applications and limitations of current markerless motion capture methods for clinical gait biomechanics. PeerJ 2022, 10, e12995. [Google Scholar] [CrossRef] [PubMed]
- Cao, Z.; Hidalgo, G.; Simon, T.; Wei, S.-E.; Sheikh, Y. OpenPose: Realtime Multi-Person 2D Pose Estimation Using Part Affinity Fields. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 43, 172–186. [Google Scholar] [CrossRef]
- Ludwig, K.; Einfalt, M.; Lienhart, R. Robust Estimation of Flight Parameters for SKI Jumpers. In Proceedings of the 2020 IEEE International Conference on Multimedia & Expo Workshops (ICMEW), London, UK, 6–10 July 2020; pp. 1–6. [Google Scholar]
- Nakai, M.; Tsunoda, Y.; Hayashi, H.; Murakoshi, H. Prediction of Basketball Free Throw Shooting by OpenPose. In Proceedings of the JSAI-isAI Workshops, Yokohama, Japan, 12–14 November 2018. [Google Scholar]
- Mendes-Neves, T.; Meireles, L.i.; Mendes-Moreira, J. A Survey of Advanced Computer Vision Techniques for Sports. arXiv 2023, arXiv:2301.07583. [Google Scholar]
- Georgiou, A.V. Pankration: An Olympic Combat Sport, 1st ed.; Xlibris Us: Bloomington, Indiana, 2005. [Google Scholar]
- Linton, F.; Kobayashi, S.; Nomizu, K. Foundations of Differential Geometry, Volume I. Am. Math. Mon. 1965, 72, 1147. [Google Scholar] [CrossRef]
- Huang, J.; Chen, L.; Izumiya, S.; Pei, D. Geometry of special curves and surfaces in 3-space form. J. Geom. Phys. 2019, 136, 31–38. [Google Scholar] [CrossRef]
- Corradi, G.; Munar, E. 510 The Curvature Effect. In The Oxford Handbook of Empirical Aesthetics; Nadal, M., Vartanian, O., Eds.; Oxford University Press: Oxford, UK, 2022. [Google Scholar]
- Pérez-Castilla, A.; García-Pinillos, F. Sports Biomechanics Applied to Performance Optimization. Appl. Sci. 2024, 14, 3590. [Google Scholar] [CrossRef]
- Fletcher, J.R.; Gallinger, T.L.; Prince, F. How Can Biomechanics Improve Physical Preparation and Performance in Paralympic Athletes? A Narrative Review. Sports 2021, 9, 89. [Google Scholar] [CrossRef]
- Majumdar, A.S.; Robergs, R.A. The Science of Speed: Determinants of Performance in the 100 m Sprint. Int. J. Sports Sci. Coach. 2011, 6, 479–493. [Google Scholar] [CrossRef]
- Bonas, A. On the Kicking Techniques of Pankration. Int. J. Hist. Sport 2023, 40, 1307–1320. [Google Scholar] [CrossRef]
- Goldsheyder, D.; Özkaya, N.; Nordin, M.; Leger, D. Fundamentals of Biomechanics: Equilibrium, Motion, and Deformation, 2016th ed.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Özkaya, N.; Leger, D.; Goldsheyder, D.; Nordin, M. Fundamentals of Biomechanics: Equilibrium, Motion, and Deformation, 2017th ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Wang, W.; Arnold, G.; Drew, T.; Gibbs, S.; Christie, I. Distance Learning Section. In Modelling Techniques; Department of Orthopaedic & Trauma Surgery, University of Dundee: Dundee, UK, 2012. [Google Scholar]
- Wang, W. Unit 3—Properties of Joints and Limbs; Drew, T., Gibbs, S., Abboud, R., Eds.; Christie, I., Illustrator; Institute of Motion Analysis and Research, College of Medicine, Dentistry and Nursing, University of Dundee: Dundee, UK, 2009. [Google Scholar]
- Winter, D.A. Biomechanics and Motor Control of Human Movement; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Poliakoff, M. Combat Sports in the Ancient World; Yale University Press: New Haven, CT, USA, 1975. [Google Scholar]
- Meriam, J.L.; Kraige, L.G. Engineering Mechanics: Statics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; Volume 1. [Google Scholar]
- Goldstein, H. Classical Mechanics; Columbia University: New York, NY, USA, 2011. [Google Scholar]
- Roberts, T.J. Contribution of elastic tissues to the mechanics and energetics of muscle function during movement. J. Exp. Biol. 2016, 219, 266–275. [Google Scholar] [CrossRef]
- Herbert, R.D.; Gandevia, S.C. Editorial: Passive Properties of Muscle. J. Appl. Physiol. 2019, 126, 1442–1444. [Google Scholar] [CrossRef]
- Gajdosik, R.L. Passive extensibility of skeletal muscle: Review of the literature with clinical implications. Clin. Biomech. 2001, 16, 87–101. [Google Scholar] [CrossRef] [PubMed]
- Dinu, D.; Louis, J.B. Biomechanical Analysis of the Cross, Hook, and Uppercut in Junior vs. Elite Boxers: Implications for Training and Talent Identification. Front. Sports Act. Living 2020, 2, 598861. [Google Scholar] [CrossRef] [PubMed]
- Barnamehei, H.; Khazaee, F.; Safaei, M.A.; Jabari, H.; Golfeshan, N.; Barnamehei, M.; Rezaei, A.; Kharazi, M.R.; Naghavi, N. Motor learning and training strategy effect on motor control; Comparison between Taekwondo and Karate front kick (Ap Chagi and Mae Geri). Int. J. Martial Arts 2020, 6, 48–65. [Google Scholar] [CrossRef]
- Andrzejewski, X.; Elbaum, L. Biomechanical Analysis of the Front Kick with the Dominant and Non-Dominant Limb in the Shito-Ryu Style of Karate. In ISBS 2005. Beijing, China: Department of Physical Therapy; Florida International University: Miami, FL, USA, 2005. [Google Scholar]
- Weerawat, T.; Jiraphon, S.; Kontorn, C.; Sorada, K. Motion Analysis of Kick Mechanism Using in Muay Thai Matial Art. IOP Conf. Ser. Mater. Sci. Eng. 2020, 717, 012023. [Google Scholar] [CrossRef]
- 47. Lucian. Anacharsis. In Lucian, Volume II: Anacharsis, Menippus, and Other Works; Harmon, A.M., Ed.; Harvard University Press: Cambridge, MA, USA, 1925; pp. 3–125. [Google Scholar]
- Poliakoff, M.B. Studies in the Terminology of the Greek Combat Sports, Hain, Konigstein, January 1982. pp. 116–121. Available online: https://books.google.co.jp/books/about/Studies_in_the_Terminology_of_the_Greek.html?id=44NwAAAAMAAJ&redir_esc=y (accessed on 17 November 2024).
- Nishikawa, K.C. Eccentric contraction: Unraveling mechanisms of force enhancement and energy conservation. J. Exp. Biol. 2016, 219, 189–196. [Google Scholar] [CrossRef] [PubMed]
- Chiu, L.Z.F.; vonGaza, G.L.; Jean, L.M.Y. Net joint moments and muscle activation in barbell squats without and with restricted anterior leg rotation. J. Sports Sci. 2017, 35, 35–43. [Google Scholar] [CrossRef]
- Hoelbling, D.; Baca, A.; Dabnichki, P. Sequential action, power generation and balance characteristics of a martial arts kick combination. Int. J. Perform. Anal. Sport 2020, 20, 766–781. [Google Scholar] [CrossRef]
- Alexis Sobarzo Soto, D.; Aedo-Muñoz, E.A.; José Brito, C.; Miarka, B. Comparisons of Motor Actions and Biomechanical Assessments of Judo Techniques Between Female Weight Categories. J. Hum. Kinet. 2020, 75, 247–255. [Google Scholar] [CrossRef] [PubMed]
- Vagner, M.; Cleather, D.J.; Olah, V.; Vacek, J.; Šťastný, P. A Systematic Review of Dynamic Forces and Kinematic Indicators of Front and Roundhouse Kicks across Varied Conditions and Participant Experience. Sports 2023, 11, 141. [Google Scholar] [CrossRef] [PubMed]
- Jia, M.; Ma, Y.; Huang, R.; Liu, L.; Wang, Z.; Lin, S.; Peng, Q.; Xiong, J.; Zheng, W. Correlation analysis between biomechanical characteristics of lower extremities during front roundhouse kick in Taekwondo and effective scores of electronic protectors. Front. Bioeng. Biotechnol. 2024, 12, 1364095. [Google Scholar] [CrossRef] [PubMed]
- Vagner, M.; Cleather, D.J.; Kubový, P.; Hojka, V.; Šťastný, P. Kinematic Determinants of Front Kick Dynamics Across Different Loading Conditions. Mil. Med. 2021, 187, e147–e153. [Google Scholar] [CrossRef] [PubMed]
- Vagner, M.; Cleather, D.J.; Kubový, P.; Hojka, V.; Šťastný, P. Effect of strength training programs on front push kick dynamics and kinematics. Arch. Budo 2021, 17. Available online: https://research.stmarys.ac.uk/id/eprint/5722/1/14458_k1%20%28002%29.pdf (accessed on 17 November 2024).
- Socci, M.; Varde’i, C.H.; Giovannelli, M.; Cejudo-Palomo, A.; D’Elia, F.; Cruciani, A.; Izzo, R. Definition of physical-dynamic parameters in circular kick in Muay Thai through latest generation inertial sensors with a critical review of the literature. In Journal of Human Sport and Exercise—2021—Autumn Conferences of Sports Science; Universidad de Alicante: Alicante, Spain, 2021. [Google Scholar]
- Székely, G.J.; Rizzo, M.L. The Uncertainty Principle of Game Theory. Am. Math. Mon. 2007, 114, 688–702. [Google Scholar] [CrossRef]
- Theocritus. Selected Poems; Bristol Classical Press: London, UK, 1991. [Google Scholar]
- Franke, M. Signal to Act: Game Theory in Pragmatics; ILLC Dissertation Series DS-2009-11; Doctoral Thesis; University of Amsterdam: Amsterdam, The Netherlands, 2009; ISBN 978-90-5776-202-4. Chapter 1; pp. 18–20. [Google Scholar]
- Brumley, L. Misperception and Its Evolutionary Value; Monash University: Clayton, Australia, 2014. [Google Scholar]
- Trejo, K.K.; Clempner, J.B.; Poznyak, A.S. A Stackelberg security game with random strategies based on the extraproximal theoretic approach. Eng. Appl. Artif. Intell. 2015, 37, 145–153. [Google Scholar] [CrossRef]
- Mendonça, L.D.M.; Bittencourt, N.F.N.; Freire, R.L.; Campos, V.C.; Ferreira, T.V.; Silva, P.L.P. Hip external rotation isometric torque for soccer, basketball, and volleyball athletes: Normative data and asymmetry index. Braz. J. Phys. Ther. 2022, 26, 100391. [Google Scholar] [CrossRef]
- Moraux, A.; Canal, A.; Ollivier, G.; Ledoux, I.; Doppler, V.; Payan, C.; Hogrel, J.-Y. Ankle dorsi- and plantar-flexion torques measured by dynamometry in healthy subjects from 5 to 80 years. BMC Musculoskelet. Disord. 2013, 14, 104. [Google Scholar] [CrossRef]
- Galen. Hygiene, Volume I: Books 1–4; Johnston, I., Ed.; Harvard University Press: Cambridge, MA, USA, 2018; Volume 535. [Google Scholar]
- Gardiner, E.N. Wrestling. I. J. Hell. Stud. 1905, 25, 14–31. [Google Scholar] [CrossRef][Green Version]
- Galen. Galen: Selected Works; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Pożarowszczyk, B.; Pawlaczyk, W.; Smoter, M.; Zarzycki, A.; Mroczek, D.; Kumorek, M.; Witkowski, K.; Adam, K. Effects of Karate Fights on Achilles Tendon Stiffness Measured by Myotonometry. J. Hum. Kinet. 2017, 56, 93–97. [Google Scholar] [CrossRef] [PubMed]
- Trybulski, R.; Kużdżał, A.; Bichowska-Pawęska, M.; Vovkanych, A.; Kawczyński, A.; Biolik, G.; Muracki, J. Immediate Effect of Cryo-Compression Therapy on Biomechanical Properties and Perfusion of Forearm Muscles in Mixed Martial Arts Fighters. J. Clin. Med. 2024, 13, 1177. [Google Scholar] [CrossRef] [PubMed]
- Zoughari, K. Tradition du mouvement dans les écoles classiques de combat du Japon. Cipango 2008, 15, 267–273. [Google Scholar] [CrossRef]
- Zoughari, K. Budo and Koryu—Articles and Interviews; Bu Shi Shuppan Publishing: Eberswalde, Germany, 2023. [Google Scholar]


| Segment | Length (cm) |
|---|---|
| Foot | 24 |
| Lower Leg | 48 |
| Upper Leg | 50 |
| Segment | Relative Mass (%) | Centre of Mass (% from Proximal End) |
|---|---|---|
| Upper Leg | 10.7 | 43.9 |
| Lower Leg | 4.7 | 42.0 |
| Foot | 1.7 | 43.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bourantanis, A.; Nomikos, N.; Wang, W. Biomechanical Insights in Ancient Greek Combat Sports: A Static Analysis of Selected Pottery Depictions. Sports 2024, 12, 317. https://doi.org/10.3390/sports12120317
Bourantanis A, Nomikos N, Wang W. Biomechanical Insights in Ancient Greek Combat Sports: A Static Analysis of Selected Pottery Depictions. Sports. 2024; 12(12):317. https://doi.org/10.3390/sports12120317
Chicago/Turabian StyleBourantanis, Andreas, Nikitas Nomikos, and Weijie Wang. 2024. "Biomechanical Insights in Ancient Greek Combat Sports: A Static Analysis of Selected Pottery Depictions" Sports 12, no. 12: 317. https://doi.org/10.3390/sports12120317
APA StyleBourantanis, A., Nomikos, N., & Wang, W. (2024). Biomechanical Insights in Ancient Greek Combat Sports: A Static Analysis of Selected Pottery Depictions. Sports, 12(12), 317. https://doi.org/10.3390/sports12120317







