Prediction and Analysis of Tensile Properties of Austenitic Stainless Steel Using Artificial Neural Network
Abstract
1. Introduction
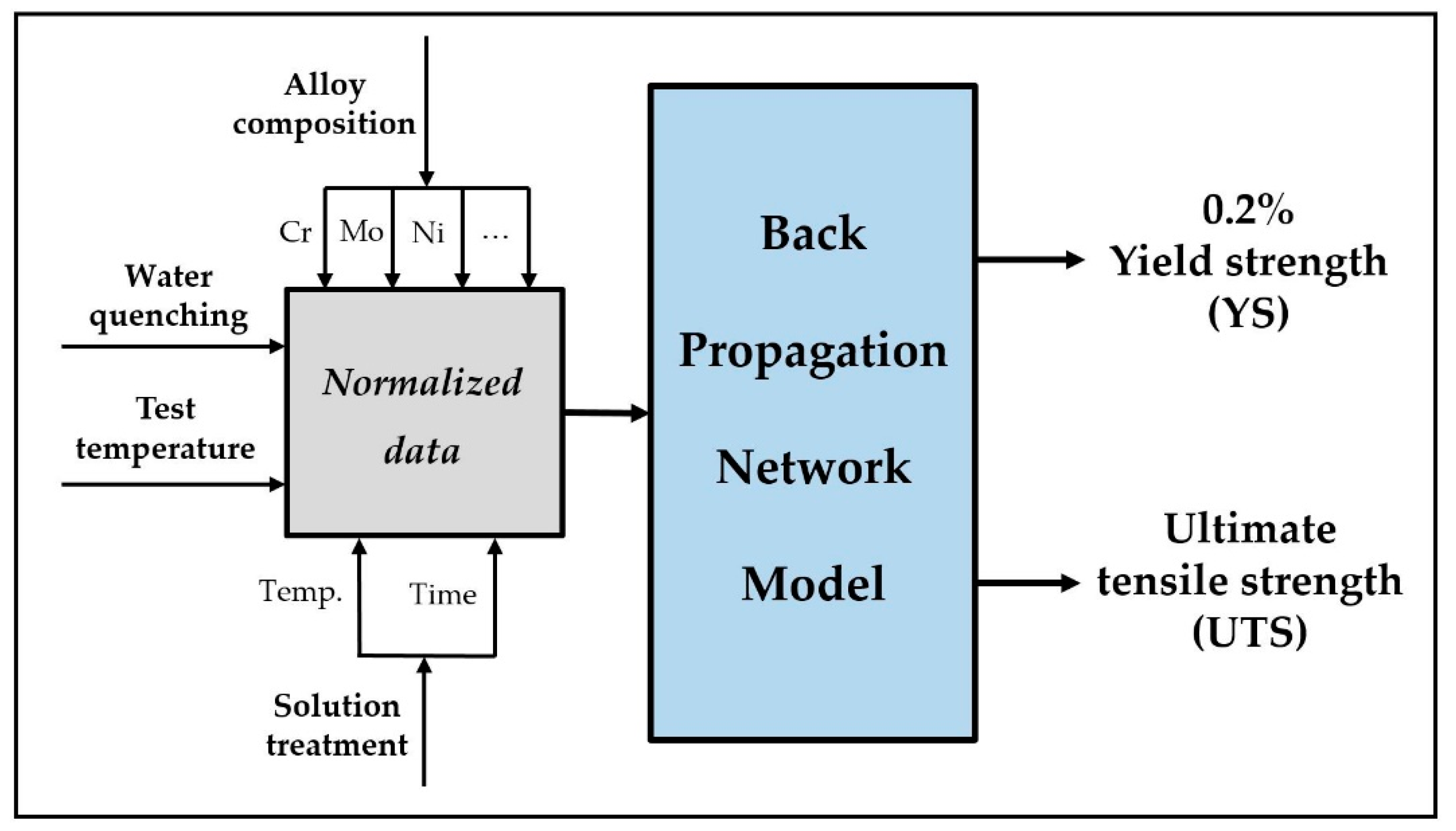
2. The Database and ANN Model
2.1. Information of the Database
2.2. Division of Data and Pre-Processing
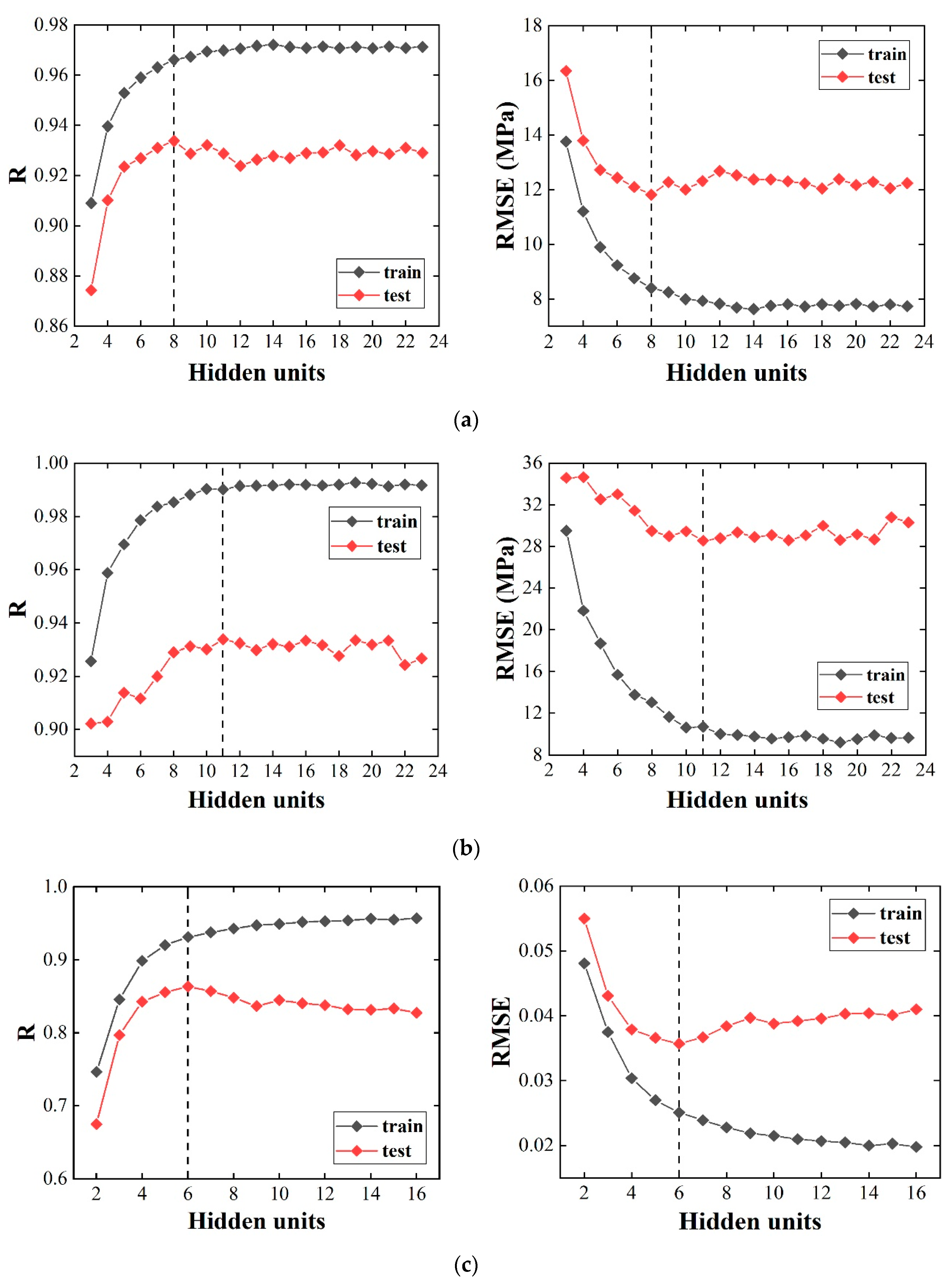
2.3. ANN Model Development
3. Results and Discussion
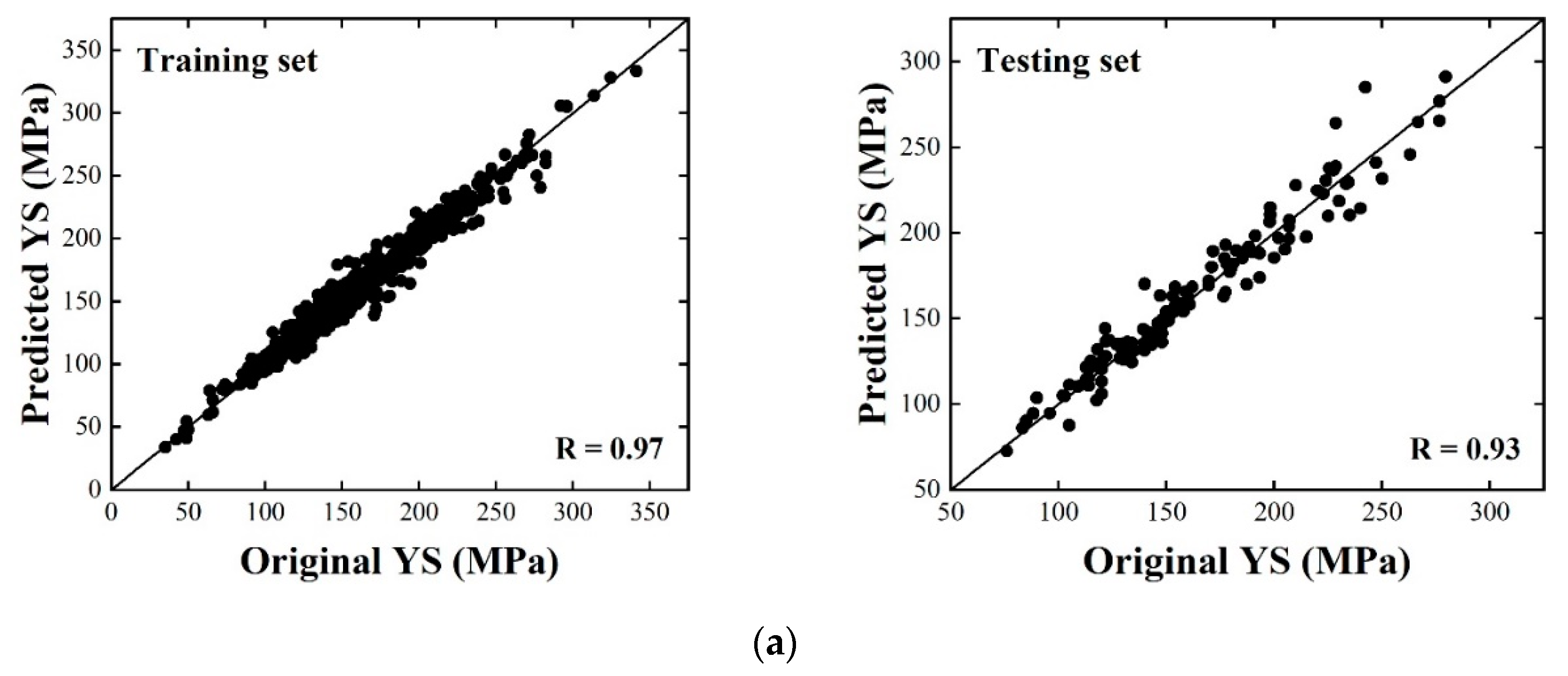
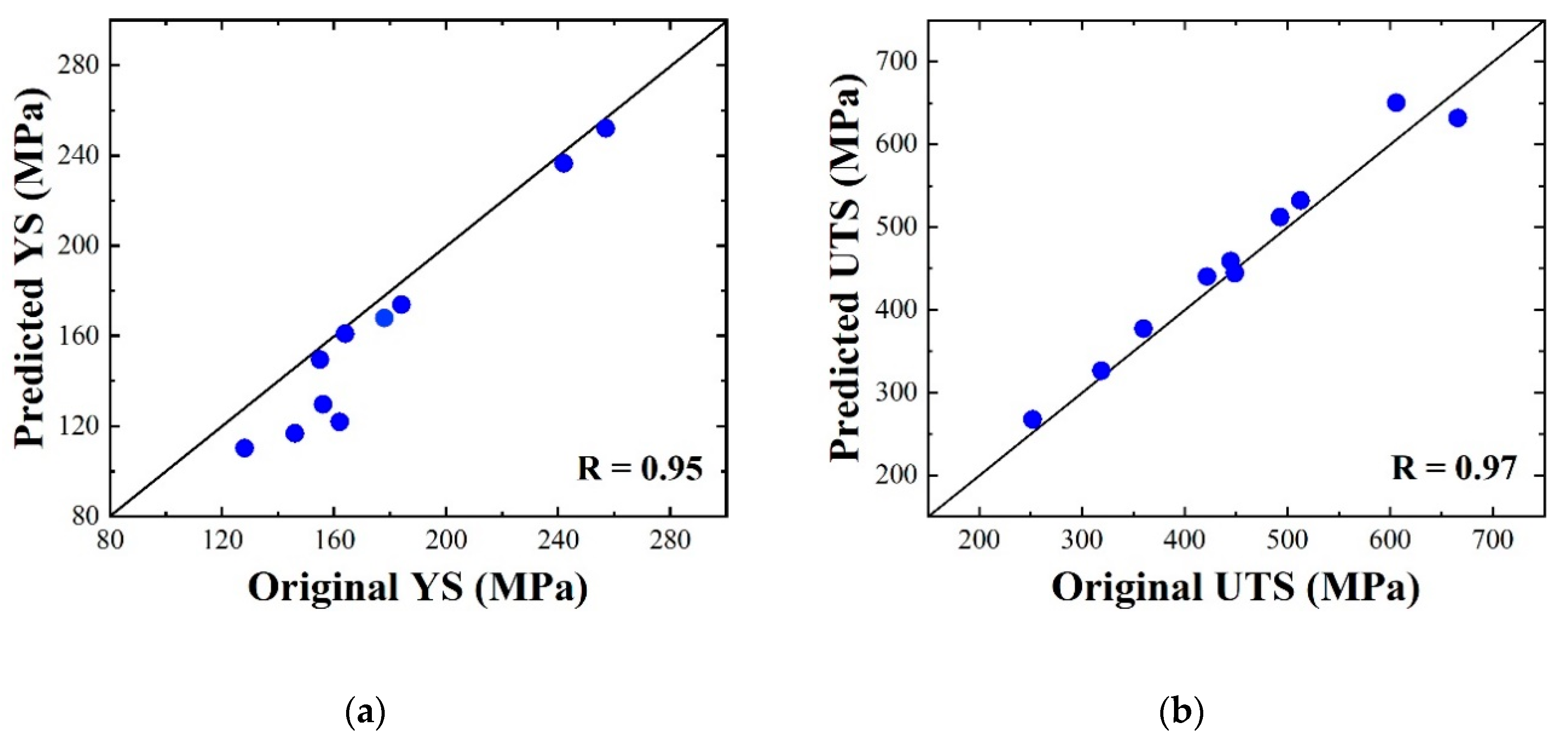
3.1. Model Performance and Validation
3.2. Feature Analysis
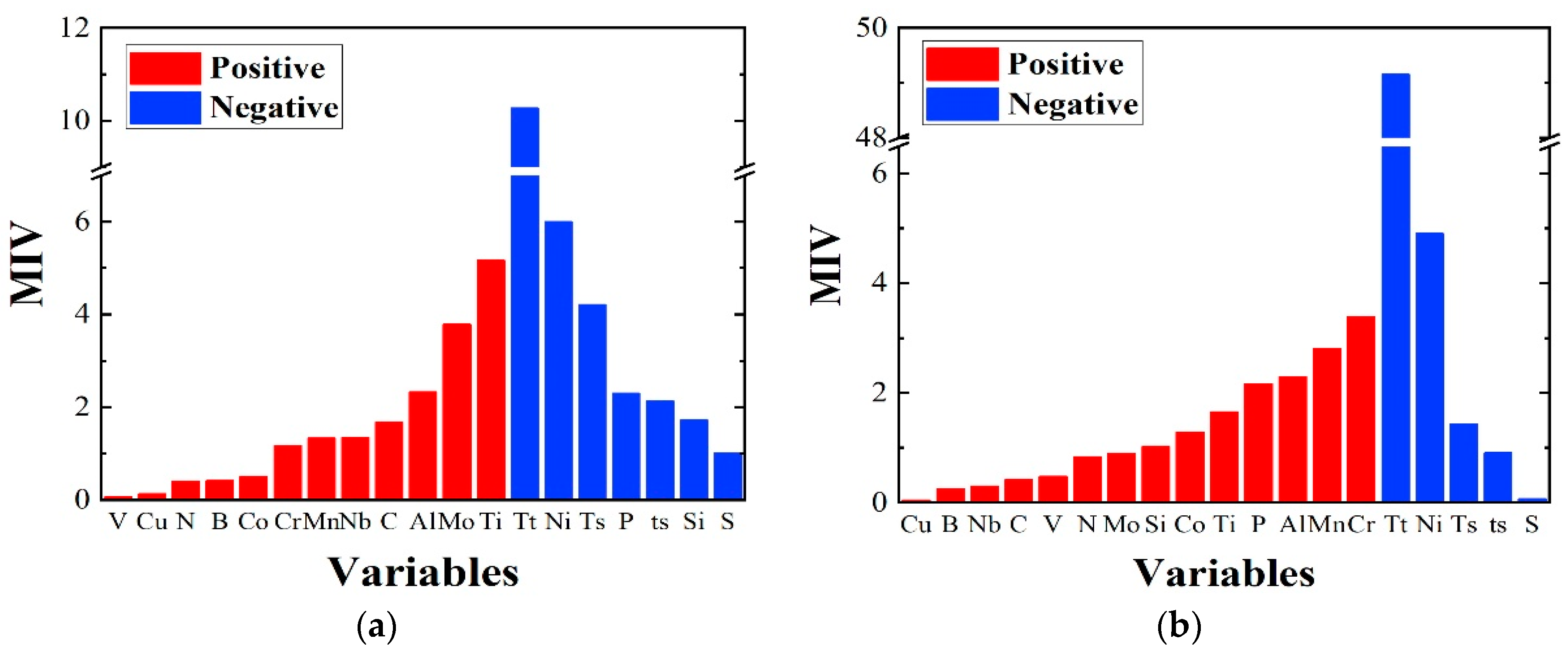
3.2.1. Mean Impact Value
- Building two new datasets by varying the magnitude of one of variables by 10% for the original training set;
- Inputting two new datasets as the simulation samples to the model and obtaining two predicted results;
- Calculating the difference value of these two predicted results, called the impact value (IV);
- According to the amount of samples in the original training set, calculating the average value of IV, that is MIV of each variable;
- Repeating the above steps in turn to get the MIV of each independent variable. It should be noted that the value of MIV indicates the positive or negative effect as well as the intensity of influence.
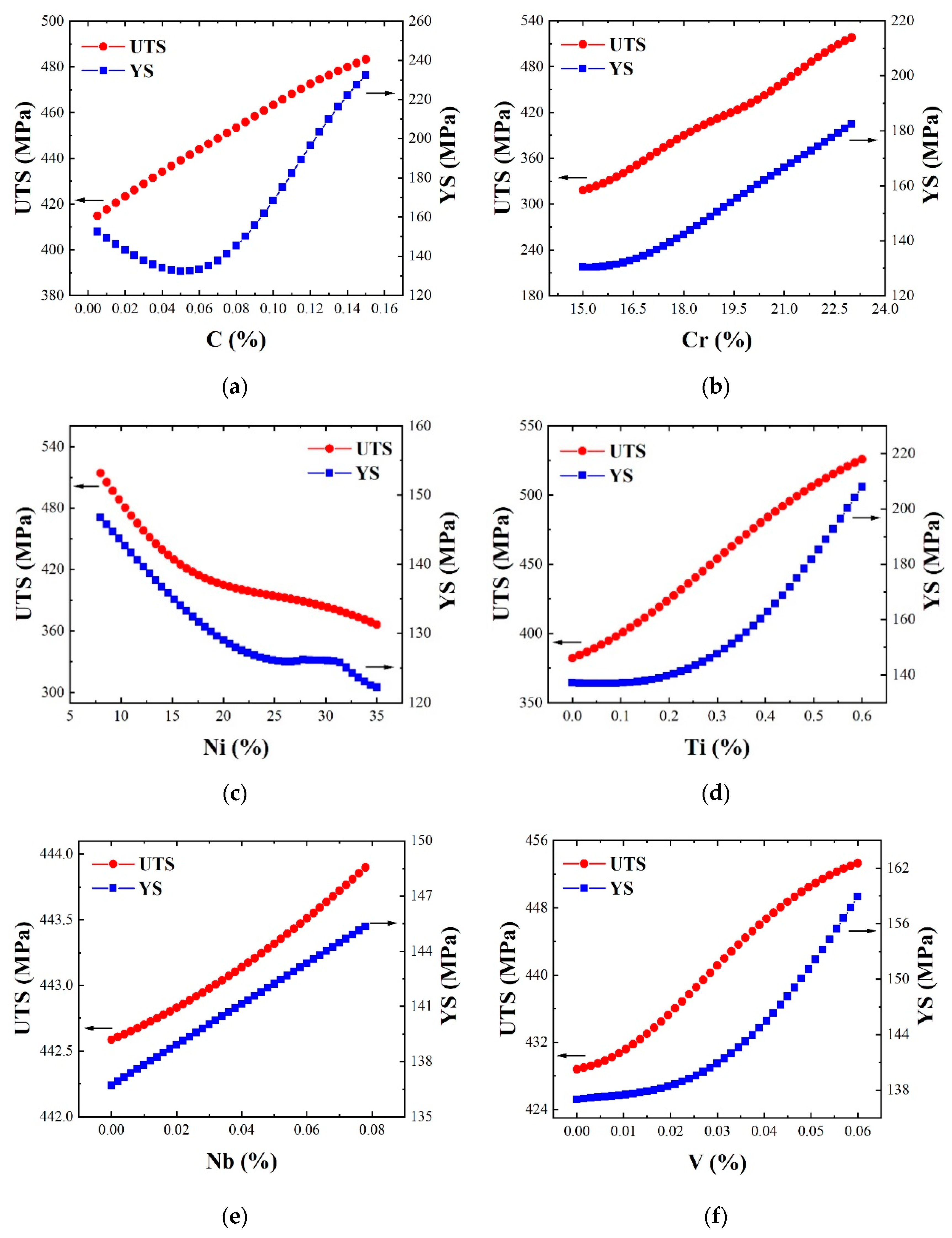
3.2.2. Influence Trends of Variables
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Variables | Range | Mean | SD |
|---|---|---|---|
| Cr | 16.39%–21.06% | 18.31% | 1.432% |
| Ni | 8.4%–34.45% | 16.4% | 9.078% |
| Mo | 0%–2.65% | 0.95% | 1.114% |
| Mn | 0.81%–1.75% | 1.39% | 0.3088% |
| Si | 0.39%–0.82% | 0.585% | 0.1194% |
| Nb | 0%–0.79% | 0.0749% | 0.2004% |
| Ti | 0%–0.53% | 0.188% | 0.2098% |
| V | 0%–0.057% | 0.0071% | 0.0166% |
| Cu | 0%–0.35% | 0.139% | 0.1101% |
| N | 0%–0.081% | 0.0197% | 0.01422% |
| C | 0.012%–0.1% | 0.0607% | 0.01556% |
| B | 0%–0.003% | 0.0005% | 0.00058% |
| P | 0%–0.038% | 0.0214% | 0.00858% |
| S | 0%–0.05% | 0.011% | 0.00829% |
| Co | 0%–0.54% | 0.115% | 0.152% |
| Al | 0%–0.52% | 0.124% | 0.188% |
| Ts | 1323–1473 K | 1378 K | 42.79 K |
| ts | 120–7200 s | 2414 s | 2397.2 s |
| Tt | 293–1273 K | 731 K | 267.42 K |
| Variables | Range | Mean | SD |
|---|---|---|---|
| Cr | 15.9%–18.3% | 17.57% | 0.4594% |
| Ni | 9.15%–12.4% | 11.1% | 1.0906% |
| Mo | 0%–2.72% | 0.856% | 1.1288% |
| Mn | 0.79%–1.71% | 1.386% | 0.2784% |
| Si | 0.29%–0.84% | 0.482% | 0.1335% |
| Nb | 0%–0.9% | 0.128% | 0.2936% |
| Ti | 0%–0.56% | 0.221% | 0.2286% |
| V | 0%–0% 2 | 0% | 0% |
| Cu | 0%–0% | 0% | 0% |
| N | 0%–0% | 0% | 0% |
| C | 0.02%–0.1% | 0.053% | 0.01167% |
| B | 0%–0.004% | 0.000081% | 0.00056% |
| P | 0%–0.04% | 0.0209% | 0.00711% |
| S | 0%–0.028% | 0.0158% | 0.00646% |
| Co | 0%–0% | 0% | 0% |
| Al | 0%–0% | 0% | 0% |
| Ts | 1293–1403 K | 1348 K | 32.7514 K |
| ts | 120–3600 s | 2117 s | 1149.61 s |
| Tt | 293–973 K | 626 K | 221.568 K |
| Variables | No.15 (SUS 316) | No.42 (SUS 304) |
|---|---|---|
| Cr | 17.05% | 18.53% |
| Ni | 12.6% | 9.1% |
| Mo | 2.24% | 0.12% |
| Mn | 1.1% | 0.88% |
| Si | 0.7% | 0.54% |
| Nb | 0.001% | 0% |
| Ti | 0.03% | 0.02% |
| V | 0% | 0% |
| Cu | 0.31% | 0.06% |
| N | 0.017% | 0.023% |
| C | 0.05% | 0.05% |
| B | 0.003% | 0% |
| P | 0.033% | 0.029% |
| S | 0.003% | 0.01% |
| Co | 0% | 0.21% |
| Al | 0.02% | 0.023% |
| Ts | 1373 K | 1373 K |
| ts | 1800 s | 1800 s |
| Water or air quenching | Water quenching (label: 1) | Water quenching (label: 1) |
| Tt | 298, 673, 773, 873, 973 K | 298, 673, 773, 873, 973 K |
References
- Callister, W.D.; Rethwisch, D.G. Materials Science and Engineering: An Introduction; John Wiley & Sons: New York, NY, USA, 2007; Volume 7. [Google Scholar]
- Krauss, G. Steels: Processing, Structure, and Performance; ASM International: Russell, OH, USA, 2015. [Google Scholar]
- Reifsnider, K.L.; Tamuzs, V. On nonlinear behavior in brittle heterogeneous materials. Compos. Sci. Technol. 2006, 66, 2473–2478. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, T. Materials discovery and design using machine learning. J. Mater. 2017, 3, 159–177. [Google Scholar] [CrossRef]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Zurada, J.M. Introduction to Artificial Neural Systems; West Publishing Company: St. Paul, MN, USA, 1992; Volume 8. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Rokach, L.; Maimon, O.Z. Data Mining with Decision Trees: Theory and Applications; World Scientific: Singapore, 2008; Volume 69. [Google Scholar]
- Council, N.R. Integrated Computational Materials Engineering: A Transformational Discipline for Improved Competitiveness and National Security; National Academies Press: Washington, DC, USA, 2008. [Google Scholar]
- Kalidindi, S.R.; Niezgoda, S.R. Microstructure informatics using higher-order statistics and efficient data-mining protocols. Jom 2011, 63, 34–41. [Google Scholar] [CrossRef]
- Rajan, K. Materials informatics. Mater. Today 2005, 8, 38–45. [Google Scholar] [CrossRef]
- Ward, L.; O’Keeffe, S.C. A machine learning approach for engineering bulk metallic glass alloys. Acta Mater. 2018, 159, 102–111. [Google Scholar] [CrossRef]
- Xue, D.; Balachandran, P.V. Accelerated search for materials with targeted properties by adaptive design. Nat. Commun. 2016, 7, 11241. [Google Scholar] [CrossRef]
- Lin, Y.; Zhang, J. Application of neural networks to predict the elevated temperature flow behavior of a low alloy steel. Comput. Mater. Sci. 2008, 43, 752–758. [Google Scholar] [CrossRef]
- Murugesan, M.; Sajjad, M. Hybrid Machine Learning Optimization Approach to Predict Hot Deformation Behavior of Medium Carbon Steel Material. Metals 2019, 9, 1315. [Google Scholar] [CrossRef]
- Kurt, H.; Oduncuoglu, M. A mathematical formulation to estimate the effect of grain refiners on the ultimate tensile strength of Al-Zn-Mg-Cu alloys. Metals 2015, 5, 836–849. [Google Scholar] [CrossRef]
- Mannodi-Kanakkithodi, A.; Pilania, G. Machine learning strategy for accelerated design of polymer dielectrics. Sci. Rep. 2016, 6, 20952. [Google Scholar] [CrossRef] [PubMed]
- Irani, K.B.; Cheng, J. Applying machine learning to semiconductor manufacturing. IEEE Expert 1993, 8, 41–47. [Google Scholar] [CrossRef]
- Yu, L.; Zunger, A. Identification of potential photovoltaic absorbers based on first-principles spectroscopic screening of materials. Phys. Rev. Lett. 2012, 108, 068701. [Google Scholar] [CrossRef] [PubMed]
- Mayer-Schönberger, V.; Cukier, K. Big Data: A Revolution that Will Transform How We Live, Work, and Think; Houghton Mifflin Harcourt: Boston, MA, USA, 2013. [Google Scholar]
- NIMS MatNavi. Available online: https://mits.nims.go.jp/index_en.html (accessed on 10 December 2019).
- MatWeb Material Property Data. Available online: http://www.matweb.com/ (accessed on 15 July 2019).
- Matmatch. Available online: https://matmatch.com/ (accessed on 22 July 2019).
- Agrawal, A.; Deshpande, P.D. Exploration of data science techniques to predict fatigue strength of steel from composition and processing parameters. Integr. Mater. Manuf. Innov. 2014, 3, 90–108. [Google Scholar] [CrossRef]
- Sourmail, T.; Bhadeshia, H. Neural network model of creep strength of austenitic stainless steels. Mater. Sci. Technol. 2002, 18, 655–663. [Google Scholar] [CrossRef]
- Guo, Z.; Sha, W. Modelling the correlation between processing parameters and properties of maraging steels using artificial neural network. Comput. Mater. Sci. 2004, 29, 12–28. [Google Scholar] [CrossRef]
- Fragassa, C.; Babic, M. Predicting the tensile behaviour of cast alloys by a pattern recognition analysis on experimental data. Metals 2019, 9, 557. [Google Scholar] [CrossRef]
- Hodgson, P.D.; Kong, L.X. The prediction of the hot strength in steels with an integrated phenomenological and artificial neural network model. J. Mater. Process. Technol. 1999, 87, 131–138. [Google Scholar] [CrossRef]
- Ramana, K.; Anita, T. Effect of different environmental parameters on pitting behavior of AISI type 316L stainless steel: Experimental studies and neural network modeling. Mater. Design 2009, 30, 3770–3775. [Google Scholar] [CrossRef]
- Mandal, S.; Sivaprasad, P. Artificial neural network modeling of composition–process–property correlations in austenitic stainless steels. Mater. Sci. Eng. A 2008, 485, 571–580. [Google Scholar] [CrossRef]
- Sivaprasad, P.; Mandal, S. Artificial neural network modelling of the tensile properties of indigenously developed 15Cr-15Ni-2.2Mo-Ti modified austenitic stainless steel. Trans. Indian Inst. Met. 2006, 59, 437–445. [Google Scholar]
- Desu, R.K.; Krishnamurthy, H.N. Mechanical properties of Austenitic Stainless Steel 304L and 316L at elevated temperatures. J. Mater. Res. Technol. 2016, 5, 13–20. [Google Scholar] [CrossRef]
- The British Steelmakers Creep Committee: BSCC High Temperature Data; The Iron and Steel Institute: London, UK, 1973.
- Materials Algorithms Project. Available online: https://www.phase-trans.msm.cam.ac.uk/map (accessed on 17 June 2019).
- Shen, C.; Wang, C. Physical metallurgy-guided machine learning and artificial intelligent design of ultrahigh-strength stainless steel. Acta Mater. 2019, 179, 201–214. [Google Scholar] [CrossRef]
- Bhadeshia, H. Neural networks in materials science. ISIJ Int. 1999, 39, 966–979. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Hecht-Nielsen, R. Theory of the backpropagation neural network. In Neural Networks for Perception; Academic Press: New York, USA, 1992; pp. 65–93. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E. Learning representations by back-propagating errors. Cognitive Modeling. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Burden, F.; Winkler, D. Bayesian regularization of neural networks. In Artificial Neural Networks; Humana Press: Totowa, NJ, USA, 2008; pp. 23–42. [Google Scholar]
- Statistics and Machine Learning Toolbox. Available online: https://www.mathworks.com/products/statistics.html (accessed on 23 December 2019).
- Bhadeshia, H. Bainite in Steels. Cambridge: The Institute of Materials; The University Press: London, UK, 1992. [Google Scholar]
- Dombi, G.W.; Nandi, P. Prediction of rib fracture injury outcome by an artificial neural network. J. Trauma Acute Care 1995, 39, 915–921. [Google Scholar] [CrossRef]
- McGuire, M.F. Stainless Steels for Design Engineers; ASM International: Russell, OH, USA, 2008. [Google Scholar]
- Martins, L.F.M.; Plaut, R.L. Effect of Carbon on the Cold-worked State and Annealing Behavior of Two 18wt% Cr–8wt% Ni Austenitic Stainless Steels. ISIJ Int. 1998, 38, 572–579. [Google Scholar] [CrossRef]
- Farahat, A.I.Z.; El-Bitar, T. Effect of Nb, Ti and cold deformation on microstructure and mechanical properties of austenitic stainless steels. Mater. Sci. Eng. A 2010, 527, 3662–3669. [Google Scholar] [CrossRef]
- Marshall, P. Austenitic Stainless Steels: Microstructure and Mechanical Properties; Springer Science & Business Media: New York, NY, USA, 1984. [Google Scholar]
- Totten, G.E. Steel Heat Treatment: Metallurgy and Technologies; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Yin, R. Metallurgical Process Engineering; Springer Science & Business Media: New York, NY, USA, 2011. [Google Scholar]
- Wu, H.; Yang, B. Effect of Solution Temperature on the Microstructure and Mechanical Properties of Wrought 316LN Stainless Steel. Adv. Mater. Res. 2014, 915, 576–582. [Google Scholar] [CrossRef]



| Number | Variables | Number | Variables |
|---|---|---|---|
| 1 | Chromium (Cr, wt%) | 11 | Carbon (C, wt%) |
| 2 | Nickel (Ni, wt%) | 12 | Boron (B, wt%) |
| 3 | Molybdenum (Mo, wt%) | 13 | Phosphorus (P, wt%) |
| 4 | Manganese (Mn, wt%) | 14 | Sulfur (S, wt%) |
| 5 | Silicon (Si, wt%) | 15 | Cobalt (Co, wt%) |
| 6 | Niobium (Nb, wt%) | 16 | Aluminum (Al, wt%) |
| 7 | Titanium (Ti, wt%) | 17 | Solution treatment temperature (Ts, K) |
| 8 | Vanadium (V, wt%) | 18 | Solution treatment time (ts, s) |
| 9 | Copper (Cu, wt%) | 19 | Water-quenched or Air-quenched |
| 10 | Nitrogen (N, wt%) | 20 | Test temperature (Tt, K) |
| Tensile Properties | Hidden Units | Training | Testing | ||||
|---|---|---|---|---|---|---|---|
| (83% of the Data) | (17% of the Data) | ||||||
| MAPE | RMSE | R | MAPE | RMSE | R | ||
| (%) | (MPa) | (%) | (MPa) | ||||
| YS | 8 | 4.09 | 8.40 | 0.97 | 5.21 | 11.82 | 0.93 |
| UTS | 11 | 1.76 | 10.69 | 0.99 | 3.56 | 28.54 | 0.93 |
| YS / UTS | 6 | 4.80 | 0.025 1 | 0.93 | 5.91 | 0.035 1 | 0.86 |
| Tensile Properties | MAPE (%) | RMSE (MPa) | R |
|---|---|---|---|
| YS | 9.61 | 5.27 | 0.95 |
| UTS | 4.16 | 6.06 | 0.97 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wu, X.; Li, X.; Xie, Z.; Liu, R.; Liu, W.; Zhang, Y.; Xu, Y.; Liu, C. Prediction and Analysis of Tensile Properties of Austenitic Stainless Steel Using Artificial Neural Network. Metals 2020, 10, 234. https://doi.org/10.3390/met10020234
Wang Y, Wu X, Li X, Xie Z, Liu R, Liu W, Zhang Y, Xu Y, Liu C. Prediction and Analysis of Tensile Properties of Austenitic Stainless Steel Using Artificial Neural Network. Metals. 2020; 10(2):234. https://doi.org/10.3390/met10020234
Chicago/Turabian StyleWang, Yuxuan, Xuebang Wu, Xiangyan Li, Zhuoming Xie, Rui Liu, Wei Liu, Yange Zhang, Yichun Xu, and Changsong Liu. 2020. "Prediction and Analysis of Tensile Properties of Austenitic Stainless Steel Using Artificial Neural Network" Metals 10, no. 2: 234. https://doi.org/10.3390/met10020234
APA StyleWang, Y., Wu, X., Li, X., Xie, Z., Liu, R., Liu, W., Zhang, Y., Xu, Y., & Liu, C. (2020). Prediction and Analysis of Tensile Properties of Austenitic Stainless Steel Using Artificial Neural Network. Metals, 10(2), 234. https://doi.org/10.3390/met10020234






