Microstructural Evolution and Mechanical Behavior of an Al-6061 Alloy Processed by Repetitive Corrugation and Straightening
Abstract
:1. Introduction
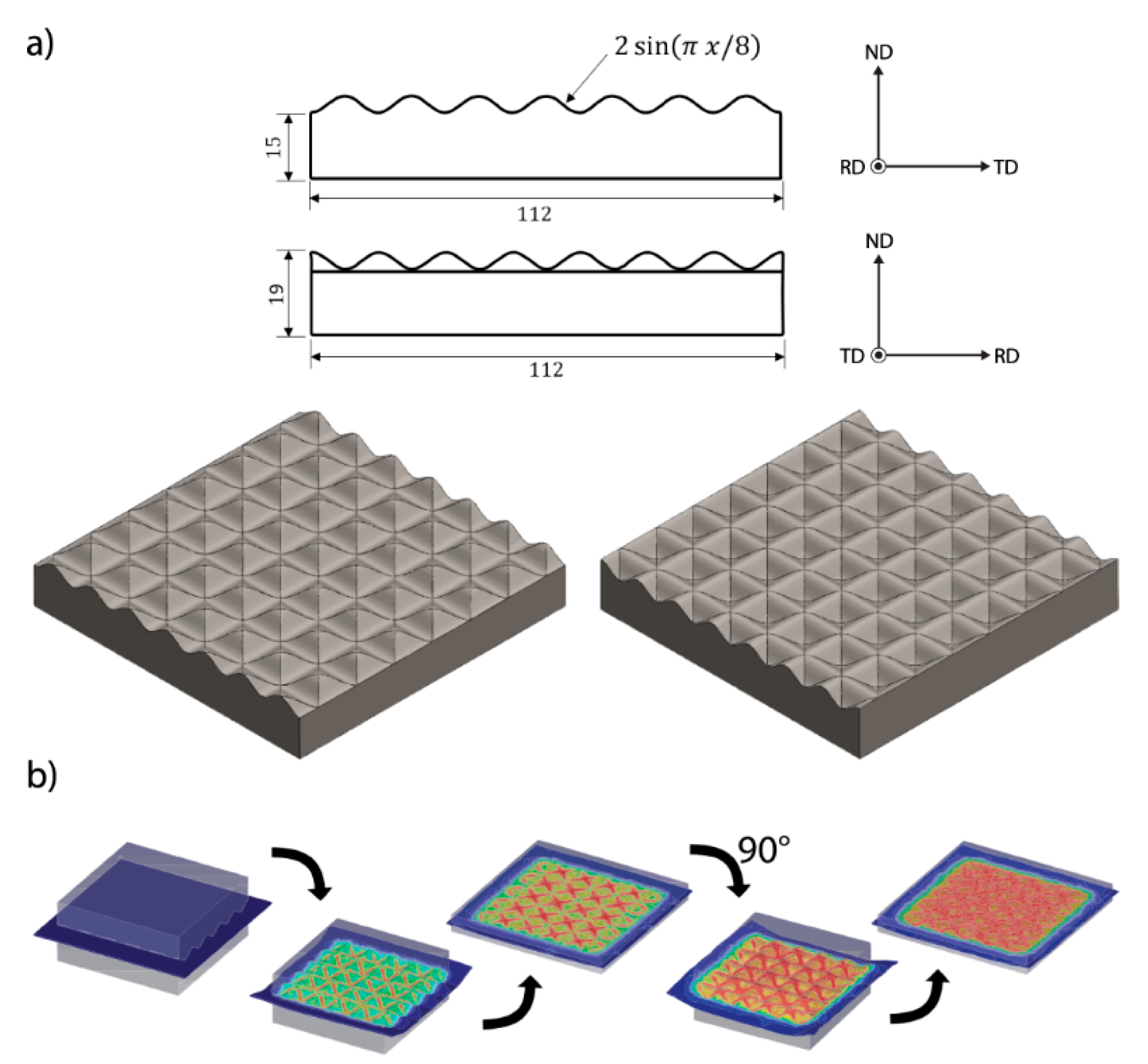
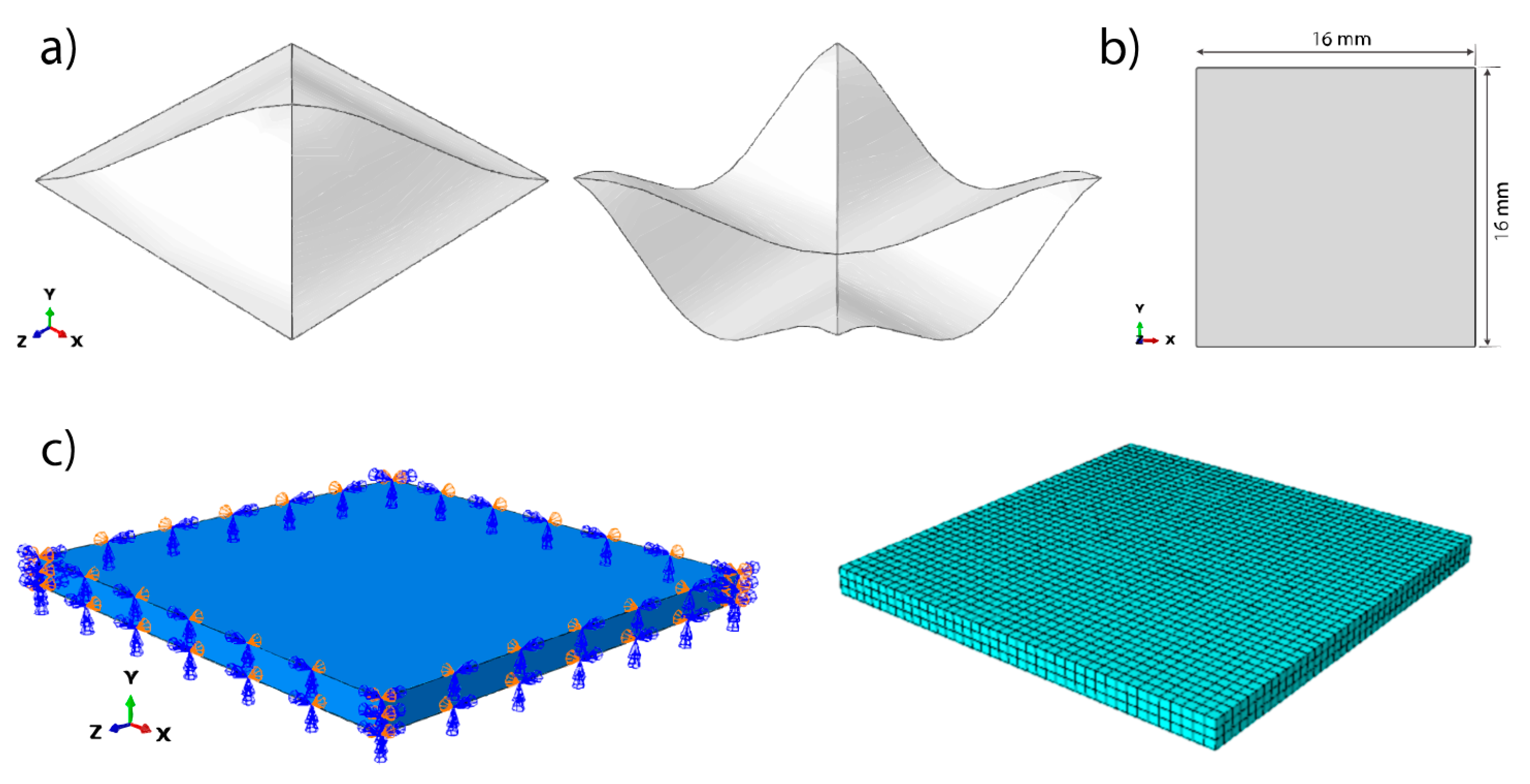
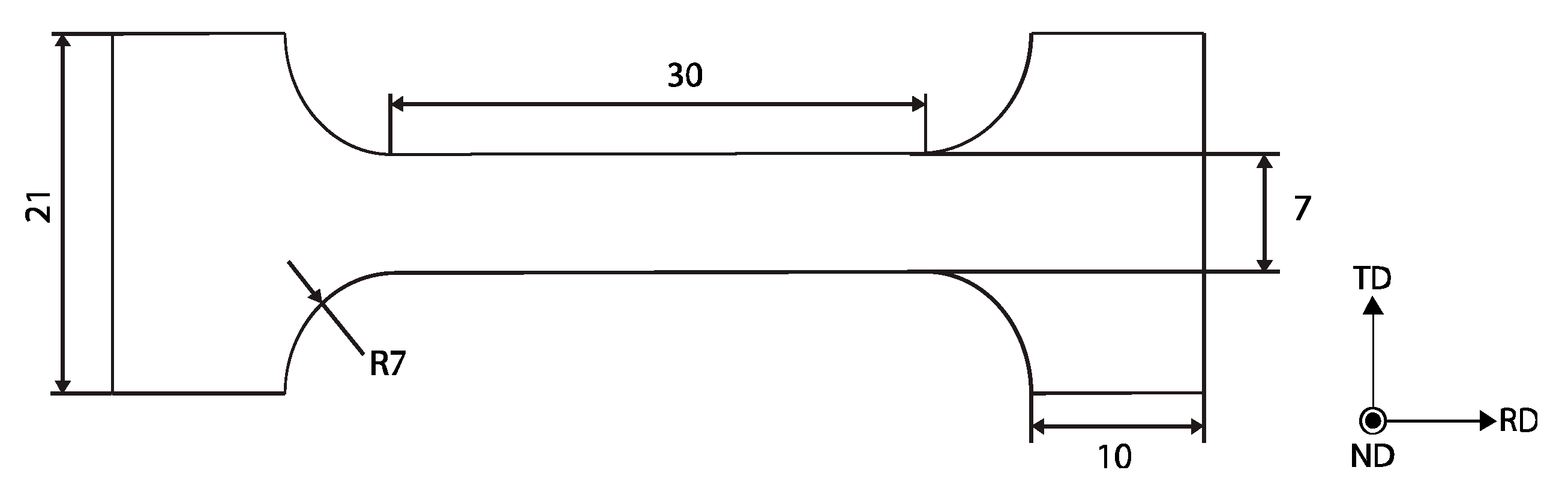
2. Materials and Methods
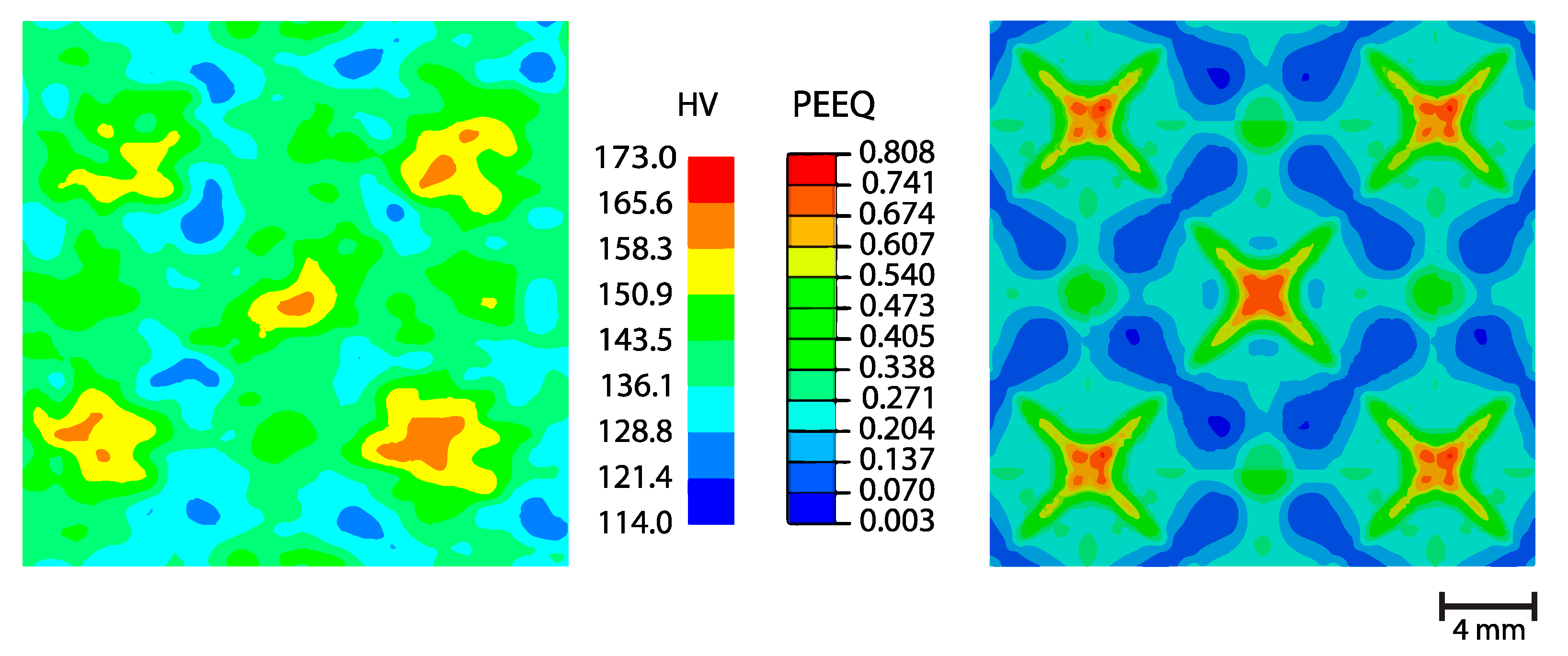
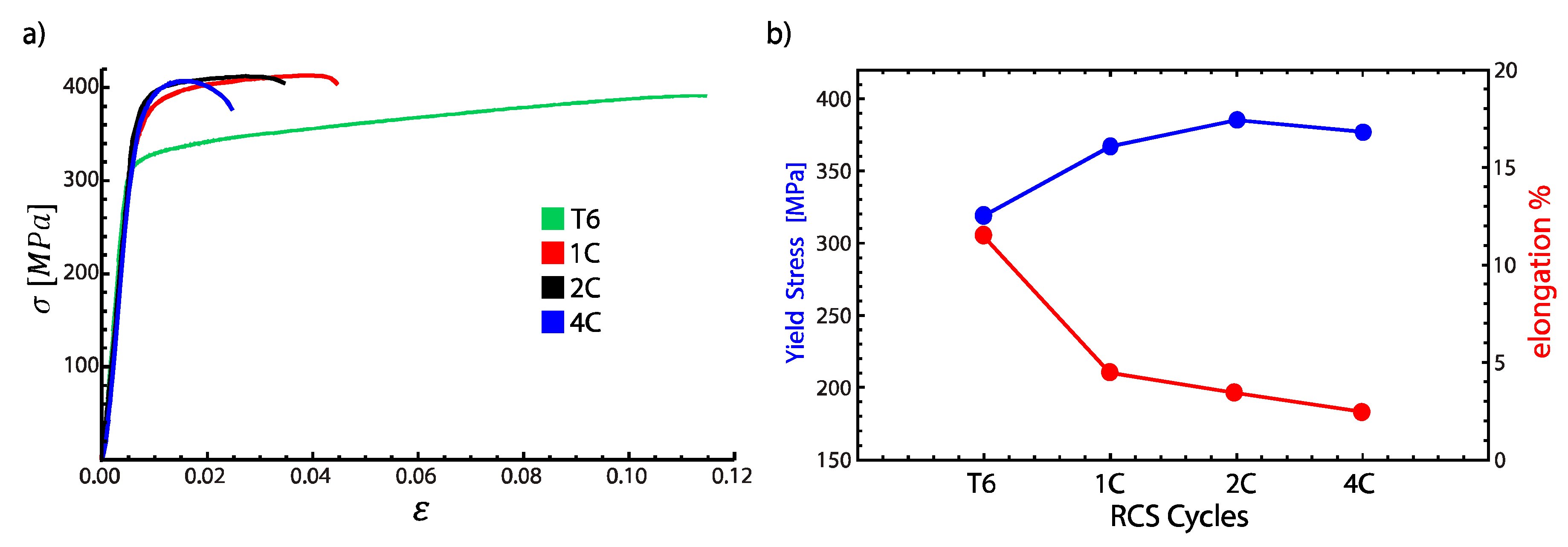
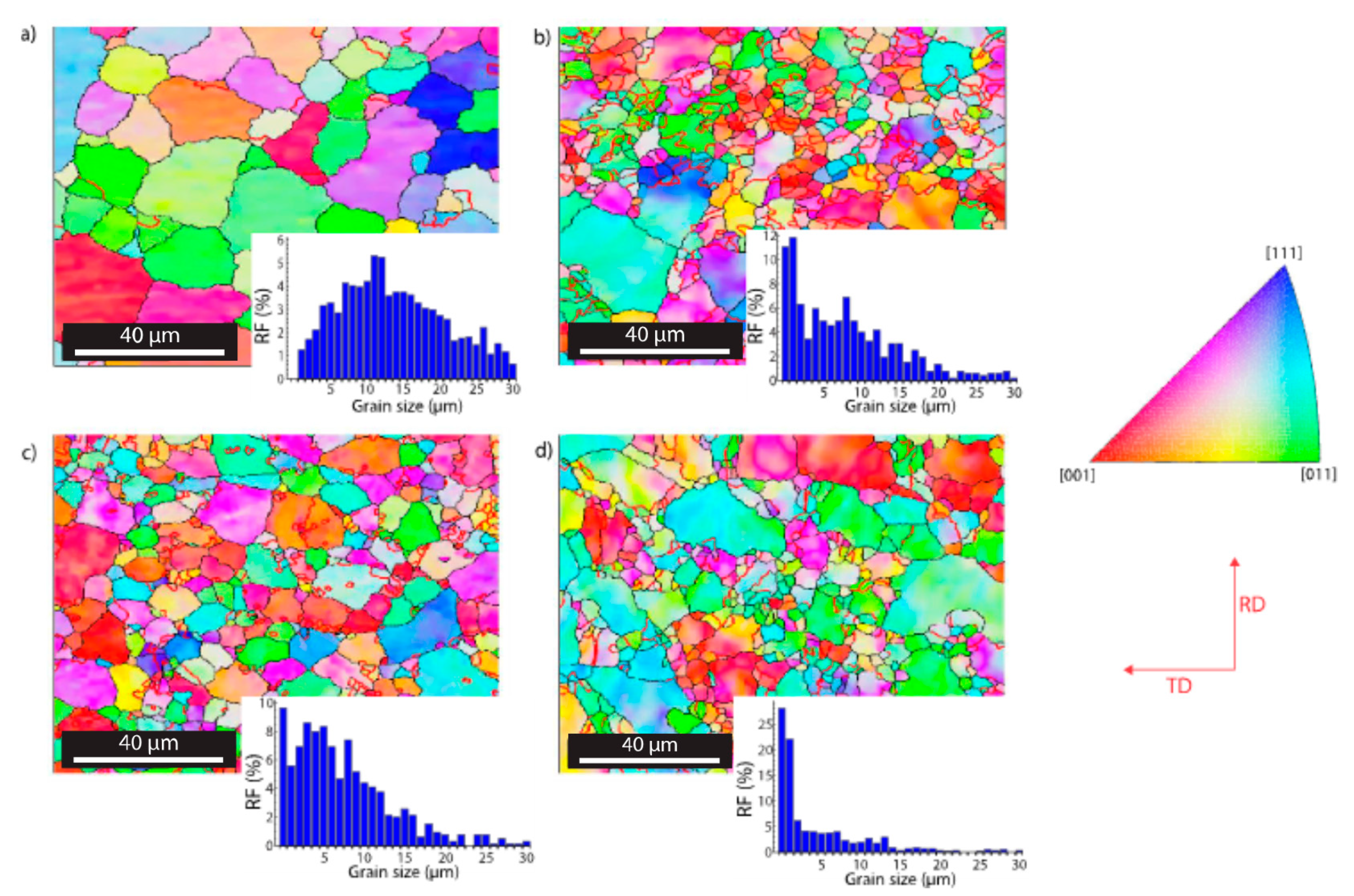
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bobruk, E.V.; Kazykhanov, V.U.; Murashkin, M.Y.; Valiev, R.Z. Enhanced Strengthening in Ultrafine-Grained Al-Mg-Si Alloys Produced via ECAP with Parallel Channels. Adv. Eng. Mater. 2015, 17, 1733–1737. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Islamgaliev, R.K.; Alexandrov, I.V. Bulk nanostructured materials from severe plastic deformation. Prog. Mater. Sci. 2000, 45, 103–189. [Google Scholar] [CrossRef]
- Yu, H.; Su, L.; Lu, C.; Tieu, K.; Li, H.; Li, J.; Godbole, A.; Kong, C. Enhanced mechanical properties of ARB-processed aluminum alloy 6061 sheets by subsequent asymmetric cryorolling and ageing. Mater. Sci. Eng. A 2016, 674, 256–261. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Zhu, Y.T.; Alexander, D.J.; Liao, X.; Lowe, T.C.; Asaro, R.J. Development of repetitive corrugation and straightening. Mater. Sci. Eng. A 2004, 371, 35–39. [Google Scholar] [CrossRef]
- Shin, D.H.; Park, J.J.; Kim, Y.S.; Park, K.T. Constrained groove pressing and its application to grain refinement of aluminum. Mater. Sci. Eng. A 2002, 328, 98–103. [Google Scholar] [CrossRef]
- Hosseini, E.; Kazeminezhad, M. Implementation of a constitutive model in finite element method for intense deformation. Mater. Des. 2011, 32, 487–494. [Google Scholar] [CrossRef]
- Sunil, B.R. Repetitive Corrugation and Straightening of Sheet Metals. Mater. Manuf. Process. 2015, 30, 1262–1271. [Google Scholar] [CrossRef]
- Thangapandian, N.; Balasivanandha Prabu, S.; Padmanabhan, K.A. Effects of die profile on grain refinement in Al-Mg alloy processed by repetitive corrugation and straightening. Mater. Sci. Eng. A 2016, 649, 229–238. [Google Scholar] [CrossRef]
- Rajinikanth, V.; Arora, G.; Narasaiah, N.; Venkateswarlu, K. Effect of repetitive corrugation and straightening on Al and Al-0.25Sc alloy. Mater. Lett. 2008, 62, 301–304. [Google Scholar] [CrossRef]
- Mirab, S.; Nili-Ahmadabadi, M.; Khajezade, A.; Jafarian, H.R. Correlation between poly-modal grain size and peculiar mechanical properties of pure aluminum deformed by RCSR process. Mater. Sci. Eng. A 2017, 700, 416–424. [Google Scholar] [CrossRef]
- Orlov, D.; Todaka, Y.; Umemoto, M.; Tsuji, N. Formation of bimodal grain structures in high purity Al by reversal high pressure torsion. Scr. Mater. 2011, 64, 498–501. [Google Scholar] [CrossRef]
- Mirsepasi, A.; Nili-Ahmadabadi, M.; Habibi-Parsa, M.; Ghasemi-Nanesa, H.; Dizaji, A.F. Microstructure and mechanical behavior of martensitic steel severely deformed by the novel technique of repetitive corrugation and straightening by rolling. Mater. Sci. Eng. A 2012, 551, 32–39. [Google Scholar] [CrossRef]
- Ozturk, F.; Sisman, A.; Toros, S.; Kilic, S.; Picu, R.C. Influence of aging treatment on mechanical properties of 6061 aluminum alloy. Mater. Des. 2010, 31, 972–975. [Google Scholar] [CrossRef]
- Ezequiel, M.; Figueroa, I.A.; Elizalde, S.; Cabrera, J.M.; Braham, C.; Morin, L.; Gonzalez, G. Numerical and experimental study of a 5754-aluminum alloy processed by heterogeneous repetitive corrugation and straightening. J. Mater. Res. Technol. 2019, 1–7. [Google Scholar] [CrossRef]
- Kim, W.J.; Kim, J.K.; Park, T.Y.; Hong, S.I.; Kim, D.I.; Kim, Y.S.; Lee, J.D. Enhancement of strength and superplasticity in a 6061 Al alloy processed by equal-channel-angular-pressing. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2002, 33, 3155–3164. [Google Scholar] [CrossRef]
- Rezaei, M.R.; Toroghinejad, M.R.; Ashrafizadeh, F. Effects of ARB and ageing processes on mechanical properties and microstructure of 6061 aluminum alloy. J. Mater. Process. Technol. 2011, 211, 1184–1190. [Google Scholar] [CrossRef]
- Sakai, T.; Belyakov, A.; Kaibyshev, R.; Miura, H.; Jonas, J.J. Dynamic and post-dynamic recrystallization under hot, cold and severe plastic deformation conditions. Prog. Mater. Sci. 2014, 60, 130–207. [Google Scholar] [CrossRef] [Green Version]
- Bacca, M.; Hayhurst, D.R.; McMeeking, R.M. Continuous dynamic recrystallization during severe plastic deformation. Mech. Mater. 2015, 90, 148–156. [Google Scholar] [CrossRef] [Green Version]
- Jenix Rino, J.; Balasivanandha Prabu, S.; Padmanabhan K., A. On the influence of repetitive corrugation and straightening on the microstructure and mechanical properties of AA 8090 Al-Li alloy. Arch. Civ. Mech. Eng. 2018, 18, 280–290. [Google Scholar]
- Totten, G.E.; MacKenzie, D.S. (Eds.) Handbook of Aluminum; Marcel Dekker, Inc: New York, NY, USA, 2003; ISBN 0824704940. [Google Scholar]
- Cabibbo, M.; Evangelista, E.; Scalabroni, C. EBSD FEG-SEM, TEM and XRD techniques applied to grain study of a commercially pure 1200 aluminum subjected to equal-channel angular-pressing. Micron 2005, 36, 401–414. [Google Scholar] [CrossRef] [PubMed]



| Element | Si | Fe | Cu | Mn | Mg | Cr | Zn | Ti | Al |
|---|---|---|---|---|---|---|---|---|---|
| wt% nominal | 0.4−0.8 | 0.7 | 0.15−0.4 | 0.15 | 0.8−1.2 | 0.04−0.3 | 0.25 | 0.15 | balance |
| wt% real | 0.77 | 0.24 | 0.16 | 0.03 | 1.03 | 0.07 | 0.03 | 0.02 | balance |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elizalde, S.; Ezequiel, M.; Figueroa, I.A.; Cabrera, J.M.; Braham, C.; Gonzalez, G. Microstructural Evolution and Mechanical Behavior of an Al-6061 Alloy Processed by Repetitive Corrugation and Straightening. Metals 2020, 10, 489. https://doi.org/10.3390/met10040489
Elizalde S, Ezequiel M, Figueroa IA, Cabrera JM, Braham C, Gonzalez G. Microstructural Evolution and Mechanical Behavior of an Al-6061 Alloy Processed by Repetitive Corrugation and Straightening. Metals. 2020; 10(4):489. https://doi.org/10.3390/met10040489
Chicago/Turabian StyleElizalde, Sergio, Marco Ezequiel, Ignacio A. Figueroa, José M. Cabrera, Chedly Braham, and Gonzalo Gonzalez. 2020. "Microstructural Evolution and Mechanical Behavior of an Al-6061 Alloy Processed by Repetitive Corrugation and Straightening" Metals 10, no. 4: 489. https://doi.org/10.3390/met10040489
APA StyleElizalde, S., Ezequiel, M., Figueroa, I. A., Cabrera, J. M., Braham, C., & Gonzalez, G. (2020). Microstructural Evolution and Mechanical Behavior of an Al-6061 Alloy Processed by Repetitive Corrugation and Straightening. Metals, 10(4), 489. https://doi.org/10.3390/met10040489







