Constitutive Model of 30CrMoA Steel with Strain Correction
Abstract
1. Introduction
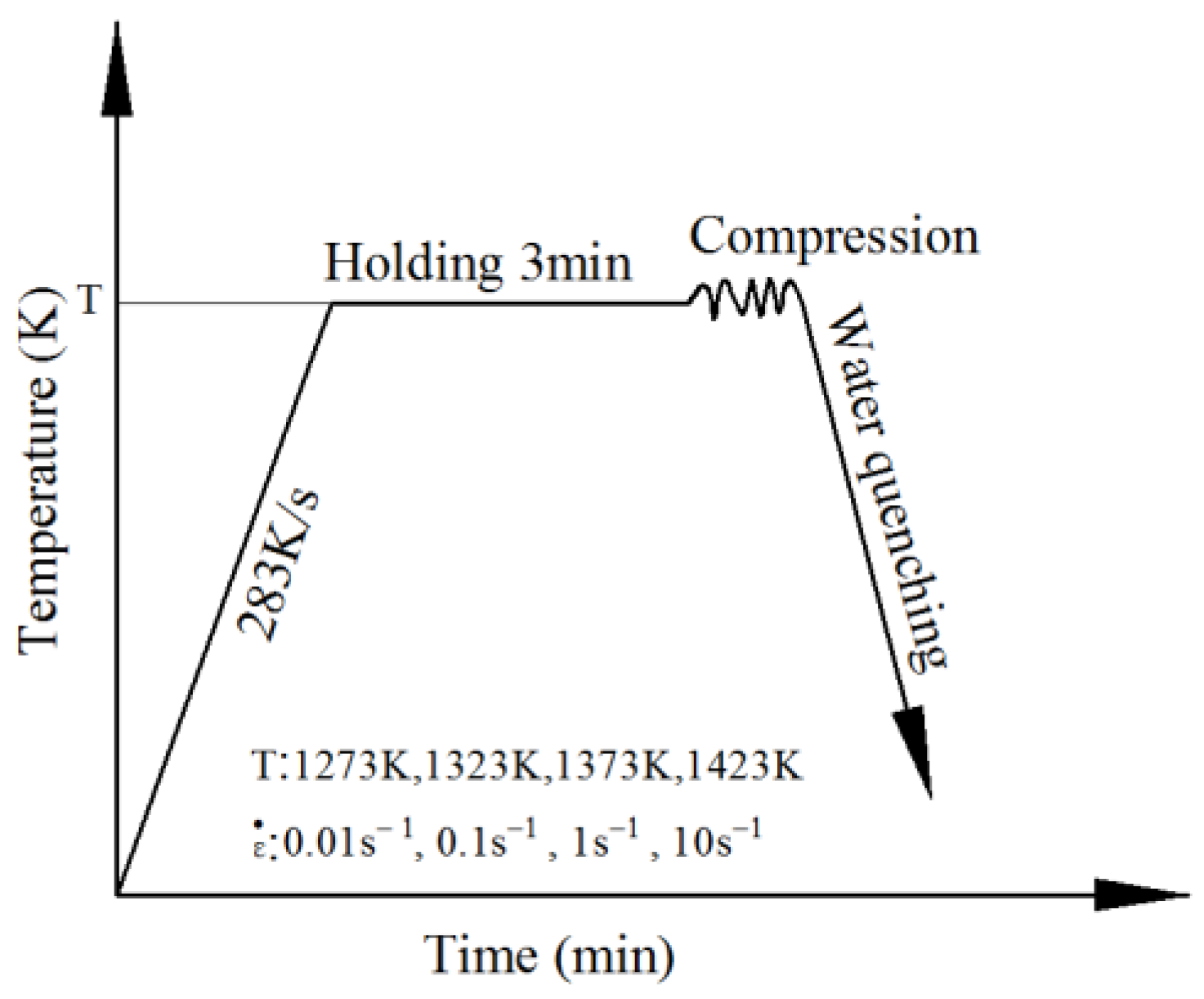
2. Experimental Materials and Methods
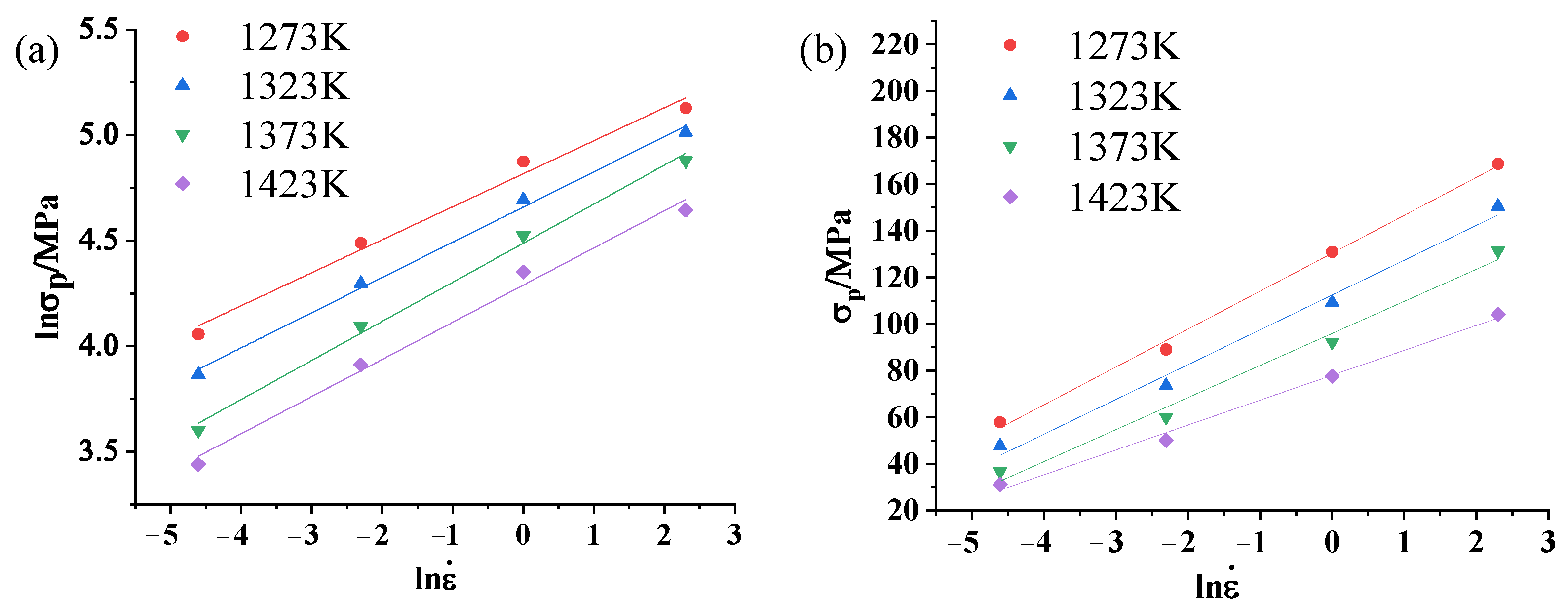
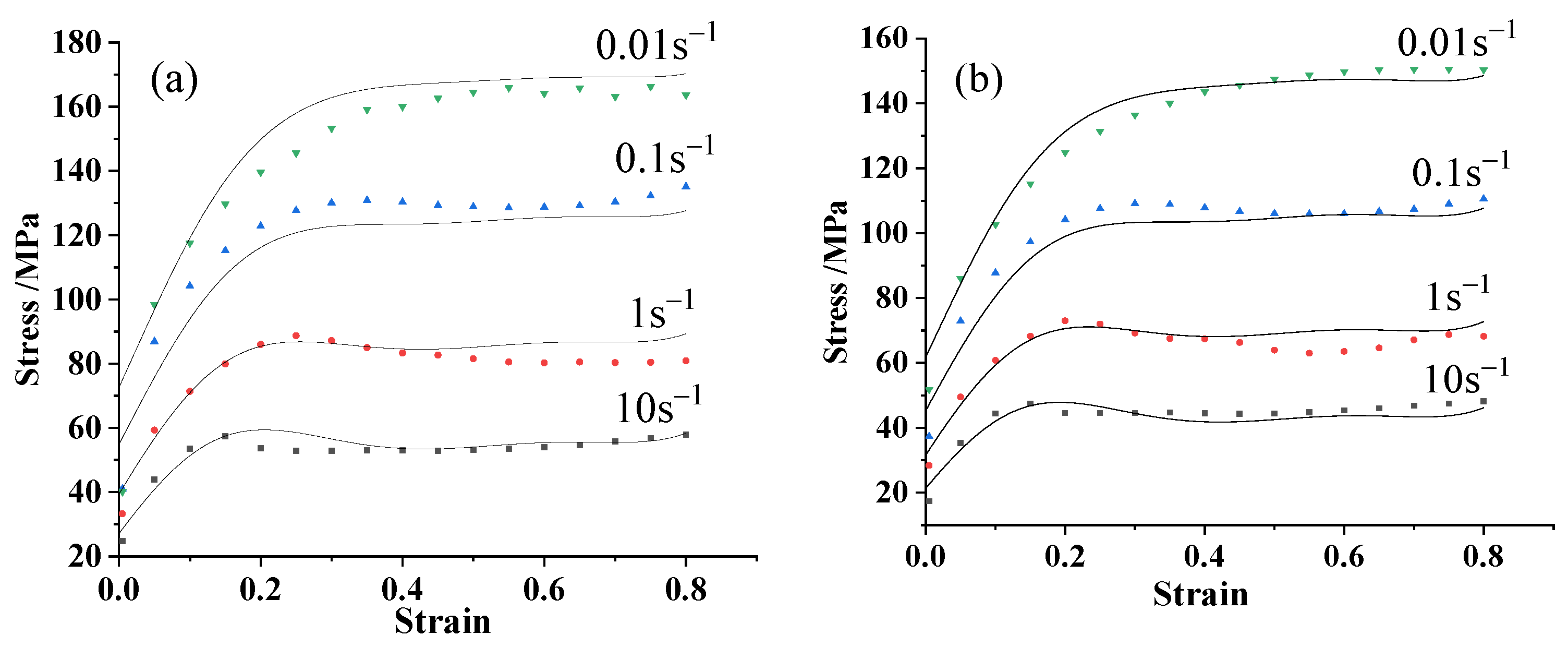
3. Measurement Results and Analysis of Experimental Stress–Strain Curves
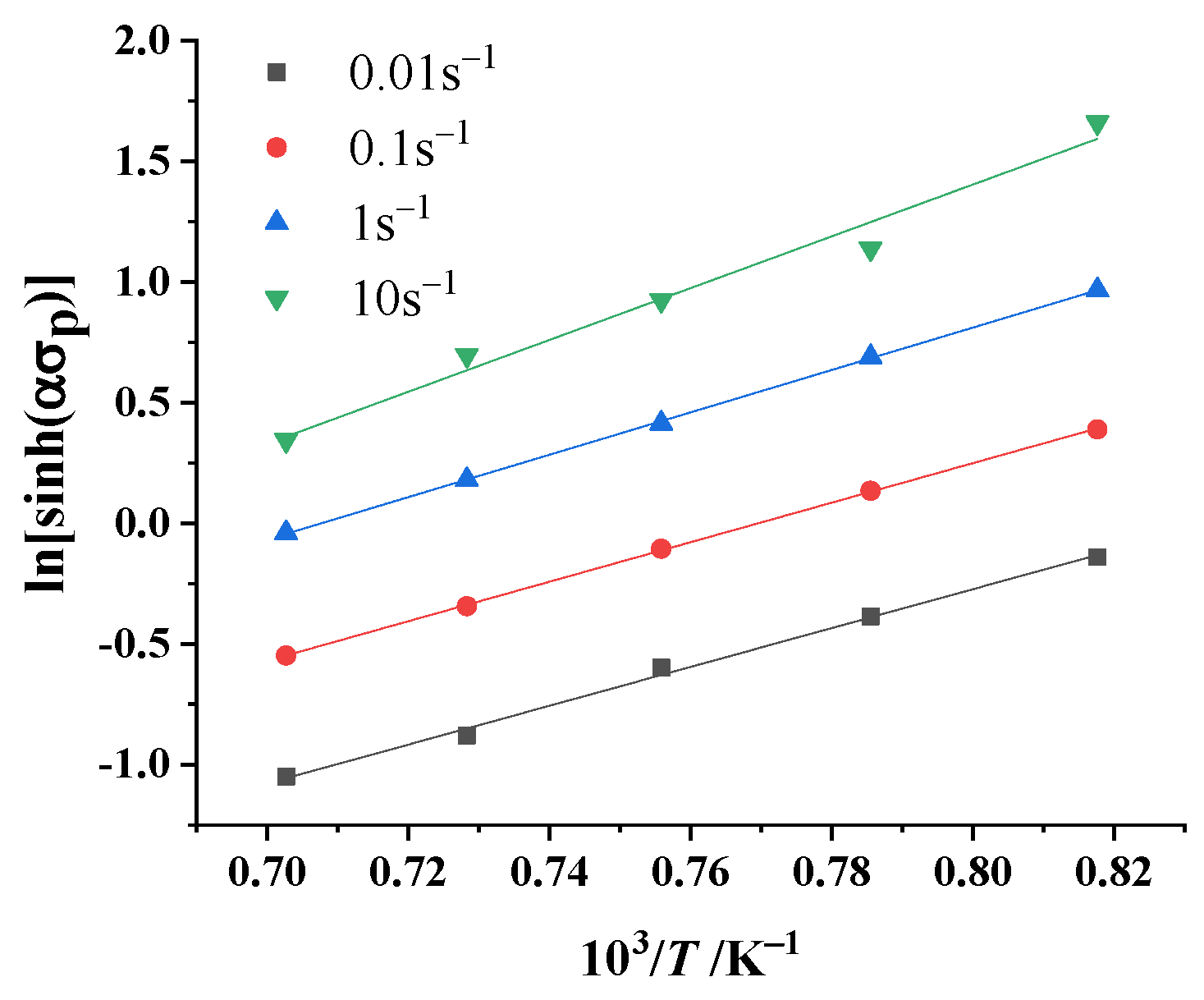
4. Establishment of Empirical Constitutive Model
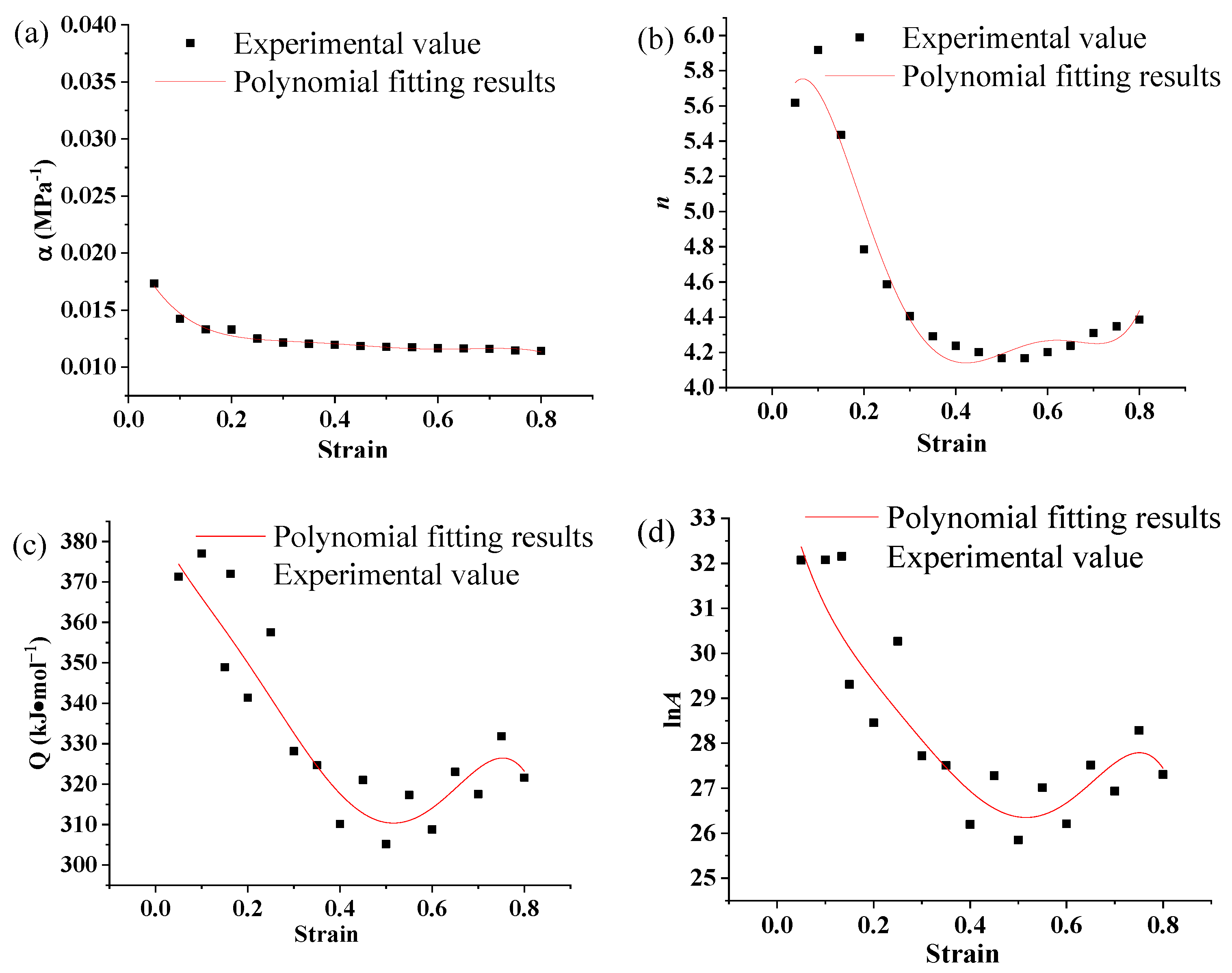
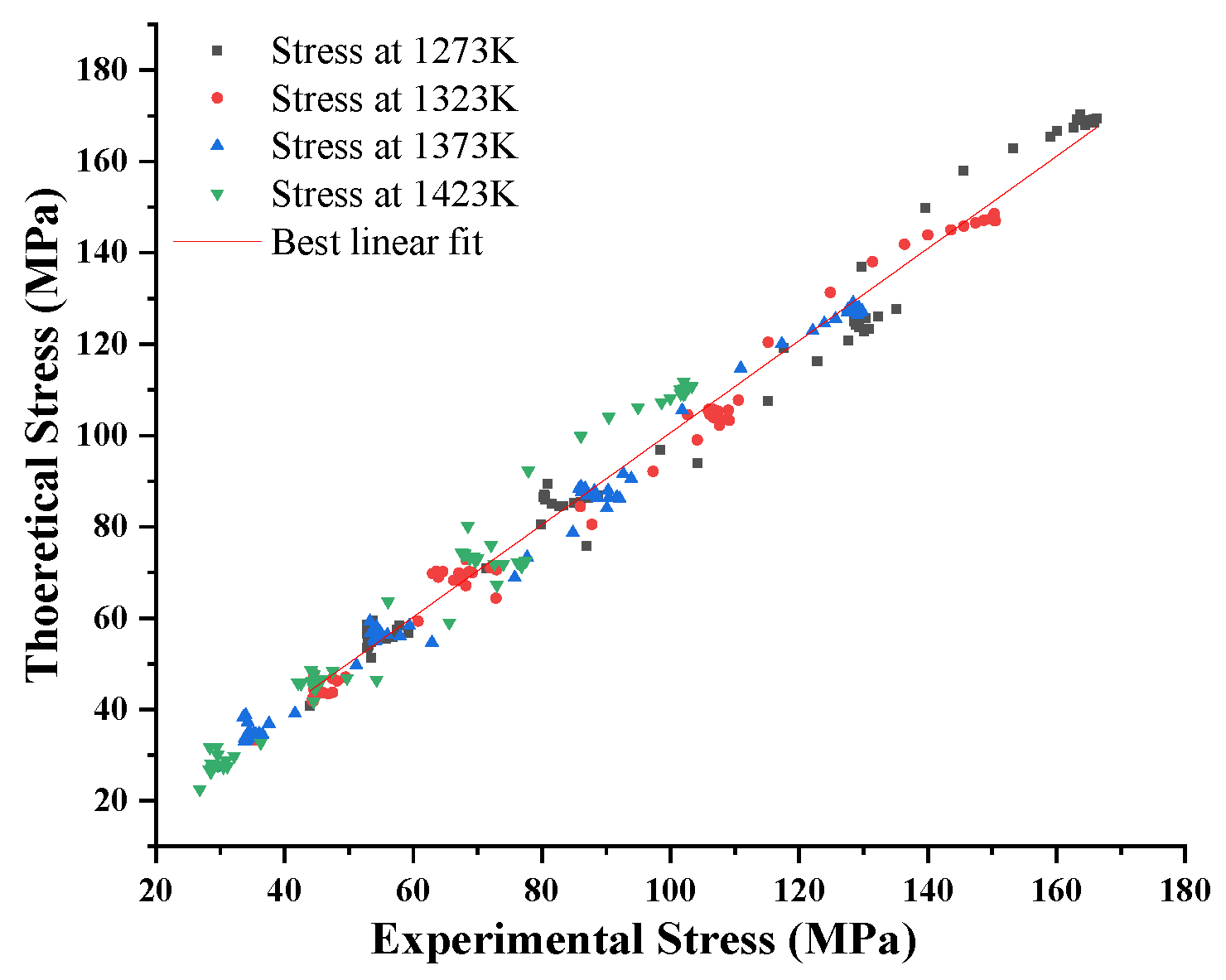
5. Strain Correction for Empirical Constitutive Models
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xiao, J.; Li, D.; Li, X.; Deng, T. Constitutive modeling and microstructure change of Ti–6Al–4V during the hot tensile deformation. J. Alloy. Compd. 2012, 541, 346–352. [Google Scholar] [CrossRef]
- Wang, B.; Yi, Z.; Lai, X.; Zhang, K. Analysis on heating performance and thermal forming of lightweight alloy using pulse current heating. Procedia Eng. 2017, 207, 639–644. [Google Scholar] [CrossRef]
- Fang, H.; Wang, G.; Liu, S.; Li, X. Research on Resistance Heating Behavior of High-Strength Steel and its Hot-Stamping Forming. J. Mater. Eng. Perform. 2018, 27, 4829–4837. [Google Scholar] [CrossRef]
- Shu, X.D.; Zhang, S.; Wang, J.T.; Shi, J.N.; Xia, Y.X. Flow stress behavior of 30CrMoA steel under high temperature compression. Metalurgija 2020, 59, 313–316. [Google Scholar]
- Zhang, S.; Shu, X.; Xu, C.; Wang, J.; Li, Z. Research on Wall Thickness Uniformity of Hollow Axles by Three-Roll Skew Rolling. In Proceedings of the ASME 2019 International Mechanical Engineering Congress and Exposition, Salt Lake City, UT, USA, 11–14 November 2019. [Google Scholar] [CrossRef]
- Peng, H.B.; Zhang, H.J. Research Development of the Constitutive Models of Metal Materials. Mater. Mechan. Eng. 2012, 3, 9–14, 79. [Google Scholar]
- Silva, T.E.F.; Gain, S.; Pinto, D.; de Jesus, A.M.P.; Xavier, J.; Reis, A.; Rosa, P.A.R. Fracture Characterization of a Cast Aluminium Alloy Aiming Machining Simulation. J. Mater. Design Appl. 2019, 233, 402–412. [Google Scholar]
- Lin, Y.C.; Chen, M.S.; Zhong, J. Flow stress behaviors of 42CrMo steel during hot compression. J. Cent. South Univ. 2008, 39, 549–553. [Google Scholar]
- Wang, W.; Zhao, J.; Zhai, R.X.; Ma, R. Arrhenius-Type Constitutive Model and Dynamic Recrystallization Behavior of 20Cr2Ni4A Alloy Carburizing Steel. Steel Res. Int. 2016, 88, 1600196. [Google Scholar] [CrossRef]
- Dou, K.; Liu, Q. Hot deformation behavior and constitutive modelling of low carbon micro-alloyed steel YQ450NQR1 during isothermal compression. Mech. Mater. 2020, 148, 103430. [Google Scholar] [CrossRef]
- Galiyev, A.; Kaibyshev, R.; Gottstein, G. Correlation of plastic deformation and dynamic recrystallization in magnesium alloy ZK60. Acta Mater. 2001, 49, 1199–1207. [Google Scholar] [CrossRef]
- Cai, J.; Li, F.; Liu, T.; Chen, B.; He, M. Constitutive equations for elevated temperature flow stress of Ti–6Al–4V alloy considering the effect of strain. Mater. Des. 2011, 32, 1144–1151. [Google Scholar] [CrossRef]
- Ding, Z.-Y.; Hu, Q.; Zeng, L.; Li, J.-G. Hot deformation characteristics of as-cast high-Cr ultra-super-critical rotor steel with columnar grains. Int. J. Miner. Met. Mater. 2016, 23, 1275–1285. [Google Scholar] [CrossRef]
- Duan, H.L.; Huang, X.M.; Ji, H.C.; Li, Y.G. The arrhenius constitutive model of steel 42CrMo for gear. Metalurgija 2020, 59, 63–66. [Google Scholar]
- Sellars, C.; McTegart, W. On the mechanism of hot deformation. Acta Met. 1966, 14, 1136–1138. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, H. Effect of strain-rate upon the plastic flow of steel. J. Appl. Phys. 1944, 15, 22–27. [Google Scholar] [CrossRef]
- Li, L.; Zhou, J.; Duszczyk, J. Determination of a constitutive relationship for AZ31B magnesium alloy and validation through comparison between simulated and real extrusion. J. Mater. Process. Technol. 2006, 172, 372–380. [Google Scholar] [CrossRef]
- Lin, Y.; Chen, X.-M. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working. Mater. Des. 2011, 32, 1733–1759. [Google Scholar] [CrossRef]
- Li, H.-Y.; Li, Y.-H.; Wei, D.-D.; Liu, J.-J.; Wang, X.-F. Constitutive equation to predict elevated temperature flow stress of V150 grade oil casing steel. Mater. Sci. Eng. A 2011, 530, 367–372. [Google Scholar] [CrossRef]
- Saravanan, L.; Senthilvelan, T. Constitutive equation and microstructure evaluation of an extruded aluminum alloy. J. Mater. Res. Technol. 2016, 5, 21–28. [Google Scholar] [CrossRef]



| C | Si | Mn | S | P | Cr | Ni | Cu | Mo |
|---|---|---|---|---|---|---|---|---|
| 0.3 | 0.27 | 0.55 | 0.025 | 0.025 | 0.92 | 0.03 | 0.025 | 0.2 |
| α | n | Q | lnA |
|---|---|---|---|
| B0 = 0.0212 | C0 = 5.3224 | D0 = 384.4796 | E0 = 34.3975 |
| B1 = −0.1016 | C1 = 14.6506 | D1 = −232.1799 | E1 = −50.4492 |
| B2 = 0.4679 | C2 = −149.9067 | D2 = 783.9559 | E2 = 228.8592 |
| B3 = −1.0624 | C3 = 443.1788 | D3 = −3628.0330 | E3 = −686.5489 |
| B4 = 1.1558 | C4 = −541.2405 | D4 = 6761.6676 | E4 = 983.5824 |
| B5 = −0.4804 | C5 = 238.4013 | D5 = −3934.6870 | E5 = −501.7943 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Shu, X.; Wang, J.; Xia, Y. Constitutive Model of 30CrMoA Steel with Strain Correction. Metals 2020, 10, 1214. https://doi.org/10.3390/met10091214
Zhang S, Shu X, Wang J, Xia Y. Constitutive Model of 30CrMoA Steel with Strain Correction. Metals. 2020; 10(9):1214. https://doi.org/10.3390/met10091214
Chicago/Turabian StyleZhang, Song, Xuedao Shu, Jitai Wang, and Yingxiang Xia. 2020. "Constitutive Model of 30CrMoA Steel with Strain Correction" Metals 10, no. 9: 1214. https://doi.org/10.3390/met10091214
APA StyleZhang, S., Shu, X., Wang, J., & Xia, Y. (2020). Constitutive Model of 30CrMoA Steel with Strain Correction. Metals, 10(9), 1214. https://doi.org/10.3390/met10091214







