Non-Destructive Micromagnetic Determination of Hardness and Case Hardening Depth Using Linear Regression Analysis and Artificial Neural Networks
Abstract
:1. Introduction
1.1. Micromagnetic Measurements and Data Evaluation
1.2. Regression Analysis
1.3. Artificial Neural Networks
2. Materials and Methods
3. Results and Discussion
3.1. Calibration by Use of Regression Analysis
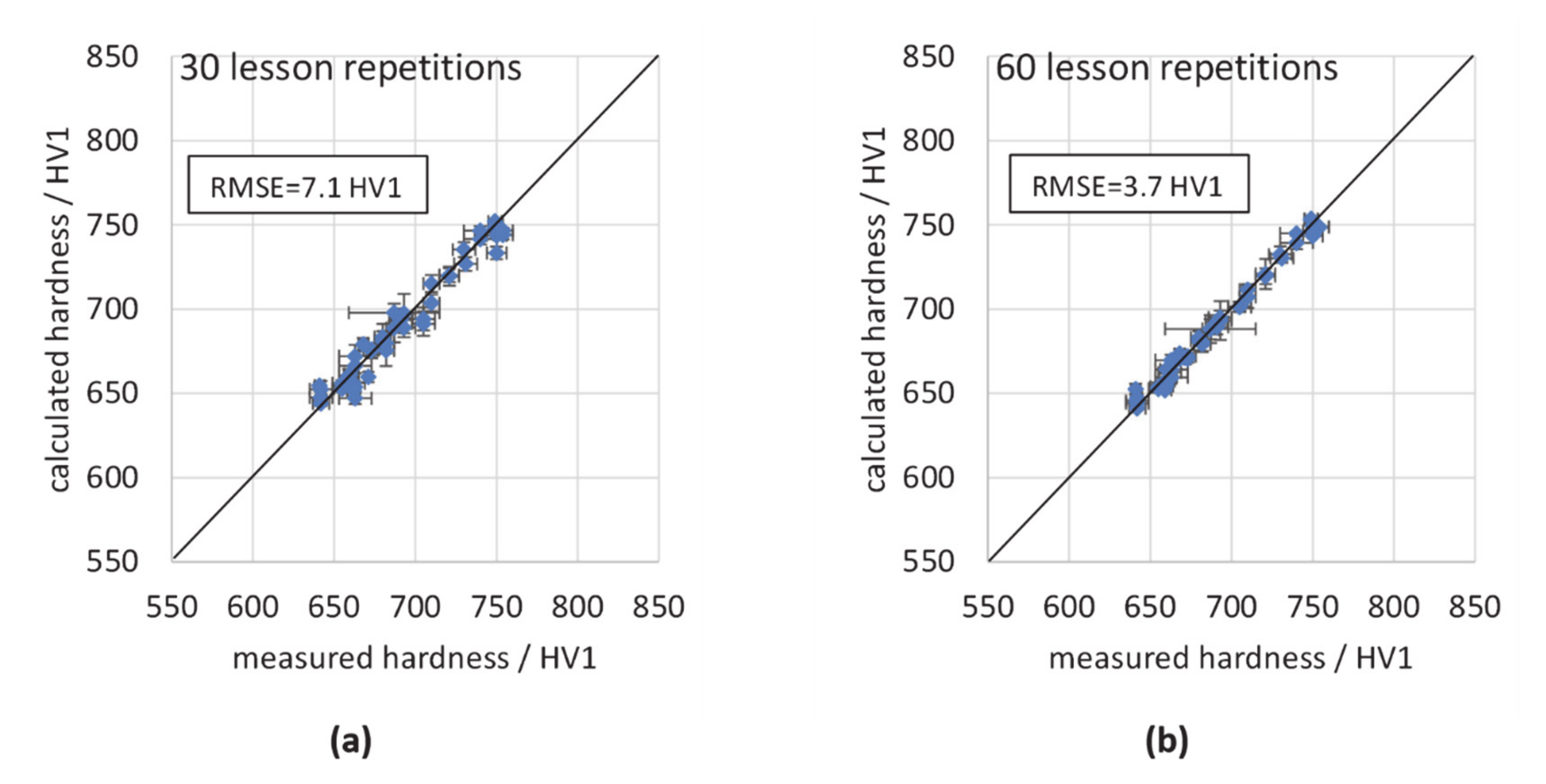
3.2. Calibration by Use of Artificial Neural Networks
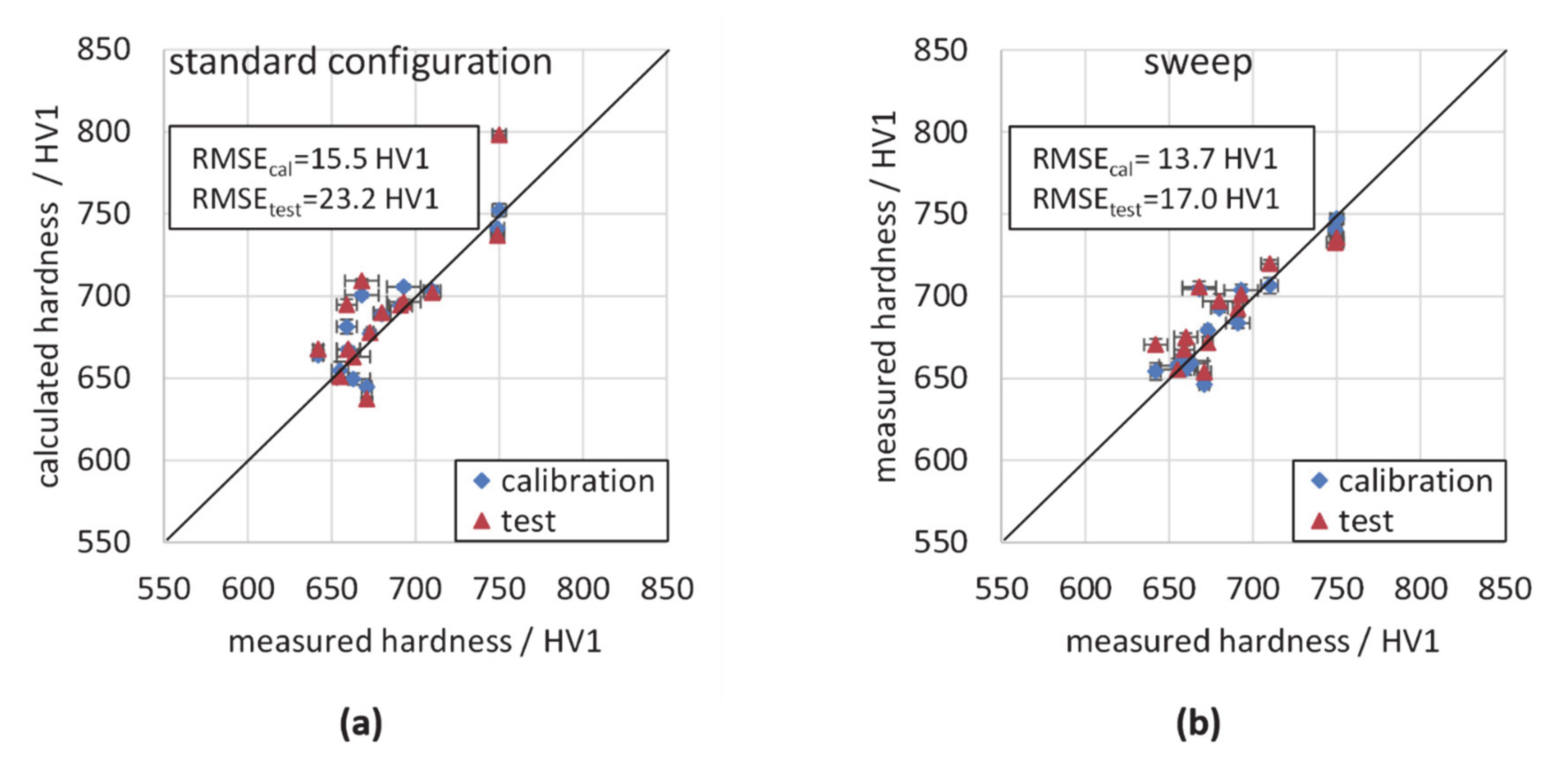
3.3. Calibration with Standard Configuration and Variation of Measurement Parameters
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Target | Measured | ||||||
|---|---|---|---|---|---|---|---|
| Surface Carbon Content/wt. % | CHD/mm | Tempering Temperature/°C | Surface Carbon Content/wt. % | Carburization Depth/mm | Hardness/HV1 | ||
| 0.6 | 0.5 | 150 | 0.6 | 0.55 | 750 | ± | 4 |
| 0.6 | 0.5 | 180 | 0.6 | 0.55 | 687 | ± | 28 |
| 0.6 | 0.5 | 210 | 0.6 | 0.55 | 659 | ± | 6 |
| 0.6 | 1 | 150 | 0.61 | 0.91 | 721 | ± | 6 |
| 0.6 | 1 | 180 | 0.61 | 0.91 | 668 | ± | 10 |
| 0.6 | 1 | 210 | 0.61 | 0.91 | 662 | ± | 4 |
| 0.6 | 2 | 150 | 0.64 | 1.87 | 710 | ± | 5 |
| 0.6 | 2 | 180 | 0.64 | 1.87 | 663 | ± | 7 |
| 0.6 | 2 | 210 | 0.64 | 1.87 | 663 | ± | 10 |
| 0.7 | 0.5 | 150 | 0.68 | 0.55 | 750 | ± | 6 |
| 0.7 | 0.5 | 180 | 0.68 | 0.55 | 680 | ± | 5 |
| 0.7 | 0.5 | 210 | 0.68 | 0.55 | 670 | ± | 3 |
| 0.7 | 1 | 150 | 0.72 | 0.85 | 749 | ± | 4 |
| 0.7 | 1 | 180 | 0.72 | 0.85 | 705 | ± | 7 |
| 0.7 | 1 | 210 | 0.72 | 0.85 | 671 | ± | 3 |
| 0.7 | 2 | 150 | 0.73 | 1.85 | 754 | ± | 6 |
| 0.7 | 2 | 180 | 0.73 | 1.85 | 691 | ± | 7 |
| 0.7 | 2 | 210 | 0.73 | 1.85 | 660 | ± | 4 |
| 0.8 | 0.5 | 150 | 0.79 | 0.57 | 730 | ± | 7 |
| 0.8 | 0.5 | 180 | 0.79 | 0.57 | 682 | ± | 5 |
| 0.8 | 0.5 | 210 | 0.79 | 0.57 | 642 | ± | 3 |
| 0.8 | 1 | 150 | 0.77 | 0.87 | 740 | ± | 4 |
| 0.8 | 1 | 180 | 0.77 | 0.87 | 673 | ± | 2 |
| 0.8 | 1 | 210 | 0.77 | 0.87 | 642 | ± | 7 |
| 0.8 | 2 | 150 | 0.81 | 1.88 | 731 | ± | 10 |
| 0.8 | 2 | 180 | 0.81 | 1.88 | 693 | ± | 7 |
| 0.8 | 2 | 210 | 0.81 | 1.88 | 655 | ± | 5 |
| Measured Variable x | Regression Function | R2 |
|---|---|---|
| Hardness | ||
| Vmag (350 Hz) | 1861x + 2795 | 0.03 |
| A3 (120 Hz) | −10.6x + 707 | 0.02 |
| A7 (100 Hz) | 74.3x + 688 | 0.003 |
| P3 (50 Hz) | 67.5x + 633 | 0.07 |
| P3 (150 Hz) | 21x + 670 | 0.03 |
| P5 (30 Hz) | −52.8x + 775 | 0.04 |
| P7 (120 Hz) | −5.7x + 696 | 0.01 |
| Hco (50 Hz) | 3.1x + 620 | 0.08 |
| Mmax (350 Hz) | −835x + 861 | 0.2 |
| Mr (350 Hz) | −667x + 795 | 0.25 |
| Hcm (80 Hz, HP 100 kHz) | −1529x + 729.92 | 0.07 |
| µr (120 Hz, 100 kHz) | −2472.9x + 1025 | 0.64 |
| µr (120 Hz, 250 kHz) | −916.2x + 867.7 | 0.3 |
| µr (150 Hz) | −2801x + 1001 | 0.62 |
| DH25µ (120Hz, 60 kHz) | 11.1x +365 | 0.24 |
| Carburization Depth | ||
| Vmag (30 Hz) | 7.7x + 5.5 | 0.08 |
| Vmag (150 Hz) | −2.97x + 5.7 | 0.16 |
| Vmag (350 Hz) | −1.98x + 6.8 | 0.17 |
| P3 (30 Hz) | −2.5x + 2.8 | 0.18 |
| P3 (40 Hz) | −2.4x + 3.03 | 0.25 |
| P3 (250 Hz) | −0.44x + 1.5 | 0.05 |
| P7 (50 Hz) | −1.15x + 4.3 | 0.3 |
| K (200 Hz) | 0.58x + 0.1 | 0.3 |
| K (300 Hz) | 1.029x − 0.83 | 0.48 |
| Hco (50 Hz) | −0.1x + 3.36 | 0.35 |
| Hco (350 Hz) | 0.01x + 0.9 | 0.01 |
| Hcm (80 Hz) | 0.281x − 1.53 | 0.57 |
| Hcm (250 Hz) | 0.15x − 0.23 | 0.31 |
| DH50m (80 Hz) | −0.09x + 4.26 | 0.07 |
| µmax (30 Hz) | 15.9x+6.6 | 0.11 |
| DH25µ (250 Hz) | −0.04x + 4.8 | 0.03 |
| Ph3 (120 Hz) | 807x + 8.4 | 0.01 |
References
- Gorgels, C. Schleifbarkeit von Einsatzstählen—Untersuchungen zur Schleifbarkeit Unterschiedlich Wärmebehandelter Einsatzstähle für die Zahnradfertigung—Abschlussbericht FVA 329 III.; Forschungsvereinigung Antriebstechnik e.V.: Frankfurt, Germany, 2008. [Google Scholar]
- Sackmann, D.; Epp, J. Sichere Schädigungsdetektion von Randzonenschädigungen Antriebstechnischer Bauteile Infolge Einer Hartfeinbearbeitung Mithilfe von Zerstörungsfreien Mikromagnetischen Prüfverfahren—Abschlussbericht FVA 723 I.; Forschungsvereinigung Antriebstechnik e.V.: Frankfurt, Germany, 2018. [Google Scholar]
- Jedamski, R.; Heinzel, J.; Rößler, M.; Epp, J.; Eckebrecht, J.; Gentzen, J.; Putz, M.; Karpuschewski, B. Potential of Magnetic Barkhausen Noise analysis for In-Process Monitoring of Surface Layer Properties of steel components in Grinding. TM Tech. Mess. 2020, 87, 787–798. [Google Scholar] [CrossRef]
- Wolter, B.; Gabi, Y.; Conrad, C. Nondestructive Testing with 3MA—An Overview of Principles and Applications. Appl. Sci. 2019, 9, 1068. [Google Scholar] [CrossRef] [Green Version]
- Sorsa, A.; Santa-aho, S.; Aylott, C.; Shaw, B.A.; Vippola, M.; Leiviskä, K. Case Depth Prediction of Nitrided Samples with Barkhausen Noise Measurement. Metals. 2019, 9, 325. [Google Scholar] [CrossRef] [Green Version]
- Send, S.; Dapprich, D.; Thomas, J.; Suominen, L. Non-destructive Case Depth Determination by Means of Low-Frequency Barkhausen Noise Measurements. J. Nondestruct. Eval. 2018, 37, 82. [Google Scholar] [CrossRef]
- Santa-Aho, S.; Vippola, M.; Sorsa, A.; Leiviskä, K.; Lindgren, M.; Lepistö, T. Utilization of Barkhausen noise magnetizing sweeps for case-depth detection from hardened steel. NDT E Int. 2012, 52, 95–102. [Google Scholar] [CrossRef]
- Szielasko, K. Entwicklung Messtechnischer Module zur Mehrparametrischen Elektromagnetischen Werkstoffcharakterisierung und -Prüfung. Ph.D. Thesis, Universität des Saarlandes, Saarbrücken, Germany, 18 August 2009. [Google Scholar]
- Epp, J.; Szielasko, K. Weiterentwicklung Der Mikromagnetischen Multiparameter-Methode zur ZerstöRungsfreien Ermittlung von GefüGe- und Spannungsgradienten in RandschichtgehäRteten und Verfestigten ZustäNden—Schlussbericht IGF 18171 N. 2017.
- Liu, X.; Zhang, R.; Wu, B.; He, C. Quantitative Prediction of Surface hardness in 12 CrMoV Steel Plate on Magnetic Barkhausen Noise and Tangential Magnetic Field Measurements. J. Nondestruct. Eval. 2018, 37, 2. [Google Scholar]
- Ahadi Akhlaghi, I.; Kahrobaee, S.; Akbarzadeh, A.; Kashefi, M.; Krause, T.W. Predicting hardness of steel specimens subjected to Jominy test using an artificial neural network and electromagnetic nondestructive technique. Nondestruct. Test. Eval. 2020, 35, 1–17. [Google Scholar] [CrossRef]
- Liu, X.; Shang, W.; He, C.; Zhang, R.; Wu, B. Simultaneous quantitative prediction of tensile stress, surface hardness and case depth in medium carbon steel rods based on multifunctional magnetic testing techniques. Measurement 2018, 128, 455–463. [Google Scholar] [CrossRef]
- Sorsa, A.; Santa-aho, S.; Vippola, M.; Leiviskä, K. Comparison of some data-driven modelling techniques applied to Barkhausen noise data sets. In Proceedings of the 11th International Conference on Barkhausen noise and Micromagnetic Testing, Aydin, Kusadasi, Turkey, 18–21 June 2015. [Google Scholar]
- Gür, C.H. Microstructure Characterization of Heat-Treated Ferromagnetic Steels by Magnetic Barkhausen Noise Method. In Proceedings of the 5th World Congress on Mechanical, Chemical and Material Engineering, Lisbon, Portugal, 1 August 2019. [Google Scholar]
- Hizli, H.; Gür, H.C. Applicability of the Magnetic Barkhausen Noise Method for Nondestructive Measurement of Residual Stresses in the Carburized and Tempered 19CrNi5H Steels. Res. Nondestruct. Eval. 2018, 29, 221–236. [Google Scholar] [CrossRef]
- Srivastava, A.; Awale, A.; Vashista, M.; Yusufzai, M.Z.K. Monitoring of thermal damages upon grinding of hardened steel using Barkhausen noise analysis. J. Mech. Sci. Technol. 2020, 34, 2145–2151. [Google Scholar] [CrossRef]
- Knyazeva, M.; Rozo Vasquez, J.; Gondecki, L.; Weibring, M.; Pohl, F.; Kipp, M.; Tenberge, P.; Theisen, W.; Walther, F.; Biermann, D. Micro-Magnetic and Microstructural Characterization of Wear Progress on Case-Hardened 16MnCr5 Gear Wheels. Materials 2018, 11, 2290. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Srivastava, A.; Awale, A.; Vashista, M.; Yusufzai, M.Z.K. Characterization of Ground Steel Using Nondestructive Magnetic Barkhausen Noise Technique. J. Mater. Eng. Perform 2020, 29, 4617–4625. [Google Scholar] [CrossRef]
- Sorsa, A.; Leiviskä, K.; Santa-aho, S.; Lepistö, T. Quantitative prediction of residual stress and hardness in case-hardened steel based on the Barkhausen noise measurement. NDT E Int. 2012, 46, 100–106. [Google Scholar] [CrossRef]
- Altpeter, I.; Boller, C.; Kopp, M.; Wolter, B.; Fernath, R.; Hirninger, B.; Werner, S. Zerstörungsfreie Detektion von Schleifbrand. In Proceedings of the DGZfP-Jahrestagung, Bremen, Germany, 30 May–1 June 2011. [Google Scholar]
- Kneller, E. Ferromagnetismus—Mit einem Beitrag Quantentheorie und Elektronentheorie des Ferromagnetismus; Springer: Berlin/Heidelberg, Germany, 1962. [Google Scholar]
- Cullity, B.D.; Graham, C.D. Introduction to Magnetic Materials, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Karpuschewski, B.; Bleicher, O.; Beutner, M. Surface integrity inspection on gears using Barkhausen noise inspection. Procedia Eng. 2011, 19, 162–171. [Google Scholar] [CrossRef] [Green Version]
- Szielasko, K.; Kopp, M.; Tschuncky, K.; Lugin, S.; Altpeter, I. Barkhausenrausch- und Wirbelstrommikroskopie zur ortsaufgelösten Charakterisierung von dünnen Schichten. In Proceedings of the DGZfP-Jahrestagung 2004, Salzburg, Austria, 17–19 May 2004. [Google Scholar]
- Altpeter, I.; Tschuncky, R.; Szielasko, K. Electromagnetic techniques for materials characterization. In Materials Characterization Using Nondestructive Evaluation (NDE) Methods; Woodhead Publishing: Sawston, UK, 2016. [Google Scholar]
- Jiles, D.C. Dynamics of Domain Magnetization and the Barkhausen Effect. Chechoslov. J. Phys. 2000, 50, 893–988. [Google Scholar] [CrossRef]
- Stupakov, A.; Perevertov, A.; Neslušan, M. Reading depth of the magnetic Barkhausen noise. II. Two-phase surface-treated steels. J. Magn. Magn. Mater. 2020, 513, 167239. [Google Scholar] [CrossRef]
- Fahrmeir, L.; Heumann, C.; Künstler, R.; Pigeot, I.; Tutz, G. Statistik—Der Weg zur Datenanalyse; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Nalbant, M.; Gokkaya, H.; Toktas, I. Comparison of Regression and Artificial Neural Network Models for Surface Roughness Prediction with the Cutting Parameters in CNC Turning. Model. Simul. Eng 2007, 2007, 92717. [Google Scholar] [CrossRef] [Green Version]
- Specht, D.F. A General Regression Neural Network. IEEE T. Neural Networ. 1991, 2, 568–576. [Google Scholar] [CrossRef] [Green Version]
- Hecht-Nielsen, R. Theory of Backpropagation Neural Network. Neural Netw. 1988, 1, 593–605. [Google Scholar] [CrossRef]
- Palau, A.; Velo, E.; Puigjaner, L. Use of neural networks and expert systems to control a gas/solid sorption. Int. J. Refrig. 1999, 22, 59–66. [Google Scholar] [CrossRef]
- Membrain Neuronale Netze Editor und Simulator. Available online: https://membrain-nn.de/index.htm (accessed on 16 October 2020).
- Popko, A.; Jakubowski, M.; Wawer, R. Membrain Neural Network for Visual Pattern Recognition. Sci. Adv. 2013, 7, 54–59. [Google Scholar] [CrossRef]
- Woernle, I.A. Anwendbarkeit Künstlicher Neuronaler Netze zur Untergrundbewertung in der Oberflächennahen Geothermie. Ph.D. Thesis, Universität Fridericiana zu Karlsruhe, Karlsruhe, Germany, 2008. [Google Scholar]



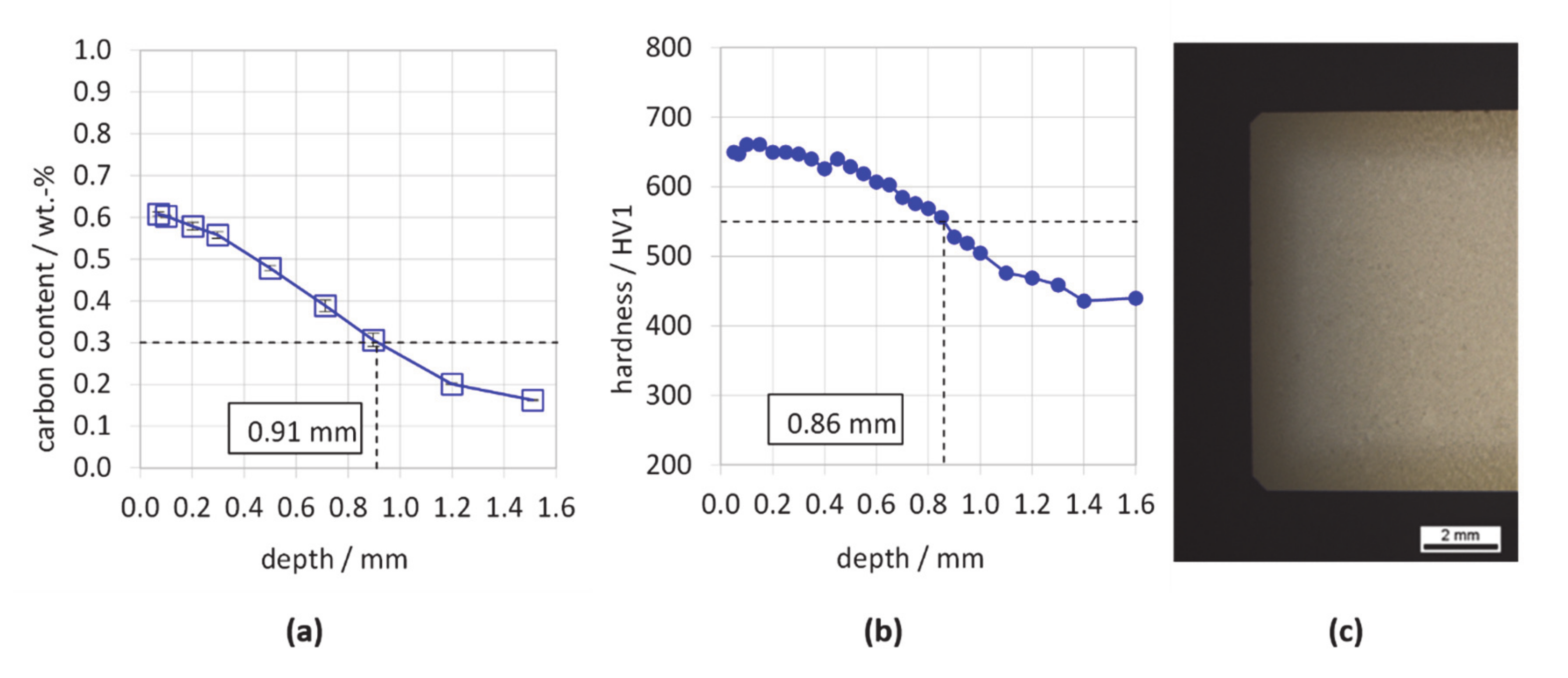






| C | Si | Mn | P | S | Cr | Mo | Ni |
|---|---|---|---|---|---|---|---|
| 0.17 | 0.39 | 0.51 | 0.01 | <0.002 | 1.56 | 0.26 | 1.43 |
| Surface Carbon Content/wt. % | Case Hardening Depth/mm | Tempering Temperature/°C |
|---|---|---|
| 0.6/0.7/0.8 | 0.5/1/2 | 150/180/210 |
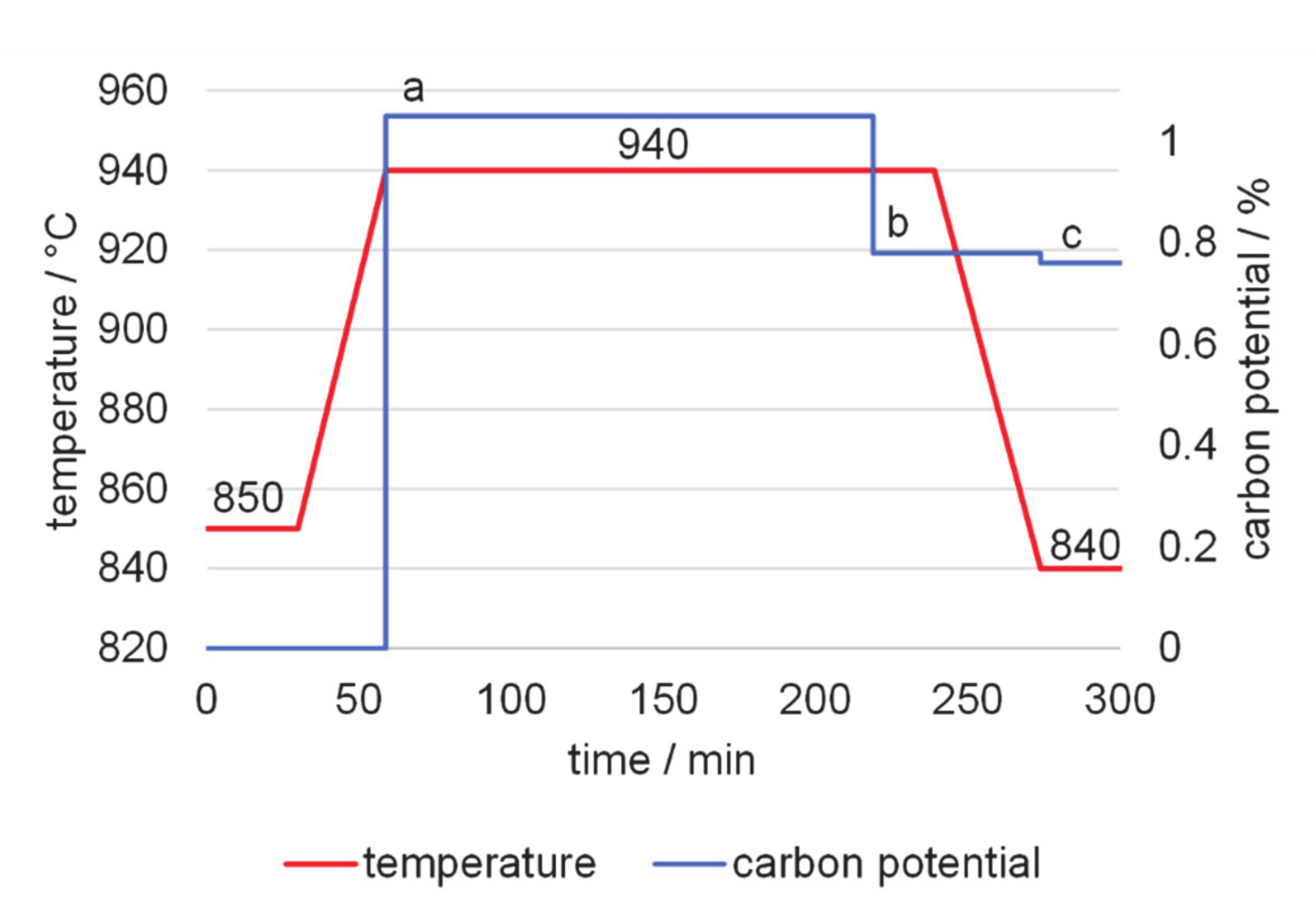
| Variation | 850 °C | a | 940 °C | b | 840 °C | c |
|---|---|---|---|---|---|---|
| 0.5 mm, 0.6 wt. % | 30 min | 0.9 vol. % | 20 min | 0.57 vol. % | 30 min | 0.57 vol. % |
| 0.5 mm, 0.7 wt. % | 30 min | 0.9 vol. % | 80 min | 0.68 vol. % | 30 min | 0.68 vol. % |
| 0.5 mm, 0.8 wt. % | 30 min | 0.9 vol. % | 80 min | 0.79 vol. % | 30 min | 0.79 vol. % |
| 1 mm, 0.6 wt. % | 30 min | 1.0 vol. % | 200 min | 0.55 vol. % | 30 min | 0.55 vol. % |
| 1 mm, 0.7 wt. % | 30 min | 1.05 vol. % | 180 min | 0.68 vol. % | 30 min | 0.66 vol. % |
| 1 mm, 0.8 wt. % | 30 min | 1.05 vol. % | 180 min | 0.78 vol. % | 30 min | 0.76 vol. % |
| 2 mm, 0.6 wt. % | 120 min | 1.05 vol. % | 740 min | 0.55 vol. % | 60 min | 0.55 vol. % |
| 2 mm, 0.7 wt. % | 120 min | 1.1 vol. % | 720 min | 0.65 vol. % | 60 min | 0.64 vol. % |
| 2 mm, 0.8 wt. % | 120 min | 1.1 vol. % | 720 min | 0.75 vol. % | 60 min | 0.75 vol. % |
| Standard Configuration | ||
| Method | Magnetization Frequency | 120 Hz |
| Harmonic analysis (HA) | Magnetization amplitude | 75 A/cm |
| Barkhausen noise (BN) | Magnetization amplitude | 75 A/cm |
| Highpass frequency | 100 kHz | |
| Lowpass frequency | No limitation | |
| Incremental permeability (IP) | Magnetization amplitude | 75 A/cm |
| Eddy current frequency | 250 kHz | |
| Eddy current (EC) | Magnetization amplitude | 65 A/cm |
| Frequencies | 3,5 kHz, 1 MHz, 2 MHz, 5 MHz | |
| Sweeps | ||
| HA, BN, IP | Magnetization frequency | 20 Hz, 30 Hz, 40 Hz, 50 Hz, 60 Hz, 80 Hz, 100 Hz, 150 Hz, 200 Hz, 250 Hz, 300 Hz, 350 Hz |
| BN | High pass frequency | no limitation, 500 kHz, 1 MHz |
| IP | Eddy current frequency | 10 kHz, 20 kHz, 60 kHz, 80 kHz, 100 kHz, 150 kHz, 200 kHz, 300 kHz, 350 kHz |
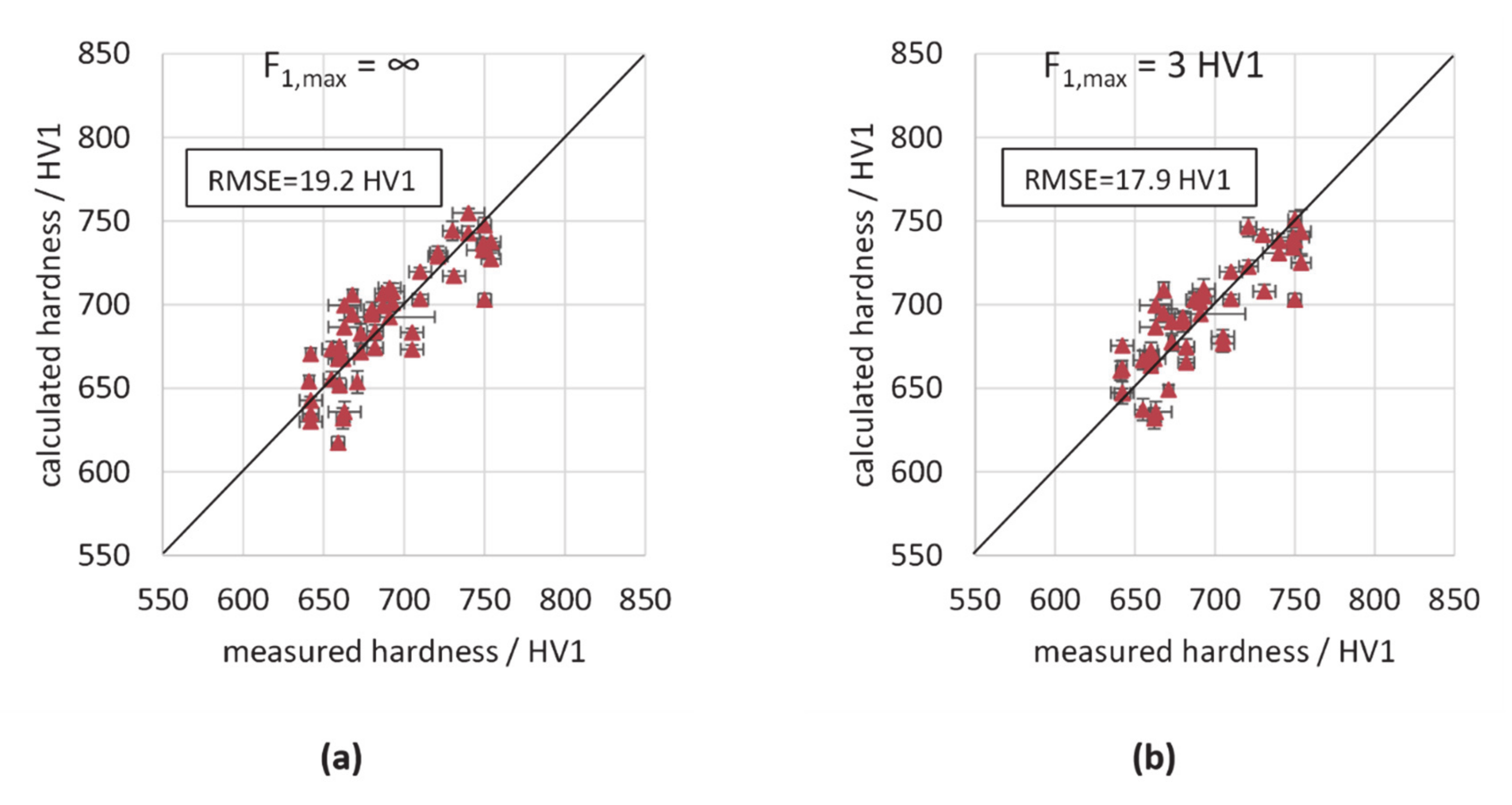
| F1,max/HV1 | F1/HV1 | R2 | RMSE/HV1 |
|---|---|---|---|
| ∞ | 9.274 | 0.8709 | 12.919 |
| 9 | 5.582 | 0.8772 | 12.599 |
| 5 | 4.887 | 0.8662 | 13.151 |
| 4 | 3.489 | 0.8669 | 13.116 |
| 3 | 2.819 | 0.8571 | 13.59 |
| 2 | 1.899 | 0.837 | 14.514 |
| 1 | 0.961 | 0.723 | 18.923 |
| F1,max = ∞ | F1,max = 3 HV1 | ||
|---|---|---|---|
| 2882.68 | 1 | 1640.43 | 1 |
| −44.3 | A3 (120 Hz) | −697.51 | A7 (100 Hz) |
| −3397.44 | Mmax (350 Hz) | −19.5 | P52 (30 Hz) |
| 274.2 | √P3 (50 Hz) | −0.36 | Hcm2 (80 Hz, HP 100 kHz) |
| −0.12 | Hco2 (50 Hz) | 411.53 | √A7 (100 Hz) |
| −142.44 | √DH25µ (120Hz, 60 kHz) | −5.59 | P72 (120 Hz) |
| −772.37 | √µr (120 Hz, 100 kHz) | −240.26 | √µr (120 Hz, 250 kHz) |
| 56.74 | P32 (150 Hz) | −1582.39 | √µr (150 Hz) |
| −33.69 | Vmag2 (350 Hz) | 1974.5 | Mr2 (350 Hz) |
| 7305.07 | Mmax2 (350 Hz) | −926.19 | √Mr (350 Hz) |
| Maximum Number of Regression Terms | F1/HV1 | R2 | RMSE/HV1 | RMSEtest/HV1 |
|---|---|---|---|---|
| 20 | 581.163 | 0.9457 | 8.375 | 13.5 |
| 10 | 9.274 | 0.8709 | 12.919 | 19.2 |
| 8 | 6.738 | 0.8548 | 13.7 | - |
| 6 | 7.174 | 0.8198 | 15.260 | 18.7 |
| 4 | 3.916 | 0.7674 | 17.341 | - |
| 2 | 3.496 | 0.6183 | 22.210 | - |
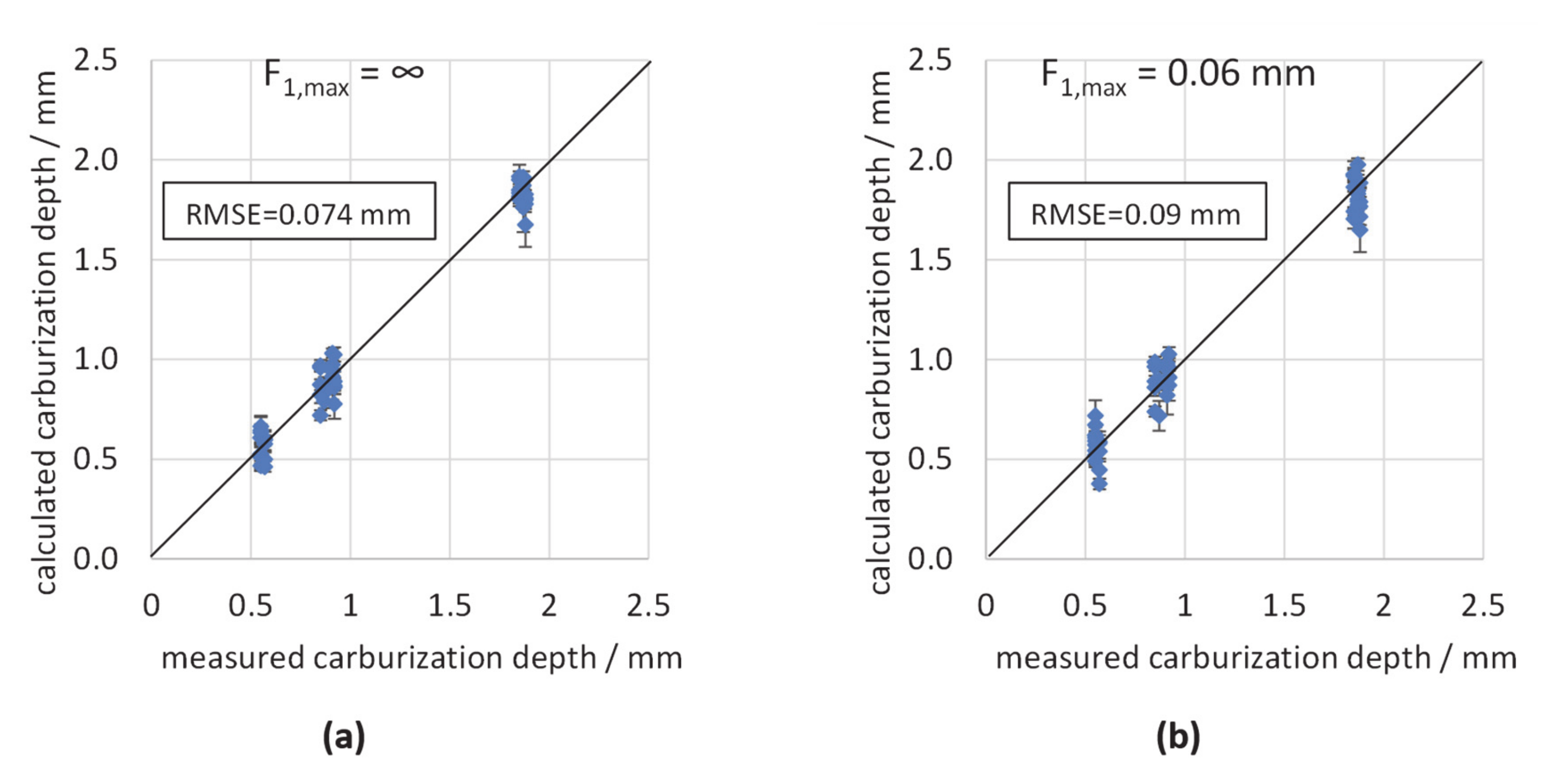
| F1,max/mm | F1/mm | R2 | RMSE/mm |
|---|---|---|---|
| ∞ | 0.267 | 0.9539 | 0.117 |
| 0.2 | 0.191 | 0.9495 | 0.123 |
| 0.1 | 0.084 | 0.949 | 0.124 |
| 0.08 | 0.076 | 0.927 | 0.148 |
| 0.07 | 0.069 | 0.9246 | 0.150 |
| 0.06 | 0.059 | 0.9446 | 0.129 |
| 0.05 | 0.038 | 0.9333 | 0.141 |
| 0.03 | 0.029 | 0.9423 | 0.131 |
| F1,Max = ∞ | F1,Max = 0.06 mm | ||
|---|---|---|---|
| −25.23 | 1 | 14.39 | 1 |
| 46.78 | √Vmag (30 Hz) | 0.72 | K (300 Hz) |
| −1.82 | √P3 (30 Hz) | −6.16 | √P3 (40 Hz) |
| 9.25 | √µmax (30 Hz) | −0.08 | P72 (50 Hz) |
| −0.07 | P72 (50 Hz) | 0.7 | √Hco (50 Hz) |
| 0.001 | Hcm2 (80 Hz) | −0.0005 | DH50m 2 (80 Hz) |
| −4.7 | Vmag2 (150 Hz) | −7.87 | √Ph3 (120 Hz) |
| 0.66 | √K (200 Hz) | 0.005 | Hcm2 (250 Hz) |
| 0.44 | √P3 (250 Hz) | −0.0003 | DH25µ2 (250 Hz) |
| 0.36 | √Hco (350 Hz) | −0.31 | Vmag2 (350 Hz) |
| Maximum Number of Regression Terms | F1/mm | R2 | RMSE/mm | RMSEtest/mm |
|---|---|---|---|---|
| 20 | 180.252 | 0.984 | 0.069 | 0.315 |
| 10 | 0.267 | 0.9539 | 0.117 | 0.130 |
| 8 | 0.178 | 0.9421 | 0.132 | - |
| 6 | 0.115 | 0.9198 | 0.155 | 0.156 |
| 4 | 0.06 | 0.842 | 0.217 | - |
| 2 | 0.047 | 0.5361 | 0.372 | - |
| Calibration Method | Hardness | Carburization Depth | ||
|---|---|---|---|---|
| - | RMSEcal/HV1 | RMSEtest/HV1 | RMSEcal/mm | RMSEtest/mm |
| linear regression (standard configuration) | 15.5 | 23.2 | 0.12 | 0.22 |
| linear regression (sweep) | 13.7 | 17.0 | 0.07 | 0.13 |
| ANN (standard configuration) | 12.7 | 15.0 | 0.06 | 0.13 |
| ANN (sweep) | 7.2 | 16.5 | 0.02 | 0.04 |
| Calibration Method | Hardness | Carburization Depth | ||
|---|---|---|---|---|
| - | RMSEcal/HV1 | RMSEtest/HV1 | RMSEcal/mm | RMSEtest/mm |
| linear regression (F1,max unlim.) | 12.1 | 19.1 | 0.074 | 0.130 |
| linear regression (F1,max lim.) | 12.5 | 17.9 | 0.090 | 0.140 |
| ANN (30 repetitions) | 7.1 | 16.4 | 0.030 | 0.103 |
| ANN (60 repetitions) | 3.7 | 18.6 | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jedamski, R.; Epp, J. Non-Destructive Micromagnetic Determination of Hardness and Case Hardening Depth Using Linear Regression Analysis and Artificial Neural Networks. Metals 2021, 11, 18. https://doi.org/10.3390/met11010018
Jedamski R, Epp J. Non-Destructive Micromagnetic Determination of Hardness and Case Hardening Depth Using Linear Regression Analysis and Artificial Neural Networks. Metals. 2021; 11(1):18. https://doi.org/10.3390/met11010018
Chicago/Turabian StyleJedamski, Rahel, and Jérémy Epp. 2021. "Non-Destructive Micromagnetic Determination of Hardness and Case Hardening Depth Using Linear Regression Analysis and Artificial Neural Networks" Metals 11, no. 1: 18. https://doi.org/10.3390/met11010018





