A Numerical and Experimental Assessment of the Small Punch Creep Test for 316L(N) Stainless Steels
Abstract
:1. Introduction
2. Model Description
2.1. Constitutive Model
2.1.1. The Elastoplastic Constitutive Model
2.1.2. The Creep Constitutive Model
2.2. Finite Element Model of the Small Punch Creep Test
3. Experimental Results SPC
4. Small Punch Creep Analysis
4.1. Numerical Simulation Cases
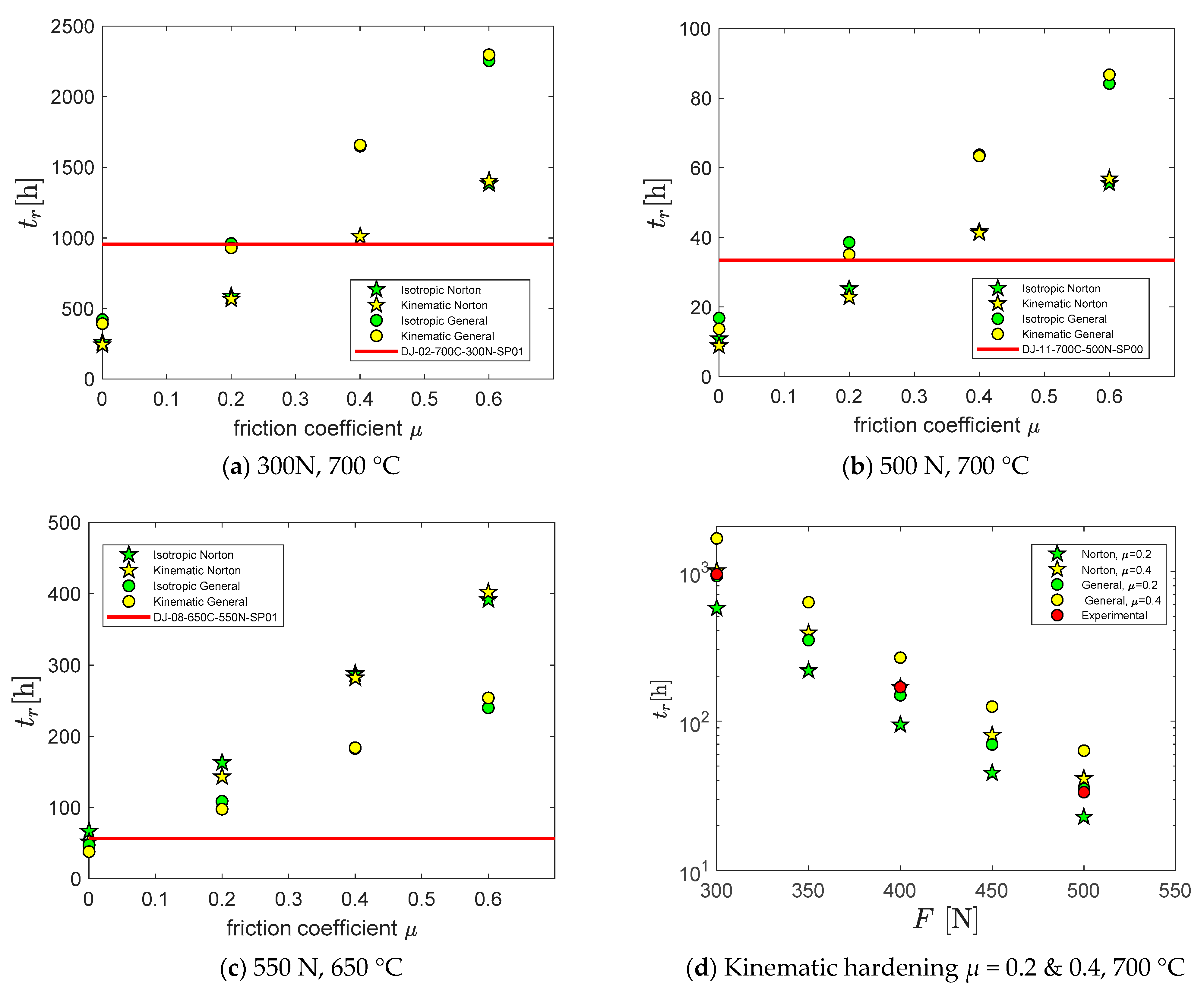
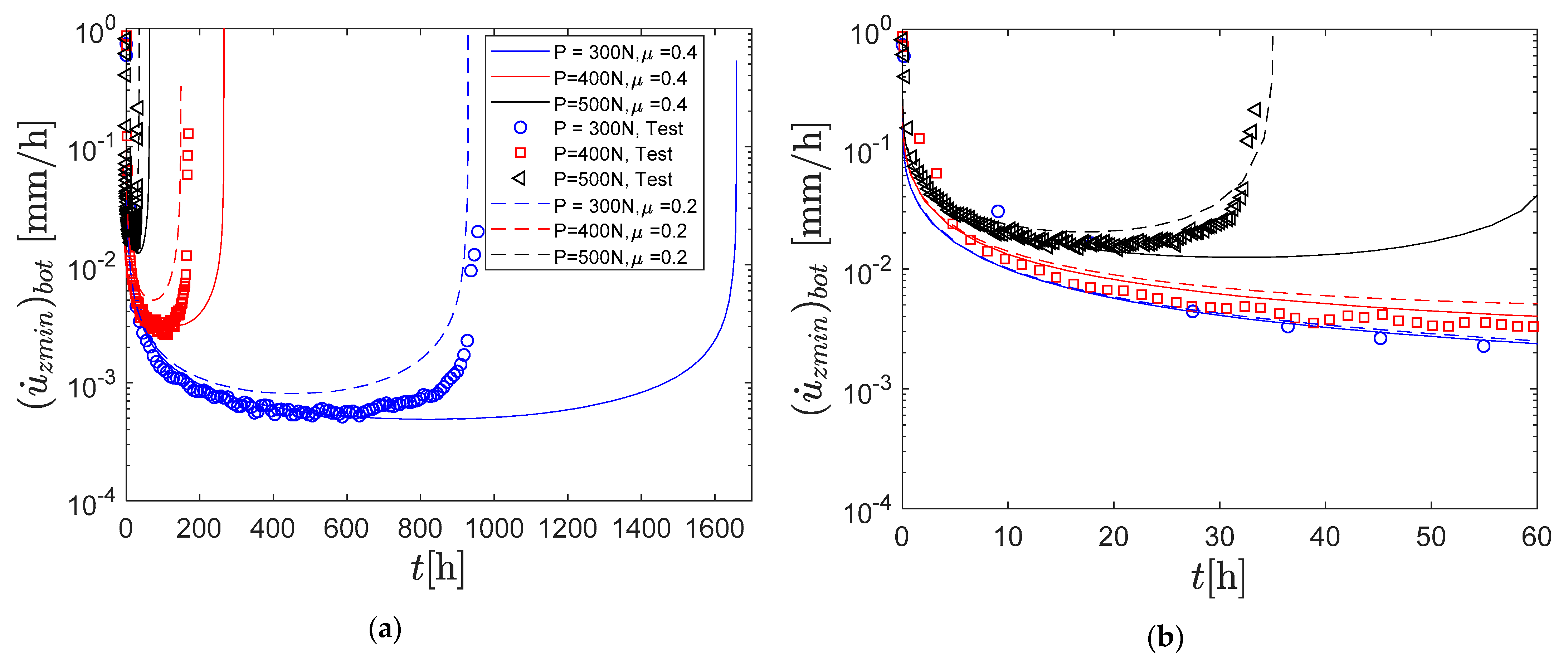
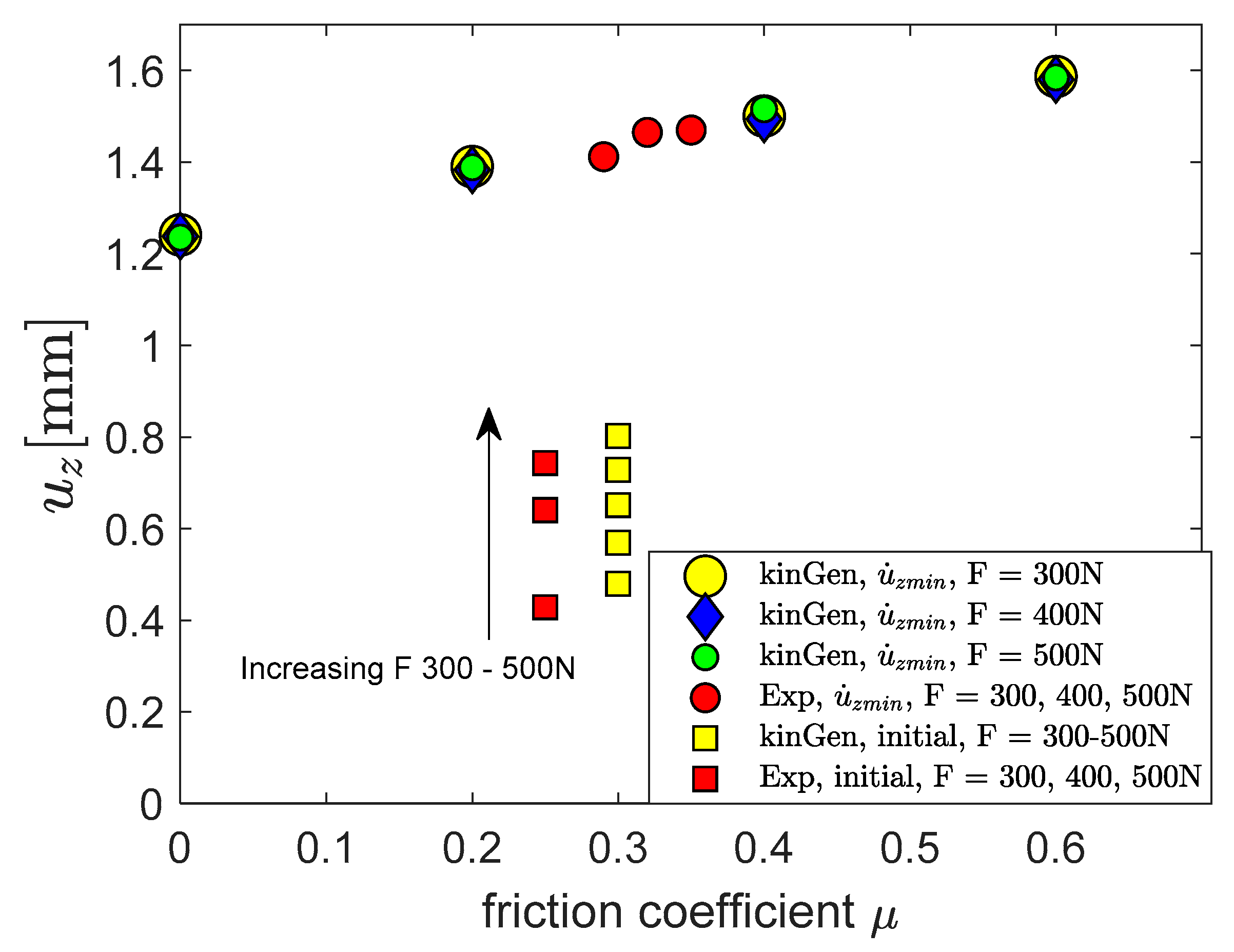
4.2. Deflection and Time to Rupture
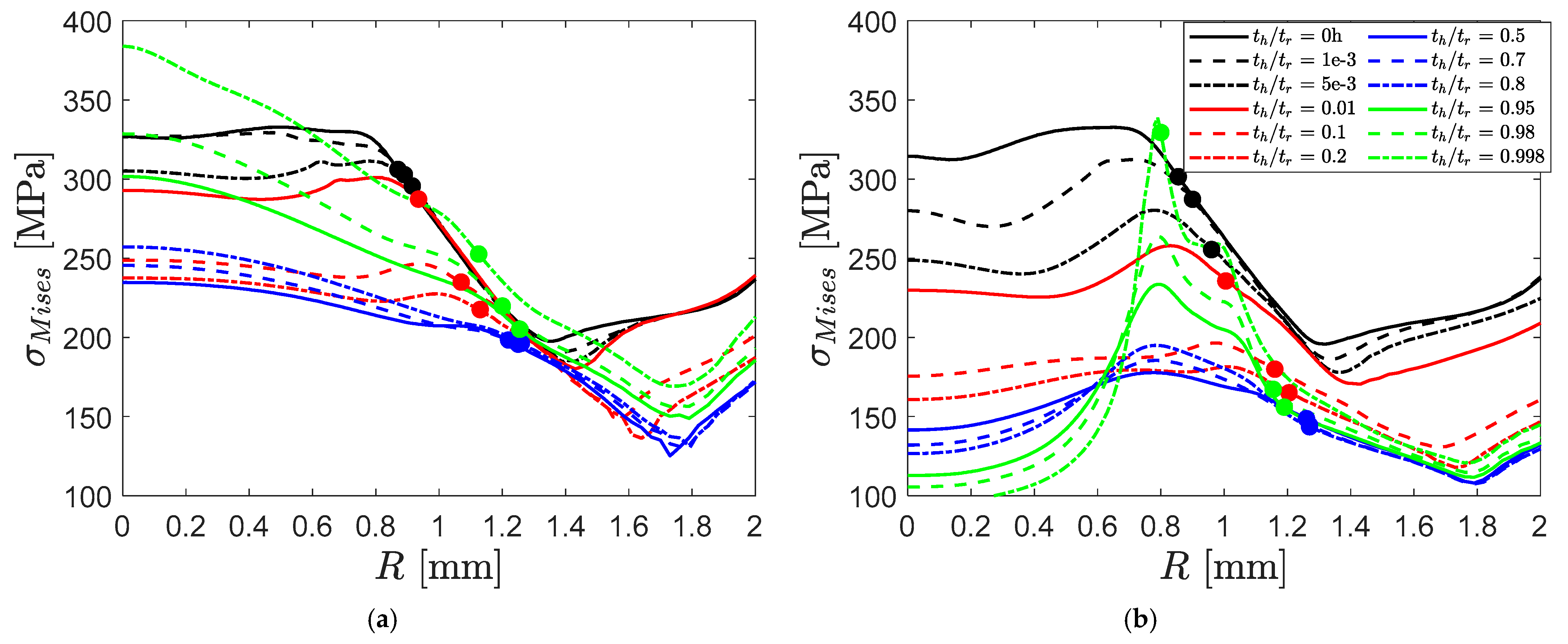
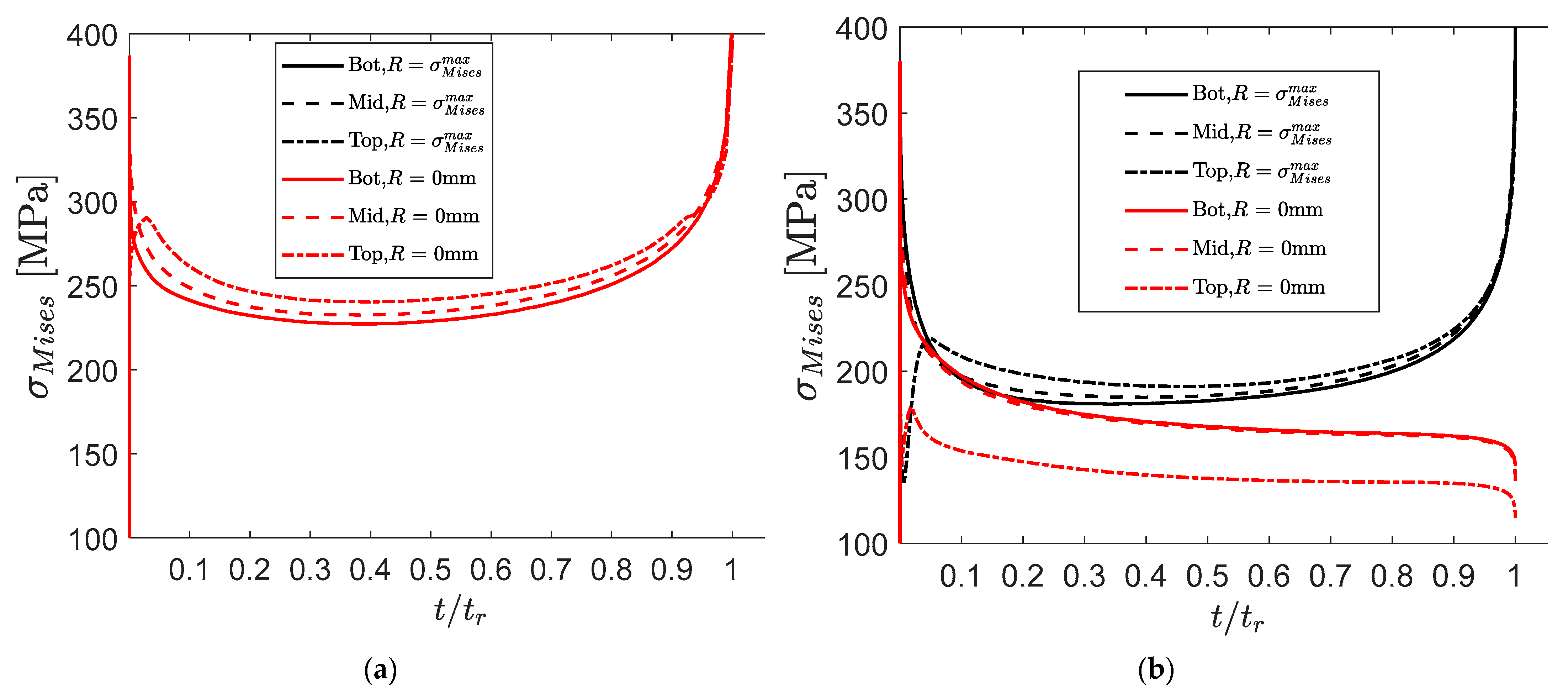
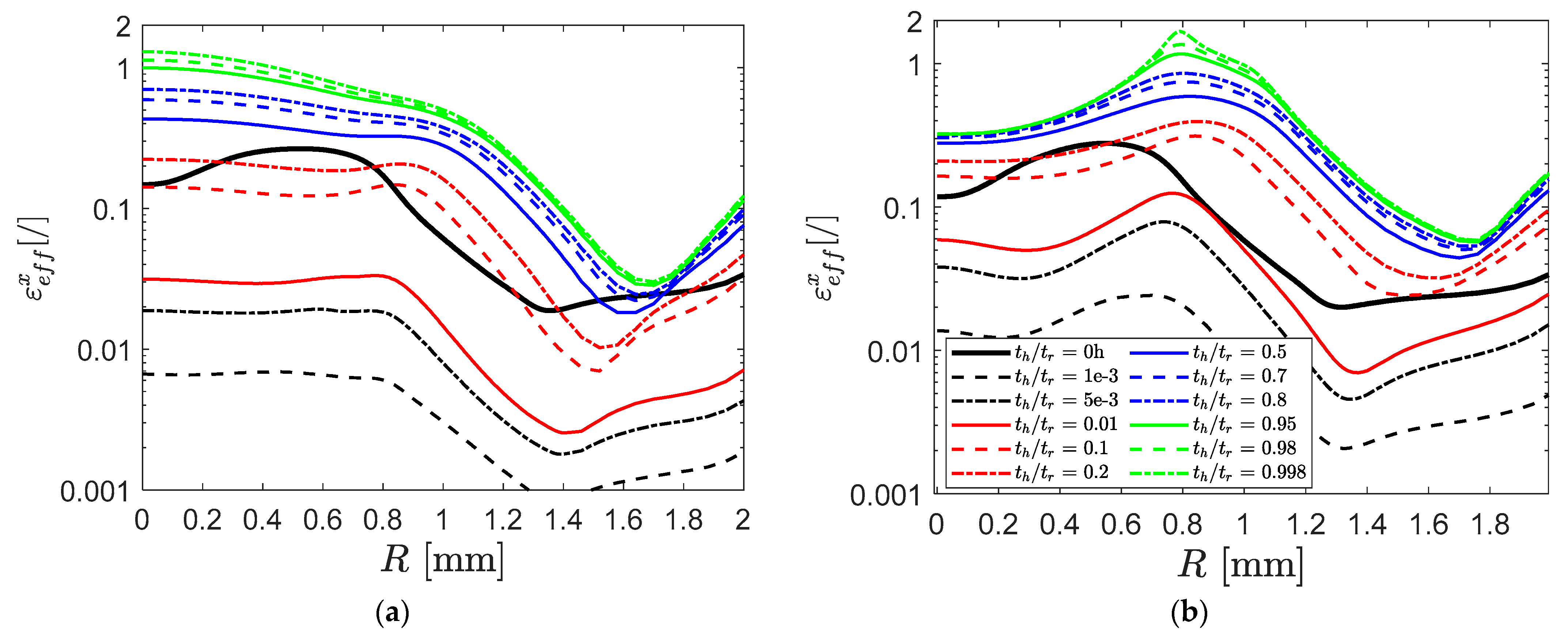
4.3. Computed Stresses and Strains
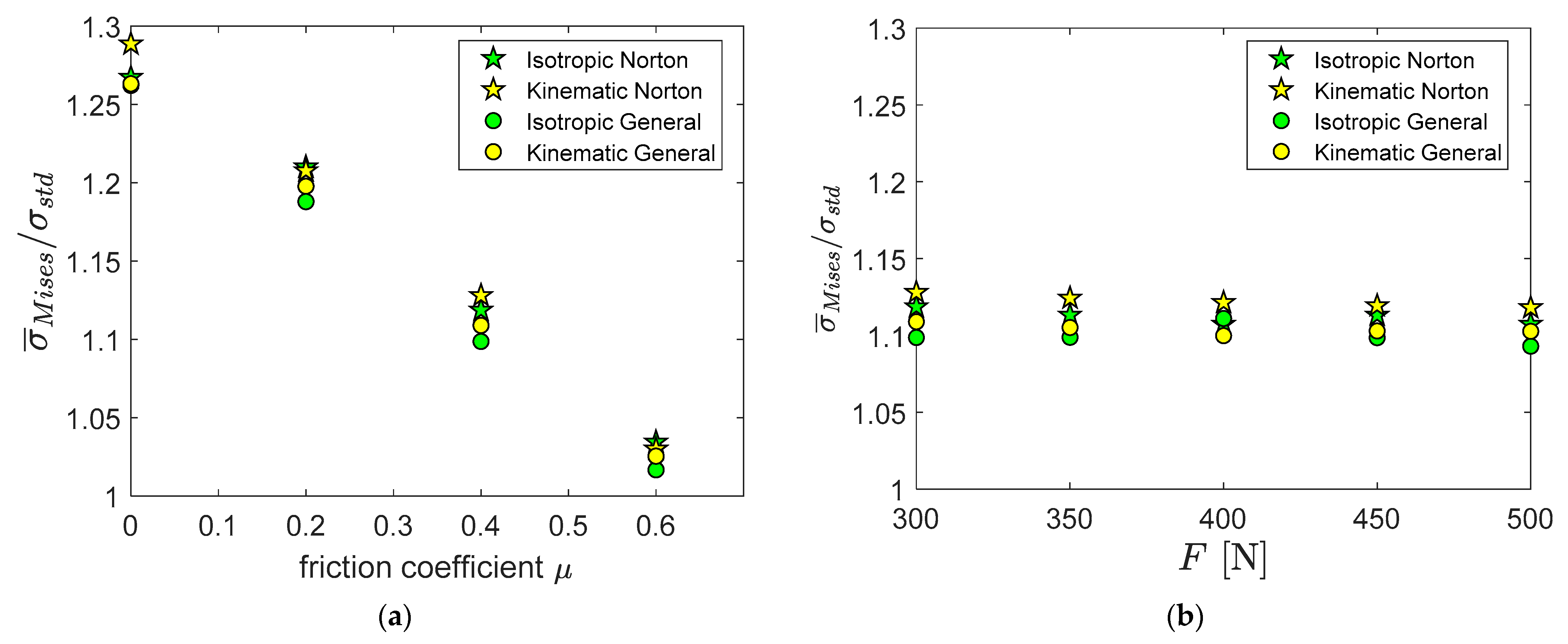
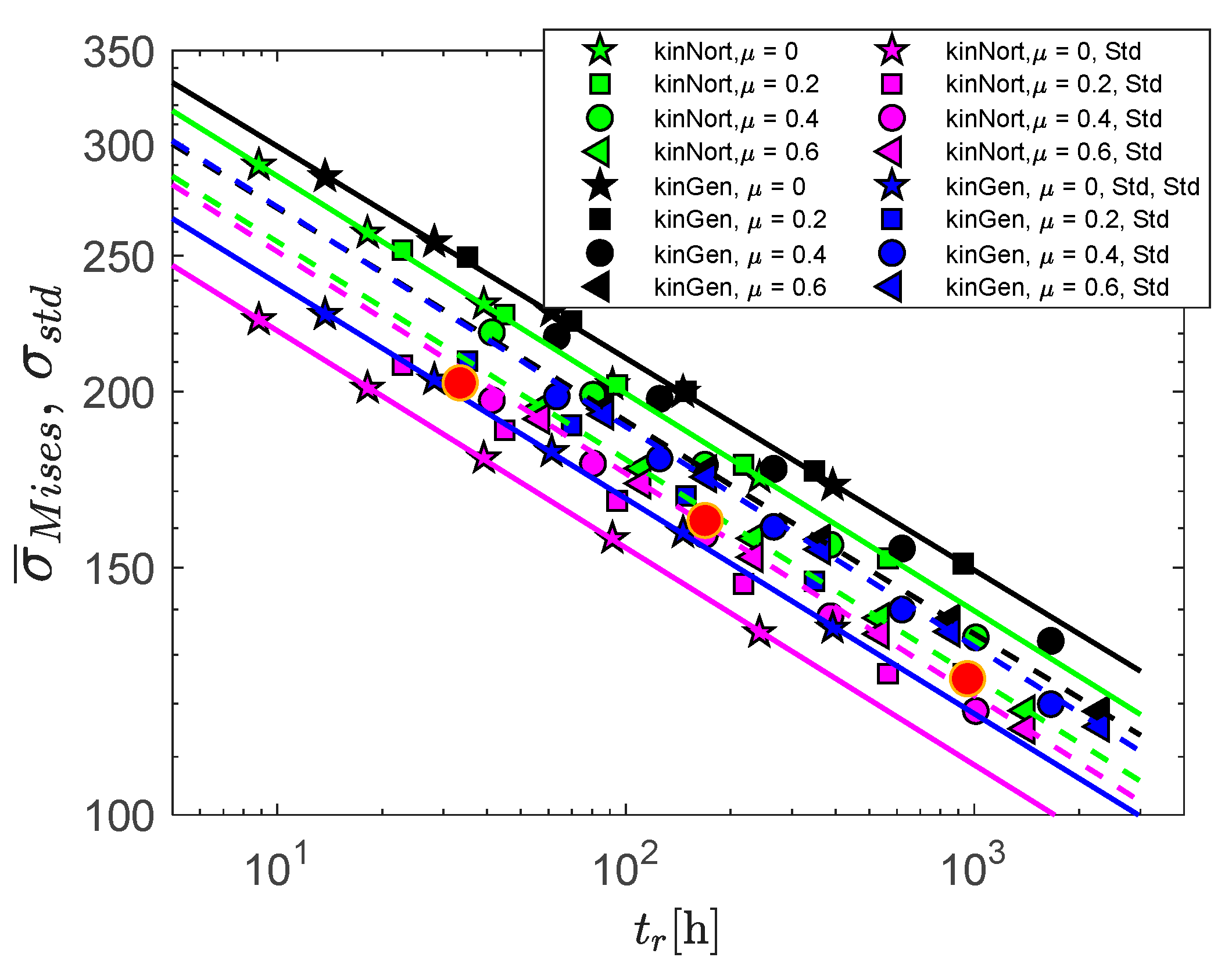
4.4. Comparison with the Standard
5. Discussion
- to assess to what extent the experimental observations can be predicted and explained by numerical simulation;
- to evaluate the importance of complexity for visco-plastic constitutive models with respect to prediction accuracy and computational effort;
- to investigate whether the RCC-MRx design data predict the SPC behaviour;
- to assess and quantify the effect of friction between the sample and the indenter for the test results;
- to compare computed results to the new small punch standard and practical aspects of the small punch creep test as an engineering tool.
6. Conclusions
- The normalized computed deflection rate versus time agrees very well with experimental data and is independent of the applied load and temperature, as well as the creep model and friction coefficient. The deflection rate has a very distinct initial decrease followed by a shallow minimum value and sharp increase prior to rupture.
- The reason for this is that the stress relaxation that occurs at the beginning of the creep homogenizes the stress distribution across the sample, and at the very end, the deflection rate increases due to increased true stress.
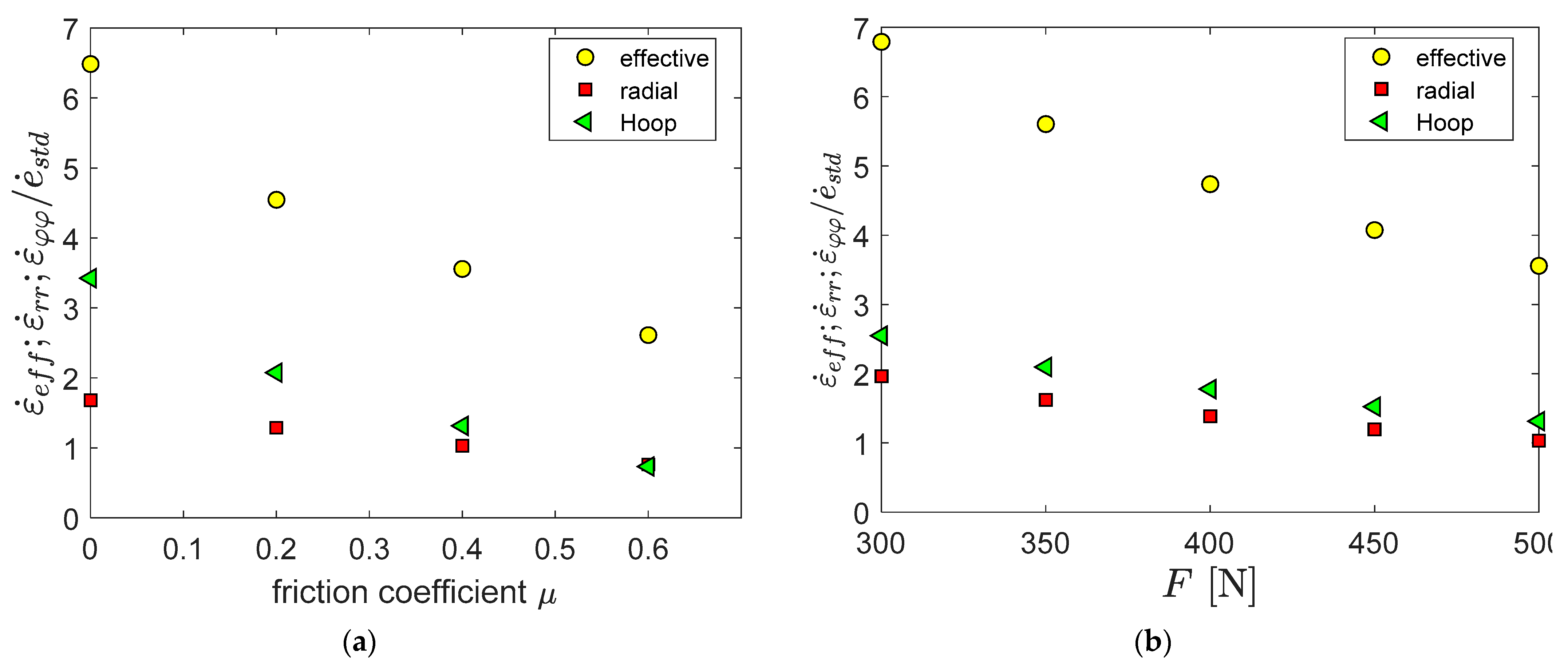
- The time to rupture increases linearly with the friction coefficient. This could potentially be used as a method to estimate the friction coefficient. The friction coefficient is affected by sample preparation and differences in measured time to rupture may be related to different sample preparations.
- Increasing friction results in an increasing localization that also moves away from the centre of the sample, but more importantly, the mean stress is reduced which explains the increase in time to rupture and a very slight increase in deflection at the minimum deflection rate.
- The time to rupture versus deflection rate is independent of the friction coefficient. Thus, friction does not affect the capability for ranking time to rupture by the SPC test.
- The time to rupture in SPC can be accurately predicted by simulation, provided that a) initial tensile properties so that the initial elastoplastic deformation is captured; b) the friction coefficient is known; and c) the creep model captures the average creep rate and ideally also creep damage in the tertiary stage.
- The small punch test is potentially better suited to estimate creep properties than tensile properties by virtue of the stress relaxation and associated stress homogenization.
- The SPC standard, which is based on the equivalence between uniaxial and small punch creep is purely empirical. Given the very different nature of the uniaxial and small punch creep, the equivalence is not obvious. Better understanding through modelling and testing of both cases could be very helpful to better assess the equivalence (or lack thereof) and guide further development of the standard.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dobeš, F.; Milička, K. Application of creep small punch testing in assessment of creep lifetime. Mater. Sci. Eng. A510-511 2009, 4, 440–443. [Google Scholar] [CrossRef]
- Dymáček, P. Recent developments in small punch testing: Applications at elevated temperatures. Theor. Appl. Fract. Mech. 2016, 86, 25–33. [Google Scholar] [CrossRef]
- Hyde, T.H.; Stoyanov, M.; Sun, W.; Hyde, C. On the interpretation of results from small punch creep tests. J. Strain Anal. Eng. Des. 2010, 45, 141–164. [Google Scholar] [CrossRef]
- Ganesh Kumar, J.; Laha, K. Small Punch Creep deformation and rupture behaviour of 316L(N) stainless steel. Mater. Sci. Eng. A 2015, 641, 315–322. [Google Scholar] [CrossRef]
- Kim, J.H.; Ro, U.; Lee, H.; Kang, S.J.; Lee, B.H.; Kim, M.K. A direct assessment of creep life based on small punch creep test. Theor. Appl. Fract. Mech. 2019, 104, 102346. [Google Scholar] [CrossRef]
- Lorenzo, M.; Cuesta, I.I.; Alegre, J.M. The relationship between the Uniaxial Creep Test and the Small Punch Creep Test of the AZ31 magnesium alloy. Mater. Sci. Eng. A 2014, 614, 319–325. [Google Scholar] [CrossRef]
- Milička, K.; Dobeš, F. Small punch testing of P91 steel. Int. J. Press. Vessel. Pip. 2006, 83, 625–634. [Google Scholar] [CrossRef]
- Saucedo-Muñoz, M.L.; Komazaki, S.-I.; Takahashi, T.; Hashida, T.; Shoji, T. Creep property measurement of service-exposed SUS 316 austenitic stainless steel by the small-punch creep-testing technique. J. Mater. Res. 2002, 17, 1945–1953. [Google Scholar] [CrossRef]
- Ule, B.; Šuštar, T.; Dobeš, F.; Milička, K.; Bicego, V.; Tettamanti, S.; Maile, K.; Schwarzkopf, C.; Whelan, M.; Kozlowski, R.; et al. Small punch test method assessment for the determination of the residual creep life of service exposed components: Outcomes from an interlaboratory exercise. Nucl. Eng. Des. 1999, 192, 1–11. [Google Scholar] [CrossRef]
- Evans, R.W.; Evans, M. Numerical modelling of small disc creep test. Mater. Sci. Technol. 2006, 22, 1155–1162. [Google Scholar] [CrossRef]
- Evans, M.; Wang, D. The small punch creep test: Some results from a numerical model. J. Mater. Sci. 2008, 43, 1825–1835. [Google Scholar] [CrossRef]
- Li, R.; Hyde, T.H.; Sun, W.; Dogan, B. Modelling and Data Interpretation of Small Punch Creep Testing. In Proceedings of the ASME 2011 Pressure Vessels and Piping Conference: American Society of Mechanical Engineer, Baltimore, MD, USA, 17–21 July 2011; Volume 6, pp. 1119–1127. [Google Scholar]
- Cortellino, F.; Rouse, J.P.; Cacciapuoti, ·B.; Sun, W.; Hyde, T.H. Experimental and Numerical Analysis of Initial Plasticity in P91 Steel Small Punch Creep Samples. Exp. Mech. 2017, 57, 1193–1212. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, L.; Song, K.; Xu, L.; Han, Y.; Jing, H.; Zhang, Y.; Li, H. Determination of creep properties of an advanced Fe-Cr-Ni alloy using small punch creep test with a modified creep strain model. Theor. Appl. Fract. Mech. 2019, 104, 102324. [Google Scholar] [CrossRef]
- Song, K.; Zhao, L.; Xu, L.; Han, Y.; Jing, H. Experimental and numerical analysis of creep and damage behavior of P92 steel by small punch tests. Theor. Appl. Fract. Mech. 2019, 100, 181–190. [Google Scholar] [CrossRef]
- CEN CWA 15627 Workshop Agreement: Small Punch Test Method for Metallic Materials (Part A A Code of Practice for Small Punch Creep Testing); European Committee for Standardization: Brussels, Belgium, 2006.
- DIN EN 10371:2021; Metallic Materials. Small Punch Test Method; English Version; German Institute for Standardization: Berlin, Germany, 2021.
- Holmström, S.; Li, Y.; Dymacek, P.; Vacchieri, E.; Jeffs, S.; Lancaster, R.; Omacht, D.; Kuboň, Z.; Anelli, E.; Rantala, J.; et al. Creep strength and minimum strain rate estimation from Small Punch Creep tests. Mater. Sci. Eng. A 2018, 731, 161–172. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Z.-W. Relationship between strain and central deflection in small punch creep specimens. Int. J. Press. Vessel. Pip. 2003, 80, 397–404. [Google Scholar] [CrossRef]
- Dymáček, P.; Milička, K. Creep small-punch testing and its numerical simulations. Mater. Sci. Eng. A 2009, 510–511, 444–449. [Google Scholar] [CrossRef]
- Wu, W.; Xiaozhe, J.; Hao, L.; Wie, S. Determination of creep damage properties from small punch creep tests considering pre-straining effect using an inverse approach. Mech. Mater. 2019, 139, 103171. [Google Scholar]
- Yang, S.; Zheng, Y.; Ling, X. Evaluation of multiaxial creep and damage evolution for small punch creep test considering critical-strain criterion. Eng. Fail. Anal. 2018, 91, 99–107. [Google Scholar] [CrossRef]
- Ling, X.; Zheng, Y.; You, Y.; Chen, Y. Creep damage in small punch creep specimens of Type 304 stainless steel. Int. J. Press. Vessel. Pip. 2007, 84, 304–309. [Google Scholar] [CrossRef]
- Arunkumar, S. Small Punch Creep Test: An Overview. Met. Mater. Int. 2020, 1–18. [Google Scholar] [CrossRef]
- Cortellino, F.; Sun, W.; Hyde, T. On the effects of friction modelling on small punch creep test responses: A numerical in-vestigation. J. Strain Analysis 2016, 51, 493–506. [Google Scholar] [CrossRef]
- Nakata, T.; Komazaki, S.I.; Kohno, Y.; Tanigawa, H. Development of a small punch testing method to evaluate the creep Property of high Cr ferritic steel:PartII—Stress analysis of small punch Test specimen by finite element method. Mater. Sci. Eng. A 2016, 666, 80–87. [Google Scholar] [CrossRef]
- Deliktaş, B.; Sönmez, M.; Türker, H.T. Characterization of Creep Behavior of high Temperature P91 steel using Uniaxial Creep and Small Punch Tests. In Proceedings of the 2016 World Congress on Advances in Civil, Environmental and Materials Research (ACEM16), Jeju, Korea, 28 August–1 September 2016; Available online: http://www.i-asem.org/publication_conf/acem16/6.ICAM16/T2F.1.MR360_1217F1.pdf, (accessed on 20 May 2021).
- Abendroth, M. Identification of creep properties for P91 steels at high temperatures using the small punch test. In Proceedings of the First International Conference SSTT, Ostrava, Czech Republic, 31 August–2 September 2010. [Google Scholar]
- Wang, L.-Y.; Song, Z.-M.; Luo, H.M.; Zhang, G.-P. 3D X-ray tomography characterization of creep cavities in small-punchtested 316 stainless steels. Mater. Sci. Eng. A 2018, 724, 69–74. [Google Scholar] [CrossRef]
- Ganesh Kumar, J.; Laha, K.; Ganesan, V.; Reddy, G.V.P. Analyses of Small Punch Creep Deformation Behavior of 316LN Stainless Steel Having Different Nitrogen Contents. J. Mater. Eng. Perform. 2018, 27, 2545–2555. [Google Scholar] [CrossRef]
- RCC-MRx; Design and Construction Rules for Mechanical Components of Nuclear Installations: High Temperature, Research and Fusion Reactors; Afcen RCC-MRx Code 2018 Edition; Afcen: Courbevoie, France, 2018.
- Baraldi, D.; Holmström, S.; Nilsson, K.-F.; Bruchhausen, M.; Simonovski, I. 316L(N) Creep Modeling with Phenomenological Approach and Artificial Intelligence Based Methods. Metals 2021, 11, 698. [Google Scholar] [CrossRef]
- Abaqus Software. Available online: https://www.3ds.com/products-services/simulia/products/abaqus/ (accessed on 10 January 2019).
- Zmat Material Model Library Software. Available online: http://www.zset-software.com/products/z-mat/ (accessed on 10 January 2019).
- Rouse, J.P.; Cortellino, F.; Sun, W.; Hyde, T.H.; Shingledecker, J. Small punch creep testing: Review on modelling and data interpretation. Mater. Sci. Technol. 2013, 29, 1328–1345. [Google Scholar] [CrossRef]
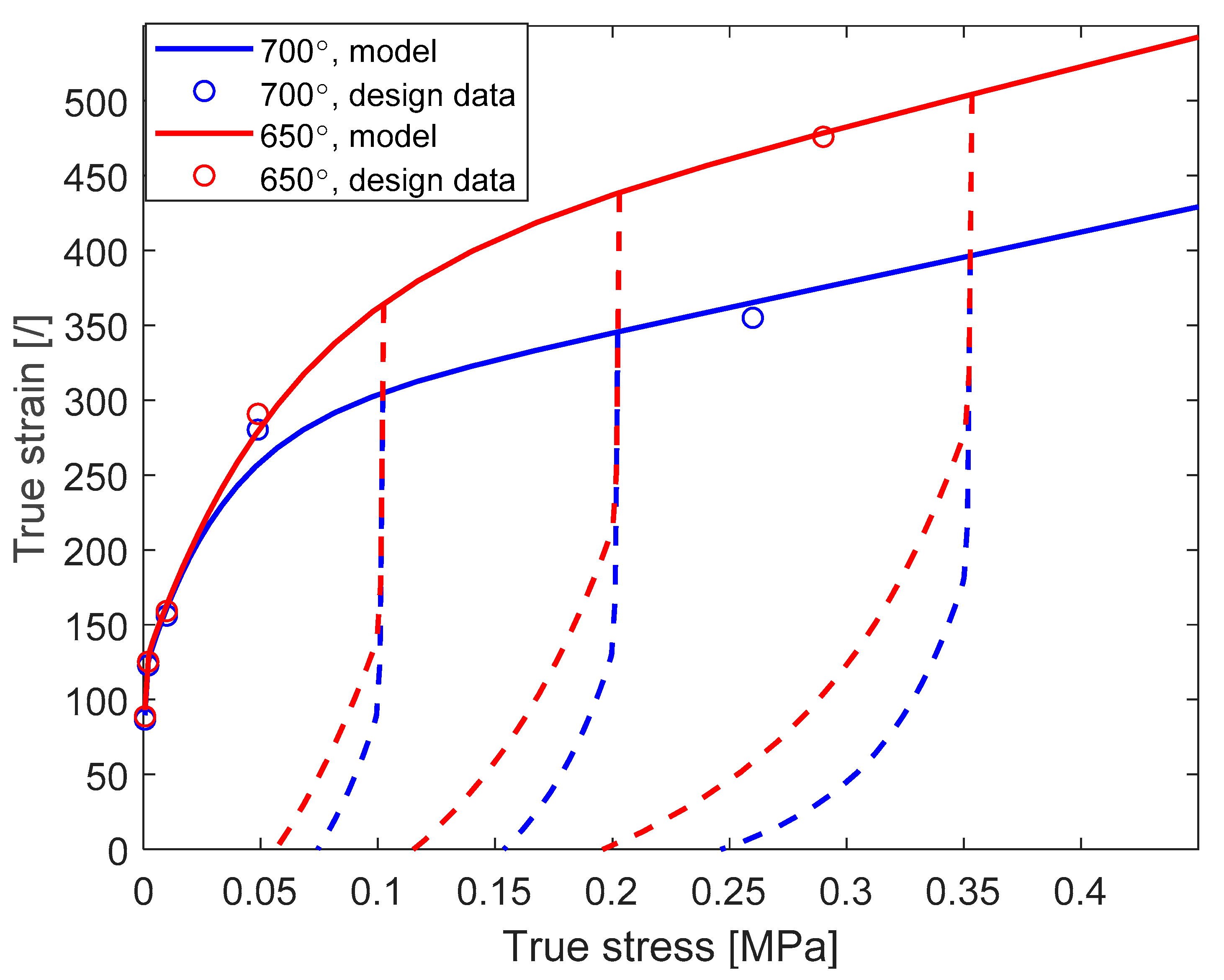





| T [°C] | E [GPa] | ν | R0 [MPa] | H (MPa) | Q1 [MPa] | b1 | Q2 [MPa] | b2 |
|---|---|---|---|---|---|---|---|---|
| 700 | 142.3 | 0.3 | 89.74 | 336.4 | 158.2 | 30.64 | 30.80 | 2545 |
| 650 | 146.5 | 0.3 | 93.24 | 392.5 | 242.2 | 17.5 | 32.05 | 2086 |
| T [°C] | Creep Model | A1 [MPa] | B1 | A2 [MPa] | B2 | A3 [MPa] | B3 | A4 [MPa] | B4 | A5 [MPa] | B5 | n |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 700 | Gen. | 1210 | 0 | 592 | 0 | 650 | 0 | 122 | 0 | 13 | 0 | 6.43 |
| Norton mean | 1682 | - | - | - | - | - | - | - | - | - | 6.24 | |
| Norton min | 1779 | - | - | - | - | - | - | - | - | - | 6.43 | |
| 650 | Gen. | 1159 | −0.19 | 890 | 0.38 | 279 | 0 | 470 | 0.075 | 16.07 | 0 | 7.39 |
| Norton mean | 1903 | - | - | - | - | - | - | - | - | - | 7.08 | |
| Norton Min | 1952 | - | - | - | - | - | - | - | - | - | 7.39 |
| Specimen | T [°C] | F [N] | u0 [mm] | umin [mm] | utr/2 (mm) | [h] | tr [h] | [µm/h] | [µm/h] | σmin [MPa] | σtr/2 [MP] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| DJ-08-650C-550N-SP01 | 650 | 550 | 0.86 | 1.36 | 1.36 | 29 | 56.6 | 7.12 | 6.65 | 234 | 231 |
| DJ-11-700C-500N-SP00 | 700 | 500 | 0.743 | 1.47 | 1.413 | 17.1 | 33.4 | 15.7 | 15.0 | 203 | 205 |
| DJ-01-700C-400N-SP01 | 700 | 400 | 0.64 | 1.46 | 1.46 | 85.8 | 169 | 2.73 | 2.69 | 162 | 160 |
| DJ-02-700C-300N-SP00 | 700 | 300 | 0.428 | 1.41 | 1.35 | 487 | 956 | 0.515 | 0.560 | 125 | 127 |
| T [°C] | F (N) | μ | Model |
|---|---|---|---|
| 700 | 300, 350, 400, 450, 500 | 0, 0.2, 0.4, 0.6 | IsoNort, KinNort, isoGen, KinGen |
| 650 | 350, 400, 450, 500, 550 | 0, 0.2, 0.4, 0.6 | IsoNort, KinNort, isoGen, KinGen |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nilsson, K.-F.; Baraldi, D.; Holmström, S.; Simonovski, I. A Numerical and Experimental Assessment of the Small Punch Creep Test for 316L(N) Stainless Steels. Metals 2021, 11, 1609. https://doi.org/10.3390/met11101609
Nilsson K-F, Baraldi D, Holmström S, Simonovski I. A Numerical and Experimental Assessment of the Small Punch Creep Test for 316L(N) Stainless Steels. Metals. 2021; 11(10):1609. https://doi.org/10.3390/met11101609
Chicago/Turabian StyleNilsson, Karl-Fredrik, Daniele Baraldi, Stefan Holmström, and Igor Simonovski. 2021. "A Numerical and Experimental Assessment of the Small Punch Creep Test for 316L(N) Stainless Steels" Metals 11, no. 10: 1609. https://doi.org/10.3390/met11101609
APA StyleNilsson, K.-F., Baraldi, D., Holmström, S., & Simonovski, I. (2021). A Numerical and Experimental Assessment of the Small Punch Creep Test for 316L(N) Stainless Steels. Metals, 11(10), 1609. https://doi.org/10.3390/met11101609






