Next Article in Journal
Effect of Strain Rate and Extrinsic SIZE Effect on Micro-Mechanical Properties of Zr-Based Bulk Metallic Glass
Next Article in Special Issue
Improving the Effectiveness of the Solid-Solution-Strengthening Elements Mo, Re, Ru and W in Single-Crystalline Nickel-Based Superalloys
Previous Article in Journal
A Numerical and Experimental Assessment of the Small Punch Creep Test for 316L(N) Stainless Steels
Previous Article in Special Issue
The Creep and Oxidation Behaviour of Pesting-Resistant (Mo,Ti)5Si3-Containing Eutectic-Eutectoid Mo-Si-Ti Alloys
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Metals
Volume 11
Issue 10
10.3390/met11101610
metals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Ultra-High Temperature Creep of Ni-Based SX Superalloys at 1250 °C

by
Satoshi Utada
1,2,
Lucille Despres
1,3 and
Jonathan Cormier
1,*
1
Institut Pprime, UPR CNRS 3346, Physics and Mechanics of Materials Department, ISAE-ENSMA, 1 Avenue Clément Ader, BP 40109, CEDEX, 86961 Futuroscope-Chasseneuil, France
2
Department of Materials, University of Oxford, Parks Road, Oxford OX1 3PH, UK
3
Institut de Recherche sur les Céramiques (IRCER), Université de Limoges, UMR CNRS 7315, 12 Rue Atlantis, 87068 Limoges, France
*
Author to whom correspondence should be addressed.
Metals 2021, 11(10), 1610; https://doi.org/10.3390/met11101610
Submission received: 20 August 2021 / Revised: 19 September 2021 / Accepted: 25 September 2021 / Published: 11 October 2021
(This article belongs to the Special Issue Creep Behavior of Metals and Alloys)
Browse Figures
Versions Notes

Abstract

:
Very high temperature creep properties of twelve different Ni-based single crystal superalloys have been investigated at 1250 °C and under different initial applied stresses. The creep strength at this temperature is mainly controlled by the remaining γ′ volume fraction. Other parameters such as the γ′ precipitate after microstructure evolution and the γ/γ′ lattice parameter mismatch seem to affect the creep strength to a lesser degree in these conditions. The Norton Law creep exponent lies in the range 6–9 for most of the alloys studied, suggesting that dislocation glide and climb are the rate limiting deformation mechanisms. Damage mechanisms in these extreme conditions comprise creep strain accumulation leading to pronounced necking and to recrystallization in the most severely deformed sections of the specimens.

1. Introduction

Ni-based single crystal (SX) superalloys are key materials for the manufacture of blades and vanes used in the hottest parts of the most advanced aero-engines and industrial gas turbines [1,2,3]. These alloys are currently used at temperatures of up to 1100 °C–1150 °C during operation of civil and military aero-engines owing to a combination of both good environmental resistance to corrosion and oxidation and excellent mechanical properties, especially under high temperature creep conditions. These properties are inherited from the specific microstructure of Ni-based superalloys consisting of a high volume fraction (>50%) of the γ′ phase (L12 structure) strengthening precipitates embedded coherently in an FCC disordered γ matrix with a high content of solid solution strengthening elements.
Many previous research has focused on the creep strength, deformation mechanisms, and microstructure evolution at temperatures between 700 °C and 1150 °C [3,4,5,6,7,8,9,10,11,12,13,14,15], corresponding to regular service conditions. Hence, ultra-high temperature creep performance data of Ni-based SX superalloys at temperatures above 1200 °C are limited to only a few studies [4,16,17,18,19,20]. It is important to characterize the creep behavior under such extreme conditions; since overheatings of gas turbine engine systems can occur in specific cases, such as single engine operation (the so-called “One Engine Inoperative” event, or OEI regimes) and emergency landing abort that lead to operation at contingency power [21,22]. For example, the tip of a turbine blade can be exposed to overheated temperature as high as 1260 °C [23]. Contingency power operation is especially crucial for helicopter engines [24]. Extreme temperatures can also be met during acceleration stages of supersonic flights whether it is for future commercial aircraft or military applications such as interceptor fighter jets, missiles, and target drones. Therefore, understanding the creep behavior and damage of various Ni-based SX superalloys under overheated temperature conditions is an important topic to guide future design of materials, components, and gas turbine systems.
In the very few attempts at investigating the creep behavior of SX superalloys at or above 1200 °C, studies have mainly focused on the role of alloying elements on the creep strength [18,19], on understanding the role of temperature changes compared to isothermal conditions [25,26,27] or on the use of such very high temperature creep data for constitutive modelling [4,18]. The most advanced understanding of the creep performance of an alloy at extreme temperatures has been presented by A. Epishin et al., studying CMSX-4 (second generation alloy) in tension creep tests at 1288 °C, i.e. at nearly the γ′-solvus temperature of the alloy [17]. This study was primarily developed to better understand deformation mechanisms during the Hot Isostatic Pressing (HIP) of this Ni-based SX superalloy and to obtain data to simulate this process for the purpose of casting pore closure. According to the findings of Epishin et al., there is a significant creep anisotropy at this temperature (even greater than the one usually observed in the 700–800 °C temperature range [8]), as well as glide-climb operating deformation mechanisms. This study has been complemented more recently by similar research in the 1150–1288 °C temperature range of a single-phase γ-analogue of the CMSX-4 alloy, with similar conclusions [20].
With the aim of better defining the actual temperature capability for future civil and military aero-engine components, and to obtain a reliable database for benchmarking with other classes of high temperature materials (e.g. ceramic matrix composites, high entropy alloys, Nb-based silicides etc.), creep tests at 1250 °C were performed in air using 12 different Ni-based SX superalloys (Mar-M200+Hf, Mar-M247LC, AM1, CMSX-4, Rene N5, PWA 1484, CMSX-4 Plus, Rene N6, CMSX-10N, MCNG, TMS-238, TROPEA). A range of minimum creep strain rates over six decades were investigated, allowing an objective evaluation of the intrinsic creep performance of the above alloys. In the present study, special attention was paid to the microstructural stability at such extremely high temperatures as a function of the alloys’ chemistry, as well as to the Norton Law exponent of the alloys studied.

2. Experimental Methods

2.1. Materials

A total of 12 different Ni-based SX superalloys were characterized in this study. The alloys and their compositions are given in Table 1. All the materials were cast using a standard Bridgman process by different suppliers. Solution heat treatment and two/three stage aging treatments were applied to all specimens to obtain a cubic γ/γ′ microstructure with precipitate size ranging between 0.3–0.6 µm. Heat treatment conditions are available in references [27,28]. Representative initial microstructures are shown in Figure 1.

2.2. Creep Tests

SX bars or plates were machined first by electric discharge machining from rods having a longitudinal crystallographic misorientation within 10° of the <001> direction. Materials were then machined by turning operations into tensile creep testing specimens having a geometry of a 14 mm gauge length and a 4 mm diameter. Parallel portions of the cylindrical specimens were mechanically polished down to P4000 SiC abrasive paper to remove residual stresses inherited from machining, which helps to prevent surface recrystallization during high temperature testing.
Tensile creep tests were performed in air using a Setra SF 2400 in-house-customized creep testing frame equipped with a radiant heating furnace [29,30]. The temperature of a specimen was controlled within 1250 ± 2 °C by a Eurotherm 2408 temperature controller (Eurotherm Ltd., Worthing, UK) connected to an S-type thermocouple spot-welded in the middle of the gauge section, in accordance with TMF Code of Practice [31]. Elongation of a specimen was monitored by a Keyence LS7070T contactless optical extensometer (Keyence Corp., Osaka, Japan) that detects a distance between markers attached to each end of the specimen’s gauge length. A heating rate of 100 °C/min was used from 600 °C to 1230 °C, followed by manual temperature control up to 1250 °C to ensure overheating did not occur. This last ramp from 1230 °C up to 1250 °C lasted no more than 2 min. The mechanical load was applied to a specimen with a soak time of 1 min after reaching 1250 °C to avoid microstructural changes as much as possible. Creep-tested specimens were cooled rapidly after failure at a rate greater than 10 °C/s down to ~900 °C, to minimize γ′ evolution during the cooling and thus enable observation of γ′ precipitates that were retained during creep loading at 1250 °C [30].

2.3. Microstructural Characterization

The γ/γ′ microstructure was observed by scanning electron microscopy, either by secondary or backscatter electron imaging using a JEOL JSM-7000F field emission gun scanning electron microscope (JEOL Ltd., Tokyo, Japan) operated at 25 kV. Longitudinal sections of specimens were mechanically polished down to 1-μm diamond powder spray and then chemically etched using Aqua Regia for 8–10 s at around 4 °C to reveal their γ/γ′ microstructure. The volume fraction of γ′ phase was measured near the fracture surface of the specimens after the creep test (i.e. 3 mm away from the fracture surface, in an area where no pronounced stress triaxiality was encountered due to necking) using in-house algorithms previously developed at Institut Pprime [32].
Aside from creep tested specimens, samples were prepared to measure equilibrium γ′ volume fraction at different temperatures between 900 °C and 1350 °C. The same creep test specimens were subjected to creep loading at 1050 °C/140 MPa for durations ranging between 50 h and 200 h to have a complete γ′-rafted structure. The gauge length section of pre-crept specimens was cut into pieces to have different aging temperature. A resistance heating furnace was kept at ± 2 °C from the set temperature and pieces were aged for 1 h to have equilibrated microstructures [25,26]. The same preparation and observation methods as employed for creep ruptured specimens were employed to obtain images of the microstructure for stereological analyses. The observation plane was parallel to the loading direction. Measurement methods explained above were the same as those used for CMSX-4, CMSX-4 Plus, and TROPEA in a previous study by the same authors [33].

3. Results

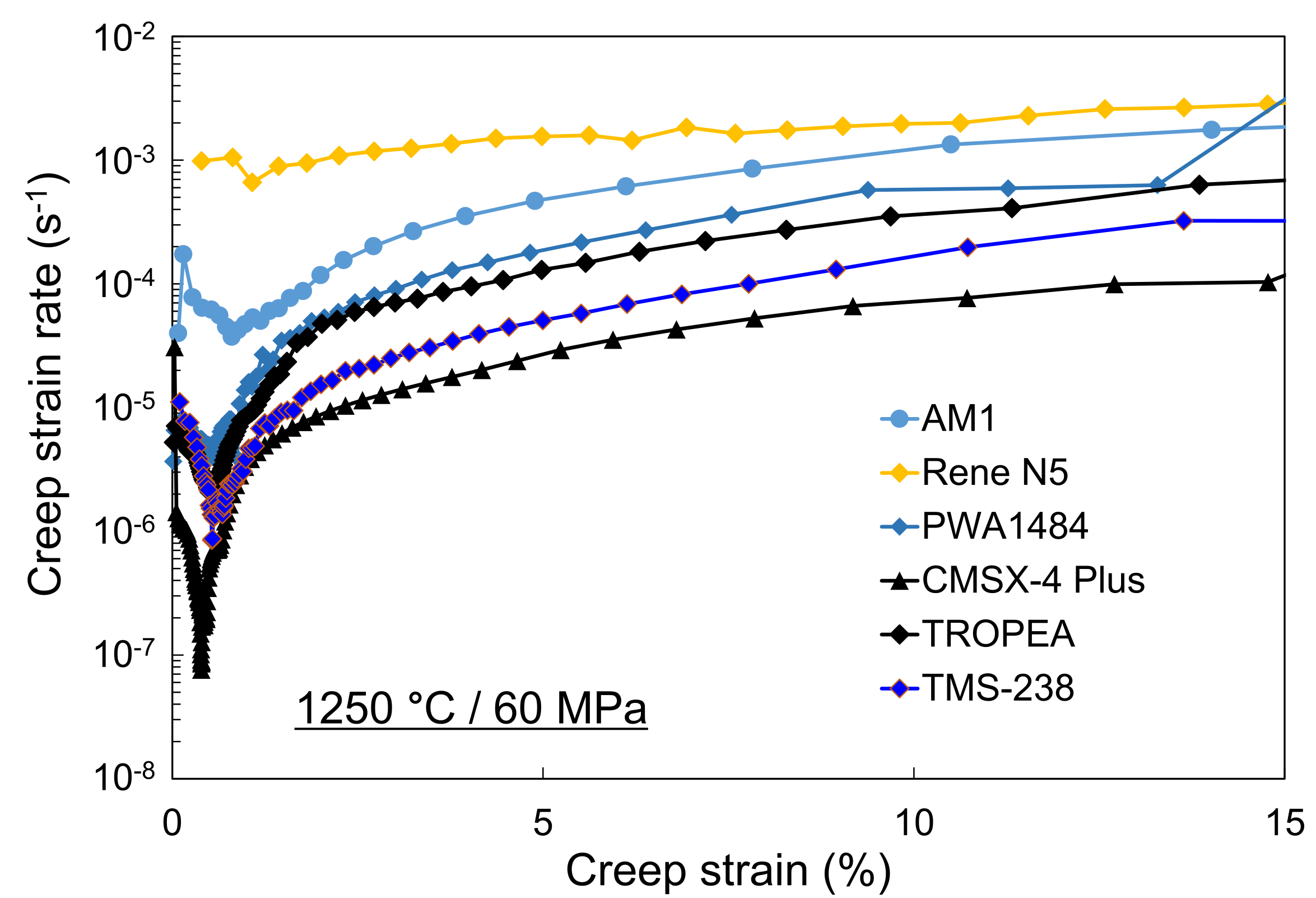
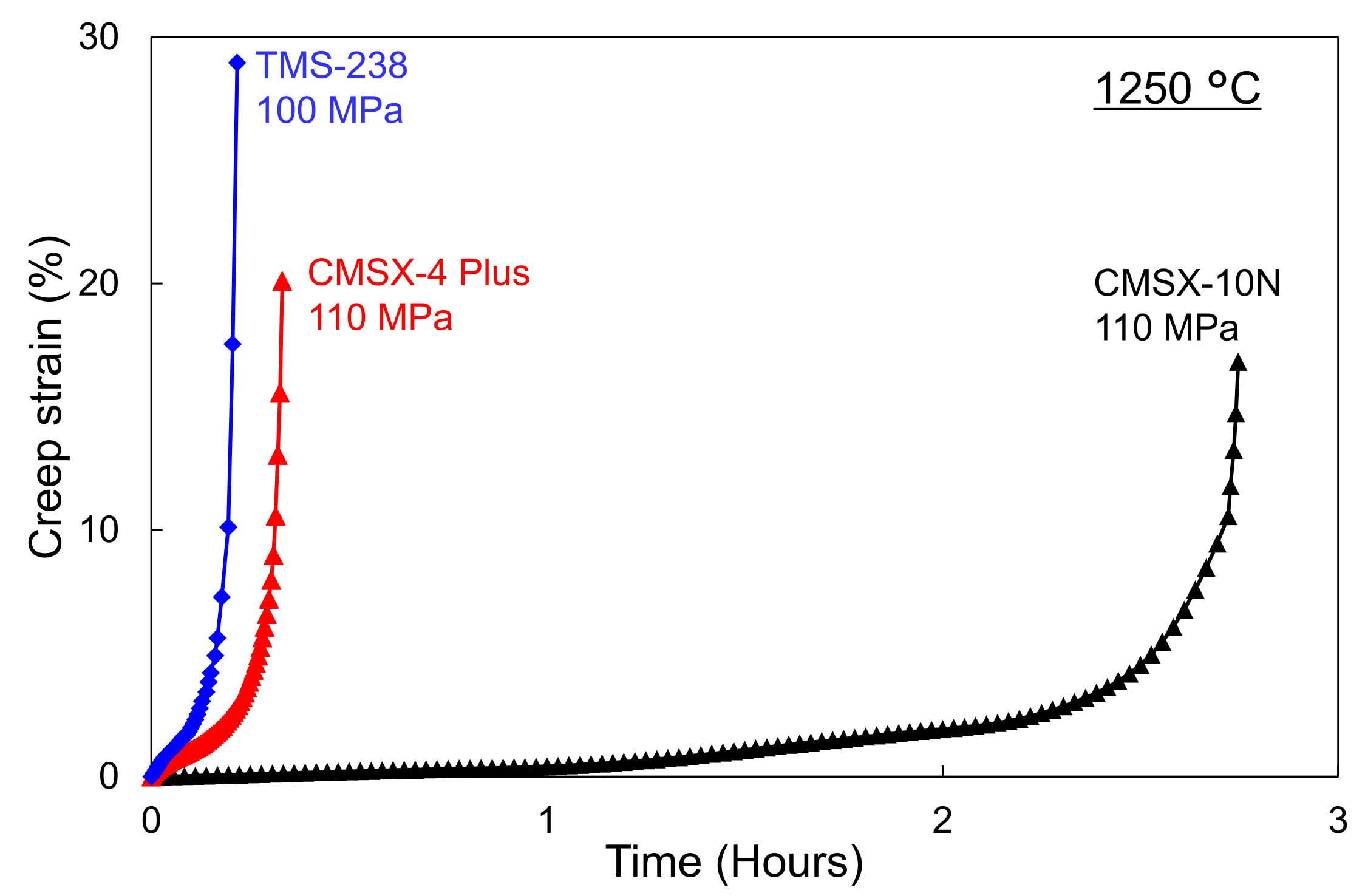
3.1. Creep Tests at 1250 °C

Results of creep tests at 1250 °C/60 MPa are shown as creep curves in Figure 2. CMSX-10N was interrupted at 31 h with 0.79% creep strain, which is a significantly longer test duration than all the other SX superalloys tested at this condition. TMS-238 and CMSX-4 Plus have relatively smaller creep strain at rupture, around 20%, compared to the other alloys. Most of the materials displayed clear primary and tertiary creep stages with a varying strain rate during steady state, which can be confirmed by the enlarged creep curves in Figure 2b and the creep strain rate curves at 1250 °C/60 MPa in Figure 3. Figure 3 shows that material with a smaller minimum creep strain rate has a higher creep rupture life, which is in accordance with other studies focusing on creep deformation of SX superalloys at temperatures above 1150 °C [4,16,17,18,19,34]. Mar-M200+Hf and Mar-M247LC were strained at a constant rate until rupture with above 50% strain at rupture. These materials could not support the target applied stress of 60 MPa and the strain rate represents the displacement rate of a lever arm that was connected to the loading line. In fact, as will be seen later in this article, these alloys are in the γ′ supersolvus condition at this temperature. Rene N5 also had a very short creep life at this condition; however, the material reached the target applied stress, and the strain at rupture was 39%, which is significantly smaller than that of Mar-M200+Hf and Mar-M247LC. Contrary to the other alloys used for the comparison in Figure 3, Rene N5 at 1250 °C/60 MPa shows no strain hardening within the first 2–3% of creep deformation.
The three alloys with the best creep life at 1250 °C/60 MPa were CMSX-10N, CMSX-4 Plus, and TMS-238, and these materials were further tested with higher applied stresses. Creep curves at 1250 °C/100-110 MPa are shown in Figure 4. At these conditions, TMS-238 showed a nearly 30% strain at rupture, which is similar to the behavior of AM1 or CMSX-4 at 1250 °C/60 MPa. Even in this extreme creep condition at 1250 °C/110 MPa, CMSX-10N had very small primary creep strain and longer creep life compared to most of the other alloys tested at 1250 °C/60 MPa.
Creep strain rate curves of some representative materials tested with different applied stresses are shown in Figure 5. Strain at minimum strain rate for CMSX-4 Plus (Figure 5a) and TMS-238 (Figure 5b) is increasing with the initial applied load. This trend was also reported for CMSX-4 tested at 1288 °C and 1200 °C [4,17]. TROPEA at 1250 °C/80 MPa (Figure 5c) and Rene N5 at 1250 °C/60 MPa (Figure 5d) are examples of creep strain rate curves that do not present clear secondary creep stage and lead to very short creep life.
The minimum creep rate evolution of all the materials tested at 1250 °C with different initial applied stresses is plotted in Figure 6a with the Norton exponent n labeled. The relationship of minimum creep rate and initial applied stress of SX superalloys tested at a temperature above 1200 °C from references [4,16,17,34] and other results from databases at Institut Pprime/ISAE-ENSMA are plotted in Figure 6b. The Norton exponent n for all of these creep conditions ranged between 6 to 9. Moreover, another study by Walston et al. also presented n = 6.1 for Rene N6 creep tested at 1204 °C [35].

3.2. Mirostructure Analyses

Representative microstructures of samples after creep tests at 1250 °C are shown in this section. Mar-M200+Hf and Mar-M247LC had homogeneously distributed very fine precipitates (Figure 7a,c) and recrystallized grains in wide areas of the specimen which was confirmed by different contrast obtained by backscatter electron (BSE) imaging (black arrows in Figure 7b). These microstructures indicate that γ′ precipitates were completely dissolved and recrystallization was triggered at 1250 °C, which is the γ′ supersolvus temperature for Mar-M200+Hf and Mar-M247LC [27,37]. Since heating was almost immediately stopped after specimen failure (after 5 to 10 s) followed by a very fast cooling, dynamic recrystallization in areas of increased stress triaxiality is the most likely recrystallization mechanism [38]. Very fine γ′ precipitates were re-precipitated during cooling from the testing temperature (see Figure 7a), which is in good agreement with previous studies using the same creep testing rig [30,39,40,41].
Figure 8 shows the microstructures of Rene N5, PWA1484, and TROPEA after creep rupture tests at 1250 °C/60 MPa. In Rene N5, there was almost no remaining γ′ precipitates near the fracture surface (Figure 8a), however, they were observed 5 mm away from the fracture surface (Figure 8d). This suggests that 1250 °C is close to the solvus temperature of Rene N5 [27] and that the temperature 5 mm away from fracture surface is slightly lower than at the gauge center. PWA1484 and TROPEA have higher volume fraction of γ′ phase in both sections compared to Rene N5. γ′ precipitates in TROPEA show a trend of directional coarsening at 5 mm away from the fracture surface (Figure 8f) and they are disturbed in a wavy form near the fracture surface (Figure 8c). This is similar for PWA1484, however, because PWA1484 has smaller precipitates than TROPEA, γ′ precipitates in Figure 8b seemed to be elongated along the loading direction as if they were sheared. This greater waviness of γ′ precipitates in areas of larger stress triaxiality is in very good agreement with prior results of R.C. Reed et al. who tested CMSX-4 in creep at 1150 °C [5]. Some of the γ′ precipitates show evidence of shearing as indicated by black arrows in Figure 9. Moreover, recrystallized grain boundaries were observed inside γ′ precipitates near the fracture surface as indicated by the white arrows in Figure 9. Although recrystallization was not confirmed in the present results using techniques such as EBSD, similar observations have been reported in other studies [16,42].
A substantially high γ′ phase volume fraction (49.6%) was retained in CMSX-10N after creep testing at 1250 °C / 60 MPa for 31 h as shown in Figure 10b. Even at such an extremely high temperature, topologically closed packed (TCP) phase precipitation occurred in the primary and the secondary dendrite arms of CMSX-10N (Figure 10a). However, as can be seen from creep test results, the retained high γ′ phase fraction contributed to the creep resistance at 1250 °C. The area fraction of TCP phase in a region consisting of two secondary dendrite arms and three interdendritic regions (lower magnification of Figure 10a) was 0.47%, which is below a level that is considered to affect creep properties of a Ni-based SX superalloy at γ′-rafting regime conditions [43].
The γ/γ′ microstructure of all creep specimens tested at 1250 °C/60 MPa was observed near the fracture surface (at a distance not further than 3 mm from the fracture surface) and the volume fraction of γ′ phase was measured. The measured γ′ volume fraction and minimum creep rate are compared in Figure 11. A clear trend of decreasing minimum creep rate with increasing γ′ volume fraction is shown in this figure. This trend is in good agreement with previous studies devoted to the isothermal creep behavior of Ni-based SX superalloys at temperatures above 1180 °C [18,19], or to the thermal cycling creep resistance during which most of the creep damage developed during overheating stages at 1160 °C [27].
The microstructures in Figure 12 correspond to specimens after creep rupture tests, the results of which are shown in Figure 4. Disturbed γ′-rafted microstructure near the fracture surface and recrystallized grain boundaries are similar to the microstructures in Figure 8. The volume fraction of γ′ phase was measured for these samples and the values were 33.6% (Figure 12a), 42.4% (Figure 12b), and 21.9% (Figure 12c) for CMSX-4 Plus at 1250 °C/110 MPa, CMSX-10N at 1250 °C/110 MPa, and TMS-238 at 1250 °C/100 MPa, respectively. These γ′ volume fraction values are very similar to the ones shown in Figure 11.
Experimentally measured equilibrium γ′ volume fraction of different Ni-based SX superalloys is presented in Figure 13. Data for CMSX-4, CMSX-4 Plus, and TROPEA are the same as the ones presented in reference [33]. Figure 13 confirms that the γ′ volume fraction measurements performed for CMSX-4 Plus, TROPEA, and TMS-238 after the creep tests at 1250 °C (Figure 11 and Figure 12) are reasonably accurate.
Representative low magnification images of creep ruptured specimens are shown in Figure 14. PWA1484 and CMSX-4 Plus which were tested at 1250 °C/60 MPa showed strong necking as reported in reference [17]. PWA1484 in Figure 14a showed almost no internal void formation and cracking. CMSX-4 Plus had voids and associated cracks elongated towards the loading direction and the tip of the fracture surface (Figure 14b). Those specimens which showed large necking at the failure cross-section showed necking anisotropy as reported in the previous study [17]. On the contrary, the fracture surface and creep voids in CMSX-10N (Figure 14c) are similar to Ni-based SX specimens tested in the γ′-rafting regime showing crack propagation from the creep void toward the perpendicular to the loading direction [5,13,44,45].

4. Discussion

The results of the present study generally agree well with the study performed by Epishin et al., which provides the most detailed analyses of the creep deformation of one Ni-based SX superalloy (CMSX-4) at ultra-high temperature [17]. Their creep tests were performed at 1288 °C, which is slightly above the solvus temperature, and hence the material was deformed in a single phase γ state. They have validated that octahedral slip is the main deformation mechanism taking place in their testing conditions [17,20]. The explanations presented in their study can be applied to the results of the present study including the glide activity, a high stress exponent (n = 6.6, see Figure 6), and necking anisotropy. The observation of microstructure shearing in Figure 9 supports the fact that slip is strongly active during creep deformation. However, the role of γ′ phase fraction/morphology was not discussed in their pioneering article because the precipitates were all dissolved at 1288 °C and because they were working with only one alloy chemical composition [17].

4.1. Creep Deformation Mechanisms of Ni-Based SX Superalloys at 1250 °C

The materials such as CMSX-4 Plus and TMS-238 have a very high content of refractory elements that generally decrease bulk diffusivity. However, comparing volume fraction values at 1250 °C/60 MPa in Figure 11 and that measured using Figure 12, which were obtained from specimens tested at higher applied stresses, γ′ volume fraction seemed to reach a near equilibrium value at 1250 °C rather rapidly, in less than an hour. This very short time required for the γ′ fraction to reach thermodynamic equilibrium under creep loading at 1250 °C is in accordance with a previous study [25]. Overall, the γ′ dissolution process is not strongly affected by the alloy composition at the testing temperature of 1250 °C. Moreover, the materials used in this study have different initial precipitate sizes as shown in Figure 1 due to the different aging time/temperature and interdiffusivity at the aging temperature. However, because of rapid microstructure evolution during creep loading at 1250 °C, the initial γ′ size does not seem to be an important factor controlling the creep strength in these conditions.
In Figure 2b, PWA1484, TROPEA, MCNG, and TMS-238 all exhibit very similar primary creep stages. During creep deformation of Ni-based SX superalloys in the rafting regime (above 1000 °C with a low applied stress for typical SX superalloys), the primary creep response indirectly expresses the kinetics of γ′-rafting. In other words, the end of the primary creep stage in these conditions corresponds to the completion of γ′-rafting [12,39,46,47,48,49,50,51,52]. γ′ volume fraction at the creep temperature, elastic strain energy at the γ/γ′ interface, bulk diffusivity, and γ/γ′ lattice misfit are known as major factors contributing to the creep behavior during primary stage in the rafting regime [39,46,49,50,51,53]. Indeed, PWA1484, TROPEA, MCNG, and TMS-238 have different chemical compositions and should possess different values for those major parameters. For example, TMS-238 is designed to have a very large absolute γ/γ′ lattice misfit at high temperature compared to 2nd generation alloys like PWA1484 and generates a very fine γ′-raft structure that retards dislocation movement, providing an extremely high creep strength up to a temperature of ~1150 °C without inducing a significant γ′ dissolution [49,53,54,55]. Another example is TROPEA, which has a high γ′ volume fraction above 1200 °C and a small absolute γ/γ′ lattice misfit for improved γ′ precipitate stability, realized by a unique Pt addition [33]. Because the microstructure rapidly evolves toward a γ′-rafted structure with equilibrated γ′ volume fraction, the creep durability at 1250 °C is primarily dependent on the remaining γ′ precipitates, as clearly illustrated in Figure 11.
In the rafting regime, climbing dislocations at the γ/γ′ interfaces of the γ′-rafted structure and shearing of dislocations into the γ′ phase are operative deformation mechanisms during the steady state secondary creep stage [14]. Associated with the dislocation climb, vacancies are transported, and creep void nucleation/growth occur [13,56]. Crack initiation and propagation from creep voids leads to a steep tertiary creep stage and failure [5,57]. Voids were observed in many creep ruptured specimens in this study (see example in, e.g., Figure 14b); however, when a specimen is subjected to significant necking, crack initiation from creep voids does not play a role in the failure mechanism. Even some specimens such as PWA1484 showed very few pores, as displayed in Figure 14a. This is another indication that the gliding dislocation activity is the main creep deformation process, and the failure is controlled in most of the specimens by creep strain accumulation with increasing true stress, due to the decrease of the load bearing section while the applied load was constant.
Large and recrystallized grains migrating in a large portion of the gauge section were only observed for Mar-M200+Hf and Mar-M247LC (materials with a solvus lower than 1250 °C). The occurrence of dynamic recrystallization all along the gauge section is a reason for the very large 50% creep strain at rupture. This phenomenon is similarly observed during certain recrystallization behaviors in forged superalloys [38,58,59,60]. For all other materials, recrystallization was also observed, but only near the fracture surface (example in Figure 9) and not in sections 5 mm away from the fracture surface (Figure 8). Recrystallization of the SX superalloy during creep testing at a low stress condition has been reported in a limited number of studies [17,61]. The size of recrystallized grains shown in Figure 9 is less than 1 μm, which agrees with recrystallization observed in Rene N5 after creep testing at 982 °C / 206 MPa [61] and pre-deformed AM1 tested at 1050 °C/140 MPa that locally accumulates very high strain [16,42]. Therefore, dynamic recrystallization is suggested to occur during the very last stages of creep deformation due to the local strain accumulation where substantial necking occurs.

4.2. Effect of Chemical Composition on the Damage Mechanisms

As shown in Figure 11, the creep strain rate and the resulting creep rupture life are mainly determined by the γ′ volume fraction at the temperature of testing. This correlation is similar to the contribution of the γ′ volume fraction in isothermal creep at temperatures above 1100 °C [62,63] and non-isothermal creep properties of different SX superalloys [27]. Because dislocation glide is enhanced with a large γ fraction and width of the γ matrix, having more γ′ precipitates can be considered as a valid reason of a better creep resistance as they become obstacles for the microstructure shearing.
Focusing on the materials with identical primary creep (PWA1484, TROPEA, MCNG, and TMS-238 in Figure 2b), their different creep rate during the secondary stage (more precisely, the minimum creep rate) expresses the material’s resistance to the dislocation glide activity after the equilibrated γ′ volume fraction is reached. Although the overall trend suggests that the γ′ volume fraction is the main creep controlling factor under these conditions, some materials do not follow this trend. For example, the creep durability of TMS-238 is higher than TROPEA at 1250 °C/60 MPa but their γ′ volume fractions are 24.8% (TMS-238) and 33.4% (TROPEA), respectively. Several materials have 20~25% γ′ volume fraction in Figure 11 (MCNG, AM1, CMSX-4, PWA1484, TMS-238), however, they perform differently in a test with the same creep condition. This is a clear indication that other factors such as individual strength of the γ′ precipitate and the γ matrix and effect of γ/γ′ lattice misfit can contribute to the material’s creep performance in these extreme conditions. The lattice misfit of AM1 and CMSX-4 is positive or near zero at low temperature, and slightly negative or near zero at 1250 °C because of almost no remaining γ′ phase [64,65]. PWA1484 and TMS-238 have a negative lattice misfit for wide temperature ranges and the value decreases with increasing temperature [55,65]. Large absolute lattice misfit helps to prevent dislocation shearing into the γ′ phase. Compared to TROPEA, MCNG and TMS-238 have a higher content of Re and Ru that contributes to the solid solution strengthening of the γ phase [20] which counterbalances the lower γ′ volume fraction of these alloys, leading to a better creep resistance overall.
The only exception to the explanations above is CMSX-10N which exhibits a very stable γ′-rafted structure and TCP phase precipitation at 1250 °C/60 MPa. Typical commercial Ni-based SX superalloys dissolve TCP forming elements at temperatures above 1200 °C [66,67,68], which is a reason why a TCP phase was not observed in all other materials. The very high content of Re and the absence of stabilizing elements such as Ru are reasons for TCP precipitation in CMSX-10N, and this usually becomes an issue during creep between 1000–1100 °C [69,70]. Despite the TCP precipitation, CMSX-10N is the strongest among all tested materials for this creep temperature and TCP phases do not influence the creep deformation mechanisms. Moreover, only one TCP precipitate was found in CMSX-10N after the test at 1250 °C/110 MPa in the analyzed image having an area of 8.7 × 10−3 mm2, and it was not at a crack. Overall, creep properties of CMSX-10N at 1250 °C can be considered as within the rafting regime which leads to failure with crack initiation and propagation from creep voids as seen in Figure 14c. Dodecahedral creep void before crack initiation was also observed in CMSX-10N after 31 h at 1250 °C/60 MPa (not shown here).
The above comparison between different alloys means that the creep strength at the extremely high temperature of 1250 °C cannot be extrapolated from lower temperature conditions. Good examples are TROPEA, TMS-238, and CMSX-10N. TROPEA has a lower creep resistance in the 900–1100 °C range compared to other 2nd to 6th generation alloys but has very good creep and tensile properties at around 700 °C with relatively good creep properties at 1250 °C [33]. TMS-238 is known to have the best creep properties from 700 °C to 1150 °C among all other Ni-based SX superalloys [55,69,71], but not at 1250 °C. Although TMS-238 has much lower creep life and lower γ′ volume fraction at 1250 °C compared to CMSX-10N and CMSX-4 Plus, creep ruptured TMS-238 specimens contained creep voids and associated crack propagation near the fracture surface. CMSX-10N has outstanding creep properties at 1250 °C owing to a very high γ′ volume fraction, and CMSX-10 series alloys including CMSX-10K and CMSX-10N have relatively good creep properties at temperatures above 1050 °C, but not as good compared to TMS-238 at temperatures below 1150 °C [69,72]. The combination of very large absolute γ/γ′ lattice misfit and solid solution in the γ phase are suggested to alter the contributions of different deformation processes (particularly for TMS-238). Also, it is worth noting that TCP precipitation is always a risk when a very high content of Re is alloyed without Ru and if the material is exposed at 1000–1100 °C for longer periods [67,72,73,74].
Further study is required to understand the role of different factors related to residual γ′ phase and the transition of the creep deformation mechanisms from the rafting regime to this ultra-high temperature regime. The effect of oxidation is not discussed in the present study since significant surface cracks were rarely observed. However, when it comes to a design of a thin-walled turbine blade, oxidation and γ′-depletion at the surface can be critical at extremely high temperatures where diffusion is very rapid. Thus, it will be of great importance to study such questions should Ni-based SX superalloys be more widely used at such extreme temperatures during service operations.

5. Conclusions

The creep properties of twelve different Ni-based single crystal superalloys (Mar-M200+Hf, Mar-M247LC, AM1, CMSX-4, Rene N5, PWA 1484, CMSX-4 Plus, Rene N6, CMSX-10N, MCNG, TMS-238, TROPEA) at 1250 °C have been evaluated and analyzed in this study. This is the first study that reports creep performance of superalloys from different generations and presents a large reference dataset for future material and component designs. The main conclusions of this study are:
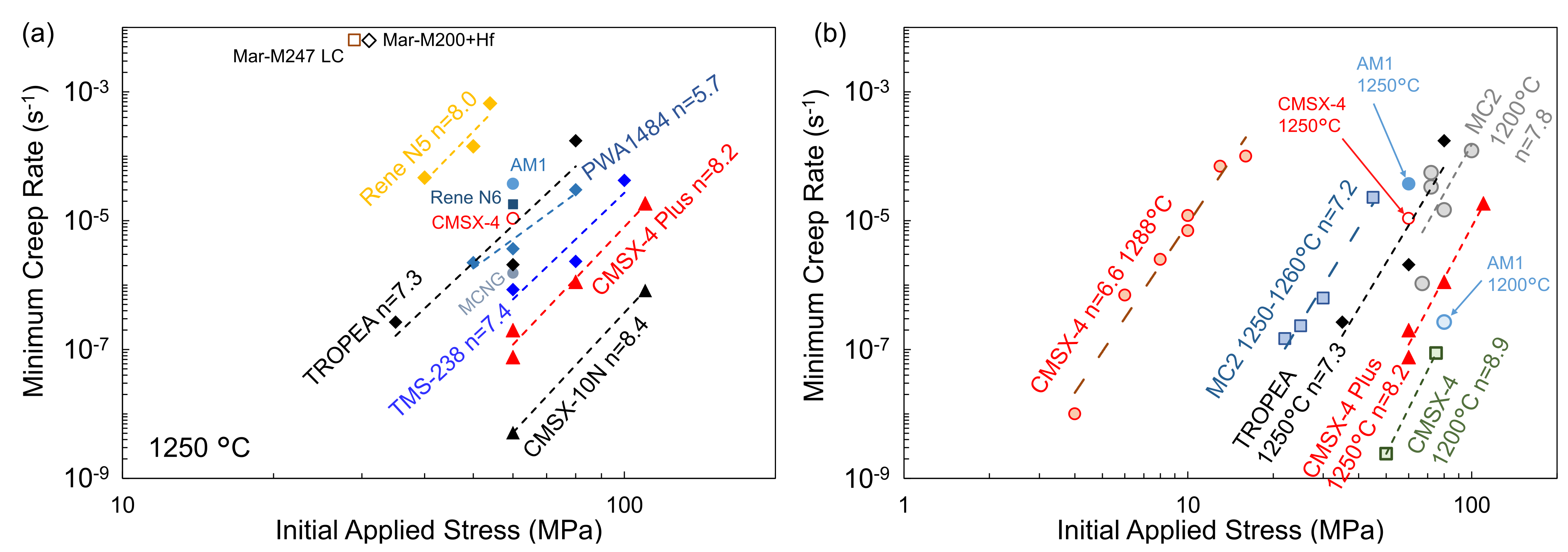
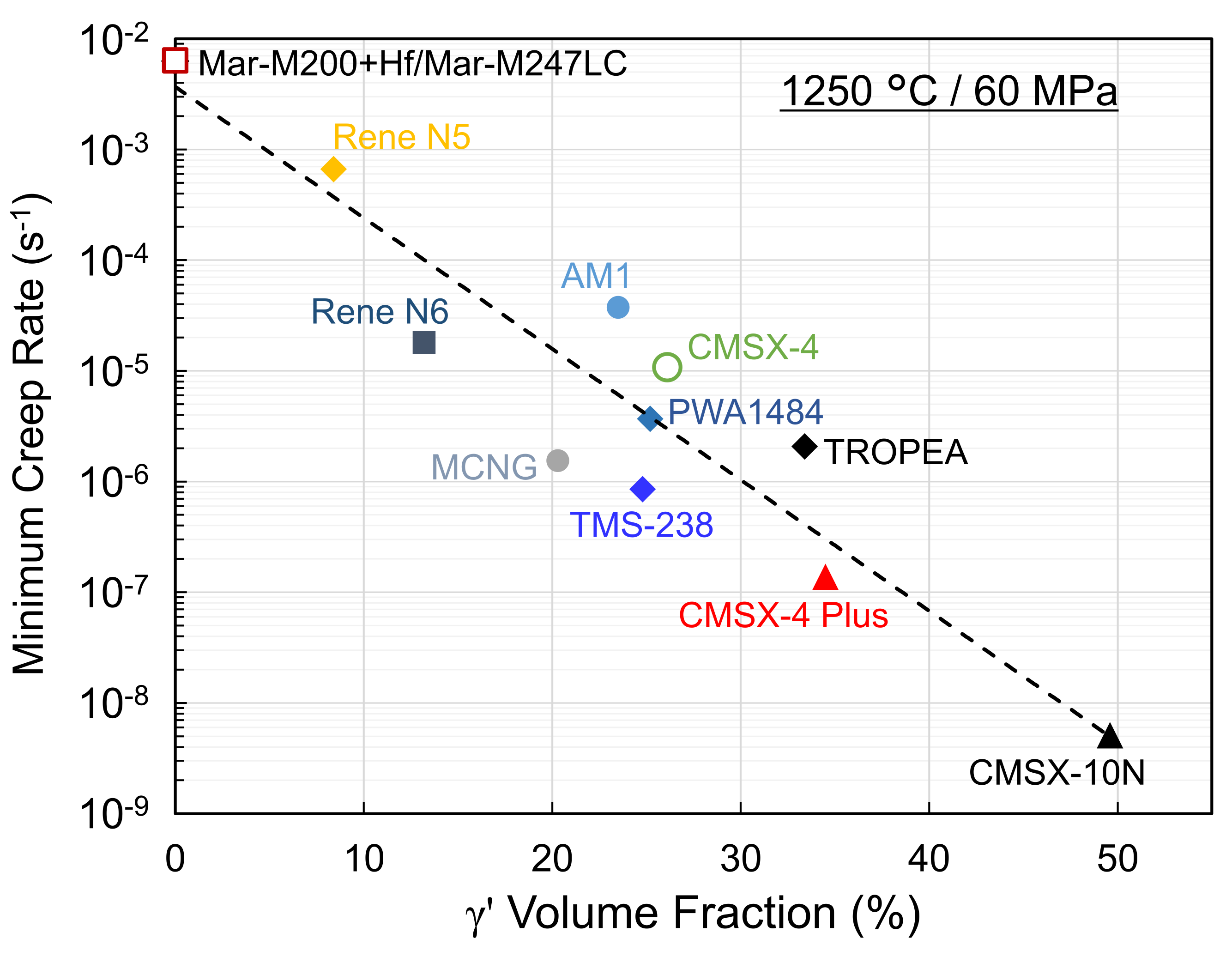
  • The creep resistance of Ni-based single crystal superalloys at ultra-high temperature conditions at 1250 °C is mainly determined by the γ′ volume fraction that controls creep strain rate. Regardless of the alloy composition and the γ′ volume fraction at 1250 °C, the creep exponent in Norton’s power law is between 6 and 9, indicating that creep deformation mechanisms at this temperature are mainly by the glide of dislocations in the γ phase.
  • Materials with similar γ′ volume fraction after creep tests at 1250 °C/ 60 MPa (MCNG, AM1, CMSX-4, PWA1484, TMS-238) exhibit different creep behavior. Alloy compositions influence the creep strength at 1250 °C by affecting the strength of the γ′ precipitates and the γ matrix and γ/γ′ lattice misfit.
  • For most of the alloys, the main damage and failure mechanism in these conditions is accumulation of creep strain that leads to very severe necking. The exception is CMSX-10N, which shows damage mechanisms typical of those observed in the γ′-rafting regime, which are crack initiation and propagation from creep voids.
  • With a relatively high applied stress, materials with a γ′ solvus temperature lower than 1250 °C (Mar-M200+Hf and Mar-M247LC) undergo dynamic recrystallization in a large area of the gauge section. Other creep ruptured materials also show recrystallization near the fracture surface. Recrystallization is presumed to occur during the last stages of creep failure due to the locally accumulated strain.

Author Contributions

Conceptualization, J.C.; methodology, S.U., L.D. and J.C.; validation, S.U., L.D. and J.C.; formal analysis, S.U. and J.C.; investigation, S.U., L.D. and J.C.; resources, J.C.; data curation, J.C.; writing—original draft preparation, S.U.; writing—review and editing, S.U. and J.C.; visualization, S.U.; supervision, J.C.; project administration, J.C.; funding acquisition, J.C. All authors have read and agreed to the published version of the manuscript.

Funding

Institut Pprime gratefully acknowledges “Contrat de Plan Etat—Région Nouvelle-Aquitaine (CPER)” as well as the “Fonds Européen de Développement Régional (FEDER)” for their financial support to the reported work.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Acknowledgments

National Institute for Materials Science (NIMS, K. Kawagishi and H. Harada), MTU Aero Engines (C. Schwalbe), Safran Aircraft Engines (A. Longuet and J. Rame), Safran Helicopter Engines (Z. Hervier), Safran Tech (V. Jaquet), GE Global Research (A. Suzuki) and L. Mataveli Suave (formerly at Safran Tech) are acknowledged for providing materials. Technical assistance from Luciana Maria Bortoluci Ormastroni and Benoît Mansoz (both at Institut Pprime) is gratefully acknowledged. The authors are grateful to D. Graham McCartney (University of Oxford) for his diligent proofreading of this manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Reed, R.C. The Superalloys: Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 2006; ISBN 9780521070119. [Google Scholar]
  2. Pollock, T.M.; Tin, S. Nickel-Based Superalloys for Advanced Turbine Engines: Chemistry, Microstructure and Properties. J. Propuls. Power 2006, 22, 361–374. [Google Scholar] [CrossRef]
  3. Long, H.; Mao, S.; Liu, Y.; Zhang, Z.; Han, X. Microstructural and compositional design of Ni-based single crystalline superalloys—A review. J. Alloys Compd. 2018, 743, 203–220. [Google Scholar] [CrossRef]
  4. Reed, R.C.; Matan, N.; Cox, D.C.; Rist, M.A.; Rae, C.M.F. Creep of CMSX-4 superalloy single crystals: Effects of rafting at high temperature. Acta Mater. 1999, 47, 3367–3381. [Google Scholar] [CrossRef]
  5. Reed, R.C.; Cox, D.C.; Rae, C.M.F. Damage accumulation during creep deformation of a single crystal superalloy at 1150 °C. Mater. Sci. Eng. A 2007, 448, 88–96. [Google Scholar] [CrossRef]
  6. MacKay, R.A.; Maier, R.D. The influence of orientation on the stress rupture properties of nickel-base superalloy single crystals. Metall. Trans. A 1982, 13, 1747–1754. [Google Scholar] [CrossRef]
  7. Caron, P.; Henderson, P.J.; Khan, T.; McLean, M. On the effects of heat treatments on the creep behaviour of a single crystal superalloy. Scr. Metall. 1986, 20, 875–880. [Google Scholar] [CrossRef]
  8. Caron, P.; Ohta, Y.; Nakagawa, Y.G.; Khan, T. Creep deformation anisotropy in single crystal superalloys. In Proceedings of the Superalloys 1988; Reichman, S., Duhl, D.N., Maurer, G., Antolovich, S.D., Lund, C., Eds.; The Minerals, Metals, & Materials Society: Pittsburg, PA, USA, 1988; pp. 215–224. [Google Scholar]
  9. Yuan, Y.; Kawagishi, K.; Koizumi, Y.; Kobayashi, T.; Yokokawa, T.; Harada, H. Creep deformation of a sixth generation Ni-base single crystal superalloy at 800 °C. Mater. Sci. Eng. A 2014, 608, 95–100. [Google Scholar] [CrossRef]
  10. Pollock, T.M.; Argon, A.S. Creep resistance of CMSX-3 nickel base superalloy single crystals. Acta Metall. Mater. 1992, 40, 1–30. [Google Scholar] [CrossRef]
  11. Zhang, J.X.; Murakumo, T.; Harada, H.; Koizumi, Y. Dependence of creep strength on the interfacial dislocations in a fourth generation SC superalloy TMS-138. Scr. Mater. 2003, 48, 287–293. [Google Scholar] [CrossRef]
  12. Rae, C.M.F.; Reed, R.C. Primary creep in single crystal superalloys: Origins, mechanisms and effects. Acta Mater. 2007, 55, 1067–1081. [Google Scholar] [CrossRef]
  13. le Graverend, J.-B.; Adrien, J.; Cormier, J. Ex-situ X-ray tomography characterization of porosity during high-temperature creep in a Ni-based single-crystal superalloy: Toward understanding what is damage. Mater. Sci. Eng. A 2017, 695, 367–378. [Google Scholar] [CrossRef]
  14. Agudo Jácome, L.; Nörtershäuser, P.; Somsen, C.; Dlouhý, A.; Eggeler, G. On the nature of γ′ phase cutting and its effect on high temperature and low stress creep anisotropy of Ni-base single crystal superalloys. Acta Mater. 2014, 69, 246–264. [Google Scholar] [CrossRef]
  15. Ai, S.H.; Lupinc, V.; Maldini, M. Creep fracture mechanisms in single crystal superalloys. Scr. Metall. Mater. 1992, 26, 579–584. [Google Scholar] [CrossRef]
  16. Hamadi, S.; Hamon, F.; Delautre, J.; Cormier, J.; Villechaise, P.; Utada, S.; Kontis, P.; Bozzolo, N. Consequences of a Room-Temperature Plastic Deformation During Processing on Creep Durability of a Ni-Based SX Superalloy. Metall. Mater. Trans. A 2018, 49, 4246–4261. [Google Scholar] [CrossRef]
  17. Epishin, A.; Fedelich, B.; Nolze, G.; Schriever, S.; Feldmann, T.; Ijaz, M.F.; Viguier, B.; Poquillon, D.; Le Bouar, Y.; Ruffini, A.; et al. Creep of Single Crystals of Nickel-Based Superalloys at Ultra-High Homologous Temperature. Metall. Mater. Trans. A 2018, 49, 3973–3987. [Google Scholar] [CrossRef] [Green Version]
  18. Ru, Y.; Zhang, H.; Pei, Y.; Li, S.; Zhao, X.; Gong, S.; Xu, H. Improved 1200 °C stress rupture property of single crystal superalloys by γ′-forming elements addition. Scr. Mater. 2018, 147, 21–26. [Google Scholar] [CrossRef]
  19. Tan, X.P.; Liu, J.L.; Jin, T.; Hu, Z.Q.; Hong, H.U.; Choi, B.G.; Kim, I.S.; Jo, C.Y.; Mangelinck, D. Effect of Ru additions on very high temperature creep properties of a single crystal Ni-based superalloy. Mater. Sci. Eng. A 2013, 580, 21–35. [Google Scholar] [CrossRef]
  20. Epishin, A.I.; Fedelich, B.; Viguier, B.; Schriever, S.; Svetlov, I.L.; Petrushin, N.V.; Saillard, R.; Proietti, A.; Poquillon, D.; Chyrkin, A. Creep of single-crystals of nickel-base γ-alloy at temperatures between 1150 °C and 1288 °C. Mater. Sci. Eng. A 2021, 825, 141880. [Google Scholar] [CrossRef]
  21. Cormier, J.; Milhet, X.; Champion, J.-L.; Mendez, J. Simulation of Very High Temperature Overheating During Isothermal Creep of Single Crystal Ni-Base Superalloy. Adv. Eng. Mater. 2008, 10, 56–61. [Google Scholar] [CrossRef]
  22. Cormier, J.; Milhet, X.; Mendez, J. Non-isothermal creep at very high temperature of the nickel-based single crystal superalloy MC2. Acta Mater. 2007, 55, 6250–6259. [Google Scholar] [CrossRef]
  23. Guo, X.; Zheng, W.; Xiao, C.; Li, L.; Antonov, S.; Zheng, Y.; Feng, Q. Evaluation of microstructural degradation in a failed gas turbine blade due to overheating. Eng. Fail. Anal. 2019, 103, 308–318. [Google Scholar] [CrossRef]
  24. Guidance for 30-second and 2-minute one-engine-inoperative (OEI) ratings for rotercraft turbine engines. In Advisory Circulars; Federal Aviation Administration: Washington, DC, USA, 2009.
  25. Giraud, R.; Hervier, Z.; Cormier, J.; Saint-Martin, G.; Hamon, F.; Milhet, X.; Mendez, J. Strain Effect on the γ′ Dissolution at High Temperatures of a Nickel-Based Single Crystal Superalloy. Metall. Mater. Trans. A 2013, 44, 131–146. [Google Scholar] [CrossRef]
  26. Cormier, J.; Milhet, X.; Mendez, J. Effect of very high temperature short exposures on the dissolution of the γ′ phase in single crystal MC2 superalloy. J. Mater. Sci. 2007, 42, 7780–7786. [Google Scholar] [CrossRef]
  27. Cormier, J. Thermal Cycling Creep Resistance of Ni-Based Single Crystal Superalloys. In Proceedings of the Superalloys 2016; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016; pp. 383–394. [Google Scholar]
  28. Bortoluci Ormastroni, L.M.; Utada, S.; Rame, J.; Mataveli Suave, L.; Kawagishi, K.; Harada, H.; Villechaise, P.; Cormier, J. Tensile, low cycle fatigue and very high cycle fatigue characterizations of advanced single crystal nickel-based superalloys. In Proceedings of the Superalloys 2020; Tin, S., Hardy, M., Clews, J., Cormier, J., Feng, Q., Marcin, J., O’Brien, C., Suzuki, A., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 341–351. [Google Scholar]
  29. Schwalbe, C.; Cormier, J.; Jones, C.N.; Galindo-Nava, E.; Rae, C.M.F. Investigating the Dislocation-Driven Micro-mechanical Response Under Non-isothermal Creep Conditions in Single-Crystal Superalloys. Metall. Mater. Trans. A 2018, 49, 3988–4002. [Google Scholar] [CrossRef] [Green Version]
  30. Cormier, J.; Jouiad, M.; Hamon, F.; Villechaise, P.; Milhet, X. Very high temperature creep behavior of a single crystal Ni-based superalloy under complex thermal cycling conditions. Philos. Mag. Lett. 2010, 90, 611–620. [Google Scholar] [CrossRef]
  31. Hähner, P.; Affeldt, E.; Beck, T.; Klingelhöffer, H.; Loveday, M.; Rinaldi, C. Final Version of the Validated Code-of-Practice for Strain-Controlled Thermo-Mechanical Fatigue Testing; Office for Official Publications of the European Communities: Luxembourg, 2006; ISBN 92-79-02216-4. [Google Scholar]
  32. Vaunois, J.-R.; Cormier, J.; Villechaise, P.; Devaux, A.; Flageolet, B. Influence of both γ′ distribution and grain size on the tensile properties of UDIMET 720Li at room temperature. In Proceedings of the 7th International Conference on Superalloys 718 and Derivatives, Pittsburg, PA, USA, 10–13 Octobe 2010; The Minerals, Metals, & Materials Society: Pittsburg, PA, USA, 2010; pp. 199–213. [Google Scholar]
  33. Rame, J.; Utada, S.; Bortoluci Ormastroni, L.M.; Mataveli Suave, L.; Menou, E.; Després, L.; Kontis, P.; Cormier, J. Platinum containing new generation nickel-based superalloy for single crystalline application. In Proceedings of the Superalloys 2020; Tin, S., Hardy, M., Clews, J., Cormier, J., Feng, Q., Marcin, J., O’Brien, C., Suzuki, A., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 71–81. [Google Scholar]
  34. Cormier, J. Comportement en Fluage Anisotherme à Haute et Très Haute Température du Superalliage Monocristallin MC2; ISAE-ENSMA: Poitiers, France, 2006. [Google Scholar]
  35. Walston, W.S.; O’hara, K.S.; Ross, E.W.; Pollock, T.M.; Murphy, W.H. Rene’ N6: Third Generation Single Crystal Superalloy. In Proceedings of the Superalloys 1996; Kissinger, R.D., Deye, D.J., Anton, D.L., Cetel, A.D., Nathal, M.V., Pollock, T.M., Woodford, D.A., Eds.; The Minerals, Metals, & Materials Society: Pittsburg, PA, USA, 1996; pp. 27–34. [Google Scholar]
  36. Mauget, F.; Marchand, D.; Benoit, G.; Morisset, M.; Bertheau, D.; Cormier, J.; Mendez, J.; Hervier, Z.; Ostoja-Kuczynski, E.; Moriconi, C. Development and use of a new burner rig facility to mimic service loading conditions of Ni-based single crystal superalloys. MATEC Web. Conf. 2014, 14, 20001. [Google Scholar] [CrossRef] [Green Version]
  37. Sponseller, D.L. Differential thermal analysis of nickel-base superalloys. In Proceedings of the Superalloys 1996; Kissinger, R.D., Deye, D.J., Anton, D.L., Cetel, A.D., Nathal, M.V., Pollock, T.M., Woodford, D.A., Eds.; The Minerals, Metals, & Materials Society: Pittsburg, PA, USA, 1996; pp. 259–270. [Google Scholar]
  38. Nicolaÿ, A.; Fiorucci, G.; Franchet, J.M.; Cormier, J.; Bozzolo, N. Influence of strain rate on subsolvus dynamic and post-dynamic recrystallization kinetics of Inconel 718. Acta Mater. 2019, 174, 406–417. [Google Scholar] [CrossRef]
  39. Cormier, J.; Cailletaud, G. Constitutive modeling of the creep behavior of single crystal superalloys under non-isothermal conditions inducing phase transformations. Mater. Sci. Eng. A 2010, 527, 6300–6312. [Google Scholar] [CrossRef]
  40. Cormier, J.; Caccuri, V.; le Graverend, J.-B.; Villechaise, P. Comments on ‘Selective evolution of secondary γ′ precipitation in a Ni-based single crystal superalloy both in the γ matrix and at the dislocation nodes. Scr. Mater. 2017, 129, 100–103. [Google Scholar] [CrossRef]
  41. le Graverend, J.-B.; Cormier, J.; Jouiad, M.; Gallerneau, F.; Paulmier, P.; Hamon, F. Effect of fine γ′ precipitation on non-isothermal creep and creep-fatigue behaviour of nickel base superalloy MC2. Mater. Sci. Eng. A 2010, 527, 5295–5302. [Google Scholar] [CrossRef]
  42. Utada, S.; Rame, J.; Hamadi, S.; Delautre, J.; Villechaise, P.; Cormier, J. Kinetics of creep damage accumulation induced by a room-temperature plastic deformation introduced during processing of AM1 Ni-based single crystal superalloy. Mater. Sci. Eng. A 2020, 789, 139571. [Google Scholar] [CrossRef]
  43. Simonetti, M.; Caron, P. Role and behaviour of μ phase during deformation of a nickel-based single crystal superalloy. Mater. Sci. Eng. A 1998, 254, 1–12. [Google Scholar] [CrossRef]
  44. MacLachlan, D.W.; Knowles, D.M. Modelling and prediction of the stress rupture behaviour of single crystal superalloys. Mater. Sci. Eng. A 2001, 302, 275–285. [Google Scholar] [CrossRef]
  45. Moss, S.J.; Webster, G.A.; Fleury, E. Creep deformation and crack growth behavior of a single-crystal nickel-base superalloy. Metall. Mater. Trans. A 1996, 27, 829–837. [Google Scholar] [CrossRef]
  46. Matan, N.; Cox, D.C.; Rae, C.M.F.; Reed, R.C. On the kinetics of rafting in CMSX-4 superalloy single crystals. Acta Mater. 1999, 47, 2031–2045. [Google Scholar] [CrossRef]
  47. Caccuri, V.; Cormier, J.; Desmorat, R. γ′-Rafting mechanisms under complex mechanical stress state in Ni-based single crystalline superalloys. Mater. Des. 2017, 131, 487–497. [Google Scholar] [CrossRef]
  48. le Graverend, J.-B.; Jacques, A.; Cormier, J.; Ferry, O.; Schenk, T.; Mendez, J. Creep of a nickel-based single-crystal superalloy during very high-temperature jumps followed by synchrotron X-ray diffraction. Acta Mater. 2015, 84, 65–79. [Google Scholar] [CrossRef]
  49. Zhang, J.; Wang, J.; Harada, H.; Koizumi, Y. The effect of lattice misfit on the dislocation motion in superalloys during high-temperature low-stress creep. Acta Mater. 2005, 53, 4623–4633. [Google Scholar] [CrossRef]
  50. Zhang, J.X.; Harada, H.; Koizumi, Y.; Kobayashi, T. Dislocation motion in the early stages of high-temperature low-stress creep in a single-crystal superalloy with a small lattice misfit. J. Mater. Sci. 2010, 45, 523–532. [Google Scholar] [CrossRef]
  51. Kamaraj, M. Rafting in single crystal nickel-base superalloys—An overview. Sadhana 2003, 28, 115–128. [Google Scholar] [CrossRef]
  52. Reed, R.C.; Cox, D.C.; Rae, C.M.F. Kinetics of rafting in a single crystal superalloy: Effects of residual microsegregation. Mater. Sci. Technol. 2007, 23, 893–902. [Google Scholar] [CrossRef]
  53. Zhang, J.X.; Murakumo, T.; Koizumi, Y.; Kobayashi, T.; Harada, H.; Masaki Jr, S. Interfacial dislocation networks strengthening a fourth-generation single-crystal TMS-138 superalloy. Metall. Mater. Trans. A 2002, 33, 3741–3746. [Google Scholar] [CrossRef]
  54. Kawagishi, K.; Yeh, A.; Yokokawa, T.; Kobayashi, T.; Koizumi, Y.; Harada, H. Development of an Oxidation-resistant High-Strength Sixth-Generation Single-Crystal Superalloy TMS-238. In Proceedings of the Superalloys 2012; Huron, E.S., Reed, R.C., Hardy, M.C., Mills, M.J., Montero, R.E., Portella, P.D., Telesman, J., Eds.; The Minerals, Metals, & Materials Society: Pittsburg, PA, USA, 2012; pp. 189–195. [Google Scholar]
  55. Yokokawa, T.; Harada, H.; Mori, Y.; Kawagishi, K.; Koizumi, Y.; Kobayashi, T.; Yuyama, M.; Suzuki, S. Design of Next Generation Ni-base Single Crystal Superalloys Containing Ir: Towards 1150 °C Temperature Capability. In Proceedings of the Superalloys 2016; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016; pp. 123–130. [Google Scholar]
  56. Epishin, A.; Link, T.; Klingelhöffer, H.; Fedelich, B.; Portella, P. Creep damage of single-crystal nickel base superalloys: Mechanisms and effect on low cycle fatigue. Mater. High Temp. 2010, 27, 53–59. [Google Scholar] [CrossRef]
  57. Epishin, A.; Link, T. Mechanisms of high-temperature creep of nickel-based superalloys under low applied stresses. Philos. Mag. 2004, 84, 1979–2000. [Google Scholar] [CrossRef]
  58. Charpagne, M.-A.; Billot, T.; Franchet, J.-M.; Bozzolo, N. Heteroepitaxial recrystallization: A new mechanism discovered in a polycrystalline γ-γ′ nickel based superalloy. J. Alloys Compd. 2016, 688, 685–694. [Google Scholar] [CrossRef] [Green Version]
  59. Medeiros, S.C.; Prasad, Y.V.R.; Frazier, W.G.; Srinivasan, R. Microstructural modeling of metadynamic recrystallization in hot working of IN 718 superalloy. Mater. Sci. Eng. A 2000, 293, 198–207. [Google Scholar] [CrossRef]
  60. Semiatin, S.L.; Weaver, D.S.; Kramb, R.C.; Fagin, P.N.; Glavicic, M.G.; Goetz, R.L.; Frey, N.D.; Antony, M.M. Deformation and recrystallization behavior during hot working of a coarse-grain, nickel-base superalloy ingot material. Metall. Mater. Trans. A 2004, 35, 679–693. [Google Scholar] [CrossRef]
  61. Rettberg, L.H.; Pollock, T.M. Localized recrystallization during creep in nickel-based superalloys GTD444 and René N5. Acta Mater. 2014, 73, 287–297. [Google Scholar] [CrossRef]
  62. Murakumo, T.; Kobayashi, T.; Koizumi, Y.; Harada, H. Creep behaviour of Ni-base single-crystal superalloys with various γ′ volume fraction. Acta Mater. 2004, 52, 3737–3744. [Google Scholar] [CrossRef]
  63. Caron, P. High y’solvus new generation nickel-based superalloys for single crystal turbine blade applications. In Proceedings of the Superalloys 2000; The Minerals, Metals, & Materials Society: Pittsburg, PA, USA, 2000; pp. 737–746. [Google Scholar]
  64. Royer, A.; Bastie, P.; Bellet, D.; Strudel, J.L. Temperature dependence of the lattice mismatch of the AM1 superalloy influence of the γ′ precipitates’ morphology. Philos. Mag. A 1995, 72, 669–689. [Google Scholar] [CrossRef]
  65. Huang, S.; An, K.; Gao, Y.; Suzuki, A. Determination of γ/γ′ Lattice Misfit in Ni-Based Single-Crystal Superalloys at High Temperatures by Neutron Diffraction. Metall. Mater. Trans. A 2018, 49, 740–751. [Google Scholar] [CrossRef]
  66. Pessah, M.; Caron, P.; Khan, T. Effect of µ Phase on the Mechanical Properties of a Nickel-Base Single Crystal Superalloy. In Proceedings of the Superalloys 1992; Antolovich, S.D., Stusrud, R.W., MacKay, R.A., Anton, D.L., Khan, T., Kissinger, R.D., Klarstrom, D.L., Eds.; The Minerals, Metals, & Materials Society: Pittsburg, PA, USA, 1992; pp. 567–576. [Google Scholar]
  67. Rae, C.; Karunaratne, M.; Small, C.; Broomfield, R.; Jones, C.; Reed, R. Topologically Close Packed Phases in an Experimental Rhenium-Containing Single Crystal Superalloy. In Proceedings of the Superalloys 2000; The Minerals, Metals, & Materials Society: Pittsburg, PA, USA, 2000; pp. 767–776. [Google Scholar]
  68. Utada, S.; Joh, Y.; Osawa, M.; Yokokawa, T.; Sugiyama, T.; Kobayashi, T.; Kawagishi, K.; Suzuki, S.; Harada, H. Creep Property and Phase Stability of Sulfur-Doped Ni-Base Single-Crystal Superalloys and Effectiveness of CaO Desulfurization. Metall. Mater. Trans. A 2018, 49, 4029–4041. [Google Scholar] [CrossRef]
  69. Koizumi, Y.; Yokokawa, T.; Sugiyama, T.; Yuyama, M.; Harada, H.; Kawagishi, K.; Takata, Y.; Kobayashi, T.; Sakamoto, M.; Suzuki, S. Creep and environmental properties of Ni-base single crystal superalloys, CMSX-4, CMSX-4 Plus, CMSX-10N and TMS-238. In Proceedings of the 46th Annual Conference of GTSJ; GTSJ: Kagoshima, Japan, 2018; p. B-13. [Google Scholar]
  70. Yeh, A.-C.; Sato, A.; Kobayashi, T.; Harada, H. On the creep and phase stability of advanced Ni-base single crystal superalloys. Mater. Sci. Eng. A 2008, 490, 445–451. [Google Scholar] [CrossRef]
  71. Yuan, Y.; Kawagishi, K.; Koizumi, Y.; Kobayashi, T.; Yokokawa, T.; Harada, H. Creep Deformation of a 6th Generation Ni-Base Single Crystal Superalloy at 800 °C and 735 MPa. In Proceedings of the Superalloys 2016; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2016; pp. 675–682. [Google Scholar]
  72. Hobbs, R.A.; Zhang, L.; Rae, C.M.F.; Tin, S. The effect of ruthenium on the intermediate to high temperature creep response of high refractory content single crystal nickel-base superalloys. Mater. Sci. Eng. A 2008, 489, 65–76. [Google Scholar] [CrossRef]
  73. Erickson, G.L. The Development and Application of CMSX®-10. In Proceedings of the Superalloys 1996; Kissinger, R.D., Deye, D.J., Anton, D.L., Cetel, A.D., Nathal, M.V., Pollock, T.M., Woodford, D.A., Eds.; The Minerals, Metals, & Materials Society: Pittsburg, PA, USA, 1996; pp. 35–44. [Google Scholar]
  74. Acharya, M.V.; Fuchs, G. The effect of long-term thermal exposures on the microstructure and properties of CMSX-10 single crystal Ni-base superalloys. Mater. Sci. Eng. A 2004, 381, 143–153. [Google Scholar] [CrossRef]
Metals 11 01610 g001 550
Figure 1. Microstructures of SX superalloys after heat treatments. (a) Mar-M200+Hf, (b) AM1, (c) PWA1484, (d) Rene N5, (e) CMSX-4 Plus, (f) CMSX-10N, (g) TMS-238, (h) TROPEA.
Figure 1. Microstructures of SX superalloys after heat treatments. (a) Mar-M200+Hf, (b) AM1, (c) PWA1484, (d) Rene N5, (e) CMSX-4 Plus, (f) CMSX-10N, (g) TMS-238, (h) TROPEA.
Metals 11 01610 g001
Metals 11 01610 g002 550
Figure 2. Result of creep tests on SX superalloys at 1250 °C/60 MPa. Scale of (a) is enlarged in (b) to show difference in primary creep stage. Note that CMSX-10N creep test has been interrupted after 31 h and 0.79% creep strain.
Figure 2. Result of creep tests on SX superalloys at 1250 °C/60 MPa. Scale of (a) is enlarged in (b) to show difference in primary creep stage. Note that CMSX-10N creep test has been interrupted after 31 h and 0.79% creep strain.
Metals 11 01610 g002
Metals 11 01610 g003 550
Figure 3. Creep strain rate curves of different SX superalloys tested at 1250 °C/60 MPa.
Figure 3. Creep strain rate curves of different SX superalloys tested at 1250 °C/60 MPa.
Metals 11 01610 g003
Metals 11 01610 g004 550
Figure 4. Result of creep tests on CMSX-4 Plus and CMSX-10N at 1250 °C/110 MPa and TMS-238 at 1250 °C/100 MPa.
Figure 4. Result of creep tests on CMSX-4 Plus and CMSX-10N at 1250 °C/110 MPa and TMS-238 at 1250 °C/100 MPa.
Metals 11 01610 g004
Metals 11 01610 g005 550
Figure 5. Creep strain rate curves of CMSX-4 Plus (a), TMS-238 (b), TROPEA (c), and Rene N5 (d) tested at 1250 °C with different applied stresses.
Figure 5. Creep strain rate curves of CMSX-4 Plus (a), TMS-238 (b), TROPEA (c), and Rene N5 (d) tested at 1250 °C with different applied stresses.
Metals 11 01610 g005
Metals 11 01610 g006 550
Figure 6. Minimum creep strain rate as a function of the initial applied stress for Ni-based SX superalloys tested in this study (a) and with data from references (b). CMSX-4 at 1288 °C [17], MC2 at 1200 °C [34], CMSX-4 at 1200 °C [4], AM1 at 1200 °C [16]. MC2 at 1250-1260 °C is from internal database in Institut Pprime tested using the MAATRE burner rig [36].
Figure 6. Minimum creep strain rate as a function of the initial applied stress for Ni-based SX superalloys tested in this study (a) and with data from references (b). CMSX-4 at 1288 °C [17], MC2 at 1200 °C [34], CMSX-4 at 1200 °C [4], AM1 at 1200 °C [16]. MC2 at 1250-1260 °C is from internal database in Institut Pprime tested using the MAATRE burner rig [36].
Metals 11 01610 g006
Metals 11 01610 g007 550
Figure 7. Microstructures after creep rupture tests at 1250 °C/60 MPa. (a) Mar-M200+Hf, 5 mm from the fracture surface. (b,c) Mar-M247LC, middle of the gauge section. (b) was obtained using BSE imaging mode. Black arrows are pointing at grain boundaries.
Figure 7. Microstructures after creep rupture tests at 1250 °C/60 MPa. (a) Mar-M200+Hf, 5 mm from the fracture surface. (b,c) Mar-M247LC, middle of the gauge section. (b) was obtained using BSE imaging mode. Black arrows are pointing at grain boundaries.
Metals 11 01610 g007
Metals 11 01610 g008 550
Figure 8. Microstructures after creep rupture tests at 1250 °C/60 MPa. (a,d) Rene N5, (b,d) PWA1484, and (c,f) TROPEA. (a–c) Near fracture surface and (d–f) 5 mm from the fracture surface.
Figure 8. Microstructures after creep rupture tests at 1250 °C/60 MPa. (a,d) Rene N5, (b,d) PWA1484, and (c,f) TROPEA. (a–c) Near fracture surface and (d–f) 5 mm from the fracture surface.
Metals 11 01610 g008
Metals 11 01610 g009 550
Figure 9. Near the fracture surface of AM1 (a) and CMSX-4 Plus (b) after creep rupture tests at 1250 °C/60 MPa. White arrows are pointing at grain boundaries in γ′ phase. Black arrows are indicating shearing traces.
Figure 9. Near the fracture surface of AM1 (a) and CMSX-4 Plus (b) after creep rupture tests at 1250 °C/60 MPa. White arrows are pointing at grain boundaries in γ′ phase. Black arrows are indicating shearing traces.
Metals 11 01610 g009
Metals 11 01610 g010 550
Figure 10. Microstructures at middle of CMSX-10N after creep test at 1250 °C/60 MPa, interrupted at 31 h and 0.79% creep strain (a). (b) is magnified image of (a).
Figure 10. Microstructures at middle of CMSX-10N after creep test at 1250 °C/60 MPa, interrupted at 31 h and 0.79% creep strain (a). (b) is magnified image of (a).
Metals 11 01610 g010
Metals 11 01610 g011 550
Figure 11. Minimum creep rate as a function of γ′ volume fraction of SX superalloys after creep tests at 1250 °C/60 MPa.
Figure 11. Minimum creep rate as a function of γ′ volume fraction of SX superalloys after creep tests at 1250 °C/60 MPa.
Metals 11 01610 g011
Metals 11 01610 g012 550
Figure 12. Microstructures after creep rupture tests on CMSX-4 Plus at 1250 °C/110 MPa (a,d), CMSX-10N at 1250 °C/110 MPa (b,e), and TMS-238 at 1250 °C/100 MPa (c,f). (a–c) Near fracture surface and (d–f) 5 mm from the fracture surface.
Figure 12. Microstructures after creep rupture tests on CMSX-4 Plus at 1250 °C/110 MPa (a,d), CMSX-10N at 1250 °C/110 MPa (b,e), and TMS-238 at 1250 °C/100 MPa (c,f). (a–c) Near fracture surface and (d–f) 5 mm from the fracture surface.
Metals 11 01610 g012
Metals 11 01610 g013 550
Figure 13. Relationship between γ′ volume fraction at thermodynamical equilibrium and temperature in Ni-based SX superalloys AM1, CMSX-4, CMSX-4 Plus, TMS-238, and TROPEA. Data for CMSX-4, CMSX-4 Plus, and TROPEA are taken from a reference [33]. The vertical dotted line is drawn to show 1250 °C.
Figure 13. Relationship between γ′ volume fraction at thermodynamical equilibrium and temperature in Ni-based SX superalloys AM1, CMSX-4, CMSX-4 Plus, TMS-238, and TROPEA. Data for CMSX-4, CMSX-4 Plus, and TROPEA are taken from a reference [33]. The vertical dotted line is drawn to show 1250 °C.
Metals 11 01610 g013
Metals 11 01610 g014 550
Figure 14. Necking and voids of PWA1484 tested at 1250 °C/60 MPa (a), CMSX-4 Plus tested at 1250 °C/60 MPa (b), and CMSX-10N tested at 1250 °C/110 MPa (c).
Figure 14. Necking and voids of PWA1484 tested at 1250 °C/60 MPa (a), CMSX-4 Plus tested at 1250 °C/60 MPa (b), and CMSX-10N tested at 1250 °C/110 MPa (c).
Metals 11 01610 g014
Table
Table 1. Chemical compositions of experimental alloys in wt. % (Ni-bal).
Table 1. Chemical compositions of experimental alloys in wt. % (Ni-bal).
AlloyCoCrMoWTaAlTiNbReRuPtHfCBZr
Mar-M200+Hf10.09.0 12.5 5.02.01.0 1.60.150.0150.05
Mar-M247LC9.08.00.510.03.25.60.7 1.40.070.0150.01
AM16.77.62.05.68.05.31.2 0.05
CMSX-49.76.40.66.46.55.61.1 2.9 0.10
PWA148410.15.01.95.98.55.6 3.0 0.10
Rene N57.57.01.55.06.56.2 3.0 0.160.05
CMSX-4 Plus10.03.50.66.08.05.70.85 4.8 0.10
Rene N612.04.01.15.96.95.6 5.3 0.19
CMSX-10N3.01.50.45.08.05.80.10.057.0
MCNG 4.01.05.05.06.00.5 4.04.0 0.10
TMS-2386.54.61.14.07.65.9 6.45.0 0.10
TROPEA8.96.40.66.19.15.41.0 1.0 1.950.08
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Utada, S.; Despres, L.; Cormier, J. Ultra-High Temperature Creep of Ni-Based SX Superalloys at 1250 °C. Metals 2021, 11, 1610. https://doi.org/10.3390/met11101610

AMA Style

Utada S, Despres L, Cormier J. Ultra-High Temperature Creep of Ni-Based SX Superalloys at 1250 °C. Metals. 2021; 11(10):1610. https://doi.org/10.3390/met11101610

Chicago/Turabian Style

Utada, Satoshi, Lucille Despres, and Jonathan Cormier. 2021. "Ultra-High Temperature Creep of Ni-Based SX Superalloys at 1250 °C" Metals 11, no. 10: 1610. https://doi.org/10.3390/met11101610

APA Style

Utada, S., Despres, L., & Cormier, J. (2021). Ultra-High Temperature Creep of Ni-Based SX Superalloys at 1250 °C. Metals, 11(10), 1610. https://doi.org/10.3390/met11101610

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop