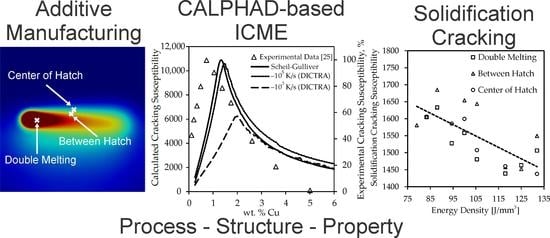
Integration of Processing and Microstructure Models for Non-Equilibrium Solidification in Additive Manufacturing

Abstract

Integration of models that capture the complex physics of solidification on the macro and microstructural scale with the flexibility to consider multicomponent materials systems is a significant challenge in modeling additive manufacturing processes. This work aims to link process variables, such as energy density, with non-equilibrium solidification by integrating additive manufacturing process simulations with solidification models that consider thermodynamics and diffusion. Temperature histories are generated using a semi-analytic laser powder bed fusion process model and feed into a CALPHAD-based ICME (CALPHAD: Calculation of Phase Diagrams, ICME: Integrated Computational Materials Engineering) framework to model non-equilibrium solidification as a function of both composition and processing parameters. Solidification cracking susceptibility is modeled as a function of composition, cooling rate, and energy density in Al-Cu Alloys and stainless steel 316L (SS316L). Trends in solidification cracking susceptibility predicted by the model are validated by experimental solidification cracking measurements of Al-Cu alloys. Non-equilibrium solidification in additively manufactured SS316L is investigated to determine if this approach can be applied to commercial materials. Modeling results show a linear relationship between energy density and solidification cracking susceptibility in additively manufactured SS316L. This work shows that integration of process and microstructure models is essential for modeling solidification during additive manufacturing.

1. Introduction

Deviation from equilibrium during solidification in additive manufacturing and welding processes causes microsegregation, reduction in the solidus temperature, and increased solidification cracking susceptibility (SCS) [1,2,3]. Computational models with the flexibility to predict non-equilibrium solidification in multicomponent materials are limited, and new computational frameworks are desired to design the next generation of additively manufactured materials. CALPHAD-based ICME (CALPHAD: Calculation of Phase Diagrams, ICME: Integrated Computational Materials Engineering) [4,5] frameworks have shown the ability to model the effects of non-equilibrium solidification in both welding and additive manufacturing process [6,7,8,9]. However, these models typically fail to couple the thermodynamics and kinetics of materials with changes in processing parameters. Overcoming this challenge requires the integration of macroscale process simulations with microstructure level models [10] for non-equilibrium solidification.

The Scheil-Gulliver model [11] for solidification is commonly coupled with CALPHAD-based thermodynamics and provides a simple approximation of non-equilibrium solidification in the case of a well-mixed liquid and no solid back-diffusion. Scheil-Gulliver models are frequently used to model solidification in additively manufactured materials and have demonstrated success in modeling SCS using the models proposed by Clyne [12] and Kou [13,14] et al. Due to its simplicity, the Scheil-Gulliver model cannot quantitatively consider changes in the cooling rate or the effect of cyclic heating and cooling encountered during additive manufacturing processes. One-dimensional kinetic models provide a more robust prediction by considering the effect of back-diffusion across mobile phase boundaries [11] and dynamic changes in the cooling rate caused by variable processing conditions. Although one-dimensional kinetic models are more computationally expensive than Scheil-Gulliver models, they are still more efficient than high-fidelity microstructure simulation approaches such as phase-field modeling, particularly in the case of multicomponent systems. The diffusion-controlled transformations (DICTRA) software module within Thermo-Calc software [15] for modeling diffusion-controlled phase transformations can be used to construct one-dimensional solidification models. Lippard et al. [16] modeled the microsegregation behavior during solidification of high-alloy steel using DICTRA and found good agreement between the model prediction and experimental measurements of microsegregation using electron dispersive spectroscopy. Zhang et al. [17] showed that reliable mobility and thermodynamic databases are necessary to accurately model solidification using DICTRA. Valiente et al. [18] used DICTRA to estimate the ferrite content in austenitic stainless-steel welds and found good agreement with the experimentally observed phase fraction. Work by Keller and Lindwall et al. [19,20] demonstrated the potential of applying one-dimensional kinetic models to additive manufacturing processes by coupling DICTRA with a finite element process model to predict microsegregation in additively manufactured Inconel 718 and 625. These efforts have demonstrated the ability of one-dimensional kinetic models to approximate non-equilibrium solidification in additively manufactured materials. However, these previous works have focused on a small number of calculations and have not investigated the effects of changes in composition or processing conditions on DICTRA solidification models using high-throughput calculations. The recent development of the Thermo-Calc Python (TC-Python) application programing interface has enabled high-throughput DICTRA calculations by adding the capability to automatically setup and post-processing batches of DICTRA calculations that cover large ranges in composition and processing parameters. Furthermore, DICTRA solidification models have never been coupled with models for SCS. Integrating process models with DICTRA solidification calculations and the Kou SCS criteria can be used to extend SCS models to the process level, enabling SCS to be investigated as a function of processing variables and composition. Integrating these models in a high-throughput computational framework creates a linkage between processing and microstructural effects that reveals new relationships between the additive manufacturing process and non-equilibrium solidification.

2. Materials and Methods

One-dimensional DICTRA solidification models are implemented using the TC-Python application programming interface to enable batch calculations as a function of both processing conditions and composition. The semi-analytic laser powder bed fusion (LPBF) process model developed by Wolfer et al. [21], which uses a Green’s function approach, is coupled with DICTRA simulations and the Kou SCS model [13,14] to create a CALPHAD-based ICME framework for modeling non-equilibrium solidification in additively manufactured materials. Temperature histories under different processing conditions are used as an input for DICTRA solidification calculations to investigate the relationship between the additive manufacturing process and non-equilibrium solidification. This approach couples alloy thermodynamics and diffusion with process variables such as laser power, scan speed, and energy density to model the effect of process parameters on non-equilibrium solidification.

Figure 1 shows how the models used in this work are coupled together using the TC-Python application programing interface to create an automated CALPHAD-based ICME framework for modeling solidification in additively manufactured materials. The TC-Python application programing interface is used to automate the Scheil-Gulliver, equilibrium, and DICTRA solidification calculations presented in this work. Integrating the LPBF process model, DICTRA calculations, and the SCS model defined by Kou using the TC-Python application programing interface expedites the tedious process of running models and post-processing data. Calculation results, such as microsegregation and SCS, are automatically post-processed and saved in a convenient text file format. This automated workflow enables the user to efficiently model large ranges in processing conditions and multicomponent composition space. The connection between macroscale process simulations and CALPHAD solidification models simplifies the complex process-microstructure relationship in additively manufactured materials into a resolvable problem by considering processing effects on the temperature history at a microstructural scale.

Setting up solidification calculations using DICTRA requires the user to have a prior understanding of the expected solidification pathway. The liquid and solid phases present during solidification and the type of solidification reaction must be known to properly setup the calculation. For example, SS316L typically undergoes a peritectic reaction with the liquid phase solidifying as BCC and then transforming into FCC. Modeling peritectic type solidification with DICTRA requires that the primary and secondary solidification phases be initialized on the same side of the one-dimensional diffusion cell. For eutectic type solidification reactions, such as the eutectic in the Al-Cu system, the primary and secondary solidification phases must be initialized on opposite sides of the one-dimensional DICTRA simulation. Conversely, the Scheil-Gulliver model does not require prior knowledge of the materials system and can be used to gain insight into the expected solidification pathway in cases where there is limited kinetic knowledge available. From the Scheil-Gulliver model, the expected solidification phases and reaction type can be determined and used to set up a higher fidelity solidification calculation using DICTRA. Using information from the Scheil-Gulliver model to determine the solidification pathway and automate the construction of high-throughput DICTRA calculations gives the modeling framework flexibility to investigate large ranges of unexplored composition space by dynamically changing the phase transformation model. Although significant challenges, such as numerical convergence issues and a deficiency of multicomponent mobility databases still limit this approach, the CALPHAD-based ICME framework outlined in this work takes a step towards utilizing high-throughput DICTRA calculations as a tool for materials design and discovery.

Solidification cracking, also referred to as hot tearing and hot cracking, is caused by the contraction of solid in the mushy zone during solidification. When the liquid becomes trapped between dendrite arms, it causes stress resulting from the lower density of the liquid when compared to the solid. SCS is related to the ability of the liquid to move out of the area between dendrite arms when shrinkage occurs. The ability of the liquid to escape the region between dendrite arms is referred to as liquid feeding ability and is related to the slope of the temperature versus the square root of the solid fraction as defined by the Kou SCS model [13,14]. The Kou SCS model can predict trends in SCS but cannot quantitatively determine if hot cracking will occur. This work aims to extend the Kou criteria to the process level by using DICTRA calculations to rank SCS based on processing parameters. The temperature versus the square root of the solid fraction is obtained using the Scheil-Gulliver or DICTRA solidification models and used to calculate the SCS according to Equation (1),

$$SCS=max\left|\frac{dT}{d\left(f_s^{1/2}\right)}\right|,$$

(1)

where f_s and T are the total solid fraction and temperature, respectively. Various modifications of Equation (1) [13,14] have been investigated in previous works and in general, yield similar results. The present form of Equation (1) was selected because it is easily implemented with numerical simulations for solidification. Computing the derivative shown in Equation (1) from DICTRA results causes numerical issues because the time and temperature step size vary throughout the simulation. The time step of the DICTRA model used in this work is controlled by the movement of phase boundaries to ensure that changes in the rate of phase transformations are captured by the model. Variations in the time and temperature step size implies that standard finite difference approximations of Equation (1) cannot be applied. Lagrange polynomial differentiation is used to overcome this limitation because a constant point spacing is not required for the derivative to be calculated. The numerical approximation of Equation (1) using three-point central Lagrange polynomial differentiation [22] is given in Equation (2),

$$\left|\frac{d{T}_{i+1}}{d\left(f_{s_{i+1}}^{1/2}\right)}\right|\approx \left|\begin{array}{c}\left(\frac{f_{s_{i+1}}^{1/2}-f_{s_{i+2}}^{1/2}}{\left(f_{s_i}^{1/2}-f_{s_{i+1}}^{1/2}\right)\left(f_{s_i}^{1/2}-f_{s_{i+2}}^{1/2}\right)}\right)T_i\\ +\left(\frac{2f_{s_{i+1}}^{1/2}-f_{s_i}^{1/2}-f_{s_{i+2}}^{1/2}}{\left(f_{s_{i+1}}^{1/2}-f_{s_i}^{1/2}\right)\left(f_{s_{i+1}}^{1/2}-f_{s_{i+2}}^{1/2}\right)}\right)T_{i+1}+\left(\frac{f_{s_{i+1}}^{1/2}-f_{s_i}^{1/2}}{\left(f_{s_{i+2}}^{1/2}-f_{s_i}^{1/2}\right)\left(f_{s_{i+2}}^{1/2}-f_{s_{i+1}}^{1/2}\right)}\right)T_{i+2}\end{array}\right|$$

(2)

The thermal model used to generate temperature histories for the LPBF process is the fast semi-analytical method developed by Wolfer et al. [21]. This method is utilized because it is an order of magnitude faster than an equivalent finite element model, allowing the user to quickly sweep the chosen parameter space while introducing minimal error. The model treats the powder bed as a homogeneous continuum with uniform and constant material properties and ignores explicit melt pool dynamics, focusing instead on a conduction-based approximation. With some calibration, this conduction-only method can be used to reproduce, with a reasonable degree of accuracy, the melt pool dimensions generated by high-fidelity simulations [23]. This calibration involves the adjustment of the volumetric source term and a selection of material properties that are representative of the material at elevated temperatures. When high-temperature material properties are unavailable or the materials system is unstudied, CALPHAD databases can be used to determine the density, specific heat, conductivity, and Gibbs free energy as a function of composition and temperature [10]. The significant speed increase over traditional methods is achieved by using a Green’s function solution to the reduced-order conduction-based model. This semi-analytical solution takes the form of a Gaussian filtering function and is fast because it is computationally simple and allows for the use of larger time steps and coarser meshes. Though the large time step results in a more complicated laser source term, it can be re-used for identical time-steps, maintaining the speed of the model.

3. Results

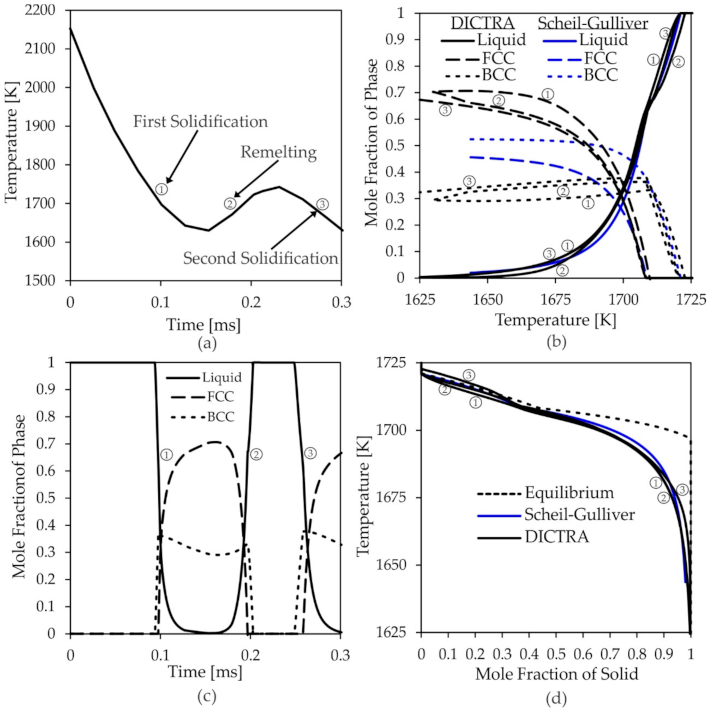
3.1. Modeling Non-Equilibrium Solidification of Al-Cu Alloys

Non-equilibrium solidification of Al-Cu alloys is modeled to validate the ability of DICTRA to predict trends in SCS as a function of the cooling rate. DICTRA calculations for the Al-Cu system are set up using the eutectic phase transformation model, a cell size of 1 µm, and a constant cooling rate. The TCAL7 and MOBAL5 databases released with Thermo-Calc software version 2020b are used (Thermo-Calc Software AB, Stockholm, Sweden). The liquid, FCC, and Al₂Cu phases are included in the model, all metastable phases are suspended, and the system is assumed to be closed. The effect of nucleation barriers is also neglected, and a planar geometry is used for all calculations. Three constant cooling rates, −10², −10⁴, and −10⁵ K/s, were investigated to determine if DICTRA can accurately model the reduction in the solidus temperature caused by microsegregation and match the experimentally observed trend of SCS reported in the literature. Figure 2a shows the solidus and liquidus temperature predicted using the equilibrium, Scheil-Gulliver, and DICTRA models for solidification. DICTRA predicts a decreasing solidus temperature with an increase in the cooling rate. As the cooling rate is increased, the solidus temperature predicted by DICTRA approaches the result of the Scheil-Gulliver model. The liquidus temperature is predicted to be the same by all models investigated in this work because all nucleation barriers are assumed to be negligible. Figure 2b shows the SCS predicted by the Scheil-Gulliver and DICTRA models with a cooling rate of −10², −10⁴, and −10⁵ K/s. SCS is calculated using the model proposed by Kou et al. [13,14] and is compared with experimental SCS % data on a secondary axis. The experimental data shown in Figure 2b were collected by Yan et al. [12], summarized by Campbell et al. [24], and originally produced by [25,26,27]. Model results are plotted using a five-point moving average to smooth out the numerical error associated with calculating the derivative at higher copper content.

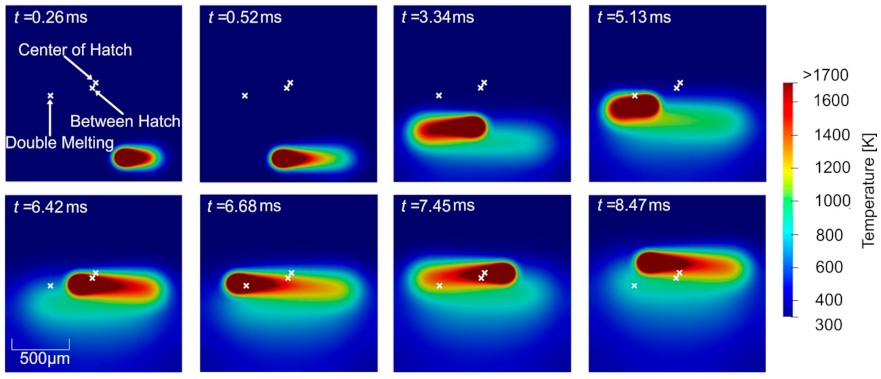
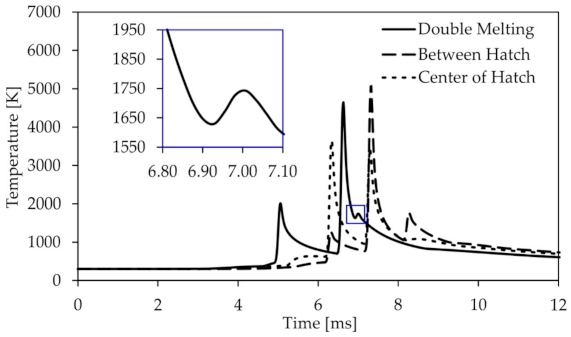
3.2. Predicting Thermal History during the Laser Powder Bed Fusion Process

The LPBF process model used in this work to predict the temperature history during additive manufacturing of SS316L consisted of a single layer 1080 µm square with a bidirectional raster scanning pattern and a 90 µm hatch spacing. The material properties were taken at 700 K by performing a linear interpolation of the properties given by Khairallah et al. [28], yielding a density of 7.9 g/(cm³), thermal conductivity of 20.2 W/(m·K), and specific heat of 470 J/(kg·K). This temperature was chosen as previous results have shown that the melt pool dimensions in SS316L are more accurate when modeled using material properties from this elevated temperature range. Zero flux boundary conditions are applied to the top and sides of the substrate and the bottom has a constant temperature consistent with the initial temperature (300 K). These boundary conditions are consistent with those used during the validation of the thermal model. The model was run with a selection of laser velocities, 0.8–1.2 m/s varying by 0.2 m/s, and laser powers 170–190 W varying by 10 W based on the optimal parameters proposed by Yan et al. [29]. A range of processing parameters was investigated to determine if the CALPHAD-based ICME framework can predict the effect of processing conditions on non-equilibrium solidification. The results were then inspected to determine which locations may be of interest to the microstructural model. These points were chosen to give a broad representation of thermal histories produced by the model. Three subsets of points were selected; the first were points from a cross section of the melt pool to capture dependence on relative location. Second, points were selected that melted more than once. Lastly, points were selected with higher and lower than average cooling rates. These points were down-selected to three points; one which rapidly remelted, one at the center of the path, and one between subsequent passes. This down-selection was carried out to avoid convergence issues with the DICTRA model for certain cooling curves. Figure 3 shows the development of the thermal field as the laser moves through the bidirectional raster scanning pattern. The white X’s shown in Figure 3 mark the location of temperature histories used as inputs to the CALPHAD-based ICME framework.

Temperature histories taken from the locations marked in Figure 3 are shown as a function of time in Figure 4. The location that undergoes rapid double melting was screened for by finding the location where the liquidus temperature is reached consecutively in the shortest period. Rapid double melting was investigated to determine if the non-equilibrium DICTRA solidification model is affected. The inset plot shown in Figure 4 highlights the rapid double melting cycle. One feature of the thermal histories that is worth addressing is the high peak temperatures predicted at the point of incidence of the laser during melting. As the thermal model uses a conduction-only approach (combined with calibrated effective transport parameters) to capture multiple heat transfer mechanisms, it produces peak melt temperatures that are beyond what is expected. However, because the model was calibrated using high-fidelity numerical simulations by comparison of the melt pool geometry, it is hypothesized that the accuracy of the predicted thermal field outside of the melt pool would be reasonable. Since the boundary of the melt pool is constrained to the melting temperature, it is analogous to a Dirichlet boundary condition and the thermal field calculated inside the melt pool can be ignored as it has no effect on the overall thermal field. This hypothesis was verified by comparing the isotherms predicted by the thermal model with those obtained by ALE3D, a high-fidelity multi-physics simulation code produced by Lawrence Livermore National Lab which has itself been validated experimentally [23,28,30].

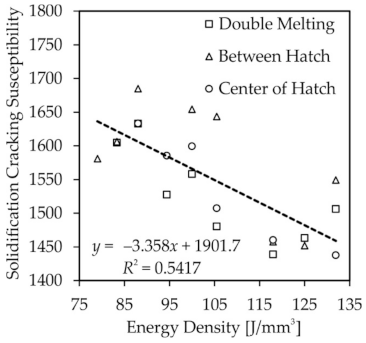
3.3. Solidification of SS316L during Additive Manufacturing

Non-equilibrium solidification of SS316L is modeled using the CALPHAD-based ICME framework shown in Figure 1 to test the convergence of DICTRA models under different temperature histories and investigate the effect of processing conditions on non-equilibrium solidification. A six-component system, consisting of Fe66.985-Cr17-Ni12-Mn1.5-Mo2.5-C0.015 in weight percent, is considered using the TCFE10 and MOBFE5 databases available in the 2020b release of Thermo-Calc software. The effects of nucleation barriers are neglected, and a closed system with a constant cell size of 10 nm and planar geometry is used for all calculations. Temperature histories generated from the LPBF process model for various processing conditions and locations throughout a single layer build are used as inputs to the DICTRA solidification model. Figure 5 shows the results of a representative DICTRA simulation from a location in the LPBF process model that undergoes multiple remelting cycles. The temperature history is directly used from the LPBF process model as shown in Figure 5a. Cutoff temperatures, defined as the solidus and liquidus, are used to select only the portion of the temperature history that relates to solidification. This minimizes the computational expense of each model and enables high-throughput calculations by only modeling phase transformations during solidification. The phase fraction of BCC and FCC as a function of temperature predicted by DICTRA deviates significantly from the Scheil-Gulliver prediction as shown in Figure 5b. Thus, the effect of back-diffusion is significant in SS316L at the high cooling rates seen in additive manufacturing processes. During the second solidification cycle, the phase fraction of BCC and FCC moves closer to the Scheil-Gulliver prediction, indicating that multiple remelting cycles cause solidification to deviate further from equilibrium if segregation in the liquid is not given enough time to homogenize. Figure 5c shows the phase fraction as a function of time predicted by DICTRA and highlights the rapid solidification and remelting that occurs because of the temperature history shown in Figure 5a. The plot of temperature versus the total solid fraction shown in Figure 5d shows reasonable agreement between the Scheil-Gulliver and DICTRA prediction.

Figure 6 shows the results of the Kou SCS model applied to DICTRA solidification calculations for SS316L as a function of energy density. Energy density is defined as the laser power divided by the product of hatch spacing, layer height, and scanning speed. A linear relationship is observed between SCS and the energy density used in the LPBF process model. Considering the inherent numerical error associated with DICTRA, the relationship between the Kou SCS model prediction and energy density is significant. The correlation between energy density and SCS is related to changes in the cooling rate during solidification. Temperature histories generated by the LPBF process model under processing conditions with lower energy density yielded faster cooling rates and higher SCS. No significant difference in the Kou SCS model is found based on the location the temperature history is taken from. Some calculations resulted in convergence issues and could not be resolved. However, convergence was achieved in most temperature histories tested in this work.

4. Discussion

Non-equilibrium solidification of Al-Cu alloys is used as a case study to demonstrate the ability of DICTRA to correlate changes in the cooling rate with SCS as a function of composition. In general, the trend in SCS predicted by the Scheil-Gulliver and DICTRA models is consistent with experimental solidification crack length measurements. The peak in SCS predicted by the Scheil-Gulliver and DICTRA models occurs at slightly higher Cu content than the experimentally observed peak reported by Campbell et al. [24]. However, the characteristic lambda shape commonly observed in SCS measurements of binary aluminum alloys [8] matches reasonably well with the experimental data as shown in Figure 2b. It is also observed that increasing the cooling rate during solidification pushes the solidification reaction further from equilibrium which, reduces the solidus temperature, increases microsegregation, and leads to increased SCS. The experimentally observed trend in SCS is reasonably reproduced by the model, demonstrating its ability to correlate process-level variables with microstructural effects. Intuitively, the model also predicts a reduction in the SCS with a decrease in the cooling rate.

The linear relationship between energy density and SCS predicted for SS316L made by LPBF demonstrates the value of coupling process models with microstructure level CALPHAD models. Increasing the energy density generally decreases the cooling rate because a larger amount of thermal energy is applied to the material, thus taking a longer time to cool. Reductions in the cooling rate led to a reduced SCS at higher energy density. Future work may be able to correlate changes in scanning strategy with SCS, microsegregation, and phase fraction using high-throughput DICTRA calculations by investigating the effect of temperature histories at various locations throughout a single layer build. No trends in SCS based on the location in the LPBF process model were found. However, switching to a material with higher SCS than SS316L, such as Ti-6Al-4V or Al-Cu, may reveal a spatial dependence.

Non-equilibrium solidification is an important metallurgical phenomenon to consider in materials design for additive manufacturing. Optimization of new alloys should focus on controlling solidification during the additive manufacturing process to obtain improved properties in the as-built condition. Models for predicting microsegregation, SCS, and phase transformations in additively manufactured materials as a function of processing parameters and composition are limited and the potential for impact in the field is apparent. The CALPHAD-based ICME framework proposed in this work attempts to address the disconnect between macroscale processing effects and microstructure level models for solidification. This work falls short of defining a quantitative process-microstructure relationship but demonstrates that modern materials models can predict qualitative relationships in additive manufacturing processes.

Improvement of the numerical solver within DICTRA is needed to realize the full potential of the CALPHAD-based ICME framework developed in this work. Convergence issues with DICTRA affected about half of the temperature histories tested in this work and limited the ability to use DICTRA in high-throughput calculations. This work also highlights the importance of reliable thermodynamic and mobility databases of critical materials systems. Improvement of thermodynamic and mobility databases will directly improve the ability of the CALPHAD approach to design the next generation of additively manufactured materials.

5. Conclusions

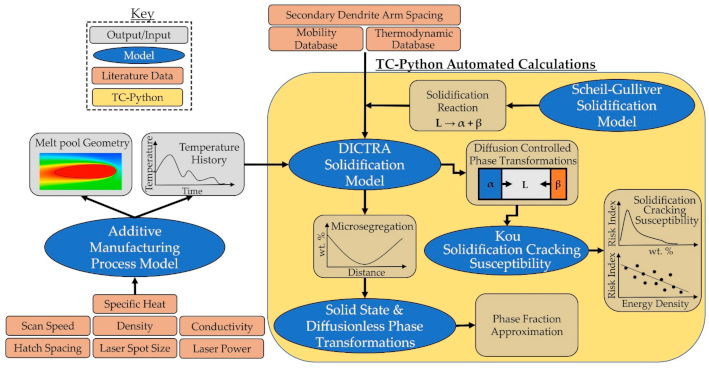
• The TC-Python application programing interface is used to couple a thermal model for the LPBF process with a DICTRA solidification model to simulate the process-microstructure relationship between processing variables and non-equilibrium solidification in additively manufactured materials. Automation of the CALPHAD-based ICME framework with the TC-Python application programing interface enables DICTRA calculations to be used as a high-throughput computational materials design tool. Improvement of numerical algorithms within DICTRA is necessary to enhance the computational efficiency of diffusion simulations.
• Experimental measurements of SCS for the binary Al-Cu system are in good agreement with DICTRA solidification calculations using the model proposed by Kou et al. [13,14].
• A linear relationship between SCS and energy density in SS316L manufactured by LPBF is predicted using a CALPHAD-based ICME framework. A location-dependent relationship with SCS in SS316L is not found.
• The ICME modeling framework developed in this work demonstrates the importance of integrating mechanical and materials models for design simulations in additive manufacturing. The developed modeling framework can be used to guide alloy design and process optimization for additive manufacturing. This framework can also be applied to other processing techniques provided a suitable thermal model is available. Since the present ICME model is based on thermodynamics and diffusion model-predictions, sustainable improvement of the CALPAHD database fidelity is critical to sustaining model accuracy.