Inelastic Strength for Fire Resistance of Composite I-Beam Covered by Insulation Material Subjected to Basic Loading Condition
Abstract
1. Introduction
2. Moment Resistance of Composite Beams
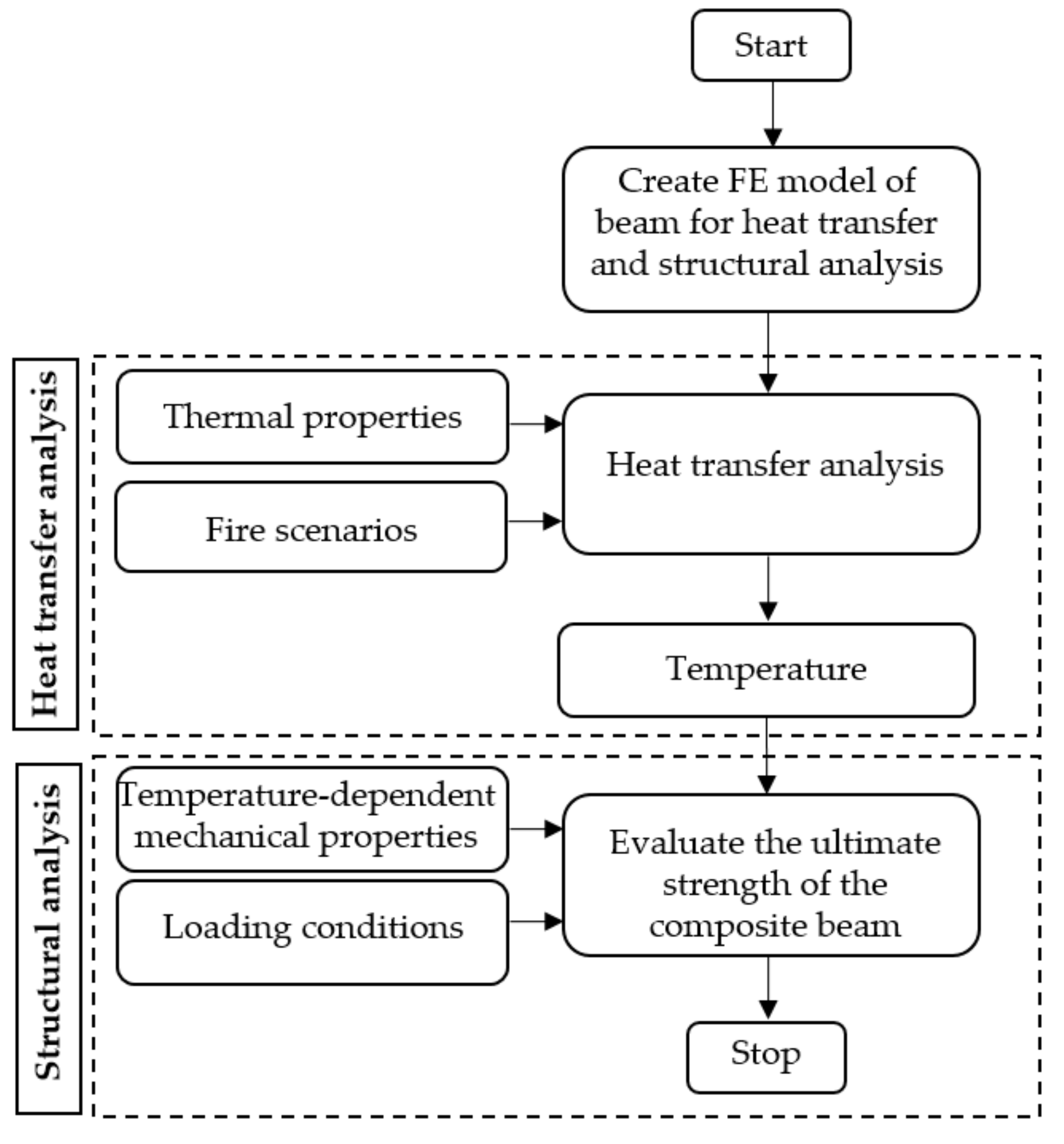
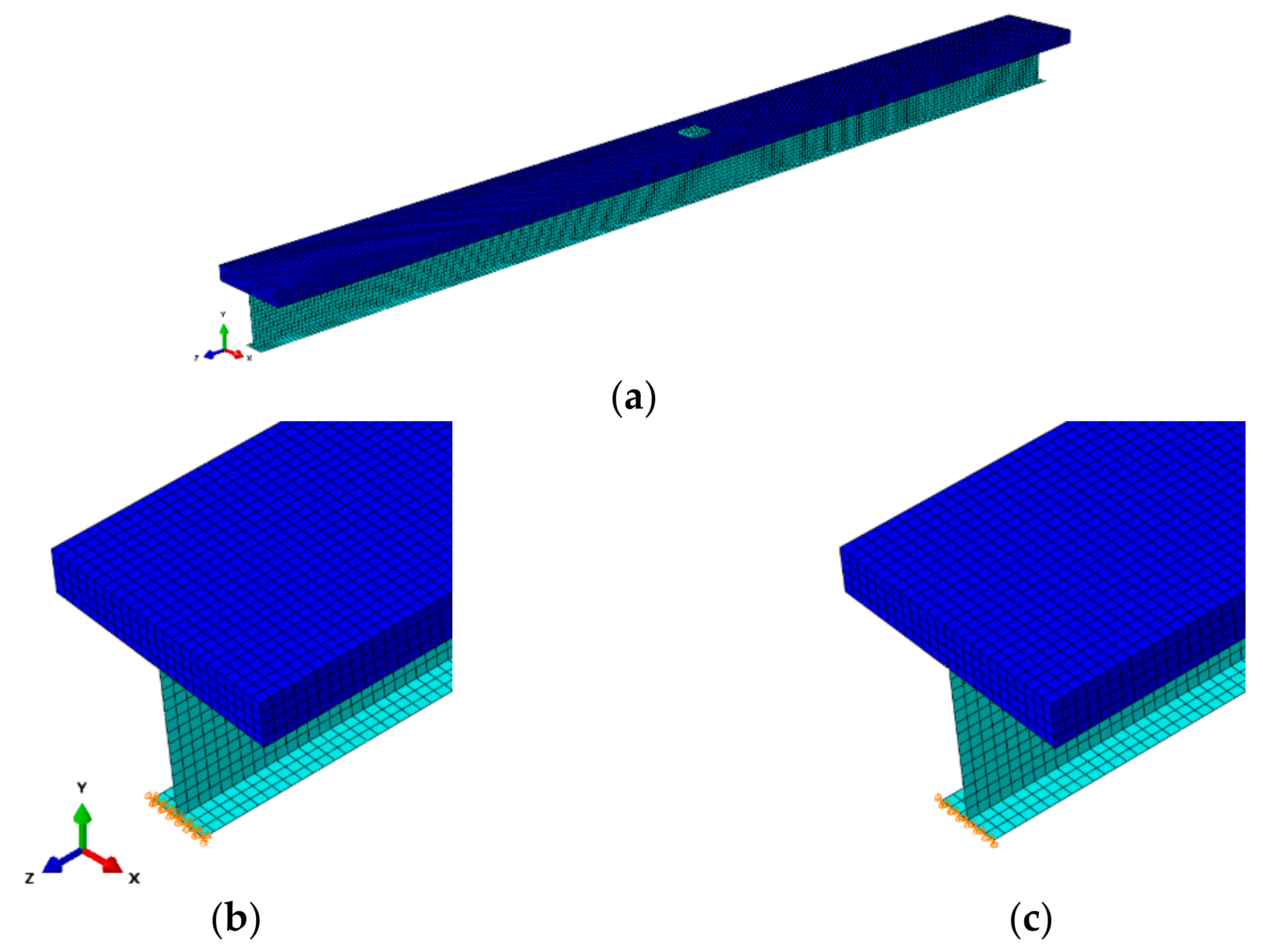
3. Finite Element Analysis
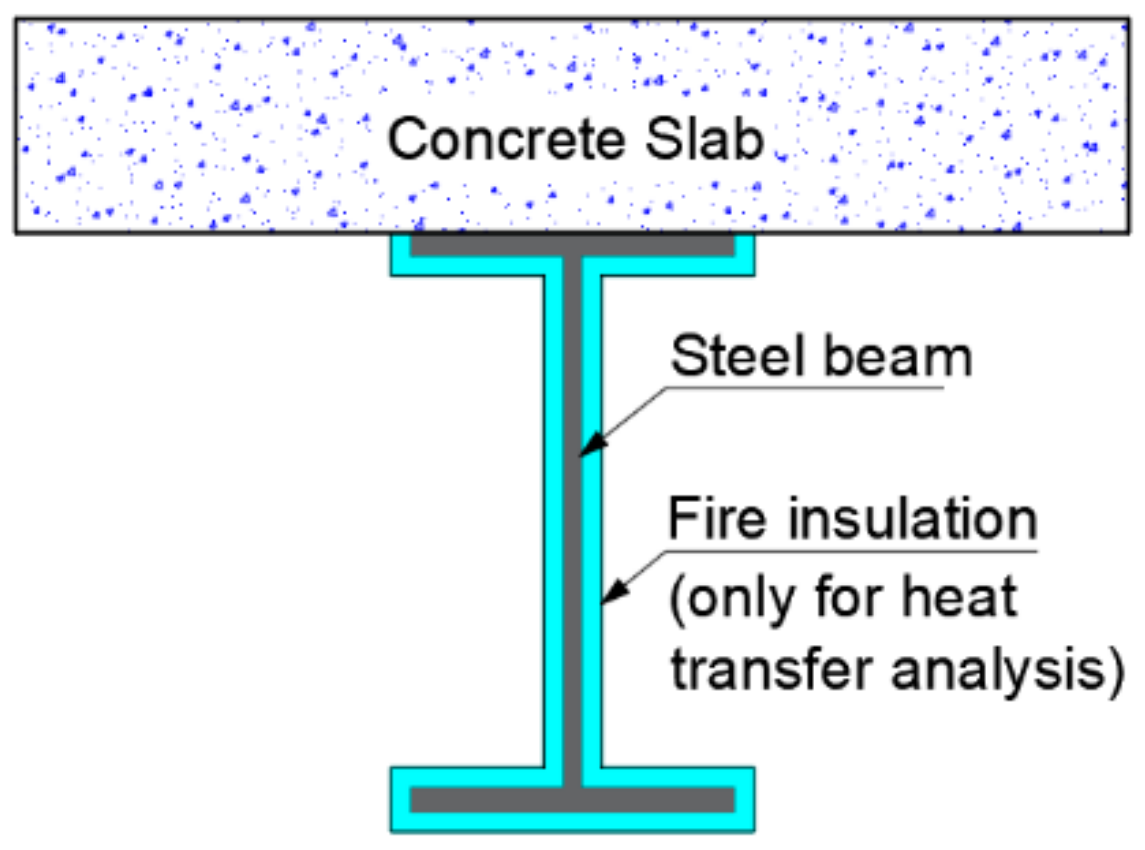
3.1. Heat Transfer Analysis
3.2. Structural Analysis
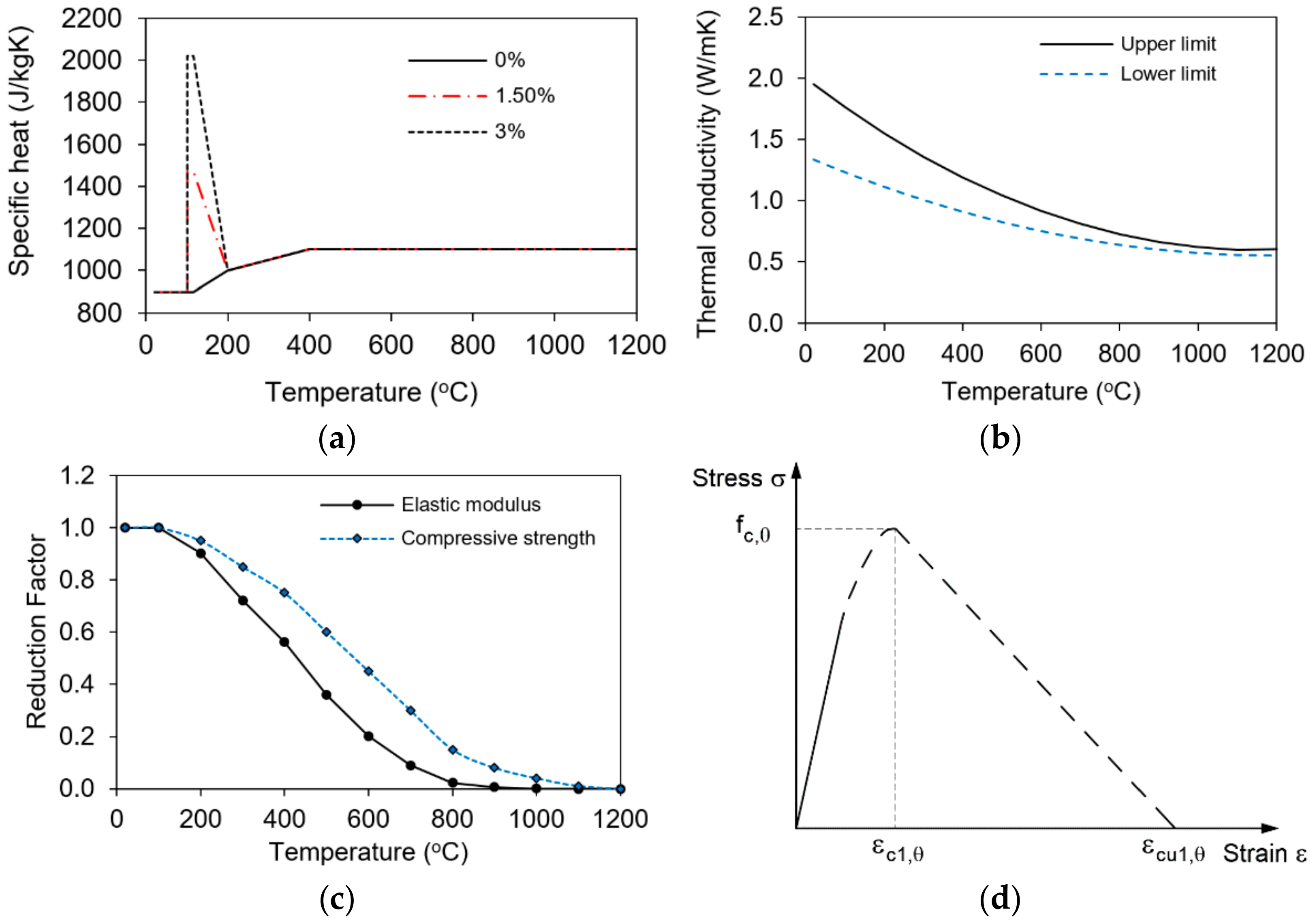
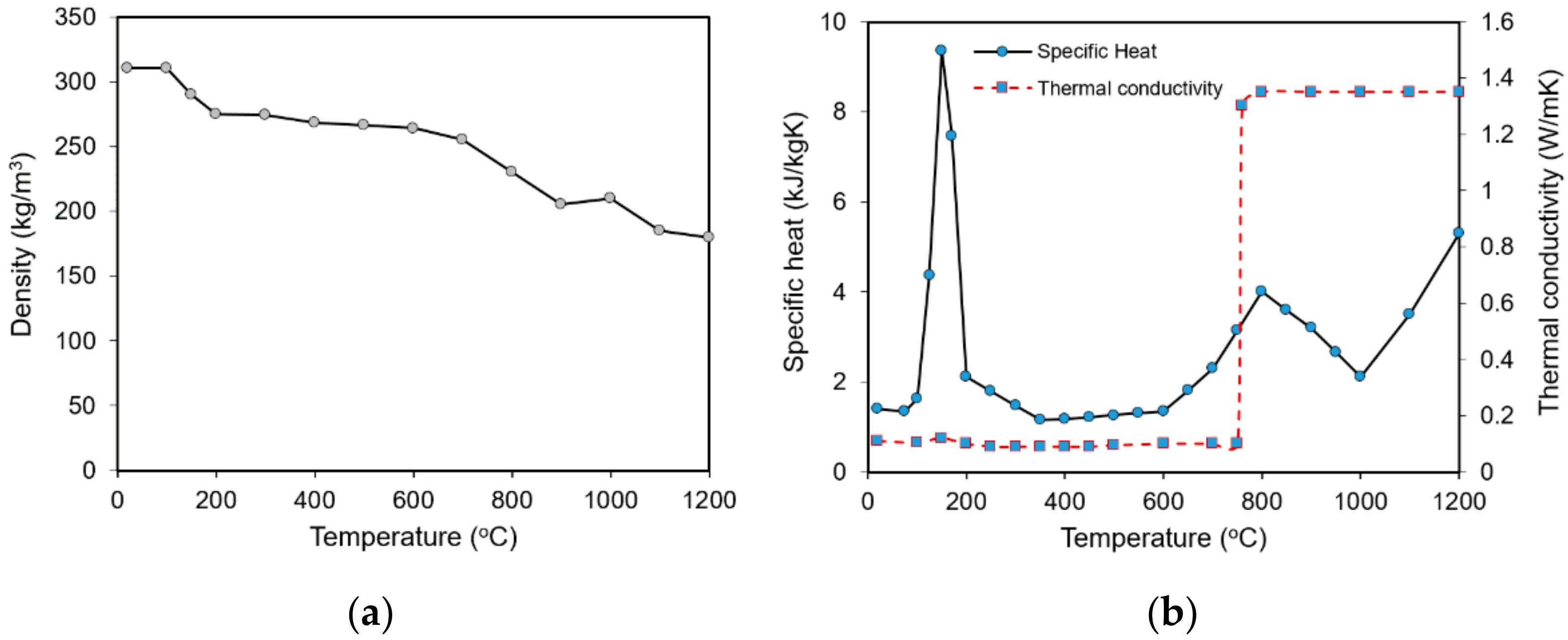
3.3. Material Properties
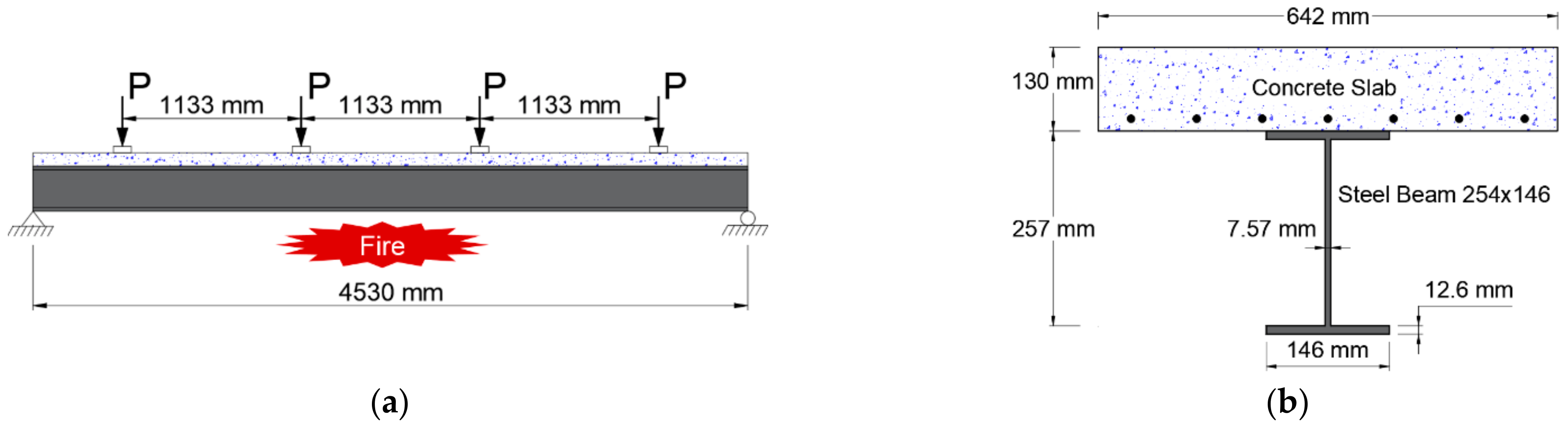
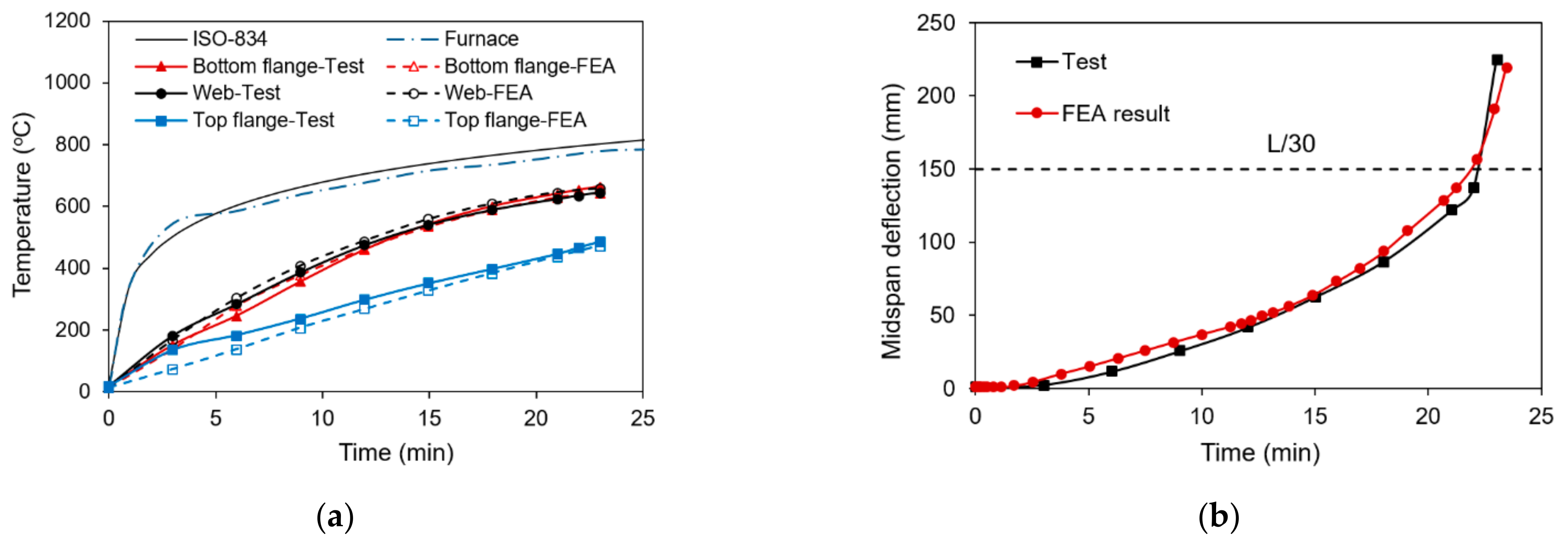
4. Validation of Model
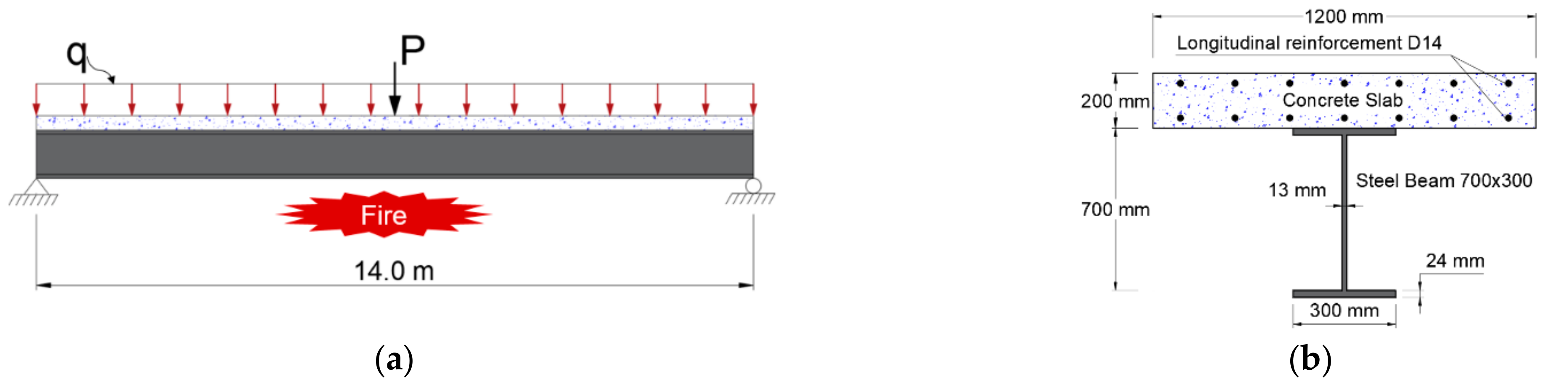
5. Model Properties
6. Finite Element Analysis Results
6.1. Temperature Distribution in the Beam
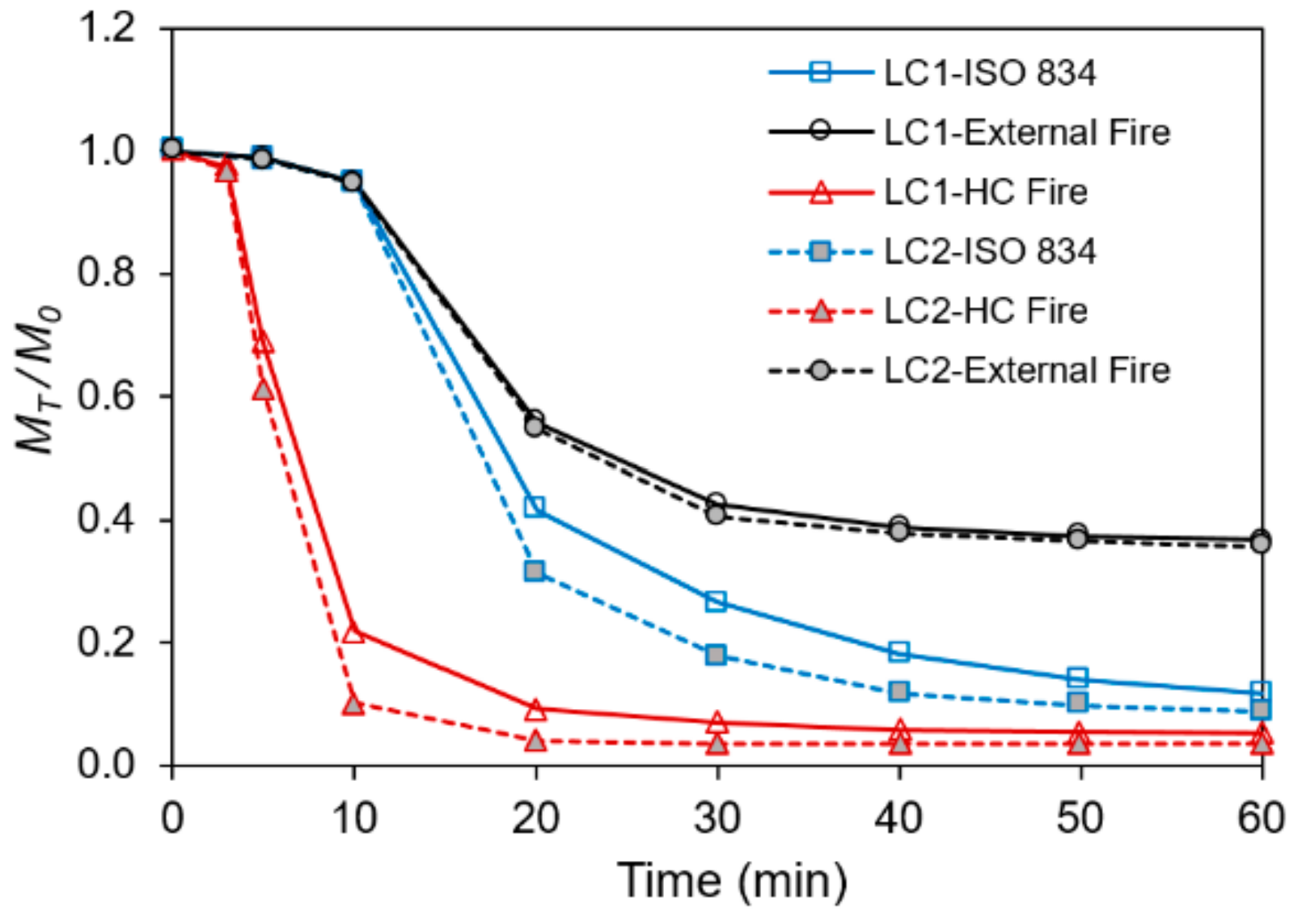
6.2. Influence of Fire Scenarios and Load Cases on the Moment Resistance
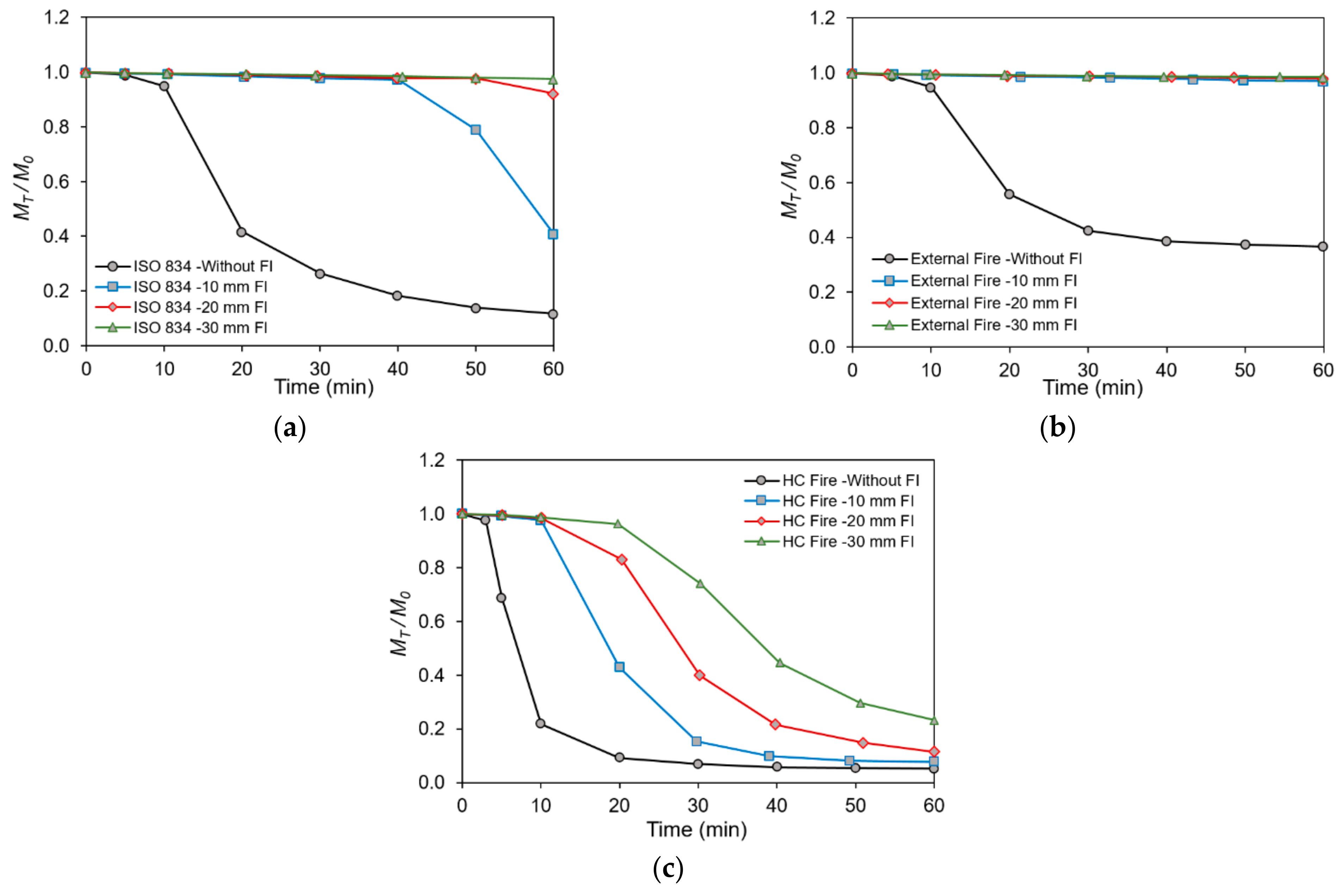
6.3. Influence of Fire Insulation Thickness on the Moment Resistance
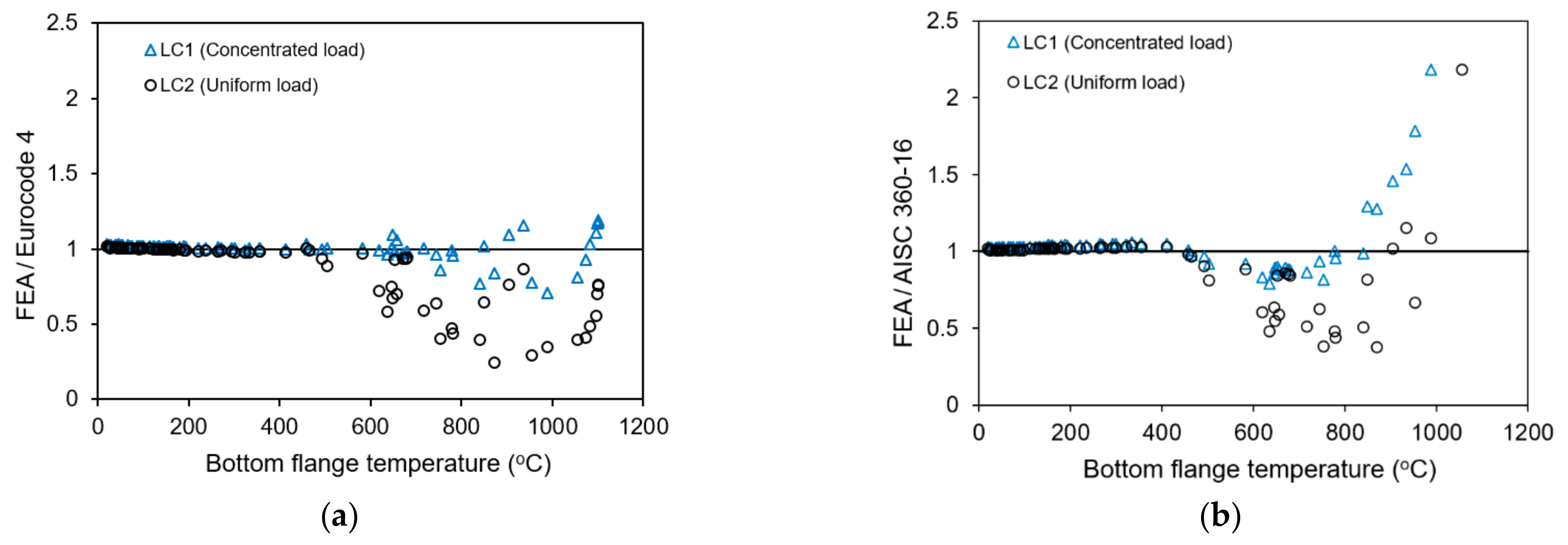
6.4. Comparison with Design Codes
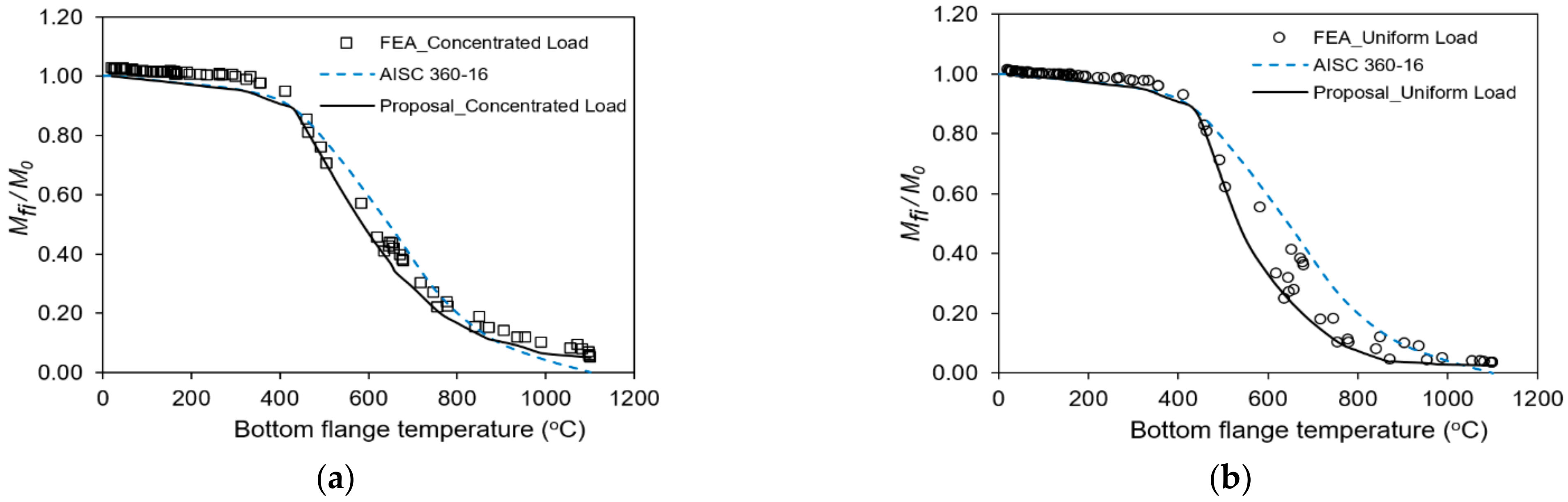
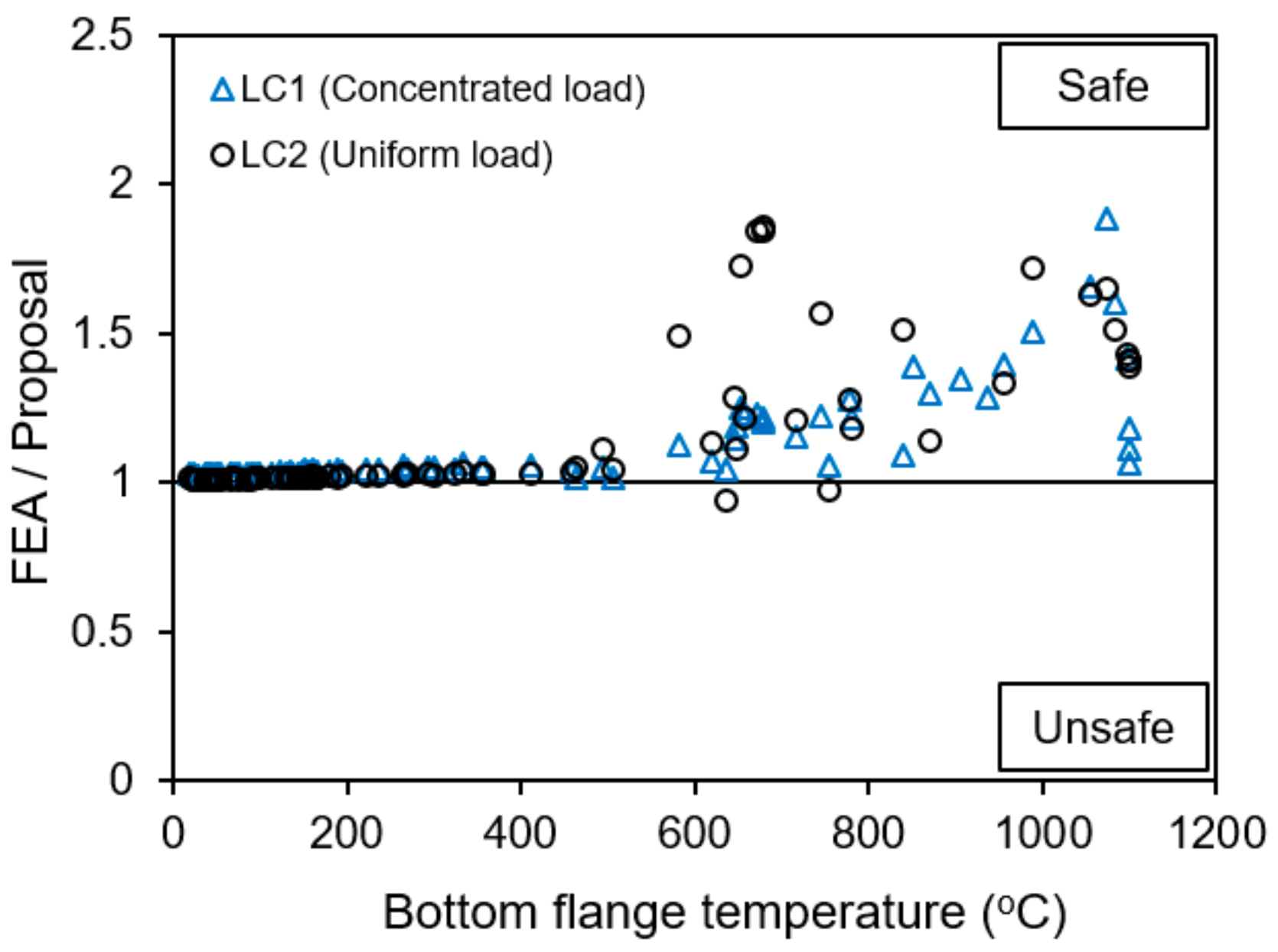
6.5. Proposal for Fire Resistance Moment
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Cases | Time, Min | Bottom Flange Temperature, °C | Eurocode 4 | AISC | FEA | Proposal | ||
|---|---|---|---|---|---|---|---|---|
| LC1, LC2 | LC1, LC2 | LC1 | LC2 | LC1 | LC2 | |||
| ISO834-Without FI | 0 | 20 | 2819.3 | 2819.3 | 2900.1 | 2859.31 | 2819.3 | 2819.3 |
| 5 | 158 | 2819.3 | 2758.9 | 2869.0 | 2818.03 | 2758.9 | 2758.9 | |
| 10 | 355 | 2751.0 | 2623.9 | 2752.5 | 2708.72 | 2623.9 | 2623.9 | |
| 20 | 646 | 1202.3 | 1404.4 | 1206.2 | 897.87 | 1054.6 | 698.1 | |
| 30 | 745 | 801.3 | 820.0 | 769.3 | 510.29 | 627.7 | 325.6 | |
| 40 | 850 | 521.7 | 408.9 | 529.1 | 335.60 | 380.5 | 133.9 | |
| 50 | 905 | 368.8 | 276.0 | 402.3 | 280.23 | 299.2 | 105.0 | |
| 60 | 936 | 291.9 | 219.3 | 337.1 | 252.71 | 263.0 | 98.1 | |
| External fire-Without FI | 5 | 160 | 2819.3 | 2757.7 | 2869.2 | 2816.69 | 2757.7 | 2757.7 |
| 10 | 356 | 2750.0 | 2622.5 | 2751.8 | 2707.87 | 2622.5 | 2622.5 | |
| 20 | 582 | 1610.9 | 1763.1 | 1617.5 | 1560.86 | 1433.5 | 1044.9 | |
| 30 | 652 | 1251.2 | 1371.3 | 1233.9 | 1161.45 | 986.1 | 671.8 | |
| 40 | 672 | 1158.2 | 1254.1 | 1121.3 | 1079.58 | 913.6 | 585.3 | |
| 50 | 677 | 1112.0 | 1219.6 | 1082.7 | 1042.74 | 891.9 | 561.4 | |
| 60 | 679 | 1084.6 | 1209.2 | 1065.0 | 1020.45 | 885.3 | 554.3 | |
| HC fire-Without FI | 5 | 505 | 1979.8 | 2163.4 | 1991.6 | 1751.24 | 1955.8 | 1673.5 |
| 10 | 780 | 658.7 | 662.2 | 631.6 | 290.19 | 519.2 | 245.8 | |
| 20 | 1073 | 286.3 | 31.6 | 266.0 | 116.45 | 141.0 | 70.5 | |
| 30 | 1096 | 180.9 | 4.6 | 199.7 | 100.93 | 141.0 | 70.5 | |
| 40 | 1099 | 141.8 | 0.8 | 166.2 | 99.29 | 141.0 | 70.5 | |
| 50 | 1100 | 131.5 | 0.2 | 156.4 | 99.10 | 141.0 | 70.5 | |
| 60 | 1100 | 128.1 | 0.0 | 150.4 | 98.05 | 141.0 | 70.5 | |
| ISO834-10 mm FI | 5 | 42 | 2819.3 | 2809.6 | 2885.1 | 2836.86 | 2809.6 | 2809.6 |
| 10 | 85 | 2819.3 | 2790.9 | 2876.7 | 2823.33 | 2790.9 | 2790.9 | |
| 20 | 153 | 2819.3 | 2761.3 | 2853.8 | 2805.58 | 2761.3 | 2761.3 | |
| 30 | 221 | 2819.3 | 2727.4 | 2837.1 | 2780.76 | 2727.4 | 2727.4 | |
| 40 | 300 | 2819.3 | 2688.3 | 2820.0 | 2758.08 | 2688.3 | 2688.3 | |
| 50 | 464 | 2300.6 | 2350.6 | 2290.6 | 2275.33 | 2257.5 | 2164.8 | |
| 60 | 658 | 1118.4 | 1336.1 | 1184.2 | 784.20 | 964.6 | 644.9 | |
| External fire-10 mm FI | 5 | 45 | 2819.3 | 2808.5 | 2900.1 | 2835.94 | 2808.5 | 2808.5 |
| 9 | 66 | 2819.3 | 2799.3 | 2884.5 | 2824.55 | 2799.3 | 2799.3 | |
| 21 | 151 | 2819.3 | 2762.2 | 2877.7 | 2807.03 | 2762.2 | 2762.2 | |
| 29 | 189 | 2819.3 | 2743.5 | 2861.9 | 2794.46 | 2743.5 | 2743.5 | |
| 43 | 265 | 2819.3 | 2705.9 | 2852.9 | 2778.78 | 2705.9 | 2705.9 | |
| 50 | 293 | 2819.3 | 2691.8 | 2835.4 | 2764.42 | 2691.8 | 2691.8 | |
| 60 | 334 | 2817.4 | 2656.9 | 2819.6 | 2754.25 | 2656.9 | 2656.9 | |
| HC fire-10 mm FI | 5 | 75 | 2819.3 | 2795.5 | 2876.8 | 2826.11 | 2795.5 | 2795.5 |
| 10 | 265 | 2819.3 | 2705.8 | 2828.6 | 2776.21 | 2705.8 | 2705.8 | |
| 20 | 648 | 1138.4 | 1393.2 | 1241.3 | 765.41 | 1043.7 | 689.1 | |
| 30 | 840 | 570.7 | 445.2 | 440.4 | 224.35 | 403.6 | 148.3 | |
| 39 | 988 | 404.9 | 131.2 | 286.9 | 142.10 | 190.6 | 82.5 | |
| 49 | 1055 | 288.4 | 52.6 | 233.9 | 115.04 | 141.0 | 70.5 | |
| 60 | 1082 | 219.4 | 21.1 | 226.0 | 106.86 | 141.0 | 70.5 | |
| ISO834-20 mm FI | 5 | 29 | 2819.3 | 2815.3 | 2889.4 | 2846.56 | 2815.3 | 2815.3 |
| 11 | 53 | 2819.3 | 2805.0 | 2883.5 | 2837.19 | 2805.0 | 2805.0 | |
| 21 | 98 | 2819.3 | 2785.6 | 2869.5 | 2822.49 | 2785.6 | 2785.6 | |
| 30 | 133 | 2819.3 | 2770.2 | 2859.4 | 2811.07 | 2770.2 | 2770.2 | |
| 40 | 166 | 2819.3 | 2754.8 | 2838.0 | 2801.11 | 2754.8 | 2754.8 | |
| 50 | 236 | 2817.7 | 2720.1 | 2831.8 | 2782.86 | 2720.1 | 2720.1 | |
| 60 | 412 | 2686.4 | 2537.1 | 2676.1 | 2619.82 | 2537.1 | 2537.1 | |
| External fire-20 mm FI | 5 | 27 | 2819.3 | 2816.1 | 2887.5 | 2837.53 | 2816.1 | 2816.1 |
| 11 | 54 | 2819.3 | 2804.7 | 2883.4 | 2825.48 | 2804.7 | 2804.7 | |
| 20 | 90 | 2819.3 | 2789.0 | 2873.5 | 2819.75 | 2789.0 | 2789.0 | |
| 30 | 124 | 2819.3 | 2774.3 | 2867.2 | 2815.33 | 2774.3 | 2774.3 | |
| 41 | 148 | 2819.3 | 2763.8 | 2858.4 | 2808.62 | 2763.8 | 2763.8 | |
| 49 | 165 | 2819.3 | 2755.3 | 2849.7 | 2800.07 | 2755.3 | 2755.3 | |
| 60 | 194 | 2819.0 | 2740.8 | 2842.7 | 2794.45 | 2740.8 | 2740.8 | |
| HC fire-20 mm FI | 5 | 50 | 2819.3 | 2806.5 | 2883.3 | 2839.45 | 2806.5 | 2806.5 |
| 10 | 179 | 2819.3 | 2748.6 | 2856.5 | 2806.73 | 2748.6 | 2748.6 | |
| 20 | 459 | 2334.9 | 2376.5 | 2407.6 | 2336.41 | 2302.4 | 2248.2 | |
| 30 | 636 | 1197.5 | 1460.8 | 1155.9 | 701.58 | 1110.3 | 745.1 | |
| 40 | 754 | 729.2 | 767.6 | 626.5 | 291.80 | 591.2 | 299.4 | |
| 51 | 871 | 514.9 | 336.0 | 430.1 | 125.86 | 330.7 | 110.5 | |
| 60 | 954 | 428.6 | 187.1 | 333.6 | 124.16 | 238.7 | 93.0 | |
| ISO834-30 mm FI | 5 | 24 | 2819.3 | 2817.3 | 2892.9 | 2851.94 | 2817.3 | 2817.3 |
| 10 | 39 | 2819.3 | 2810.9 | 2886.9 | 2842.53 | 2810.9 | 2810.9 | |
| 20 | 70 | 2819.3 | 2797.4 | 2876.4 | 2833.12 | 2797.4 | 2797.4 | |
| 29 | 99 | 2819.3 | 2785.0 | 2869.4 | 2822.57 | 2785.0 | 2785.0 | |
| 41 | 130 | 2819.3 | 2771.5 | 2853.2 | 2812.02 | 2771.5 | 2771.5 | |
| 50 | 164 | 2818.6 | 2756.0 | 2840.8 | 2802.80 | 2756.0 | 2756.0 | |
| 60 | 270 | 2813.7 | 2703.1 | 2827.0 | 2784.13 | 2703.1 | 2703.1 | |
| External fire-30 mm FI | 5 | 25 | 2819.3 | 2817.2 | 2888.2 | 2851.04 | 2817.2 | 2817.2 |
| 10 | 39 | 2819.3 | 2811.2 | 2886.5 | 2844.35 | 2811.2 | 2811.2 | |
| 19 | 65 | 2819.3 | 2799.8 | 2877.7 | 2835.50 | 2799.8 | 2799.8 | |
| 30 | 92 | 2819.3 | 2788.1 | 2869.7 | 2826.64 | 2788.1 | 2788.1 | |
| 40 | 113 | 2819.3 | 2779.0 | 2861.6 | 2821.47 | 2779.0 | 2779.0 | |
| 54 | 136 | 2819.3 | 2768.9 | 2857.8 | 2816.16 | 2768.9 | 2768.9 | |
| 60 | 143 | 2819.3 | 2765.8 | 2854.9 | 2810.26 | 2765.8 | 2765.8 | |
| HC fire-30 mm FI | 5 | 39 | 2819.3 | 2811.2 | 2887.0 | 2846.17 | 2811.2 | 2811.2 |
| 10 | 134 | 2819.3 | 2769.8 | 2863.4 | 2818.41 | 2769.8 | 2769.8 | |
| 20 | 324 | 2819.3 | 2672.3 | 2789.7 | 2753.56 | 2672.3 | 2672.3 | |
| 30 | 493 | 2151.4 | 2217.2 | 2147.9 | 2004.16 | 2038.9 | 1797.8 | |
| 40 | 619 | 1304.9 | 1555.4 | 1291.5 | 938.84 | 1206.8 | 829.5 | |
| 51 | 717 | 855.0 | 987.7 | 857.5 | 504.52 | 741.6 | 416.2 | |
| 60 | 777 | 677.8 | 670.6 | 672.0 | 319.34 | 524.9 | 250.0 | |
References
- Fike, R.; Kodur, V. Enhancing fire resistance of composite beam-slab assemblies through steel fiber reinforced concrete. Eng. Struct. 2011, 33, 2870–2878. [Google Scholar] [CrossRef]
- Aziz, E.; Kodur, V. An approach for evaluating the residual strength of fire exposed bridge girders. J. Constr. Steel Res. 2013, 88, 34–42. [Google Scholar] [CrossRef]
- Aziz, E.M.; Kodur, V.K.; Glassman, J.D.; Moreyra Garlock, M.E. Behavior of steel bridge girders under fire conditions. J. Constr. Steel Res. 2015, 106, 11–22. [Google Scholar] [CrossRef]
- Zhou, H.; Li, S.; Chen, L.; Zhang, C. Fire tests on composite steel-concrete beams prestressed with external tendons. J. Constr. Steel Res. 2018, 143, 62–71. [Google Scholar] [CrossRef]
- Kodur, V.K.R.; Naser, M.Z. Designing steel bridges for fire safety. J. Constr. Steel Res. 2019, 156, 46–53. [Google Scholar] [CrossRef]
- Bihina, G.; Zhao, B.; Bouchaïr, A. Behaviour of composite steel-concrete cellular beams in fire. Eng. Struct. 2013, 56, 2217–2228. [Google Scholar] [CrossRef]
- Sucharda, O.; Konecny, P. Recommendation for the modelling of 3D non-linear analysis of RC beam tests. Comput. Concr. 2018, 21, 11–20. [Google Scholar]
- Bresler, B.; Scordelis, A.C. Shear strength of reinforced concrete beams. J. Am. Concr. Inst. 1963, 60, 51–72. [Google Scholar]
- Vecchio, F.J.; Shim, W. Experimental and analytical reexamination of classic concrete beam tests. J. Struct. Eng. 2004, 130, 460–469. [Google Scholar] [CrossRef]
- Agrawal, A.; Kodur, V. Residual response of fire-damaged high-strength concrete beams. Fire Mater. 2019, 43, 310–322. [Google Scholar] [CrossRef]
- Thanaraj, D.P.; Anand, N.; Arulraj, P.; Al-Jabri, K. Investigation on structural and thermal performance of reinforced concrete beams exposed to standard fire. J. Build. Eng. 2020, 32, 101764. [Google Scholar] [CrossRef]
- Lee, S.H.; Choi, B.J. Post fire residual strength of the Wall-Slab using siliceous concrete. Materials 2021, 14, 1793. [Google Scholar] [CrossRef]
- Selden, K.L.; Fischer, E.C.; Varma, A.H. Experimental Investigation of Composite Beams with shear connection subjected to fire loading. J. Struct. Eng. 2016, 142, 04015118. [Google Scholar] [CrossRef]
- Selden, K.L.; Varma, A.H. Composite beams under fire loading: Numerical modeling of behavior. J. Struct. Fire Eng. 2016, 7, 142–157. [Google Scholar] [CrossRef]
- Pak, H.; Kang, M.S.; Kang, J.W.; Kee, S.H.; Choi, B.J. A Numerical Study on the Thermo mechanical Response. Int. J. Steel Struct. 2018, 18, 1177–1190. [Google Scholar] [CrossRef]
- Kodur, V.K.R.; Naser, M.Z. Effect of local instability on capacity of steel beams exposed to fire. J. Constr. Steel Res. 2015, 111, 31–42. [Google Scholar] [CrossRef]
- Naser, M.Z.; Kodur, V.K.R. Factors governing onset of local instabilities in fire exposed steel beams. Thin Wall. Struct. 2016, 98, 48–57. [Google Scholar] [CrossRef]
- Naser, M.Z.; Kodur, V.K.R. Comparative fire behavior of composite girders under flexural and shear loading. Thin Wall. Struct. 2017, 116, 82–90. [Google Scholar] [CrossRef]
- Naser, M.Z.; Kodur, V. Response of fire exposed composite girders under dominant flexural and shear loading. J. Struct. Fire Eng. 2017, 9, 108–125. [Google Scholar] [CrossRef]
- Kodur, V.K.R.; Naser, M.Z. Approach for shear capacity evaluation of fire exposed steel and composite beams. J. Constr. Steel Res. 2018, 141, 91–103. [Google Scholar] [CrossRef]
- Kodur, V.K.R.; Cheng, F.P.; Wang, T.C.; Sultan, M.A. Effect of strength and fiber reinforcement on fire resistance of high-strength concrete columns. J. Struct. Eng. 2003, 192, 253–259. [Google Scholar] [CrossRef]
- Bilodeau, A.; Kodur, V.K.; Hoff, G. Optimization of the type and amount of polypropylene fibres for preventing the spalling of lightweight concrete subjected to hydrocarbon fire. Cem. Concr. Compos. 2004, 26, 163–174. [Google Scholar] [CrossRef]
- Jin, L.; Zhang, R.; Dou, G.; Du, X. Fire resistance of steel fiber reinforced concrete beams after low-velocity impact loading. Fire Saf. J. 2018, 98, 24–37. [Google Scholar] [CrossRef]
- Shoaei, P.; Ghassemi, P.; Ameri, F.; Musaeei, H.R.; Ban, C.C.; Ozbakkaloglu, T. Comparative study on the effect of fiber type and content on the fire resistance of alkali-activated slag composites. Constr. Build. Mater. 2021, 288, 123136. [Google Scholar] [CrossRef]
- Kodur, V.; Aziz, E.; Dwaikat, M. Evaluating Fire Resistance of Steel Girders in Bridges. J. Bridge Eng. 2013, 18, 633–643. [Google Scholar] [CrossRef]
- Kang, H.; Lee, D.H.; Hwang, J.H.; Oh, J.Y.; Kim, K.S.; Kim, H.Y. Structural performance of prestressed composite members with corrugated webs exposed to fire. Fire Technol. 2015, 52, 1957–1981. [Google Scholar] [CrossRef]
- Kodur, V.K.; Aziz, E.M.; Naser, M.Z. Strategies for enhancing fire performance of steel bridges. Eng. Struct. 2017, 131, 446–458. [Google Scholar] [CrossRef]
- Kang, M.S.; Kang, J.W.; Kee, S.H.; Choi, B.J. Damage Evaluation of Composite Beams under Fire Conditions. Int. J. Steel Struct. 2020, 20, 1996–2008. [Google Scholar] [CrossRef]
- Martinez, J.; Jeffers, A.E. Analysis of restrained composite beams exposed to fire. Eng. Struct. 2021, 234, 111740. [Google Scholar] [CrossRef]
- ABAQUS. Standard User’s Manual. Version 2020; Dassault Systèmes: Johnston, RI, USA, 2020. [Google Scholar]
- EN 1994-1-2. Eurocode 4: Design of Composite Steel and Concrete Structures—Part 1-2: General Rules—Structural Fire Design; European Committee for Standardisation: Brussels, Belgium, 2005. [Google Scholar]
- ANSI/AISC 360–16. Specification for Structural Steel Buildings; American Institute of Steel Construction: Chicago, IL, USA, 2016. [Google Scholar]
- EN 1994-1-1. Eurocode 4: Design of Composite Steel and Concrete Structures—Part 1-1: General Rules and Rules for Buildings; European Committee for Standardisation: Brussels, Belgium, 2005. [Google Scholar]
- Hozjan, T.; Saje, M.; Srpčič, S.; Planinc, I. Fire analysis of steel-concrete composite beam with interlayer slip. Comput. Struct. 2011, 89, 189–200. [Google Scholar] [CrossRef]
- Nguyen, X.T.; Park, J.S. Nonlinear buckling strength of steel H-beam under localized fire and pure bending. KSCE J. Civ. Eng. 2021, 25, 561–573. [Google Scholar] [CrossRef]
- EN 1991-1-2. Eurocode 1: Action on Structures—Part 1-2: General Action—Action on Structures Exposed to Fire; European Committee for Standardisation: Brussels, Belgium, 2002. [Google Scholar]
- EN 1992-1-2. Eurocode 2: Design of Concrete Structures—Part 1-2: General Rules—Structural Fire Design; European Committee for Standardisation: Brussels, Belgium, 2004. [Google Scholar]
- EN 1993-1-2. Eurocode 3: Design of Steel Structures—Part 1-2: General Rules–Structural fire Design; European Committee for Standardisation: Brussels, Belgium, 2005. [Google Scholar]
- Kodur, V.K.R.; Shakya, A.M. Effect of temperature on thermal properties of spray applied fire resistive materials. Fire Saf. J. 2013, 61, 314–323. [Google Scholar] [CrossRef]
- Dwaikat, M.M.S.; Kodur, V.K.R. A simplified approach for predicting temperatures in fire exposed steel members. Fire Saf. J. 2013, 55, 87–96. [Google Scholar] [CrossRef]
- Imran, M.; Mahendran, M.; Keerthan, P. Heat Transfer Modelling of CFRP Strengthened and Insulated Steel Tubular Columns. Constr. Build. Mater. 2018, 184, 278–294. [Google Scholar] [CrossRef]
- Wainman, D.E.; Kirby, B.R. Compendium of UK Standard Fire Test Data for Unprotected Structural Steel-1; British Steel Corporation and Swinden Laboratories: Rotherham, UK, 1988. [Google Scholar]
- ISO834. Fire Resistance Tests—Elements of Building Construction; International Organization for Standardization: Geneva, Switzerland, 1999. [Google Scholar]
- Hyundai Steel. Online Products Guide. 2015. Available online: https://www.hyundai-steel.com/kr/down/ProductsGuide.pdf (accessed on 16 April 2021).




| Bottom Flange Temperature (°C) | rT |
|---|---|
| 20 | 1.00 |
| 150 | 0.98 |
| 320 | 0.95 |
| 430 | 0.89 |
| 540 | 0.71 |
| 650 | 0.49 |
| 760 | 0.26 |
| 870 | 0.12 |
| 980 | 0.05 |
| 1100 | 0.00 |
| Types | Properties | Values |
|---|---|---|
| Steel beam | Beam height, h (mm) | 700 |
| Flange width, bf (mm) | 300 | |
| Flange thickness, tf (mm) | 24 | |
| Web thickness, tw (mm) | 13 | |
| Elastic modulus, E (GPa) | 210 | |
| Yield stress, fy (MPa) | 275 | |
| Poisson’s ratio, μs | 0.3 | |
| Concrete slab | Slab thickness, ts (mm) | 200 |
| Slab width, bc (mm) | 1200 | |
| (MPa) | 30 | |
| Poission’s ratio, μc | 0.2 |
| Temperature (°C) | Steel Beam | Concrete Slab | ||
|---|---|---|---|---|
| Yield Stress, fy (MPa) | Elastic Modulus, E (MPa) | Compressive Strength, (MPa) | Elastic Modulus, E (MPa) | |
| 20 | 275.00 | 210,000 | 30.00 | 30,588.56 |
| 100 | 275.00 | 210,000 | 30.00 | 30,588.56 |
| 200 | 275.00 | 189,000 | 28.50 | 27,606.18 |
| 300 | 275.00 | 168,000 | 25.50 | 22,100.24 |
| 400 | 275.00 | 147,000 | 22.50 | 17,206.07 |
| 500 | 214.50 | 126,000 | 18.00 | 11,011.88 |
| 600 | 129.25 | 65,100 | 13.50 | 6194.18 |
| 700 | 63.25 | 27,300 | 9.00 | 2752.97 |
| 800 | 30.25 | 18,900 | 4.50 | 688.24 |
| 900 | 16.50 | 14,175 | 2.40 | 195.77 |
| 1000 | 11.00 | 9450 | 1.20 | 48.94 |
| Cases | Temperature in Steel Beam | Temperature in Slab and FI |
|---|---|---|
| Without FI | 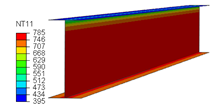 |  |
| FI (t = 10 mm) | 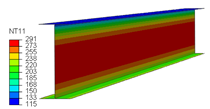 | 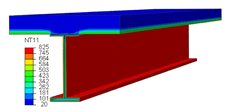 |
| FI (t = 20 mm) | 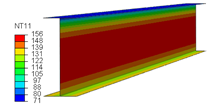 | 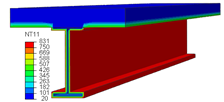 |
| FI (t = 30 mm) | 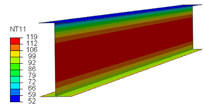 | 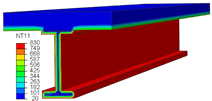 |
| Load Cases | Bottom Flange Temperature, T (°C) | f | rT |
|---|---|---|---|
| LC1 | T ≤ 430 | 1 | AISC * |
| 430 < T ≤ 650 | 0.0016T + 0.2982 | AISC * | |
| 650 < T ≤ 800 | −0.0009T + 1.9771 | AISC * | |
| 800 < T ≤ 1000 | −0.0028T + 3.4557 | AISC * | |
| T = 1100 | 1 | 0.05 | |
| LC2 | T ≤ 430 | 1 | AISC * |
| 430 < T ≤ 870 | 0.0051T − 1.2825 | AISC * | |
| 870 < T ≤ 1000 | −0.0124T + 13.846 | AISC * | |
| T = 1100 | 1 | 0.025 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, X.T.; Park, J.S. Inelastic Strength for Fire Resistance of Composite I-Beam Covered by Insulation Material Subjected to Basic Loading Condition. Metals 2021, 11, 739. https://doi.org/10.3390/met11050739
Nguyen XT, Park JS. Inelastic Strength for Fire Resistance of Composite I-Beam Covered by Insulation Material Subjected to Basic Loading Condition. Metals. 2021; 11(5):739. https://doi.org/10.3390/met11050739
Chicago/Turabian StyleNguyen, Xuan Tung, and Jong Sup Park. 2021. "Inelastic Strength for Fire Resistance of Composite I-Beam Covered by Insulation Material Subjected to Basic Loading Condition" Metals 11, no. 5: 739. https://doi.org/10.3390/met11050739
APA StyleNguyen, X. T., & Park, J. S. (2021). Inelastic Strength for Fire Resistance of Composite I-Beam Covered by Insulation Material Subjected to Basic Loading Condition. Metals, 11(5), 739. https://doi.org/10.3390/met11050739






