1. Introduction
AISI H11 (1.2343) hot-work tool steel, is a typical representative of the group of chromium hot-work tool steels. It is widely used for the production of tools and dies for high-pressure die casting and forging. The higher concentration of carbide-forming alloying elements improves the high-temperature softening resistance of the steel [
1,
2]. Since hot-work tool steels usually operate at elevated temperatures, the high-temperature oxidation behaviour of H11 hot-work tool steel is of great importance. Several authors [
3,
4,
5,
6,
7,
8,
9] have studied the effect of elevated temperatures on the mechanical and physical properties of hot-work tool steels. With this consideration, we investigate the oxidation kinetics of AISI H11 in the temperature range between 400 °C and 700 °C.
Oxidation is one of the most important types of corrosion. Metals and alloys begin to oxidize in air or other atmospheres containing oxygen [
10,
11,
12,
13]. Assuming that oxygen is in the gaseous state, metals (M) are converted to oxides (M
aO
b), and the reaction proceeds according to the following chemical reaction [
12]:
Since the chemical reactions of oxidation are well known, one can calculate the Gibbs free energy of the reactions. The Equation (2) for the Gibbs free energy of reaction (1), is given as [
12]:
where
μ is the chemical potential,
a is the activity,
R is the gas constant,
p is the pressure and
T is the temperature. Assuming that
;
and
atm (101 325 Pa), Equation (3) can be derived from Equation (2) [
12]:
Then the Gibbs free energy for the chemical reaction (1) can be determined [
12]:
where
K is the equilibrium chemical reaction constant and
is the Gibbs free energy change per mole of the reaction at standard conditions. Some of the chemical reactions for the oxidation of metals can be found in the well-known Ellingham diagram [
14]. Let us first consider the oxidation of pure metals, it depends on the growth kinetics of the oxide layer, on whether it will protect the metal from oxidizing or not. From a thermodynamic point of view, the chemical reaction (1) proceeds spontaneously from left to right when the total change in Gibbs free energy is negative [
10,
11,
12,
13,
15].
The oxidation kinetics of metals and alloys can follow several different laws, the most common of which are linear, parabolic, cubic, logarithmic, and inverse logarithmic. In fact, the kinetics is very complex and can also consist of a combination of several laws (linear and parabolic, etc.). The chemical reaction (1) follows a kinetic law that can be described by the following equation [
10,
11,
12,
13,
15,
16,
17]:
where
ξ is a measure of the extent of the reaction at time
t, and
n is the number of moles [
10,
11,
12,
13,
15,
16,
17]. However, the most common method for studying the oxidation rate is to measure the weight gain of the sample over time. Gravimetry is a particularly suitable method, where the change in weight over time can be measured continuously or discontinuously [
17].
Several authors studied high-temperature oxidation of iron in air or pure oxygen atmosphere [
11,
13,
17,
18,
19,
20,
21]. The high-temperature oxidation kinetics of iron in the temperature range 700–1250 °C can be expressed by Tammann-type parabolic equation [
21]:
where,
x is the total thickness of the oxide layer,
t is the oxidation time,
x0 is the initial thickness of the oxide layer (if some oxides are already present on the surface, otherwise the value is 0) of the parabolic oxidation, and
is a constant of the parabolic rate usually given in cm
2 s
−1. However, since oxidation kinetics are usually studied by a change in mass as a function of oxidation time, a parabolic law can be expressed by the Pilling-Bedworth equation [
21,
22]:
where
W is the change in mass per unit area, due to oxidation of iron, and
kp (=
) is the parabolic constant in g
2 cm
−4 s
−1, and
W0 is the initial mass at the time (
t = 0) of parabolic oxidation. In the original Pilling-Bedworth equation [
22],
W0 is equal to 0. In the considered temperature range, the oxidation follows the parabolic law, the resulting oxide layer consists of a very thin outer sublayer of hematite, a thin intermediate sublayer of magnetite and a thick inner sublayer of wüstite [
21,
23].
On the other hand, the oxidation of iron below 700 °C is much more complex, so that even the published results of different authors [
21,
24,
25,
26,
27] are less consistent. In previous studies, it was found that the kinetics of isothermal oxidation of iron in the temperature range (570–700 °C) follows a parabolic law. However, the thicknesses of the individual oxide layers differ from study to study [
24,
25,
26,
27].
Regarding the high-temperature oxidation of steels, many studies [
21,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37] in which the high-temperature oxidation of various steels has been investigated have been carried out. Many ways have been proposed to calculate the rate constant of oxidation kinetics. The most suitable method to obtain the equation to calculate the oxidation rate constant of steel under continuous heating or cooling was developed by Kofstad [
38]. According to his interpretation, oxidation following a linear, parabolic, or cubic law can be generally expressed as:
where
W is defined as the change in mass per unit area over time
t,
n is a constant with values of 1, 2, or 3 for the linear, parabolic, or cubic law, and
kn is a time-independent rate constant expressed as:
where,
B is the constant,
T is the absolute temperature,
R is the gas constant, and
Q is the activation energy. There is also an alternative [
39], but since the mass change was measured over time, we used the Kofstad method. Regarding the high-temperature oxidation of hot-work tool steels, there are some studies [
40,
41,
42,
43,
44] have been carried out. Bidibadi et al. [
40] investigated the oxidation behaviour of CrMoV steel, the study sets out the composition of the oxide layers in detail and proves that the inner oxide layer contains spinel-like oxides. Zhang et al. [
41] studied the high-temperature oxidation resistance of H13 steel, from the TG curves, there is a mass decrease between 250 °C and 500 °C during the heating, when the oxide layer has already formed, but unfortunately, no further analysis was performed regarding the cause the of mass decrease. On the other hand, Min et al. [
42] carried out a prediction and analysis of the oxidation of H13 hot-work tool steel. Using the software Thermo-Calc the compositions of the oxide layers were calculated as a function of oxygen partial pressure, and the oxidation mechanisms in different atmospheres were discussed. Regarding the oxidation of H11 steel, Pieraggi et al. [
43] explained the oxidation behaviour of H11 steel in dry and wet air at 600 °C and 700 °C. It was found that the oxidation kinetics follows the parabolic law and is also quite sensitive to the presence of water vapour. Bruckel et al. [
44] investigated the isothermal oxidation behaviour of an X38CrMoV5 hot-work tool steel at 600 °C and 700 °C. It was also found that the oxidation kinetics is very sensitive to the presence of water vapour. On the other hand, it was proved that the oxide layer is duplex consisting of an outer hematite sublayer and an inner (Fe, Cr)
3O
4 sublayer. It was mentioned that carbides could play an important role in the growth process of the oxide layer. These studies served as a first insight into what the formed oxide layers might consist of and how the oxidation kinetics might behave.
2. Materials and Methods
We investigated the H11 (EN X37CrMoV5-1) hot-work tool steel with the chemical composition given in
Table 1, measured by wet chemical analysis and infrared absorption after combustion with ELTRA CS-800 (ELTRA GmbH, Haan, Germany).
First the heat treatment of H11 hot-work tool steel was carried out. The austenitization temperature was 1020 °C and the soaking time was 30 min. Quenching was carried out in oil, followed by two-stage tempering, at 550 °C and 620 °C for 2 h, for reaching the hardness 42–44 HRC. The heat treatment was carried out in Bosio EUP-K 6/1200 (Bosio d.o.o., Celje, Slovenia) chamber furnace. Since air atmosphere was used, we had to mill off 2 mm of the steel surface, due to decarburization and oxidation during the heat treatment. Sample preparation using a CNC (Computer Numerical Control) Deckel Maho DMC 63V (Deckel Maho Pfronten GmbH, Pfronten, Germany) machine was next. three different types of samples were prepared, the first ones were cubes with dimensions of 10 mm × 10 mm × 10 mm (length × width × height), which were used during the high-temperature oxidation in the chamber furnace. These samples were specially prepared for further analysis by light optical microscope and SEM (Scanning Electron Microscope). The second set of samples were cuboids with dimensions 10 mm × 10 mm × 5 mm, which were also used during high-temperature oxidation in the chamber furnace. The dimensions are different because the height of the XRD (X-ray Diffraction) sample holder is limited. The last ones are cylinders with dimensions h = 4 mm and Φ = 4 mm, which were used in the high-temperature oxidation in NETZSCH STA (Simultaneous Thermal Analyzer) Jupiter 449C (NETZSCH Holding, Selb, Germany) instrument. All surfaces were polished with 1 μm polycrystalline diamond suspension, after polishing, the samples were ultrasonically cleaned with ethanol and dried on hot air, this procedure was also repeated before each oxidation test.
To get a first insight into the composition of the oxide layers, CALPHAD (CALculation of PHAse Diagrams) simulations were performed with the software Thermo-Calc (Thermo-Calc 2020a, Thermo-Calc Software AB, Stockholm, Sweden) using the thermodynamic database TCOX9 [
45] (Metal Oxide Solutions Database). In the diagrams the amount of phase is shown on the
Y-axis and the activity of O
2 is shown on
X-axis. The composition of the oxide sublayers in the formed oxide layer in the studied temperature range (400–700 °C), was calculated. Thermo-Calc software and HSC Chemistry software (HSC Chemistry 9.0, Metso Outotec Finland Oy, Tampere, Finland) were also used to calculate the Gibbs free energy of the oxidation reactions.
High-temperature oxidation was studied at 400 °C, 500 °C, 600 °C, and 700 °C in air atmosphere for 100 h. The samples analysed by light optical microscope, SEM and XRD were oxidised in Bosio EUP-K 6/1200 (Bosio d.o.o., Celje, Slovenia) chamber furnace. The heating rate was 15 °C min−1 and the high-temperature oxidation was carried out in air atmosphere. To improve the oxidation conditions, additional air (79 vol% nitrogen, 21 vol% oxygen 0.9 vol% argon and 0.1 vol% of hydrocarbons and other inert gases) was injected into the furnace at a flow rate of 0.3 L min−1. Cooling was performed in the chamber furnace at the cooling rate of 0.5 C min−1, which was intentionally slow. The main reason was not to damage the oxide layer.
The samples used for the study of kinetics were oxidized in the NETZSCH STA Jupiter 449C (NETZSCH Holding, Selb, Germany) instrument. The heating and cooling rate were 10 °C min−1, in addition air was injected into the furnace at a flow rate of 30 mL min−1 (during the heating/cooling and the isothermal section). Correction runs were also performed prior to sample runs with an empty Al2O3 pedestal on which the samples were located during oxidation. TGA (Thermogravimetric Analysis) was used to study the kinetics.
The samples for SEM analysis were ground and polished. An FEG-SEM (Field Emission Gun Scanning Electron Microscopy) ThermoFisher Scientific Quattro S (ThermoFisher Scientific, Waltham, MA, USA) was used to examine the composition and thickness of the oxide layers. The composition was investigated using EDS (Energy-Dispersive X-ray Spectroscopy) analysis (Ultim® Max, Oxford Instruments, Abingdon, UK). EBSD (Electron Backscatter Diffraction) analysis was also performed using ZEISS CrossBeam 550 (Carl Zeiss AG, Oberkochen, Germany) SEM with HikariSuper EBSD camera (EDAX, Mahwah NJ, USA). In addition, the samples were ground, polished, and etched with Vilella’s reagent for optical microscopy. Microphot FXA, Nikon (Nikon, Minato City, Japan) with 3CCD video camera Hitachi HV-C20A (Hitachi, Ltd., Tokyo, Japan) was used for microstructure analysis. Vickers hardness was measured using Instron Tukon 2100B (Instron, Norwood, MA, USA). The hardness measurements were performed on the metallographically prepared samples (ground and polished), and we only measured the hardness of the steels. PANalytical XPert Pro PW3040/60 (Malvern Panalytical, Malvern, England, UK), X-ray diffractometer with Cu anode (λ = 0.15419 nm) using Bragg-Bretano geometry with a theta-theta goniometer with a radius of 240 mm was used to study the types of oxides in the oxide layers.
Since we were investigating samples in two different conditions soft annealed and hardened and tempered condition, we marked the first ones with H11 (soft annealed) and the second ones with H11-HT (hardened and tempered).
4. Discussion
For discussion, we plotted a diagram of Gibbs free energies (
Figure 18) for oxidation reactions of some carbides, alloying elements, and oxides, calculated using Thermo-Calc and HSC Chemistry software. All chemical reactions have been normalized to 1 mol O
2 for better comparability.
The results of all analyses were used to explain the oxidation kinetics of H11 steel. The oxidation kinetics (
Figure 16) is unstable below 700 °C, which can also be seen from the fluctuating oxidation curves. As evidenced by thermodynamic calculations and metallographic analysis, the microstructure of the steel in the soft annealed state consists of a ferrite matrix and spherical carbides (Cr, Mo, Fe)
23C
6 and VC, and some Ti(C,N). In the case of hardened and tempered state, the microstructure consists of a martensitic matrix and primary (VC and TiCN), and secondary (Cr, Mo, Fe)
23C
6) carbides. There are more of the latter, as they are precipitated during tempering.
The oxidation kinetics (
Figure 16) during heating (Part 1) show in all cases the beginnings of the parabolic or cubic law (best described by the exponential growth function). Under isothermal conditions (part 2), the slope of the curves begins to decrease, except at 700 °C in the case of a soft annealed sample. As can be seen from the results presented, an oxide layer forms during heating and becomes thicker, as the oxidation temperature increases. The weight increases on average from 0.7 mg at 400 °C to 1.1 mg at 700 °C. The reason for this is that oxidation of the matrix and alloying elements and carbides occurs simultaneously during heating. It depends on the formed oxide layer, whether it protects the steel from further oxidation. In other words, whether a formed oxide layer is in thermodynamic equilibrium with the atmosphere under the given conditions or not.
Namely, in the transition from heating to the isothermal part of oxidation, it is crucial, whether the oxide layer is already in thermodynamic equilibrium with the atmosphere and protects the steel from further oxidation or not. The curves decrease at lower temperatures (400–600 °C) and increase at oxidation temperatures of 700 °C in the case of a soft annealed sample. Here it is essential, which has a greater influence on the oxidation rate or which process controls the oxidation kinetics. The oxidation of the iron matrix is on one side and the oxidation of carbides and other alloying elements in the matrix on the other side. In this case, mainly chromium, molybdenum, silicon, and vanadium. At lower temperatures (T < 700 °C), the oxidation of carbides and alloying elements dissolved in the matrix has been shown to have a greater effect on the oxidation kinetics than the oxidation of iron, even though the iron concentration in the matrix is highest. It has been shown that the oxide layer in this temperature range consists of three sublayers, namely the outer hematite, the middle magnetite, and the inner spinel. It is the latter that best protects the steel from further oxidation. Magnetite grows by the predominant transport of Fe
2+ cations to wüstite (not yet thermodynamically stable) and Fe
3+ to hematite. At the same time, grain boundaries in the oxide layer below 600 °C are very important for diffusion in both magnetite and hematite [
12,
46,
47,
48]. However, in this temperature range, diffusion is limited precisely because of the inner oxide sublayer, which consists of spinel oxide, so that the diffusion of iron and oxygen, and thus the growth of the magnetite oxide sublayer is also impeded. This is also contributed by the very fine crystalline grains of magnetite in the inner oxide sublayer (
Figure 10,
Figure 11 and
Figure 12), which further impede diffusion. As a result, oxygen is mainly used for the oxidation of carbides, which are most oxidized at the interface between the middle/inner oxide sublayers. From the calculated Gibbs free energies (
Figure 18), chromium should oxidize first, then chromium spinels are formed, afterwards the oxidation of M
23C
6 carbide starts, followed by the oxidation of iron and finally carbon. The oxidation of the carbides themselves has been reported by several authors [
49,
50,
51,
52,
53]. It was found that M
23C
6 carbides start to oxidize in the air atmosphere at elevated temperatures and thus can affect the oxidation kinetics, while MC carbides do not have a much effect on the oxidation kinetics. Recent research [
49] has shown that M
23C
6 (Cr
23C
6) carbides in high-silicon ferritic/martensitic steel begin to oxidize under isothermal conditions in an atmosphere of air at 823 K. It was found that carbides and areas around (with increased alloying elements) can serve as potential sites for the formation of chromium oxides. In the case of Cr
23C
6, chromium begins to form chromium oxide (Cr
2O
3), which is a product of carbide oxidation. At the same time, the oxidation of the carbide itself also produces CO
2 [
51], which is also a product of oxidation, the chemical reaction proceeds as follows:
The remaining molybdenum, silicon and iron also diffuse into the spinel oxide and partially into the magnetite. However, chromium, will not form a single oxide (Cr
2O
3), due to its low chromium content (5% by weight) [
49,
54,
55]. As a result, it will react with iron and oxygen after a chemical reaction (16) to form a spinel-shaped oxide that forms the inner oxide sublayer.
At the same time, MC (VC) carbides themselves do not have a significant effect on the oxidation kinetics because, as can be seen from the Gibbs free energy calculations (
Figure 18), they oxidize last, slowly decompose into the inner oxide sublayer during oxidation, vanadium slowly diffuses into spinel oxides due to the decomposition of carbides and increases the density of the inner oxide sublayer. At the same time, it has been demonstrated [
35,
49] that silicon is also incorporated into the spinel oxide.
There are more causes of curve oscillations (
Figure 16). As can be seen from the chemical reaction (15) and the oxidation reactions of other carbides (
Figure 18), CO
2 is the product of carbide oxidation. This means that the local gas volume in the inner oxide sublayer will increase, especially at the interface with the middle sublayer, as carbide oxidation is most intense there. At the same time, the expansion coefficients (α) of the individual oxides formed must be considered. The CO
2 formed during the oxidation of carbides will leave the oxide layer, which is seen on the curve as a slope in the negative direction, as at the same time stresses are created in the oxide layer, causing cracking, and some oxide to fall off. It has been proven by other authors that if the resulting gas (CO or CO
2, as in our case) cannot escape through micro channels (micro pores and cracks), its pressure begins to increase, leading to the formation of new pores or even cracking or oxide layer fractures [
21,
56]. Mainly for the purpose of demonstrating that part of the oxide layer is crumbling, we also took an image of the morphology of the oxide layer (
Figure 19—orange circles) with a SEM to explain the oscillations of the curves obtained with TG.
At high-temperature oxidation at 700 °C, the aforementioned effect is still visible in a hardened and tempered sample, but in the soft annealed condition, it is only visible at the beginning of the oxidation, after which the oxidation rate depends mainly on oxygen and iron diffusion. This means that there is a faster diffusion of oxygen and iron in the soft annealed sample, and the resulting inner oxide sublayer and carbide oxidation no longer control the oxidation kinetics. In this case, chromium rich M23C6 carbides are no longer oxidized as intensively, but begin to decompose and thus the alloying elements begin to diffuse into the magnetite and form an inner oxide sublayer as is the case with other carbides. This can also be seen by the fact that both the inner and middle oxide sublayers are thicker than those that form in the temperature range between 400 °C and 600 °C. In addition, wüstite begins to form in the inner oxide sublayer, where iron diffusion is most rapid. In the hardened and tempered sample, the influence of carbide oxidation is still present, which is also evident from the curves. The curves at about 55 h oxidation slowly begin to flatten their shape (no oscillations are visible), indicating that the oxidation of the carbides no longer controls the oxidation kinetics.
In the soft annealed samples, the oxide grows throughout the crystal grain and on the carbides. In a hardened and tempered sample, the areas with increased contents of alloying elements and carbides oxidize first and then the matrix begins to oxidize.
Regarding the composition of the oxide layer, in all cases the oxide layer has the same composition and differs only in the thicknesses, which increase with temperature. Thus, the oxide layer consists of three sublayers, namely the outer hematite, the middle magnetite and the inner one of spinel oxide (Fe, Cr)
3O
4. At the oxidation temperature of 700 °C in the case of the soft annealed sample, the inner oxide sublayer consists of spinel and some wüstite. However, in the case of the hardened and tempered sample, no wüstite was detected. At the same time, a hematite band also appears on the contact surface between the steel and the inner oxide sublayer at the temperature of 700 °C. A similar composition of the oxide layer has also been reported by other researchers [
40,
57,
58]. The thicknesses increase from 3.8 μm to 154.2 μm for the soft annealed sample and from 0.1 μm to 117.1 μm for the hardened and tempered sample (
Table 3).
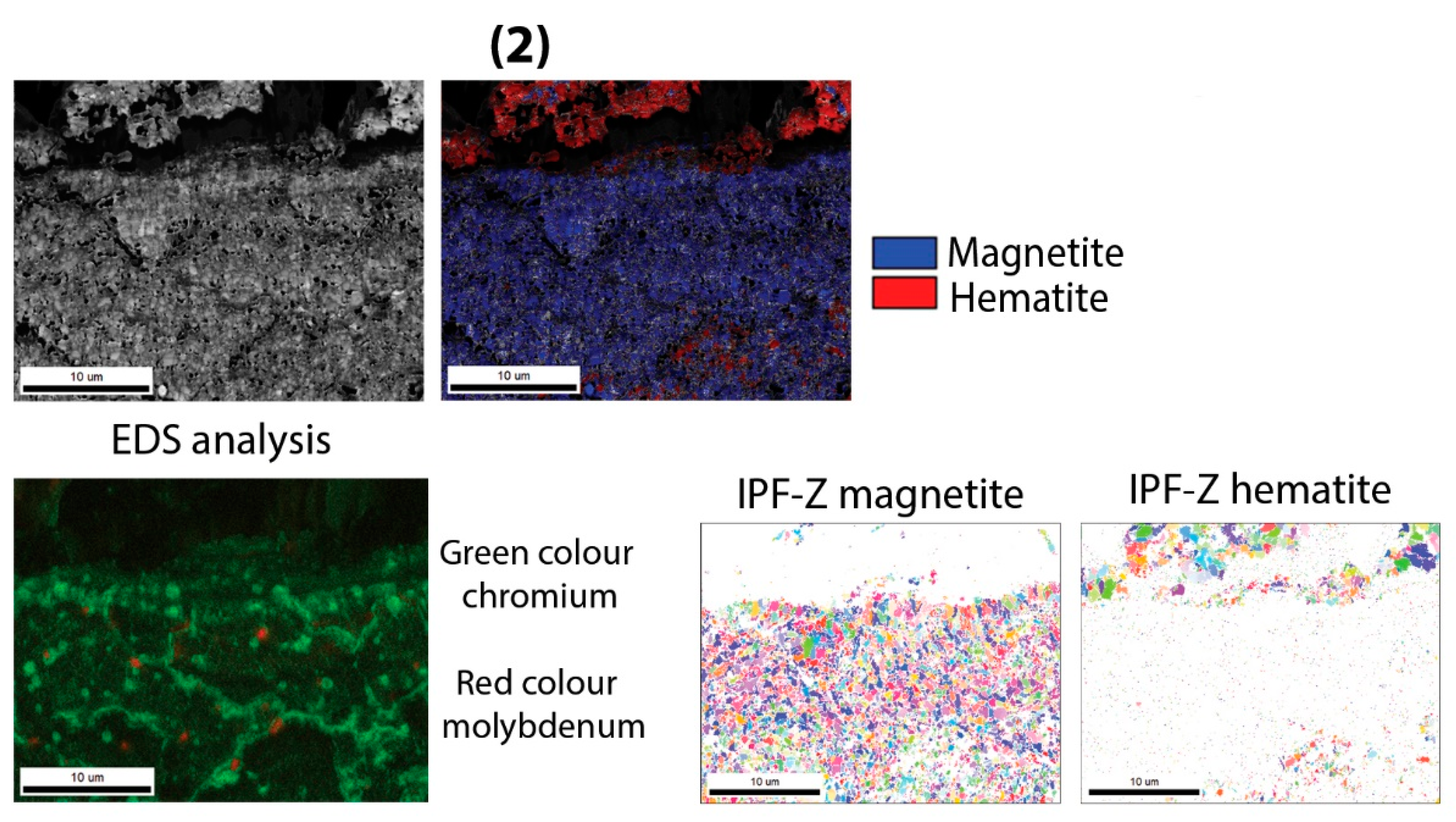
In the temperature range 400–600 °C, the oxide layer also consists of three sublayers (
Figure 5). The inner oxide sublayer consists of spinel oxide ((Fe, Cr)
3O
4), which also contains increased concentrations of molybdenum, silicon, vanadium, and manganese. The middle oxide sublayer is also composed of magnetite, in which the concentrations of chromium, molybdenum, silicon, manganese and vanadium are much lower. The outer oxide sublayer, which is very thin, consists of hematite. This is also consistent with thermodynamic calculations, except in the case of molybdenum oxide, which was not formed. Thermodynamic calculations also indicated that internal oxidation should take place, which can be confirmed only in the case of the hardened and tempered sample, namely after oxidation at the temperature of 600 °C.
Figure 20 shows the oxide layer of the H11 hot-work tool steel in soft annealed state, after oxidation at 500 °C. There are no differences in the composition of the oxide layer between soft annealed and hardened and tempered samples up to 700 °C. The only difference is the density of the inner oxide sublayer, which is denser in the hardened and tempered samples, as shown by the EBSD results.
At 700 °C (
Figure 21) in the case of the soft annealed state, the outer oxide sublayer also consists of hematite, the middle of magnetite and some hematite, and the inner of magnetite (Fe, Cr)
3O
4, hematite bands, and some wüstite. On the other hand, the oxide layer formed on the hardened and tempered sample after oxidation at a temperature of 700 °C was denser and did not contain any wüstite, as shown by the results of the EBSD analysis (
Figure 15).
The morphology of the oxide layer formed in soft annealed (H11) and hardened and tempered (H11-HT) samples after oxidation at a temperature of 400 °C is shown in
Figure 22. In the case of the soft annealed sample, the oxide starts to grow over the entire surface. On the other hand, in the case of the hardened and tempered sample, the areas with elevated concentrations of alloying elements and carbides begin to oxidize first.
5. Conclusions
Chemical composition affects high-temperature oxidation. It depends on the alloying elements, their content and affinity for oxygen, whether they form independent oxides or whether they are involved in oxidation processes at all. In the case of AISI H11 hot-work tool steel, silicon has the greatest affinity to oxygen, followed by chromium, molybdenum, carbon, and others. However, silicon did not have much influence on the high-temperature oxidation, since it was not present in the carbides (only in the matrix) and on the other hand soft annealed samples had faster oxidation kinetics. So, we assumed that chromium is the element that starts to oxidize first, since it was also present in the carbides.
Carbides and areas around (with increased concentration of alloying elements) can serve as potential sites for the formation of oxides. This is most evident at lower temperatures 400–500 °C, where oxidation of the Cr23C6 carbides controls the oxidation kinetics. Oxidation of the carbides causes stresses in the inner oxide sublayer, leading to pores and cracks, but can also lead to crumbling of the oxide layer, which is most evident in the oxidation kinetics at 400 °C. The higher the temperature, the smaller the effect, as diffusion is already so rapid that oxidation of the carbides no longer affects the oxidation kinetics of the steel, so that even Cr23C6 carbides (≥700 °C) begin to slowly dissolve into the inner oxide sublayer at higher temperatures. Other carbides present, however, have no significant influence on oxidation.
The oxide layers formed during heating are in some cases sufficient protection to preserve the steel from further oxidation. The result is that the mass, which has increased during heating remains almost unchanged during further oxidation under isothermal conditions. This is observed at a temperature of 500 °C, and even more so at a temperature of 600 °C for both samples (soft annealed and hardened and tempered). Similarly, for the hardened and tempered sample at a temperature of 700 °C. In these cases, the change in mass is minimal, confirming the assumption that an oxide layer formed during heating provides sufficient protection to keep the steel from further oxidation.
Oxidation kinetics are also affected by the heat treatment of the steel. In general, the oxidation kinetics of the hardened and tempered samples are slower than the oxidation kinetics of the soft annealed samples. Small differences occur at a temperature of 400 °C and 500 °C. However, at 600 °C and 700 °C a difference is seen between soft annealed and hardened and tempered samples, with the oxidation kinetics of the latter being slower. This is largely influenced by the alloying elements dissolved in the matrix. More alloying elements are dissolved in the hardened and tempered samples and consequently the inner oxide sublayer formed is denser, preventing further diffusion of iron and oxygen.
Heat treatment affects the growth of the oxide layer and the size of the crystal grains in the oxide layer. As has been shown, the oxide layer, especially the inner sublayer, is denser in hardened and tempered samples. As a result, the growth of the oxide layer is slower because the diffusion of oxygen, iron and other alloying elements is impeded. Consequently, since the crystal grains in the matrix of the hardened and tempered samples are much smaller, the crystal grains in the oxide layer, especially in the inner sublayer, are also smaller than in the soft annealed samples.
Thermodynamic calculations give a first insight into the composition of the oxide layer. From the calculated thermodynamic results, one can conclude which oxides will form after oxidation at a given temperature. It has been shown that the calculations can be very accurate, provided we set all the input data correctly.