Combined Effects of EMBr and SEMS on Melt Flow and Solidification in a Thin Slab Continuous Caster
Abstract
:1. Introduction
2. Compact Strip Production Process
3. Numerical Model
3.1. Fluid Flow
3.2. Solidification and Melting Model
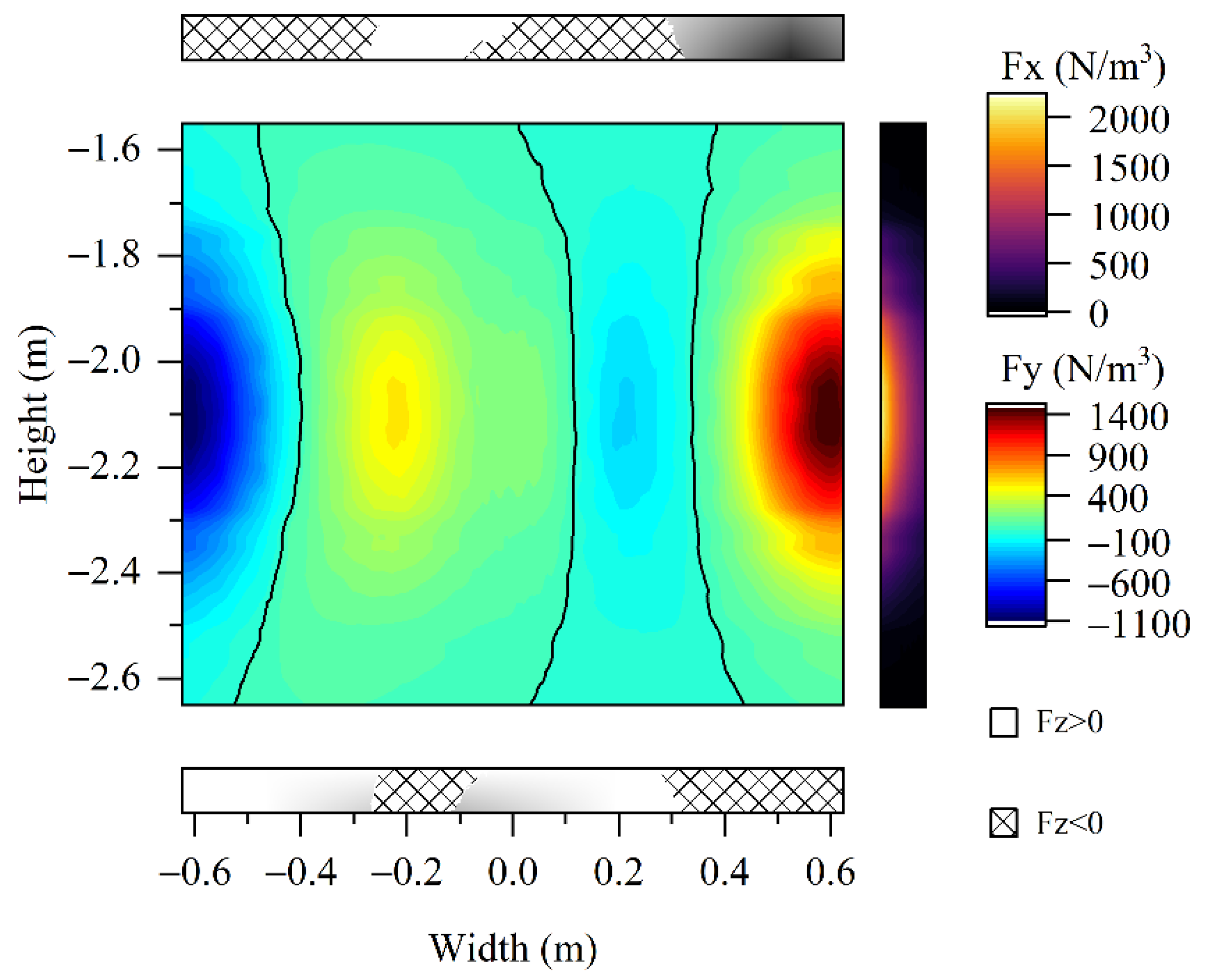
3.3. Electromagnetic Stirring Force
3.4. Electric Potential Method
3.5. Boundary Conditions
4. Simulation Results and Discussion
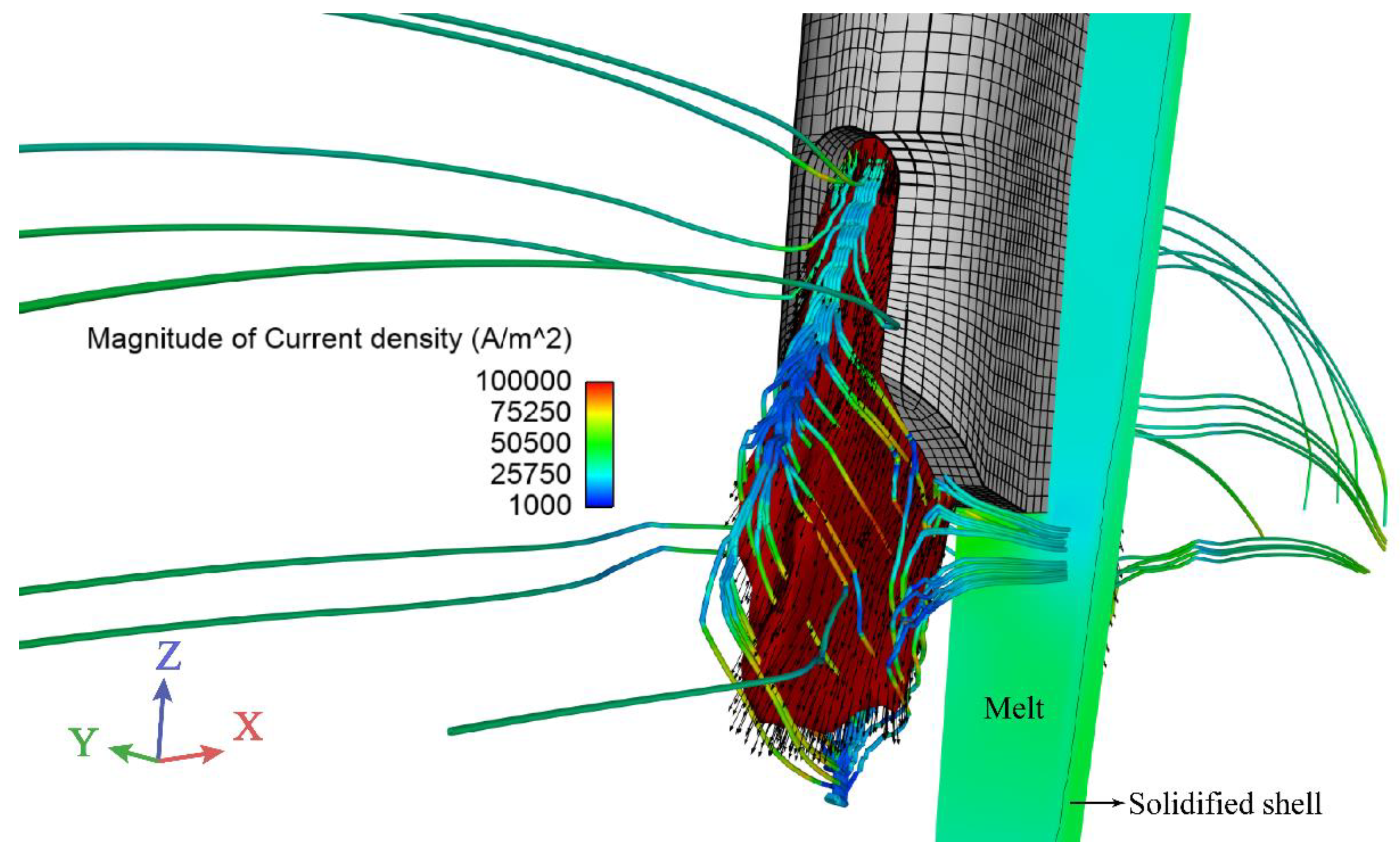
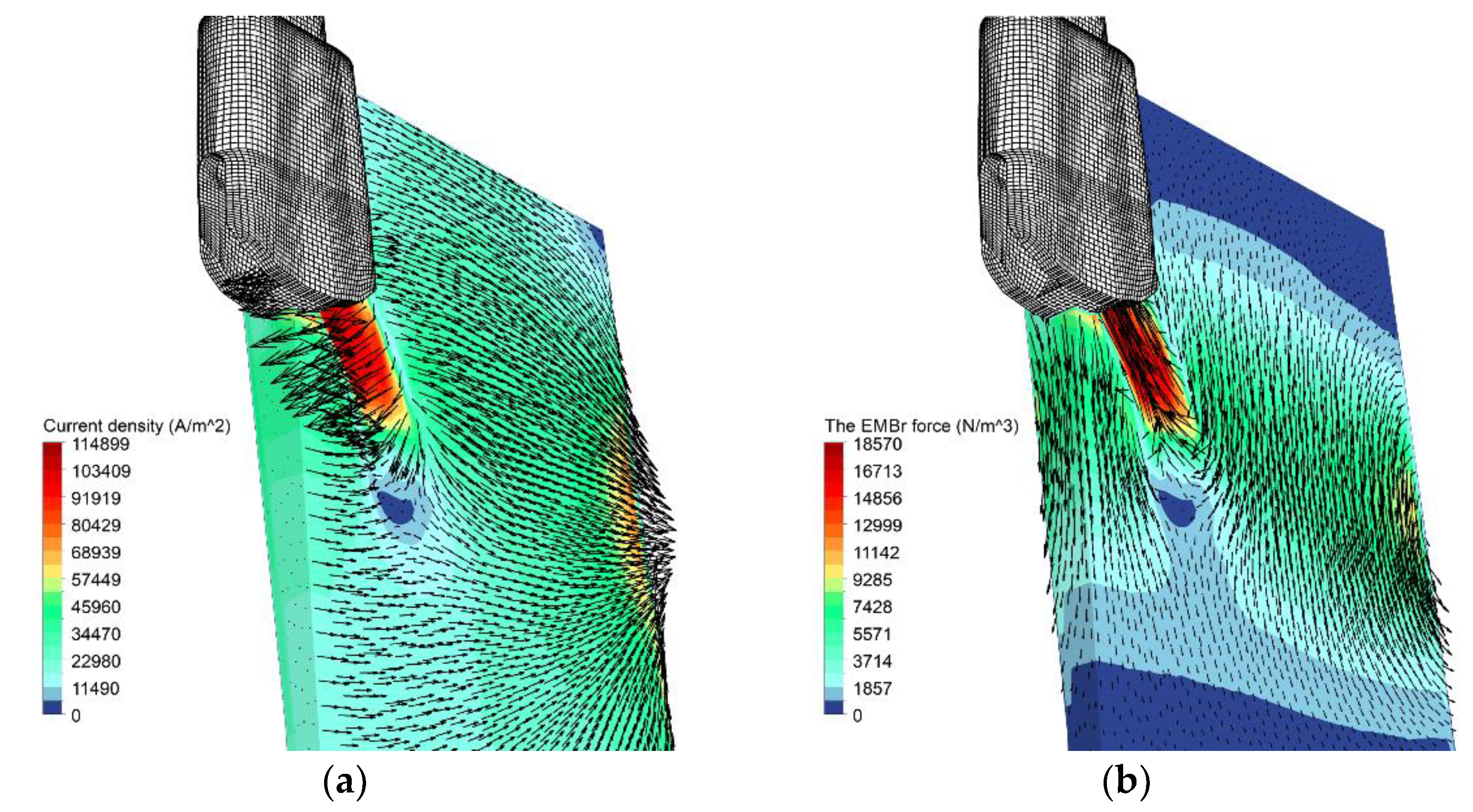
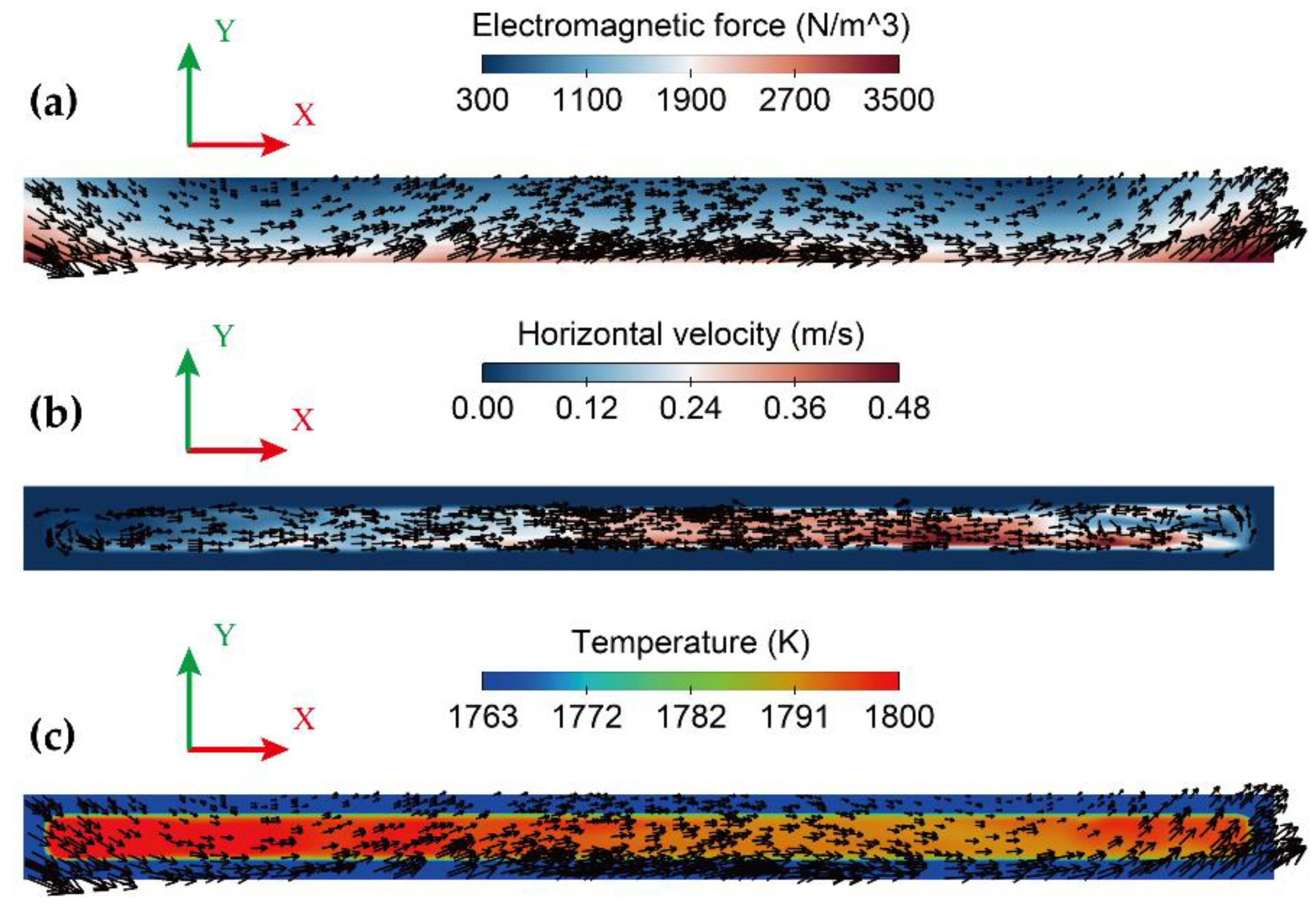
4.1. Electromagnetic Fields
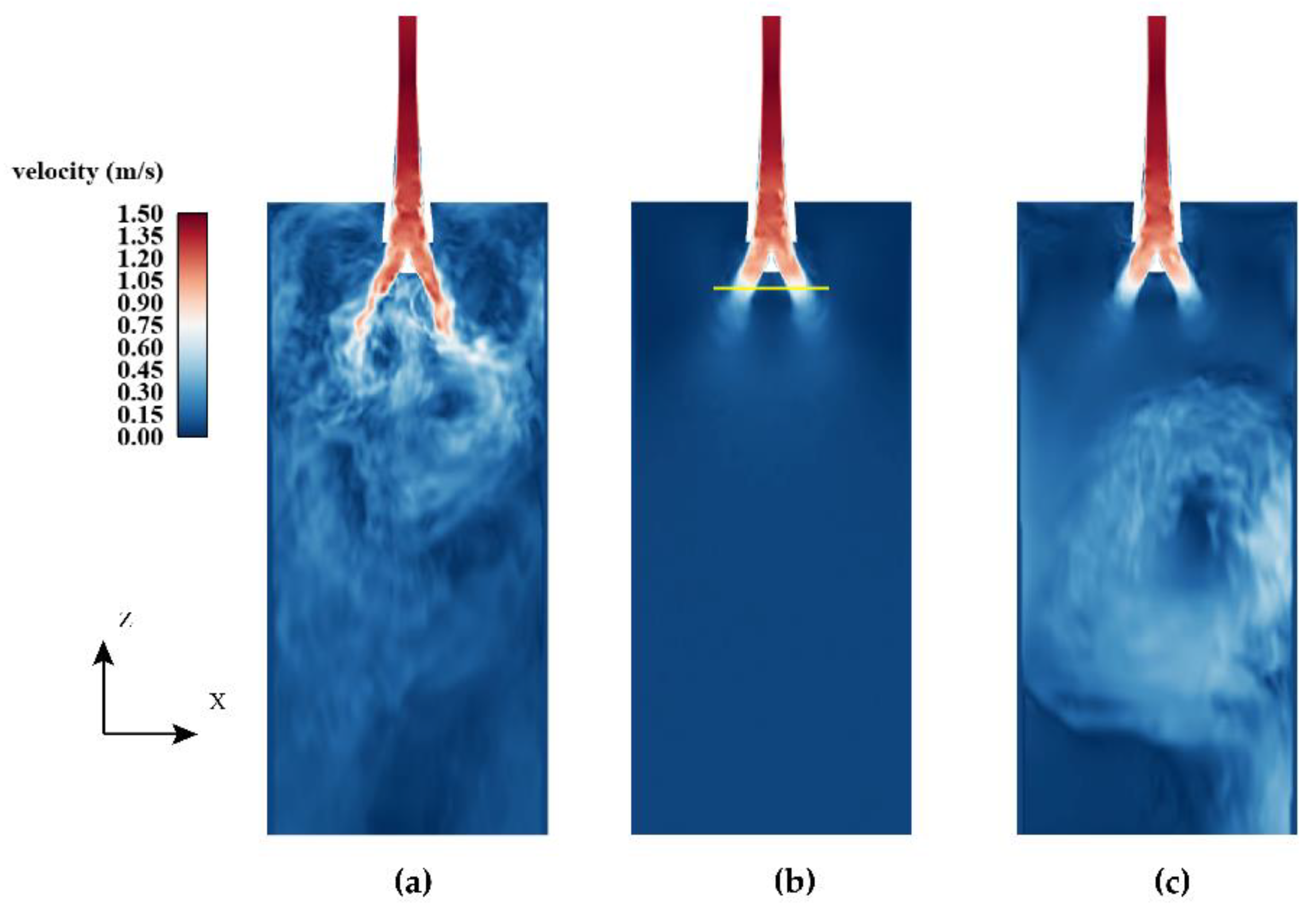
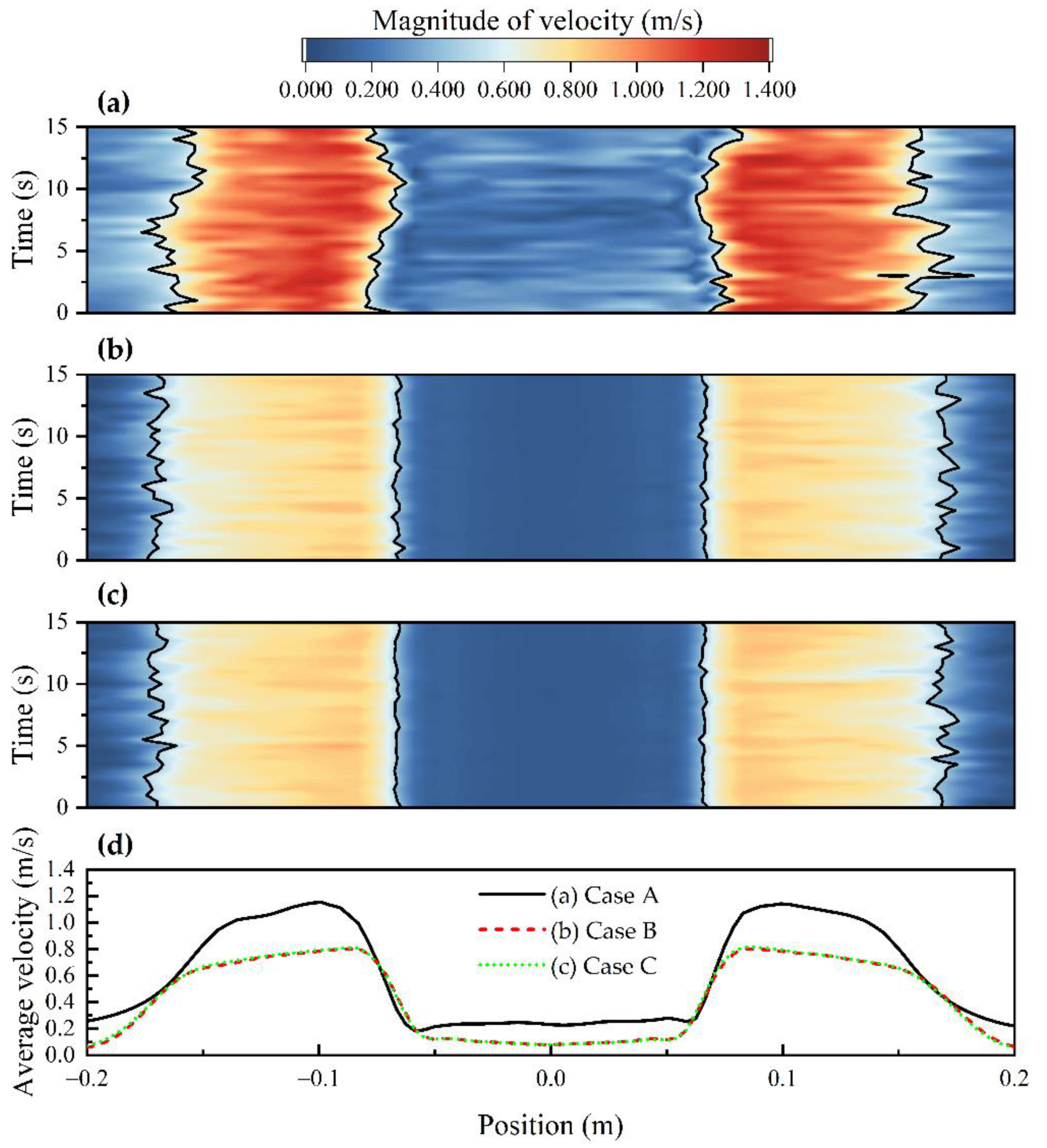
4.2. Melt Flow Field
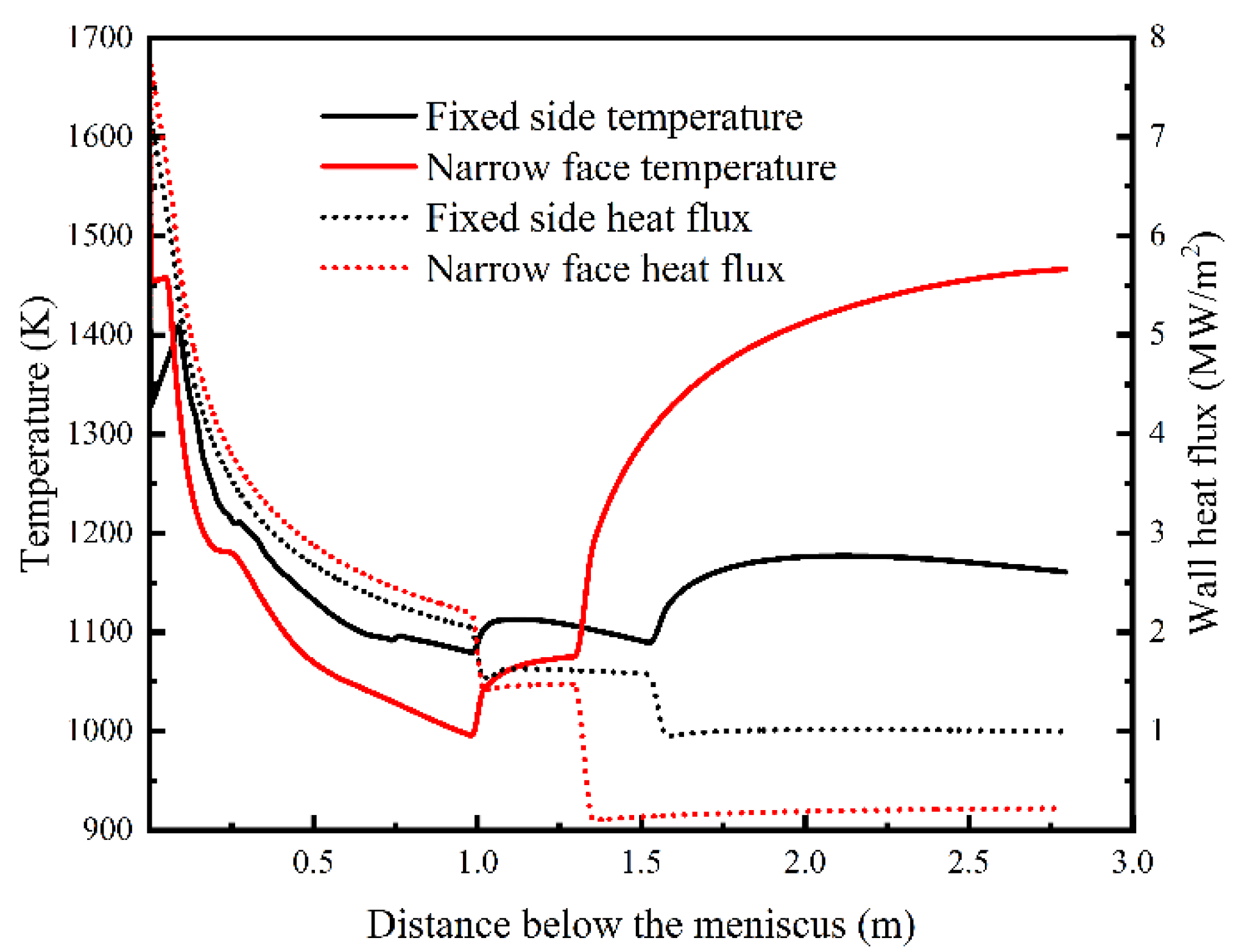
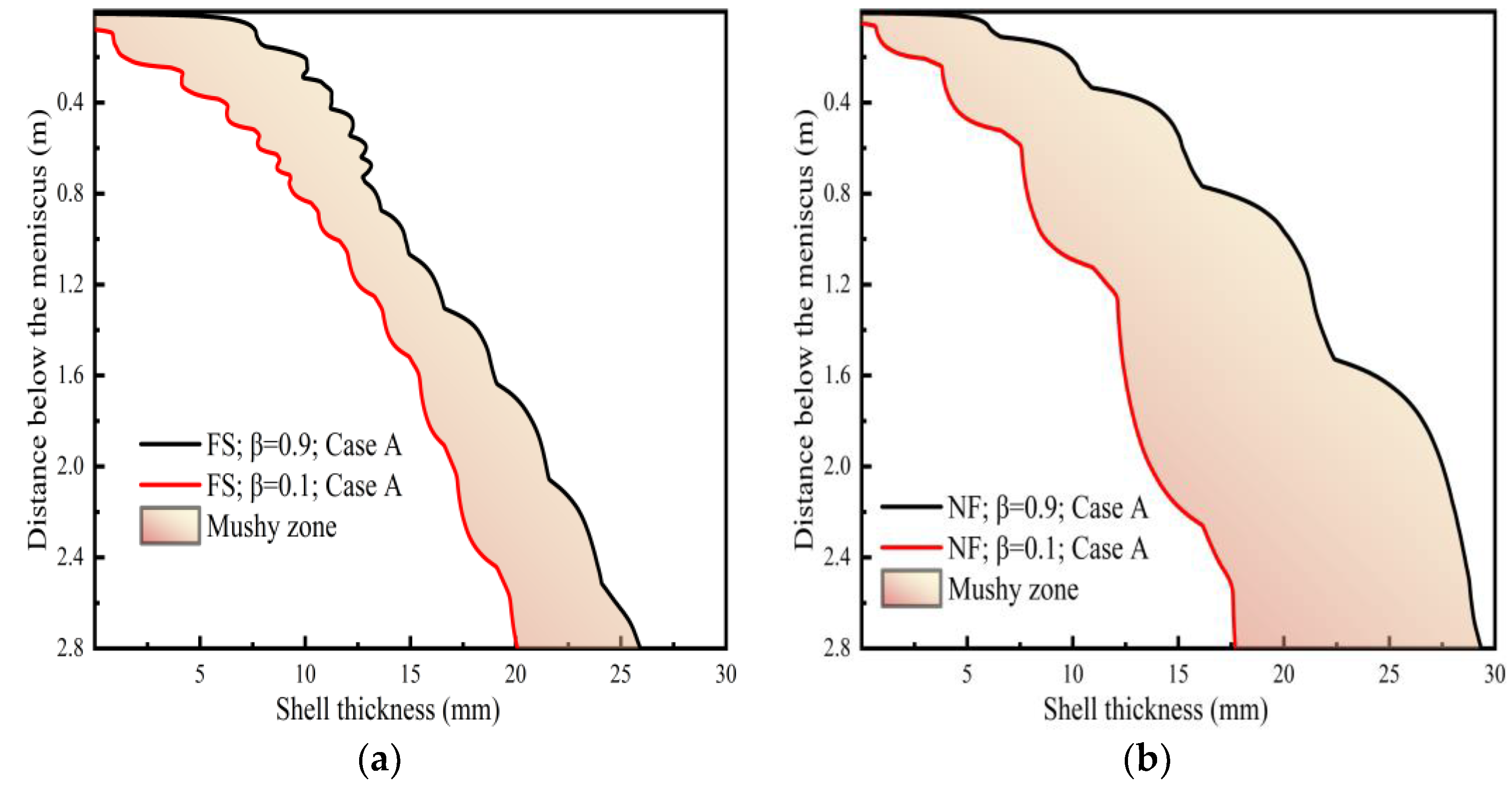
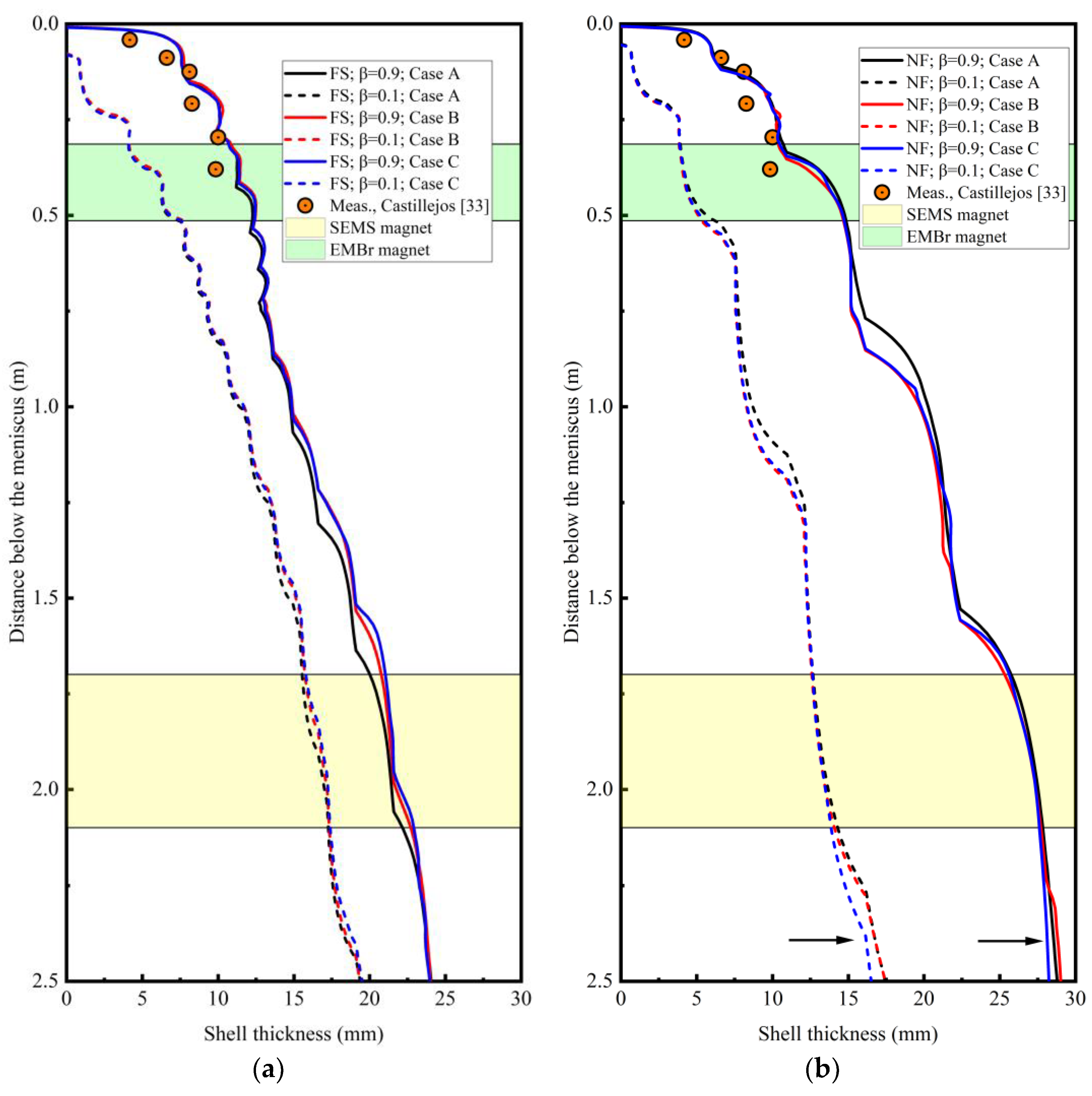
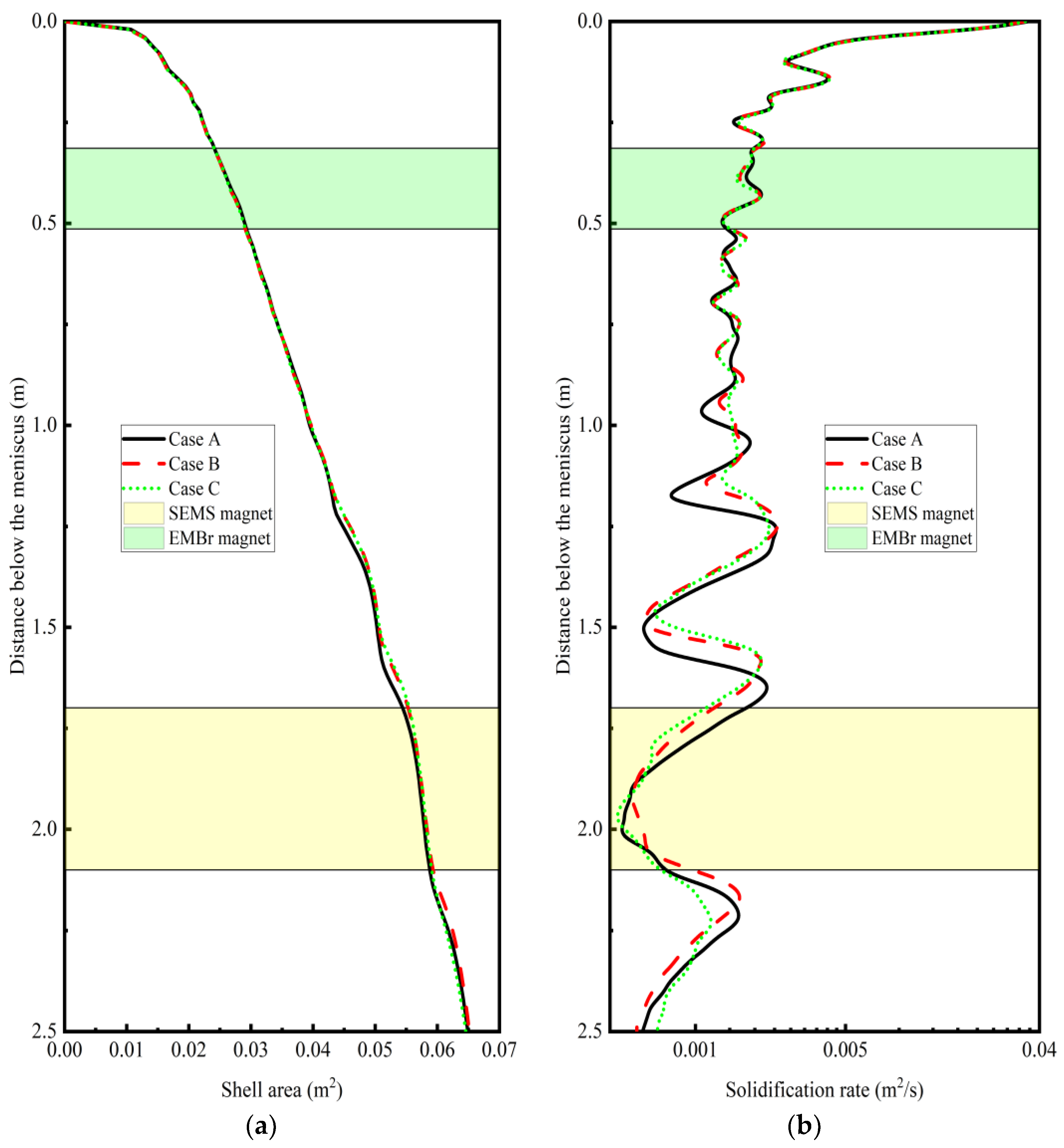
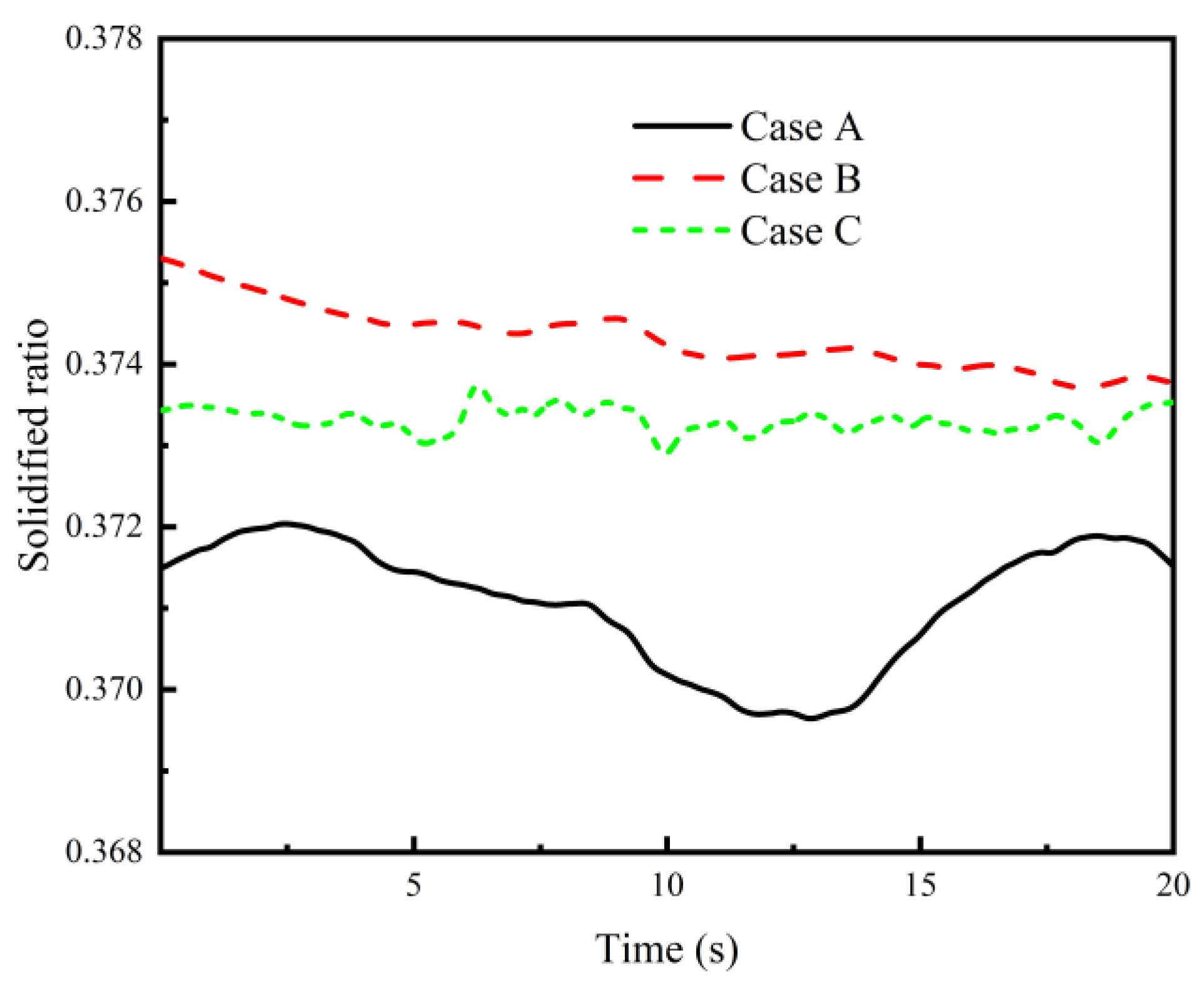
4.3. Heat Transfer and Solidification
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Michel, J.P.; Jonas, J.J. Precipitation kinetics and solute strengthening in high temperature austenites containing al and n. Acta Met. 1981, 29, 513–526. [Google Scholar] [CrossRef]
- Kang, Y.L.; Yu, H.; Fu, J.; Wang, K.; Wang, Z.B. Morphology and precipitation kinetics of aln in hot strip of low carbon steel produced by compact strip production. Mater. Sci. Eng. A Struct. Mater. Prop. 2003, 351, 265–271. [Google Scholar] [CrossRef]
- Park, J.K.; Thomas, B.G.; Samarasekera, I.V.; Yoon, U.S. Thermal and mechanical behavior of copper molds during thin-slab casting (i): Plant trial and mathematical modeling. Met. Mater. Trans. B 2002, 33, 425–436. [Google Scholar] [CrossRef]
- Morales, R.D.; Tang, Y.; Nitzl, G.; Eglsaeer, C.; Hackl, G. Design of a submerged entry nozzle for thin slab molds operating at high casting speeds. ISIJ Int. 2012, 52, 1607–1615. [Google Scholar] [CrossRef] [Green Version]
- Qiao, J.L.; Guo, F.H.; Hu, J.W.; Xiang, L.; Qiu, S.T.; Wang, H.J. Precipitates in compact strip production (csp) process non-oriented electrical steel. Metals 2020, 10, 1301. [Google Scholar] [CrossRef]
- Cho, S.M.; Thomas, B.G. Electromagnetic forces in continuous casting of steel slabs. Metals 2019, 9, 471. [Google Scholar] [CrossRef] [Green Version]
- Cukierski, K.; Thomas, B.G. Flow control with local electromagnetic braking in continuous casting of steel slabs. Met. Mater. Trans. B 2008, 39, 94–107. [Google Scholar] [CrossRef]
- Wang, Y.F.; Zhang, L.F. Fluid flow-related transport phenomena in steel slab continuous casting strands under electromagnetic brake. Met. Mater. Trans. B 2011, 42, 1319–1351. [Google Scholar] [CrossRef]
- Li, F.; Wang, E.G.; Feng, M.J.; Li, Z. Simulation research of flow field in continuous casting mold with vertical electromagnetic brake. ISIJ Int. 2015, 55, 814–820. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Wang, E.G.; Zhang, L.T.; Xu, Y.; Deng, A.Y. Influence of vertical electromagnetic brake on the steel/slag interface behavior in a slab mold. Met. Mater. Trans. B 2017, 48, 2389–2402. [Google Scholar] [CrossRef]
- Singh, R.; Thomas, B.G.; Vanka, S.P. Large eddy simulations of double-ruler electromagnetic field effect on transient flow during continuous casting. Met. Mater. Trans. B 2014, 45, 1098–1115. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.Q.; Zhang, L.F. Influence of fc-mold on the full solidification of continuous casting slab. JOM 2016, 68, 2170–2179. [Google Scholar] [CrossRef]
- Xu, L.; Wang, E.G.; Karcher, C.; Deng, A.Y.; Xu, X.J. Numerical simulation of the effects of horizontal and vertical embr on jet flow and mold level fluctuation in continuous casting. Met. Mater. Trans. B 2018, 49, 2779–2793. [Google Scholar] [CrossRef]
- Chaudhary, R.; Thomas, B.G.; Vanka, S.P. Effect of electromagnetic ruler braking (embr) on transient turbulent flow in continuous slab casting using large eddy simulations. Met. Mater. Trans. B 2012, 43, 532–553. [Google Scholar] [CrossRef]
- Schurmann, D.; Glavinic, I.; Willers, B.; Timmel, K.; Eckert, S. Impact of the electromagnetic brake position on the flow structure in a slab continuous casting mold: An experimental parameter study. Met. Mater. Trans. B 2020, 51, 61–78. [Google Scholar] [CrossRef]
- Chaudhary, R.; Ji, C.; Thomas, B.G.; Vanka, S.P. Transient turbulent flow in a liquid-metal model of continuous casting, including comparison of six different methods. Met. Mater. Trans. B 2011, 42, 987–1007. [Google Scholar] [CrossRef]
- Li, B.K.; Tsukihashi, F. Effects of electromagnetic brake on vortex flows in thin slab continuous casting mold. ISIJ Int. 2006, 46, 1833–1838. [Google Scholar] [CrossRef] [Green Version]
- Harada, H.; Toh, T.; Ishii, T.; Kaneko, K.; Takeuchi, E. Effect of magnetic field conditions on the electromagnetic braking efficiency. ISIJ Int. 2001, 41, 1236–1244. [Google Scholar] [CrossRef]
- Tian, X.Y.; Li, B.W.; He, J.C. Electromagnetic brake effects on the funnel shape mold of a thin slab caster based on a new type magnet. Met. Mater. Trans. B 2009, 40, 596–604. [Google Scholar] [CrossRef]
- Dubke, M.; Tacke, K.-H.; Spitzer, K.-H.; Schwerdtfeger, K. Flow fields in electromagnetic stirring of rectangular strands with linear inductors: Part i. Theory and experiments with cold models. Met. Trans. B 1988, 19, 581–593. [Google Scholar] [CrossRef]
- Dubke, M.; Tacke, K.-H.; Spitzer, K.-H.; Schwerdtfeger, K. Flow fields in electromagnetic stirring of rectangular strands with linear inductors: Part ii. Computation of flow fields in billets, blooms, and slabs of steel. Met. Trans. B 1988, 19, 595–602. [Google Scholar] [CrossRef]
- Kunstreich, S. Electromagnetic stirring for continuous casting (part 2). Rev. Met. Cah. Inf. Technol. 2003, 100, 1043–1061. [Google Scholar] [CrossRef]
- Gong, J.; Liu, H.P.; Wang, X.H.; Bao, Y.P. Numerical simulation of electromagnetic field and flow pattern in a continuous slab caster with in-roll type strand electromagnetic stirring. J. Iron Steel Res. Int. 2015, 22, 414–422. [Google Scholar] [CrossRef]
- Niu, L.; Qiu, S.T.; Zhao, J.X.; Chen, Y.Q.; Yang, S.F. Processing parameter optimization for continuous casting of 38crmoal round bloom based on a prediction model of the equiaxed crystal ratio. Ironmak. Steelmak. 2019, 46, 835–844. [Google Scholar] [CrossRef]
- Shibata, H.; Itoyama, S.; Kishimoto, Y.; Takeuchi, S.; Siekiguchi, H. Prediction of equiaxed crystal ratio in continuously cast steel slab by simplified columnar-to-equiaxed transition model. ISIJ Int. 2006, 46, 921–930. [Google Scholar] [CrossRef]
- Vakhrushev, A.; Wu, M.; Ludwig, A.; Tang, Y.; Hackl, G.; Nitzl, G. Numerical investigation of shell formation in thin slab casting of funnel-type mold. Met. Mater. Trans. B 2014, 45, 1024–1037. [Google Scholar] [CrossRef]
- Vakhrushev, A.; Kharicha, A.; Wu, M.; Ludwig, A.; Nitzl, G.; Tang, Y.; Hackl, G.; Watziger, J.; Rodrigues, C.M.G. On modelling viscoplastic behavior of the solidifying shell in the funnel-type continuous casting mold. IOP Conf. Ser. Mater. Sci. Eng. 2019, 529, 012081. [Google Scholar] [CrossRef]
- Vakhrushev, A.; Kharicha, A.; Wu, M.; Ludwig, A.; Nitzl, G.; Tang, Y.; Hackl, G.; Watzinger, J.; Rodrigues, C.M.G. Modelling viscoplastic behavior of solidifying shell under applied electromagnetic breaking during continuous casting. IOP Conf. Ser. Mater. Sci. Eng. 2020, 861, 012015. [Google Scholar] [CrossRef]
- Miao, X.C.; Timmel, K.; Lucas, D.; Ren, Z.M.; Eckert, S.; Gerbeth, G. Effect of an electromagnetic brake on the turbulent melt flow in a continuous-casting mold. Met. Mater. Trans. B 2012, 43, 954–972. [Google Scholar] [CrossRef]
- Singh, R.; Thomas, B.G.; Vanka, S.P. Effects of a magnetic field on turbulent flow in the mold region of a steel caster. Met. Mater. Trans. B 2013, 44, 1201–1221. [Google Scholar] [CrossRef]
- Vakhrushev, A.; Kharicha, A.; Liu, Z.Q.; Wu, M.H.; Ludwig, A.; Nitzl, G.; Tang, Y.; Hackl, G.; Watzinger, J. Electric current distribution during electromagnetic braking in continuous casting. Met. Mater. Trans. B 2020, 51, 2811–2828. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Vakhrushev, A.; Wu, M.H.; Karimi-Sibaki, E.; Kharicha, A.; Ludwig, A.; Li, B.K. Effect of an electrically-conducting wall on transient magnetohydrodynamic flow in a continuous-casting mold with an electromagnetic brake. Metals 2018, 8, 609. [Google Scholar] [CrossRef] [Green Version]
- Camporredondo, S.J.E.; Castillejos, E.A.H.; Acosta, G.F.A.; Gutiérrez, M.E.P.; Herrera, G.M.A. Analysis of thin-slab casting by the compact-strip process: Part i. Heat extraction and solidification. Met. Mater. Trans. B 2004, 35, 541–560. [Google Scholar] [CrossRef]
- Tian, X.Y.; Zou, F.; Li, B.W.; He, J.C. Numerical analysis of coupled fluid flow, heat transfer and macroscopic solidification in the thin slab funnel shape mold with a new type embr. Metall. Mater. Trans. B 2010, 41, 112–120. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow. Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- ANSYS FLUENT 14. 5-Theory Guide; ANSYS. Inc.: Canonsburg, PA, USA, 2012. [Google Scholar]
- Singh, V.; Das, S.K. Thermo-fluid mathematical modeling of steel slab caster: Progress in 21st century. ISIJ Int. 2016, 56, 1509–1518. [Google Scholar] [CrossRef] [Green Version]
- Schneider, M.C.; Gu, J.P.; Beckermann, C.; Boettinger, W.J.; Kattner, U.R. Modeling of micro- and macrosegregation and freckle formation in single-crystal nickel-base superalloy directional solidification. Met. Mater. Trans. A 1997, 28, 1517–1531. [Google Scholar] [CrossRef]
- Wang, Y.D.; Chen, W.; Jiang, D.B.; Zhang, L.F. Effect of the gap between copper mold and solidified shell on the fluid flow in the continuous casting strand with mold electromagnetic stirring. Steel Res. Int. 2020, 91, 1900470. [Google Scholar] [CrossRef]
- Li, X.L.; Li, B.K.; Liu, Z.Q.; Niu, R.; Huang, X.C. Large eddy simulation of electromagnetic three-phase flow in a round bloom considering solidified shell. Steel Res. Int. 2019, 90, 1800133. [Google Scholar] [CrossRef]
- Liu, H.P.; Yang, C.Z.; Zhang, H.; Zhai, Q.J.; Gan, Y. Numerical simulation of fluid flow and thermal characteristics of thin slab in the funnel-type molds of two casters. ISIJ Int. 2011, 51, 392–401. [Google Scholar] [CrossRef] [Green Version]
- Camporredondo, S.J.E.; Acosta, G.F.A.; Castillejos, E.A.H.; Gutiérrez, M.E.P.; González de la, P.R. Analysis of thin-slab casting by the compact-strip process: Part ii. Effect of operating and design parameters on solidification and bulging. Met. Mater. Trans. B 2004, 35, 561–573. [Google Scholar] [CrossRef]
- Petrus, B.; Zheng, K.; Zhou, X.; Thomas, B.G.; Bentsman, J. Real-time, model-based spray-cooling control system for steel continuous casting. Met. Mater. Trans. B 2010, 42, 87–103. [Google Scholar] [CrossRef]
- Yang, J.; Xie, Z.; Ning, J.; Liu, W.H.; Ji, Z.P. A framework for soft sensing of liquid pool length of continuous casting round blooms. Met. Mater. Trans. B 2014, 45, 1545–1556. [Google Scholar] [CrossRef]
- Timmel, K.; Eckert, S.; Gerbeth, G. Experimental investigation of the flow in a continuous-casting mold under the influence of a transverse, direct current magnetic field. Met. Mater. Trans. B 2011, 42, 68–80. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Li, L.M.; Li, B.K.; Jiang, M.F. Large eddy simulation of transient flow, solidification, and particle transport processes in continuous-casting mold. JOM 2014, 66, 1184–1196. [Google Scholar] [CrossRef]
- Gäumann, M.; Bezençon, C.; Canalis, P.; Kurz, W. Single-crystal laser deposition of superalloys: Processing–microstructure maps. Acta Mater. 2001, 49, 1051–1062. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Niu, R.; Wu, Y.D.; Li, B.K.; Gan, Y.; Wu, M. Physical and numerical simulation of mixed columnar-equiaxed solidification during cold strip feeding in continuous casting. Int. J. Heat Mass Transf. 2021, 173, 121237. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| Mold | |
| Width | 1250 mm |
| Funnel Part Height | 850 mm |
| Vertical Part Height | 250 mm |
| Vertical Part Thickness | 85 mm |
| Maximum Thickness | 195 mm |
| Casting Speed | 4 m/min |
| SEN | |
| Inlet Diameter | 80 mm |
| Port Height | 135 mm |
| Port Width | 33.8 mm |
| Inlet Velocity | 1.38 m/s |
| Submergence Depth | 180 mm |
| EMBr | |
| Magnet Width | 1200 mm |
| Magnet Height | 200 mm |
| Windings Per Coil | 100 |
| Current | 250 A |
| SEMS | |
| Magnet Height | 400 mm |
| Windings Per Coil | 100 |
| Max Current | 600 A |
| Frequency | 4 Hz |
| Cases | |
| Case A | No EMBr, No SEMS |
| Case B | EMBr, No SEMS |
| Case C | EMBr, SEMS |
| Parameter | Value | |
|---|---|---|
| Wide Faces | ||
| Mold (Cooling Water) | Flow Rate | 6200 L/min |
| Temperature Increase | 18 K | |
| Grid | Length | 0.49 m |
| Water Flow Rate | 1964 L/min | |
| Seg.2 | Length | 1.27 m |
| Water Flow Rate | 1668 L/min | |
| Narrow Faces | ||
| Mold (Cooling Water) | Flow Rate | 230 L/min |
| Temperature Increase | 15 K | |
| Wide and Narrow Faces | ||
| Ring | Length | 0.06 m |
| Water Flow Rate | 300 L/min | |
| Natural Convection | 8.7 W/(m2 K) | |
| Ambient Temperature | 300 K | |
| Parameter | Value |
|---|---|
| Density, ρ | 6949 kg/m3 |
| Specific Heat, cp | 700 J/(kg K) |
| Conductivity, λl | 35 W/(m K) |
| Laminar Viscosity, μl | 0.006 kg/(m s) |
| Latent Heat, L | 271,000 J/kg |
| Solidus Temperature, Tsolidus | 1763.2 K |
| Liquidus Temperature, Tliquidus | 1790.5 K |
| Electrical Conductivity of Liquid Steel, σliq | 714,000 S/m |
| Electrical Conductivity of Solid Steel, σsol | 999,600 S/m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Liu, Z.; Li, B. Combined Effects of EMBr and SEMS on Melt Flow and Solidification in a Thin Slab Continuous Caster. Metals 2021, 11, 948. https://doi.org/10.3390/met11060948
Wang C, Liu Z, Li B. Combined Effects of EMBr and SEMS on Melt Flow and Solidification in a Thin Slab Continuous Caster. Metals. 2021; 11(6):948. https://doi.org/10.3390/met11060948
Chicago/Turabian StyleWang, Changjun, Zhongqiu Liu, and Baokuan Li. 2021. "Combined Effects of EMBr and SEMS on Melt Flow and Solidification in a Thin Slab Continuous Caster" Metals 11, no. 6: 948. https://doi.org/10.3390/met11060948
APA StyleWang, C., Liu, Z., & Li, B. (2021). Combined Effects of EMBr and SEMS on Melt Flow and Solidification in a Thin Slab Continuous Caster. Metals, 11(6), 948. https://doi.org/10.3390/met11060948






