Fatigue Behavior of Nonreinforced Hand-Holes in Aluminum Light Poles
Abstract
:1. Introduction
2. Materials and Methods
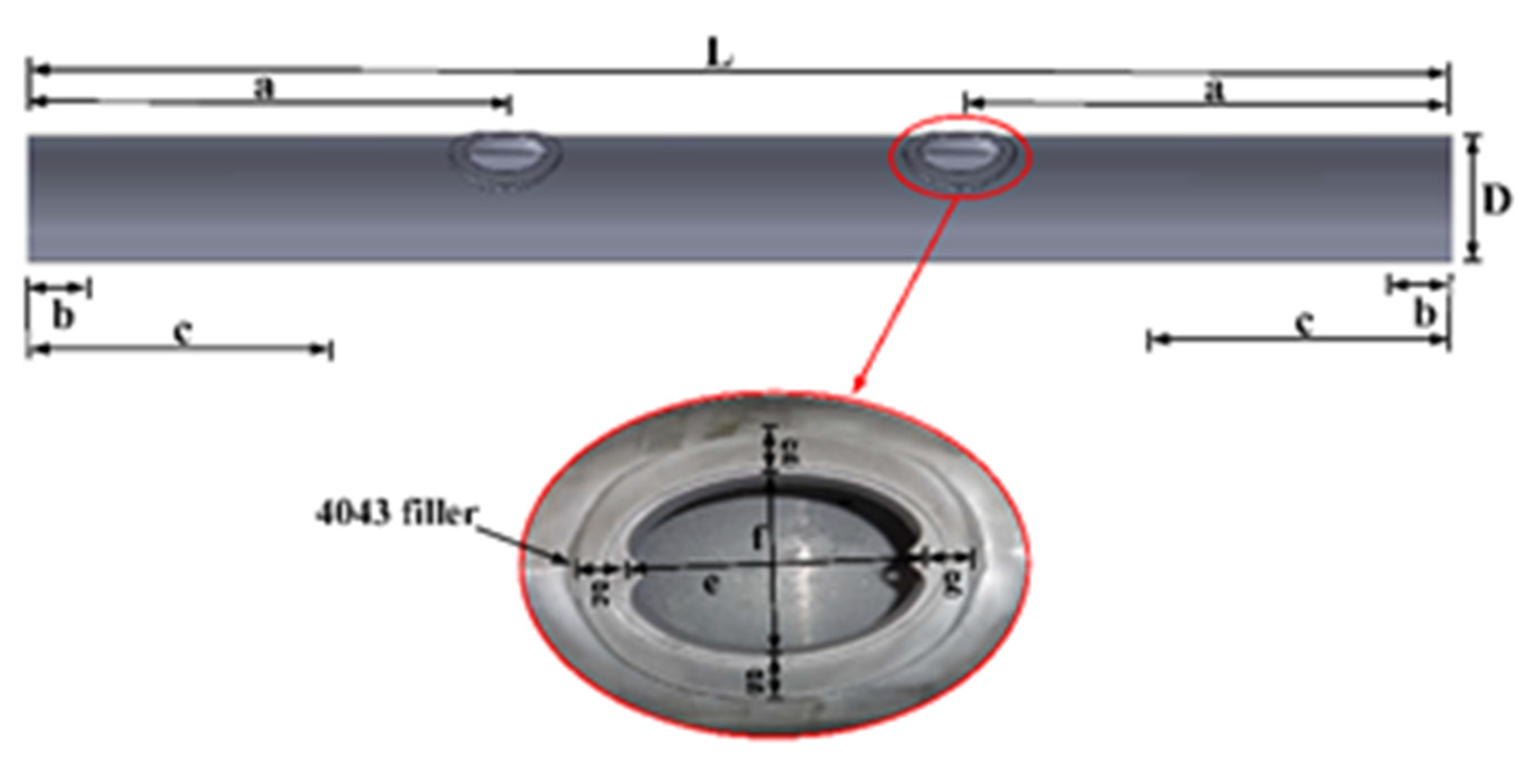
2.1. Pole Geometry and Material Properties
2.2. Fatigue Tests
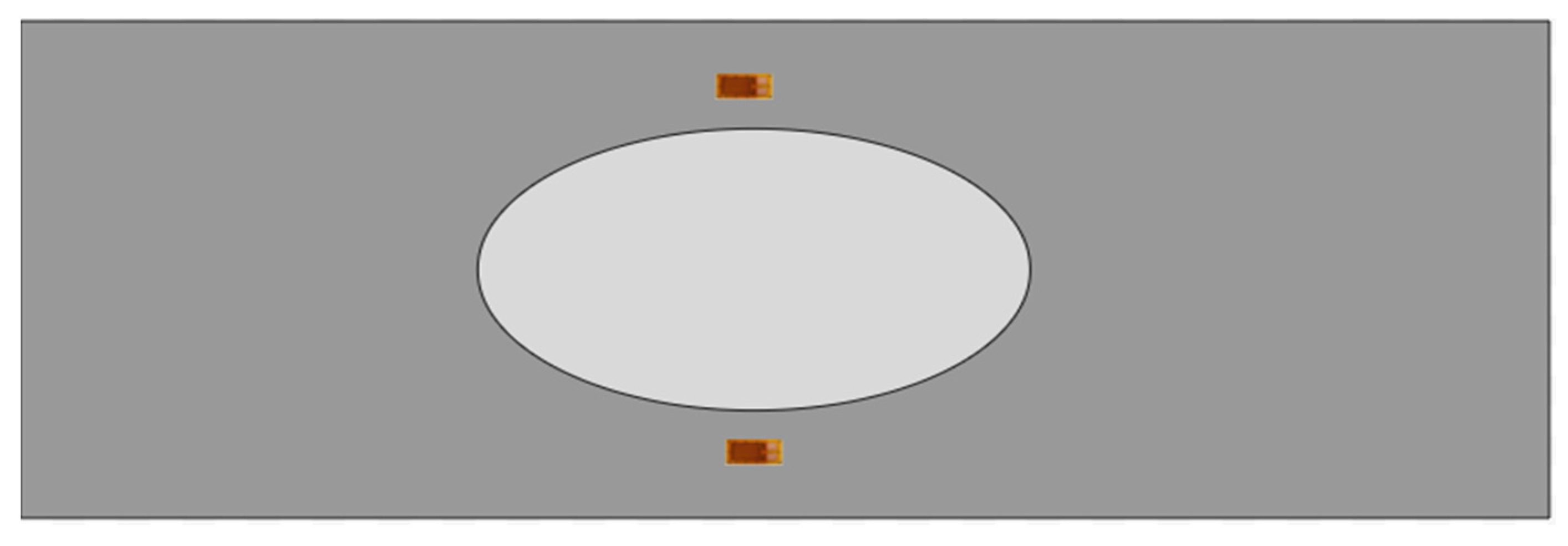
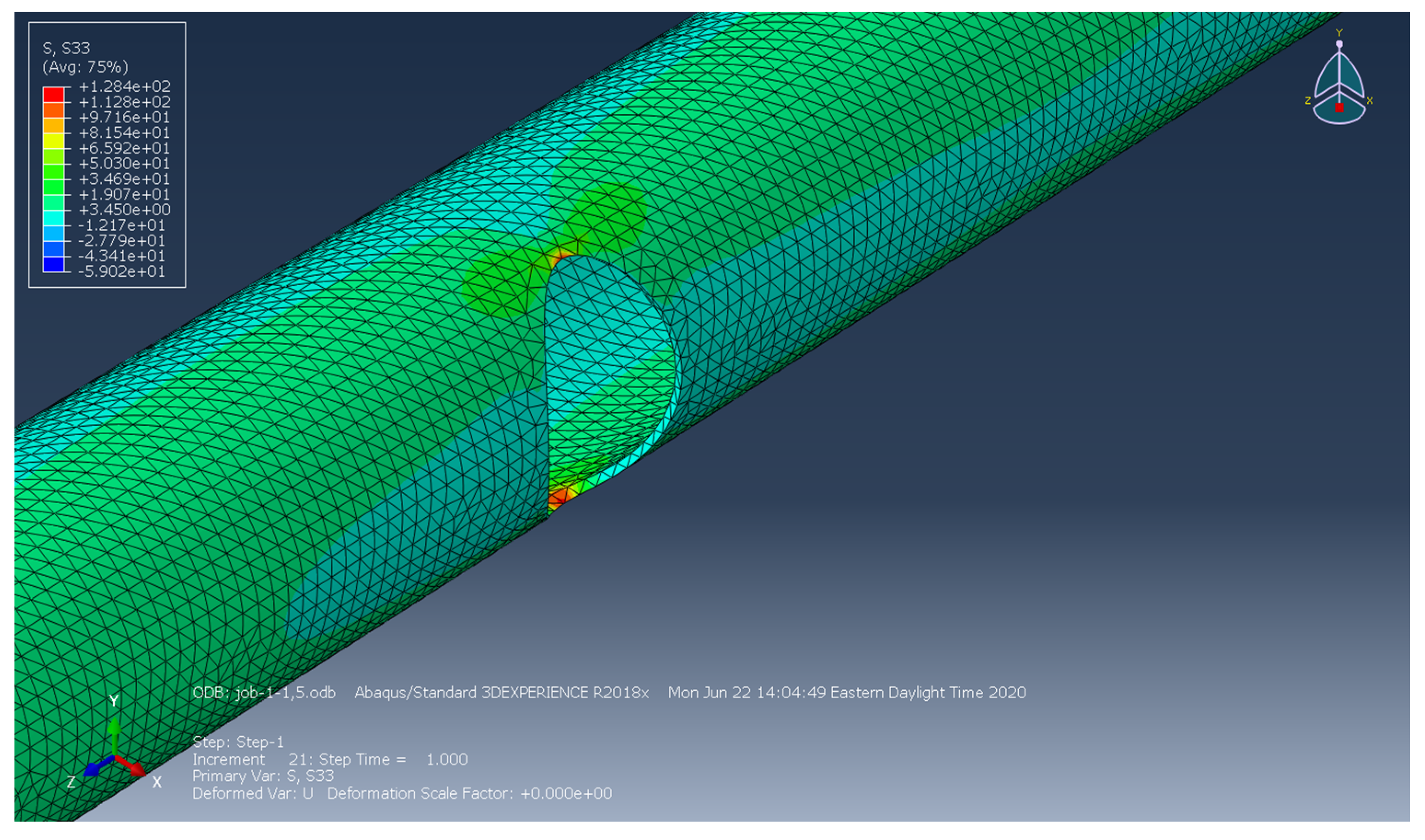
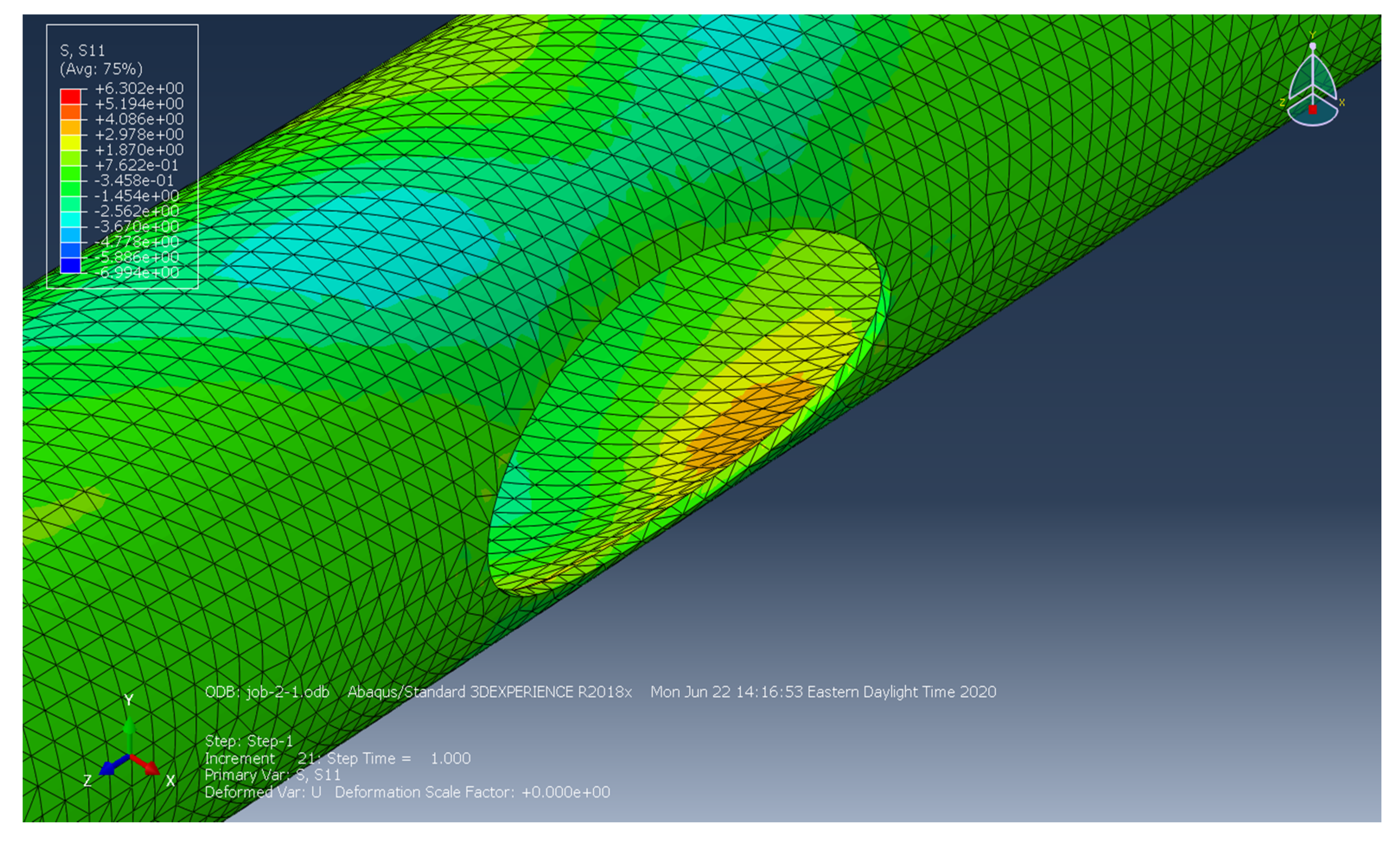
2.3. Finite Element Models
3. Results
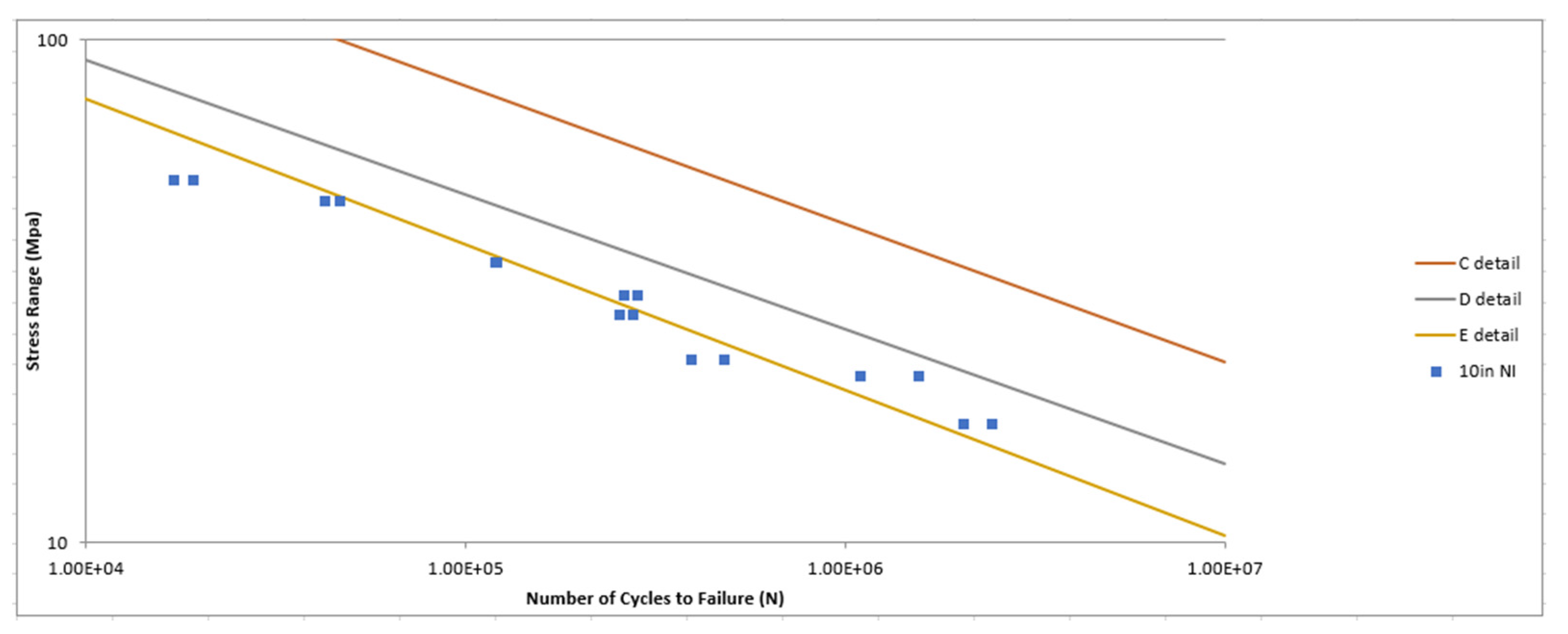
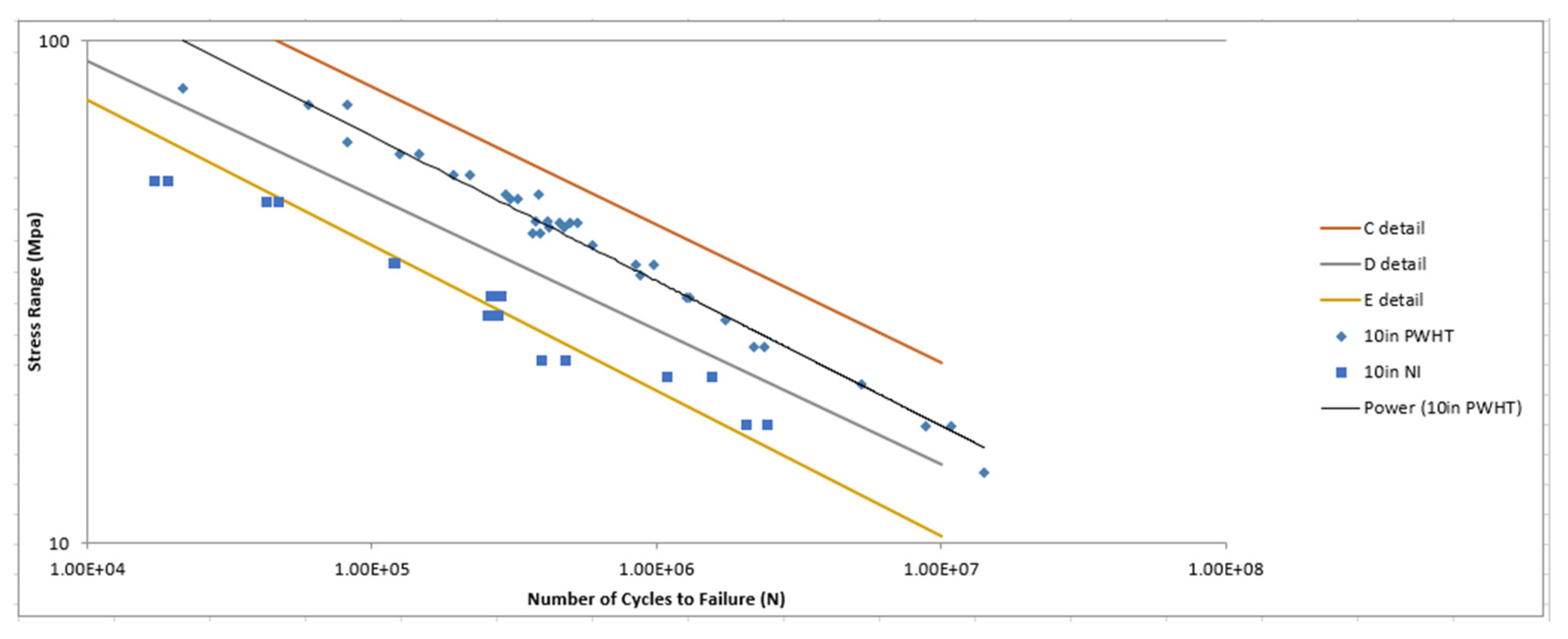
3.1. Fatigue Tests Results
3.2. Finite Element Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Murthy, M.V.V.; Rao, K.P.; Rao, A.K. On stresses around an arbitrarily oriented crack in a cylindrical shell. Int. J. Struct. 1974, 10, 1243–1269. [Google Scholar] [CrossRef]
- Durelli, A.J.; Parks, V.J.; Feng, H.C. Stresses around an elliptical hole in a finite plate subjected to axial loading. J. Appl. Mech. 1966, 33, 192–195. [Google Scholar] [CrossRef]
- The Aluminum Association. Aluminum Design Manual: Specification for Aluminum Structures; The Aluminum Association: Arlington, VA, USA, 2010. [Google Scholar]
- Fisher, J.W.; Kulak, G.L.; Smith, I.F.C. A Fatigue Primer for Structural Engineers; National Steel Bridge Alliance & AISC: Chicago, IL, USA, 1998. [Google Scholar]
- Roy, S.; Park, Y.C.; Sause, R.; Fisher, J.W.; Kaufmann, E.J. Cost-effective connection details for highway sign, luminaire, and traffic signal structures. In NCHRP 10-70 Web-Only Doc. 176; Transportation Research Board: Washington, DC, USA, 2011. [Google Scholar]
- AASHTO (American Association of State Highway and Transportation Officials). Standard Specifications for Structural Supports for Highway Signs, Luminaires and Traffic Signals (LRFDLTS-1); AASHTO (American Association of State Highway and Transportation Officials): Washington, DC, USA, 2015. [Google Scholar]
- Dexter, R.J.; Ricker, N.J. Fatigue-Resistant Design of Cantilevered Signal, Sign, and Light Supports. In NCHRP Report 469; University of Minnesota: Minneapolis, MN, USA, 2002. [Google Scholar]
- Menzemer, C. Examination of Several Mullica River Bridge Light Poles, Corresponding to J; Bowman, Hapco: Abingdon, VA, USA, 2012. [Google Scholar]
- Daneshkhah, A.R.; Schlatter, C.R.; Rusnak, C.R.; Menzemer, C.C. Fatigue behavior of reinforced welded hand-holes in aluminum light poles. Eng. Struct. Mater. 2019, 188, 60–68. [Google Scholar] [CrossRef]
- Rusnak, C.R. Fatigue Behavior in Reinforced Electrical Access Holes in Aluminum Light Pole Support Structures. Master’s Thesis, The University of Akron, Akron, OH, USA, 2019. [Google Scholar]
- Hilty, E.; Menzemer, C.; Manigandan, K.; Srivatsan, T. Influence of welding and heat treatment on microstructure, properties and fracture behavior of a wrought aluminum alloy. Emerg. Mater. Res. 2014, 3, 230–242. [Google Scholar] [CrossRef]

















| Part Name | Alloy | Tensile Yield Strength | Ultimate Tensile Strength |
|---|---|---|---|
| Tube | 6063-T6 | 213.7 MPa (31 ksi) | 241.3 MPa (35 ksi) |
| Aspect Ratio | Longitudinal | Transverses |
|---|---|---|
| 1-1.5 | 118.8 | 5.0 |
| 1-1.25 | 72.0 | 0.9 |
| 1-1 | 48.4 | 0.1 |
| 1.5-1 | 44.0 | 0.0 |
| 1.75-1 | 38.5 | 0.0 |
| 2-1 | 36.7 | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rusnak, C.R.; Menzemer, C.C. Fatigue Behavior of Nonreinforced Hand-Holes in Aluminum Light Poles. Metals 2021, 11, 1222. https://doi.org/10.3390/met11081222
Rusnak CR, Menzemer CC. Fatigue Behavior of Nonreinforced Hand-Holes in Aluminum Light Poles. Metals. 2021; 11(8):1222. https://doi.org/10.3390/met11081222
Chicago/Turabian StyleRusnak, Cameron R., and Craig C. Menzemer. 2021. "Fatigue Behavior of Nonreinforced Hand-Holes in Aluminum Light Poles" Metals 11, no. 8: 1222. https://doi.org/10.3390/met11081222
APA StyleRusnak, C. R., & Menzemer, C. C. (2021). Fatigue Behavior of Nonreinforced Hand-Holes in Aluminum Light Poles. Metals, 11(8), 1222. https://doi.org/10.3390/met11081222





