Weld-Quality Prediction Algorithm Based on Multiple Models Using Process Signals in Resistance Spot Welding
Abstract
:1. Introduction
2. Experiments
2.1. Materials
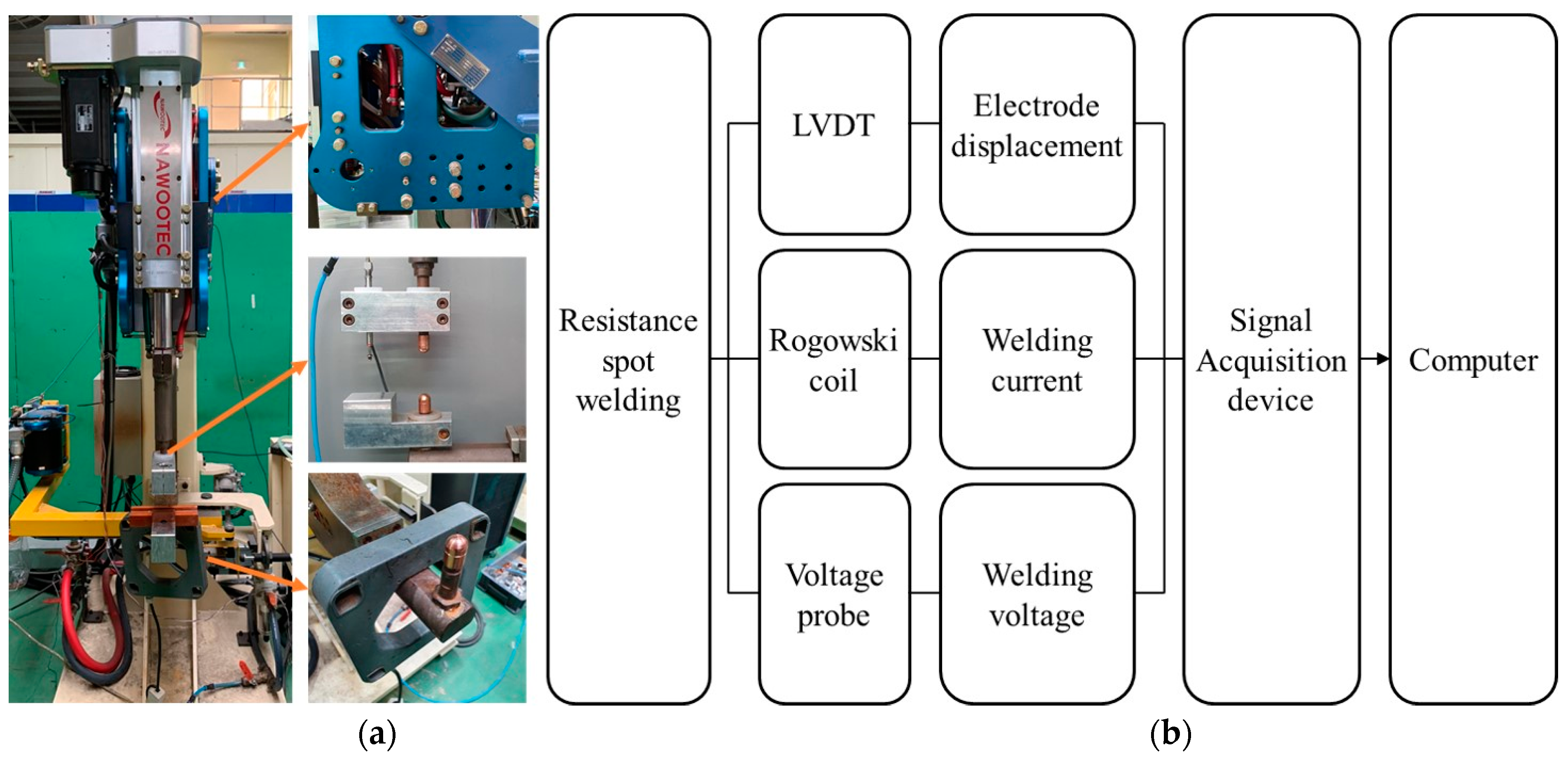
2.2. Experimental Setup
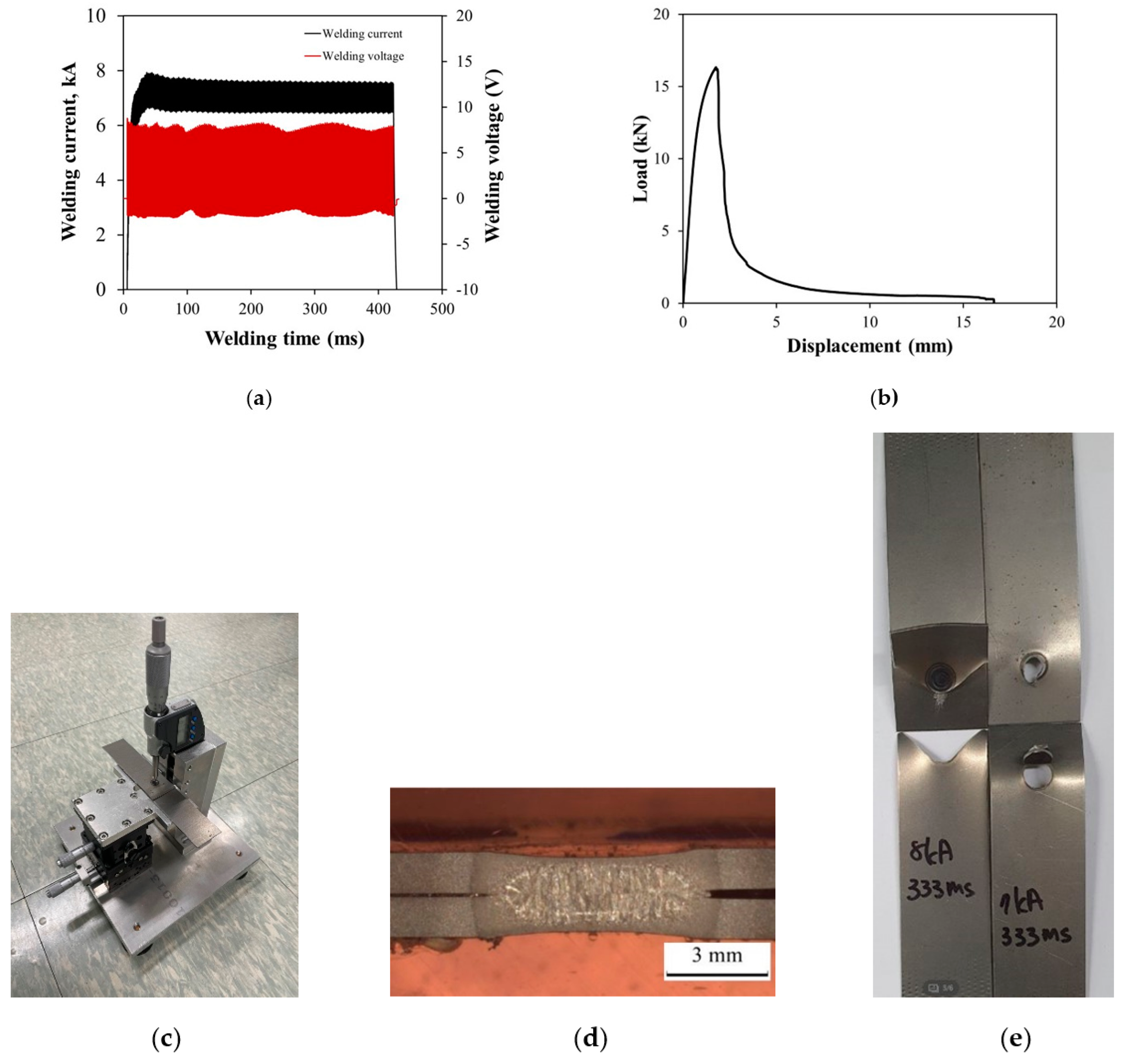
2.3. Experimental Procedure
2.4. Regression Model
2.4.1. Polynomial Regression Model
2.4.2. Logistic Regression Model
3. Results and Discussion
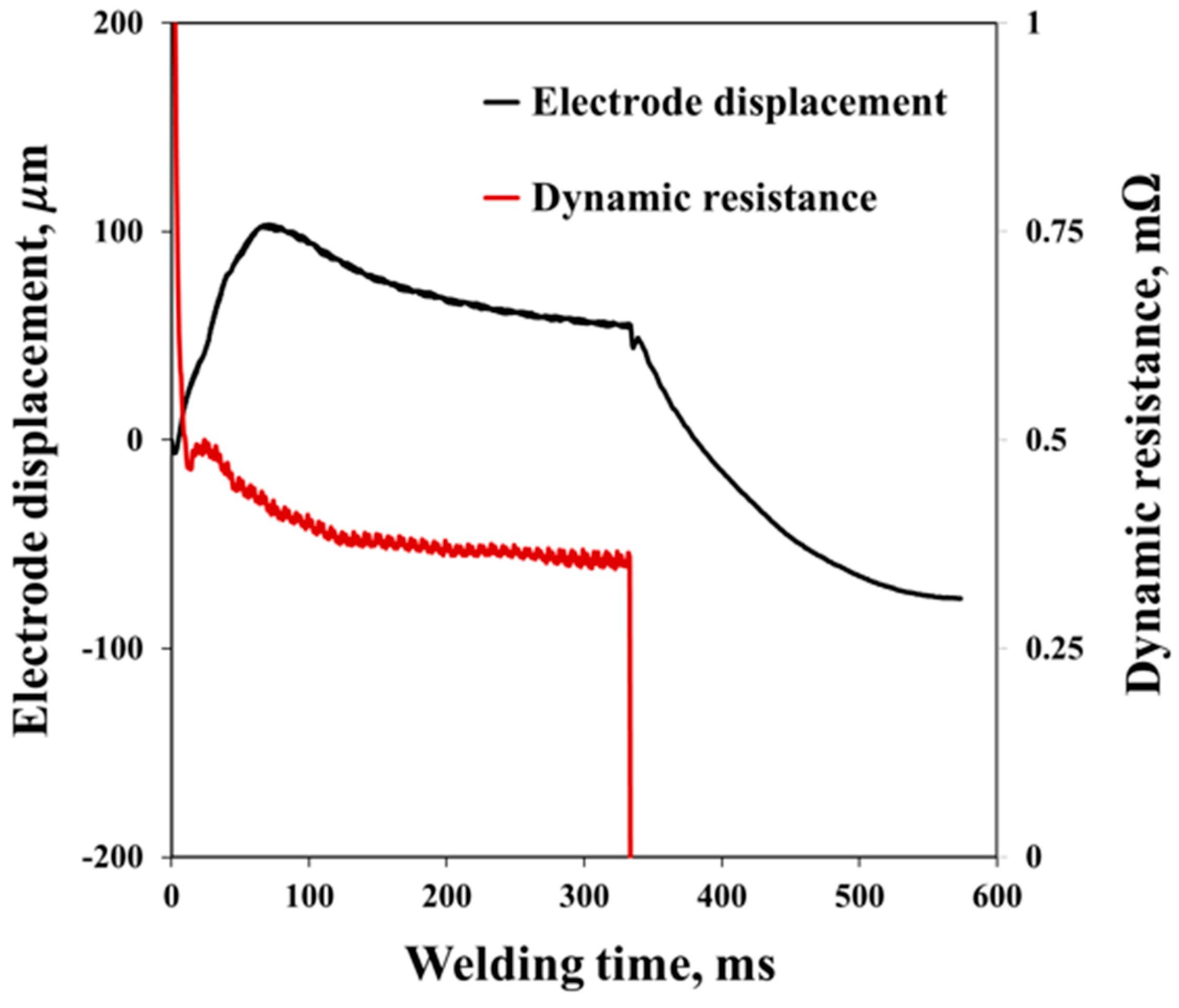
3.1. Independent Variables for Regression Models
3.2. Correlation Analysis
3.3. Estimation of Prediction Models
3.3.1. Prediction Model for Expulsion Occurrence
3.3.2. Prediction Model for Failure Mode
3.3.3. Prediction Model for Indentation Depth
3.3.4. Prediction Model for Tensile Shear Strength
3.4. Weld Quality Prediction Using Prediction Models
3.5. Weld Quality Evaluation Algorithm
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xinmin, L.; Xiaoyun, Z.; Yansong, Z.; Guanlong, C. Weld quality inspection based on online measured indentation from servo encoder in resistance spot welding. IEEE Trans. Instrum. Meas. 2007, 56, 1501–1505. [Google Scholar] [CrossRef]
- Oikawa, H.; Murayama, G.; Hiwatashi, S.; Matsuyama, K. Resistance spot weldability of high strength steel sheets for automobiles and the quality assurance of joints. Weld. World 2007, 51, 7–18. [Google Scholar] [CrossRef]
- Zhang, H. Expulsion and its influence on weld quality. Weld. J. N. Y. 1999, 78, 373-s. [Google Scholar]
- Varjenja, O.N.P.O.S.; To, P.U.; Naprednega, K.V.; Jekla, F.-M.V.T. Dependence of the fracture mode on the welding variables in the resistance spot welding of ferrite-martensite DP980 advanced high-strength steel. Mater. Tehnol. 2012, 46, 665–671. [Google Scholar]
- Evaluation of Non-Destructive Testing Methods for Automatic Quality Checking of Spot Welds. Available online: http://www.diva-portal.org/smash/record.jsf?pid=diva2%3A642618&dswid=4158 (accessed on 15 September 2021).
- Blitz, J.; Simpson, G. Ultrasonic Methods of Non-Destructive Testing, 2nd ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1995; p. 5. [Google Scholar]
- Zhang, B.; Wei, Z.; Osman, A. An ultrasonic non-destructive testing method for evaluating resistance spot welding quality. In Proceedings of the International Symposium on Structural Health Monitoring and Nondestructive Testing, Saarbruecken, Germany, 4–5 October 2018. [Google Scholar]
- Zhang, H.; Senkara, J. Resistance Welding: Fundamentals and Applications, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2012; p. 182. [Google Scholar]
- Zhang, P.; Zhang, H.; Chen, J.; Ma, Y. Quality monitoring of resistance spot welding based on electrode displacement characteristics analysis. Front. Mech. Eng. China 2007, 2, 330–335. [Google Scholar] [CrossRef]
- Yu, J. Quality estimation of resistance spot weld based on logistic regression analysis of welding power signal. Int. J. Precis. Eng. Manuf. 2015, 16, 2655–2663. [Google Scholar] [CrossRef]
- Yu, J. Adaptive resistance spot welding process that reduces the shunting effect for automotive high-strength steels. Metals 2018, 8, 775. [Google Scholar] [CrossRef] [Green Version]
- Hwang, I.; Yun, H.; Yoon, J.; Kang, M.; Kim, D.; Kim, Y.-M. Prediction of resistance spot weld quality of 780 MPa grade steel using adaptive resonance theory artificial neural networks. Metals 2018, 8, 453. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Hou, Y.; Yang, T.; Zhang, Q.; Zhao, J. Welding quality evaluation of resistance spot welding using the time-varying inductive reactance signal. Meas. Sci. Technol. 2018, 29, 055601. [Google Scholar] [CrossRef]
- Xia, Y.-J.; Su, Z.-W.; Li, Y.-B.; Zhou, L.; Shen, Y. Online quantitative evaluation of expulsion in resistance spot welding. J. Manuf. Process. 2019, 46, 34–43. [Google Scholar] [CrossRef]
- Choi, S.G.; Hwang, I.; Kim, Y.M.; Kang, B.; Kang, M. Prediction of the Weld Qualities Using Surface Appearance Image in Resistance Spot Welding. Metals 2019, 9, 831. [Google Scholar] [CrossRef] [Green Version]
- Dejans, A.; Kurtov, O.; Van Rymenant, P. Acoustic emission as a tool for prediction of nugget diameter in resistance spot welding. J. Manuf. Process. 2021, 62, 7–17. [Google Scholar] [CrossRef]
- Kim, S.; Hwang, I.; Kang, M.; Park, J.; Yu, J. Prediction of Indentation Depth of Resistance Spot Welding Using Electrode Displacement Signal. J. Weld. Join. 2021, 39, 314–322. [Google Scholar] [CrossRef]
- Su, Z.-W.; Xia, Y.-J.; Shen, Y.; Li, Y.-B. A novel real-time measurement method for dynamic resistance signal in medium frequency DC resistance spot welding. Meas. Sci. Technol. 2020, 31, 055011. [Google Scholar] [CrossRef]
- Ostertagová, E. Modelling using Polynomial Regression. Procedia Eng. 2012, 48, 500–506. [Google Scholar] [CrossRef] [Green Version]
- Peng, C.-Y.J.; Lee, K.L.; Ingersoll, G.M. An Introduction to Logistic Regression Analysis and Reporting. J. Educ. Res. 2010, 96, 3–14. [Google Scholar] [CrossRef]
- Dickinson, D.W.; Franklin, J.E.; Stanya, A. Characterization of spot welding behavior by dynamic electrical parameter monitoring. Weld. J. 1980, 59, 170–176. [Google Scholar]
- Wan, X.; Wang, Y.; Zhao, D.; Huang, Y.; Yin, Z. Weld quality monitoring research in small scale resistance spot welding by dynamic resistance and neural network. Measurement 2017, 99, 120–127. [Google Scholar] [CrossRef]
- Zhao, D.; Ivanov, M.; Wang, Y.; Du, W. Welding quality evaluation of resistance spot welding based on a hybrid approach. J. Intell. Manuf. 2021, 32, 1819–1832. [Google Scholar] [CrossRef]
- Xing, B.; Xiao, Y.; Qin, Q.H. Characteristics of shunting effect in resistance spot welding in mild steel based on electrode displacement. Meas. J. Int. Meas. Confed. 2018, 115, 233–242. [Google Scholar] [CrossRef] [Green Version]
- ISO 18595. Resistance Welding—Spot Welding of Aluminium and Aluminium Alloys—Weldability, Welding and Testing, 1st ed.; British Standards Institution (BSI): Geneva, Switzerland, 2007; pp. 11–13. [Google Scholar]
- AWS D8.1M. Specification for Automotive Weld Quality—Resistance Spot Welding of Steel; American Welding Society (AWS): Miami, FL, USA, 2013. [Google Scholar]




| Material Grade | Thickness (mm) | Tensile Strength (MPa) | Yield Strength (MPa) |
|---|---|---|---|
| SPFC590 | 1.2 | 600 | 512 |
| SPFC780Y | 1.2 | 807 | 519 |
| SPFC980Y | 1.2 | 1002 | 712 |
| SPFC980Y | 1.4 | 1002 | 712 |
| SPFC980Y | 1.6 | 1002 | 712 |
| SPFC590 | 1.0 | 600 | 512 |
| SGFC980Y | 1.2 | 1000 | 708 |
| SGAFC980Y | 1.2 | 1005 | 715 |
| Item | Condition |
|---|---|
| Welding machine | Medium-frequency direct current welding machine |
| Electrode force (kN) | 2.94 |
| Welding current (kA) | 4.0, 5.0, 6.0, 7.0, 8.0 |
| Welding time (ms) | 250, 333, 417 |
| Hold time (ms) | 167 |
| Independent Variable | Definition | Independent Variable | Definition | Independent Variable | Definition |
|---|---|---|---|---|---|
| Coating | Thickness | Tensile strength of test materials | |||
| Displacement at A | Displacement at B | Displacement at C | |||
| Welding time at A | Welding time at B | Average of dynamic resistance | |||
| Area of dynamic resistance waveform | Dynamic resistance at D | - | - |
| Response Variable (↓) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Expulsion occurrence | −0.045 | 0.039 | 0.019 | 0.196 | −0.622 | 0.783 | −0.456 | 0.009 | −0.549 | −0.385 | −0.524 |
| Failure mode | −0.100 | −0.266 | −0.332 | 0.249 | −0.137 | 0.285 | −0.367 | 0.071 | −0.573 | −0.357 | −0.548 |
| Indentation depth | 0.249 | −0.048 | 0.092 | 0.172 | −0.760 | 0.922 | −0.494 | 0.097 | −0.793 | −0.486 | −0.748 |
| Tensile shear strength | 0.148 | 0.299 | 0.423 | 0.463 | −0.131 | 0.487 | −0.404 | 0.047 | −0.631 | −0.410 | −0.575 |
| Term | SE Coefficient | p Value | VIF |
|---|---|---|---|
| Constant | 3.150 | 0.000 | - |
| 0.0170 | 0.000 | 15.14 | |
| 0.0191 | 0.000 | 15.21 | |
| 0.0120 | 0.006 | 1.06 |
| Term | SE Coefficient | p Value | VIF |
|---|---|---|---|
| Constant | 2.050 | 0.000 | - |
| 0.001 | 0.000 | 1.11 | |
| 3.880 | 0.000 | 1.11 |
| Term | p Value |
|---|---|
| constant | 0.015 |
| 0.000 | |
| 0.000 | |
| 0.001 | |
| 0.004 | |
| 0.759 | |
| 0.006 | |
| 0.000 | |
| 0.000 | |
| 0.000 | |
| 0.001 | |
| 0.000 | |
| 0.003 | |
| 0.000 | |
| 0.006 | |
| 0.004 |
| Term | p Value |
|---|---|
| constant | 0.000 |
| 0.000 | |
| 0.000 | |
| 0.851 | |
| 0.004 | |
| 0.393 | |
| 0.456 | |
| 0.183 | |
| 0.515 | |
| 0.000 | |
| 0.076 | |
| 0.001 | |
| 0.000 | |
| 0.000 | |
| 0.000 | |
| 0.000 | |
| 0.045 | |
| 0.003 | |
| 0.000 | |
| 0.000 | |
| 0.065 | |
| 0.002 | |
| 0.000 |
| Actual Class | Positive | Negative | |
|---|---|---|---|
| Predicted Class | |||
| Positive | 18 | 0 | |
| Negative | 2 | 60 | |
| Actual Class | Positive | Negative | |
|---|---|---|---|
| Predicted Class | |||
| Positive | 18 | 2 | |
| Negative | 10 | 50 | |
| Quality Metric | Criterion | |||
|---|---|---|---|---|
| Expulsion (ISO 18595) | No expulsion | |||
| Failure mode (ISO 18595) | Button failure | |||
| Indentation depth (AWS D8.1M) | Indentation should be less than 30% of the thickness of each outside sheet of the welded joint | |||
| Tensile shear strength (AWS D8.1M) | Material grade | Thickness (mm) | Tensile strength (MPa) | Criterion (kN) |
| SPFC590 | 1.2 | 600 | 5.7 | |
| SPFC780Y | 1.2 | 807 | 7.4 | |
| SPFC980Y | 1.2 | 1002 | 8.8 | |
| SPFC980Y | 1.4 | 1002 | 11.1 | |
| SPFC980Y | 1.6 | 1002 | 13.5 | |
| SPFC590 | 1.0 | 600 | 4.3 | |
| SGFC980Y | 1.2 | 1000 | 8.8 | |
| SGAFC980Y | 1.2 | 1005 | 8.8 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Hwang, I.; Kim, D.-Y.; Kim, Y.-M.; Kang, M.; Yu, J. Weld-Quality Prediction Algorithm Based on Multiple Models Using Process Signals in Resistance Spot Welding. Metals 2021, 11, 1459. https://doi.org/10.3390/met11091459
Kim S, Hwang I, Kim D-Y, Kim Y-M, Kang M, Yu J. Weld-Quality Prediction Algorithm Based on Multiple Models Using Process Signals in Resistance Spot Welding. Metals. 2021; 11(9):1459. https://doi.org/10.3390/met11091459
Chicago/Turabian StyleKim, Sehyeon, Insung Hwang, Dong-Yoon Kim, Young-Min Kim, Munjin Kang, and Jiyoung Yu. 2021. "Weld-Quality Prediction Algorithm Based on Multiple Models Using Process Signals in Resistance Spot Welding" Metals 11, no. 9: 1459. https://doi.org/10.3390/met11091459






