Comprehensive Weldability Criterion for Magnetic Pulse Welding of Dissimilar Materials
Abstract
:1. Introduction
2. Numerical Modeling and Experimental Method
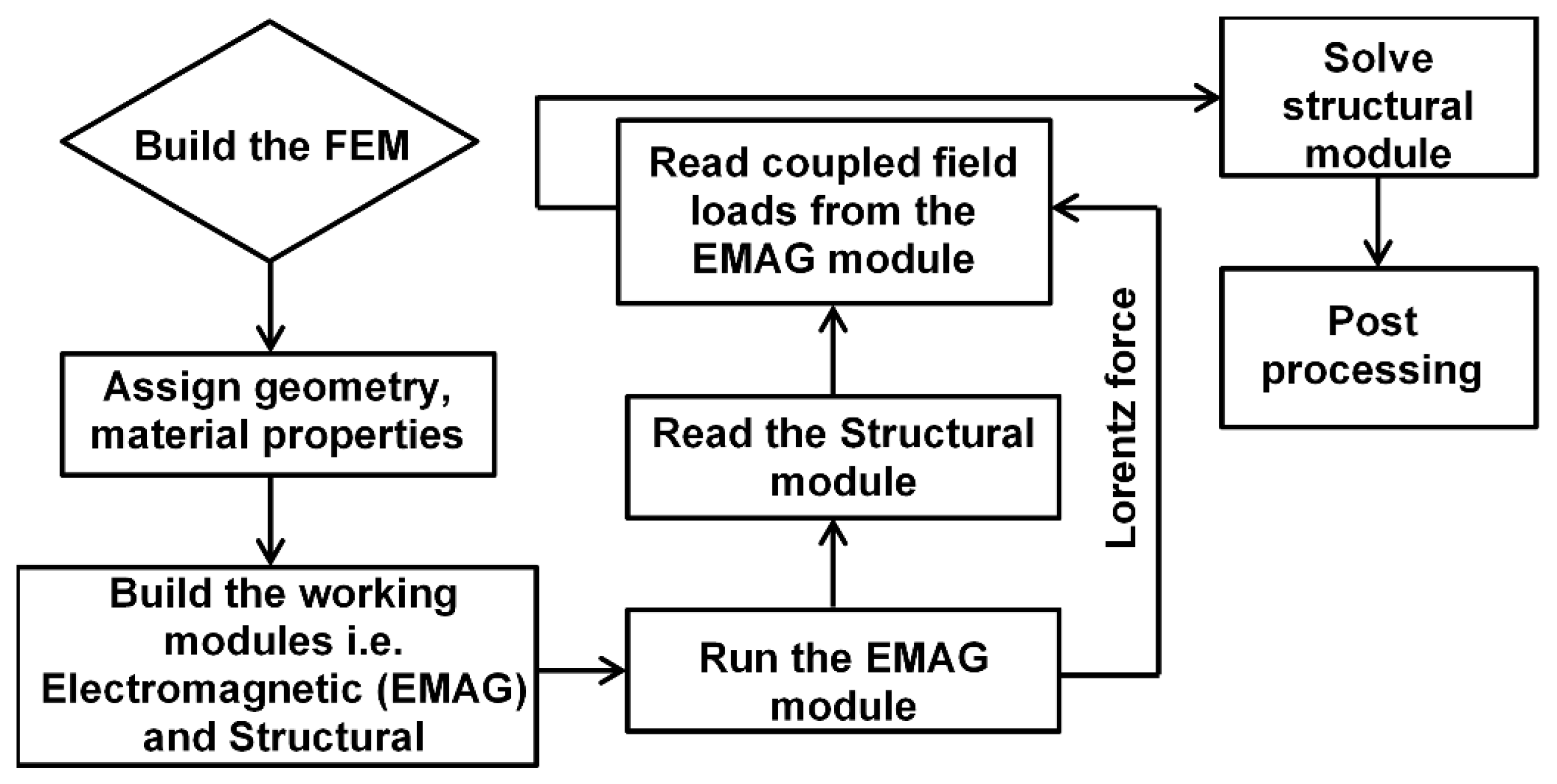
2.1. Finite Element Model
2.2. Experimental Method
3. Algorithmic Approach for Shop-Floor-Applicable Process Parameters
3.1. Development of Weldability Criteria: Threshold Velocity vs. Effective Velocity
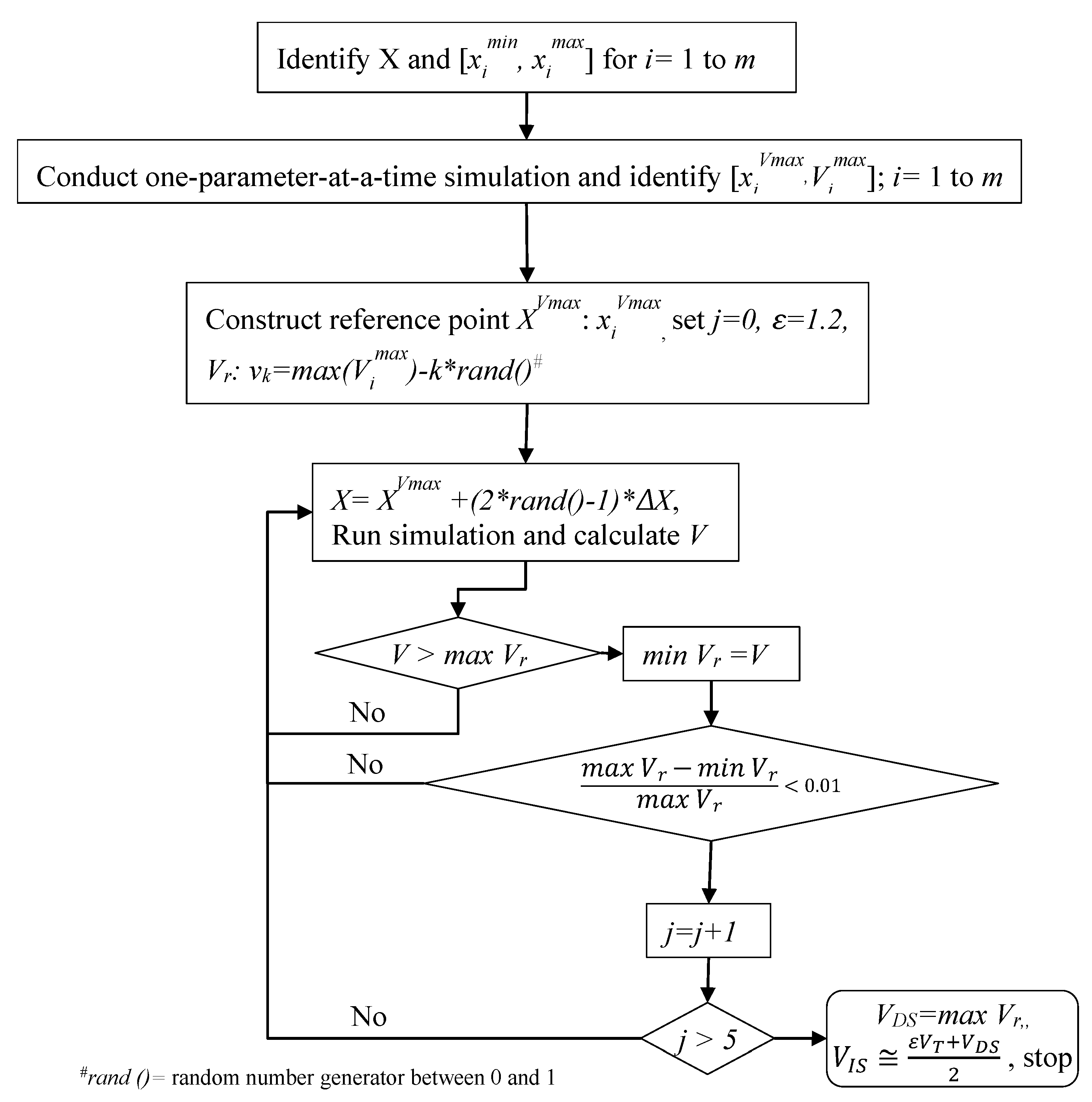
3.2. Algorithm for Selection of Shop-Floor Applicable Parameters
4. Results and Discussion
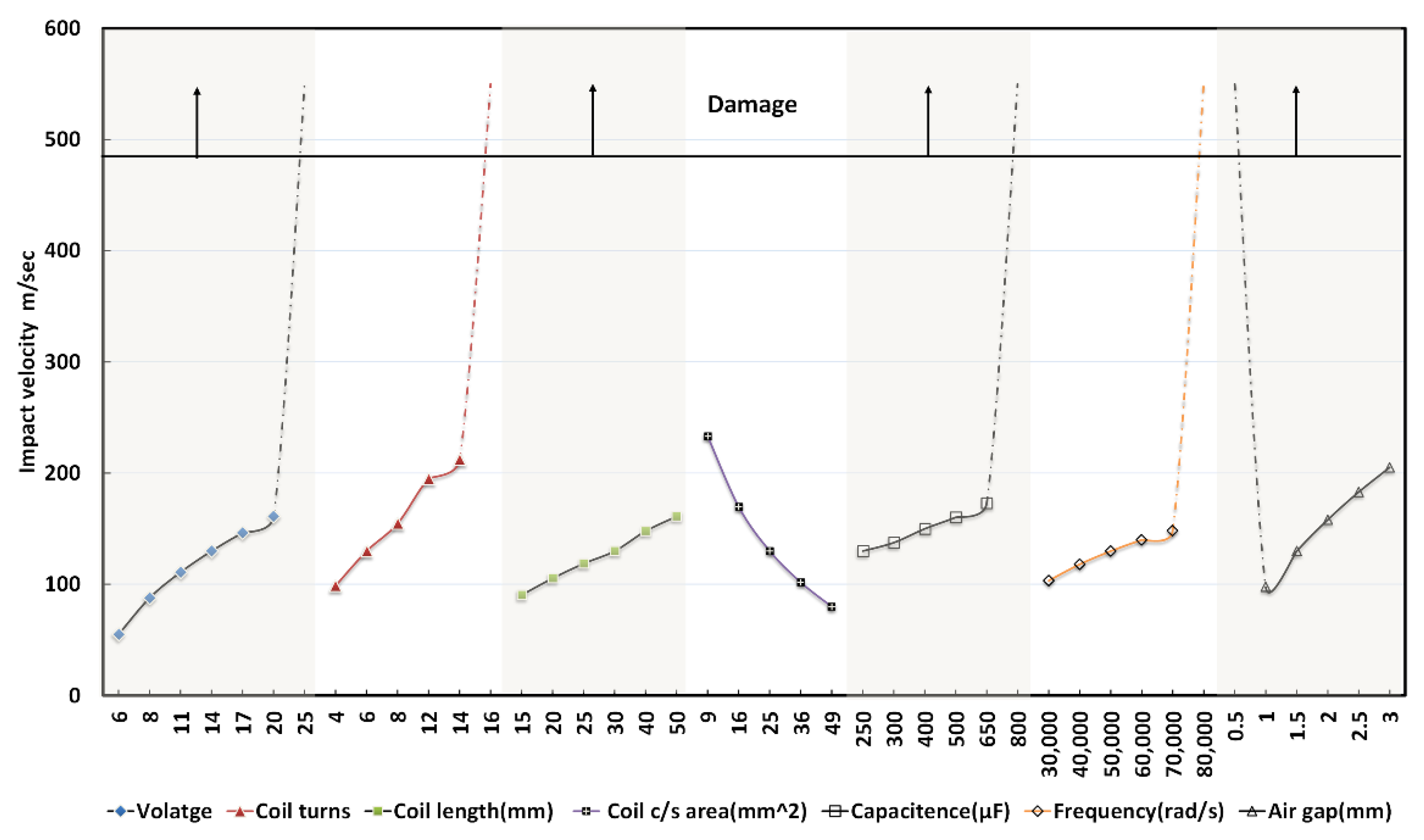
4.1. Process Parameter Identification
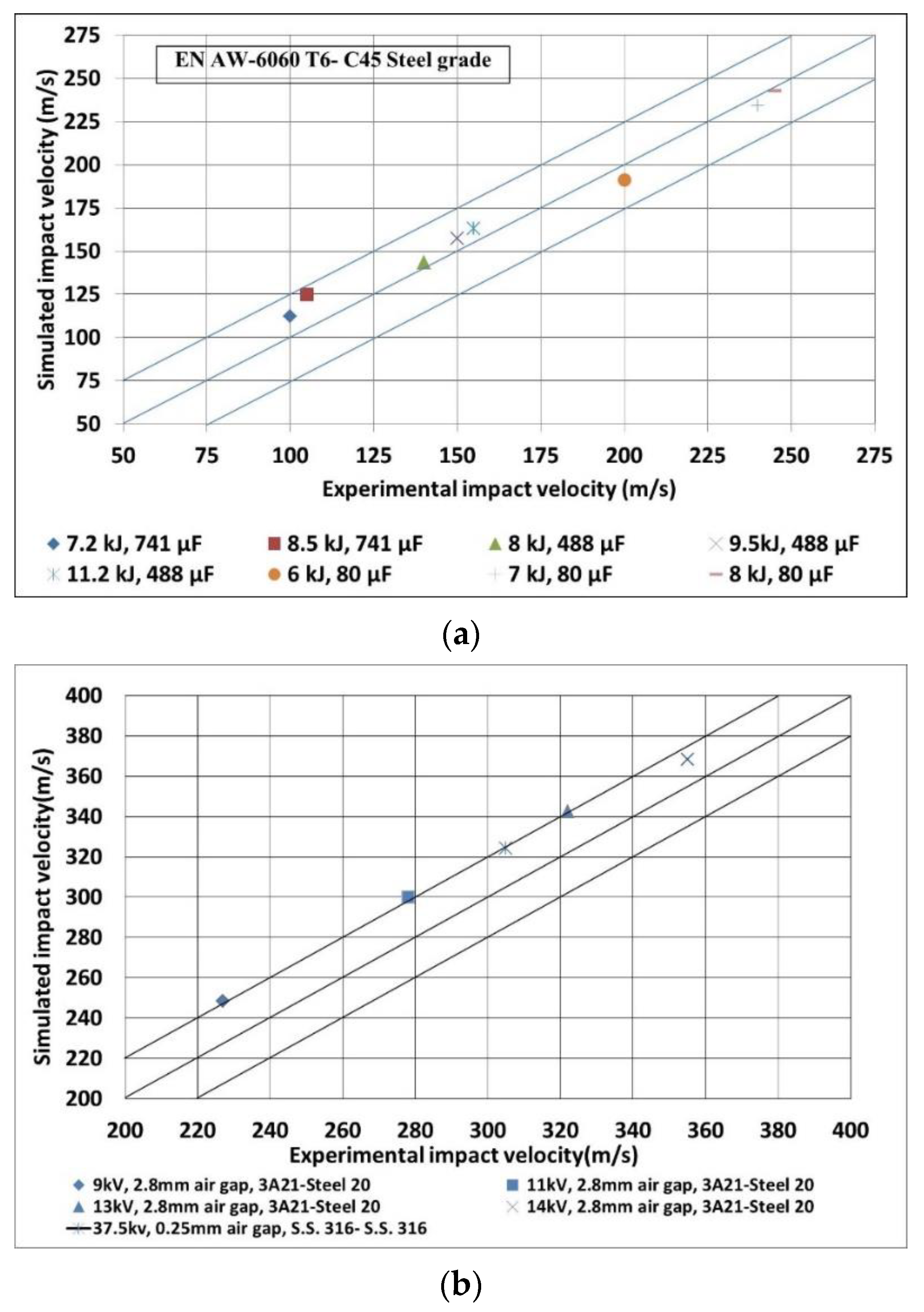
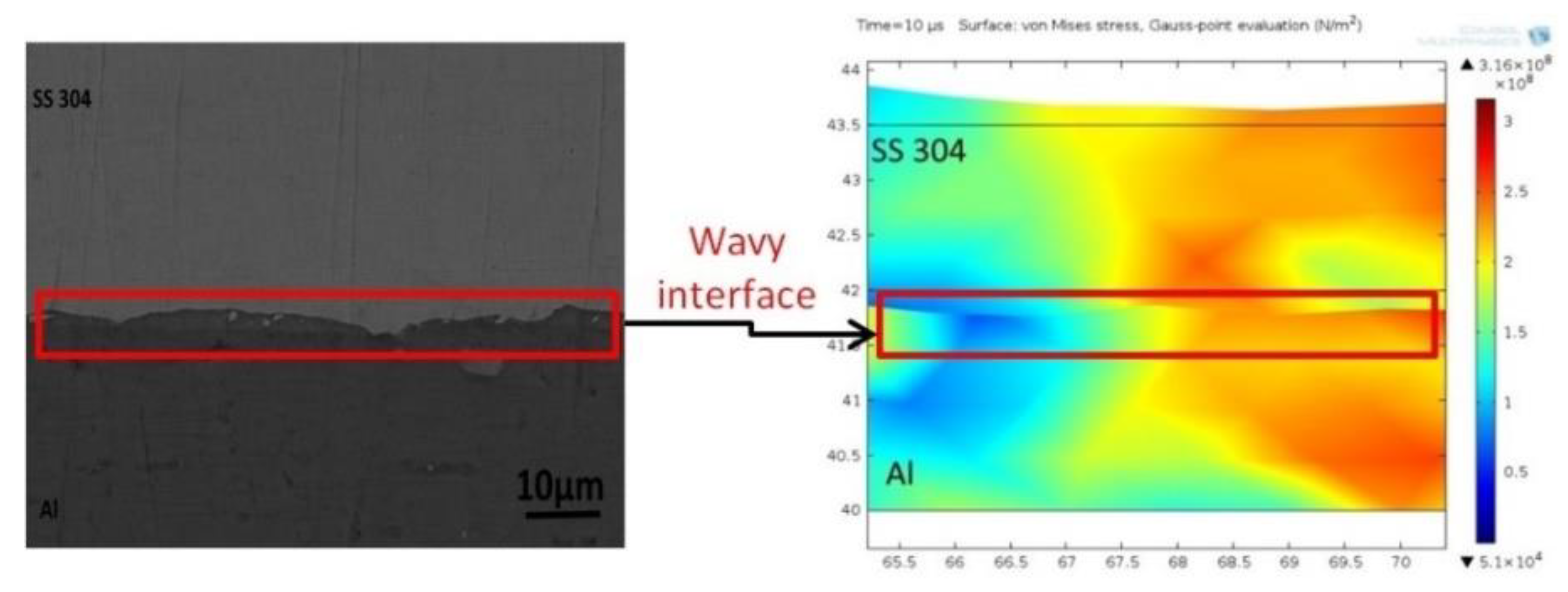
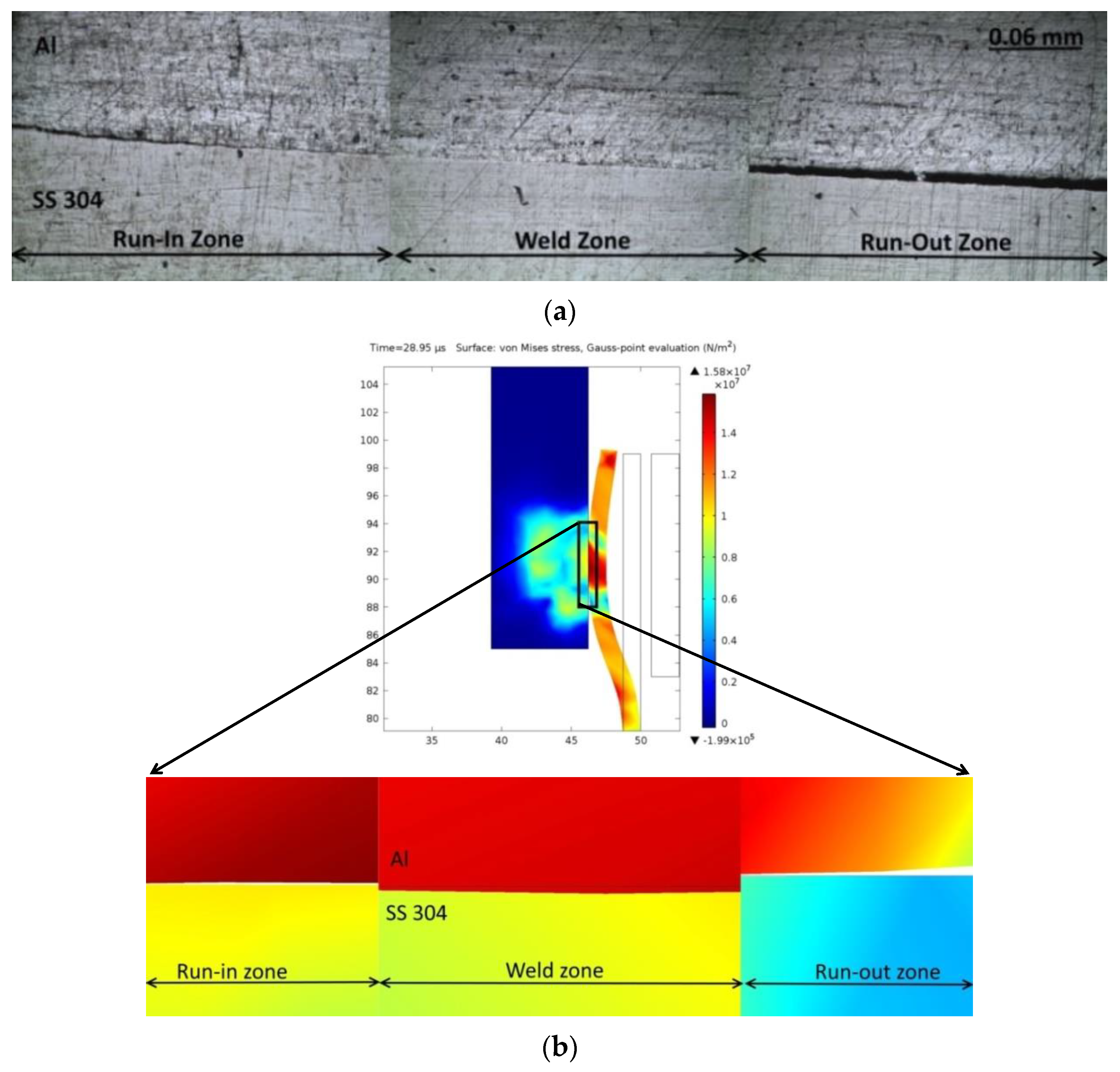
4.2. Experimental Corroboration of FEM Observations
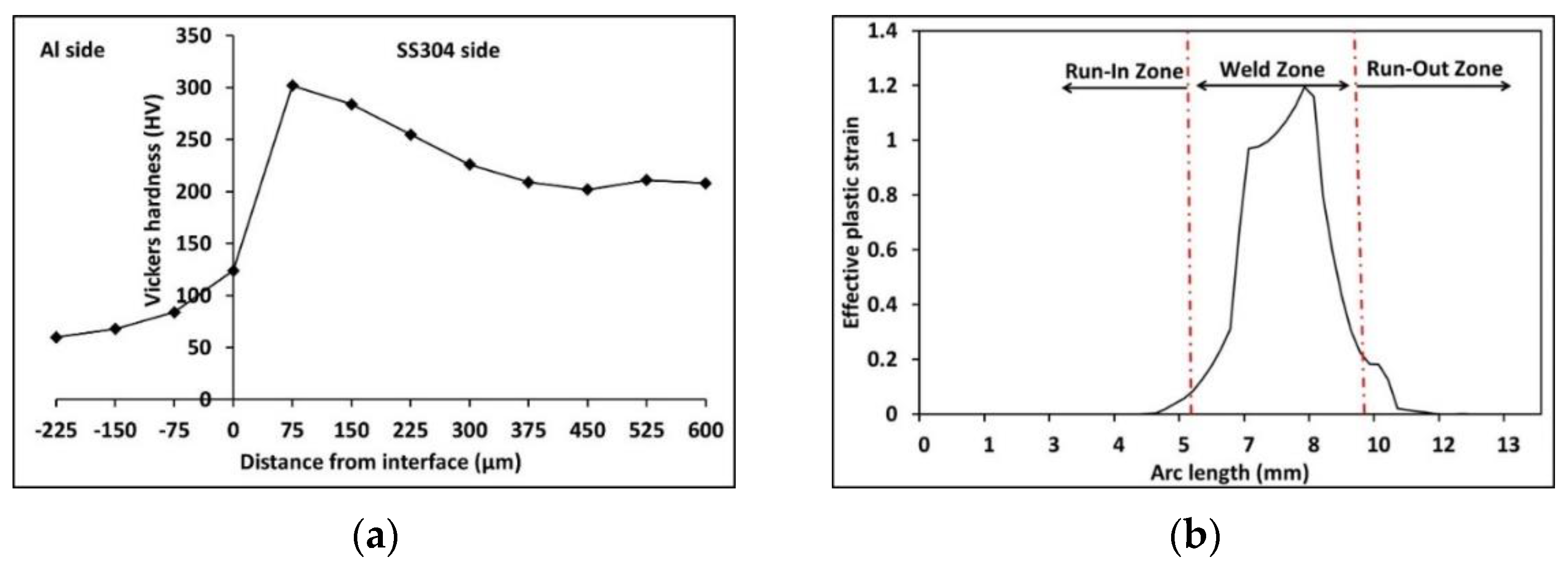
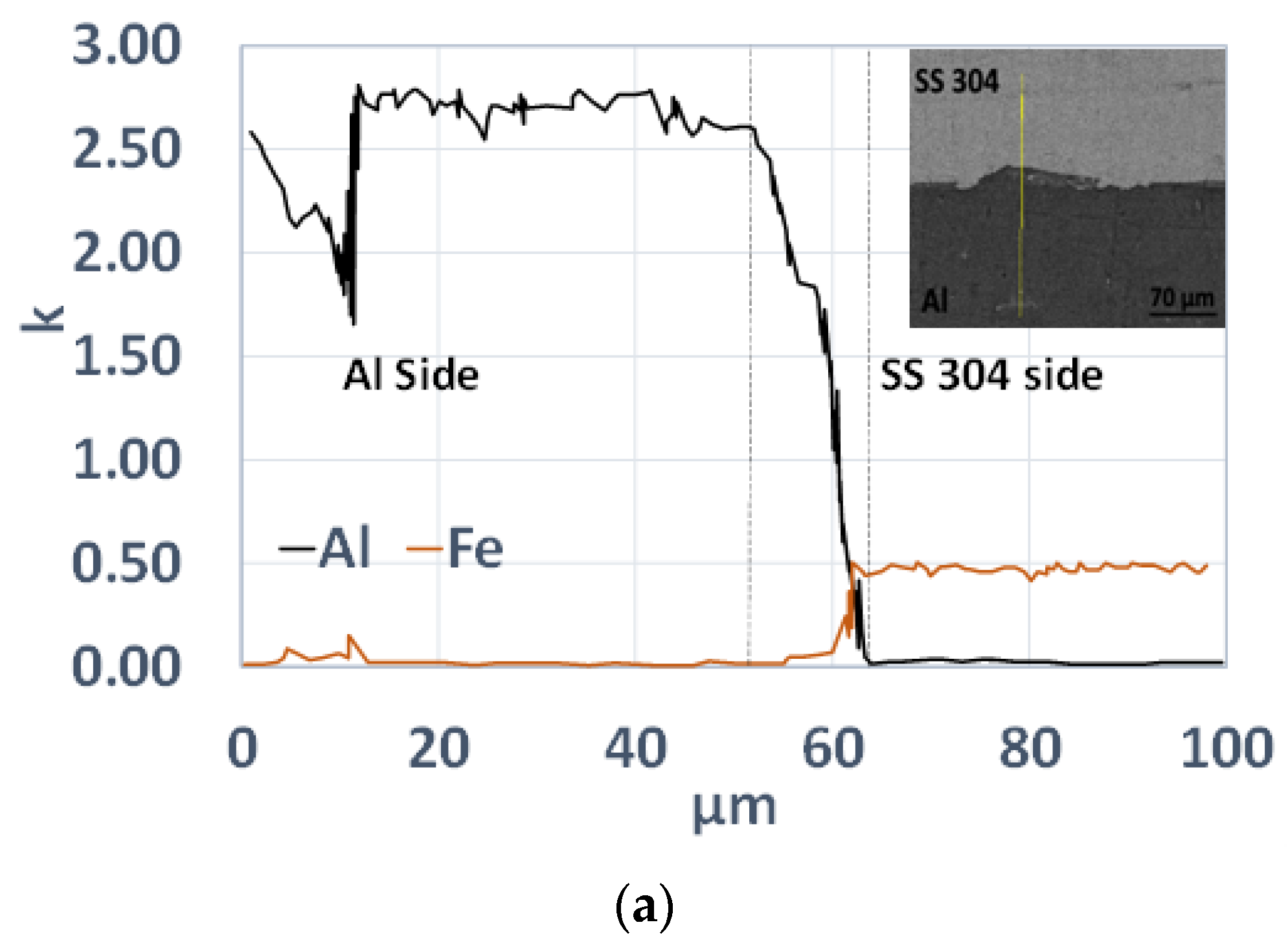
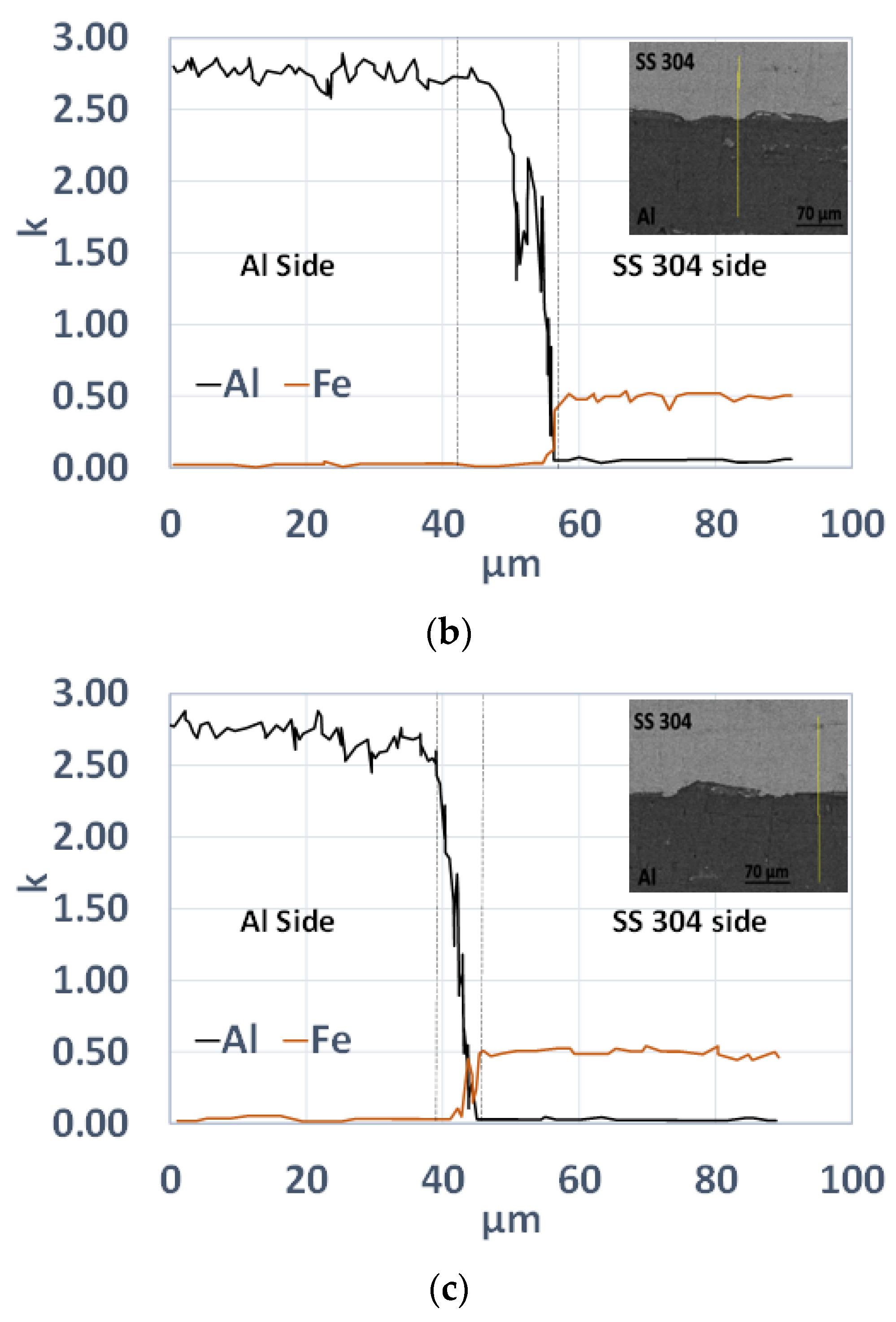
4.3. Metallurgical Investigation
5. Conclusions
- The conventional weldability criterion (threshold impact velocity) is necessary but insufficient, as it is calculated using material properties without considering the geometry of the electromagnetic coil, electrical and physical parameters, such as air gap and plate thickness, and surface imperfections. Such a criterion does not identify suitable process parameters for shop-floor applications.
- A new criterion (effective impact velocity) is proposed, in which the effective impact velocity is the average of the threshold and maximum possible velocity without damage. The investigation offers a numeric algorithm to compute effective impact velocity, wherein the maximum possible velocity without damage is obtained through FEM simulation.
- The proposed weldability criterion overcomes the existing limitations and can be numerically computed and inversely modeled, and thus can be used to prescribe shop-floor applicable process parameters.
- The weld samples obtained with numerically computed parameters were consistent with the experiments in terms of interface morphology, the intermediate layer’s width, and plastic strain distribution. The joints cleared lap shear tests, wherein fracture occurred outside the welded region—increased hardness in and around the interface zone corresponded with the predicted plastic strain in the FEM simulation. Surface energy dispersive spectroscopy also showed that the increased hardness was associated with element transfer at the interface during the severe plastic deformation at the time of impact.
- The proposed approach is an experimentally corroborated and time-saving method that will encourage using finite element modeling to obtain shop-floor-applicable process parameters. Moreover, the cost will be reduced as use of the electromagnetic coil will be restricted to that of a few (essential for FEM validation), unlike conventional methods, wherein several coils are to be tested.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Kapil, A.; Sharma, A. Magnetic pulse welding: An efficient and environmentally friendly multi-material joining technique. J. Clean. Prod. 2015, 100, 35–58. [Google Scholar] [CrossRef]
- Martinsen, K.; Hu, S.J.; Carlson, B.E. Joining of dissimilar materials. CIRP ANN-Manuf. Techn. 2015, 64, 679–699. [Google Scholar] [CrossRef] [Green Version]
- Stern, A.; Aizenshtein, M. Bonding zone formation in magnetic pulse welds. Sci. Technol. Weld. Join. 2002, 7, 339–342. [Google Scholar] [CrossRef]
- Akbari Mousavi, S.A.A.; Al-Hassani, S.T.S. Numerical and experimental studies of the mechanism of the wavy interface formations in explosive/impact welding. J. Mech. Phys. Solids 2005, 53, 2501–2528. [Google Scholar] [CrossRef]
- Kapil, A.; Lee, T.; Vivek, A.; Bockbrader, J.; Abke, T.; Daehn, G. Benchmarking strength and fatigue properties of spot impact welds. J. Mater. Process. Technol. 2018, 255, 219–233. [Google Scholar] [CrossRef]
- Kore, S.D.; Date, P.P.; Kulkarni, S.V. Effect of process parameters on electromagnetic impact welding of aluminum sheets. Int. J. Impact Eng. 2007, 34, 1327–1341. [Google Scholar] [CrossRef]
- Aizawa, T.; Kashani, M.; Okagawa, K. Application of magnetic pulse welding for aluminum alloys and SPCC steel sheet joints. Weld. J. 2007, 86, 119–124. [Google Scholar]
- Hisashi, S.; Isao, S.; Sherif, R.; Hidekazu, M. Numerical study of joining process in magnetic pressure seam welding. Trans. JWRI 2009, 38, 63–68. [Google Scholar]
- Zhang, Y.; Daehn, G.; L’Eplattenier, P.; Babu, S. Experimental study and numerical simulation on magnetic pulse welding for pre-flanged AA6061-t6 and CU101 sheets. In Trends in Welding Research, Proceeding of the 8th International Conference, Pine Mountain, GA, USA, 1–6 June 2008; ASM International: Materials Park, OH, USA, 2009; pp. 715–720. [Google Scholar]
- Kore, S.D.; Dhanesh, P.; Kulkarni, S.V.; Date, P.P. Numerical modeling of electromagnetic welding. Int. J. Appl. Electrom. 2010, 32, 1–19. [Google Scholar]
- Shim, J.Y.; Kang, B.Y.; Kim, I.S.; Kang, M.J.; Park, D.H.; Kim, I.J. A study on distributions of electromagnetic force of the dissimilar metal joining in MPW using a FEM. Adv. Mat. Res. 2010, 83–86, 214–221. [Google Scholar] [CrossRef]
- Kakizaki, S.; Watanabe, M.; Kumai, S. Simulation and Experimental Analysis of Metal Jet Emission and Weld Interface Morphology in Impact Welding. Mater. Trans. 2011, 52, 1003–1008. [Google Scholar] [CrossRef] [Green Version]
- Zhidan, X.U.; Junjia, C.; Haiping, Y.U.; Chunfeng, L.I. Research on the impact velocity of magnetic impulse welding of pipe fitting. Mater. Des. 2013, 49, 736–745. [Google Scholar]
- Fan, Z.; Yu, H.; Li, C. Plastic deformation behavior of bi-metal tubes during magnetic pulse cladding: FE analysis and experiments. J. Mater. Process. Technol. 2016, 229, 230–243. [Google Scholar] [CrossRef]
- Yu, H.; Tong, Y. Magnetic pulse welding of aluminum to steel using uniform pressure electromagnetic actuator. Int. J. Adv. Manuf. Technol. 2017, 91, 2257–2265. [Google Scholar] [CrossRef]
- Garg, A.; Panda, B.; Shankhwar, K. Investigation of the joint length of weldment of environmental-friendly magnetic pulse welding process. Int. J. Adv. Manuf. Technol. 2016, 87, 2415–2426. [Google Scholar] [CrossRef]
- Psyk, V.; Scheffler, C.; Linnemann, M.; Landgrebe, D. Process analysis for magnetic pulse welding of similar and dissimilar material sheet metal joints. Procedia Eng. 2017, 207, 353–358. [Google Scholar] [CrossRef]
- Li, J.S.; Raoelison, R.N.; Sapanathan, T.; Hou, Y.L.; Rachik, M. Interface evolution during magnetic pulse welding under extremely high strain rate collision: Mechanisms, thermomechanical kinetics and consequences. Acta Mater. 2020, 195, 404–415. [Google Scholar] [CrossRef]
- Shotri, R.; Racineux, G.; De, A. Magnetic pulse welding of metallic tubes–experimental investigation and numerical modelling. Sci. Technol. Weld. Join. 2020, 25, 273–281. [Google Scholar] [CrossRef]
- Khalil, C.; Marya, S.; Racineux, G. Magnetic pulse welding and spot welding with improved coil efficiency—Application for dissimilar welding of automotive metal alloys. J. Manuf. Mater. Process. 2020, 4, 69. [Google Scholar] [CrossRef]
- Li, J.S.; Raoelison, R.N.; Sapanathan, T.; Zhang, Z.; Chen, X.G.; Marceau, D.; Hou, Y.L.; Rachik, M. An anomalous wave formation at the Al/Cu interface during magnetic pulse welding. Appl. Phys. Lett. 2020, 116, 161601. [Google Scholar] [CrossRef] [Green Version]
- Shotri, R.; Faes, K.; De, A. Magnetic pulse welding of copper to steel tubes—Experimental investigation and process modelling. J. Manuf. Process. 2020, 58, 249–258. [Google Scholar] [CrossRef]
- Li, J.S.; Sapanathan, T.; Raoelison, R.N.; Hou, Y.L.; Simar, A.; Rachik, M. On the complete interface development of Al/Cu magnetic pulse welding via experimental characterizations and multiphysics numerical simulations. J. Mater. Process. Technol. 2021, 296, 117185. [Google Scholar] [CrossRef]
- Zhang, S.; Lueg-Althoff, J.; Hahn, M.; Tekkaya, A.E.; Kinsey, B. Effect of process parameters on wavy interfacial morphology during magnetic pulse welding. J. Manuf. Sci. Eng. 2021, 143, 011010. [Google Scholar] [CrossRef]
- Zhang, S.; Kinsey, B.L. Influence of material properties on interfacial morphology during magnetic pulse welding of al1100 to copper alloys and commercially pure titanium. J. Manuf. Mater. Process. 2021, 5, 64. [Google Scholar] [CrossRef]
- Khalil, C.; Marya, S.; Racineux, G. Construction of physical welding windows for magnetic pulse welding of 5754 aluminum with DC04 steel. Int. J. Mater. Form. 2021, 14, 843–854. [Google Scholar] [CrossRef]
- Drehmann, R.; Scheffler, C.; Winter, S.; Psyk, V.; Kräusel, V.; Lampke, T. Experimental and numerical investigations into magnetic pulse welding of aluminum alloy 6016 to hardened steel 22mnb5. J. Manuf. Mater. Process. 2021, 5, 66. [Google Scholar] [CrossRef]
- Shotri, R.; Racineux, G.; De, A. Probing magnetic pulse welding of aluminium and steel sheets. J. Manuf. Process. 2021, 72, 309–319. [Google Scholar] [CrossRef]
- Jiang, H.; Liao, Y.; Jing, L.; Gao, S.; Li, G.; Cui, J. Mechanical properties and corrosion behavior of galvanized steel/Al dissimilar joints. Arch. Civ. Mech. Eng. 2021, 21, 168. [Google Scholar] [CrossRef]
- Chi, L.; Liang, S.; Wang, X.; Ran, Y.; Wang, Y. Simulation and Experimental Study on Forming Process of Wavy Interface in Electromagnetic Pulse Welding Based on Metallic Jet. Mater. Trans. 2022, 63, 33–42. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, N.; Li, X.; Wang, Q.; Ding, H. Optimization design and experimental research of magnetic pulse welding system based on uniform pressure electromagnetic actuator. Int. J. Adv. Manuf. Technol. 2022, 121, 8447–8465. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, H.; Wu, H.; Peng, W. Process simulation and experimental investigation on joining of Al/Ti sheets by magnetic pulse welding. Int. J. Adv. Manuf. Technol. 2022, 121, 5463–5472. [Google Scholar] [CrossRef]
- Yao, Y.; Jing, L.; Wang, S.; Li, G.; Cui, J.; Tang, X.; Jiang, H. Mechanical properties and joining mechanisms of Al-Fe magnetic pulse welding by spot form for automotive application. J. Manuf. Process. 2022, 76, 504–517. [Google Scholar] [CrossRef]
- Li, Z.; Peng, W.; Chen, Y.; Liu, W.; Zhang, H. Simulation and experimental analysis of Al/Ti plate magnetic pulse welding based on multi-seams coil. J. Manuf. Process. 2022, 83, 290–299. [Google Scholar] [CrossRef]
- Dang, H.; Yu, H. Improving the quality of Al-Fe tube joints manufactured via magnetic pulse welding using an inclined-wall field shaper. J. Manuf. Process. 2022, 73, 78–89. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, C.; Shi, X.; Wang, P.; Shen, T.; Mi, Y.; Ma, Y. Evaluation model of electromagnetic pulse welding effect based on Vc-β trajectory curve. J. Mater. Res. Technol. 2022, 20, 616–626. [Google Scholar] [CrossRef]
- Li, Y.; Yang, D.; Yang, W.; Wu, Z.; Liu, C. Multiphysics Numerical Simulation of the Transient Forming Mechanism of Magnetic Pulse Welding. Metals 2022, 12, 1149. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, S.; Li, G.; Cui, J.; Yu, Y.; Jiang, H. A sandwich structure realizing the connection of CFRP and Al sheets using magnetic pulse welding. Compos. Struct. 2022, 295, 115865. [Google Scholar] [CrossRef]
- Athar, M.H.; Tolaminejad, B. Weldability window and the effect of interface morphology on the properties of Al/Cu/Al laminated composites fabricated by explosive welding. Mater. Des. 2015, 86, 516–525. [Google Scholar] [CrossRef]
- Ribeiro, J.B.; Mendes, R.; Loureiro, A. Review of the weldability window concept and equations for explosive welding. J. Phys. Conf. 2014, 500, 052038. [Google Scholar] [CrossRef] [Green Version]
- Cowper, G.R.; Symonds, P.S. Strain Hardening and Strain-Rate Effects in the Impact Loading of Cantilever Beams; Report No. 28; Brown University Division of Applied Mathematics: Providence, RI, USA, 1957. [Google Scholar]
- Kapil, A.; Sharma, A. Advances in Material Forming and Joining; Springer: New Delhi, India, 2015; pp. 255–272. [Google Scholar]
- Kapil, A.; Mastanaiah, P.; Sharma, A. Process Parameter Sensitivity in Magnetic Pulse Welding: An Artificial Neural Network approach. In Proceedings of the 9th International Conference on High-Speed Forming, Dortmund, Germany, 13–15 October 2021. [Google Scholar]
- Stankevic, V.; Lueg-Althoff, J.; Hahn, M.; Tekkaya, A.E.; Zurauskiene, N.; Dilys, J.; Klimantavicius, J.; Kersulis, S.; Simkevicius, C.; Balevicius, S. Magnetic field measurements during magnetic pulse welding using CMR-B-scalar sensors. Sensors 2020, 20, 5925. [Google Scholar] [CrossRef]
- Bellmann, J.; Lueg-Althoff, J.; Schulze, S.; Gies, S.; Beyer, E.; Tekkaya, A.E. Measurement of collision conditions in magnetic pulse welding processes. J. Phys. Sci. Appl. 2017, 7, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Kapil, A.; Vivek, A.; Daehn, G. Process-Structure-Property Relationship in Dissimilar Al-High-Strength Steel Impact Spot Welds Created Using Vaporizing Foil Actuator Welding. SAE Int. J. Mater. Manuf. 2021, 14, 17. [Google Scholar] [CrossRef]
- Raoelison, R.N.; Racine, D.; Zhang, Z.; Buiron, N.; Marceau, D.; Rachik, M. Magnetic pulse welding: Interface of Al/Cu joint and investigation of intermetallic formation effect on the weld features. J. Manuf. Process. 2014, 16, 427–434. [Google Scholar] [CrossRef]
- Raoelison, R.N.; Sapanathan, T.; Buiron, N.; Rachik, M. Magnetic pulse welding of Al/Al and Al/Cu metal pairs: Consequences of the dissimilar combination on the interfacial behavior during the welding process. J. Manuf. Process. 2015, 20, 112–127. [Google Scholar] [CrossRef]
- Ben-Artzy, A.; Stern, A.; Frage, N.; Shribman, V.; Sadot, O. Wave formation mechanism in magnetic pulse welding. Int. J. Impact Eng. 2010, 37, 397–404. [Google Scholar] [CrossRef]
- Gobel, G.; Kaspar, J.; Herrmannsdorfer, T.; Brenner, B.; Beyer, E. Insights into intermetallic phases on pulse welded dissimilar metal joints. In Proceedings of the 4th International Conference on High-Speed Forming, Columbus, OH, USA, 9–10 March 2010; pp. 127–136. [Google Scholar]
- Lueg-Althoff, J.; Lorenz, A.; Gies, S.; Weddeling, C.; Goebel, G.; Tekkaya, A.E.; Beyer, E. Magnetic pulse welding by electromagnetic compression: Determination of the impact velocity. Adv. Mater. Res. 2014, 966, 489–499. [Google Scholar] [CrossRef]
- Desai, S.V.; Kumar, S.; Satyamurthy, P.; Chakravartty, J.K.; Chakravarthy, D.P. Analysis of the effect of collision velocity in electromagnetic welding of aluminum strips. Int. J. Appl. Electromagn. 2010, 34, 131–139. [Google Scholar] [CrossRef]





| Investigators | Material Pair | Work Reported |
|---|---|---|
| Hisashi et al. [8] | Al-Fe | Examined magnetic pressure seam welding through numerical simulations |
| Zhang et al. [9] | Al-Cu | Determination of process parameters through experiments and numerical simulations |
| Kore et al. [10] | Al-SS | Weld formation criteria for plate joint based on numerical simulations and experiments |
| Shim et al. [11] | Al-Cu | Electromagnetic force estimation in dissimilar MPW using finite element method (FEM) |
| Kakizaki et al. [12] | Al-Cu, Al-Ni | Numerical and experimental study on weld interface formation for dissimilar metal lap joints |
| Zhidan et al. [13] | Al-Fe | Calculation of impact rate in the dissimilar tubular joint through numerical simulations and experiments |
| Fan et al. [14] | Al-mild steel | Development of a numerical scheme to better understand the deformation mechanisms |
| Yu and Tong [15] | Al-Steel | Development of a weldability window through experiments |
| Garg et al. [16] | Al-Cu | Experimental and numerical investigation based on genetic programming |
| Psyk et al. [17] | Al-Cu | Analysis of the influence of process parameters on collision parameters and weld quality |
| Li et al. [18] | Al-Cu | Formation mechanisms of wakes, vortices, swirls, and mesoscale cavities at the interface |
| Shotri et al. [19] | Al-SS | Analysis of the electromagnetic field and force, and its effect on the impact and plastic deformation |
| Khalil et al. [20] | Al-Steel | Effect of coil design on the process performance |
| Li et al. [21] | Al-Cu | Mechanism of anomalous wave formation at the interface |
| Shotri et al. [22] | Cu-Steel | Examined the influence of the stand-off distance and target tube wall thickness on the nature of its plastic deformation |
| Li et al. [23] | Al-Cu | Understanding various interface characteristics and underlying mechanisms |
| Zhang et al. [24] | Al-Cu | Investigation of the effects of impact velocity, target tube thickness, and mandrel inclusion on the interface characteristics |
| Zhang et al. [25] | Cu-CP-Ti | Investigation of the interfacial morphology and dependence on parent material properties |
| Khalil et al. [26] | Al-Steel | Identification of physical weldability window |
| Drehmann et al. [27] | Al-Steel | Development of process windows for high-quality welds |
| Shotri et al. [28] | Al-Steel | Unveiling underlying phenomena and identification of suitable process conditions for defect-free weld production |
| Jiang et al. [29] | Al-Steel | Comparison of the mechanical properties and corrosion behavior of Al–Steel electromagnetic self-pieced riveting, adhesive, and hybrid riveted and adhesive joints |
| Chi et al. [30] | Cu-Steel | Revealed the mechanism of wavy interface and vortex formation. |
| Zhang et al. [31] | Al-SS | Optimized design for the uniform pressure welding and maximization of magnetic pressure |
| Chen et al. [32] | Al-Ti | Establishment of Al–Ti welding and exploration of MPW dynamic characteristics |
| Yao et al. [33] | Al-Steel | Study of structural aspects of magnetic pulse spot welding (MPSW) |
| Li et al. [34] | Al-Ti | New multi-seam structural coil design |
| Dang et al. [35] | Al-Steel | Optimized field shaper design |
| Zhou et al. [36] | Al-Cu | Scientific approach for optimal design of MPW equipment and process parameter selection |
| Li et al. [37] | Al-Mg | Multiphysics simulation of the transient forming process in MPW |
| Liu et al. [38] | Al-CFRP | Evaluation of the mechanical properties, interfacial characteristics, joining and failure mechanisms of the CFRP/AA5052 MPW joints |
| Process Parameter | Range |
|---|---|
| Voltage (kV) | 6–25 |
| Coil turns | 3–16 |
| Coil length (mm) | 15–40 |
| Coil cross-section area (mm2) | 9–49 |
| Capacitance | 250–800 |
| Frequency (rad/s) | 30,000–80,000 |
| Air gap (mm) | 0.5–3.5 |
| Attribute | Specifics | Value |
|---|---|---|
| Element size parameters (User-controlled mesh) | Maximum element size (mm) | 2 |
| Minimum element size (mm) | 0.004 | |
| Maximum element growth rate | 1.1 | |
| Curvature factor | 0.2 | |
| Time stepping | Method | Backward differentiation formula (BDF) |
| Steps taken by the solver | Free | |
| Maximum step (µs) | 0.1 | |
| Event tolerance | 0.01 |
| Material | Properties | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Flyer tube (Pure Al) | Element | Fe | Cu | Mn | Si | Mg | Zn | Ti | Al |
| Composition % | 0.40 | 0.05 | 0.05 | 0.25 | 0.05 | 0.07 | 0.05 | 99.5 | |
| Density | 2700 kg/m3 | ||||||||
| Modulus of elasticity | 70 GPa | ||||||||
| Modulus of shear | 26.2 GPa | ||||||||
| Bulk modulus | 76 GPa | ||||||||
| Speed of sound | 5305 m/s | ||||||||
| Poisson’s ratio | 0.33 | ||||||||
| Parameter ‘m’ in Equation (5) | 0.25 | ||||||||
| Parameter ‘P’ in Equation (5) | 6500 | ||||||||
| Target tube (SS304) | Element | C | Mn | Si | P | S | Cr | Ni | N |
| Composition % | 0.08 | 2 | 0.75 | 0.04 | 0.03 | 19.0 | 10.0 | 0.10 | |
| Density | 8033 kg/m3 | ||||||||
| Modulus of elasticity | 0.29 | ||||||||
| Modulus of shear | 142.5 GPa | ||||||||
| Bulk modulus | 193 GPa | ||||||||
| Speed of sound | 77.5 GPa | ||||||||
| Poisson’s ratio | 4211 kg/m3 | ||||||||
| Parameter ‘m’ in Equation (5) | 0.28 | ||||||||
| Parameter ‘P’ in Equation (5) | 996 | ||||||||
| Electromagnetic coil (Copper) | Relative permeability | 1 | |||||||
| Inductance | 10−7 nH | ||||||||
| Resistivity | 3.4 × 10−8 Ohm | ||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kapil, A.; Mastanaiah, P.; Sharma, A. Comprehensive Weldability Criterion for Magnetic Pulse Welding of Dissimilar Materials. Metals 2022, 12, 1791. https://doi.org/10.3390/met12111791
Kapil A, Mastanaiah P, Sharma A. Comprehensive Weldability Criterion for Magnetic Pulse Welding of Dissimilar Materials. Metals. 2022; 12(11):1791. https://doi.org/10.3390/met12111791
Chicago/Turabian StyleKapil, Angshuman, P. Mastanaiah, and Abhay Sharma. 2022. "Comprehensive Weldability Criterion for Magnetic Pulse Welding of Dissimilar Materials" Metals 12, no. 11: 1791. https://doi.org/10.3390/met12111791
APA StyleKapil, A., Mastanaiah, P., & Sharma, A. (2022). Comprehensive Weldability Criterion for Magnetic Pulse Welding of Dissimilar Materials. Metals, 12(11), 1791. https://doi.org/10.3390/met12111791