Determining the Optimal Cutting Parameters for Required Productivity for the Case of Rough External Turning of AISI 1045 Steel with Minimal Energy Consumption
Abstract
:1. Introduction
2. Research Task and Application
The Case Study
- Number of working days = 260 days/year;
- Maintenance operations days = 30 days/year;
- Number of working hours total (2 shifts) = 3680 h/year;
- Number of operating seconds on the machine per year = 6.624 × 106 s/year;
- 30% of time is reserved for external rough turning = 2.208 106 s/year;
- Target material volume removal rate = 1677 mm3/s.
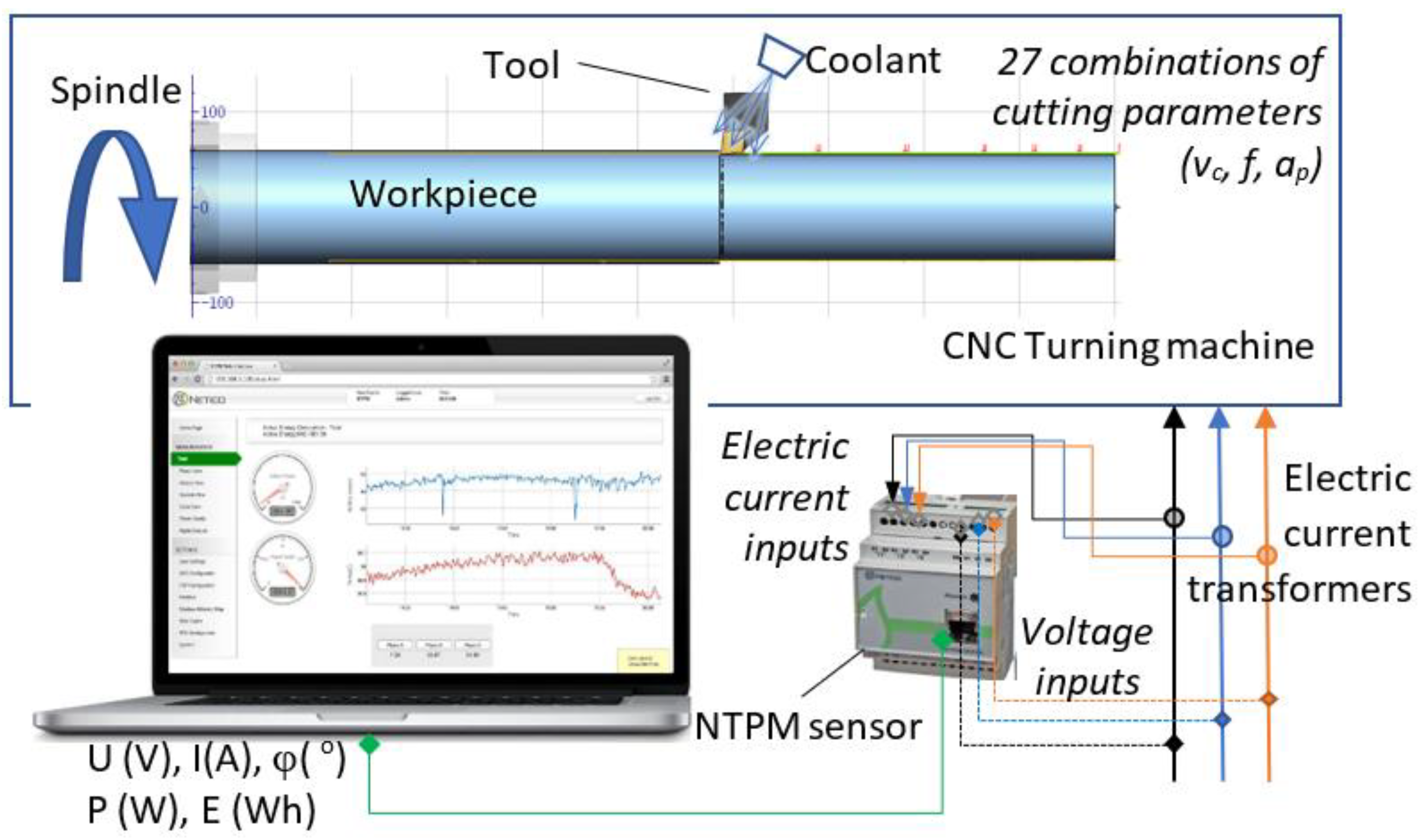
3. Experiment and Measuring Setup
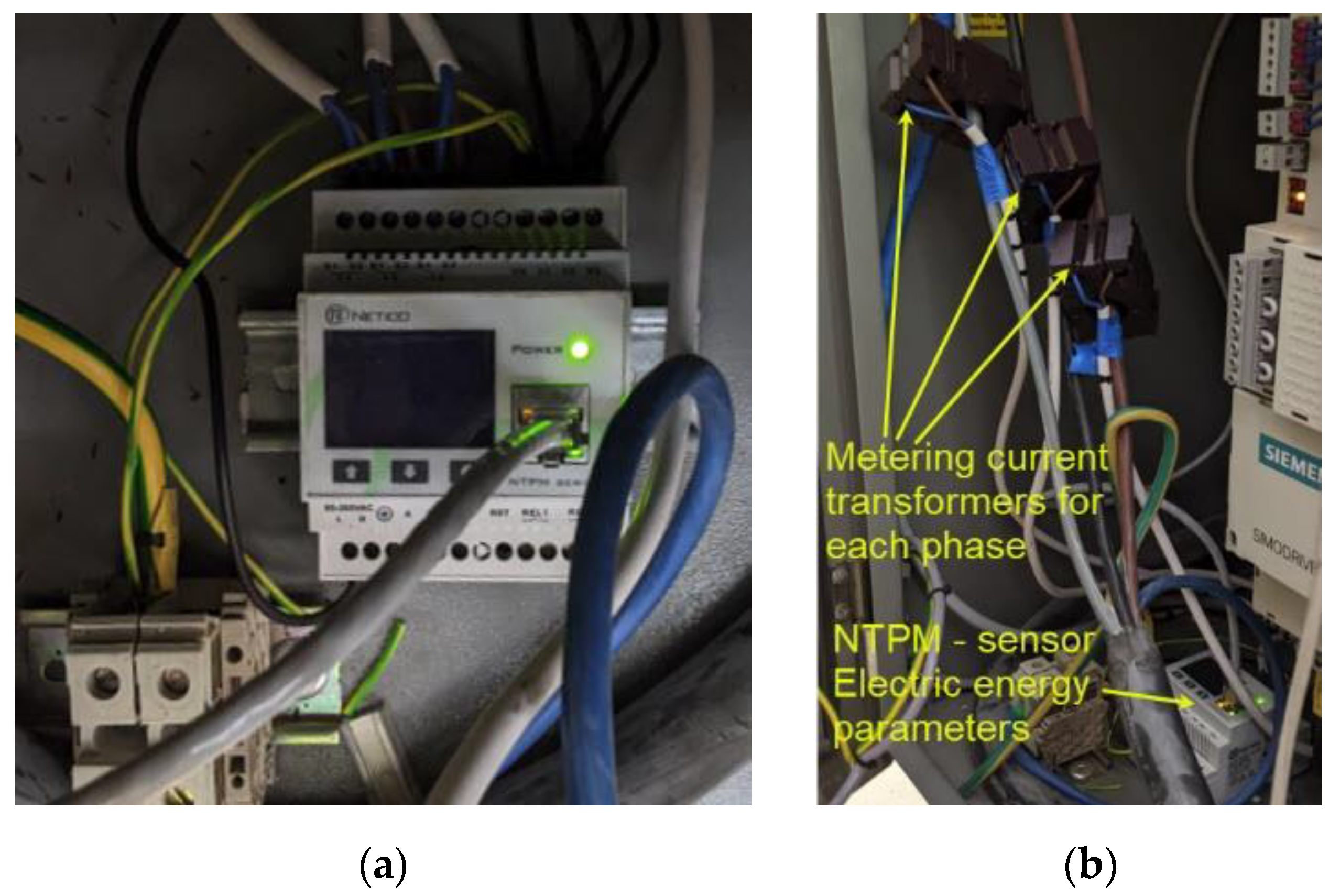
3.1. Materials: Workpiece, Machine, Tool System, Energy and Power Measuring Equipment
- ap = 0.5–4 (mm); ap_recommended = 2 mm;
- f = 0.1–0.5 (mm/rev); f_recommended =0.25 mm/rev;
- vc = 240–360 (m/min); vc_ recommended = 280 m/min.
3.2. Plan of Experiment
- ap = {1, 1.75, 2.5} mm;
- f = {0.1, 0.2, 0.3} mm/rev;
- vc = {240, 270, 300} m/min.
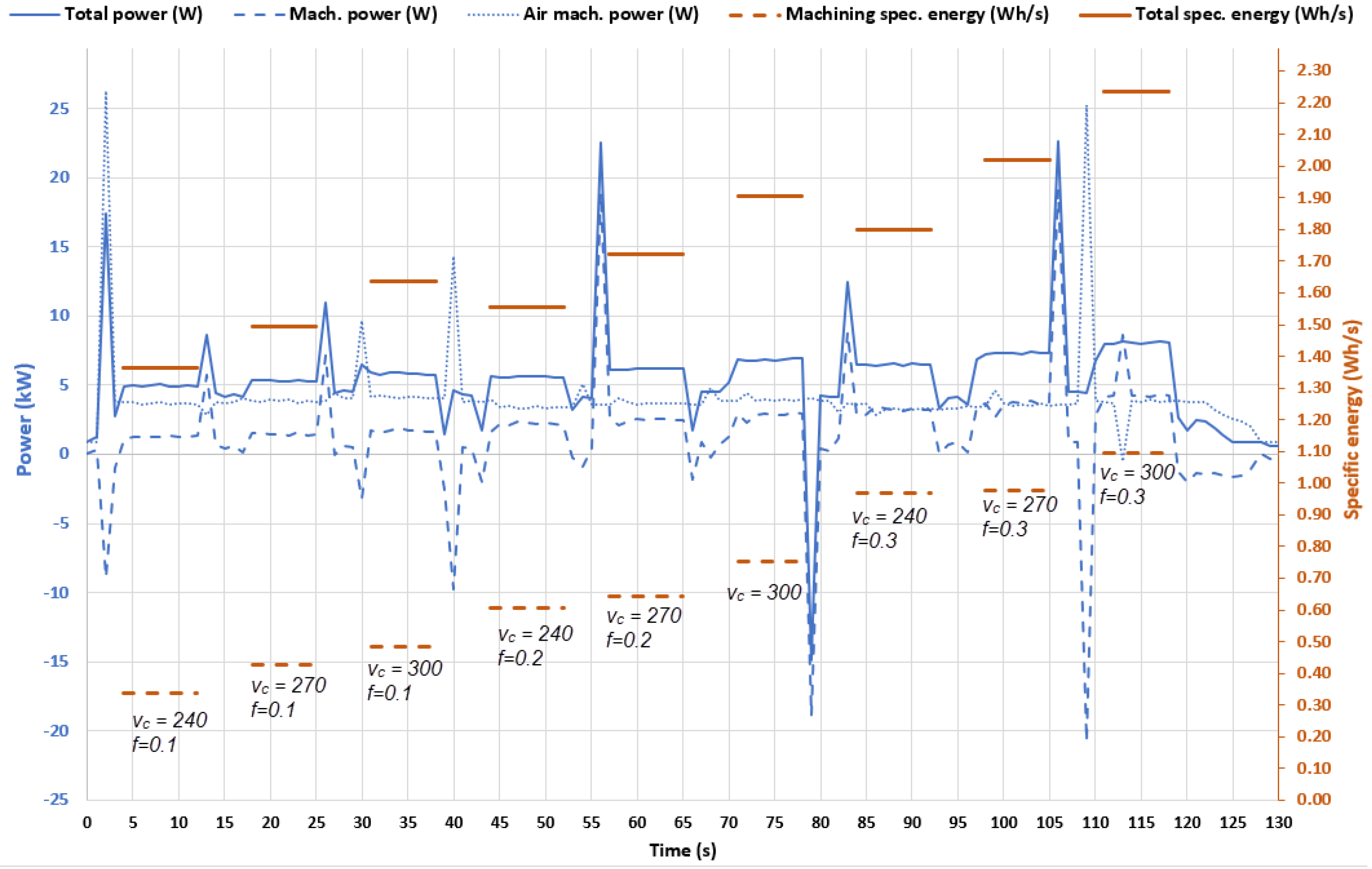
3.3. Measurements
- Idle state—the CNC lathe is turned on, but the workpiece does not rotate, nor is the coolant supplied (Figure 7).
- “Air machining”—the workpiece rotates in accordance with the NC program, the coolant floods the tool and the workpiece, the tool performs programmed movements, but the toolpath is offset 0.5 (mm) from the workpiece outer contour (Figure 8).
- Machining—the workpiece rotates in accordance with the NC program and the turret/tool perform movements in accordance with the NC program, the tool performs programmed movements, the material is removed, the coolant floods the tool, workpiece and cutting zone (Figure 8).
3.4. Energy Consumption Empirical Model
4. Results
Proposed Machining Optimization Model
5. Discussion
6. Conclusions
- The main difference from the majority of previous studies comes from the determination to deal with a specific real-practice case, which concerns a lot of small workshops limited by the existing production facility resources to find the optimal selection of cutting parameter values that are adjusted to their limitations. This kind of optimization is especially important for the machining operations that consume a large amount of energy and engage high power.
- The methods used for both modelling and optimization are not new by themselves, but the presented approach of determining the optimal cutting parameters against the additional constraints seems very usable and efficient in real practice. Thus, the practical relevance of the research is that it can be seen as a kind of template procedure that is developed for determination of optimal selection of cutting parameter values adjusted to the specific limitations originating from the real production conditions. Of course, it is worthwhile conducting the procedure for serial production where numerous repetitions of the critical operation justify it.
- The advantage of the applied procedure is the continuous change of parameters in real time and the direct monitoring of power and energy consumption. In this way, the influence of the parameters, as well as the area of research, can be determined easily. In addition, the advantage is that this method of measurement can indicate in real time whether there has been any significant wear of the tool, which would be reflected in an increase in power for the cutting summary constants;
- The proposed template procedure represents a general approach which can also be applied to other workpiece materials, cutting tool materials and machining processes, operations and features (drilling, chamfering, facing, boring, finish turning, multi-pass turning, etc).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zolfani, S.H.; Bazrafshan, R.; Akaberi, P.; Yazdani, M.; Ecer, F. Combining the suitability-feasibility-acceptability (SPA) strategy with the MCDM approach. Facta Univ. Ser. Mech. Eng. 2021, 19, 579–600. [Google Scholar]
- Stanojković, J.; Radovanović, M. Influence of the cutting parameters on force moment and surface roughness in the end milling of aluminum 6082-T6. Facta Univ. Ser. Mech. Eng. 2022, 20, 157–165. [Google Scholar] [CrossRef]
- Kara, S.; Li, W. Unit process energy consumption models for material removal processes. CIRP Ann. Manuf. Technol. 2011, 60, 37–40. [Google Scholar] [CrossRef]
- Jeswiet, J.; Kara, S. Carbon emissions and CESTM in manufacturing. CIRP Ann. Manuf. Technol. 2008, 57, 17–20. [Google Scholar] [CrossRef]
- Gutowski, T.; Dahmus, J.; Thiriez, A. Electrical energy requirements for manufacturing processes. In Proceedings of the 13th CIRP International Conference of Life Cycle Engineering, Lueven, Belgium, 31 May–2 June 2006. [Google Scholar]
- Duflou, J.R.; Sutherland, J.W.; Dornfeld, D.; Herrmann, C.; Jeswiet, J.; Kara, S.; Hauschild, M.; Kellens, K. Towards energy and resource efficient manufacturing: A processes and systems approach. CIRP Ann. Manuf. Technol. 2012, 61, 587–609. [Google Scholar] [CrossRef] [Green Version]
- Warsi, S.S.; Jaffery, S.H.I.; Ahmad, R.; Khan, M.; Ali, L.; Agha, M.H.; Akram, S. Development of energy consumption map for orthogonal machining of Al 6061-T6 alloy. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2018, 232, 2510–2522. [Google Scholar] [CrossRef]
- Zhou, L.; Li, J.; Li, F.; Meng, Q.; Li, J.; Xu, X. Energy consumption model and energy efficiency of machine tools: A comprehensive literature review. J. Clean. Prod. 2016, 112, 3721–3734. [Google Scholar] [CrossRef]
- Zhao, G.Y.; Liu, Z.Y.; He, Y.; Cao, H.J.; Guo, Y.B. Energy consumption in machining: Classification, prediction, and reduction strategy. Energy 2017, 133, 142–157. [Google Scholar] [CrossRef]
- Camposeco-Negrete, C. Optimization of cutting parameters using Response Surface Method for minimizing energy consumption and maximizing cutting quality in turning of AISI 6061 T6 aluminum. J. Clean. Prod. 2015, 91, 109–117. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, S.; Sidhu, A.S.; Pruncu, C.I. Bibliometric analysis of Specific Energy Consumption (SEC) in machining operations: A sustainable response. Sustainability 2021, 13, 5617. [Google Scholar] [CrossRef]
- Li, L.; Li, C.; Tang, Y.; Yi, Q. Influence factors and operational strategies for energy efficiency improvement of CNC machining. J. Clean. Prod. 2017, 161, 220–238. [Google Scholar] [CrossRef]
- Balogun, V.A.; Mativenga, P.T. Modelling of direct energy requirements in mechanical machining processes. J. Clean. Prod. 2013, 41, 179–186. [Google Scholar] [CrossRef]
- Mori, M.; Fujishima, M.; Inamasu, Y.; Oda, Y. A study on energy efficiency improvement for machine tools. CIRP Ann. Manuf. Technol. 2011, 60, 145–148. [Google Scholar] [CrossRef]
- Diaz, N.; Redelsheimer, E.; Dornfeld, D. Energy consumption characterization and reduction strategies for milling machine tool use. In Proceedings of the Glocalized Solutions for Sustainability in Manufacturing: Proceedings of the 18th CIRP International Conference on Life Cycle Engineering, Braunschweig, Germany, 2–4 May 2011; pp. 263–267. [Google Scholar]
- He, Y.; Liu, F.; Wu, T.; Zhong, F.P.; Peng, B. Analysis and estimation of energy consumption for numerical control machining. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2012, 226, 255–266. [Google Scholar] [CrossRef]
- Xie, J.; Liu, F.; Qiu, H. An integrated model for predicting the specific energy consumption of manufacturing processes. Int. J. Adv. Manuf. Technol. 2016, 85, 1339–1346. [Google Scholar] [CrossRef]
- Zhao, G.; Zhao, Y.; Meng, F.; Guo, Q.; Zheng, G. Prediction model of machine tool energy consumption in hard-to-process materials turning. Int. J. Adv. Manuf. Technol. 2020, 106, 4499–4508. [Google Scholar] [CrossRef]
- Jozić, S.; Dumanić, I.; Bajić, D. Experimental analysis and optimization of the contorllable parameters in turning of en AW-2011 alloy: Dry machining and alternative cooling techniques. Facta Univ. Ser. Mech. Eng. 2020, 18, 13–29. [Google Scholar]
- Rajemi, M.F.; Mativenga, P.T.; Aramcharoen, A. Sustainable machining: Selection of optimum turning conditions based on minimum energy considerations. J. Clean. Prod. 2010, 18, 1059–1065. [Google Scholar] [CrossRef]
- Guo, Y.; Loenders, J.; Duflou, J.; Lauwers, B. Optimization of energy consumption and surface quality in finish turning. Procedia CIRP 2012, 1, 512–517. [Google Scholar] [CrossRef]
- Lu, C.; Gao, L.; Li, X.; Chen, P. Energy-efficient multi-pass turning operation using multi-objective backtracking search algorithm. J. Clean. Prod. 2016, 137, 1516–1531. [Google Scholar] [CrossRef] [Green Version]
- Bagaber, S.A.; Yusoff, A.R. Multi-objective optimization of cutting parameters to minimize power consumption in dry turning of stainless steel 316. J. Clean. Prod. 2017, 157, 30–46. [Google Scholar] [CrossRef] [Green Version]
- Su, Y.; Zhao, G.; Zhao, Y.; Meng, J.; Li, C. Multi-Objective optimization of cutting parameters in turning AISI 304 austenitic stainless steel. Metals 2020, 10, 217. [Google Scholar] [CrossRef]
- Zhu, Z.; Buck, D.; Guo, X.; Xiong, X.; Xu, W.; Cao, P. Energy efficiency optimization for machining of wood plastic composite. Machines 2022, 10, 104. [Google Scholar] [CrossRef]
- Salur, E.; Kuntoglu, M.; Asian, A.; Pimenov, D.Y. The effects of MQL and dry environment on tool wear, cutting temperature, and power consumption during end milling of AISI 1040 steel. Metals 2021, 11, 1674. [Google Scholar] [CrossRef]
- Kant, G.; Sangwan, K.S. Prediction and optimization of machining parameters for minimizing power consumption and surface roughness in machining. J. Clean. Prod. 2014, 83, 151–164. [Google Scholar] [CrossRef]
- Sangwan, K.S.; Kant, G. Optimization of machining parameters for improving energy efficiency using Integrated Response Surface Methodology and Genetic Algorithm Approach. Procedia CIRP 2017, 61, 517–522. [Google Scholar] [CrossRef]
- Sidhu, A.S.; Singh, S.; Kumar, R.; Pimenov, D.Y.; Giasin, K. Prioritizing Energy-Intensive Machining Operations and Gauging the Influence of Electric Parameters: An Industrial Case Study. Energies 2021, 14, 4761. [Google Scholar] [CrossRef]
- Zębala, W.; Struzikiewicz, G.; Słodki, B. Reduction of Power Consumption by Chip Breakability Control in Ti6Al4V Titanium Alloy Turning. Materials 2020, 13, 2642. [Google Scholar] [CrossRef]
- Kuntoglu, M.; Saglam, H. Investigation of progressive tool wear for determining of optimized machining parameters in turning. Measurement 2019, 140, 427–436. [Google Scholar] [CrossRef]
- Usca, U.A.; Sap, S.; Uzun, M.; Kuntoglu, M.; Salur, E.; Karabiber, A.; Pimenov, D.Y.; Giasin, K.; Wojciechowski, S. Estimation, optimization and analysis based investigation of the energy consumption in machinability of ceramic-based metal matrix composite materials. J. Mater. Res. Technol. 2022, 17, 2987–2998. [Google Scholar] [CrossRef]
- Qasim, A.; Nisar, S.; Shah, A.; Khalid, M.S.; Sheikh, M.A. Optimization of process parameters for machining of AISI-1045 steel using Taguchi design and ANOVA. Simul. Model. Pract. Theory 2015, 59, 36–51. [Google Scholar] [CrossRef]
- Oda, Y.; Fujishima, M.; Takeuchi, Y. Energy-saving machining of multi-functional machine tools. Int. J. Autom. Technol. 2015, 9, 135–142. [Google Scholar] [CrossRef]
- Nur, R.; Yusof, N.M.; Sudin, I.; Nor, F.M.; Kurniawan, D. Determination of energy consumption during turning of hardened stainless steel using resultant cutting force. Metals 2021, 11, 565. [Google Scholar] [CrossRef]
- Jozić, S.; Bajić, D.; Dumanić, I.; Bagavac, Ž. Optimization for an efficient and highly productive turning process. Rep. Mech. Eng. 2021, 2, 212–221. [Google Scholar] [CrossRef]
- Liu, X.W. Global convergence on an active set SQP for inequality constrained optimization. J. Comput. Appl. Math. 2005, 180, 201–211. [Google Scholar] [CrossRef]
- Belegundu, A.D.; Chandrupatla, T.R. Optimization Concepts and Applications in Engineering, 3rd ed.; Cambrige University Press: Cambrige, UK, 2019. [Google Scholar]
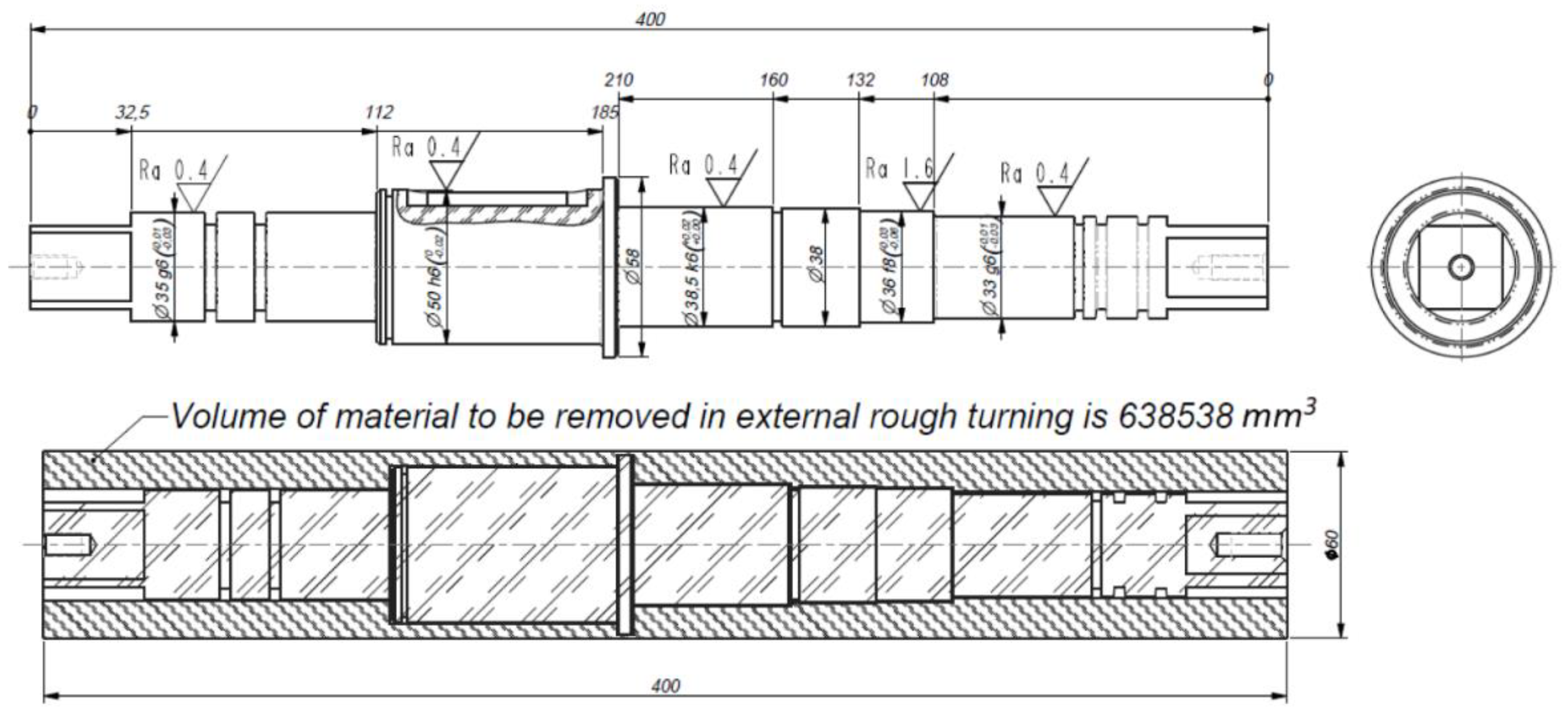






| Ref | Authors (Year) | Material (Machining Process) | Input Parameters 1 | Output Parameters | Optimization Methodology |
|---|---|---|---|---|---|
| [20] | Rajemi et al. (2010) | ASI 1040 steel (turning, dry conditions) | vc (300, 400, 500 m/min), f (0.15 mm/rev), ap (1 mm) | Energy consumption, tool wear | - |
| [21] | Guo et al. (2012) | 11SMnPb30 steel, AlCuMgPb aluminum (finish turning, dry conditions) | vc (60~800 m/min), f (0.05~0.3 mm/rev), ap (0.5~2 mm) | Energy consumption (total specific energy), surface roughness | - |
| [10] | Camposeco-Negrete (2015) | AISI 606 T6 aluminum (rough turning, wet conditions) | vc (266–434 m/min), f (0.12–0.28 mm/rev), ap (0.66–2.34 mm) | Specific energy consumption (SEC), surface roughnessMRR | Central composite design (for experiment setup), RSM |
| [22] | Lu et al. (2016) | C45 carbon steel forging bar (rough and finish multi-pass turning, wet conditions) | vc (50–500 m/min), f (0.1–0.9 mm/rev), ap (1–3 mm), number of roughing passes (1–7), tool life, etc. | Energy consumption, machining precision | MOBSA |
| [23] | Bagaber and Yusoff (2017) | AISI 316 stainless steel (turning, dry conditions) | vc (89.5–190.4 m/min), f (0.066–0.23 mm/rev), ap (0.6–1.6 mm) | Energy consumption, surface roughness, tool wear | RSM |
| [7] | Warsi et al. (2018) | Al 6061-T6 alloy (orthogonal pipe machining, dry conditions) | vc (250, 500, 750, 1000 m/min), f (0.1, 0.2, 0.3, 0.4 mm/rev) | Specific energy consumption, chip formation | - |
| [24] | Su et al. (2020) | AISI 304 austenitic stainless steel, (turning, wet conditions) | vc (50–80 m/min), f (0.15–0.35 mm/rev), ap (0.2–2.2 mm) | Specific energy consumption, surface roughnessMRR | Taguchi method, GRA, RSM |
| [31] | Kuntoglu and Saglam (2019) | AISI 1050, (turning, dry conditions) | vc (135, 194, 207 m/min), f (0.171, 0.214. 0.256 mm/rev), tool tip | Cutting tool, tangential cutting force, acoustic emission | Taguchi method, ANOVA |
| [32] | Usca et al. (2022) | Cu/B-CrC composites (milling) | vc (125, 175 m/min), f (0.2, 0.4 mm/rev), reinforcement ratio (0, 5, 10, 15%) | Energy consumption | Taguchi method, fuzzy inference system |
| Abbreviation | Meaning | Unit |
|---|---|---|
| ap | Depth of cut | mm |
| f | Feed rate | mm/rev |
| vc | Cutting speed | m/min |
| MRR | Material (volume) removal rate | cm3/s, mm3/s |
| TEC | Total active electric energy consumption | Wh |
| SEC | Specific energy consumption | Wh/mm3 |
| STEC | Specific total energy consumption in time (or Time-specific total energy consumption) | Wh/s |
| TEP | Total active engaged power | W |
| Ets | Total energy consumption for the particular shaft | kWh |
| Workpiece Number | Initial Measurement | Additional Measurements | |
|---|---|---|---|
| From D0 to D1, ap | From D0′ to D1′, ap | From D0″ to D1″, ap | |
| 1st workpiece | 58 to 56, ap = 1 mm | 56 to 52.6 ap = 1.7 mm | 52.6 to 47.6 ap = 2.5 mm |
| 2nd workpiece | 58 to 54.6, ap = 1.7 mm | 54.6 to 52.6, ap = 1 mm | 52.6 to 47.6, ap = 2.5 mm |
| 3rd workpiece | 58 to 53, ap = 2.5 mm | 53 to 51, ap = 1 mm | 51 to 47.6, ap = 1.7 mm |
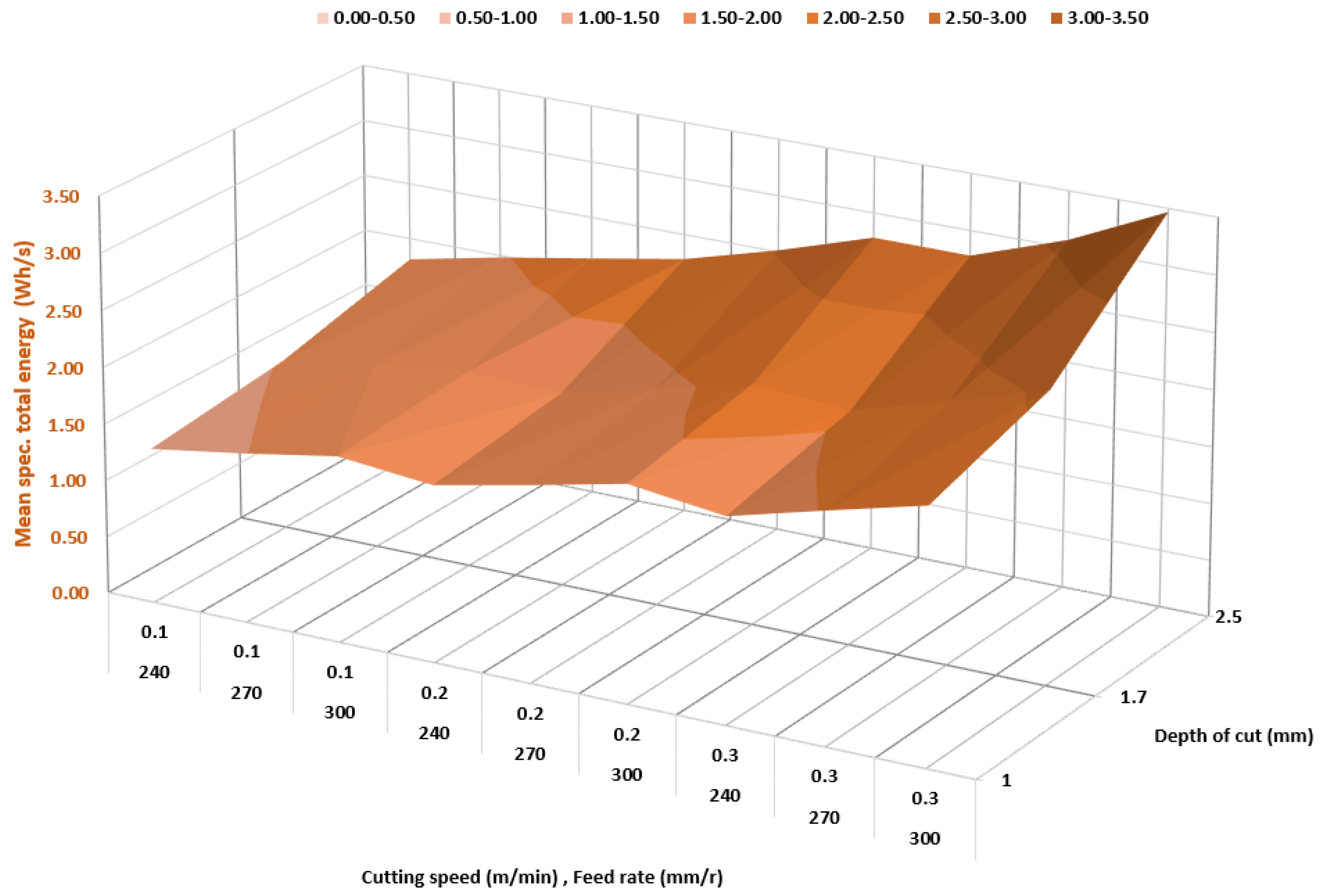
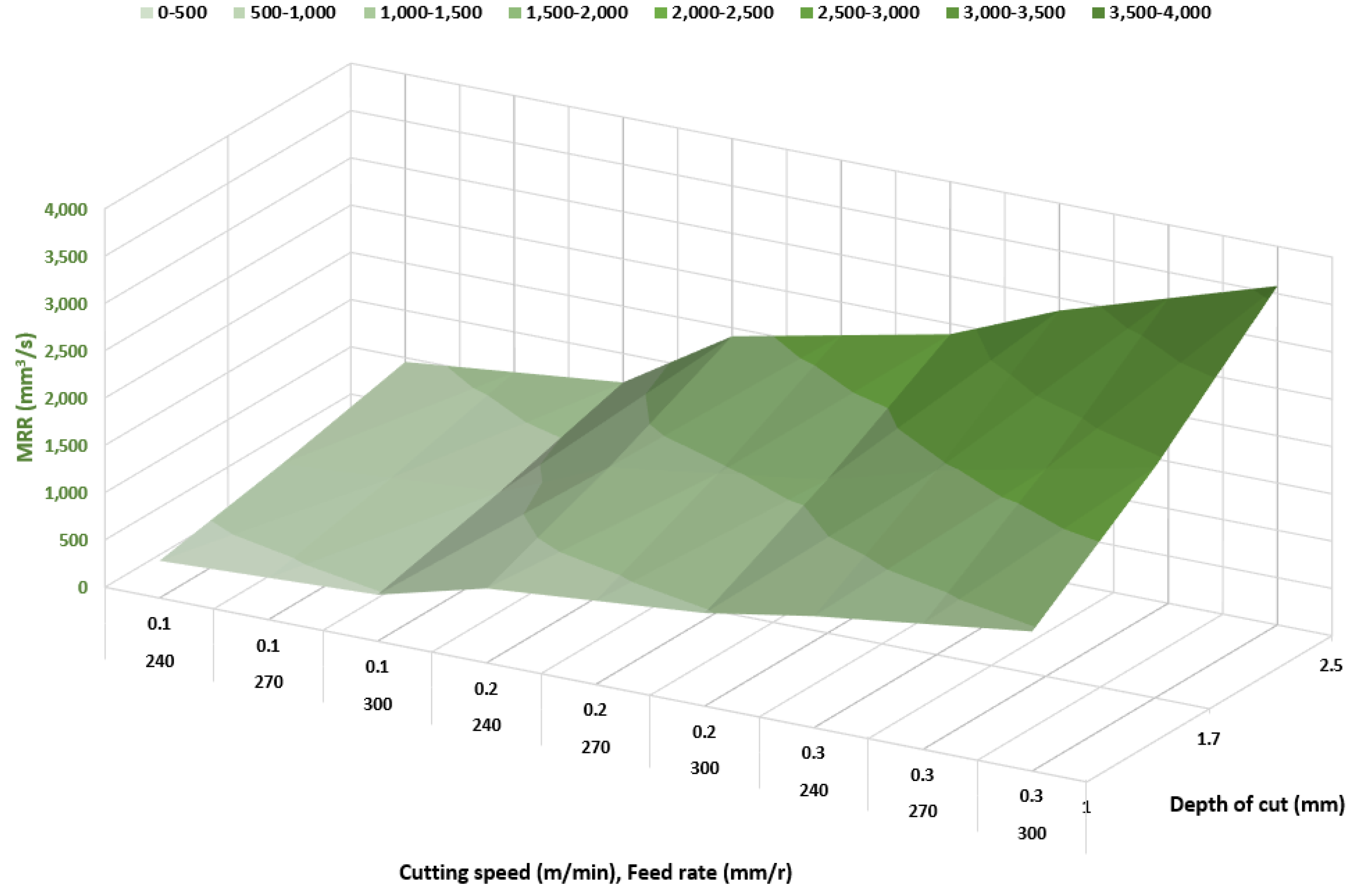
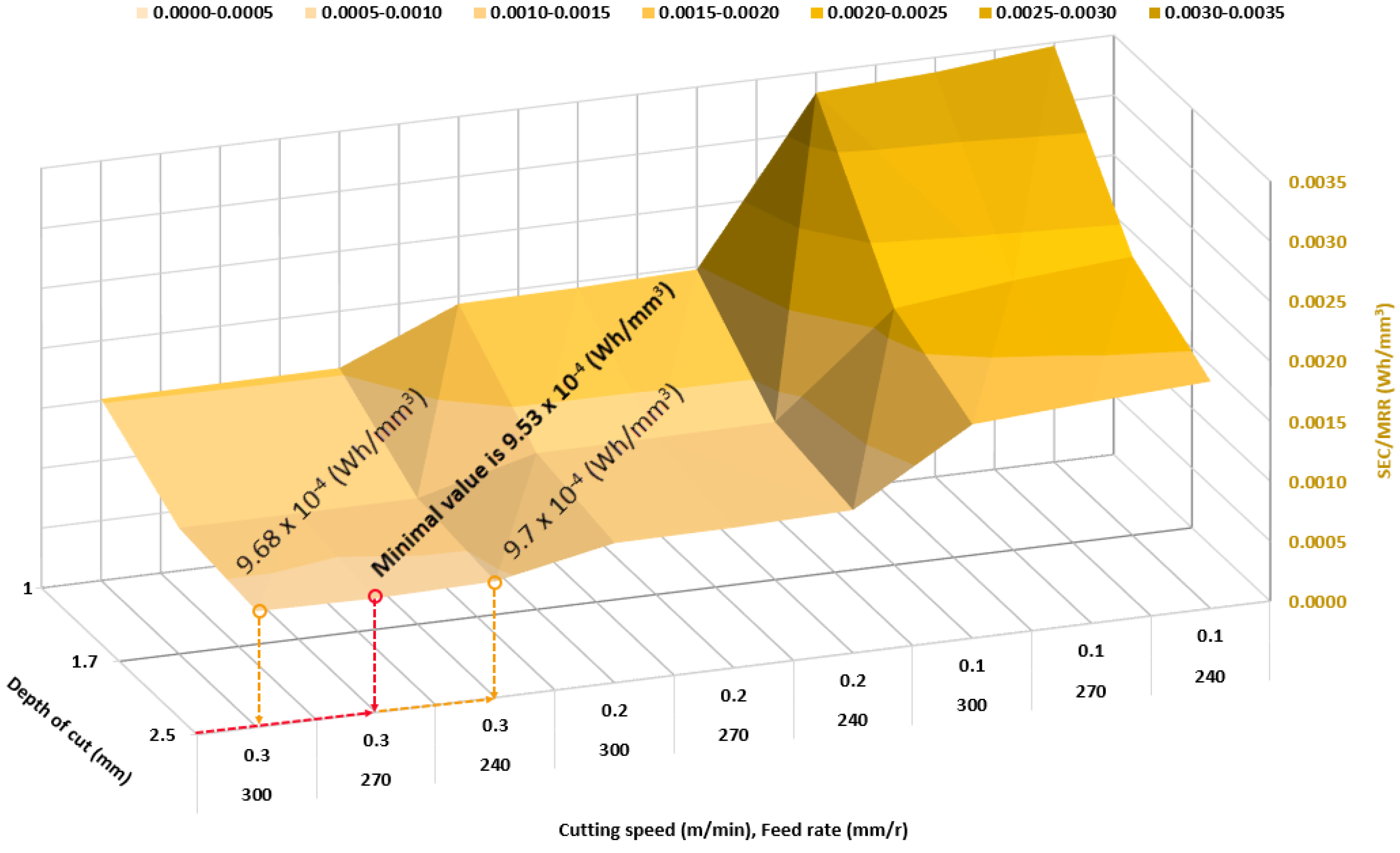
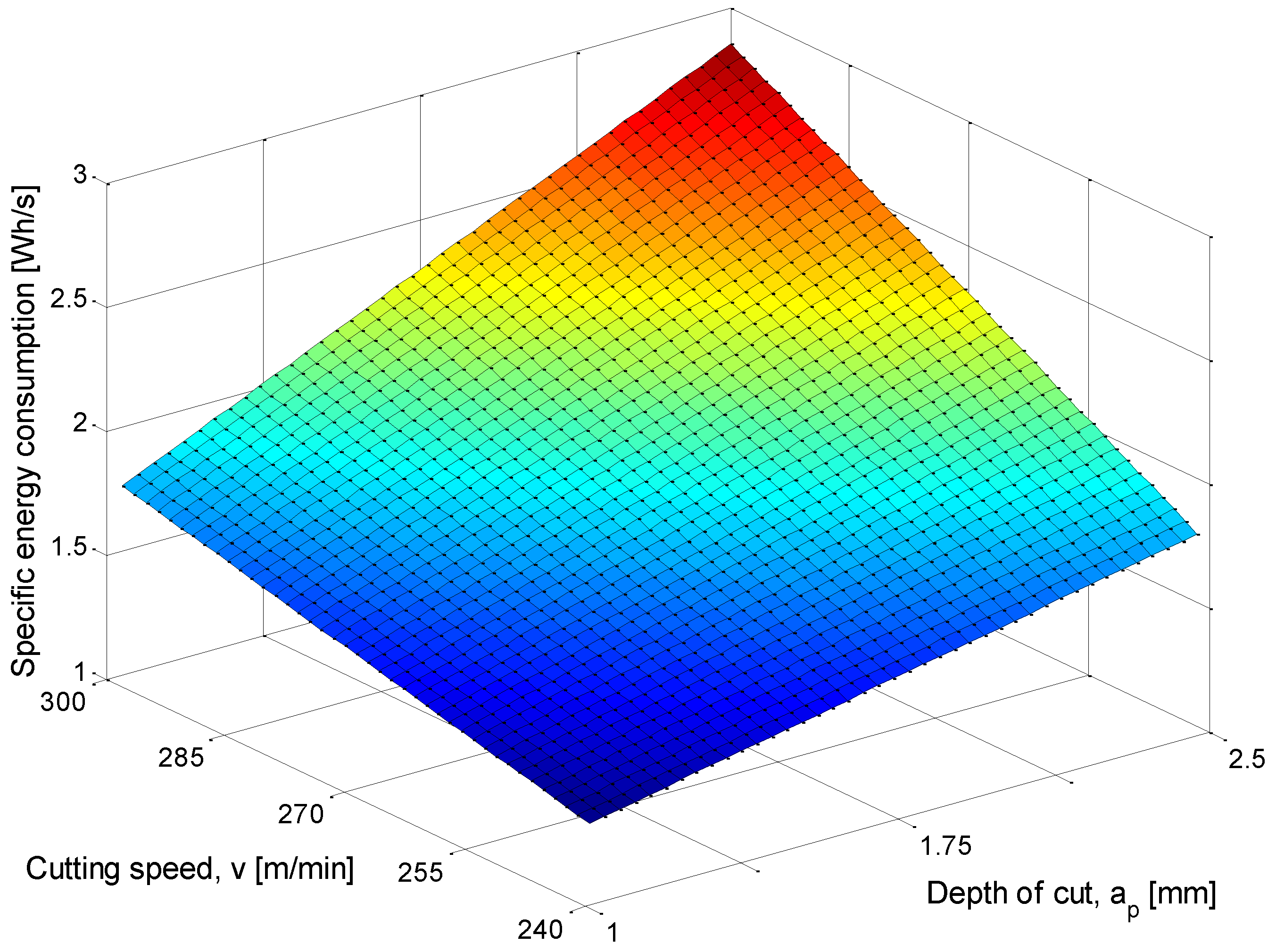
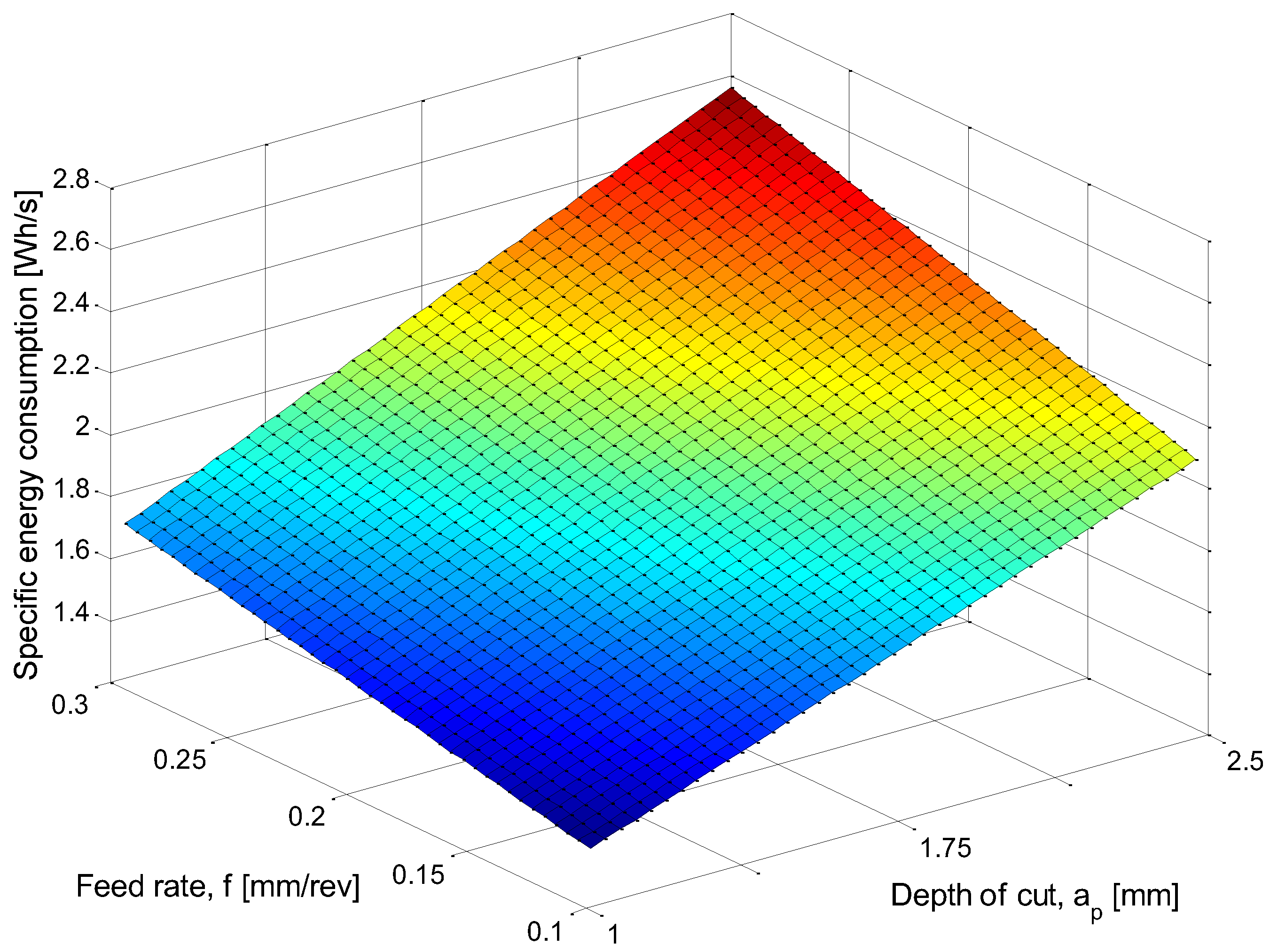
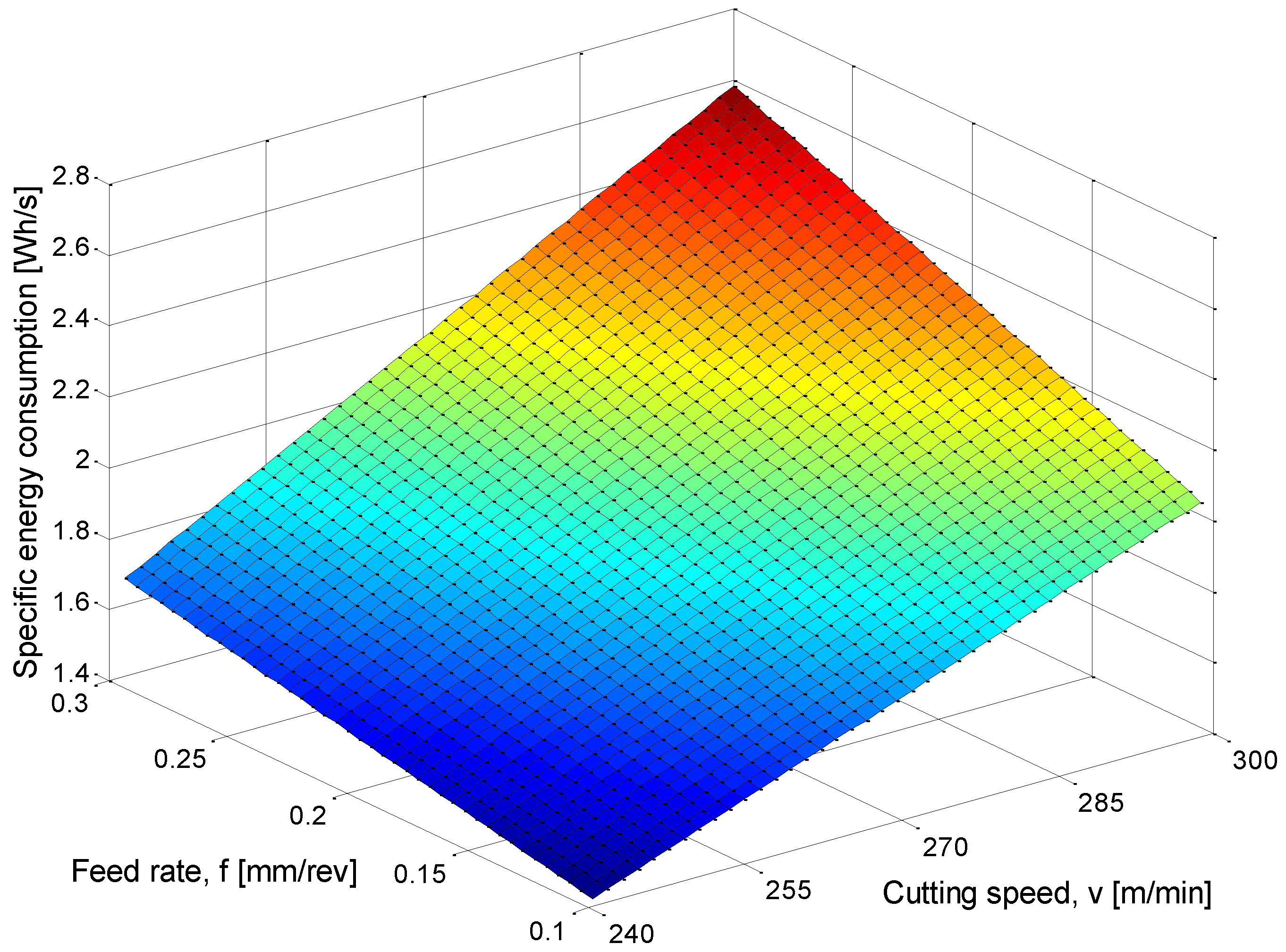
| ap (mm) | f (mm/rev) | vc (m/min) | MRR (mm3/s) | TEP (W) | STEC (Wh/s) | SEC (Wh/mm3) |
|---|---|---|---|---|---|---|
| 1 | 0.1 | 240 | 393.10 | 4935.06 | 1.37 | 3.474 × 10−3 |
| 1 | 0.1 | 270 | 442.24 | 5322.91 | 1.49 | 3.376 × 10−3 |
| 1 | 0.1 | 300 | 491.38 | 5835.52 | 1.64 | 3.329 × 10−3 |
| 1 | 0.2 | 240 | 786.21 | 5608.11 | 1.55 | 1.977 × 10−3 |
| 1 | 0.2 | 270 | 884.48 | 6175.24 | 1.72 | 1.949 × 10−3 |
| 1 | 0.2 | 300 | 982.76 | 6837.59 | 1.91 | 1.939 × 10−3 |
| 1 | 0.3 | 240 | 1179.31 | 6492.26 | 1.80 | 1.526 × 10−3 |
| 1 | 0.3 | 270 | 1326.72 | 7299.55 | 2.02 | 1.523 × 10−3 |
| 1 | 0.3 | 300 | 1474.14 | 8051.62 | 2.23 | 1.515 × 10−3 |
| 1.7 | 0.1 | 240 | 649.97 | 5512.27 | 1.51 | 2.326 × 10−3 |
| 1.7 | 0.1 | 270 | 731.22 | 5900.72 | 1.64 | 2.249 × 10−3 |
| 1.7 | 0.1 | 300 | 812.47 | 6264.62 | 1.74 | 2.140 × 10−3 |
| 1.7 | 0.2 | 240 | 1299.95 | 6199.09 | 1.71 | 1.316 × 10−3 |
| 1.7 | 0.2 | 270 | 1462.44 | 6867.04 | 1.91 | 1.309 × 10−3 |
| 1.7 | 0.2 | 300 | 1624.93 | 7592.23 | 2.12 | 1.305 × 10−3 |
| 1.7 | 0.3 | 240 | 1949.92 | 7428.40 | 2.05 | 1.052 × 10−3 |
| 1.7 | 0.3 | 270 | 2193.66 | 8340.29 | 2.30 | 1.050 × 10−3 |
| 1.7 | 0.3 | 300 | 2437.40 | 9136.01 | 2.56 | 1.051 × 10−3 |
| 2.5 | 0.1 | 240 | 955.36 | 6533.28 | 1.81 | 1.895 × 10−3 |
| 2.5 | 0.1 | 270 | 1074.78 | 7166.88 | 1.98 | 1.845 × 10−3 |
| 2.5 | 0.1 | 300 | 1194.20 | 7772.73 | 2.13 | 1.784 × 10−3 |
| 2.5 | 0.2 | 240 | 1910.71 | 8184.40 | 2.28 | 1.194 × 10−3 |
| 2.5 | 0.2 | 270 | 2149.55 | 9082.34 | 2.52 | 1.170 × 10−3 |
| 2.5 | 0.2 | 300 | 2388.39 | 10,018.38 | 2.78 | 1.165 × 10−3 |
| 2.5 | 0.3 | 240 | 2866.07 | 9995.08 | 2.78 | 9.699 × 10−4 |
| 2.5 | 0.3 | 270 | 3224.33 | 11,216.10 | 3.07 | 9.528 × 10−4 |
| 2.5 | 0.3 | 300 | 3582.59 | 12,432.05 | 3.47 | 9.681 × 10−4 |
| Average Roughness | f = 0.1 (mm/rev) | f = 0.2 (mm/rev) | f = 0.3 (mm/rev) |
|---|---|---|---|
| Ra min | 0.945 (μm) | 1.238 (μm) | 2.332 (μm) |
| Ra max | 0.986 (μm) | 1.522 (μm) | 2.789 (μm) |
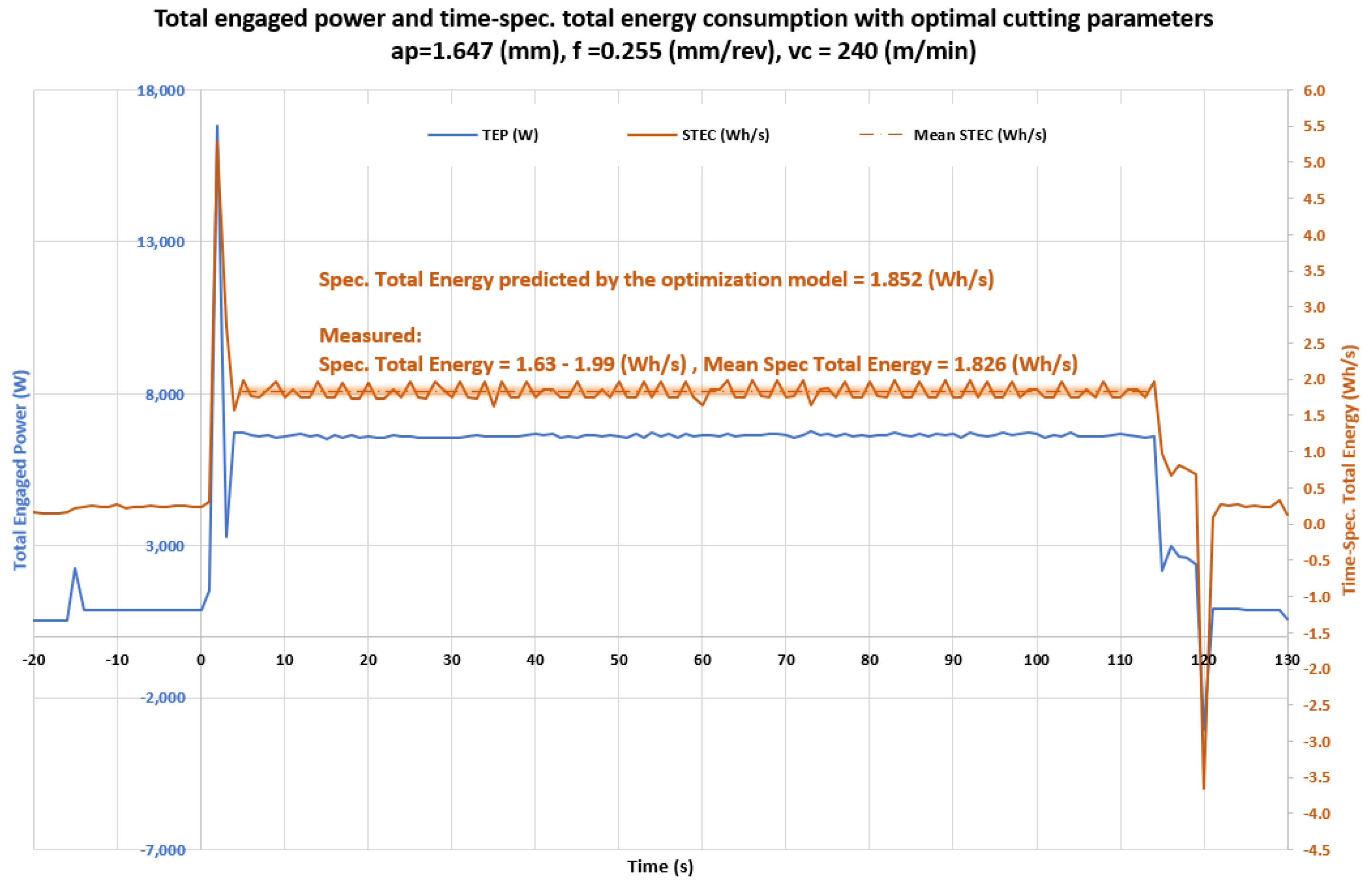
| Cutting Parameters | ap (mm) | vc (m/min) | f (mm/rev) | MRR (mm3/s) | Time 1 (s) | STEC (Wh/s) | Ets (kWh) |
|---|---|---|---|---|---|---|---|
| Determined optimization solution for minimum STEC and target MRR | 1.647 | 240 | 0.255 | 1677 | 2.208 × 106 | 1.852 | 4089 |
| Recommended cutting regime | 2 | 280 | 0.25 | 2333 | 1.587 × 106 | 2.389 | 3792 |
| According to minimum measured value of SEC (Wh/mm3) (Table 2 and Figure 10) | 2.5 | 270 | 0.3 | 3224 | 1.1486 × 106 | 3.072 | 3528 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stojković, M.; Madić, M.; Trifunović, M.; Turudija, R. Determining the Optimal Cutting Parameters for Required Productivity for the Case of Rough External Turning of AISI 1045 Steel with Minimal Energy Consumption. Metals 2022, 12, 1793. https://doi.org/10.3390/met12111793
Stojković M, Madić M, Trifunović M, Turudija R. Determining the Optimal Cutting Parameters for Required Productivity for the Case of Rough External Turning of AISI 1045 Steel with Minimal Energy Consumption. Metals. 2022; 12(11):1793. https://doi.org/10.3390/met12111793
Chicago/Turabian StyleStojković, Miloš, Miloš Madić, Milan Trifunović, and Rajko Turudija. 2022. "Determining the Optimal Cutting Parameters for Required Productivity for the Case of Rough External Turning of AISI 1045 Steel with Minimal Energy Consumption" Metals 12, no. 11: 1793. https://doi.org/10.3390/met12111793
APA StyleStojković, M., Madić, M., Trifunović, M., & Turudija, R. (2022). Determining the Optimal Cutting Parameters for Required Productivity for the Case of Rough External Turning of AISI 1045 Steel with Minimal Energy Consumption. Metals, 12(11), 1793. https://doi.org/10.3390/met12111793







