A Comparative Study on the Mathematic Models for the Ignition of Titanium Alloy in Oxygen-Enriched Environment
Abstract
:1. Introduction
2. Mathematic Model
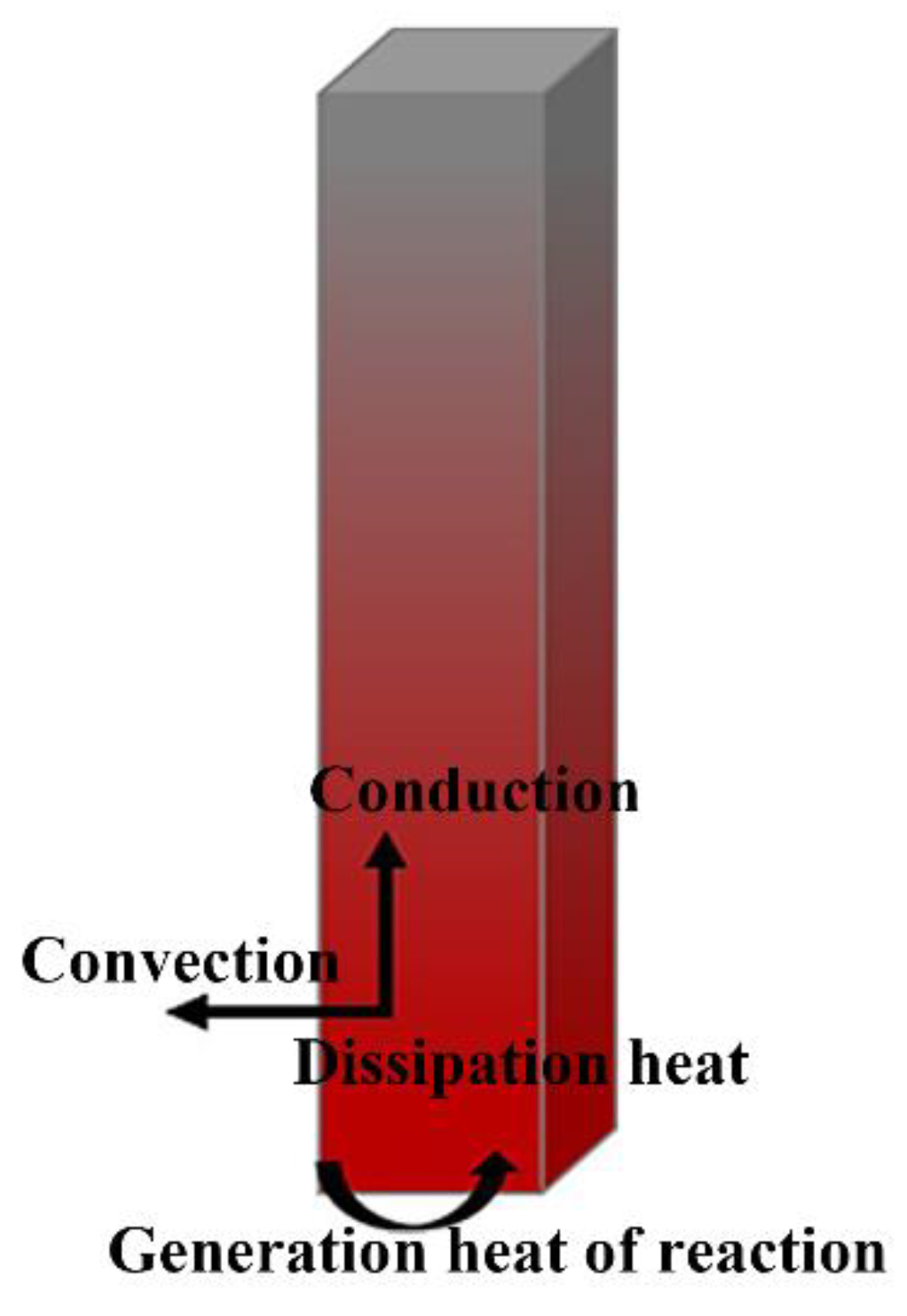
2.1. Heat Transfer Model
- The ignition ignores the internal thermal resistance of the reaction zone.
- Constant thermophysical properties for the TC17 alloy are used.
- Phase transformation of titanium alloys is neglected.
2.2. Ignition Criterion
2.2.1. The Ignition Criterion of Semenov Model
- (a)
- Chemical absorption model
- (b)
- Oxide film thickening model
2.2.2. The Ignition Criterion of Frank-Kamenetskii Model
3. Experimental
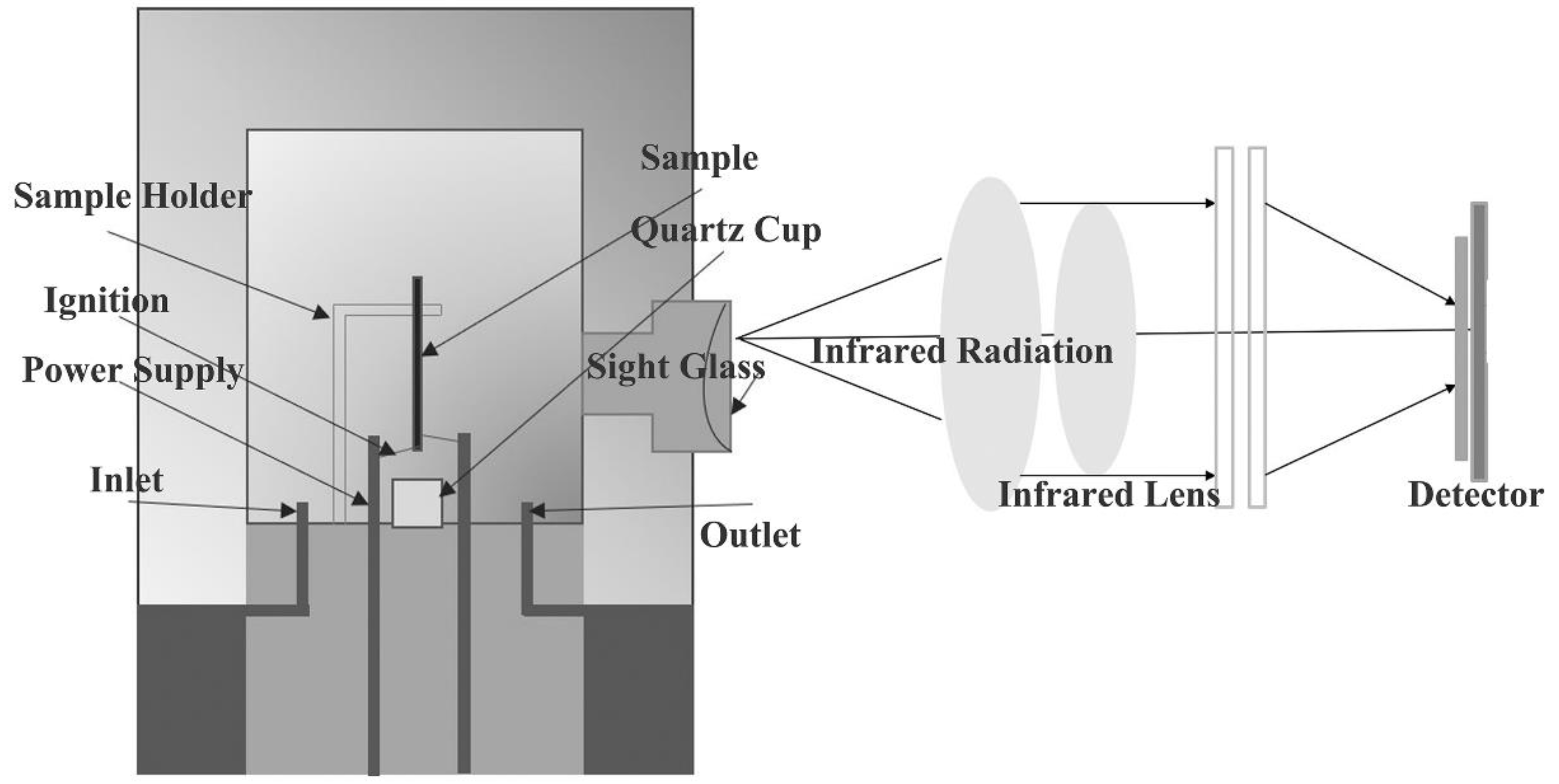
3.1. Materials
3.2. Experimental Methods
4. Result and Discussion
4.1. Effect of Size on Critical Oxygen Pressure
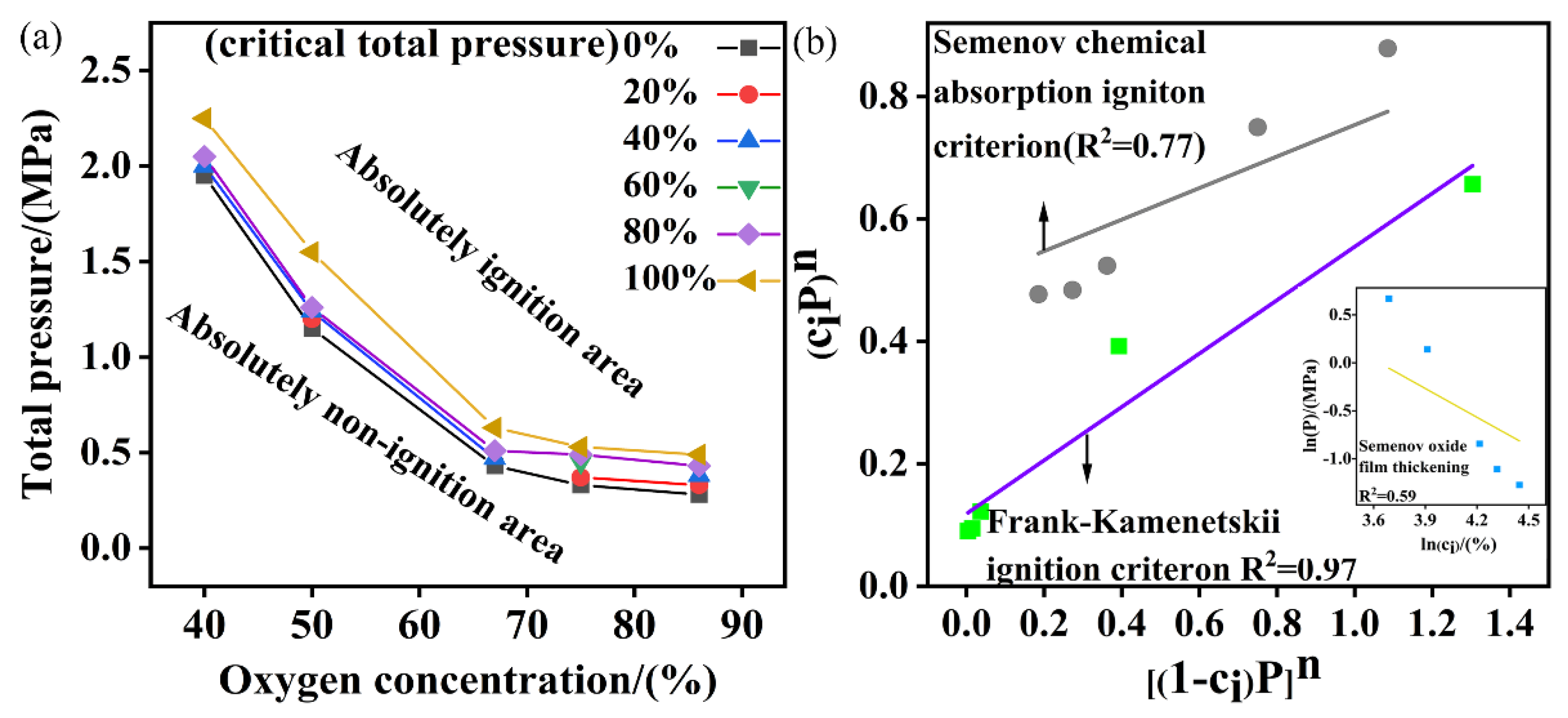
4.2. Effect of Oxygen Concentration on Critical Pressure
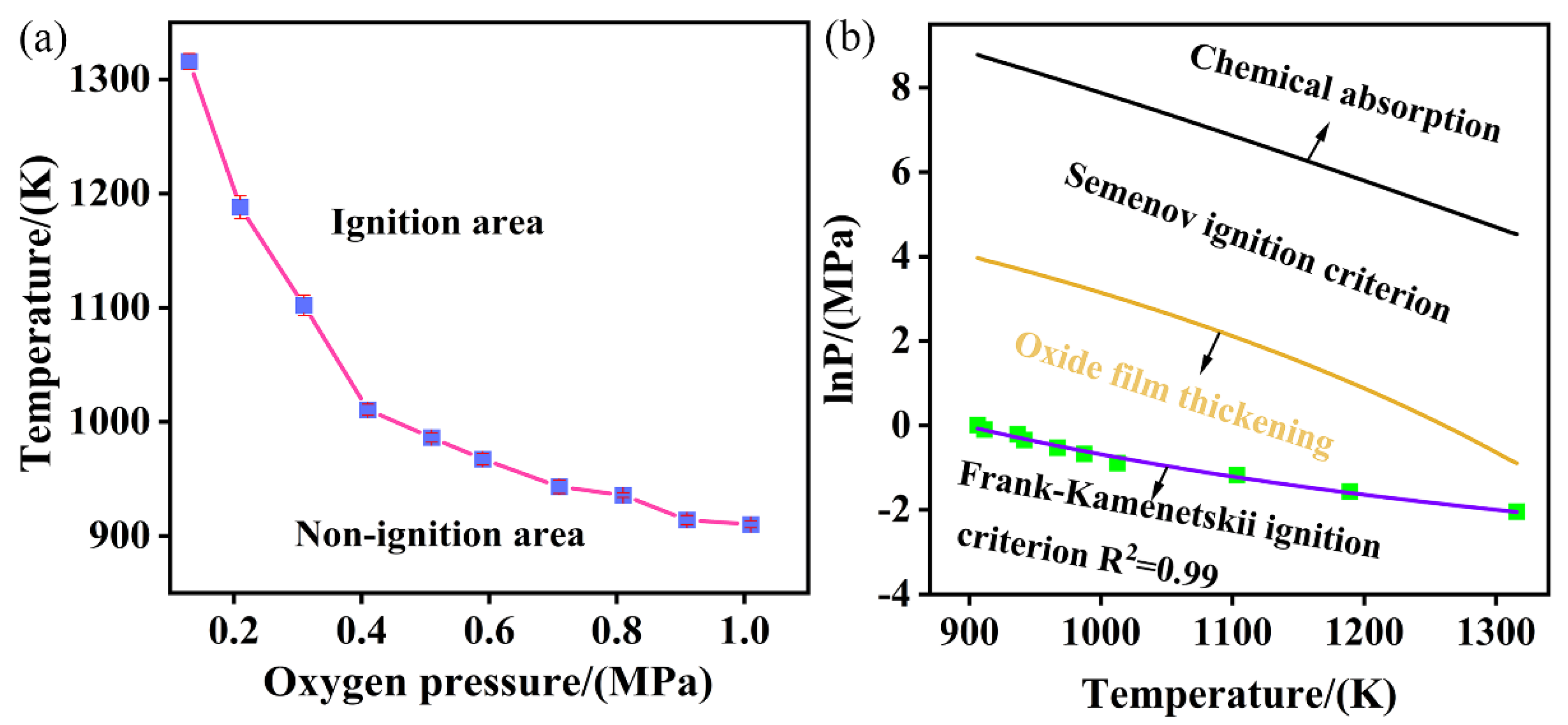
4.3. Effect of Oxygen Pressure on Ignition Temperature
4.4. The Prediction of Ignition Temperature
5. Conclusions
- The critical oxygen pressure of TC17 alloy increased with the increase of size, which can be described well by the Frank-Kamenetskii model. The critical oxygen pressure is size independent in the Semenov model (including oxide film thickening), which is inconsistent with the experimental data.
- The reaction order, absorption coefficient and activation energy of TC17 alloy in the ignition criterion of Frank-Kamenetskii model is determined to be 1.69, 4.01 MPa−1.69, and 99.23 kJ·mol−1 respectively by fitting the criterion model with the relationship between the critical oxygen pressure and size, the critical pressure and oxygen concentration, and the ignition temperature and oxygen pressure.
- The ignition temperatures of the TC17 alloy with different size are predicted by the ignition criterion of Frank-Kamenetskii model with the relative error within 3.85%, indicating that the Frank-Kamenetskii model can be suitable for describing the critical ignition conditions of bulk metallic rather than the Semenov model.
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Nomenclature | |||
| internal energy, J | atmosphere pressure, MPa | ||
| rate of enrgy generation, J·K−1 | thickness of the oxide film, m | ||
| rate of energy loss, J·K−1 | oxygen partial pressure, MPa | ||
| rate of the convection loss, J·K−1 | m | the dependence of the oxidation rate on the thickness of the oxide film | |
| surface area of the reaction zone, m2 | specific heat of the TC17 alloy, J·g−1·K−1 | ||
| heat-transfer coefficient, W·m−2·K−1 | density of the TC17 alloy, kg·m−3 | ||
| environment temperature, K | thermal conductively of the TC17 alloy, W·m−1·K−1 | ||
| heat of the reaction per unit mass, MJ·kg−1 | threshold value | ||
| activation energy, kJ·mol−1 | sample length, m | ||
| Subscripts | |||
| i | internal | ||
| Preexponent, kg·m−2·s−1 | g | generation | |
| d | dissipation | ||
| c | convection | ||
| reaction order | s | surface | |
| B | Boltzmann | ||
| environment | |||
| R | molar gas constant, J·mol−1·K−1 | r | reaction |
| oxygen concentration, % | m | TC17 alloy material | |
| adsorption coefficient, MPa−n | a | atmosphere | |
| n | convection energy | ||
| critical oxygen pressure, MPa | c | critical value | |
Appendix B
- The relationship between size and critical oxygen pressure
- 2.
- The relationship between oxygen concentration and critical pressure
- 3.
- The relationship between oxygen pressure and ignition temperature
References
- Gunaji, M.V.; Sircar, S.; Beeson, H.D. Ignition and Combustion of Titanium and Titanium Alloys. ASTM Spec. Tech. Publ. 1995, 1267, 81–85. [Google Scholar]
- Mäkipää, M.; Makkonen, P.; Fordham, R.J. Modeling of low-temperature oxidation of steel tubes in biomass combustion. Trans. Tech. Publ. 2004, 461, 999–1006. [Google Scholar] [CrossRef]
- Seltzer, R.J. Scientists Air Concerns Over Continuing Crisis in Space Science. Chem. Eng. News. 1998, 66, 27. [Google Scholar] [CrossRef]
- Isert, S.; Lane, C.D.; Gunduz, I.E.; Son, S.F. Tailoring burning rates using reactive wires in composite solid rocket propellants. Proc. Combust. Inst. 2017, 36, 2283–2290. [Google Scholar] [CrossRef]
- Petrescu, R.V.; Aversa, R.; Akash, B.; Corchado, J.; Kozaitis, S.; Abu-Lebdeh, T.; Apicella, A.; Petrescu, F.I. Airlander. J. Aircr. Spacecr. Technol. 2017, 2, 119–148. [Google Scholar] [CrossRef] [Green Version]
- Jahnke, L.P. Titanium in jet engines. Sci. Technol. Appl. Titan. 1970, 31, 1099–1115. [Google Scholar]
- Zawierucha, R.; Samant, A.V.; Million, J.F. Promoted Ignition-Combustion Behavior of Cast and Wrought Engineering Alloys in Oxygen-Enriched Atmospheres. In Flammability and Sensitivity of Materials in Oxygen-Enriched Atmospheres; ASTM: West Conshohocken, PA, USA, 2003; Volume 1454, p. 164. [Google Scholar]
- Million, J.F.; Samant, A.V.; Zawierucha, R. Promoted Ignition-Combustion Behavior of Cobalt and Nickel Alloys in Oxygen-Enriched Atmospheres. J. ASTM Int. 2009, 6, 1–8. [Google Scholar] [CrossRef]
- McIlroy, K.; Zawierucha, R.; Million, J.F. Promoted ignition-combustion behavior of alternative high performance engineering alloys in oxygen-enriched atmospheres. In Flammability and Sensitivity of Materials in Oxygen-Enriched Atmospheres; ASTM: West Conshohocken, PA, USA, 1997. [Google Scholar]
- Che, F.; Ha, S.; McEwen, J.-S. Hydrogen oxidation and water dissociation over an oxygen-enriched Ni/YSZ electrode in the presence of an electric field: A first-principles-based microkinetic model. Ind. Eng. Chem. Res. 2017, 56, 1201–1213. [Google Scholar] [CrossRef]
- Gray, B.F. Spontaneous Combustion and Self-Heating. In SFPE Handbook of Fire Protection Engineering; Springer: New York, NY, USA, 2016; Volume 20, pp. 604–632. [Google Scholar]
- Grossel, S.S.; Britton, L.G. Ignition handbook. J. Loss Prevent. Proc. 2004, 17, 97–99. [Google Scholar] [CrossRef]
- Borisova, Y.A.; Sklyarov, N.M. Fireproof titanium alloys. Phys. Metallogr. 1993, 6, 21–24. [Google Scholar]
- Khaikin, B.I.; Bloshenko, V.N.; Merzhanov, A.G. On the ignition of metal particles. Combust. Explos. Shock Waves 1970, 6, 412–422. [Google Scholar] [CrossRef]
- Bolobov, V.I. Conditions for Ignition of Iron and Carbon Steel in Oxygen. Combust. Explos. Shock Waves 2001, 37, 292–296. [Google Scholar] [CrossRef]
- Liang, X.Y.; Mi, G.B.; Li, P.J.; Huang, X.; Cao, C.X. Theoretical study on ignition of titanium alloy under high temperature friction condition. Acta Phys. Sin. 2020, 69, 216101–216112. [Google Scholar] [CrossRef]
- Semenov, N.N.N. Theories of combustion processes. Z. Phys. Chem. 1928, 48, 571–582. [Google Scholar]
- Frank-Kamenetskii, D.A. Towards temperature distributions in a reaction vessel and the stationary theory of thermal explosion. Dokl. Akad. Nauk SSSR 1938, 18, 411–412. [Google Scholar]
- Frank-Kamenetskii, D.A. Ignition and extinction of solid surfaces. Dokl. Akad. Nauk SSSR Ser. A 1941, 30, 734–737. [Google Scholar]
- Restuccia, F.; Ptak, N.; Rein, G. Self-heating behavior and ignition of shale rock. Combust. Flame 2017, 176, 213–219. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Sheng, J.J. Feasibility of using the Frank-Kamenetskii theory to predict the spontaneous ignition of crude oil-sand mixture. Energy Fuel 2019, 33, 4816–4825. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, X.; Sugai, Y.; Sasaki, K. Determination of critical self-ignition temperature of low-rank coal using a 1 m wire-mesh basket and extrapolation to industrial coal piles. Energy Fuel 2017, 31, 6700–6710. [Google Scholar] [CrossRef]
- Jones, J. Calculation of the Frank–Kamenetskii critical parameter for a cubic reactant shape from experimental results on bituminous coals. Fuel 1999, 78, 89–91. [Google Scholar] [CrossRef]
- Skinner, D.; Olson, D.; Block-Bolten, A. Electrostatic discharge ignition of energetic materials. Propell. Explos. Pyrot. 1998, 23, 34–42. [Google Scholar] [CrossRef]
- Garcia-Torrent, J.; Ramírez-Gómez, Á.; Querol-Aragón, E.; Grima-Olmedo, C.; Medic-Pejic, L. Determination of the risk of self-ignition of coals and biomass materials. J. Hazard. Mater. 2012, 213, 230–235. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Hu, Z.; Restuccia, F.; Fang, J.; Rein, G. Experimental study of the effect of the state of charge on self-heating ignition of large ensembles of lithium-ion batteries in storage. Appl. Therm. Eng. 2022, 212, 118621. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, P.; Lin, S.; Niu, H.; Huang, X. Self-heating ignition of open-circuit cylindrical Li-ion battery pile: Towards fire-safe storage and transpor. J. Energy Storage 2020, 32, 101842. [Google Scholar] [CrossRef]
- Bolobov, V.I. Possible self-ignition mechanism of titanium alloys in oxygen. Fiz. Goreniya Vzryva 2003, 39, 77–81. [Google Scholar]
- Godínez, F.; Navarrete, M.; Chávez, O.; Merlin, A.; Valdés, J. Two Fractal Versions of Newton’s Law of Cooling. Prog. Fract. Differ. Appl. Int. J. 2015, 1, 133–143. [Google Scholar]
- Bolobov, V. Theory of ignition of metals at fracture. Combust. Explos. Shock Waves 2012, 48, 689–693. [Google Scholar] [CrossRef]
- Bolobov, V.I. Possible Mechanism of Autoignition of Titanium Alloys in Oxygen. Combust. Explos. Shock Waves 2003, 39, 677–680. [Google Scholar] [CrossRef]
- Wilson, D.B.; Stoltzfus, J.M. Fundamentals of Metals Ignition in Oxygen. ASTM Spec. Tech. Publ. 1997, 1319, 272–282. [Google Scholar]
- Hardee, C.H.; Donaldson, B.A.; Lee, O.D. Predicting the critical boundary temperature of multidimensional explosives. Combust. Flame 1972, 19, 331–342. [Google Scholar] [CrossRef]
- Humphrey, G.L. The Heats of Formation of TiO, Ti2O3, Ti3O5 and TiO2 from Combustion Calorimetry. J. Am. Chem. Soc. 1951, 73, 1587–1590. [Google Scholar] [CrossRef]
- Shin, K.R.; Kim, Y.S.; Yang, H.W.; Ko, Y.G.; Shin, D.H. In vitro biological response to the oxide layer in pure titanium formed at different current densities by plasma electrolytic oxidation. Appl. Surf. Sci. 2014, 314, 221–227. [Google Scholar] [CrossRef]
- Shahmir, H.; Langdon, T.G. Characteristics of the allotropic phase transformation in titanium processed by high-pressure torsion using different rotation speeds. Mater. Sci. Eng. A 2016, 667, 293–299. [Google Scholar] [CrossRef] [Green Version]
- Causone, F.; Corgnati, S.P.; Filippi, M.; Olesen, B.W. Experimental evaluation of heat transfer coefficients between radiant ceiling and room. Energy Build. 2009, 41, 622–628. [Google Scholar] [CrossRef]
- Bolobov, V.I. Mechanism of Self-Ignition of Titanium Alloys in Oxygen. Combust. Explos. Shock Waves 2002, 38, 639–645. [Google Scholar] [CrossRef]
- Chicardi, E.; Córdoba, J.; Gotor, F.J. Kinetics of high-temperature oxidation of (Ti,Ta)(C,N)-based cermets. Corros. Sci. 2016, 102, 168–177. [Google Scholar] [CrossRef]
- ASTM. ASTM G124 Standard Test Method for Determining the Burning Behavior of Metallic Materials in Oxygen-Enriched Atmospheres, Annual Book of ASTM Standards; ASTM Int.: West Conshohocken, PA, USA, 2010; Volume 14, pp. 1–10. [Google Scholar]


| Standard Symbol | Dimension | Value |
|---|---|---|
| MPa | 1.00 | |
| R | J·mol−1·K−1 | 8.314 |
| MJ·kg−1 | 12.00 [34] | |
| kg·m−3 | 4.23 × 103 [35] | |
| kg·m−3 | 4.77 × 103 [36] | |
| W·m−1·K−1 | 15.00 [28] | |
| m | 0.070 | |
| W·m−2·K−1 | 11 [37] | |
| 0.50 [31,38] | ||
| MPa−0.5 | 0.52 [31,38] | |
| kJ·mol−1 | 44.50 [31] | |
| kg·m−2·s−1 | 4.20 [31] | |
| kJ·mol−1 | 283.50 [39] | |
| - | 1.00 or 2.00 [14] | |
| - | 1.00 [14] |
| Element | Al | Sn | Mo | Cr | Zr | Ti |
|---|---|---|---|---|---|---|
| wt.% | 4.5–5.5 | 1.5–2.5 | 3.5–4.5 | 3.5–4.5 | 1.5–2.5 | Bal. |
| a (m) | b (m) | δc (m) | |
|---|---|---|---|
| 0.001 | 0.001 | 0.005 | 1.714 |
| 0.0032 | 0.0032 | 0.005 | 2.024 |
| 0.005 | 0.005 | 0.005 | 2.520 |
| 0.008 | 0.008 | 0.005 | 3.830 |
| 0.010 | 0.010 | 0.005 | 5.040 |
| 0.012 | 0.012 | 0.005 | 6.518 |
| Model Type | Parameter | Dimension | Value |
|---|---|---|---|
| Frank-Kamenetskii | MPa−1.69 | 4.01 | |
| Frank-Kamenetskii | - | 1.69 | |
| Frank-Kamenetskii | kJ·mol−1 | 99.23 | |
| Frank-Kamenetskii | kg·m−2·s−1 | 20,230 | |
| Semenov | - | 0.50 [31,38] | |
| Semenov | MPa−0.5 | 0.52 [31,38] | |
| Semenov | kJ·mol−1 | 44.50 [31] | |
| Semenov | kg·m−2·s−1 | 4.20 [31] | |
| Semenov | kJ·mol−1 | 283.50 [39] | |
| Semenov | - | 1.00 or 2.00 [14] | |
| Semenov | - | 1.00 [14] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Li, J.; Li, Y.; Dou, C.; Jin, P.; He, G.; Song, X.; Huang, J.; Zhang, C. A Comparative Study on the Mathematic Models for the Ignition of Titanium Alloy in Oxygen-Enriched Environment. Metals 2022, 12, 1812. https://doi.org/10.3390/met12111812
Wang C, Li J, Li Y, Dou C, Jin P, He G, Song X, Huang J, Zhang C. A Comparative Study on the Mathematic Models for the Ignition of Titanium Alloy in Oxygen-Enriched Environment. Metals. 2022; 12(11):1812. https://doi.org/10.3390/met12111812
Chicago/Turabian StyleWang, Congzhen, Jianjun Li, Yajun Li, Caihong Dou, Pengfei Jin, Guangyu He, Xiping Song, Jinfeng Huang, and Cheng Zhang. 2022. "A Comparative Study on the Mathematic Models for the Ignition of Titanium Alloy in Oxygen-Enriched Environment" Metals 12, no. 11: 1812. https://doi.org/10.3390/met12111812
APA StyleWang, C., Li, J., Li, Y., Dou, C., Jin, P., He, G., Song, X., Huang, J., & Zhang, C. (2022). A Comparative Study on the Mathematic Models for the Ignition of Titanium Alloy in Oxygen-Enriched Environment. Metals, 12(11), 1812. https://doi.org/10.3390/met12111812







