Effects of Vacancy Defects on Electrical and Optical Properties of ZnO/WSe2 Heterostructure: First-Principles Study
Abstract
:1. Introduction
2. Computational Methods
3. Results and Discussion
3.1. Structure and Stability
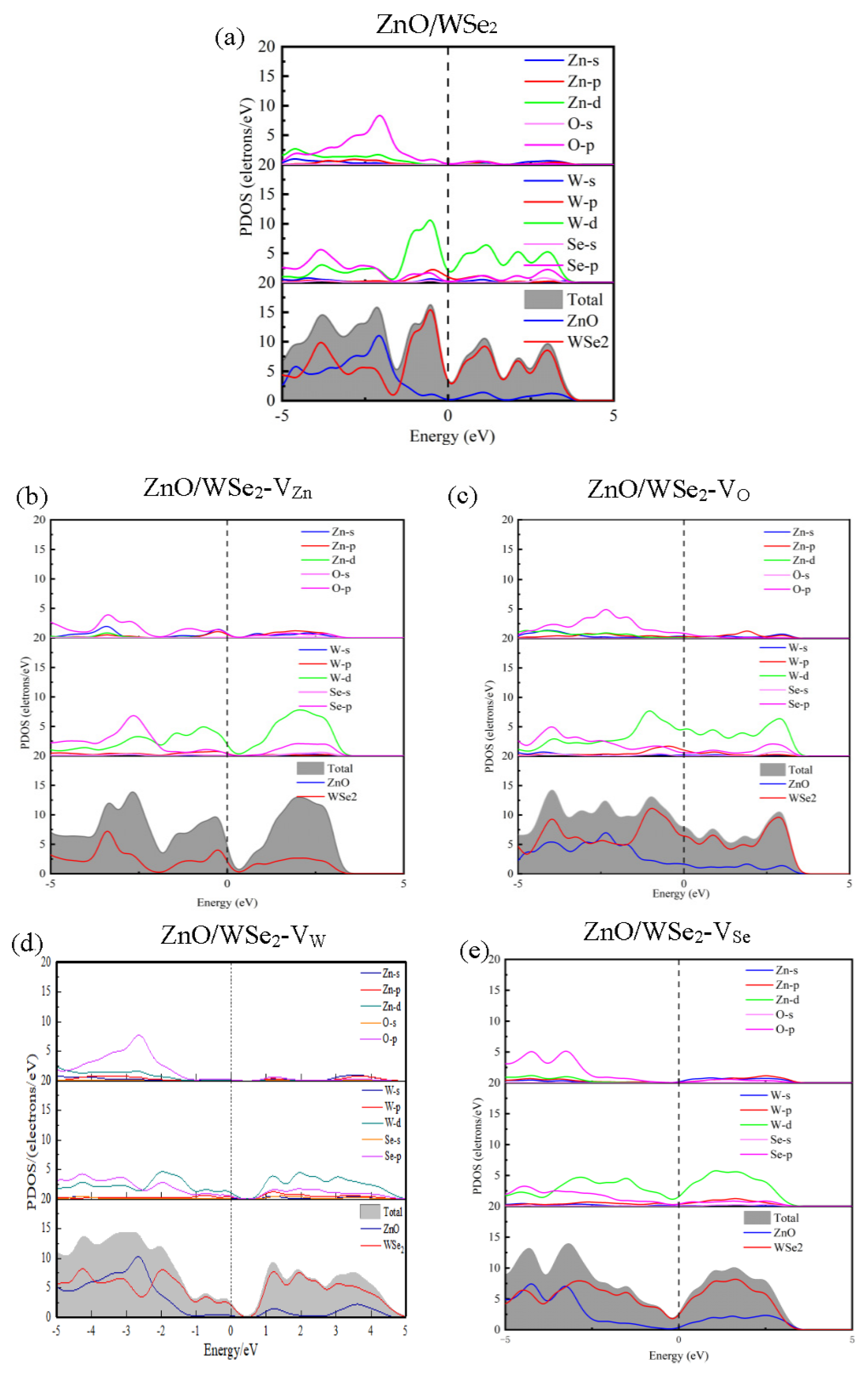
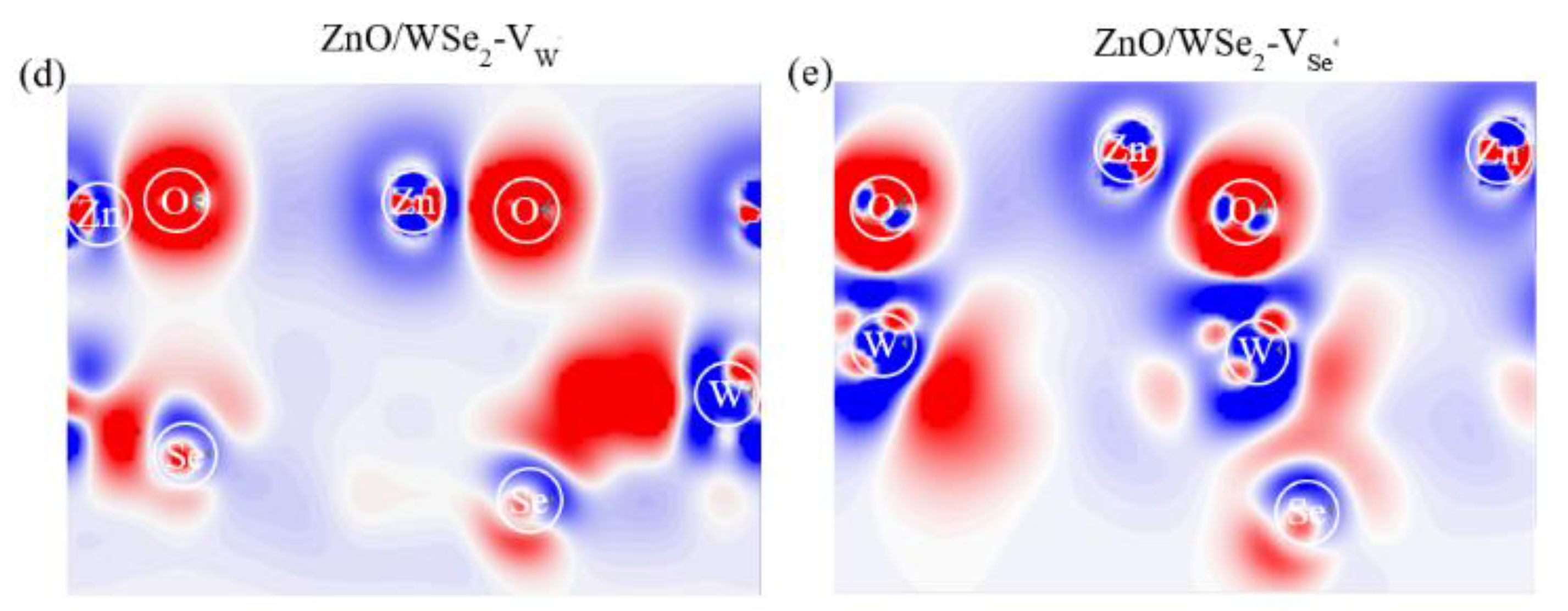
3.2. Electronic Properties
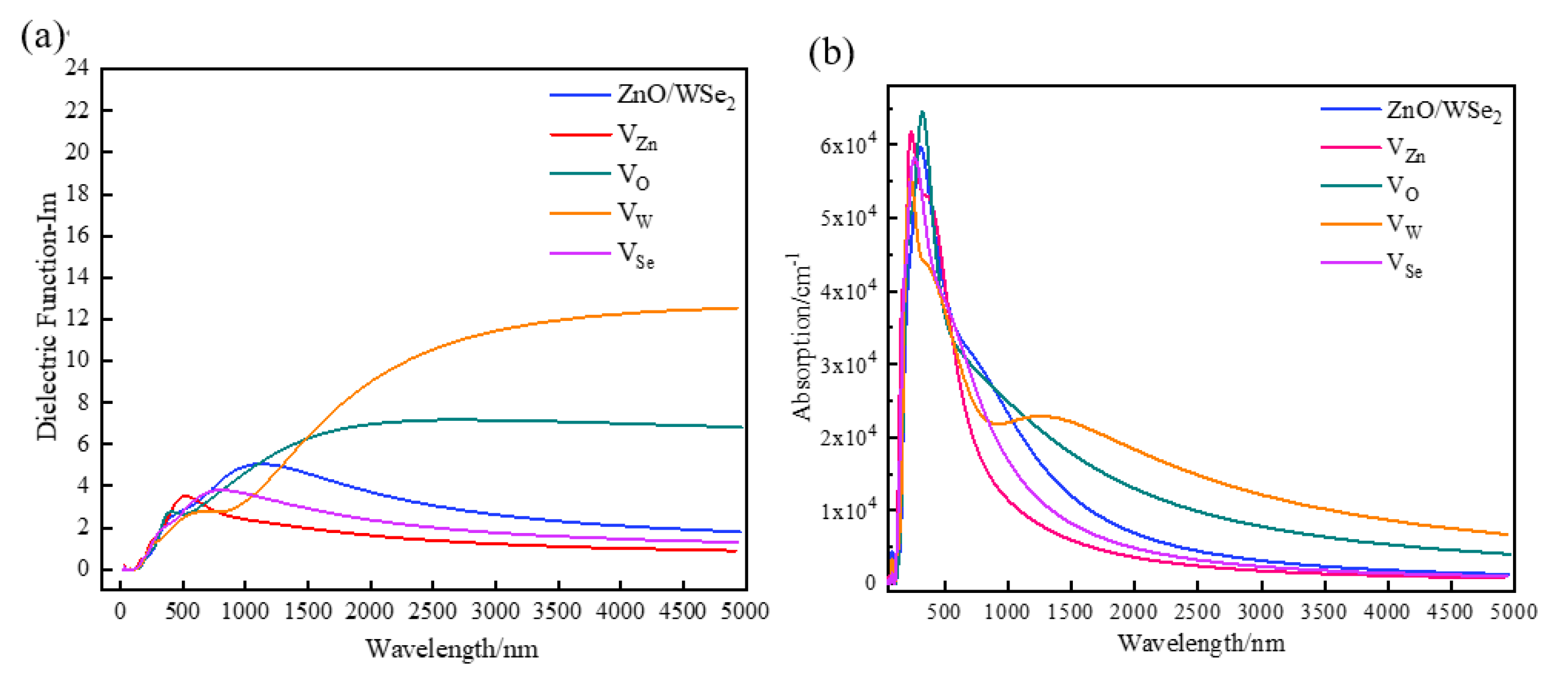
3.3. Optical Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Obeid, M.M.; Bafekry, A.; Rehman, S.U.; Nguyen, C.V. A type-II GaSe/HfS2 van der Waals heterostructure as promising photocatalyst with high carrier mobility. Appl. Surf. Sci. 2020, 534, 147607. [Google Scholar] [CrossRef]
- Wang, B.-J.; Li, X.-H.; Cai, X.-L.; Yu, W.-Y.; Zhang, L.-W.; Zhao, R.-Q.; Ke, S.-H. Blue phosphorus/Mg (OH)2 van der Waals heterostructures as promising visible-light photocatalysts for water splitting. J. Phys. Chem. C 2018, 122, 7075–7080. [Google Scholar] [CrossRef]
- Fujishima, A.; Honda, K. Electrochemical photolysis of water at a semiconductor electrode. Nature 1972, 238, 37–38. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.T.; Vu, T.V.; Binh, N.T.; Hoat, D.; Hieu, N.V.; Nguyen, C.V.; Phuc, H.V.; Jappor, H.R.; Obeid, M. Strain-tunable electronic and optical properties of monolayer GeSe: Promising for photocatalytic water splitting applications. Chem. Phys. 2020, 529, 110543. [Google Scholar] [CrossRef]
- Neto, A.H.C.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef] [Green Version]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [Green Version]
- Novoselov, K.S.; Jiang, D.; Schedin, F.; Booth, T.J.; Khotkevich, V.V.; Morozov, S.V.; Geim, A.K. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 2005, 102, 10451–10453. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.H.; Kalantar-Zadeh, K.; Kis, A.; Coleman, J.N.; Strano, M.S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 2012, 7, 699–712. [Google Scholar] [CrossRef]
- Ponce, F.A.; Bour, D.P. Nitride-based semiconductors for blue and green light-emitting devices. Nature 1997, 386, 351–359. [Google Scholar] [CrossRef]
- Green, M.A.; Bremner, S.P. Energy conversion approaches and materials for high-efficiency photovoltaics. Nat. Mater. 2017, 16, 23–34. [Google Scholar] [CrossRef]
- Polman, A.; Knight, M.; Garnett, E.C.; Ehrler, B.; Sinke, W.C. Photovoltaic materials: Present efficiencies and future challenges. Science 2016, 352, aad4424. [Google Scholar] [CrossRef] [Green Version]
- Green, M.A.; Hishikawa, Y.; Warta, W.; Dunlop, E.D.; Levi, D.H.; Hohl-Ebinger, J.; Ho-Baillie, A.W.H. Solar cell efficiency tables (version 50). Prog. Photovolt. Res. Appl. 2017, 25, 668–676. [Google Scholar] [CrossRef] [Green Version]
- Ohno, H.; Munekata, H.; Penney, T.; von Molnár, S.; Chang, L.L. Magnetotransport properties of p-type (In, Mn) As diluted magnetic III-V semiconductors. Phys. Rev. Lett. 1992, 68, 2664. [Google Scholar] [CrossRef]
- Dietl, T.; Ohno, H. Dilute ferromagnetic semiconductors: Physics and spintronic structures. Rev. Mod. Phys. 2014, 86, 187. [Google Scholar] [CrossRef] [Green Version]
- King, T.C.; Yang, Y.P.; Liou, Y.S.; Wu, C.J. Tunable defect mode in a semiconductor-dielectric photonic crystal containing extrinsic semiconductor defect. Solid State Commun. 2012, 152, 2189–2192. [Google Scholar] [CrossRef]
- Mak, K.F.; Lee, C.; Hone, J.; Shan, J.; Heinz, T.F. Atomically thin MoS2: A new direct-gap semiconductor. Phys. Rev. Lett. 2010, 105, 136805. [Google Scholar] [CrossRef] [Green Version]
- Dolui, K.; Rungger, I.; Pemmaraju, C.D.; Sanvito, S. Possible doping strategies for MoS2 monolayers: An ab initio study. Phys. Rev. B 2013, 88, 075420. [Google Scholar] [CrossRef] [Green Version]
- Komsa, H.-P.; Kotakoski, J.; Kurasch, S.; Lehtinen, O.; Kaiser, U.; Krasheninnikov, A. Two-dimensional transition metal dichalcogenides under electron irradiation: Defect production and doping. Phys. Rev. Lett. 2012, 109, 035503. [Google Scholar] [CrossRef]
- Segovia-Chaves, F.; Vinck-Posada, H. Effects of hydrostatic pressure on the band structure in two-dimensional semiconductor square photonic lattice with defect. Phys. B Condens. Matter 2018, 545, 203–209. [Google Scholar] [CrossRef]
- Zak, A.; Feldman, Y.; Lyakhovitskaya, V.; Leitus, G.; Popovitz-Biro, R.; Wachtel, E.; Cohen, H.; Reich, S.; Tenne, R. Alkali metal intercalated fullerene-like MS2 (M = W.; Mo) nanoparticles and their properties. J. Am. Chem. Soc. 2002, 124, 4747–4758. [Google Scholar] [CrossRef]
- Kabita, K.; Maibam, J.; Sharma, B.I.; Thapa, R.K.; Brojen Singh, R.K. First principle study on pressure-induced electronic structure and elastic properties of indium phosphide (InP). Indian J. Phys. 2015, 89, 1265–1271. [Google Scholar] [CrossRef]
- Mellot-Draznieks, C. Role of computer simulations in structure prediction and structure determination: From molecular compounds to hybrid frameworks. J. Mater. Chem. 2007, 17, 4348–4358. [Google Scholar] [CrossRef]
- Lejaeghere, K.; Bihlmayer, G.; Björkman, T.; Blaha, P.; Blügel, S.; Blum, V.; Caliste, D.; Castelli, I.E.; Clark, S.J.; Corso, A.D.; et al. Reproducibility in density functional theory calculations of solids. Science 2016, 351, aad3000. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef] [Green Version]
- Segall, M.D.; Lindan, P.J.D.; Probert, M.J.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [Green Version]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef] [Green Version]
- Hu, F.; Tao, L.; Ye, H.; Li, X.; Chen, X. ZnO/WSe2 vdW heterostructure for photocatalytic water splitting. J. Mater. Chem. C 2019, 7, 7104–7113. [Google Scholar] [CrossRef]
- Zheng, H.; Li, X.-B.; Chen, N.-K.; Xie, S.-Y.; Tian, W.Q.; Chen, Y.; Xia, H.; Zhang, S.B.; Sun, H.-B. Monolayer II-VI semiconductors: A first-principles prediction. Phys. Rev. B 2015, 92, 115307. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Local and Gradient-Corrected Density Functionals, Chemical Applications of Density-Functional Theory; Laird, B.B., Ross, R.B., Ziegler, T., Eds.; American Chemical Society: Washington, DC, USA, 1996; pp. 453–462. [Google Scholar]
- Zhang, Y.; Yang, W. Comment on “Generalized gradient approximation made simple”. Phys. Rev. Lett. 1998, 80, 890. [Google Scholar] [CrossRef]
- Wu, Z.; Cohen, R.E. More accurate generalized gradient approximation for solids. Phys. Rev. B 2006, 73, 235116. [Google Scholar] [CrossRef] [Green Version]
- Friák, M.; Šob, M.; Vitek, V. Ab initio study of the ideal tensile strength and mechanical stability of transition-metal disilicides. Phys. Rev. B 2003, 68, 184101. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.-S.; Mizoguchi, T.; Yamamoto, T.; Kang, S.L.; Ikuharaa, Y. First-principles calculation of defect energetics in cubic-BaTiO3 and a comparison with SrTiO3. Acta Mater. 2007, 55, 6535–6540. [Google Scholar] [CrossRef]
- Ge, F.F.; Wu, W.D.; Cao, L.H.; Wang, X.M.; Wang, H.P.; Dai, Y.; Wang, H.B.; Shen, J. The structure and defect formation energy in tetragonal PbTiO3: Ab initio calculation. Ferroelectrics 2010, 401, 154–160. [Google Scholar] [CrossRef]
- Shang, J.; Pan, L.; Wang, X.; Li, J.; Deng, H.-X.; Wei, Z. Tunable electronic and optical properties of InSe/InTe van der Waals heterostructures toward optoelectronic applications. J. Mater. Chem. C 2018, 6, 7201–7206. [Google Scholar] [CrossRef]
- Sun, S.; Meng, F.; Wang, H.; Wang, H.; Ni, Y. Novel two-dimensional semiconductor SnP3: High stability, tunable bandgaps and high carrier mobility explored using first-principles calculations. J. Mater. Chem. A 2018, 6, 11890–11897. [Google Scholar] [CrossRef]
- Yu, H.B.; Wang, W.H.; Bai, H.Y. An electronic structure perspective on glass-forming ability in metallic glasses. Appl. Phys. Lett. 2010, 96, 081902. [Google Scholar]
- Zhang, C.; Zhou, Y.; Zhang, Y.; Zhao, S.; Fang, J.; Sheng, X.; Zhang, H. Self-assembly hierarchical silica nanotubes with vertically aligned silica nanorods and embedded platinum nanoparticles. ACS Sustain. Chem. Eng. 2017, 5, 1578–1585. [Google Scholar] [CrossRef]
- Grätzel, M. Photoelectrochemical Cells. In Materials for Sustainable Energy: A Collection of Peer-Reviewed Research and Review Articles from Nature Publishing Group; Nature: London, UK, 2011; pp. 26–32. [Google Scholar]
- Zhu, L.; Cao, X.; Gong, C.; Jiang, A.; Cheng, Y.; Xiao, J. Preparation of Cu3N/MoS2 heterojunction through magnetron sputtering and investigation of its structure and optical performance. Materials 2020, 13, 1873. [Google Scholar] [CrossRef] [Green Version]
- Hassan, M.A.; Kang, J.H.; Johar, M.A.; Ha, J.-S.; Ryu, S.-W. High-performance ZnS/GaN heterostructure photoanode for photoelectrochemical water splitting applications. Acta Mater. 2018, 146, 171–175. [Google Scholar] [CrossRef]
- Djurišić, A.B.; Li, E.H. The Optical Dielectric Function: Excitonic Effects at E0 Critical Point. J. Phys. Soc. Jpn. 2001, 70, 2164–2167. [Google Scholar] [CrossRef]
- Fadaie, M.; Shahtahmassebi, N.; Roknabad, M.R. Effect of external electric field on the electronic structure and optical properties of stanene. Opt. Quantum Electron. 2016, 48, 1–12. [Google Scholar] [CrossRef]
- Sun, M.; Chou, J.-P.; Gao, J.; Cheng, Y.; Hu, A.; Tang, W.; Zhang, G. Exceptional optical absorption of buckled arsenene covering a broad spectral range by molecular doping. ACS Omega 2018, 3, 8514–8520. [Google Scholar] [CrossRef] [PubMed]
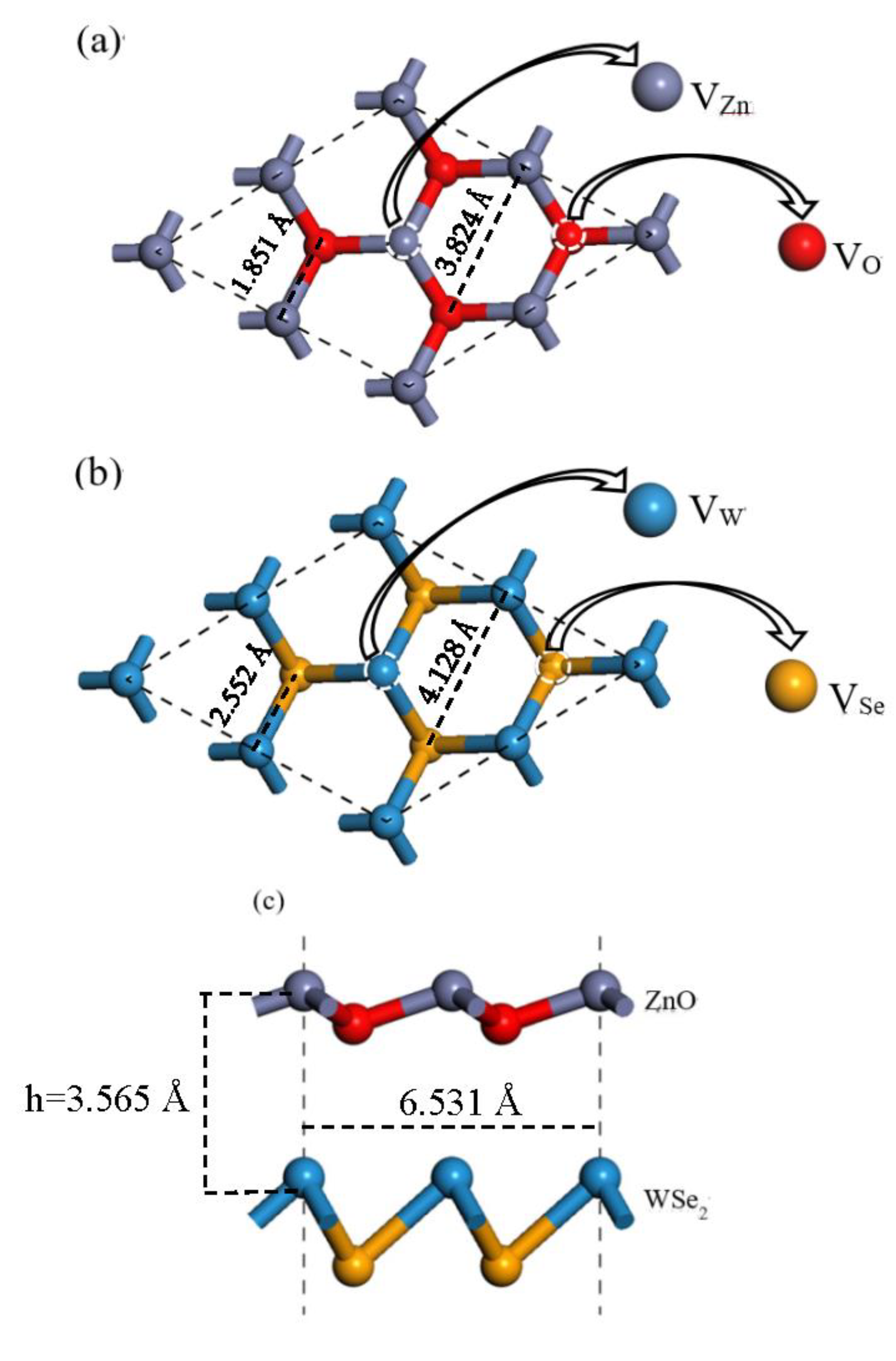
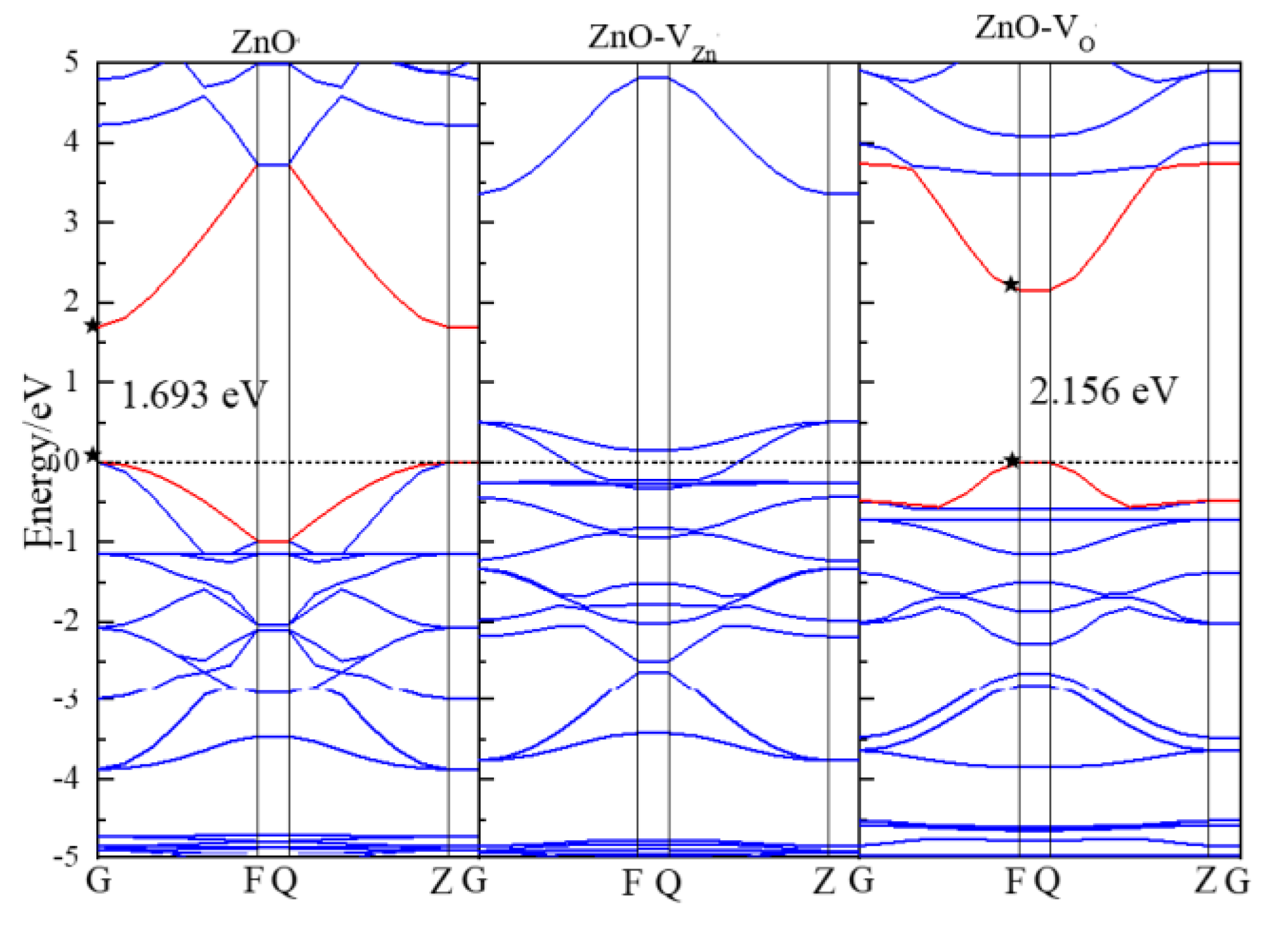
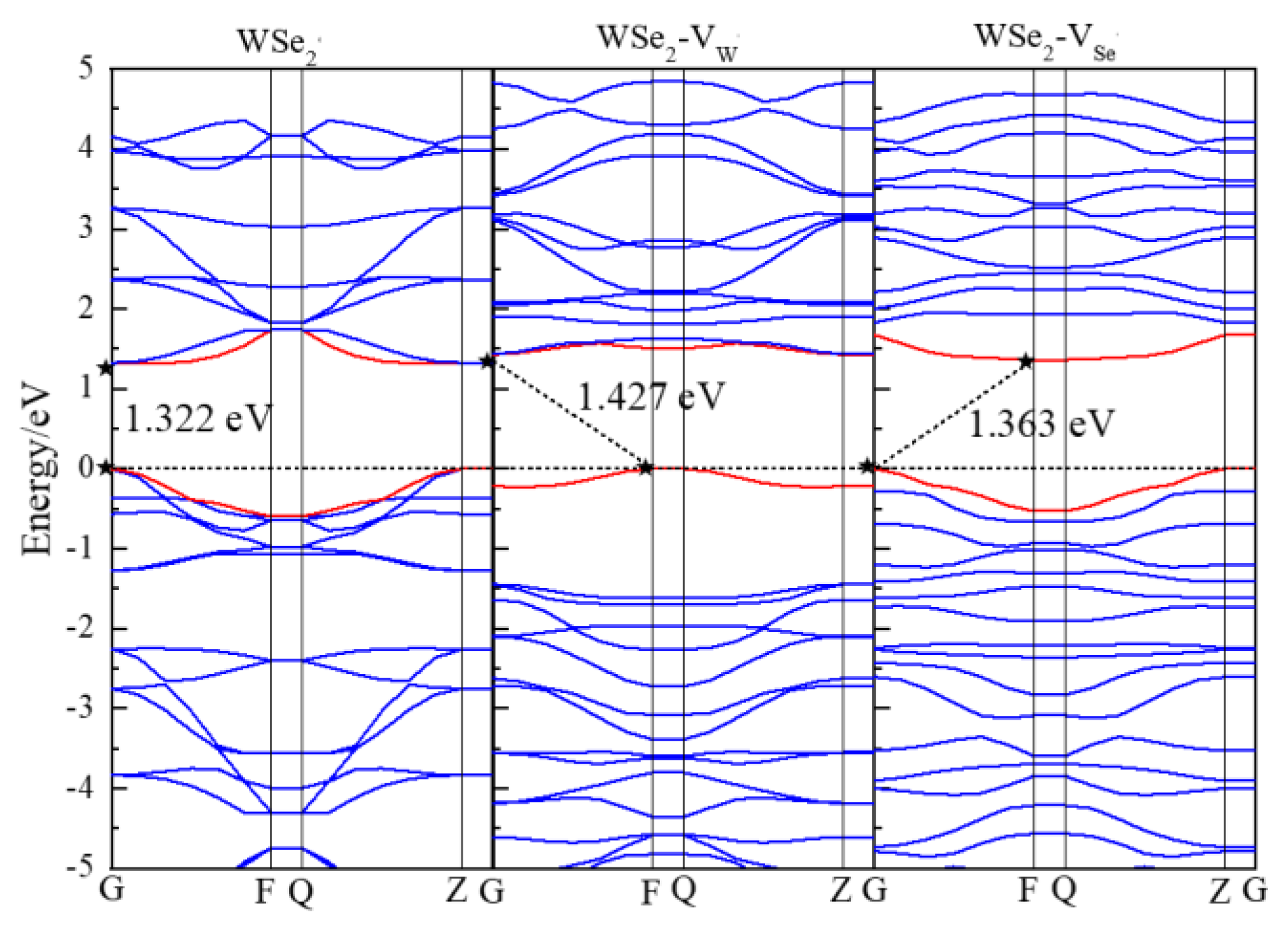
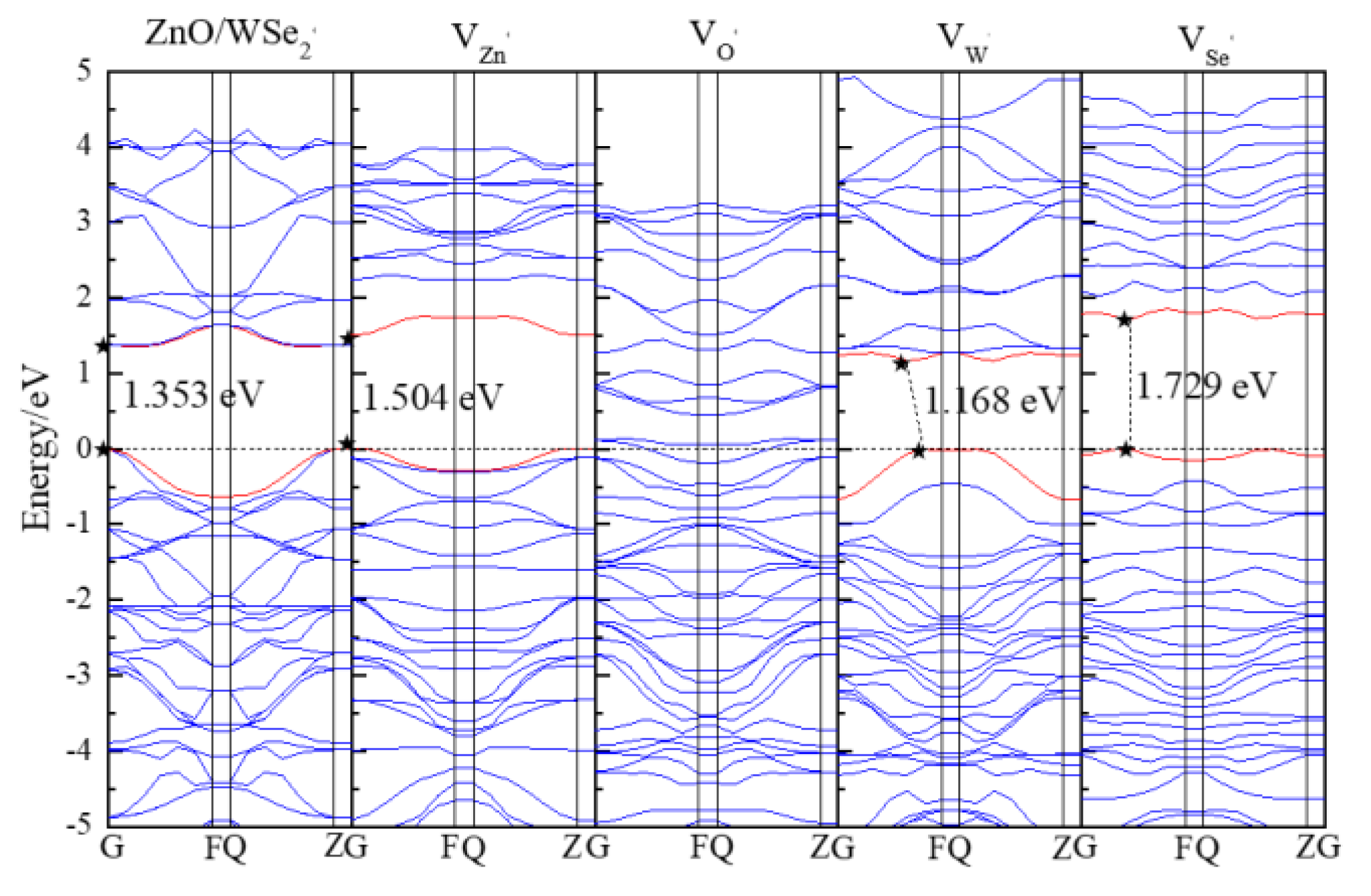

| Structure | ZnO | WSe2 | ZnO/WSe2 | |
|---|---|---|---|---|
| Vacancy | ||||
| VZn | 6.44 | −2.56 | ||
| VO | 8.13 | 7.90 | ||
| VW | 7.66 | 10.59 | ||
| VSe | 3.40 | 0.40 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yong, X.; Wang, A.; Deng, L.; Zhou, X.; Li, J. Effects of Vacancy Defects on Electrical and Optical Properties of ZnO/WSe2 Heterostructure: First-Principles Study. Metals 2022, 12, 1975. https://doi.org/10.3390/met12111975
Yong X, Wang A, Deng L, Zhou X, Li J. Effects of Vacancy Defects on Electrical and Optical Properties of ZnO/WSe2 Heterostructure: First-Principles Study. Metals. 2022; 12(11):1975. https://doi.org/10.3390/met12111975
Chicago/Turabian StyleYong, Xi, Ao Wang, Lichuan Deng, Xiaolong Zhou, and Jintao Li. 2022. "Effects of Vacancy Defects on Electrical and Optical Properties of ZnO/WSe2 Heterostructure: First-Principles Study" Metals 12, no. 11: 1975. https://doi.org/10.3390/met12111975
APA StyleYong, X., Wang, A., Deng, L., Zhou, X., & Li, J. (2022). Effects of Vacancy Defects on Electrical and Optical Properties of ZnO/WSe2 Heterostructure: First-Principles Study. Metals, 12(11), 1975. https://doi.org/10.3390/met12111975






