Thermodynamic Assessment of Ti-Al-Fe-V Quaternary System Applied to Novel Titanium Alloys Designing

Abstract

The Ti-Al-Fe-V quaternary system is a very useful system for titanium alloy development. However, there are few reports on the thermodynamic description of this system. In the present work, the experimental investigation and thermodynamic description of the relative sub-systems of the Ti-Al-Fe-V quaternary system are summarized and reviewed, wherein the Ti-Fe-V system is re-assessed by using CALPHAD (CALculation of PHAse Diagrams) approach. The thermodynamic database of the Ti-Al-Fe-V quaternary system is established by extrapolating the thermodynamic descriptions of all sub- systems. Then, a method of titanium alloy design combining Mo equivalent with CALPHAD is proposed. The pseudo-binary sections with V:Fe = 3.5:1 and Al = 0.0, 3.0, 4.5 and 6.0 wt% are calculated. Finally, three different types of titanium alloys are recommended according to the new method.

1. Introduction

As important lightweight structural materials, titanium and titanium alloys are widely used in aviation, aerospace, vehicle engineering, biomedical engineering and other fields due to their excellent performance [1,2,3]. Although titanium elements are abundant in the Earth’s crust, in 2016, the world output of titanium sponges was only 183,277 metric tons [4]. The high production cost of titanium alloys limits their development and application. Recently, the low-cost preparation of titanium alloys and the development of low-cost titanium alloys have become the focus of research [5,6,7]. Therefore, we can reduce the processing cost of titanium alloy by using methods such as short technological process, for example, the use of powder metallurgy and other near net shaping technology, and increasing the yield by optimizing the heating temperature, deformation and distortion temperature. The cost of the related processing accounts for 60% of the total cost of commercial titanium alloys, while the raw materials account for 40% [8]. On the other hand, we can use inexpensive raw materials (alloying elements) to design titanium alloys. Specifically, scholars have tried to replace expensive isomorphic β-type elements such as V, Mo and Nb with inexpensive eutectoid β-type elements such as Fe, Cr and Mn, which has proven to be an effective way to reduce the cost of titanium alloys [9]. ATI company has developed ATI 425 low-cost titanium alloy using inexpensive Fe instead of part V [10], which not only reduces the cost, but also reduces the possibility of the occurrence of brittle phase, thus this alloy keeps the good mechanical properties and can be applied to military armor materials. It is important to thoroughly understand the thermodynamics of alloys to improve their properties [11]. Therefore, it is essential to thermodynamic assessment of the Ti-Al-Fe-V quaternary system for developing novel titanium alloys containing these elements.

In this work, the thermodynamic evaluation of six sub-binary systems (Ti-Al, Ti-Fe, Ti-V, Al-Fe, Al-V and Fe-V) and four sub-ternary systems (Ti-Al-Fe, Ti-Al-V, Ti-Fe-V and Al-Fe-V) were reviewed, and the thermodynamic re-evaluation of Ti-Fe-V system was carried out, and the construction of the thermodynamic database of the Ti-Al-Fe-V quaternary system was directly extrapolated from four sub-ternary systems. Then, a method of combining Mo equivalent with CALPHAD was proposed to design novel titanium alloys. Finally, pseudo-binary sections were calculated with the V:Fe = 3.5:1 and Al = 0.0, 3.0, 4.5 and 6.0 wt%, and three novel titanium alloys were designed.

2. Literature Review

2.1. Binary Systems

The Ti-Al system was optimized by many researchers [12,13,14,15,16,17,18], which included liquid, α(Ti), β, β₀, α(Al), Ti₃Al, TiAl, Ti₃Al₅, Ti₂Al₅, TiAl₂, the high-temperature phase H_TiAl₃ and the low-temperature phase L_TiAl₃. The thermodynamic parameters of this system used in the present work are from Witusiewicz et al. [18] and the calculated Ti-Al phase diagram is shown in Figure 1. For the Ti-Fe system, several thermodynamic descriptions are available [19,20,21,22,23,24], in which liquid, γ(Fe), β, α(Ti), TiFe and Fe₂Ti were included. Bo’s [24] work is accepted in the present work and the calculated Ti-Fe phase diagram is shown in Figure 2. The Ti-V system was optimized by [25,26,27], and three phases of liquid, β and α(Ti) were included. The calculated Ti-V phase diagram using the thermodynamic parameters from Ghosh et al. [27] is shown in Figure 3. The Al-Fe system has been reported by many researchers [28,29,30] and includes liquid, β, β₀, γ(Fe), α(Al), Al₈Fe₅, Al₂Fe, Al₅Fe₂ and Al₁₃Fe₄. Sundman’s [30] thermodynamic parameters are adopted in the present work and the calculated Al-Fe phase diagram is shown in Figure 4. Several thermodynamic parameters of the Al-V system are available [31,32], in which liquid, α(Al), β, Al₂₁V₂, Al₄₅V₇, Al₂₃V₄, Al₃V and Al₈V₅ are included. The thermodynamic parameters used in the present work are from Gong et al. [32] and the calculated Al-V phase diagram is shown in Figure 5. The Fe-V system was optimized by [33,34,35], and four phases of liquid, γ(Fe), β and sigma were included. The thermodynamic parameters are accepted in the present work from Kumar et al. [35] and the calculated Fe-V phase diagram is shown in Figure 6. For the evaluation of the six binary systems mentioned above, only those that are most consistent with experimental data will be accepted in the present work. The crystallographic data of individual phases in the six binary systems [18,24,27,30,32,35] are listed in

Table 1. Crystallographic data of individual phases in the six binary systems.

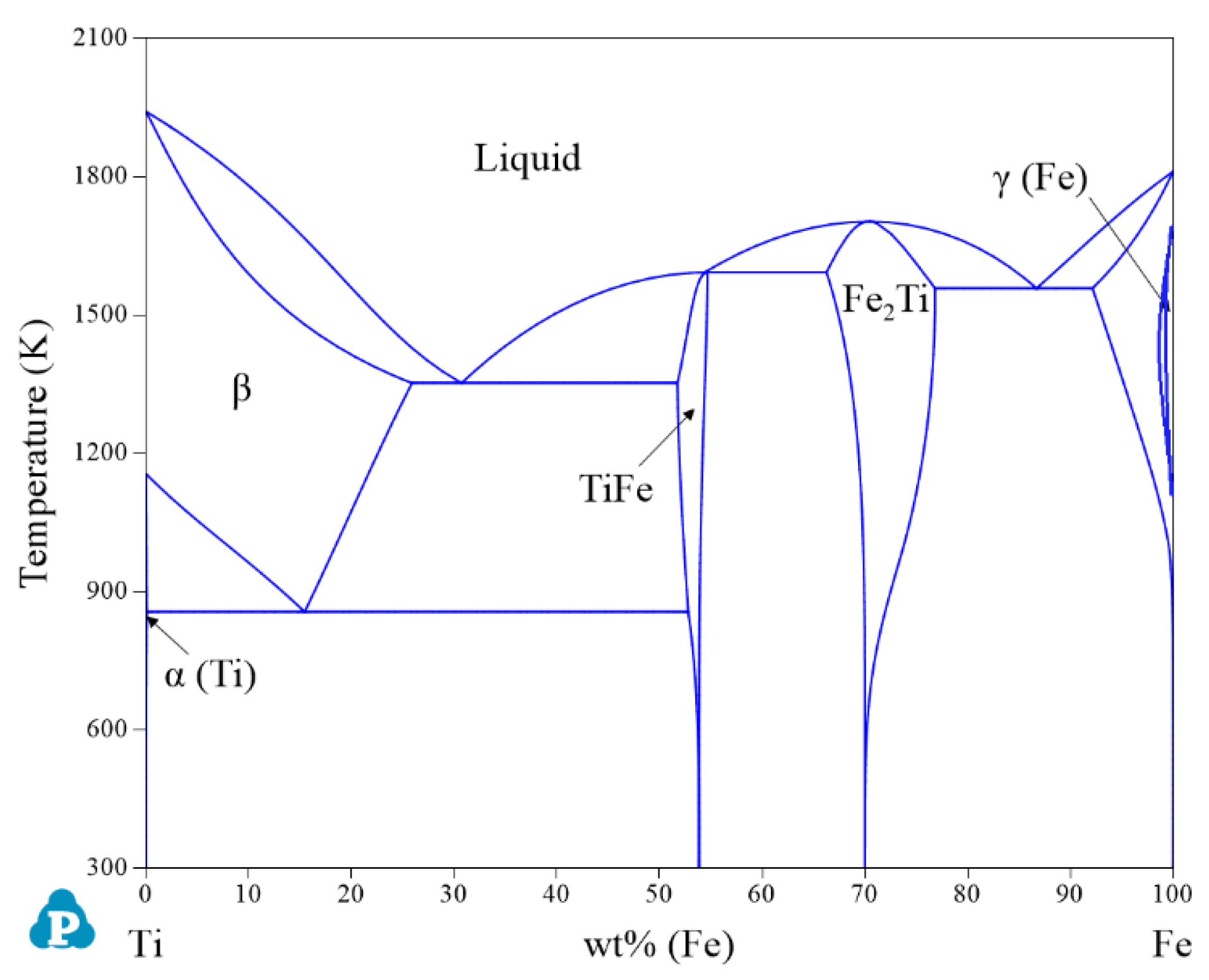
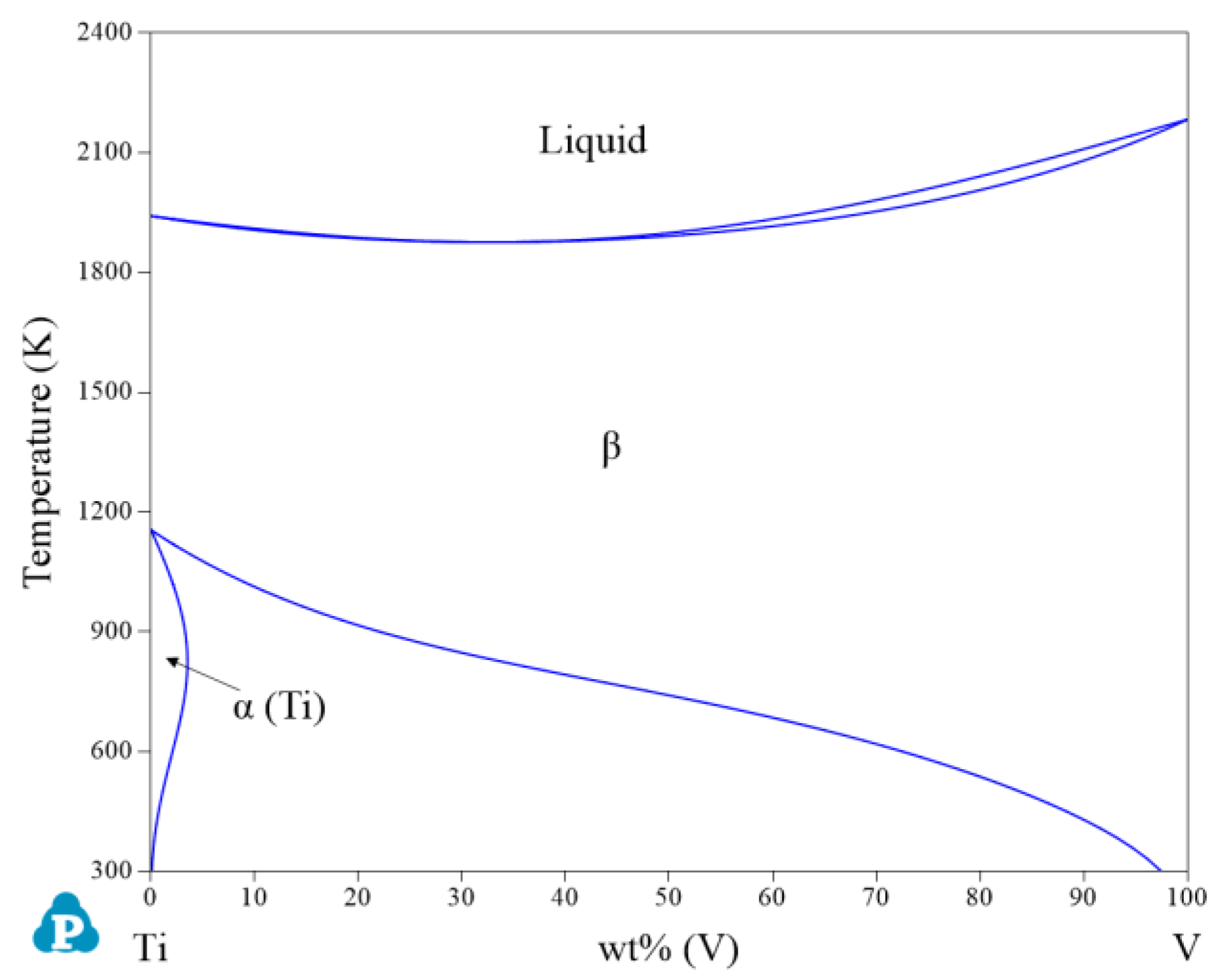
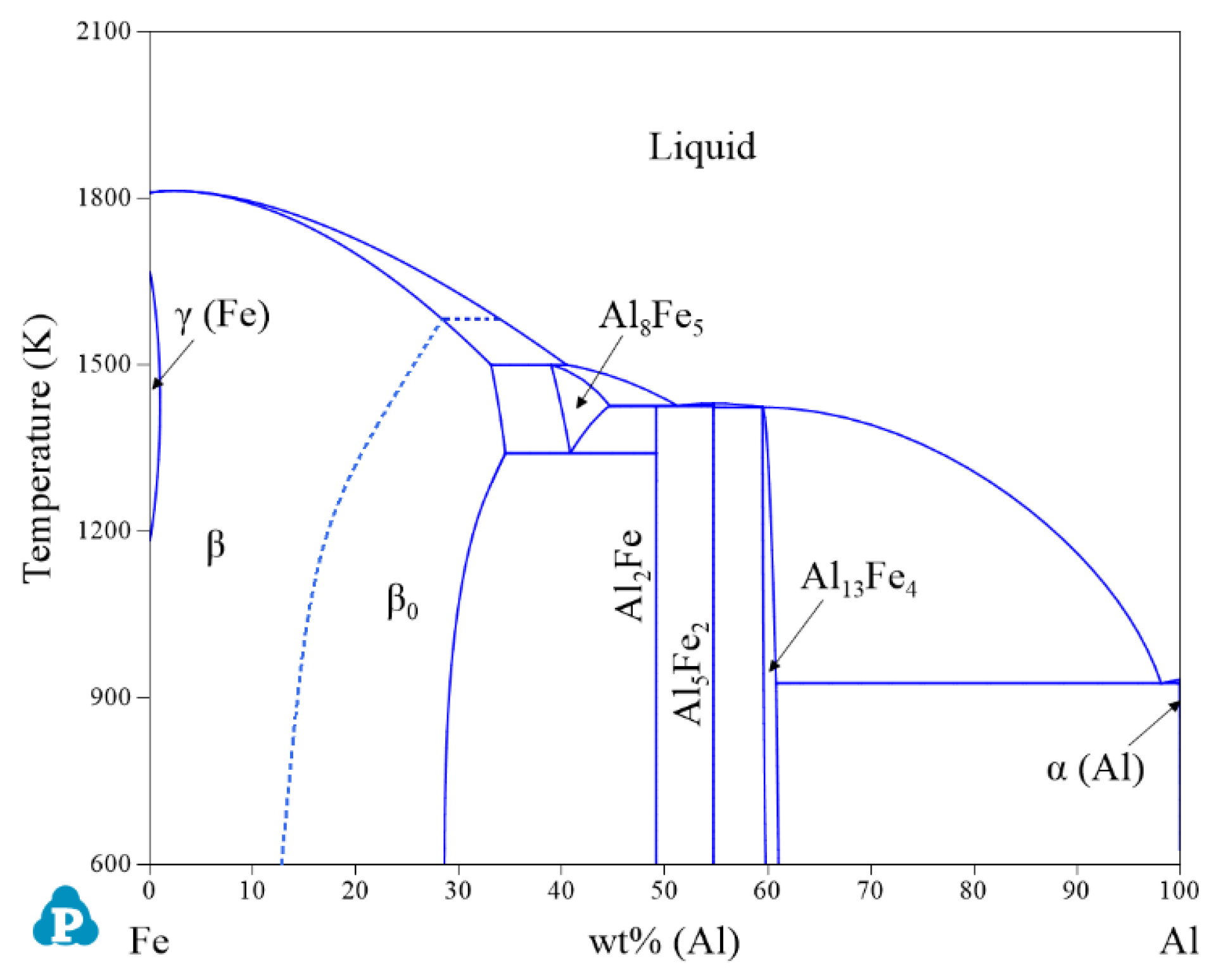
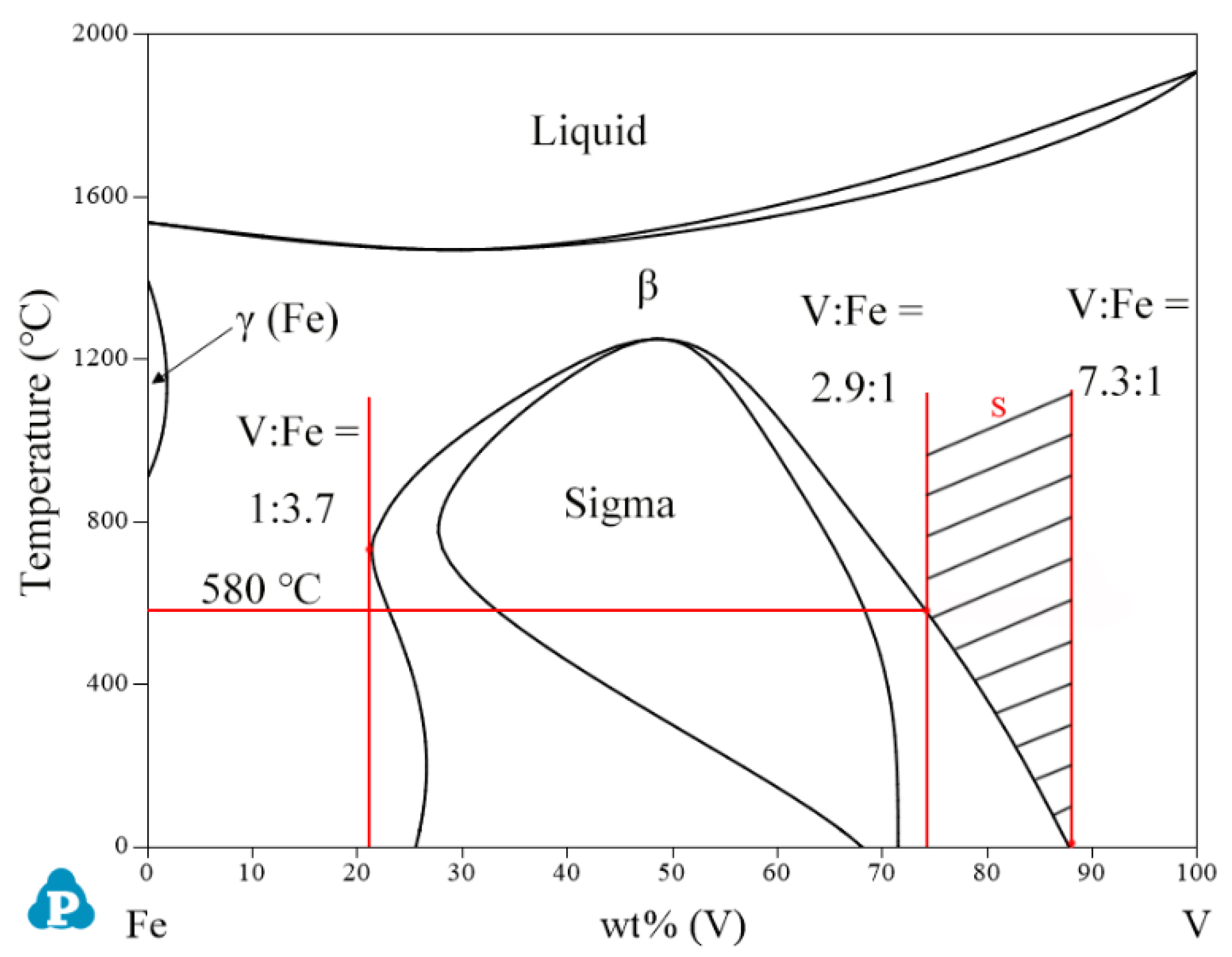
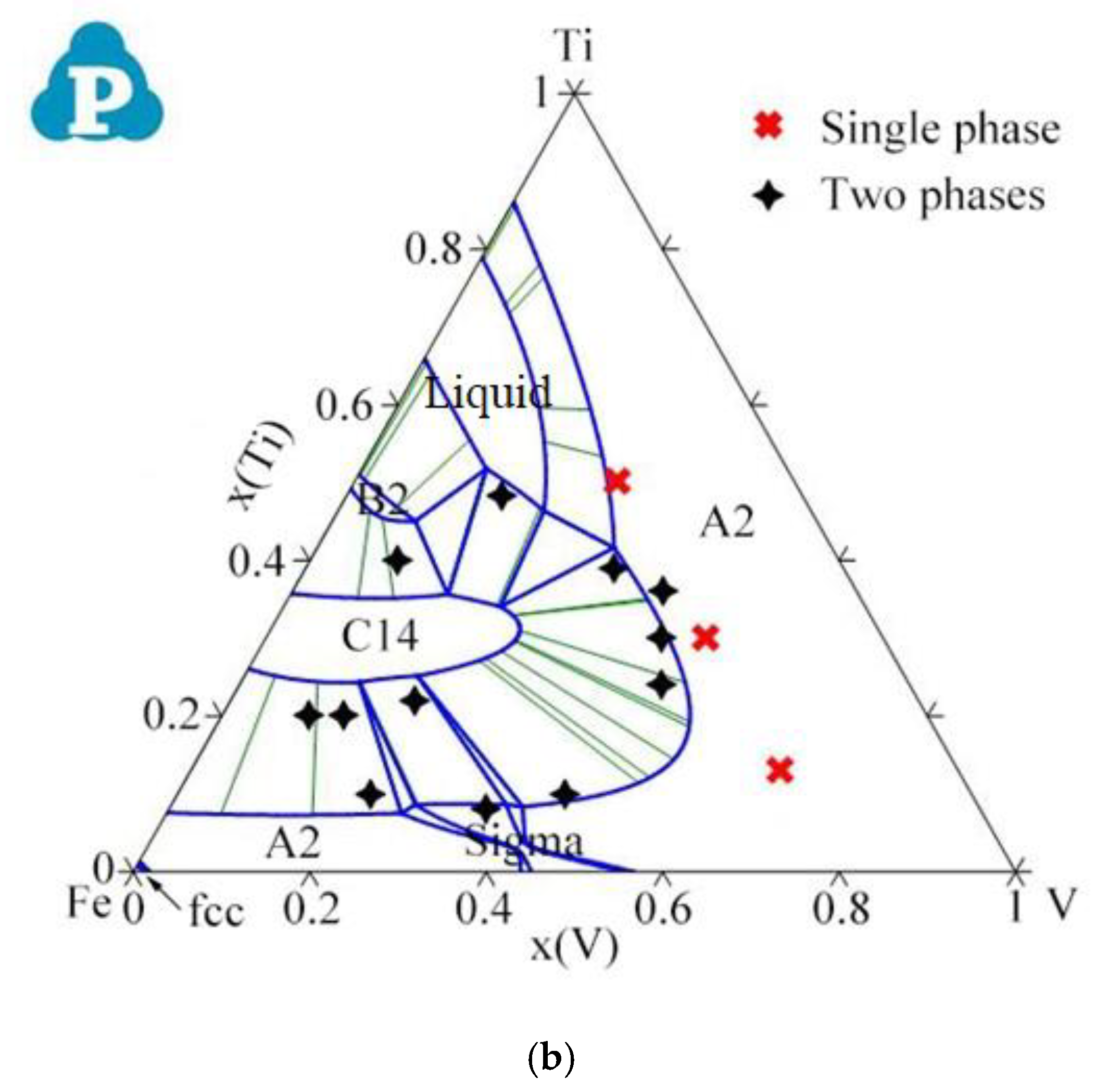
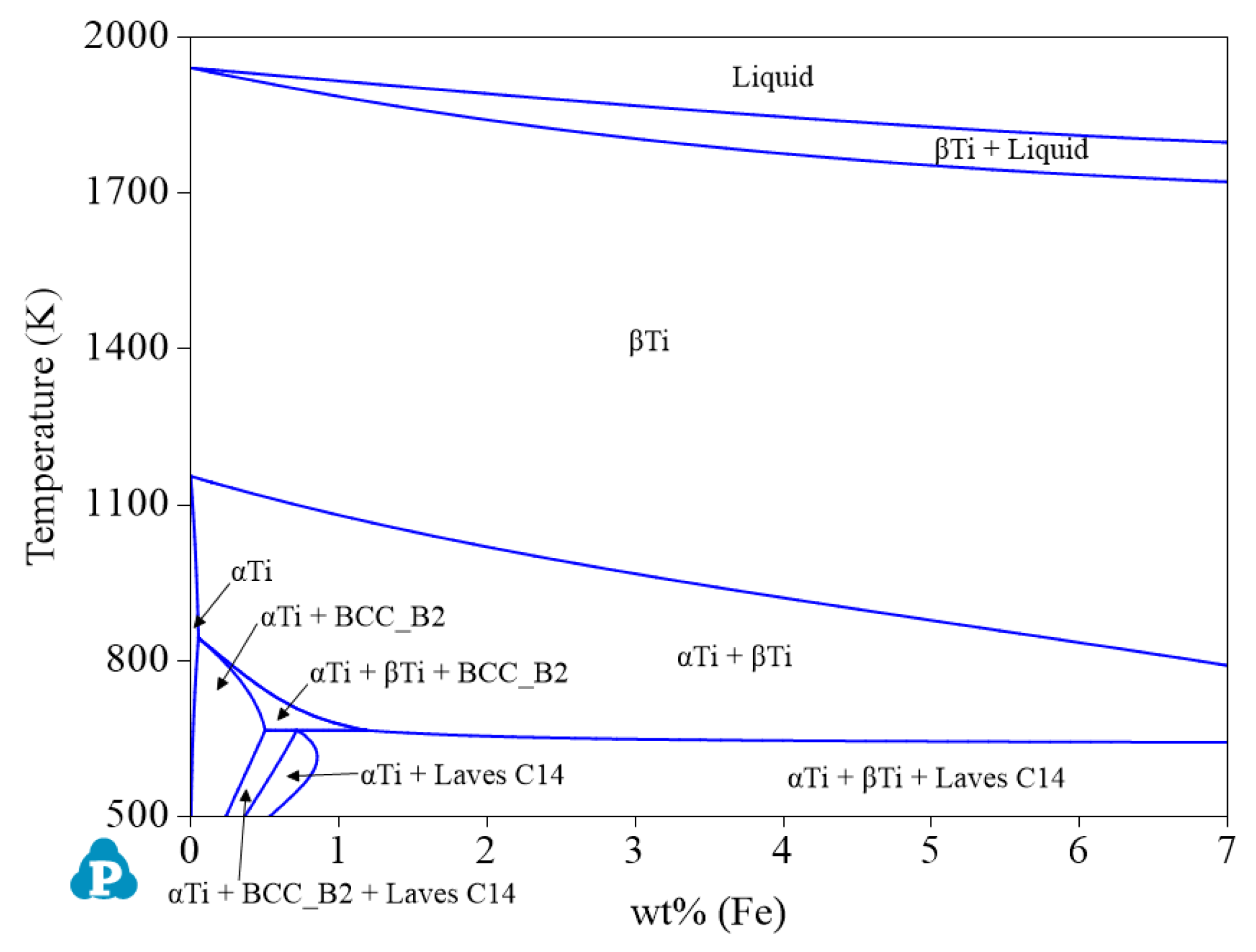
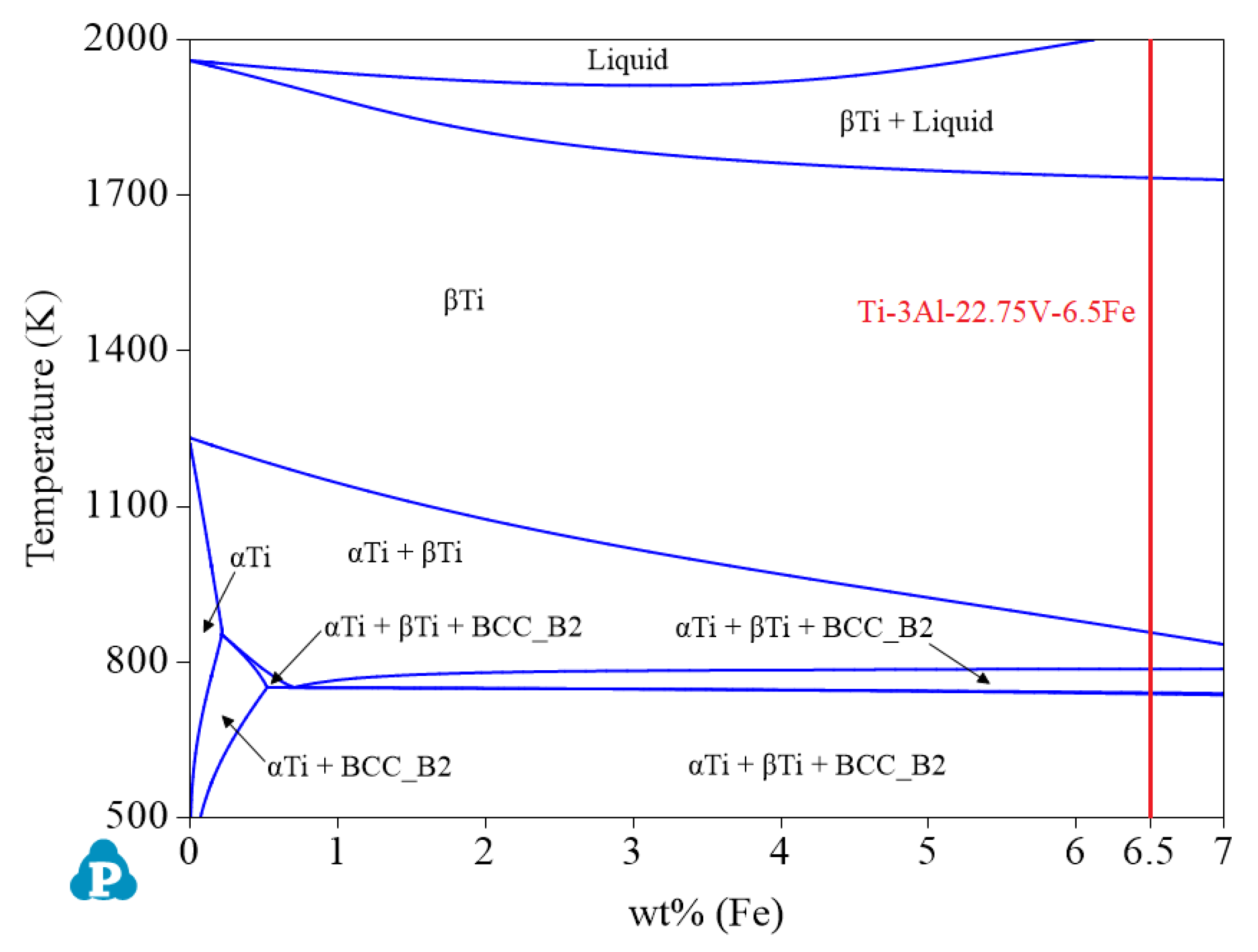
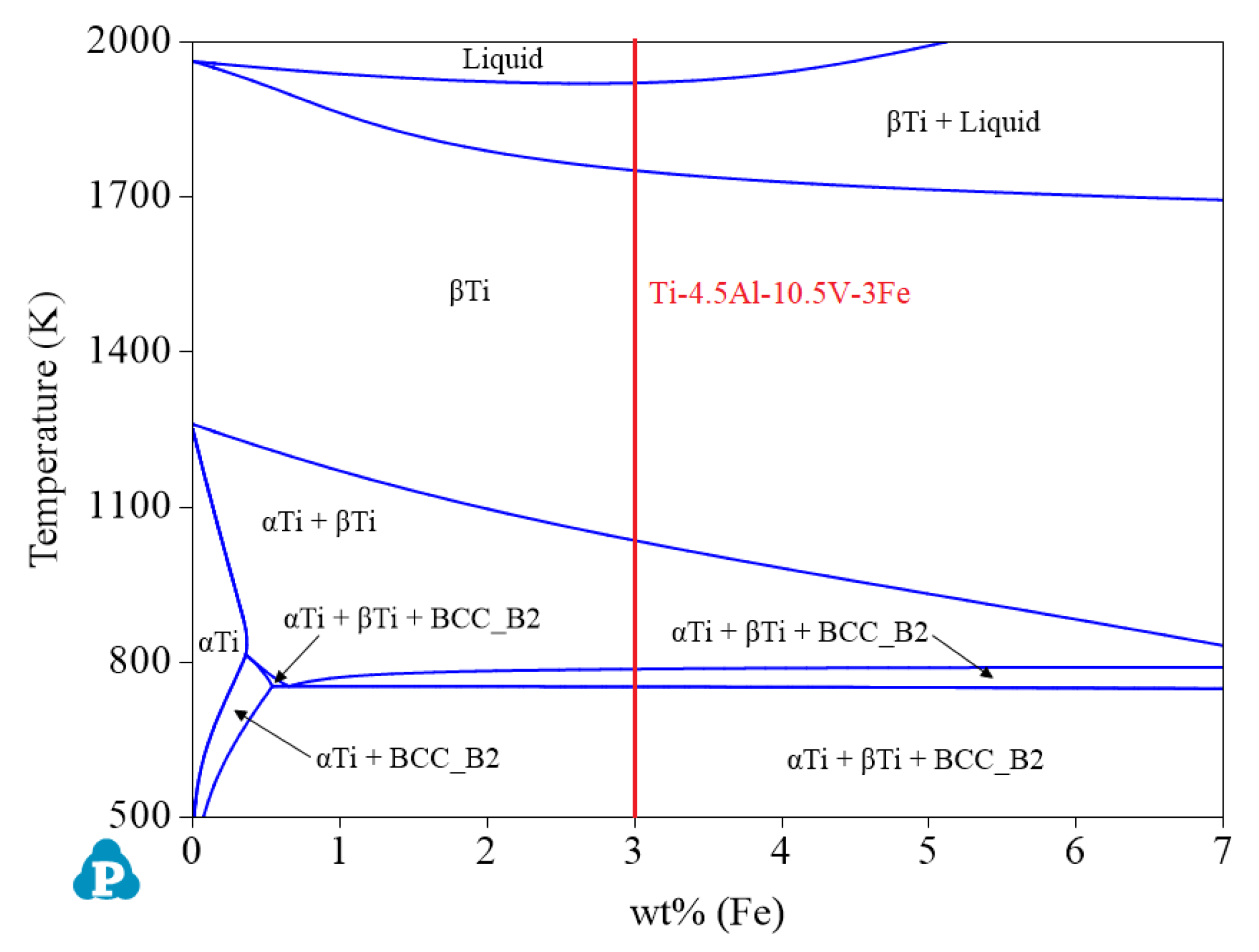
System	Phase	Struktur-Bericht	Prototype	Person Symbol	Space Group	References
Ti-Al	α(Al)	FCC_A1	Cu	cF4	$\mathrm{Fm}\overline{3}$m	[18]
	β	BCC_A2	W	cI2	$\mathrm{Im}\overline{3}$m	[18]
	β0	BCC_B2	CsCl	cI2	$\mathrm{Pm}\overline{3}$m	[18]
	α(Ti)	HCP_A3	Mg	hP2	P63/mmc	[18]
	Ti3Al	D019	Ni3Sn	hP8	P63/mmc	[18]
	TiAl	L10	AuCu	tP4	P4/mmm	[18]
	Ti3Al5	-	Ti3Al5	tP32	P4/mbm	[18]
	Ti2Al5	-	Ti2Al5	tP28	P4/mmm	[18]
	TiAl2	-	HfGa2	tI24	I41/amd	[18]
	H_TiAl3	D022	TiAl3(h)	tI8	I4/mmm	[18]
	L_TiAl3	-	TiAl3(l)	tI32	I4/mmm	[18]
Ti-Fe	γ(Fe)	FCC_A1	Cu	cF4	$\mathrm{Fm}\overline{3}$m	[36]
	β	BCC_A2	W	cI2	$\mathrm{Im}\overline{3}$m	[36]
	α(Ti)	HCP_A3	Mg	hP2	P63/mmc	[36]
	TiFe	BCC_B2	CsCl	cP2	$\mathrm{Pm}\overline{3}$m	[36]
	Fe2Ti	C14	MgZn2	hP12	P63/mmc	[36]
Ti-V	β	BCC_A2	W	cI2	$\mathrm{Im}\overline{3}$m	[27]
	α(Ti)	HCP_A3	Mg	hP2	P63/mmc	[27]
Fe-Al	γ(Fe) and α(Al)	FCC_A1	Cu	cF4	$\mathrm{Fm}\overline{3}$m	[30]
	β	BCC_A2	W	cI2	$\mathrm{Im}\overline{3}$m	[30]
	β0	BCC_B2	CsCl	cP8	$\mathrm{Pm}\overline{3}$m	[30]
	Al8Fe5	D82	Cu5Zn8	cI52	$\mathrm{I}4\overline{3}$m	[30]
	Al2Fe	-	Al2Fe	aP18	P1	[30]
	Al5Fe2	-	-	oC?	Cmcm	[30]
	Al13Fe4	-	-	mC102	C2/m	[30]
Al-V	α(Al)	FCC_A1	Cu	cF4	$\mathrm{Fm}\overline{3}$m	[37]
	β	BCC_A2	W	cI2	$\mathrm{Im}\overline{3}$m	[37]
	Al21V2	-	Al21V2	cF176	$\mathrm{Fd}\overline{3}$m	[37]
	Al45V7	-	Al45V7	mC104	C2/m	[37]
	Al23V4	-	Al23V4	hP54	P63/mmc	[37]
	Al3V	-	Al3Ti	tI8	I4/mmm	[37]
	Al8V5	-	Cu5Zn8	cI52	$\mathrm{I}\overline{4}$3m	[37]
Fe-V	γ(Fe)	FCC_A1	Cu	cF4	$\mathrm{Fm}\overline{3}$m	[38]
	β	BCC_A2	W	cI2	$\mathrm{Im}\overline{3}$m	[38]
	sigma	D8b	σCrFe	tP30	-	[38]

.

2.2. Ternary Systems

Since Ti-Al-Fe based alloys are widely used, the Ti-Al-Fe system has been very well investigated [39,40,41,42,43,44,45,46]. The thermodynamic parameters are accepted in this study from Hu et al. [46]. The Ti-Al-V ternary system was first evaluated by Hayes et al. [47] and reproduces experimental data from Farrar et al. [48]. Isothermal sections of 873 K to 1473 K were established by Ahmed et al. [49], and it was reported that at 1473 K or above, the assumed one-phase (Ti, V)₁Al₃ can be divided into two different phases. A new phase named H₂ in the alloys Al₅₅Ti₁₀V₃₅ and Al₆₂Ti₁₀V₂₈ was detected by Shao et al. [50,51] and Chang et al. [52], and the phase relationship at 1373 K was determined by Zhang et al. [53]. The thermodynamic re-assessment of this system was carried out based on the above experimental data by Kostov et al. [54], Wang et al. [55] and Lu et al. [56], and the thermodynamic parameters are accepted in this work by Lu et al. [56]. The Al-Fe-V system was studied by [57,58,59,60,61]. The Fe-rich angle phase diagram at 773 K was reported by Zhao et al. [59]. Subsequently, the Fe-rich isothermal sections at 923 K, 973 K and 1023 K were experimentally determined by Maebashi [60]. The latest thermodynamic description of this system was re-evaluated by Wang et al. [61], which was in good agreement with the above experimental data. Therefore, her work is accepted in the present work. The experimental data of the Ti-Fe-V system on the basis of previous work [62,63] were reviewed by Villars et al. [64] and recommended three isothermal sections at 300 K, 1073 K and 1273 K, two vertical sections at the FeTi-V and the Fe₂Ti-V joins and liquidus surface projection. Prima et al. [65] determined the homogeneity of V in the Fe₂Ti phase. Later, isothermal sections at 1273 K and 1473 K were confirmed by Massicot et al. [66], and a tentative liquidus surface projection with a quasi-peritectic reaction liquid + Fe₂Ti → bcc + FeTi at 1413 K was presented. Recently, the thermodynamic description of the Ti-Fe-V system was assessed by Guo et al. [67], where the model of the sigma phase is described as (Fe, Ti, V)₁₀(Fe, Ti, V)₂₀. We know that the three binary systems used in Guo’s work are Ti-V [25], Ti-Fe [23] and Fe-V [35], and the models of some phases of the latter two systems are modified. However, the literature review in Section 2.1 shows that the best evaluation of the three binary systems is the work of Ghosh et al. [27], Bo et al. [24] and Kumar et al. [35]. At the same time, to ensure the consistency of thermodynamic parameters in the present work, the thermodynamic parameters of the Ti-Fe-V system are re-optimized, and the binary systems used are Ti-V [27], Ti-Fe [24] and Fe-V [35], where the model of the sigma phase is defined as (Fe)₈(V)₄(Fe, Ti, V)₁₈.

3. Thermodynamic Modeling

3.1. Pure Elements

In the present work, the Gibbs energy function of each pure element is extracted from the SGTE (Scientific Group Thermodata Europe) compilation by Dinsdale et al. [68]. The Gibbs energy function of element i (i = Ti, Al, Fe and V) is described by the following equation:

$${}^{o}G_i^{\mathsf{\varphi }}\left(T\right)=G_i^{\mathsf{\varphi }}\left(T\right)-H_i^{SER}=a+bT+cTlnT+d{T}^2+\raisebox{1ex}{$e$}\!\left/ \!\raisebox{-1ex}{$T$}\right.+\dots$$

(1)

3.2. Solution Phases

In the Ti-Al-Fe-V quaternary system, solution phases liquid, FCC_A1, BCC_A2 and HCP_A3 are included, which are all described with the substitutional solution model. Their Gibbs energies are described by the following expression:

$${}_{}{}^{}G^{Ø}={\displaystyle \sum }_{i=1}^n{x}_i{}^{0}G_i^{Ø}+RT{\displaystyle \sum }_{i=1}^n{x}_{i}ln\left(x_i\right)+{}^{E}G^{Ø}$$

(2)

where $x_i$ is the mole fraction of the pure element $i$ (i = Ti, Al, Fe and V), ${}^{0}G_i^{Ø}$ is the Gibbs energy of the pure component $i$, n is equal to the number of elements in this system, $R$ is the gas constant and $T$ is the absolute temperature. ${}^{E}G^{Ø}$ is the excess Gibbs energy, expressed by the Redlich-Kister polynomial [69]:

$${}^{E}G^{Ø}={\displaystyle \sum }_{i,j=1\left(i\ne j\right)}^n{x}_i{x}_j{\displaystyle \sum }_{k=0}^m{L}_{\left(i,j\right)}^k{\left(x_i-x_j\right)}^k+{\displaystyle \sum }_{i,j,l=1\left(i\ne j\ne l\right)}^n{x}_i{x}_j{x}_l{\displaystyle \sum }_{k=i,j,l}{L}_k{V}_k$$

(3)

where $L_{\left(i,j\right)}^k$ is the binary interaction parameters between elements $i$ and $j$, $L_k$ is the ternary interaction parameters. The item $V_k$ is defined as:

$$V_k=x_k+(1-{\displaystyle \sum }_{p=i,j.l}{x}_p)/n$$

(4)

3.3. Intermetallic Compounds

In addition to the solution phases, other different types of intermetallic compounds are also included in the Ti-Al-Fe-V quaternary system. In the present work, different and appropriate sublattice models are used for different intermetallic compounds. The general expression of Gibbs energy of sublattice model is as follows:

$$G^{Ø}={}^{ref}G^{Ø}+{}^{id}G^{Ø}+{}^{E}G^{Ø}$$

(5)

where ${}^{ref}G^{Ø}$ is expressed in terms of compound energy and their associated sublattice species concentrations, $y_p^i$:

$${}^{ref}G^{Ø}=\sum y_p^i{y}_q^j\dots y_s^j{G}_{\left(p:q:\dots :s\right)}^0$$

(6)

where ${}^{id}G^{Ø}$ is the ideal mixing term, which assumes the random mixing of species on each sublattice:

$${}^{id}G^{Ø}=RT{\displaystyle \sum }_{i=1}^l{n}_i{\displaystyle \sum }_{p=1}^m{y}_p^{i}In\left(y_p^i\right)$$

(7)

where ${}^{E}G^{Ø}$ is the excess Gibbs energy, L is the interaction parameter between different species in the same sublattice:

$${}^{E}G^{Ø}=\sum y_p^i{y}_q^i{y}_r^j{L}_{\left(p:q:r\right)}$$

(8)

$$L_{\left(p:q:r\right)}={\displaystyle \sum }_v{L}_{\left(p:q:r\right)}^v{(y_p^i-y_q^j)}^v$$

(9)

4. Thermodynamic Optimization

The evaluations of all model parameters were carried out by recurrent runs of the Pan-optimizer module of Pandat software [70], which works by minimizing the square sum of the differences between experimental and computed values. Each piece of experimental information was given a certain weight, and the weight was varied systematically during the optimization process until most of the experimental data were accounted for within the estimated uncertainty limits. The step-by-step optimization method reported by Wang et al. [71] was used in the present work.

4.1. Ti-Fe-V System

Through the analysis in Section 2.2, combining the Ti-Fe system [24], Ti-V system [27] and Fe-V system [35], the Ti-Fe-V system is re-evaluated. The sigma phase is re-modeled as (Fe)₈(V)₄(Fe, Ti, V)₁₈, and the models of other phases refer to Guo’s [67] work to match the thermodynamic parameters of other systems in the present work. The experimental results reported by Massicot et al. [66] are used to reoptimize. The calculated isothermal sections at 1273 K and 1473 K in comparison with experimental data [66] are shown in Figure 7, and it is shown that the calculated results are in good agreement with the corresponding experimental data within the error. Figure 8 shows the calculated liquidus surface projection of the Ti-Fe-V system using the thermodynamic parameters of the present work. The thermodynamic parameters of the Fe-Ti-V system obtained in the present work are shown in

Table 2. Summary of the thermodynamic parameters in the Ti-Fe-V system.

Phase/Model	Thermodynamic Parameters	References
Liquid (Fe, Ti, V)1	${}_{}{}^{0}L{}_{Fe, Ti}^{Liquid}=-\mathrm{74,300}+17.839 T$	[24]
	${}_{}{}^{1}L{}_{Fe, Ti}^{Liquid}=8299.849-6.101 T$	[24]
	${}_{}{}^{0}L{}_{Fe, V}^{Liquid}=-\mathrm{35,963}+10.489 T$	[35]
	${}_{}{}^{1}L{}_{Fe,V}^{Liquid}=-4935+6.290 T$	[35]
	${}_{}{}^{0}L{}_{Ti,V}^{Liquid}=368.55$	[27]
	${}_{}{}^{1}L{}_{ Ti,V}^{Liquid}=2838.63$	[27]
	${}_{}{}^{0}L{}_{Fe,Ti,V}^{Liquid}=-\mathrm{99,808.75}+48.75 T$	This work
FCC_A1 (Fe, Ti, V)1	${}_{}{}^{0}L{}_{Fe, Ti}^{FCC\_A1}=-\mathrm{52,149.856}+9.265 T$	[24]
	${}_{}{}^{1}L{}_{Fe, Ti}^{FCC\_A1}=4755.900-4.982 T$	[24]
	${}_{}{}^{2}L{}_{Fe, Ti}^{FCC\_A1}=\mathrm{29,205.228}-11.046 T$	[24]
	${}_{}{}^{0}T{{}_c}_{Fe}^{FCC\_A1}=-201$	[24]
	${}_{}{}^{0}B{{}_{magn}}_{Fe}^{FCC\_A1}=-2.1$	[24]
	${}_{}{}^{0}L{}_{Fe, V}^{FCC\_A1}=-\mathrm{15,260}+1.765 T$	[35]
BCC_A2 (Fe, Ti, V)1	${}_{}{}^{0}L{}_{Fe, Ti}^{BCC\_A2}=-\mathrm{69,241.924}+25.246 T+0.0001 T^2+\mathrm{120,000} T^{-1}$	[24]
	${}_{}{}^{1}L{}_{Fe, Ti}^{BCC\_A2}=5018.986-4.992 T$	[24]
	${}_{}{}^{2}L{}_{Fe, Ti}^{BCC\_A2}=\mathrm{23,028.241}-13.110 T$	[24]
	${}_{}{}^{0}T{{}_c}_{Fe,Ti}^{BCC\_A2}=-2000$	[24]
	${}_{}{}^{0}L{}_{Fe, V}^{BCC\_A2}=-\mathrm{21,427}+6.846 T$	[35]
	${}_{}{}^{1}L{}_{Fe, V}^{BCC\_A2}=7345-1.509 T$	[35]
	${}_{}{}^{0}T{{}_c}_{Fe}^{BCC\_A2}=1043$	[35]
	${}_{}{}^{0}T{{}_c}_{Fe,V}^{BCC\_A2}=-110$	[35]
	${}_{}{}^{1}T{{}_c}_{Fe,V}^{BCC\_A2}=3075$	[35]
	${}_{}{}^{2}T{{}_c}_{Fe,V}^{BCC\_A2}=808$	[35]
	${}_{}{}^{3}T{{}_c}_{Fe,V}^{BCC\_A2}=-2169$	[35]
	${}_{}{}^{0}B{{}_{magn}}_{Fe}^{BCC\_A2}=2.22$	[35]
	${}_{}{}^{0}B{{}_{magn}}_{Fe,V}^{BCC\_A2}=-2.26$	[35]
	${}_{}{}^{0}L{}_{Ti, V}^{BCC\_A2}=6523.17$	[27]
	${}_{}{}^{1}L{}_{Ti, V}^{BCC\_A2}=2025.39$	[27]
	${}_{}{}^{0}L{}_{Fe,Ti,V}^{BCC\_A2}=-\mathrm{37,247.5}+7.5 T$	This work
HCP_A3 (Fe, Ti, V)1	${}_{}{}^{0}L{}_{Fe, Ti}^{HCP\_A3}=-\mathrm{25,000}+35.004 T$	[24]
	${}_{}{}^{0}L{}_{Ti,V}^{HCP\_A3}=\mathrm{13,223}$	[27]
BCC_B2 (Fe, Ti, V)0.5(Fe, Ti, V)0.5	${}_{}{}^{0}L{}_{Fe:Ti}^{BCC\_B2}=-\mathrm{30,028.003}+4.495 T$	[24]
	${}_{}{}^{0}L{}_{Ti:Fe}^{BCC\_B2}=-\mathrm{30,028.003}+4.495 T$	[24]
	${}_{}{}^{1}L{}_{Fe,Ti:Fe}^{BCC\_B2}=-5001.5$	[24]
	${}_{}{}^{1}L{}_{Fe:Fe,Ti}^{BCC\_B2}=-5001.5$	[24]
	${}_{}{}^{1}L{}_{Fe,Ti:Ti}^{BCC\_B2}=\mathrm{11,000}$	[24]
	${}_{}{}^{1}L{}_{Ti:Fe,Ti}^{BCC\_B2}=\mathrm{11,000}$	[24]
	${}_{}{}^{0}L{}_{Ti,V:Fe}^{BCC\_B2}=\mathrm{10,000}-1.58 T$	This work
	${}_{}{}^{0}L{}_{Fe:Ti,V}^{BCC\_B2}=\mathrm{10,000}-1.58 T$	This work
	${}_{}{}^{0}L{}_{Fe,V:Ti}^{BCC\_B2}=\mathrm{43,000}-13 T$	This work
	${}_{}{}^{0}L{}_{Ti:Fe,V}^{BCC\_B2}=\mathrm{43,000}-13 T$	This work
	${}_{}{}^{0}L{}_{Fe,Ti:V}^{BCC\_B2}=\mathrm{28,500}$	This work
	${}_{}{}^{0}L{}_{V:Fe,Ti}^{BCC\_B2}=\mathrm{28,500}$	This work
Sigma (Fe)8(V)4(Fe, Ti, V)18	${}_{}{}^{0}L{}_{Fe:V:Fe}^{Sigma}=8 {}_{}{}^{0}G{}_{Fe}^{fcc}+4 {}_{}{}^{0}G{}_V^{bcc}+18 {}_{}{}^{0}G{}_{Fe}^{bcc}-\mathrm{163,218}+41.607 T$	[35]
	${}_{}{}^{0}L{}_{Fe:V:V}^{Sigma}=8 {}_{}{}^{0}G{}_{Fe}^{fcc}+22 {}_{}{}^{0}G{}_V^{bcc}-\mathrm{183,967}-43.718 T$	[35]
	${}_{}{}^{0}L{}_{Fe:V:Ti}^{Sigma}=8 {}_{}{}^{0}G{}_{Fe}^{fcc}+4 {}_{}{}^{0}G{}_V^{bcc}+18 {}_{}{}^{0}G{}_{Ti}^{hcp}-\mathrm{231,015.15}-102.45 T$	This work
	${}_{}{}^{0}L{}_{Fe:V:Fe,Ti}^{Sigma}=-\mathrm{572,000}$	This work
	${}_{}{}^{0}L{}_{Fe:V:Ti,V}^{Sigma}=-\mathrm{388,097.5}+357.5 T$	This work
	${}_{}{}^{1}L{}_{Fe:V:Ti,V}^{Sigma}=-\mathrm{81,529}+73 T$	This work
	${}_{}{}^{0}L{}_{Fe:V:Fe,Ti,V}^{Sigma}=-\mathrm{138,521}+77 T$	This work
C14 (Fe, Ti, V)2(Fe, Ti, V)1	${}_{}{}^{0}L{}_{Fe:Fe}^{C14}=3 {}_{}{}^{0}G{}_{Fe}^{bcc}+\mathrm{15,000}$	[24]
	${}_{}{}^{0}L{}_{Fe:Ti}^{C14}=-\mathrm{85,500}+410.041 T-73.553 T lnT-0.01017 T^2+\mathrm{124,212.42} T^{-1}$	[24]
	${}_{}{}^{0}L{}_{Fe:V}^{C14}=2 {}_{}{}^{0}G{}_{Fe}^{bcc}+{}_{}{}^{0}G{}_V^{bcc}+\mathrm{15,000}$	This work
	${}_{}{}^{0}L{}_{Ti:Fe}^{C14}=3 {}_{}{}^{0}G{}_{Ti}^{hcp}+3{}_{}{}^{0}G{}_{Fe}^{bcc}+\mathrm{115,500}-410.041 T+73.553 T lnT+0.01017 T^2-\mathrm{124,212.42} T^{-1}$	[24]
	${}_{}{}^{0}L{}_{Ti:Ti}^{C14}=3 {}_{}{}^{0}G{}_{Ti}^{hcp}+\mathrm{15,000}$	[24]
	${}_{}{}^{0}L{}_{Ti:V}^{C14}=2 {}_{}{}^{0}G{}_{Ti}^{hcp}+{}_{}{}^{0}G{}_V^{bcc}+\mathrm{15,000}$	This work
	${}_{}{}^{0}L{}_{V:Fe}^{C14}=2 {}_{}{}^{0}G{}_V^{bcc}+{}_{}{}^{0}G{}_{Fe}^{bcc}+\mathrm{15,000}$	This work
	${}_{}{}^{0}L{}_{V:Ti}^{C14}=2 {}_{}{}^{0}G{}_V^{bcc}+{}_{}{}^{0}G{}_{Ti}^{hcp}+\mathrm{15,000}$	This work
	${}_{}{}^{0}L{}_{V:V}^{C14}=3 {}_{}{}^{0}G{}_V^{bcc}+\mathrm{15,000}$	This work
	${}_{}{}^{0}L{}_{Fe,V:Fe}^{C14}=-\mathrm{133,021.5}+45.5 T$	This work
	${}_{}{}^{0}L{}_{Fe,V:Ti}^{C14}=-\mathrm{82,412.5}+12.5 T$	This work
	${}_{}{}^{0}L{}_{Fe,V:V}^{C14}=-\mathrm{143,650}+50 T$	This work
	${}_{}{}^{0}L{}_{Ti,V:Ti}^{C14}=-\mathrm{10,830}$	This work
	${}_{}{}^{0}L{}_{Ti,V:V}^{C14}=-\mathrm{10,830}$	This work
	${}_{}{}^{0}L{}_{V:Fe,V}^{C14}=-5000$	This work

.

4.2. Ti-Al-Fe-V System

In view of no report on a new phase of Ti-Al-Fe-V quaternary system and the effect of the quaternary interaction parameters on the whole Gibbs energy can be ignored, the thermodynamic database of the Ti-Al-Fe-V quaternary system constructed by extrapolating from four ternary sub-systems using the Muggianu model [72]. For the four ternary sub-systems, as listed in

Table 3. Thermodynamic descriptions for constituent ternary sub-systems of the Ti-Al-Fe-V quaternary system, used in the present work.

System	Source of the Ternary Description	Constituent Binary System	Source of the Constituent Binary Description	Postscript
Ti-Al-Fe	Hu et al. [46]	Ti-Al	Witusiewicz et al. [18]	Adopted
		Ti-Fe	Bo et al. [24]
		Al-Fe	Sundman et al. [30]
Ti-Al-V	Lu et al. [56]	Ti-Al	Witusiewicz et al. [18]	Adopted
		Ti-V	Ghosh et al. [27]
		Al-V	Gong et al. [32]
Al-Fe-V	Wang et al. [61]	Al-Fe	Sundman et al. [30]	Adopted
		Al-V	Gong et al. [32]
		Fe-V	Kumar et al. [35]
Ti-Fe-V	Present work	Ti-Fe	Bo et al. [24]	Re-assessed in the present work
		Ti-V	Ghosh et al. [27]
		Fe-V	Kumar et al. [35]

, descriptions for Ti-Al-Fe [46], Ti-Al-V [56] and Al-Fe-V [61] were already available. Although a description for the Ti-Fe-V [67] system was also available, the thermodynamic parameters of Ti-Fe and Ti-V systems were derived from Keyzer et al. [23] and Zeng et al. [25]. It can be seen from Table 3 that the thermodynamic parameters of Ti-Fe and Ti-V systems accepted from Bo et al. [24] and Ghosh et al. [27] in the present work. In order to ensure the self-consistency of thermodynamic parameters, the Ti-Fe-V system was completely re-assessed covering the whole composition range.

The eventual purpose of the present work is to design novel titanium alloys containing Al, Fe and V elements by using calculated phase diagrams, and to provide theoretical guidance for the formulation of the heat treatment process of the designed titanium alloys. The next section will illustrate in detail with examples.

5. Alloy Design

The most fundamental aspect of alloy design is composition design, followed by the regulation of microstructure through smelting, processing and heat treatment to obtain excellent alloy properties. The composition design of titanium alloy refers to the determination of which alloying elements and the amount to be added to the titanium matrix under certain theoretical guidance, and then the prediction of the alloy performance. At present, the main method of composition design of titanium alloy is Mo equivalent method [73]. The formulae of Mo equivalent commonly used at present are as follows [74]:

[Mo]_eq = 1.0Mo + 0.67V + 0.44W + 0.28Nb + 0.22Ta + 2.9Fe + 1.58Cr + 1.56Mn − 1.0Al

(10)

Although Mo equivalent can guide the design of different types of titanium alloys, there are also design blind spots. When Mo equivalent method is used to design titanium alloys, the content of various alloying elements still depends on the selection of experience, and the emergence of brittle phase cannot be avoided precisely, nor can it provide theoretical guidance for subsequent heat treatment process. In the present work, for the design of titanium alloys, a method combining Mo equivalent with CALPHAD is proposed. The new method can not only jointly and accurately guide the design of alloy composition, but also provide an exact theoretical basis for subsequent heat treatment of the designed alloy. Taking the Ti-Al-Fe-V quaternary system as an example, the process of designing alloys using this new method will be described in detail below.

In the development of novel titanium alloys, Al remains the most important and commonly used α stabilizer, which can suppress the formation of ω phase to a certain extent and promote the transformation of brittle phase ω into α phase [75]. Although the ultimate solubility of Al in Ti is 7.5 wt%, when the content of Al exceeds 6.0 wt%, the brittle phase Ti₃Al will easily appear below 400 K, as shown in Figure 1, therefore, the content of Al should not exceed 6.0 wt%.

Table 4. Some titanium alloys developed in various countries.

Country	Trade Mark	Nominal Composition (wt%)	References
USA	Timetal 62S	Ti-6Al-1.7Fe-0.1Si	[78]
	Timetal 21S	Ti-15Mo-2.7Nb-3Al-0.2Si	[79]
	Ti-1023	Ti-10V-2Fe-3Al	[80]
Japan	SP-700	Ti-4.5Al-3V-2Mo-2Fe	[78]
	KSTi-9	Ti-4.5Al-2Mo-1.6V-0.5Fe-0.3Si-0.03C	[81]
China	Ti8LC	Ti-6Al-1Fe-1Mo	[78]
	Ti12LC	Ti-4.5Al-1.5Fe-6.8Mo	[78]
	-	Ti-3Al-3.7Cr-2Fe	[82]

lists some titanium alloys developed in various countries [76], and the Al content of these alloys focuses in 3.0, 4.5 and 6.0 wt%. These three Al contents were also selected in this work. When the Al content is fixed, the focus transfers to the ratio of the elements Fe and V, and this proportion can be determined by the phase diagram of the Fe-V system, as shown in Figure 6. Based on the Fe-V phase diagram, it could be known that the sigma brittle phase and β and sigma two-phase region existed in a wide range of components. To avoid the presence of sigma brittle phase in the designed alloy microstructure at room temperature, the selected component proportion should be V:Fe ≥ 7.3:1 or V:Fe ≤ 1:3.7. Although the cost of alloy is greatly reduced when V:Fe ≤ 1:3.7 is selected for alloy design, the brittle phase of Fe₂Ti is more likely to appear with increasing Fe content, which seriously affects the mechanical properties of the alloy [77]. In addition, regardless of which heat treatment method is adopted in the subsequent heat treatment process, the temperature is always higher than the recrystallization temperature of pure titanium at 853 K (580 °C), and the ratio of V:Fe corresponding to this temperature is 2.9:1, so the ratio of V:Fe is optional in the range of 2.9:1 to 7.3:1, that is, the S part marked in Figure 6. The ratio of V:Fe = 3.5:1 is recommended to design novel titanium alloys.

The pseudo-binary sections are calculated based on the thermodynamic database of the Ti-Al-Fe-V system, with the ratio of V: Fe = 3.5:1 and Al contents of 0.0, 3.0, 4.5 and 6.0 wt%. The calculation results of these pseudo-binary sections are shown in Figure 9, Figure 10, Figure 11 and Figure 12. It can be seen that with the increase in Al content, the solid solution area of α phase increases inch by inch, while the solid solution area of β phase decreases gradually. This indicates that in the Ti-Al-Fe-V system, an Al content of 6.0 wt% is suitable for the design of α titanium alloy, and an Al content of 3.0 wt% is suitable for the design of β titanium alloy. Between both, an α + β titanium alloy could be designed. Combined with these pseudo-binary sections, it can be seen that the brittle phase has been successfully avoided in the composition design of titanium alloys, thus the degradation of the titanium alloy properties is avoided. From Figure 9, Figure 10, Figure 11 and Figure 12, it can be seen that the pseudo-binary sections can not only provide guidance for the design of titanium alloys, but also provide a theoretical basis for subsequent heat treatment process of the designed titanium alloys according to the transformation temperature of (α + β)/β. Leyens [83] pointed out that the minimum value of Mo equivalent of approximately 10 is necessary to obtain the α + β dual phase titanium alloys during quenching, and around 30 for pure β titanium alloys. The critical concentrations of V and Fe for obtaining the α, α + β and β titanium alloys are determined via the formula of Mo equivalent [74], as shown in

Table 5. The critical content of the element Fe and V in different types of titanium alloys with different Al content.

The Content of Al (wt%)	The Content of Fe and V in α Titanium Alloys		The Content of Fe and V in α + β Titanium Alloys		The Content of Fe and V in β Titanium Alloys
	Fe (wt%)	V (wt%)	Fe (wt%)	V (wt%)	Fe (wt%)	V (wt%)
3.0	<2.48	<8.68	2.48–6.29	8.68–22.02	>6.29	>22.02
4.5	<2.76	<9.66	2.76–6.58	9.66–23.03	>6.58	>23.03
6.0	<3.05	<10.68	3.05–6.86	10.68–24.01	>6.86	>24.01

.

Using the method of combining Mo equivalent with CALPHAD, three different types of novel titanium alloys are suggested below:

(1)

As a strengthening element of the α phase, the α single-phase region of a keeps expanding with increasing Al content. Figure 12 shows that when the Al content is 6.0 wt%, the largest α single-phase region is observed. Therefore, if you want to design α titanium alloys of the Ti-Al-Fe-V system, 6.0 wt% Al can be preferred. At this time, the ranges of Fe and V are 0–3.05 wt% and 0–10.68 wt%, respectively. The recommended alloy composition is Ti-6Al-3.5V-1Fe, and its actual Mo equivalent is −0.755, which is considered to be 0.

(2)

V and Fe, as β phase reinforcing elements, can enlarge the β phase region. To obtain β titanium alloy, the content of elements V and Fe should be within the appropriate range as much as possible. Figure 10 shows that when the Al content is 3.0 wt%, the largest β single-phase region is observed. Therefore, if you want to design β titanium alloys of the Ti-Al-Fe-V system, 3.0 wt% Al can be preferred. At this time, the ranges of Fe and V are greater than 6.29 wt% and 22.02 wt%, respectively. The recommended alloy composition is Ti-3Al-22.75V-6.5Fe, and its Mo equivalent is 31.

(3)

Although α titanium alloys and β titanium alloys can also be designed when the Al content is 4.5 wt%, the range of options did not reach the optimal when compared with the other two concentrations. Therefore, when the Al content is 4.5 wt%, as shown in Figure 11, priority should be given to design α + β titanium alloys. At this time, the ranges of Fe and V are 2.76–6.58 wt% and 9.66–23.03 wt%, respectively. The recommended alloy composition is Ti-4.5Al-10.5V-3Fe, and its Mo equivalent is 11.2.

Figure 10, Figure 11 and Figure 12 are thermodynamic equilibrium phase diagram, from which it can be seen that the designed α, α + β and β titanium alloys cannot be obtained at room temperature. However, due to the factors of alloy diffusion kinetics, the designed α, α + β and β titanium alloys can be obtained at room temperature by adopting appropriate heat treatment process. Three types of titanium alloys have been successfully designed by the method and the properties of these alloys need to be further studied.

6. Conclusions

In the present work, the experimental investigation and thermodynamic description of the relative sub-systems of the Ti-Al-Fe-V quaternary system were summarized and reviewed. The Ti-Fe-V system was re-assessment based on critical review of experimental data, and the calculated results were in satisfactory agreement with the reported experimental data. The thermodynamic database of the Ti-Al-Fe-V quaternary system was subsequently established by extrapolating the thermodynamic descriptions of the accepted sub-binary and sub-ternary systems. Then, the method of titanium alloy design combining Mo equivalent with CALPHAD was proposed. The pseudo-binary sections with V:Fe = 3.5:1 and Al = 0.0, 3.0, 4.5 and 6.0 wt% were calculated. Finally, three different types of titanium alloys were recommended according to the proposed method: α titanium alloy (Ti-6Al-3.5V-1Fe), β titanium alloy (Ti-3Al-22.75V-6.5Fe) and α + β titanium alloy (Ti-4.5Al-10.5V-3Fe). The thermodynamic database established and the method proposed in the present work are expected to guide future development of titanium alloys containing Al, Fe and V.