Long-Term Ultrasonic Benchmarking for Microstructure Characterization with Bayesian Updating
Abstract
:1. Introduction
2. Methods
2.1. Traditional Bayesian Regression Model
2.2. Hierarchical Bayesian Regression Model
3. Experiments and Results
3.1. Experimental Preparations
3.2. Results for First Week without Updating
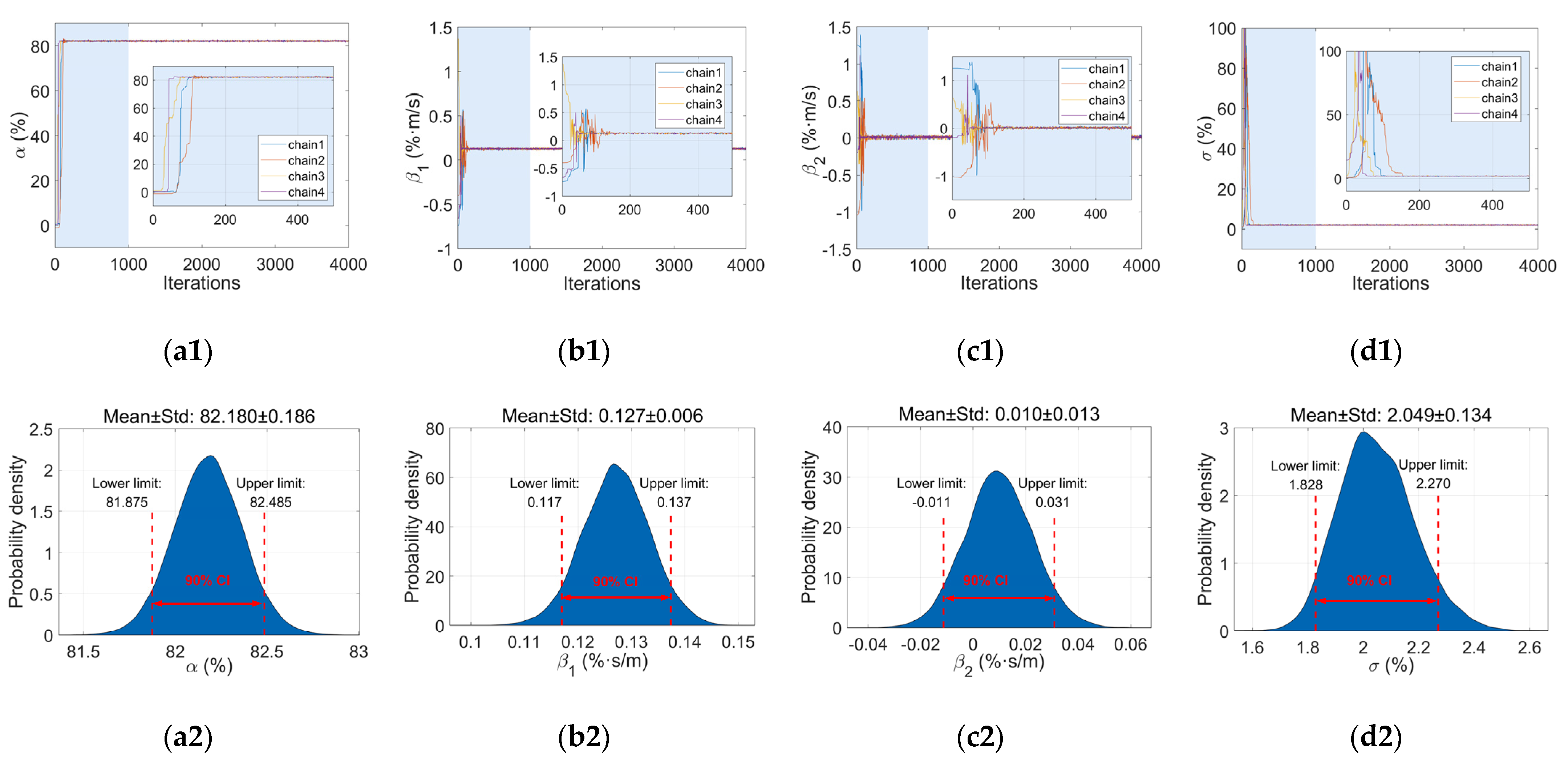
3.2.1. Traditional Model
3.2.2. Hierarchical Model
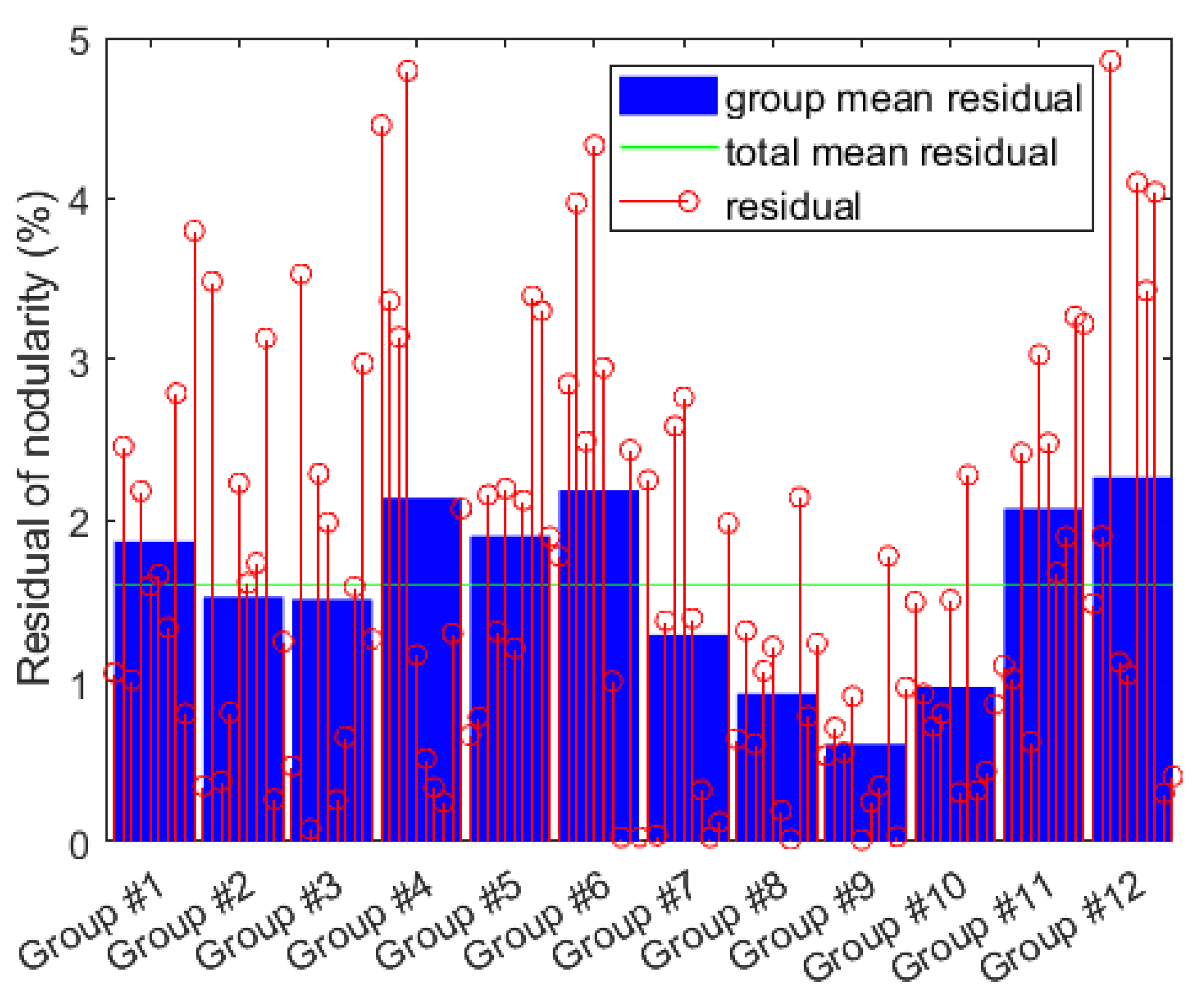
3.3. Results for Thirteen Weeks with Updating
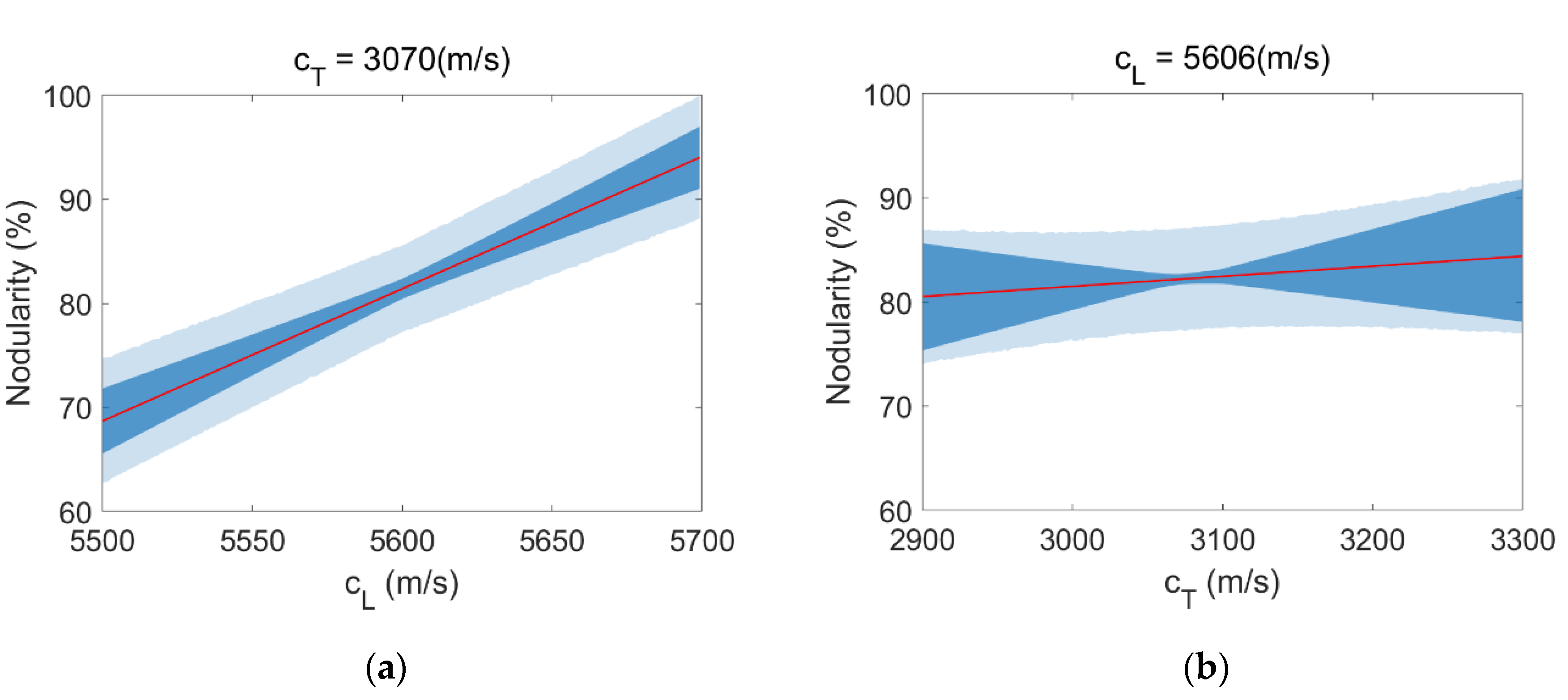
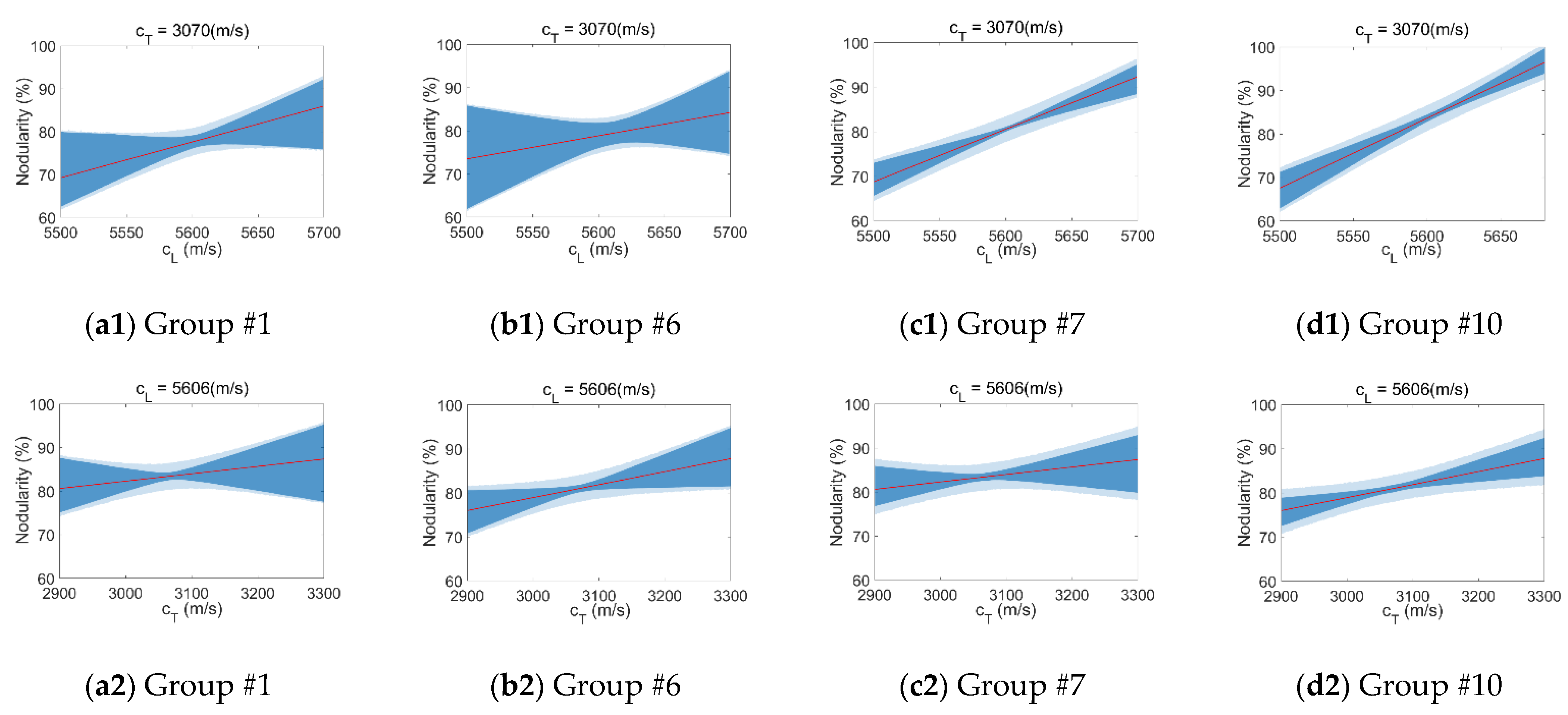
3.3.1. Traditional Model
3.3.2. Hierarchical Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cui, C.Y.; Gu, Y.F.; Yuan, Y.; Osada, T.; Harada, H. Enhanced mechanical properties in a new Ni–Co base superalloy by controlling microstructures. Mater. Sci. Eng. A 2011, 528, 5465–5469. [Google Scholar] [CrossRef]
- Huang, H.; Talreja, R. Effects of void geometry on elastic properties of unidirectional fiber reinforced composites. Compos. Sci. Technol. 2005, 65, 1964–1981. [Google Scholar] [CrossRef]
- Kumar, A.S.; Kumar, B.R.; Datta, G.L.; Ranganath, V.R. Effect of microstructure and grain size on the fracture toughness of a micro-alloyed steel. Mater. Sci. Eng. A 2010, 527, 954–960. [Google Scholar] [CrossRef]
- Liang, C.; Ma, M.X.; Jia, M.T.; Raynova, S.; Yan, J.Q.; Zhang, D.L. Microstructures and tensile mechanical properties of Ti–6Al–4V bar/disk fabricated by powder compact extrusion/forging. Mater. Sci. Eng. A 2014, 619, 290–299. [Google Scholar] [CrossRef]
- Osório, W.R.; Freire, C.M.; Garcia, A. The role of macrostructural morphology and grain size on the corrosion resistance of Zn and Al castings. Mater. Sci. Eng. A 2005, 402, 22–32. [Google Scholar] [CrossRef]
- Epp, J. 4—X-ray diffraction (XRD) techniques for materials characterization. In Materials Characterization Using Nondestructive Evaluation (NDE) Methods; Hübschen, G., Altpeter, I., Tschuncky, R., Herrmann, H.-G., Eds.; Woodhead Publishing: Duxford, UK, 2016; pp. 81–124. [Google Scholar]
- Hübschen, G. 7—Ultrasonic techniques for materials characterization. In Materials Characterization Using Nondestructive Evaluation (NDE) Methods; Hübschen, G., Altpeter, I., Tschuncky, R., Herrmann, H.-G., Eds.; Woodhead Publishing: Duxford, UK, 2016; pp. 177–224. [Google Scholar]
- Inkson, B.J. 2—Scanning electron microscopy (SEM) and transmission electron microscopy (TEM) for materials characterization. In Materials Characterization Using Nondestructive Evaluation (NDE) Methods; Hübschen, G., Altpeter, I., Tschuncky, R., Herrmann, H.-G., Eds.; Woodhead Publishing: Duxford, UK, 2016; pp. 17–43. [Google Scholar]
- Pandey, D.; Pandey, S. Ultrasonics: A Technique of Material Characterization. In Acoustic Waves; IntechOpen: Rijeka, Croatia, 2010; pp. 397–398. [Google Scholar]
- Du, H.; Turner, J.A. Ultrasonic attenuation in pearlitic steel. Ultrasonics 2014, 54, 882–887. [Google Scholar] [CrossRef] [PubMed]
- Thompson, R.B.; Margetan, F.J.; Haldipur, P.; Yu, L.; Li, A.; Panetta, P.; Wasan, H. Scattering of elastic waves in simple and complex polycrystals. Wave Motion 2008, 45, 655–674. [Google Scholar] [CrossRef]
- Chassignole, B.; Duwig, V.; Ploix, M.A.; Guy, P.; El Guerjouma, R. Modelling the attenuation in the ATHENA finite elements code for the ultrasonic testing of austenitic stainless steel welds. Ultrasonics 2009, 49, 653–658. [Google Scholar] [CrossRef] [PubMed]
- Chimenti, D.E. Review of air-coupled ultrasonic materials characterization. Ultrasonics 2014, 54, 1804–1816. [Google Scholar] [CrossRef] [PubMed]
- Yap, Y.L.; Toh, W.; Koneru, R.; Chua, Z.Y.; Lin, K.; Yeoh, K.M.; Lim, C.M.; Lee, J.S.; Plemping, N.A.; Lin, R.; et al. Finite element analysis of 3D-Printed Acrylonitrile Styrene Acrylate (ASA) with Ultrasonic material characterization. Int. J. Comput. Mater. Sci. Eng. 2019, 08, 1950002. [Google Scholar] [CrossRef]
- Schmidt, J.; Marques, M.R.G.; Botti, S.; Marques, M.A.L. Recent advances and applications of machine learning in solid-state materials science. NPJ Comput. Mater. 2019, 5, 83. [Google Scholar] [CrossRef]
- Kushibiki, J.; Ono, Y.; Ohashi, Y. Experimental considerations on water-couplant temperature for accurate velocity measurements by the LFB ultrasonic material characterization system. In Proceedings of the 2000 IEEE Ultrasonics Symposium. Proceedings. An International Symposium (Cat. No.00CH37121), San Juan, PR, USA, 22–25 October 2000; Volume 1, pp. 619–623. [Google Scholar]
- Schmerr, L.W. Simulating the Experiments of the 2004 Ultrasonic Benchmark Study. AIP Conf. Proc. 2005, 760, 1880–1887. [Google Scholar]
- Song, S.J.; Schmerr, L.W., Jr.; Thompson, R.B. Ultrasonic Benchmarking Study: Overview Up to Year 2005. AIP Conf. Proc. 2006, 820, 1844–1853. [Google Scholar] [CrossRef]
- Liu, Y.; Kalkowski, M.K.; Huang, M.; Lowe, M.J.S.; Samaitis, V.; Cicėnas, V.; Schumm, A. Can ultrasound attenuation measurement be used to characterise grain statistics in castings? Ultrasonics 2021, 115, 106441. [Google Scholar] [CrossRef] [PubMed]
- Peng, S.; Chen, X.; Wu, G.; Li, M.; Chen, H. Ultrasound Evaluation of the Primary α Phase Grain Size Based on Generative Adversarial Network. Sensors 2022, 22, 3274. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Liu, Y. Bayesian Information Fusion of Multmodality Nondestructive Measurements for Probabilistic Mechanical Property Estimation. In Proceedings of the ASME 2020 International Mechanical Engineering Congress and Exposition, Online, 16–19 November 2020. [Google Scholar]
- Guan, X.; Jha, R.; Liu, Y. Maximum Entropy Method for Model and Reliability Updating Using Inspection Data. In Proceedings of the AIAA 2010-2591. 51st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Orlando, FL, USA, 12–15 April 2010. [Google Scholar]
- Guan, X.; Jha, R.; Liu, Y. Model selection, updating, and averaging for probabilistic fatigue damage prognosis. Struct. Saf. 2011, 33, 242–249. [Google Scholar] [CrossRef]
- Yang, J.; He, J.; Guan, X.; Wang, D.; Chen, H.; Zhang, W.; Liu, Y. A probabilistic crack size quantification method using in-situ Lamb wave test and Bayesian updating. Mech. Syst. Signal Processing 2016, 78, 118–133. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, N.; Ersoy, D.; Liu, Y. Manifold-based Conditional Bayesian network for aging pipe yield strength estimation with non-destructive measurements. Reliab. Eng. Syst. Saf. 2022, 223, 108447. [Google Scholar] [CrossRef]
- Tant, K.M.M.; Galetti, E.; Mulholland, A.J.; Curtis, A.; Gachagan, A. A transdimensional Bayesian approach to ultrasonic travel-time tomography for non-destructive testing. Inverse Probl. 2018, 34, 095002. [Google Scholar] [CrossRef] [Green Version]
- Bai, L.; Le Bourdais, F.; Miorelli, R.; Calmon, P.; Velichko, A.; Drinkwater, B.W. Ultrasonic Defect Characterization Using the Scattering Matrix: A Performance Comparison Study of Bayesian Inversion and Machine Learning Schemas. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 3143–3155. [Google Scholar] [CrossRef]
- Bai, L.; Zhang, J.; Velichko, A.; Drinkwater, B.W. The use of full-skip ultrasonic data and Bayesian inference for improved characterisation of crack-like defects. NDT E Int. 2021, 121, 102467. [Google Scholar] [CrossRef]
- Austin, P.; Goel, V.; van Walraven, C. An Introduction to Multilevel Regression Models. Can. J. Public Health 2001, 92, 150–154. [Google Scholar] [CrossRef] [PubMed]
- Aldrin, J.C.; Knopp, J.S.; Sabbagh, H.A. Bayesian methods in probability of detection estimation and model-assisted probability of detection evaluation. AIP Conf. Proc. 2013, 1511, 1733–1740. [Google Scholar] [CrossRef] [Green Version]
- Chiachío, J.; Bochud, N.; Chiachío, M.; Cantero, S.; Rus, G. A multilevel Bayesian method for ultrasound-based damage identification in composite laminates. Mech. Syst. Signal Processing 2017, 88, 462–477. [Google Scholar] [CrossRef] [Green Version]
- Bürkner, P.-C. brms: An R Package for Bayesian Multilevel Models Using Stan. J. Stat. Softw. 2017, 80, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Gelman, A.; Carlin, J.; Stern, H.; Dunson, D.; Vehtari, A.; Rubin, D. Bayesian Data Analysis; Chapman and Hall/CRC: New York, NY, USA, 2013; pp. 16–31. [Google Scholar]
- Schneider, A.; Hommel, G.; Blettner, M. Linear regression analysis: Part 14 of a series on evaluation of scientific publications. Dtsch. Arztebl. Int. 2010, 107, 776–782. [Google Scholar] [CrossRef]
- Papadakis, E.P. Ultrasonic attenuation caused by Rayleigh scattering by graphite nodules in nodular cast iron. J. Acoust. Soc. Am. 1981, 70, 782–787. [Google Scholar] [CrossRef]
- ISO 945-4; Microstructure of Cast Irons—Part 4: Test Method for Evaluating Nodularity in Spheroidal Graphite Cast Irons. ISO: Geneva, Switzerland, 2019; p. 38.
- Liu, Y.; Song, Y.; Li, X.; Chen, C.; Zhou, K. Evaluating the reinforcement content and elastic properties of Mg-based composites using dual-mode ultrasonic velocities. Ultrasonics 2017, 81, 167–173. [Google Scholar] [CrossRef]
- Peter, D.H. Kernel estimation of a distribution function. Commun. Stat. —Theory Methods 1985, 14, 605–620. [Google Scholar] [CrossRef]
- Watanabe, S. Asymptotic Equivalence of Bayes Cross Validation and Widely Applicable Information Criterion in Singular Learning Theory. J. Mach. Learn. Res. 2010, 11, 3571–3594. [Google Scholar]





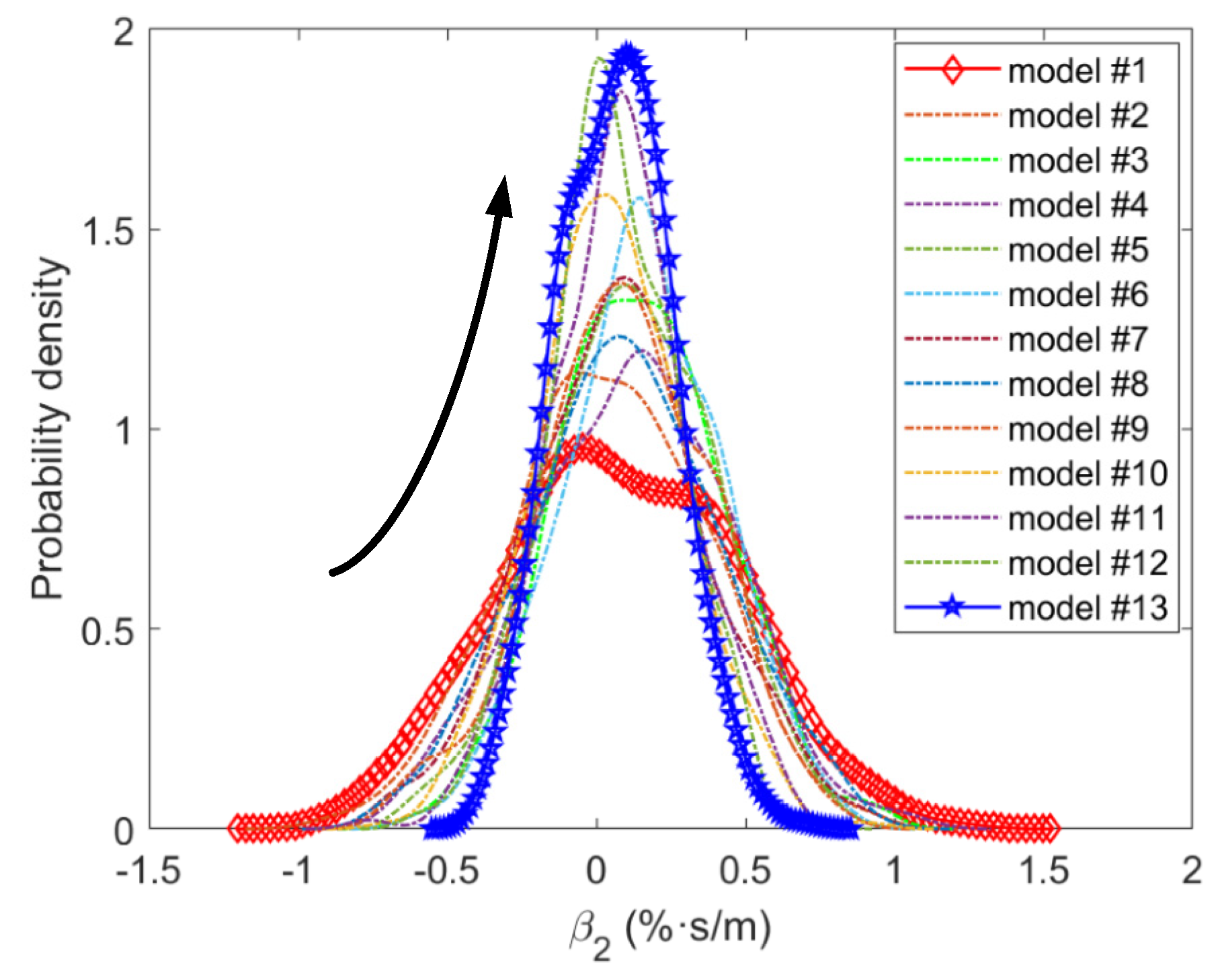
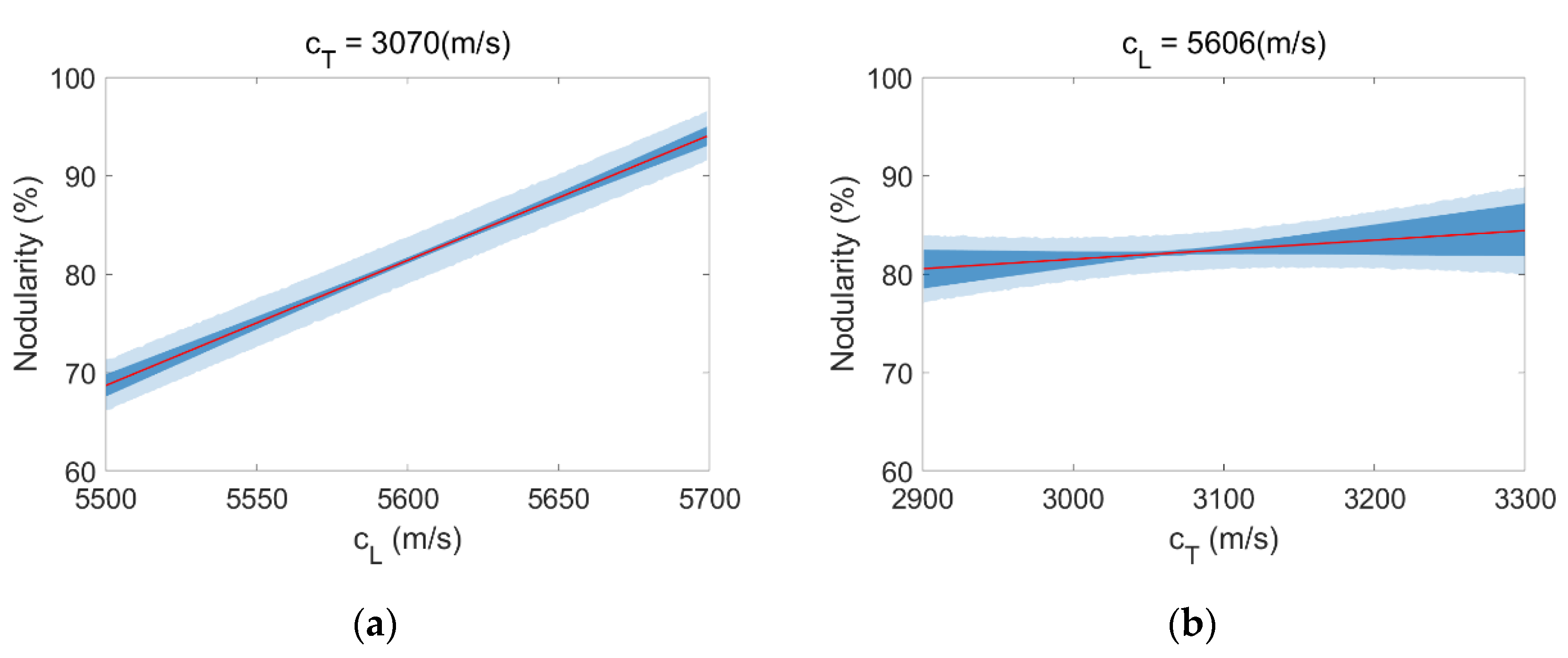
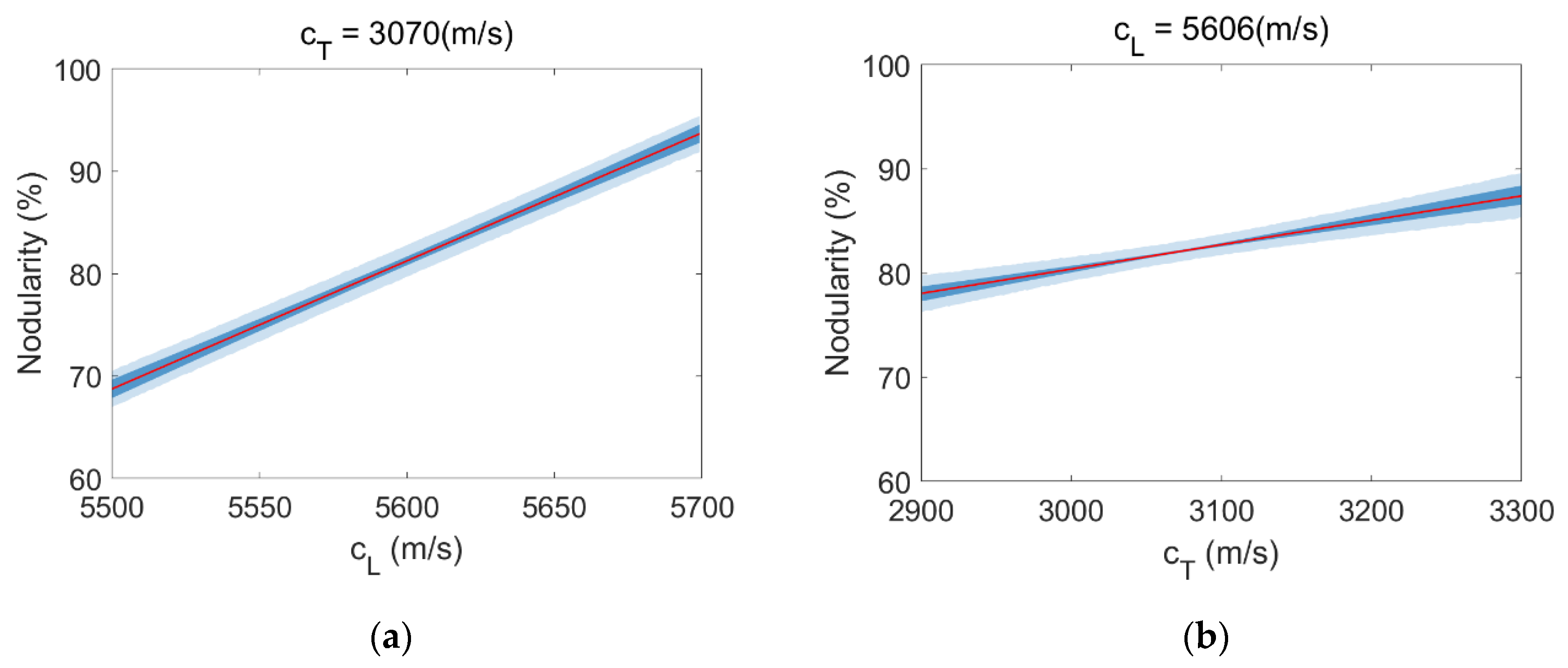
| No. | Damping (Ohms) | Expertise Level | Noise Level |
|---|---|---|---|
| 1 | 333 | Senior | High |
| 2 | 49 | Senior | High |
| 3 | 25 | Senior | High |
| 4 | 333 | Junior | High |
| 5 | 49 | Junior | High |
| 6 | 25 | Junior | High |
| 7 | 333 | Senior | Low |
| 8 | 49 | Senior | Low |
| 9 | 25 | Senior | Low |
| 10 | 333 | Junior | Low |
| 11 | 49 | Junior | Low |
| 12 | 25 | Junior | Low |
| Parameters | Mean | Standard Deviation | 90% CI | |||
|---|---|---|---|---|---|---|
| Lower Bound | Upper Bound | |||||
| Fixed effects | γα | 82.163 | 0.189 | 81.785 | 82.534 | |
| 0.128 | 0.008 | 0.115 | 0.141 | |||
| 0.053 | 0.378 | −0.641 | 1.302 | |||
| να,1 | −0.104 | 0.052 | −0.190 | 0.018 | ||
| να,2 | −0.063 | 0.056 | −0.192 | 0.056 | ||
| −0.002 | 0.002 | −0.006 | 0.001 | |||
| 0.001 | 0.003 | −0.006 | 0.007 | |||
| 0.062 | 0.213 | −0.040 | 0.642 | |||
| −0.218 | 0.589 | −2.124 | 0.017 | |||
| Random effects | Second level | 0.533 | 0.561 | 0.027 | 1.974 | |
| 0.907 | 1.002 | 0.032 | 3.446 | |||
| σα | 2.382 | 2.076 | 0.113 | 6.777 | ||
| −0.162 | 0.514 | −0.899 | 0.793 | |||
| −0.174 | 0.516 | −0.827 | 0.771 | |||
| −0.259 | 0.514 | −0.895 | 0.695 | |||
| Base level | σ | 1.721 | 0.122 | 1.521 | 1.921 | |
| Items | Metallographic Method (%) | Least-Square Fitting Method (%) | Traditional Model,1st Week (%) | Hierarchical Model, 1st Week (%) | ||
|---|---|---|---|---|---|---|
| T-1 | Mean | 77.30 | 78.15 | 79.26 | 78.89 | |
| Std | 2.3 | - | 8.9 | 5.3 | ||
| 90% CI | Lower | - | - | 64.62 | 70.17 | |
| Upper | - | - | 93.90 | 87.61 | ||
| T-2 | Mean | 81.00 | 81.96 | 79.38 | 79.30 | |
| Std | 2.7 | - | 9.1 | 4.3 | ||
| 90% CI | Lower | - | - | 64.41 | 72.23 | |
| Upper | - | - | 94.35 | 86.37 | ||
| Items | Traditional Model,6th Week (%) | Hierarchical Model, 6th Week (%) | Traditional Model, 13th Week (%) | Hierarchical Model, 13th Week (%) | ||
| T-1 | Mean | 79.04 | 78.31 | 78.33 | 77.91 | |
| Std | 4.8 | 3.6 | 3.3 | 2.3 | ||
| 90% CI | Lower | 86.94 | 72.39 | 72.90 | 74.13 | |
| Upper | 71.14 | 84.23 | 83.76 | 81.70 | ||
| T-2 | Mean | 82.22 | 80.14 | 81.75 | 80.71 | |
| Std | 5.0 | 3.8 | 3.1 | 2.3 | ||
| 90% CI | Lower | 74.00 | 86.39 | 76.65 | 76.93 | |
| Upper | 90.45 | 73.89 | 86.85 | 84.50 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Song, Y.; Li, X.; Ni, P. Long-Term Ultrasonic Benchmarking for Microstructure Characterization with Bayesian Updating. Metals 2022, 12, 1088. https://doi.org/10.3390/met12071088
Zhang F, Song Y, Li X, Ni P. Long-Term Ultrasonic Benchmarking for Microstructure Characterization with Bayesian Updating. Metals. 2022; 12(7):1088. https://doi.org/10.3390/met12071088
Chicago/Turabian StyleZhang, Feng, Yongfeng Song, Xiongbing Li, and Peijun Ni. 2022. "Long-Term Ultrasonic Benchmarking for Microstructure Characterization with Bayesian Updating" Metals 12, no. 7: 1088. https://doi.org/10.3390/met12071088





