The Influence of Laser Power and Scan Speed on the Dimensional Accuracy of Ti6Al4V Thin-Walled Parts Manufactured by Selective Laser Melting
Abstract
:1. Introduction
2. Experimental Procedure
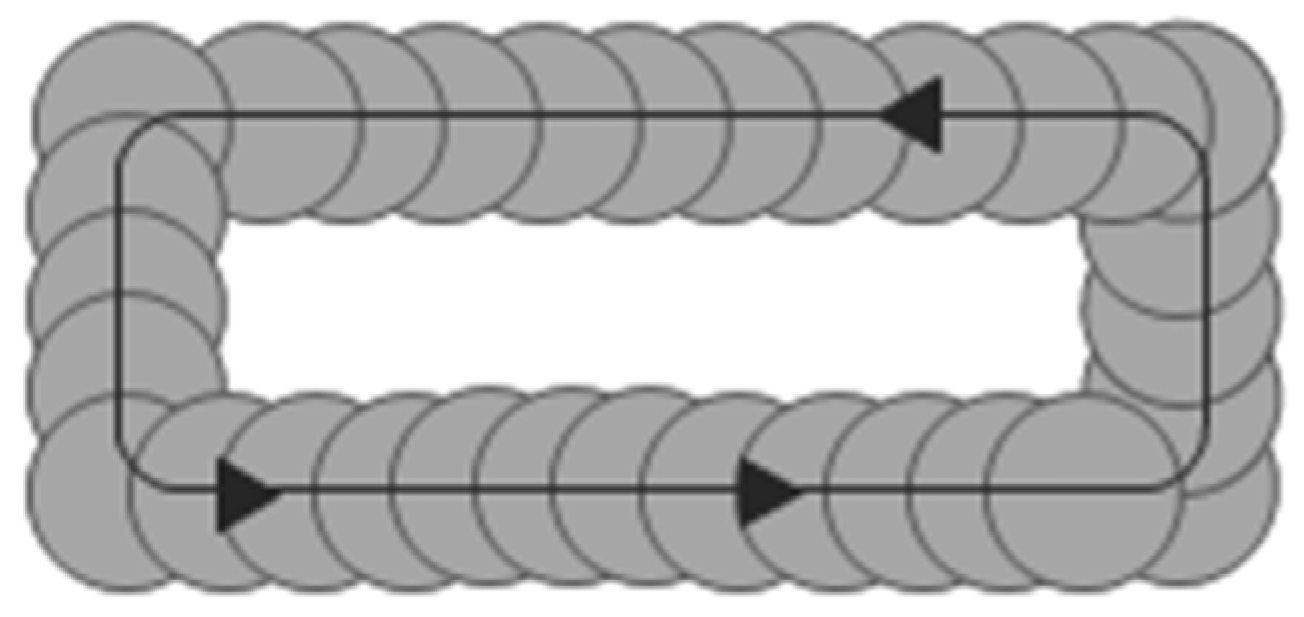
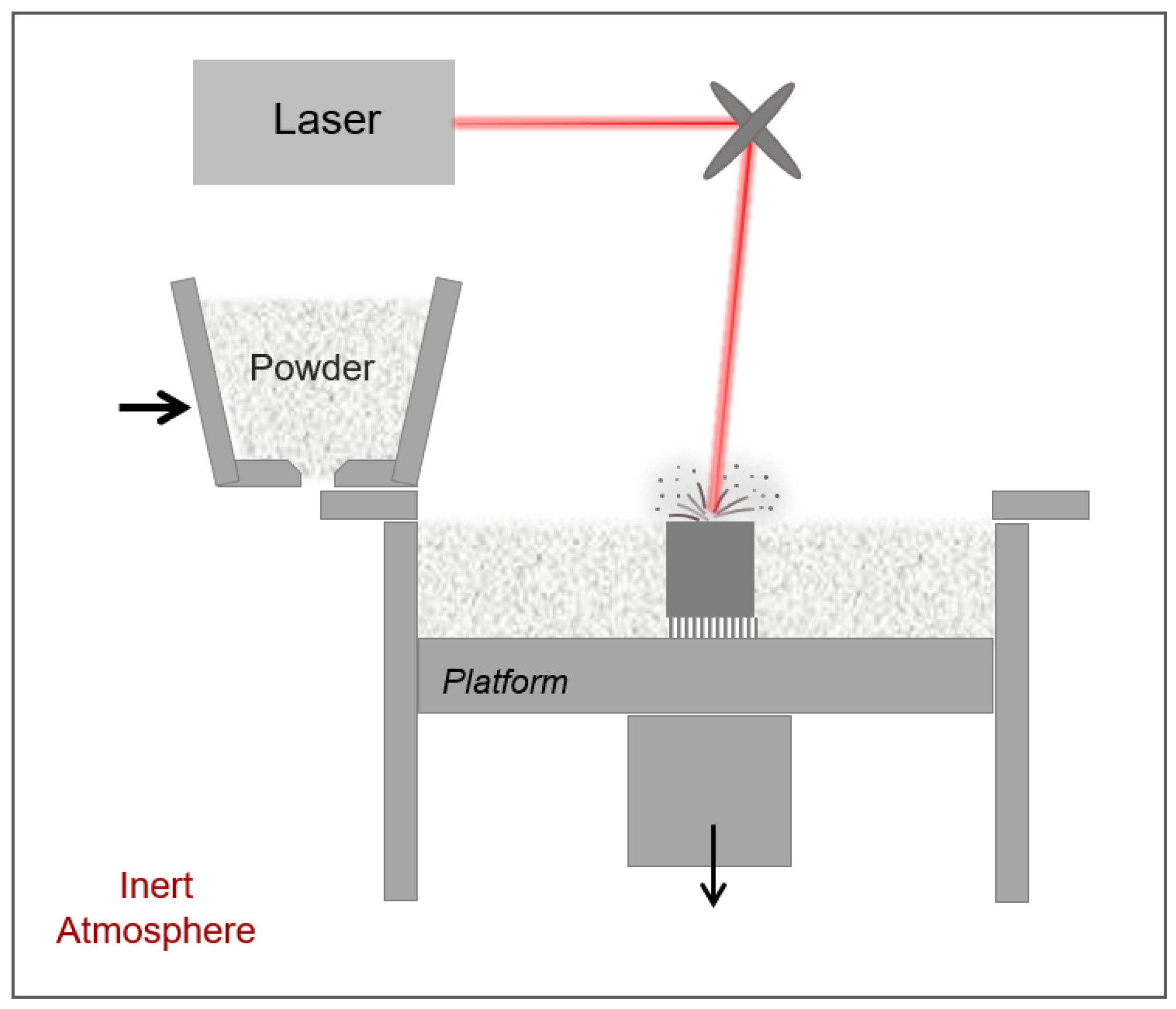
2.1. SLM Fabrication Details
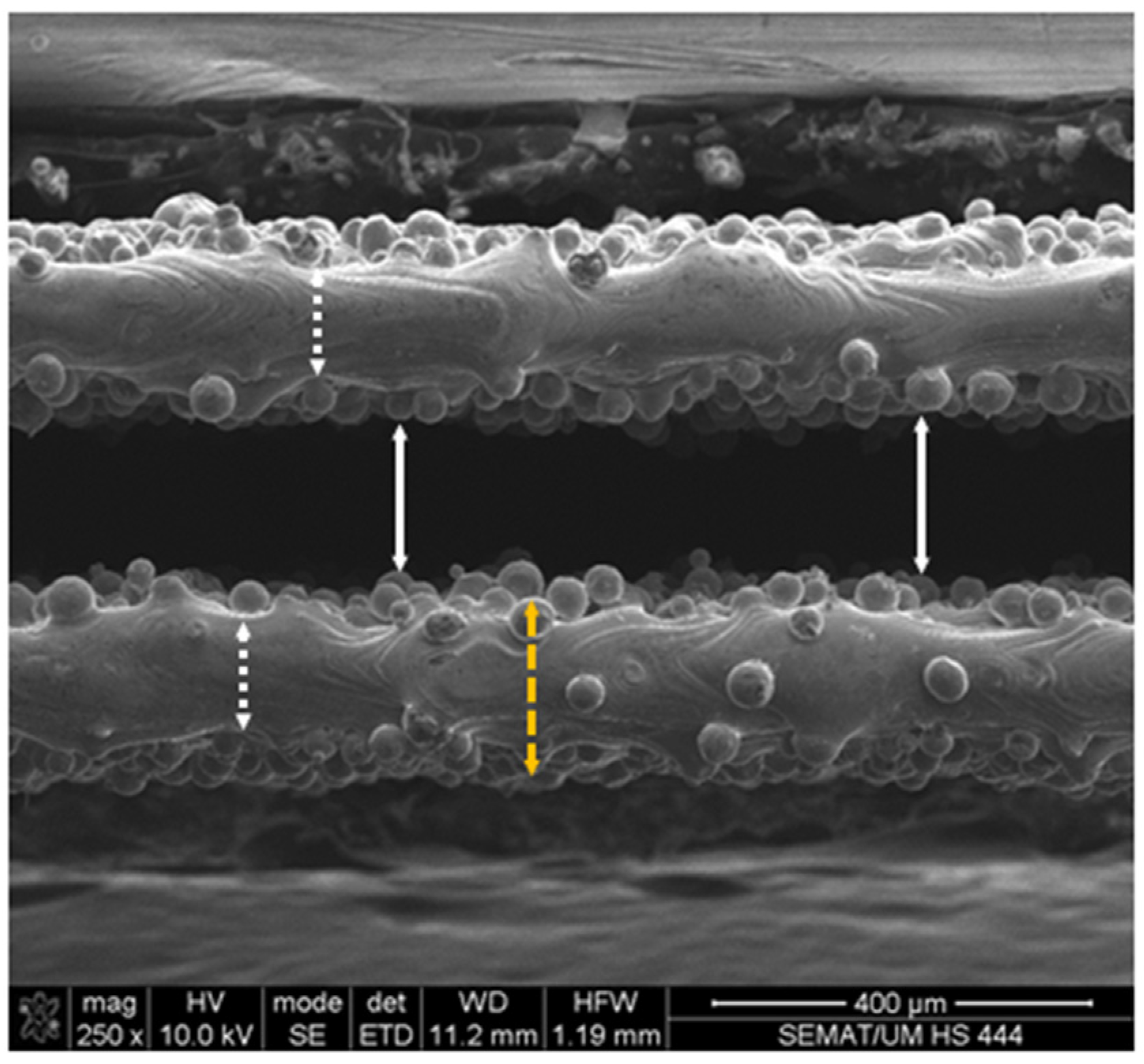
2.2. Dimensional Analysis
3. Results and Discussion
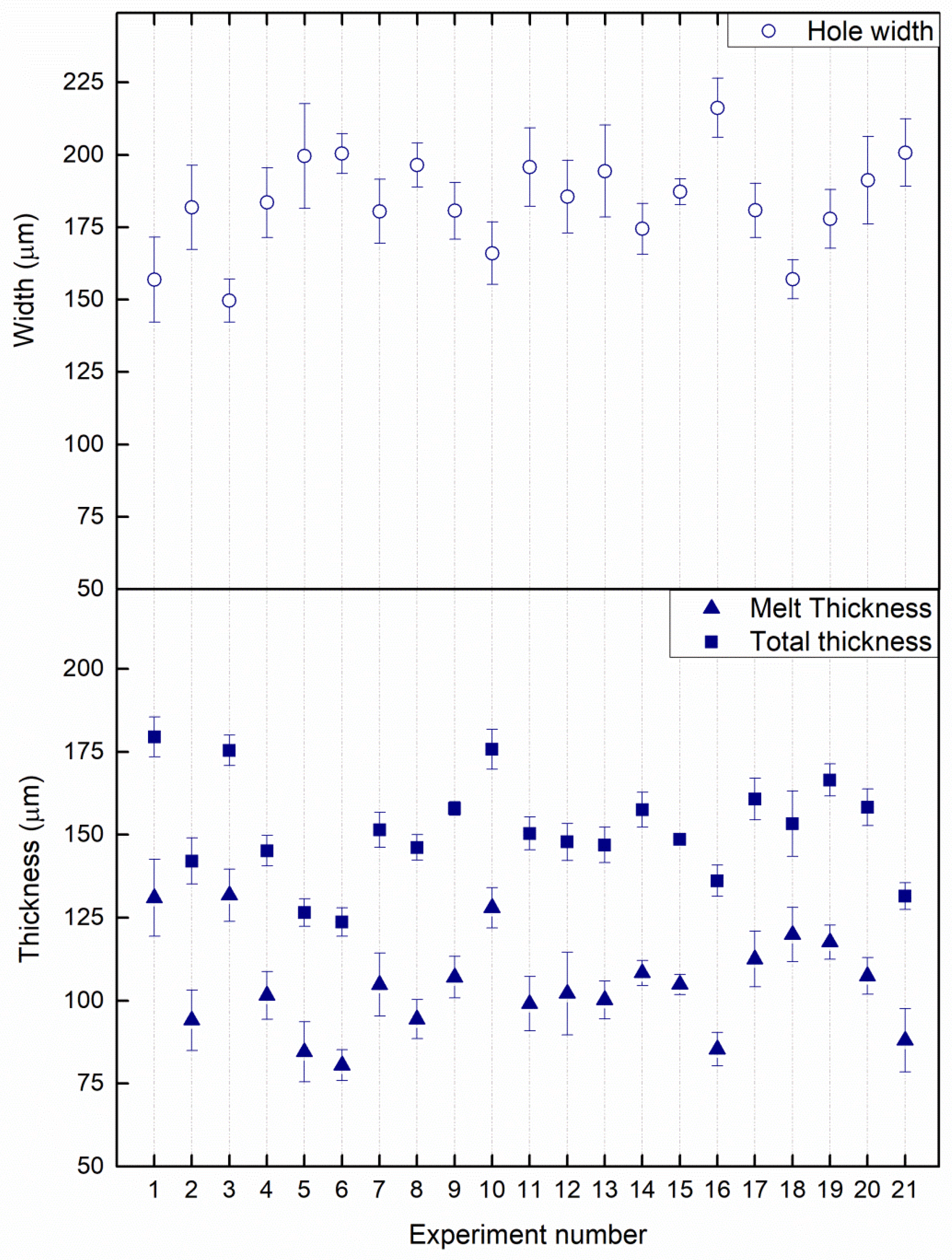
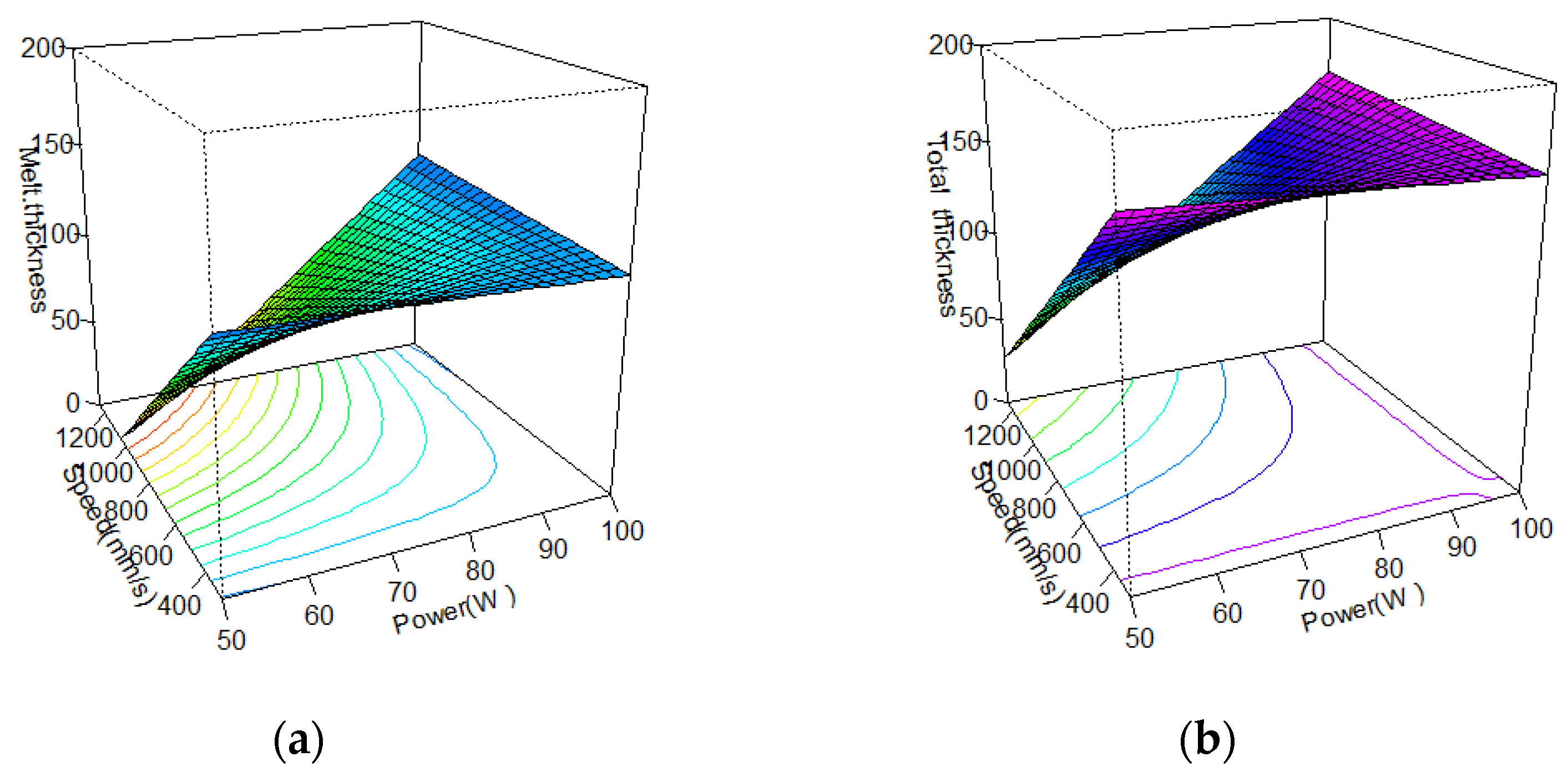
3.1. Dimensional Analysis
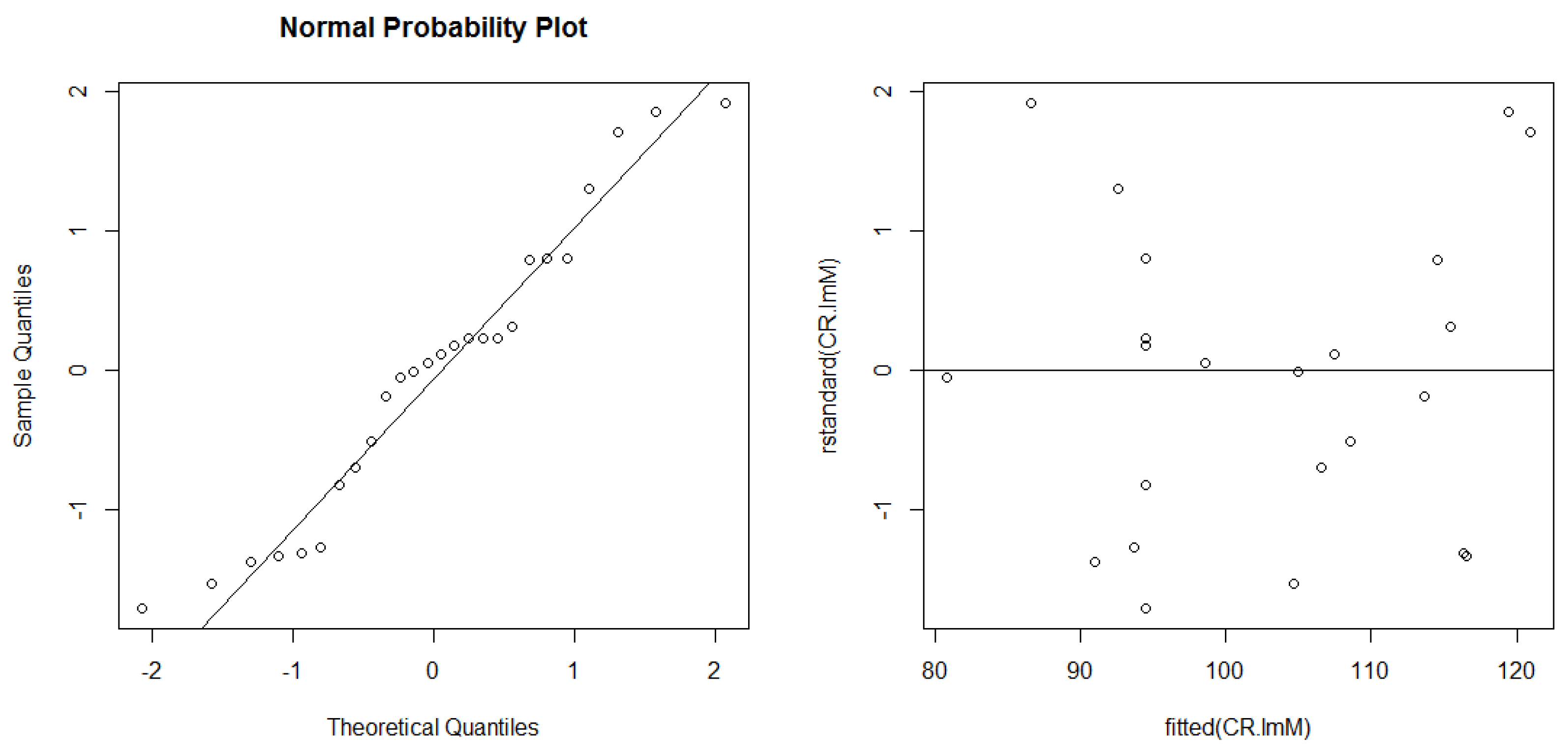
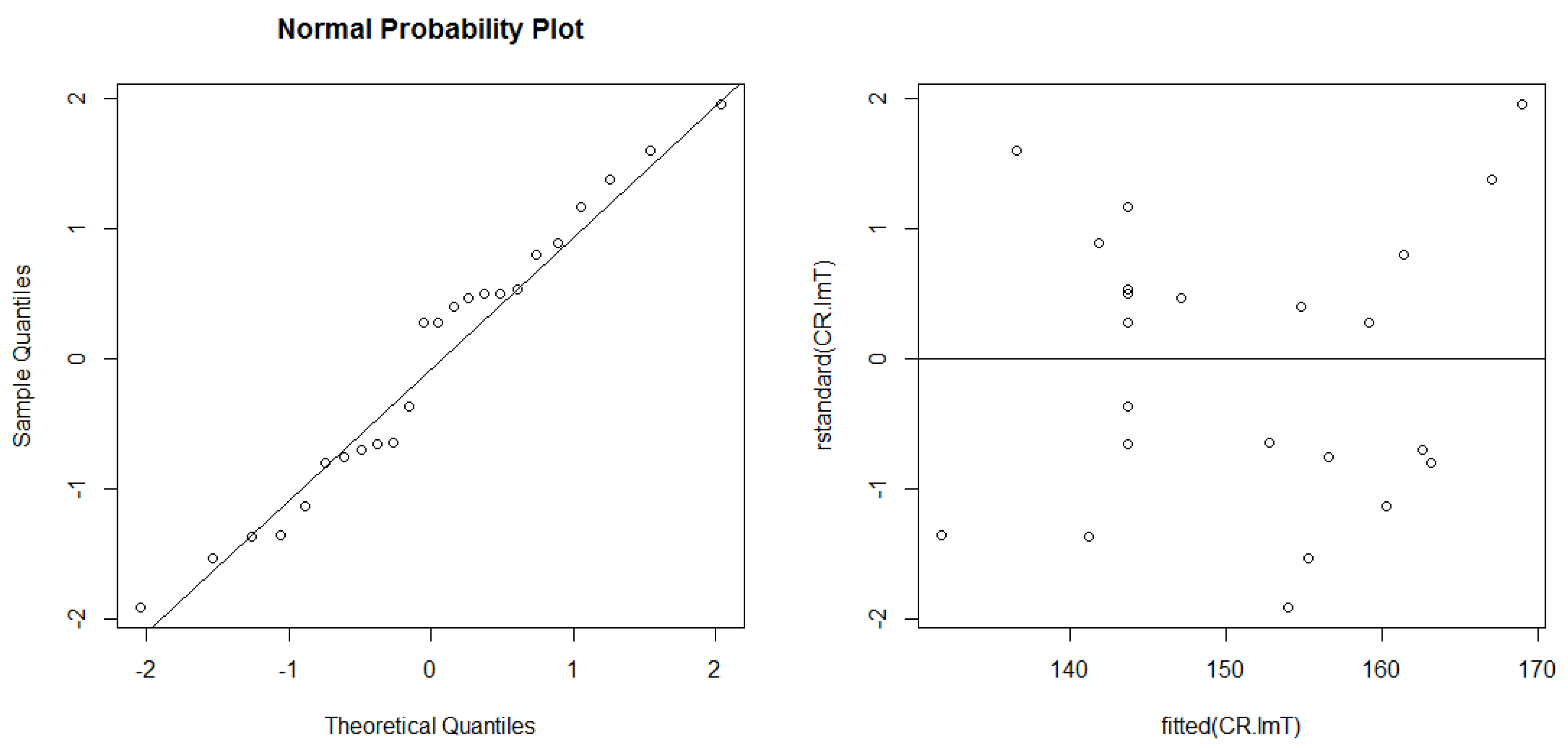
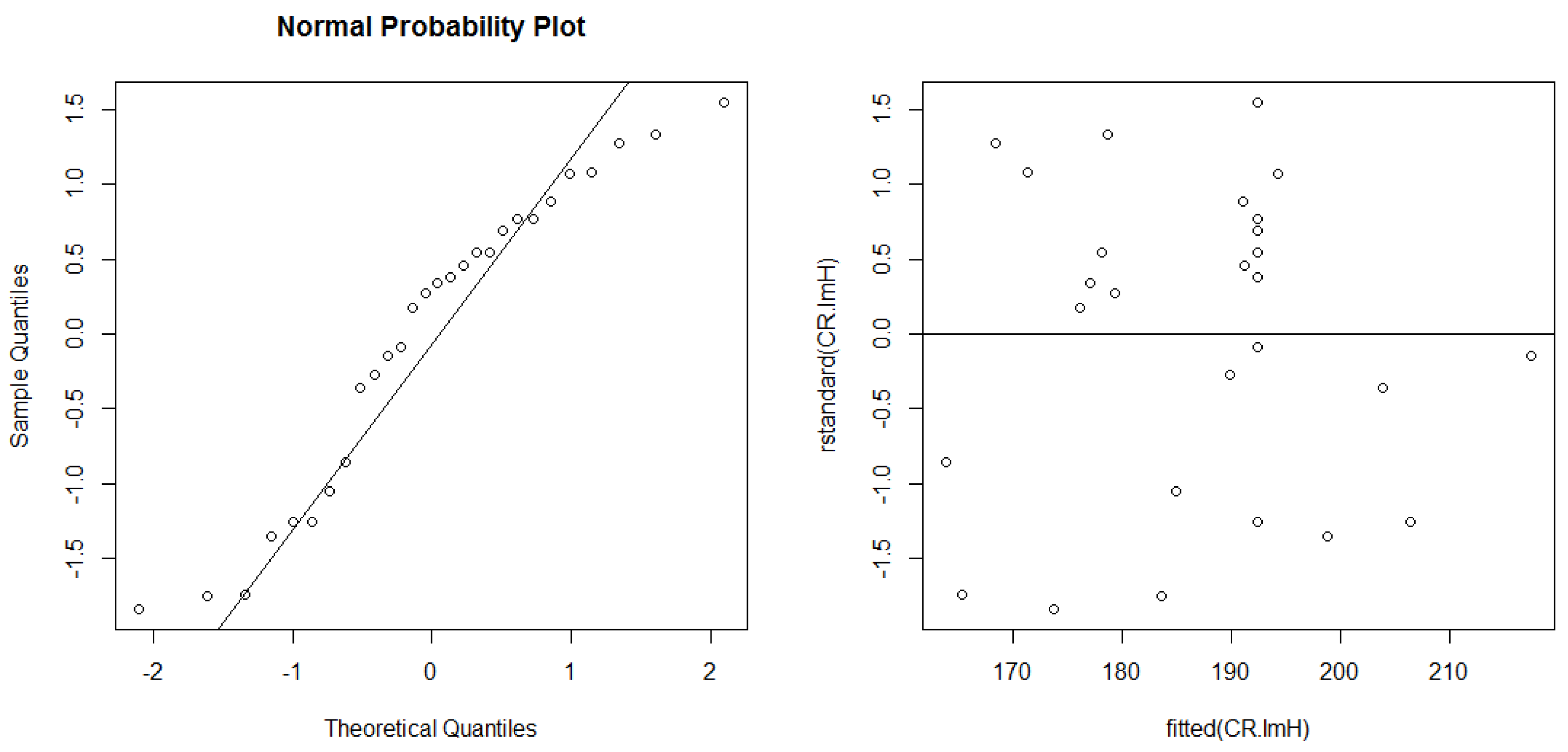
3.2. Statistical Analysis
4. Conclusions
- -
- The influence of the Selective Laser Melting (SLM) parameters laser power and scan speed on Ti6Al4V thin-walled tubes’ thickness was assessed.
- -
- Predictive models for the influence of these processing parameters (independent variables) on the thickness (dependent variable) of thin-walled tubes were developed.
- -
- The developed models prove that these micro-sized parts’ final dimensions are greatly dependent on these SLM processing parameters.
- -
- These models can be used to optimize the micro-manufacturing of Ti6Al4V thin-walled parts by SLM.
Author Contributions
Funding

Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dallago, M.; Fontanari, V.; Torresani, E.; Leoni, M.; Pederzolli, C.; Potrich, C.; Benedetti, M. Fatigue and biological properties of Ti-6Al-4V ELI cellular structures with variously arranged cubic cells made by selective laser melting. J. Mech. Behav. Biomed. Mater. 2018, 78, 381–394. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Thouas, G.A. Metallic implant biomaterials. Mater. Sci. Eng. R Rep. 2015, 87, 1–57. [Google Scholar] [CrossRef]
- Hassanin, H.; Finet, L.; Cox, S.C.; Jamshidi, P.; Grover, L.M.; Shepherd, D.E.T.; Addison, O.; Attallah, M.M. Tailoring selective laser melting process for titanium drug-delivering implants with releasing micro-channels. Addit. Manuf. 2018, 20, 144–155. [Google Scholar] [CrossRef] [Green Version]
- van Hooreweder, B.; Apers, Y.; Lietaert, K.; Kruth, J.P. Improving the fatigue performance of porous metallic biomaterials produced by Selective Laser Melting. Acta Biomater. 2017, 47, 193–202. [Google Scholar] [CrossRef]
- Sarker, A.; Tran, N.; Rifai, A.; Brandt, M.; Tran, P.A.; Leary, M.; Fox, K.; Williams, R. Rational design of additively manufactured Ti6Al4V implants to control Staphylococcus aureus biofilm formation. Materialia 2019, 5, 100250. [Google Scholar] [CrossRef]
- Wang, X.; Xu, S.; Zhou, S.; Xu, W.; Leary, M.; Choong, P.; Qian, M.; Brandt, M.; Xie, Y.M. Topological design and additive manufacturing of porous metals for bone scaffolds and orthopaedic implants: A review. Biomaterials 2016, 83, 127–141. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, S.; Zhu, H.; Hu, Z.; Wang, G.; Zeng, X. Horizontal dimensional accuracy prediction of selective laser melting. Mater. Des. 2018, 160, 9–20. [Google Scholar] [CrossRef]
- Bartolomeu, F.; Fonseca, J.; Peixinho, N.; Alves, N.; Gasik, M.; Silva, F.S.; Miranda, G. Predicting the output dimensions, porosity and elastic modulus of additive manufactured biomaterial structures targeting orthopedic implants. J. Mech. Behav. Biomed. Mater. 2019, 99, 104–117. [Google Scholar] [CrossRef] [PubMed]
- Bartolomeu, F.; Costa, M.M.; Alves, N.; Miranda, G.; Silva, F.S. Additive manufacturing of NiTi-Ti6Al4V multi-material cellular structures targeting orthopedic implants. Opt. Lasers Eng. 2020, 134, 106208. [Google Scholar] [CrossRef]
- Maconachie, T.; Leary, M.; Lozanovski, B.; Zhang, X.; Qian, M.; Faruque, O.; Brandt, M. SLM lattice structures: Properties, performance, applications and challenges. Mater. Des. 2019, 183, 108137. [Google Scholar] [CrossRef]
- Verma, S.; Yang, C.; Lin, C.; Jeng, J.Y. Additive manufacturing of lattice structures for high strength mechanical interlocking of metal and resin during injection molding. Addit. Manuf. 2022, 49, 102463. [Google Scholar] [CrossRef]
- Li, Z.; Xu, R.; Zhang, Z.; Kucukkoc, I. The influence of scan length on fabricating thin-walled components in selective laser melting. Int. J. Mach. Tools Manuf. 2018, 126, 1–12. [Google Scholar] [CrossRef]
- Pérez-Ruiz, J.D.; Marin, F.; Martínez, S.; Lamikiz, A.; Urbikain, G.; de Lacalle, L.N.L. Stiffening near-net-shape functional parts of Inconel 718 LPBF considering material anisotropy and subsequent machining issues. Mech. Syst. Signal Process. 2022, 168, 108675. [Google Scholar] [CrossRef]
- Pérez-Ruiz, J.D.; de Lacalle, L.N.L.; Urbikain, G.; Pereira, O.; Martínez, S.; Bris, J. On the relationship between cutting forces and anisotropy features in the milling of LPBF Inconel 718 for near net shape parts. Int. J. Mach. Tools Manuf. 2021, 170, 103801. [Google Scholar] [CrossRef]
- Smith, K.E.; Dupont, K.M.; Safranski, D.L.; Blair, J.; Buratti, D.; Zeetser, V.; Callahan, R.; Lin, J.; Gall, K. Use of 3D printed bone plate in novel technique to surgically correct hallux valgus deformities. Tech. Orthop. 2016, 31, 181–189. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fang, C.; Cai, H.; Kuong, E.; Chui, E.; Siu, Y.C.; Ji, T.; Drstvenšek, I. Surgical applications of three-dimensional printing in the pelvis and acetabulum: From models and tools to implants. Anwendungen des 3-dimensionalen Drucks an Becken und Acetabulum: Von Modellen und Instrumenten zu Implantaten. Unfallchirurg 2019, 122, 278–285. [Google Scholar] [CrossRef] [Green Version]
- Dall’Ava, L.; Hothi, H.; di Laura, A.; Henckel, J.; Hart, A. 3D printed acetabular cups for total hip arthroplasty: A review article. Metals 2019, 9, 729. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Escudero, G.; Jimeno Beitia, A.; Martínez de Pissón Caruncho, G.; López de Lacalle, L.N.; González-Barrio, H.; Pereira Neto, O.; Calleja-Ochoa, A. A reliable clean process for five-axis milling of knee prostheses. Int. J. Adv. Manuf. Technol. 2021, 115, 1605–1620. [Google Scholar] [CrossRef]
- Tan, J.H.; Wong, W.L.E.; Dalgarno, K.W. An overview of powder granulometry on feedstock and part performance in the selective laser melting process. Addit. Manuf. 2017, 18, 228–255. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Zhang, S.; Wang, Z.Y.; Zhang, C.H.; Wu, C.L.; Wang, M. 3D printing externally reinforced layers for high-speed railway brake discs: Adaptability of SLM processes for manufacturing gradient materials. Mater. Today Commun. 2022, 31, 103778. [Google Scholar] [CrossRef]
- Ferreira, D.F.S.; Miranda, G.; Oliveira, F.J.; Oliveira, J.M. Predictive models for an optimized fabrication of 18Ni300 maraging steel for moulding and tooling by selective laser melting. J. Manuf. Process. 2021, 70, 46–54. [Google Scholar] [CrossRef]
- Zhang, S.; Wei, Q.; Cheng, L.; Li, S.; Shi, Y. Effects of scan line spacing on pore characteristics and mechanical properties of porous Ti6Al4V implants fabricated by selective laser melting. Mater. Des. 2014, 63, 185–193. [Google Scholar] [CrossRef]
- Bartolomeu, F.; Faria, S.; Carvalho, O.; Pinto, E.; Alves, N.; Silva, F.S.; Miranda, G. Predictive models for physical and mechanical properties of Ti6Al4V produced by Selective Laser Melting. Mater. Sci. Eng. A 2016, 663, 181–192. [Google Scholar] [CrossRef]
- Wang, Z.; Xiao, Z.; Tse, Y.; Huang, C.; Zhang, W. Optimization of processing parameters and establishment of a relationship between microstructure and mechanical properties of SLM titanium alloy. Opt. Laser Technol. 2019, 112, 159–167. [Google Scholar] [CrossRef]
- Salem, H.; Carter, L.N.; Attallah, M.M.; Salem, H.G. Influence of processing parameters on internal porosity and types of defects formed in Ti6Al4V lattice structure fabricated by selective laser melting. Mater. Sci. Eng. A 2019, 767, 138387. [Google Scholar] [CrossRef]
- Leary, M. 4-Surface roughness optimisation for selective laser melting (SLM): Accommodating relevant and irrelevant surfaces. In Woodhead Publishing Series in Electronic and Optical Materials, Laser Additive Manufacturing; Brandt, M., Ed.; Woodhead Publishing: Cambridge, UK, 2017; pp. 99–118. ISBN 9780081004333. [Google Scholar] [CrossRef]





| Experiment | A | B |
|---|---|---|
| Power (W) | Scan Speed (mm/s) | |
| 1 | 50 | 300 |
| 2 | 50 | 400 |
| 3 | 60 | 300 |
| 4 | 60 | 400 |
| 5 | 60 | 500 |
| 6 | 60 | 600 |
| 7 | 70 | 400 |
| 8 | 70 | 550 |
| 9 | 80 | 300 |
| 10 | 80 | 500 |
| 11 | 80 | 600 |
| 12 | 80 | 700 |
| 13 | 80 | 800 |
| 14 | 90 | 600 |
| 15 | 90 | 700 |
| 16 | 90 | 1250 |
| 17 | 100 | 300 |
| 18 | 100 | 400 |
| 19 | 100 | 500 |
| 20 | 100 | 600 |
| 21 | 100 | 1250 |
| Model Terms | Sum of Squares | Degree of Freedom | Mean Square | F Value | p-Value |
|---|---|---|---|---|---|
| Model | 3095.734 | 3 | 1031.911 | 17.810 | <0.001 |
| A | 1732.033 | 1 | 1732.033 | 29.894 | <0.001 |
| B | 2826.825 | 1 | 2826.825 | 45.978 | <0.001 |
| AB | 1366.774 | 1 | 1366.774 | 23.590 | <0.001 |
| Residuals | 1274.63 | 22 | 57.94 | ||
| Lack of fit | 999.57 | 15 | 66.64 | 1.6959 | 0.2454 |
| Pure error | 275.06 | 7 | 39.29 | ||
| Corrected Total | 4370.364 | 25 | |||
| Press | 2204.695 | ||||
| Multiple R2: 0.7083 Adjusted R2: 0.6685 Predicted R2: 0.4955 Adequate precision: 13.4268 | |||||
| Model Terms | Sum of Squares | Degree of Freedom | Mean Square | F Value | p-Value |
|---|---|---|---|---|---|
| Model | 2337.174 | 3 | 779.058 | 16.030 | <0.001 |
| A | 1147.771 | 1 | 1147.771 | 23.617 | <0.001 |
| B | 2234.525 | 1 | 2234.525 | 45.978 | <0.001 |
| AB | 1143.759 | 1 | 1143.759 | 23.534 | <0.001 |
| Residuals | 971.91 | 20 | 48.60 | ||
| Lack of fit | 870.67 | 14 | 62.19 | 3.6857 | 0.058707 |
| Pure error | 101.24 | 6 | 16.87 | ||
| Corrected Total | 3309.084 | 23 | |||
| Press | 1813.276 | ||||
| Multiple R2: 0.7063 Adjusted R2: 0.6622 Predicted R2: 0.4520 Adequate precision: 13.06467 | |||||
| Model Terms | Sum of Squares | Degree of Freedom | Mean Square | F Value | p-Value |
|---|---|---|---|---|---|
| Model | 4244.342 | 3 | 1414.781 | 13.460 | <0.001 |
| A | 1062.045 | 1 | 1062.045 | 10.104 | 0.00404 |
| B | 3616.83 | 1 | 3616.83 | 34.410 | <0.001 |
| AB | 1399.101 | 1 | 1399.101 | 13.311 | 0.00127 |
| Residuals | 2522.60 | 24 | 105.11 | ||
| Lack of fit | 2061.35 | 17 | 121.26 | 1.8402 | 0.2098719 |
| Pure error | 461.25 | 7 | 65.89 | ||
| Corrected Total | 6766.942 | 27 | |||
| Press | 3634.965 | ||||
| Multiple R2: 0.6272 Adjusted R2: 0.5806 Predicted R2: 0.4628 Adequate precision: 13.79676 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miranda, G.; Faria, S.; Bartolomeu, F.; Pinto, E.; Alves, N.; Silva, F.S. The Influence of Laser Power and Scan Speed on the Dimensional Accuracy of Ti6Al4V Thin-Walled Parts Manufactured by Selective Laser Melting. Metals 2022, 12, 1226. https://doi.org/10.3390/met12071226
Miranda G, Faria S, Bartolomeu F, Pinto E, Alves N, Silva FS. The Influence of Laser Power and Scan Speed on the Dimensional Accuracy of Ti6Al4V Thin-Walled Parts Manufactured by Selective Laser Melting. Metals. 2022; 12(7):1226. https://doi.org/10.3390/met12071226
Chicago/Turabian StyleMiranda, Georgina, Susana Faria, Flávio Bartolomeu, Elodie Pinto, Nuno Alves, and Filipe Samuel Silva. 2022. "The Influence of Laser Power and Scan Speed on the Dimensional Accuracy of Ti6Al4V Thin-Walled Parts Manufactured by Selective Laser Melting" Metals 12, no. 7: 1226. https://doi.org/10.3390/met12071226
APA StyleMiranda, G., Faria, S., Bartolomeu, F., Pinto, E., Alves, N., & Silva, F. S. (2022). The Influence of Laser Power and Scan Speed on the Dimensional Accuracy of Ti6Al4V Thin-Walled Parts Manufactured by Selective Laser Melting. Metals, 12(7), 1226. https://doi.org/10.3390/met12071226











