Modelling Dynamic Recrystallization of A356 Aluminum Alloy during Hot Deformation

Abstract

The flow stress and dynamic recrystallization behavior of A356 aluminum alloy was studied, with a strain rate ranging from 0.001 s⁻¹ to 1 s⁻¹ and temperature ranging from 300 to 500 °C. Both the true stress–strain curves and microstructure examination of A356 aluminum alloy indicated that dynamic recrystallization occurred during the isothermal compression. A physical dynamic recrystallization model based on the Arrhenius equation was developed, and this model can accurately predict the dynamic recrystallization fraction of A356 aluminum alloy during the isothermal compression. Finally, this model was implemented in FEM software Forge, and the microstructure evolution was simulated well.

1. Introduction

The Al-Si-Mg aluminum alloy is widely used to manufacture automobile structural parts via casting, owing to its excellent castability and the possibility of precipitation strengthening [1,2]. However, those cast structural parts have gradually failed to meet the market requirements for high-performance parts (lightness and strength). Improving the mechanical properties of Al-Sil-Mg alloy through thermoplastic deformation is the preferred method to produce high-performance structural parts [3,4,5]. The microstructure evolution during the thermoplastic deformation process has been studied by many researchers for its significant influence on the mechanical properties of the formed parts. The dynamic recrystallization of three Al-Si-Mg alloys with different Si content during hot extrusion was investigated by Wu et al., and the results showed that particle-stimulated dynamic recrystallization only occurred in Si-rich zones [6]. David et al. revealed that dynamic recovery and continuous dynamic recrystallization are the main restoration mechanisms of the extruded Al-Si-Mg alloy during the hot torsion [7]. Wu et al. found that the dynamic recrystallization of the Al-Si-Mg alloy increased with the deformation temperature and reduction ratio during the hot rolling [8]. Esmaeil et al. found that the dynamic recrystallization during the equal channel angular pressing can obviously suppress dynamic mechanical damage to the Al-Si-Mg alloy [9]. Moghadam et al. found that dynamic recrystallization is the main softening mechanism of eutectic Al-Si-Mg alloy during hot deformation [10].

Besides the dynamic recrystallization mechanism and its effect, the quantitative prediction of dynamic recrystallization during the hot deformation is also important. Gan et al. developed a dynamic recrystallization model which can accurately predict the grain size of 2219 aluminum alloy [11]; Quan et al. proposed an Avrami-type model for predicting the dynamic recrystallization fraction of 7075 aluminum alloy [12]; Chen et al. proposed a model for predicting grain size and dynamic recrystallization of 7075 aluminum alloy, based on the polycrystal plasticity approach [13]; Zhang et al. established a kinetic model for dynamic recrystallization of 2195 aluminum alloy [14]. In general, the dynamic recrystallization modeling of wrought aluminum alloy has been relatively mature. However, there are few reports focused on modeling the dynamic recrystallization of cast Al-Si-Mg aluminum alloy. It is urgent to research the dynamic recrystallization modeling of cast Al-Si-Mg aluminum alloy to promote the application of the finite element method in the optimization design of structural parts.

In this study, the dynamic recrystallization behavior of A356 aluminum alloy during hot deformation was investigated. A dynamic recrystallization model based on Arrhenius equation was developed and validated. Finally, the model was implemented into the finite element software Forge (NxT 2.1, Transvalor S.A, France) to predict the dynamic recrystallization fraction of A356 alloy during hot deformation.

2. Materials and Methods

The A356 alloy was used for hot compression. Its chemical composition was obtained by X-ray fuorescence spectrometry, and the result are shown in Table 1. The isothermal hot compression tests were conducted by Gleeble-3800 (DSI, St.Paul, MN, USA) with different strain rates (1, 0.1, 0.01 and 0.001 s⁻¹) and temperatures (300, 350, 400, 450 and 500 °C). The cylindrical specimens with 15 mm in height and 10 mm in diameter were heated up to a certain temperature at 5 °C/s and held for 2 min to eliminate the thermal gradient. All specimens were compressed to true strain of 0.9 and then immediately quenched in water.

Table 1. Chemical composition of the A356 alloy (wt%).

Si	Mg	Fe	Cu	Mn	Zn	Cr	Ti	Al
7.43	0.43	0.29	0.17	0.069	0.02	0.01	0.01	Balance

The deformed specimens were sectioned along the central axis for metallurgical observation. The observation area is the central area of the sample. Specimens for the electron backscattered diffraction (EBSD) were initially mechanically polished, and then polished by Ion thinner (EM RES102, LEICA, Wetzlar, Germany) for 1 h. The orientation maps were measured by a scanning electron microscope (SU3500, Hitachi, Tokyo, Japan) with the scanning step of 0.5 μm. Grain boundaries with misorientation exceeding 15° are depicted in orientation maps as black lines, and grain boundaries with misorientation from 3 to 15° are depicted in orientation maps as red lines. The commercial FEM software Forge was used to simulate the hot compression process.

3. Results

3.1. Flow Stress Behavior

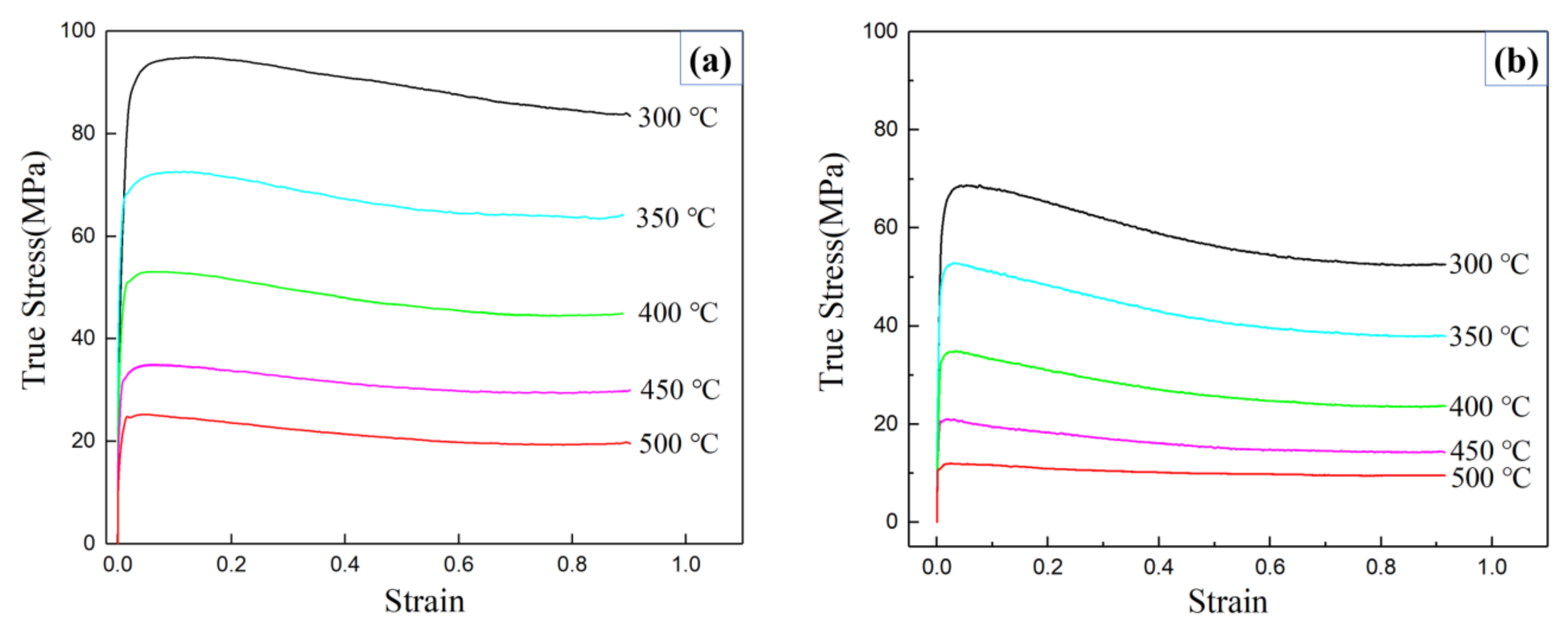
The true stress–strain curves of A356 alloy under different strain rate and temperature are illustrated in Figure 1. It can be found from the Figure 1 that the flow stress decreases obviously after reaching the peak value, and finally drives to a steady state. This phenomenon is determined by the two factors, work hardening and dynamic softening [15,16]. The work hardening is dominated by dislocation propagation and accumulation. And the dynamic recovery and dynamic recrystallization dominated the dynamic softening. The final steady state can be attributed to the equilibrium of work hardening and dynamic softening.

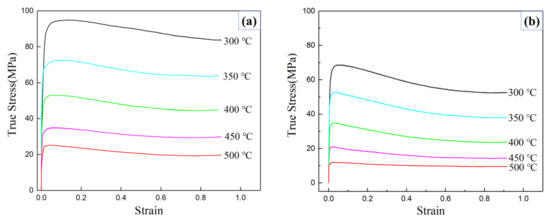
Figure 1. True stress–strain curves of A356 alloy under different strain rate: (a) $\dot{\epsilon }=0.1 {\mathrm{s}}^{-1}$; (b) $\dot{\epsilon }=0.001 {\mathrm{s}}^{-1}$.

3.2. Microstructure Evolution

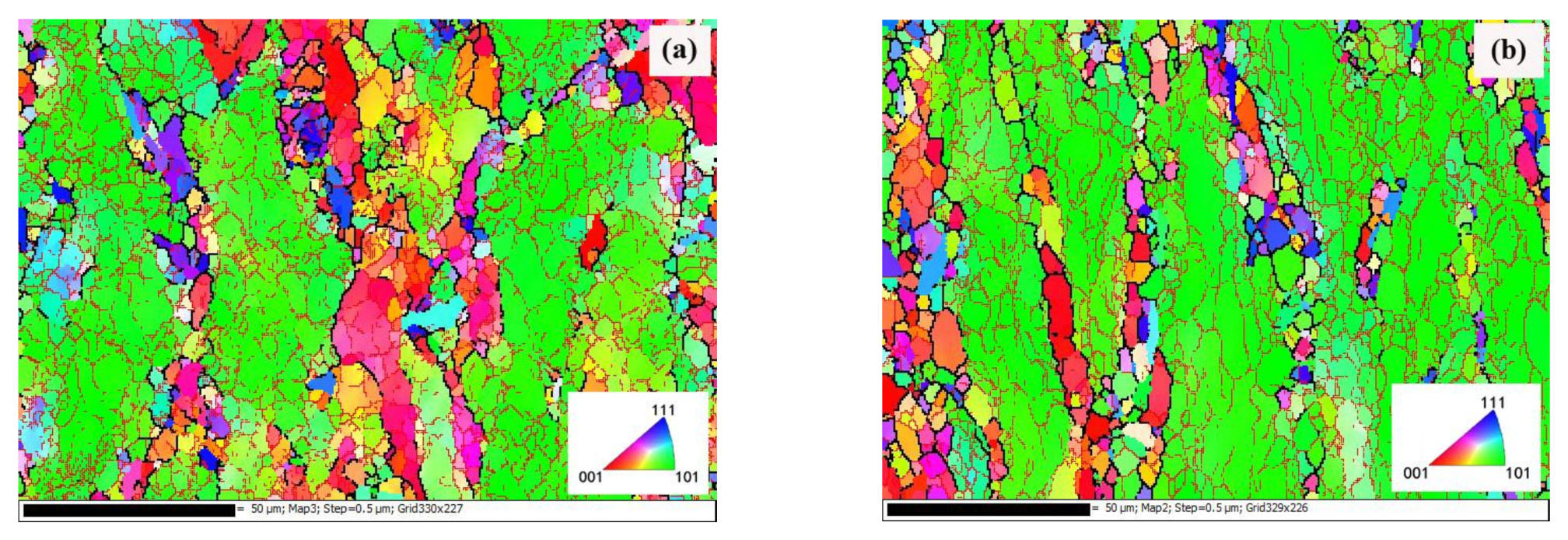
Figure 2 shows the EBSD maps of the deformed samples. It is clear that the microstructure is dominated by coarse primary Al dendrites and fine equiaxed grains. There are lots of LAGBs in the dendrites, and that characterized by typical dynamic recovery microstructure. At the same time, it can be found that fine equiaxed grains are located in the eutectic zones. With the strain increasing from 0.6 to 0.9, the fine equiaxed grain fraction increases obviously. Furthermore, this microstructure features prove that dynamic recrystallization occurred during the hot deformation.

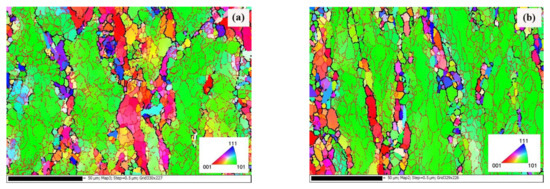
Figure 2. The EBSD maps of A356 under different loading parameters: (a) T = 400 °C, 0.1 s⁻¹, ε = 0.6; (b) T = 400 °C, 0.1 s⁻¹, ε = 0.9.

4. Modelling Dynamic Recrystallization

4.1. Modelling Procedure

The correlation between deformation temperature, strain rate and flow stress during hot deformation can be expressed by the Arrhenius-type equation [17]. At the same time, the influence of deformation temperature and the strain rate on the deformation process can be illustrated by the Zener-Holloman parameter (Z). The specific equations are given by Equations (1)–(4).

$$\dot{\epsilon }=A_1{\sigma }^{n_1}\exp \left(-\frac{Q}{RT}\right)$$

(1)

$$\dot{\epsilon }=A_2\exp \left(\beta \sigma \right)\exp \left(-\frac{Q}{RT}\right)$$

(2)

$$\dot{\epsilon }=\mathrm{A}{\left[\sin \mathrm{h}\left(\alpha \sigma \right)\right]}^n\exp \left(-\frac{Q}{RT}\right)$$

(3)

$$\mathrm{Z}=\mathrm{A}{\left[\sin \mathrm{h}\left(\alpha \sigma \right)\right]}^n=\dot{\epsilon }\exp \left(\frac{Q}{RT}\right)$$

(4)

where $A_1$, $A_2$, A, $n_1$, n, α ($\alpha =\beta /n_1$) and $\beta$ are material constants, σ is the true stress, Q is deformation activation energy, and R is the universal gas constant (8.314 J mol⁻¹ K⁻¹).

The following equations can be obtained by taking the logarithm of Equations (1) and (2):

$$\ln \dot{\epsilon }=ln{A}_1-Q/RT+n_{1}ln\sigma$$

(5)

$$\ln \dot{\epsilon }=ln{A}_2-Q/RT+\beta \sigma$$

(6)

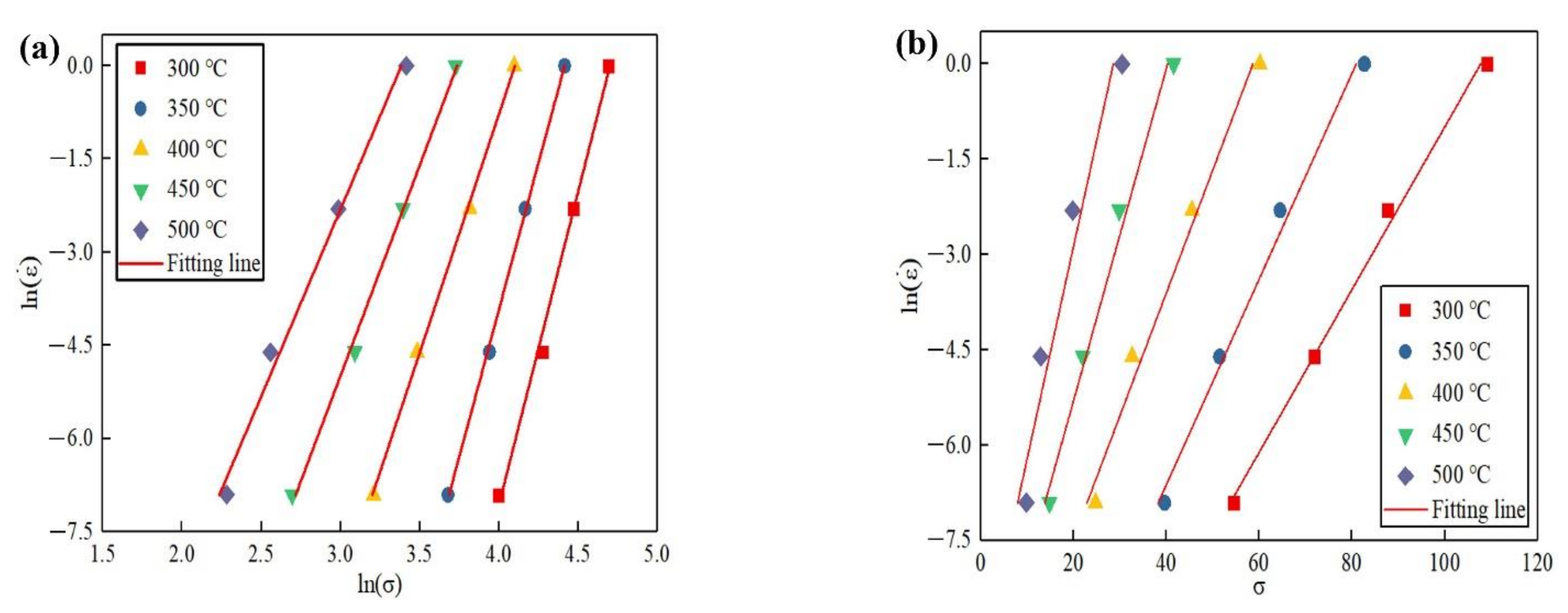
Obviously, $n_1$ and $\beta$ are the slope of Equations (5) and (6), respectively. The $n_1$ and $\beta$ can be calculated by Equations (5) and (6) with different strain. The relationship between $ln\sigma$, $\sigma$ and $\ln \dot{\epsilon }$ are showed in Figure 3. It is clear that the relation curves between $ln\sigma$, $\sigma$ and $\ln \dot{\epsilon }$ obtained with different temperature are approximate parallel lines.

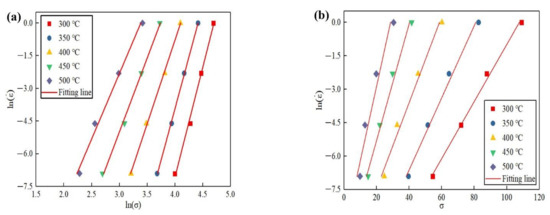
Figure 3. The relation curves between $ln\sigma$, $\sigma$ and $\ln \dot{\epsilon }$ with ε = 0.6: (a) the relation between $ln\sigma$ and $\ln \dot{\epsilon }$; (b) the relation between $\sigma$ and $\ln \dot{\epsilon }$.

The following equation can be obtained by taking the logarithm of Equation (3):

$$\ln \dot{\epsilon }=\ln \left(A_3\right)+nln\left[sinh\left(\alpha \sigma \right)\right]-\left(\frac{Q}{RT}\right)$$

(7)

At a constant temperature or strain rate, deformation activation energy Q can be obtained by partial differentiation of Equation (7):

$$\mathrm{Q}=\mathrm{R}{\left[\frac{\partial ln\dot{\epsilon }}{\partial ln\left[\sin \mathrm{h}\left(\alpha \sigma \right)\right]}\right]}_T·{\left[\frac{\partial ln\left[\sin \left(\alpha \sigma \right)\right]}{\partial \left(1/T\right)}\right]}_{\dot{\epsilon }}$$

(8)

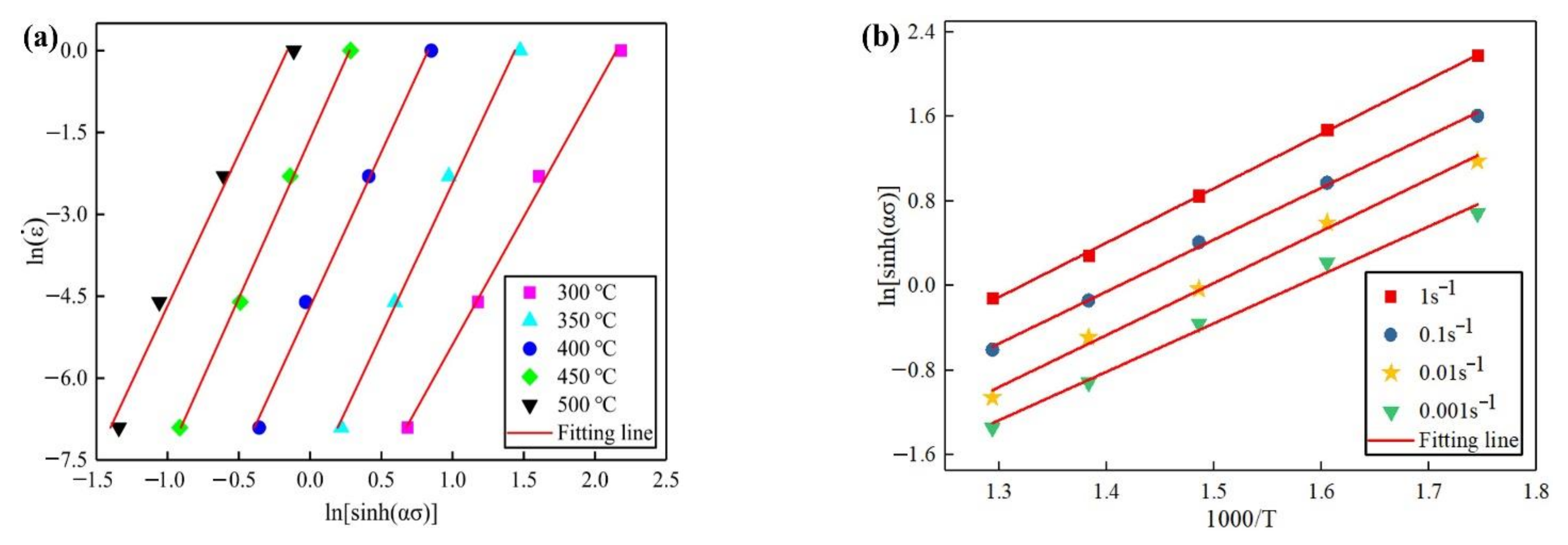
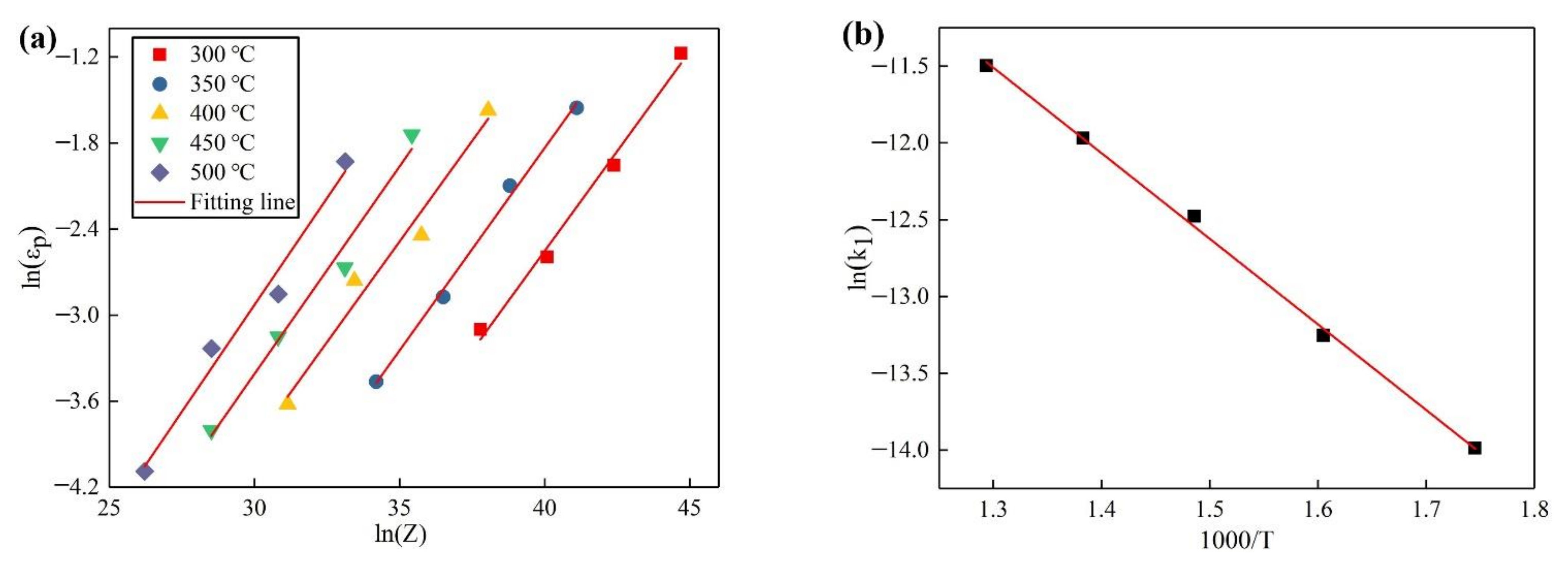
The Q value can be calculated based on slope of relation curves between $ln\left[\sin \mathrm{h}\left(\alpha \sigma \right)\right]$, $ln\dot{\epsilon }$ and $1/T$. With ε = 0.6, those curves are illustrated in Figure 4. Those curves are approximate parallel curves. Thus, Q value can be obtained based on the slope of those curves by linear regression. Then, the Z values can be calculated by Equation (4).

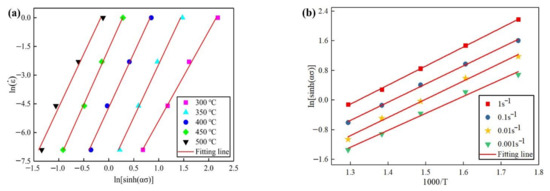
Figure 4. The relation curves between $ln\left[\sin \mathrm{h}\left(\alpha \sigma \right)\right]$, $ln\dot{\epsilon }$ and $1/T$ with ε = 0.6: (a) the relation between $ln\left[\sin \mathrm{h}\left(\alpha \sigma \right)\right]$ and $ln\dot{\epsilon }$; (b) the relation between $ln\left[\sin \mathrm{h}\left(\alpha \sigma \right)\right]$ and $1/T$.

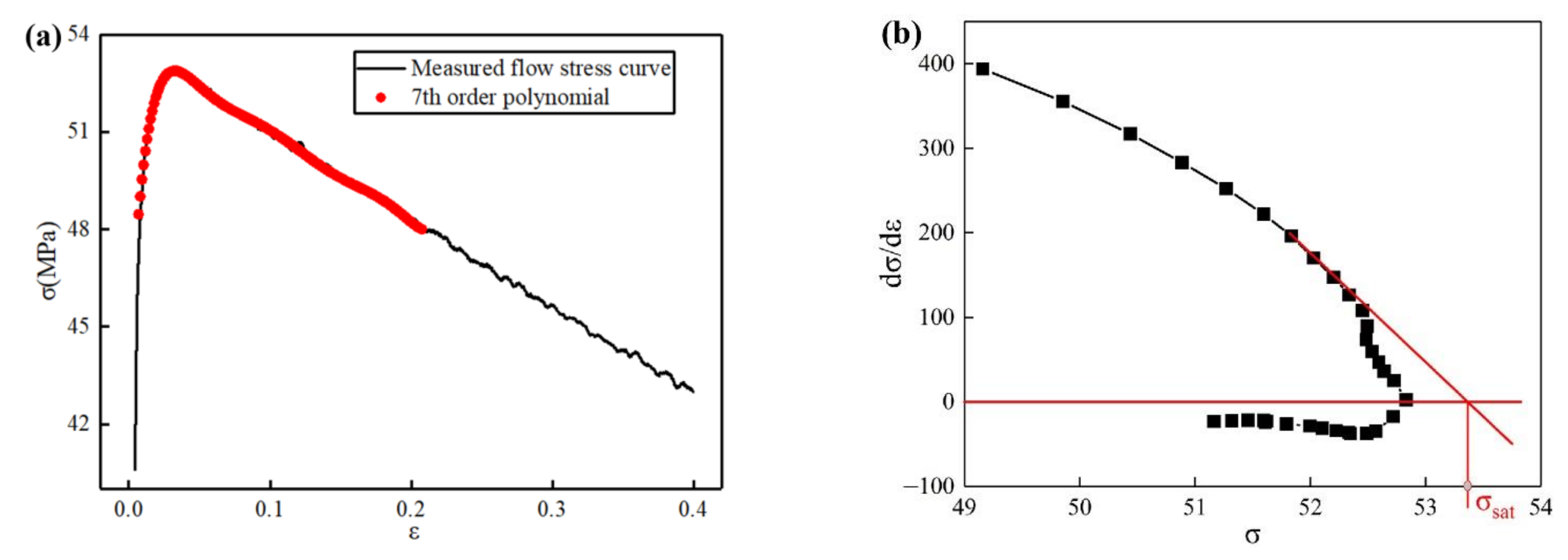
Based on the work-hardening theory [18], the recovery saturated stress (${\sigma }_{sat}$) can be calculated by relation curve of work-hardening rate and flow stress. Aim to calculate the recovery saturated stress with different deformation conditions, the true stress–strain curves are fitted by 7th polynomial. The fitting and calculating detail with deformation temperature of 350 °C and strain rate of 0.001 s⁻¹ are showed in Figure 5.

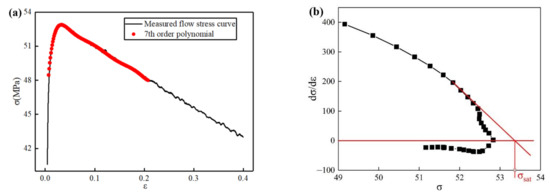
Figure 5. The recovery saturated stress calculation detail: (a) the polynomial fitting result; (b) the recovery saturated stress calculation.

According to the reported results [19], considering the fact that it is difficult to clarify the softening effect between dynamic recovery and dynamic recrystallization during the hot deformation, the dynamic recrystallization steady stress (${\sigma }_{ss}$) can be expressed by Equation (9).

$${\sigma }_{ss}=0.9{\sigma }_s$$

(9)

where ${\sigma }_s$ is steady stress of the flow stress curve.

The dynamic recrystallization fraction ($X_D$) can be expressed as the function of strain or flow stress as follows [20]:

$$X_D=1-exp\left[-k{\left(\frac{\epsilon -{\epsilon }_c}{{\epsilon }_p}\right)}^m\right]$$

(10)

$$X_D=\frac{{\sigma }_{sat}-\sigma }{{\sigma }_{sat}-{\sigma }_{ss}}$$

(11)

where k and m are material constant, the peak strain ${\epsilon }_p=k_1{Z}^{m_1}$, the critical stress ${\epsilon }_c=0.85{\epsilon }_p$. The $k_1$ and $m_1$ can be calculated by taking the logarithm of ${\epsilon }_p=k_1{Z}^{m_1}$ under different deformation conditions. The relation between Z and $\ln ({\epsilon }_p$) is showed in Figure 6a, the relation between $k_1$ and T is showed in Figure 6b.

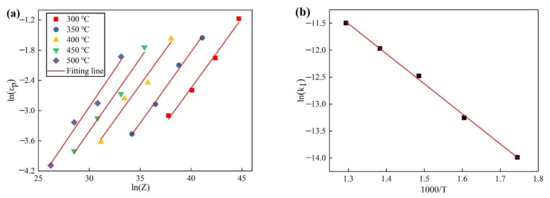
Figure 6. The relation between peak strain and Z: (a) the relation between Z and $\ln ({\epsilon }_p$); (b) the relation between $k_1$ and T.

The material constant m and k can be calculated by taking the logarithm of Equation (10):

$$\left\{\begin{array}{c}m=dln\left[-\ln \left(1-X_D\right)\right]/d\ln \left[\left(\epsilon -{\epsilon }_c\right)/{\epsilon }_p\right]\\ k=-\ln \left(1-X_D\right)/{\left[\left(\epsilon -{\epsilon }_c\right)/{\epsilon }_p\right]}^m \end{array}\right.$$

(12)

Finally, the dynamic recrystallization fraction of A356 alloy can be expressed as follows:

$$\left\{\begin{array}{l}{X}_D=1-exp\left[-2.227{\left(\left(\epsilon -{\epsilon }_c\right)/{\epsilon }_p\right)}^{0.41706}\right]\\ {\epsilon }_p=k_1{Z}^{0.2857} \\ k_1=exp\left[-\left(4.26109+5574.6/T\right)\right]\\ {\epsilon }_c=0.85{\epsilon }_p\\ Z=\dot{\epsilon }exp\left(220865/RT\right)\end{array}\right.$$

(13)

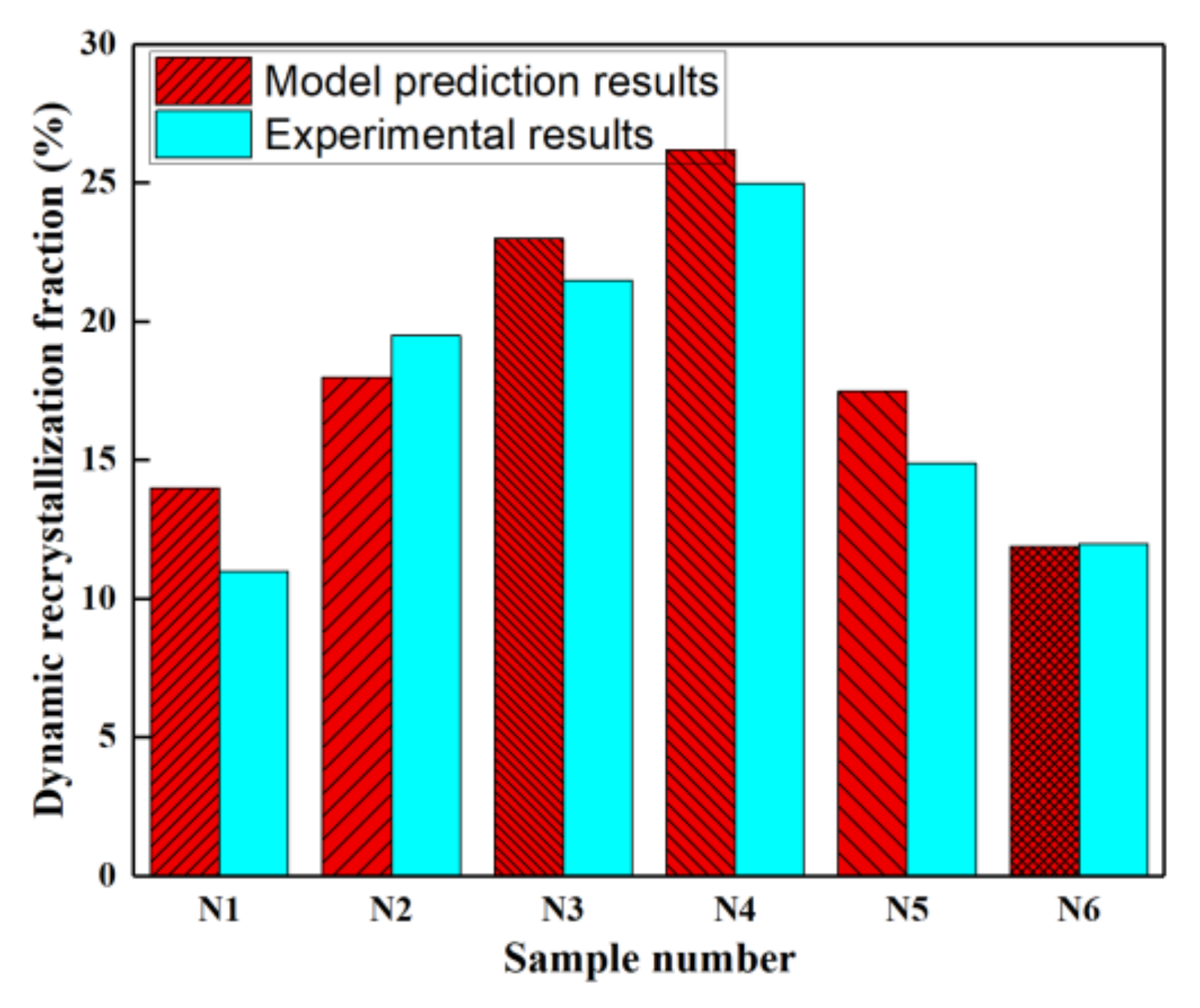
Aiming to verify the precision of this model, dynamic recrystallization fraction of the deformed specimens was tested and counted. The comparison between prediction results and experiment results is showed in Figure 7. It is clear that this model can accurately predict dynamic recrystallization fraction.

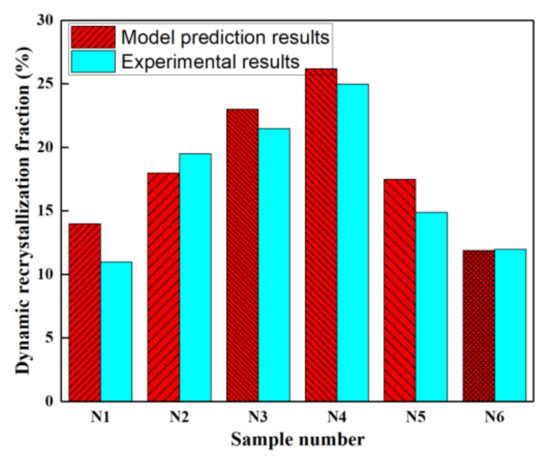
Figure 7. Comparison between experiment results and model prediction results: (N1) T = 300 °C, $\dot{\epsilon }$ = 0.01, ε = 0.6; (N2) T = 400 °C, $\dot{\epsilon }$ = 0.01, ε = 0.4; (N3) T = 400 °C, $\dot{\epsilon }$ = 0.01, ε = 0.6; (N4) T = 400 °C, $\dot{\epsilon }$ = 0.01, ε = 0.8; (N5) T = 300 °C, $\dot{\epsilon }$ = 0.1, ε = 0.6; (N6) T = 300 °C, $\dot{\epsilon }$ = 1, ε = 0.6.

4.2. FEM Application

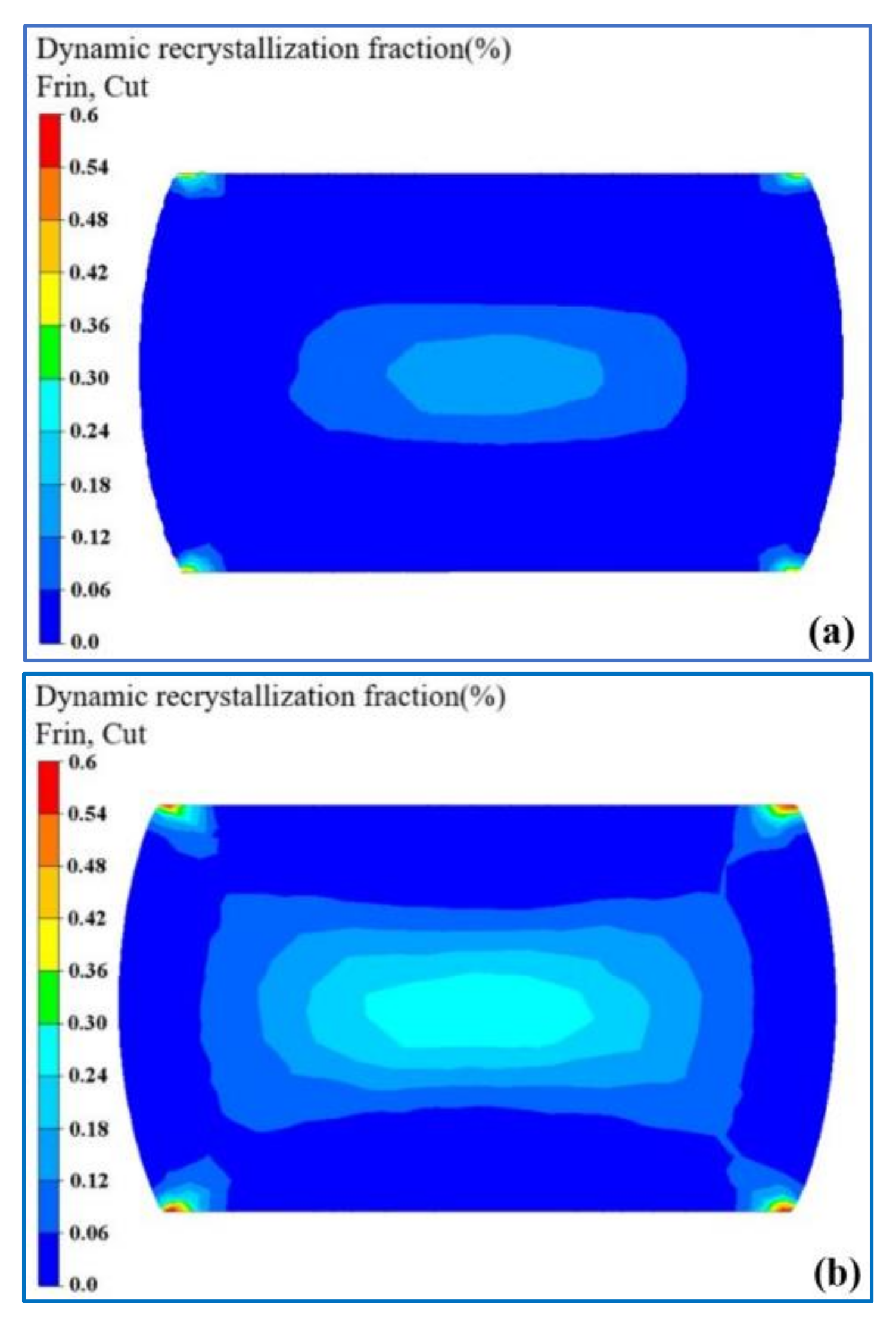
It can be concluded that the dynamic recrystallization model can accurately predict the dynamic recrystallization fraction of A356 alloy. Thus, this model was inserted into FEM software Forge by user subroutine program to simulate the hot compression process. The simulation results and experiment results are showed in Figure 8. Figure 8a shows the result with deformation temperature of 300 °C, strain rate of 0.01 s⁻¹ and reduction rate of 40%. Figure 8b shows the result with deformation temperature of 500 °C, strain rate of 0.01 s⁻¹ and reduction rate of 40%. The simulation results of the central area under those two deformation conditions are 14% and 30%, respectively. In addition, the experiment results of the central area under those two deformation conditions are 11.28% and 27.83%, respectively [21]. Obviously, the simulation results are in good agreement with the experimental results.

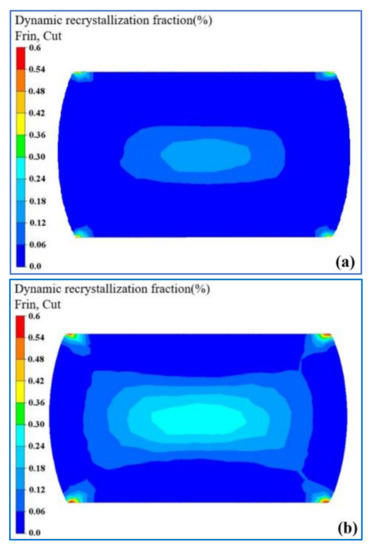
Figure 8. Comparison between the simulation results and experimental results: (a) simulation result with T = 300 °C, $\dot{\epsilon }=$ 0.01 s⁻¹ and reduction rate of 40%; (b) simulation result with T = 500 °C, $\dot{\epsilon }=$ 0.01 s⁻¹ and reduction rate of 40%.

5. Conclusions

In this paper, the flow stress and dynamic recrystallization of the A356 alloy was investigated by isothermal compression and mathematical modeling. The main conclusions can be obtained as follows:

(1)

The dynamic recrystallization of A356 aluminum alloy occurred during the thermoplastic deformation.

(2)

A dynamic recrystallization model based on Arrhenius type equation was developed to calculate the dynamic recrystallization fraction of the A356 alloy. There was a good agreement between the predicted and experimental dynamic recrystallization fraction.

(3)

The model was inserted into the FEM software Forge to simulate the microstructure evolution of A356 alloy during isothermal deformation. The maximum error between simulated and experimental dynamic recrystallization fraction is less than 3.0%.