An Improved Correlation for the Estimation of the Yield Strength from Small Punch Testing
Abstract
:1. Introduction
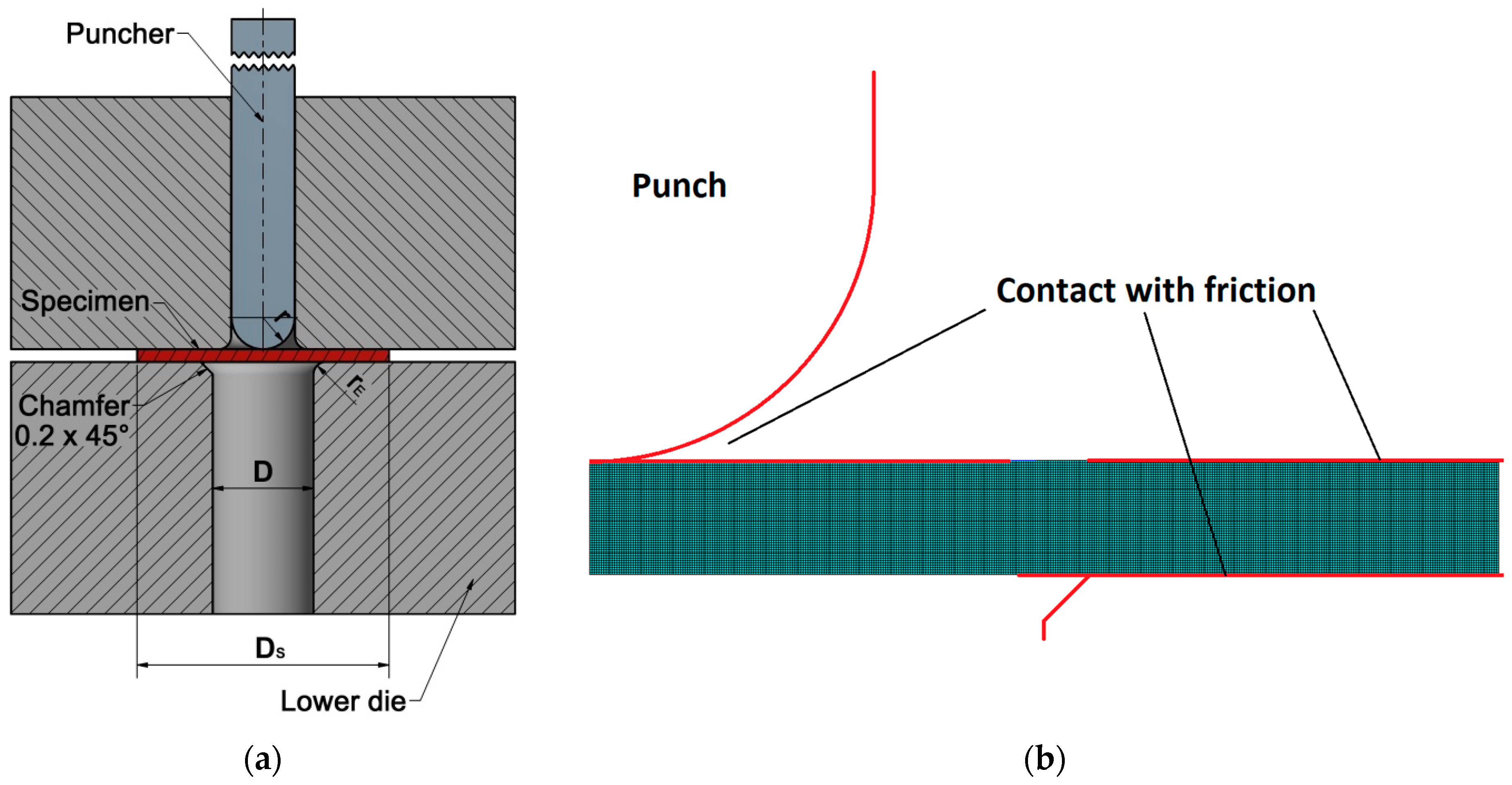
2. Modeling of the Small Punch Test
2.1. Finite Element Modeling
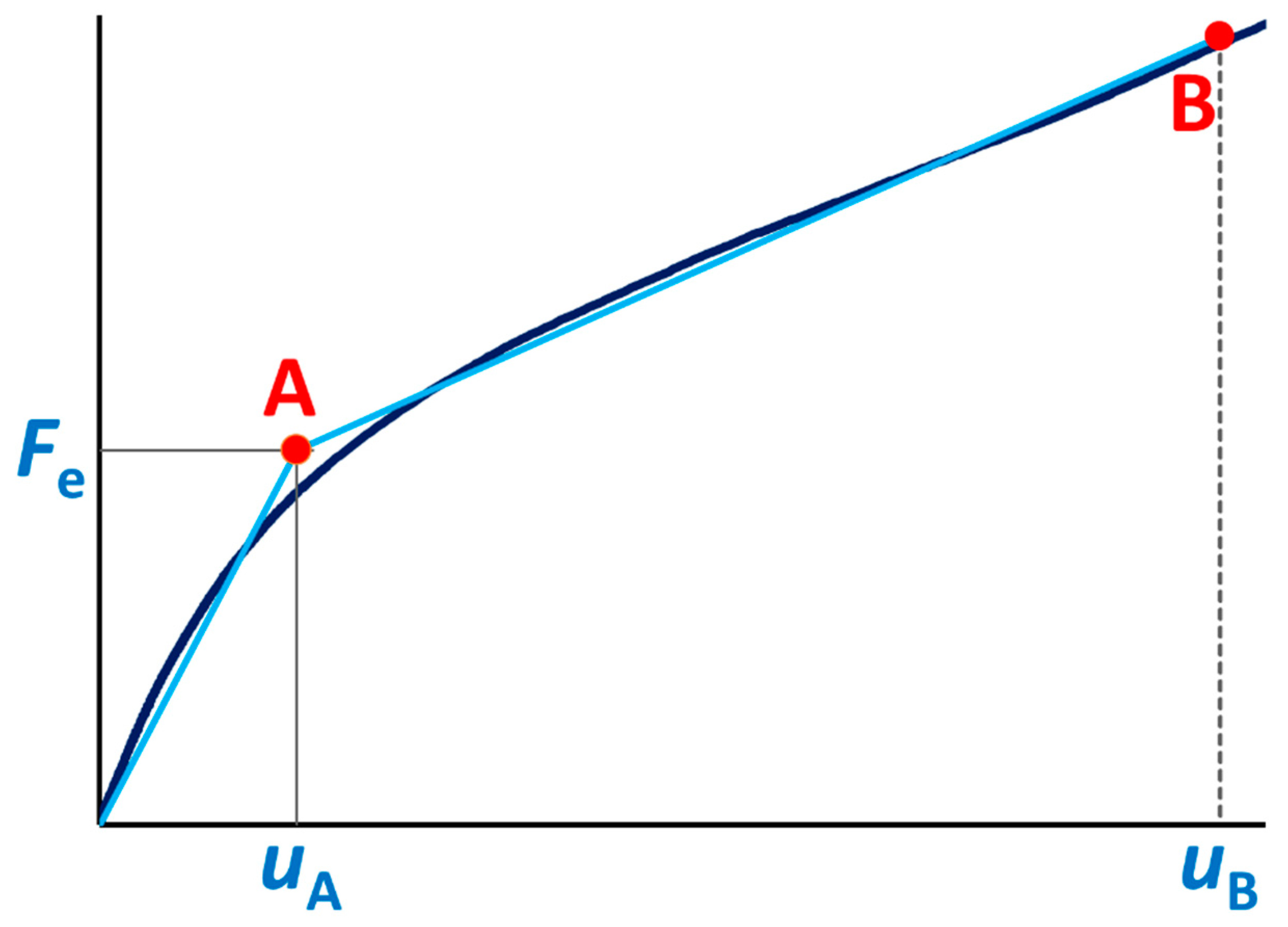
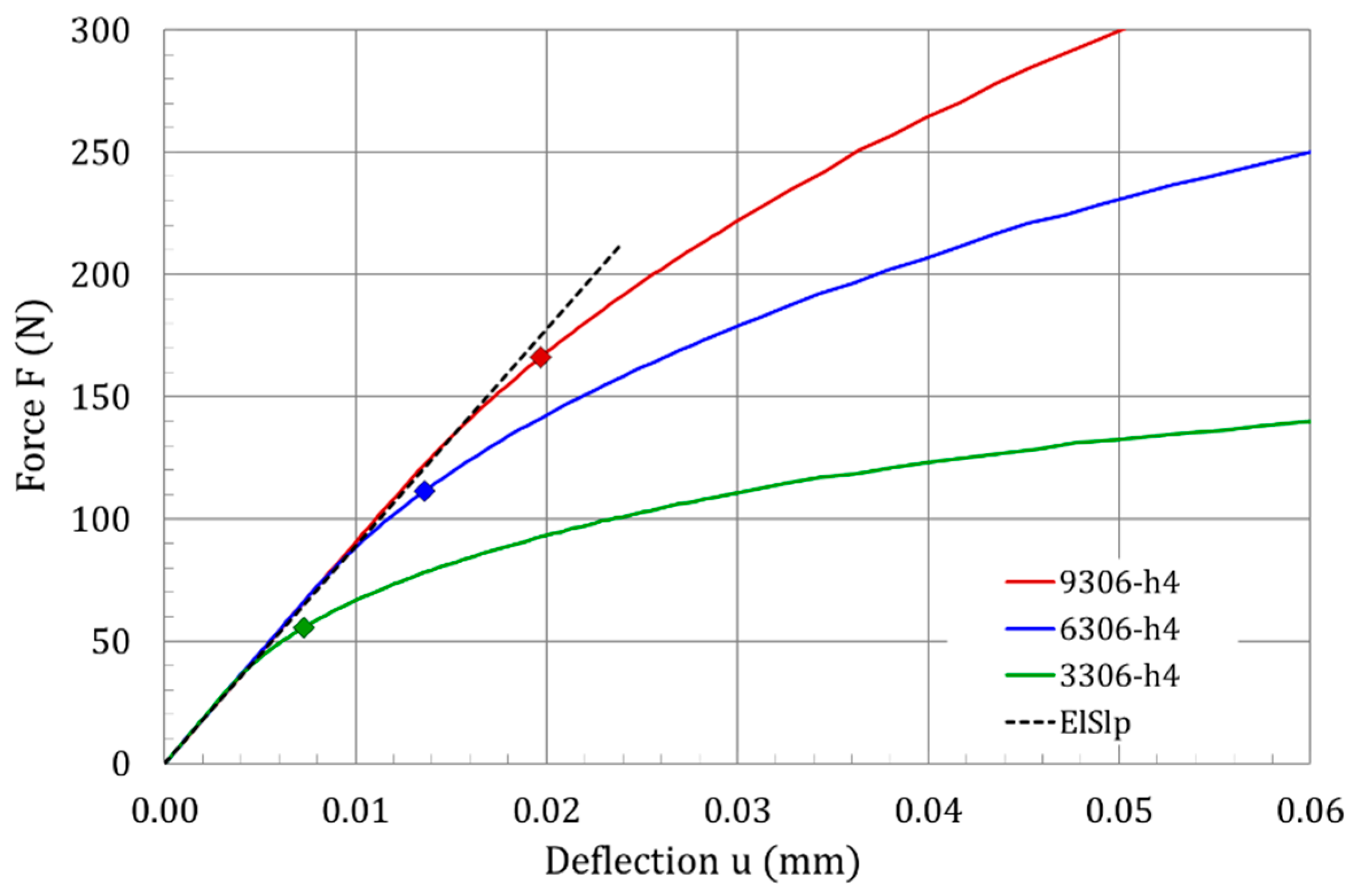
2.2. Analytical Equations for the Linear Elastic Phase of the SP Test
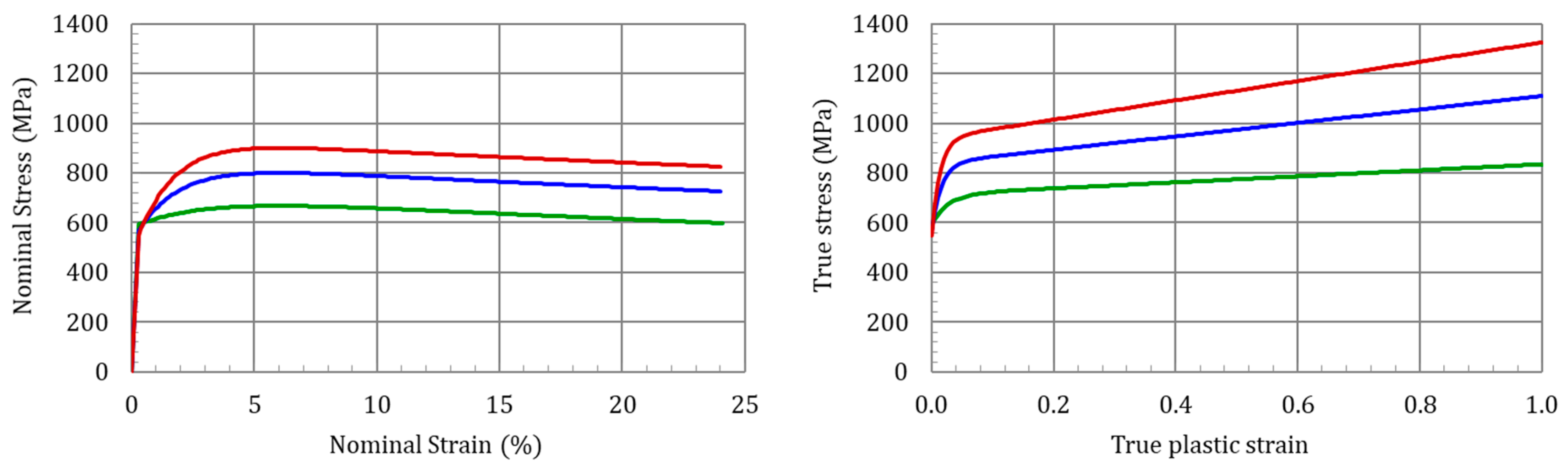
2.3. Systematic Variation of the Tensile Parameters and Specimen Thickness
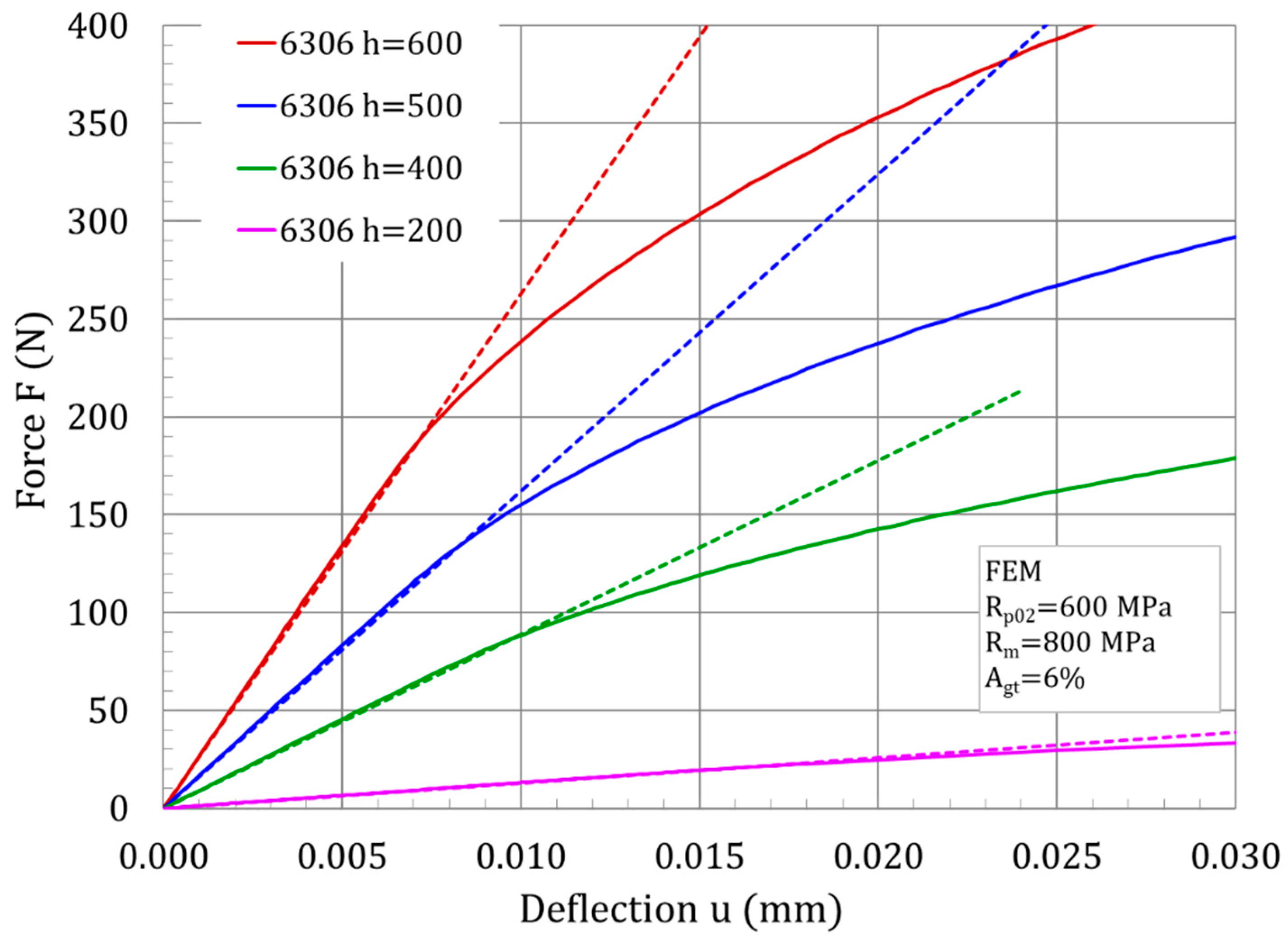
3. Results
4. Discussion
5. Conclusions
- The analytical elastic slope agrees very well with the finite element simulation;
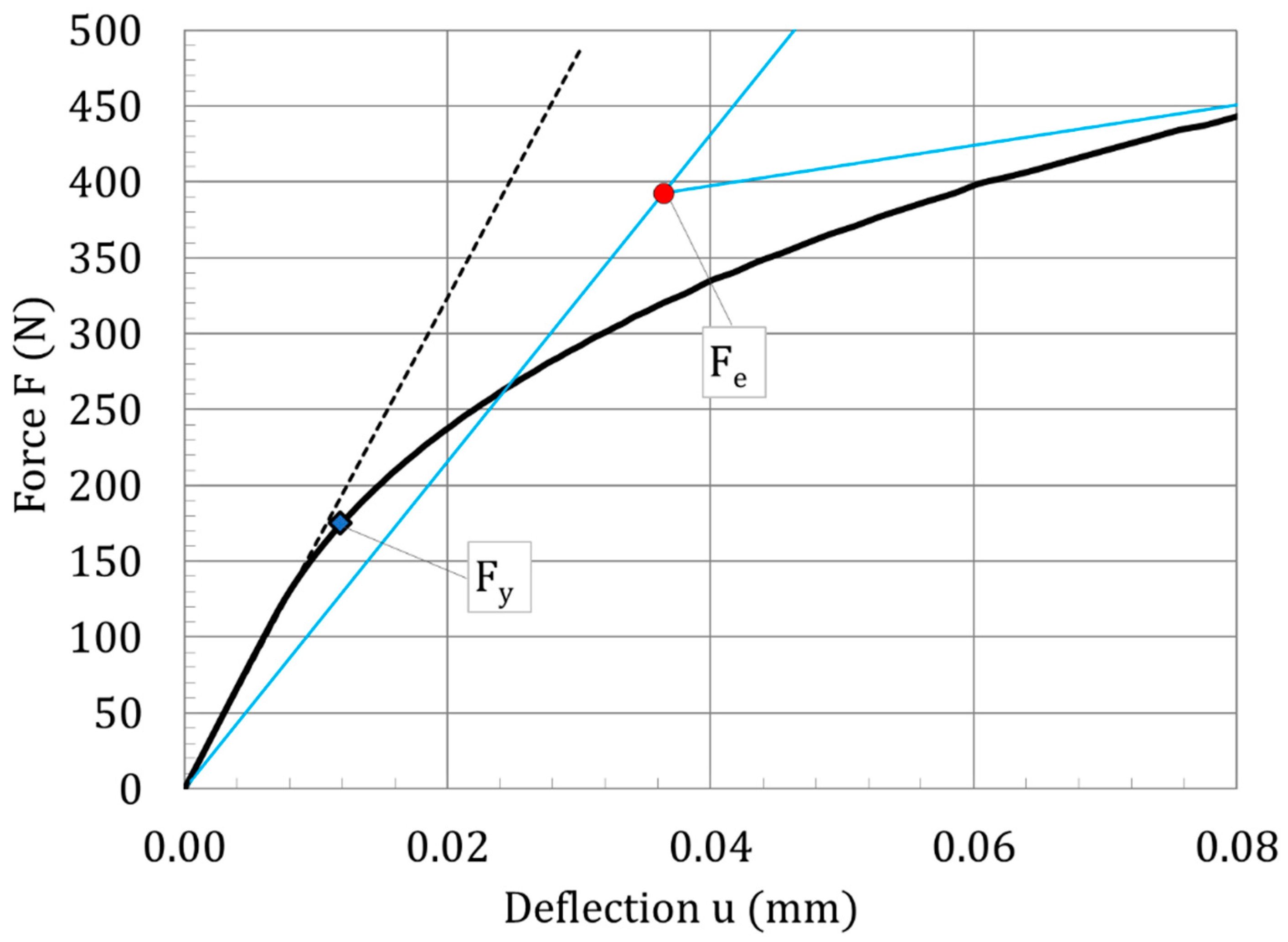
- A modified elastic–plastic transition force was proposed for the empirical yield strength correlation, which provides a significantly reduced uncertainty as compared to the elastic–plastic transition force defined in the European standard;
- With the new definition of (Equation (11)), the yield strength correlation is widely independent of the SP geometry and the flow properties of the material.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Effective lower die radius | |
| Total uniform strain (nominal strain at ) | |
| Radius of the contact area between punch and specimen | |
| Contact radius associated with the reference force | |
| Coefficient of variation (standard deviation divided by average) | |
| Diameter of lower die receiving hole | |
| Elasticity modulus | |
| Punch force | |
| Elastic–plastic transition force | |
| Reference force for the analytical calculation of the elastic slope | |
| Modified elastic–plastic transition force | |
| FE | Finite element |
| Specimens thickness | |
| Hardening exponent of the true stress–plastic strain curve | |
| Plate stiffness | |
| Puncher radius | |
| Parameter of the true stress–plastic strain curve | |
| Yield strength | |
| Ultimate tensile strength | |
| Elastic slope of the small punch plate (analytical calculation) | |
| SP | Small punch |
| UTS | Ultimate tensile strength |
| Central deflection at the specimen bottom (opposite to punch tip) | |
| Punch tip displacement | |
| Indentation depth of the punch as calculated by Hertzian contact theory | |
| YS | Yield strength |
| Empirical factor for the estimation of yield stress | |
| True strain | |
| Nominal strain | |
| Poisson’s ratio | |
| True stress | |
| Nominal stress | |
| Elasticity limit, true initial flow stress |
References
- Kameda, J. A kinetic model for ductile-brittle fracture mode transition behavior. Acta Metall. 1986, 34, 2391–2398. [Google Scholar] [CrossRef]
- Misawa, T.; Adachi, T.; Saito, M.; Hamaguchi, Y. Small punch tests for evaluating ductile-brittle transition behavior of irradiated ferritic steels. J. Nucl. Mater. 1987, 150, 194–202. [Google Scholar] [CrossRef]
- Abendroth, M.; Kuna, M. Identification of ductile damage and fracture parameters from the small punch test using neural networks. Eng. Fract. Mech. 2006, 73, 710–725. [Google Scholar] [CrossRef]
- Melkior, T.; Terentyev, D.; Chang, C.; Bakaev, A.; Holmström, S.; Lebediev, S.; Paputsia, A. Mechanical properties of structural metallic alloys for nuclear applications deduced by small punch test. J. Nucl. Mater. 2023, 583, 154521. [Google Scholar] [CrossRef]
- Shen, Y.; Lv, S.; Zhou, Q.; Shi, L.; Sun, L.; Li, Z. Microstructure Characterization and Small Punch Test Analysis in Nickel-Based Alloy 617 by High Energy Neon Implantation. Metals 2022, 12, 438. [Google Scholar] [CrossRef]
- EN Standard EN-10371; Small Punch Test Method for Metallic Materials. European Committee for Standardization: Brussels, Belgium, 2021.
- Altstadt, E.; Bergner, F.; Houska, M. Use of the small punch test for the estimation of ductile-to-brittle transition temperature shift of irradiated steels. Nucl. Mater. Energy 2021, 26, 100918. [Google Scholar] [CrossRef]
- Calaf Chica, J.; Bravo Díez, P.; Preciado Calzada, M. A New Prediction Method for the Ultimate Tensile Strength of Steel Alloys with Small Punch Test. Materials 2018, 11, 1491. [Google Scholar] [CrossRef]
- Calaf Chica, J.; Bravo Díez, P.M.; Preciado Calzada, M. Development of an improved prediction method for the yield strength of steel alloys in the Small Punch Test. Mater. Des. 2018, 148, 153–166. [Google Scholar] [CrossRef]
- Holmström, S.; Simonovski, I.; Baraldi, D.; Bruchhausen, M.; Altstadt, E.; Delville, R. Developments in the estimation of tensile strength by small punch testing. Theor. Appl. Fract. Mech. 2019, 101, 25–34. [Google Scholar] [CrossRef]
- Altstadt, E.; Houska, M.; Simonovski, I.; Bruchhausen, M.; Holmström, S.; Lacalle, R. On the estimation of ultimate tensile stress from small punch testing. Int. J. Mech. Sci. 2018, 136, 85–93. [Google Scholar] [CrossRef]
- Campitelli, E.N.; Spätig, P.; Bonadé, R.; Hoffelner, W.; Victoria, M. Assessment of the constitutive properties from small ball punch test: Experiment and modeling. J. Nucl. Mater. 2004, 335, 366–378. [Google Scholar] [CrossRef]
- Lacalle, R.; Andrés, D.; Álvarez, J.A.; Gutiérrez-Solana, F. Transition Region of Nuclear Vessel Steels: Master Curve Approach Using Small Punch Notched Specimens. Key Eng. Mater. 2017, 734, 77–86. [Google Scholar] [CrossRef]
- Andres, D.; Lacalle, R.; Cicero, S.; Alvarez, J.A. Application of the small punch test in combination with the master curve approach for the characterisation of the ductile to brittle transition region. J. Nucl. Mater. 2019, 518, 409–418. [Google Scholar] [CrossRef]
- Holmström, S.; Li, Y.; Dymacek, P.; Vacchieri, E.; Jeffs, S.P.; Lancaster, R.J.; Omacht, D.; Kubon, Z.; Anelli, E.; Rantala, J.; et al. Creep strength and minimum strain rate estimation from Small Punch Creep tests. Mater. Sci. Eng. A 2018, 731, 161–172. [Google Scholar] [CrossRef]
- Vivas, J.; Capdevila, C.; Altstadt, E.; Houska, M.; Sabirov, I.; San-Martín, D. Microstructural Degradation and Creep Fracture Behavior of Conventionally and Thermomechanically Treated 9% Chromium Heat Resistant Steel. Met. Mater. Int. 2019, 25, 343–352. [Google Scholar] [CrossRef]
- Vivas, J.; Capdevila, C.; Altstadt, E.; Houska, M.; San-Martín, D. Importance of austenitization temperature and ausforming on creep strength in 9Cr ferritic/martensitic steel. Scr. Mater. 2018, 153, 14–18. [Google Scholar] [CrossRef]
- Dymáček, P.; Jarý, M.; Dobeš, F.; Kloc, L. Tensile and Creep Testing of Sanicro 25 Using Miniature Specimens. Materials 2018, 11, 142. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Gao, M.; Zhang, H.; Geng, X.; Liu, X.; Pan, H. Small punch creep test reveals the differences of high-temperature creep behaviours for laser powder bed fusion and Rolled Inconel 718 alloys. Mater. Sci. Eng. A 2023, 886, 145698. [Google Scholar] [CrossRef]
- Huang, Y.; Kadowaki, M.; Nakano, T.; Kumada, K.; Watanabe, S.; Kawada, T.; Sato, K. Creep constitutive law prediction via short-term evaluation using a small size testing method. Energy Rep. 2023, 10, 1126–1134. [Google Scholar] [CrossRef]
- Hermanová, Š.; Kuboň, Z.; Čížek, P.; Kosňovská, J.; Rožnovská, G.; Dorazil, O.; Cieslarová, M. Study of Material Properties and Creep Behavior of a Large Block of AISI 316L Steel Produced by SLM Technology. Metals 2022, 12, 1283. [Google Scholar] [CrossRef]
- Tian, X.; Zhang, S.; Xu, H.; Li, T.; Yang, B.; Zhang, M. Assessment of Creep Properties Using Small Punch Test for a 9%Cr-Mo-Co-B Power Plant Steel. Metals 2021, 11, 1996. [Google Scholar] [CrossRef]
- Pan, H.; Peng, J.; Geng, X.; Gao, M.; Miao, X. Prediction of mechanical properties for typical pressure vessel steels by small punch test combined with machine learning. Int. J. Press. Vessels Pip. 2023, 206, 105060. [Google Scholar] [CrossRef]
- Zhong, J.; He, Z.; Guan, K.; Jiang, T. Investigation on regression model for the force of small punch test using machine learning. Int. J. Press. Vessels Pip. 2023, 206, 105031. [Google Scholar] [CrossRef]
- Kameda, J.; Mao, X. Small-punch and TEM-disc testing techniques and their application to characterization of radiation damage. J. Mater. Sci. 1992, 27, 983–989. [Google Scholar] [CrossRef]
- Bruchhausen, M.; Austin, T.; Holmström, S.; Altstadt, E.; Dymacek, P.; Jeffs, S.; Lancaster, R.; Lacalle, R.; Matocha, K.; Petzová, J. European Standard on Small Punch Testing of Metallic Materials; ASME: New York, NY, USA, 2017; p. V01AT01A065. [Google Scholar] [CrossRef]
- Altstadt, E.; Ge, H.E.; Kuksenko, V.; Serrano, M.; Houska, M.; Lasan, M.; Bruchhausen, M.; Lapetite, J.-M.; Dai, Y. Critical evaluation of the small punch test as a screening procedure for mechanical properties. J. Nucl. Mater. 2016, 472, 186–195. [Google Scholar] [CrossRef]
- Hähner, P.; Soyarslan, C.; Çakan, B.G.; Bargmann, S. Determining tensile yield stresses from Small Punch tests: A numerical-based scheme. Mater. Des. 2019, 182, 107974. [Google Scholar] [CrossRef]
- Zhong, J.; Song, M.; Guan, K.; Dymacek, P. Application of a database in the evaluation of strengths of Cr-Mo steels by means of small punch test. Int. J. Mech. Sci. 2020, 166, 105195. [Google Scholar] [CrossRef]
- Popov, V.L. Contact Mechanics and Friction: Physical Principles and Applications, English ed.; Springer: Heidelberg, Germany; New York, NY, USA, 2010. [Google Scholar]
- Mathiak, F.U. Ebene Flächentragwerke II—Grundlagen der Plattentheorie; Hochschule Neubrandenburg, Dept. Bauingenieur- und Vermessungswesen: Neubrandenburg, Germany, 2008. [Google Scholar]
- Reissner, E. On the Theory of Bending of Elastic Plates. J. Math. Phys. 1944, 23, 184–191. [Google Scholar] [CrossRef]
- Mindlin, R.D. Influence of Rotatory Inertia and Shear on Flexural Motions of Isotropic. Elastic Plates J. Appl. Mech. 1951, 18, 31–38. [Google Scholar] [CrossRef]




| Punch Diameter d = 2r (mm) | Receiving Hole Diameter D (mm) | Specimen Thickness h (mm) | Edge Size (mm) | Edge Type |
|---|---|---|---|---|
| 2.5 | 4.0 | 0.2 … 0.6 | 0.2 | Chamfer |
| Code | |||||||
|---|---|---|---|---|---|---|---|
| 3106 | 296.3 | 60.8 | 35.4 | 300 | 333 | 1.11 | 6 |
| 3306 | 285.3 | 135.1 | 59.2 | 300 | 400 | 1.33 | 6 |
| 3506 | 275.2 | 193.9 | 69.1 | 300 | 450 | 1.5 | 6 |
| 6106 | 592.2 | 121.2 | 27.5 | 600 | 667 | 1.11 | 6 |
| 6303 | 504.2 | 311.3 | 185.9 | 600 | 800 | 1.33 | 3 |
| 6306 | 569.0 | 270.0 | 62.6 | 600 | 800 | 1.33 | 6 |
| 6312 | 587.7 | 298.6 | 22.1 | 600 | 800 | 1.33 | 12 |
| 6506 | 547.5 | 388.8 | 73.4 | 600 | 900 | 1.5 | 6 |
| 9106 | 887.9 | 179.2 | 39.4 | 900 | 1000 | 1.11 | 6 |
| 9306 | 851.0 | 404.9 | 66.2 | 900 | 1200 | 1.33 | 6 |
| 9506 | 816.3 | 585.3 | 78.3 | 900 | 1350 | 1.5 | 6 |
| Simulation ID | ||||
|---|---|---|---|---|
| 3106-h5 | 81.9 | 196.4 | 0.916 | 0.382 |
| 3306-h2 | 13.3 | 24.8 | 0.900 | 0.484 |
| 3306-h4 | 55.8 | 124.7 | 0.860 | 0.385 |
| 3306-h5 | 85.5 | 202.5 | 0.877 | 0.370 |
| 3306-h6 | 120.1 | 301.0 | 0.899 | 0.359 |
| 3506-h5 | 88.5 | 209.6 | 0.848 | 0.358 |
| 6106-h5 | 164.2 | 370.6 | 0.914 | 0.405 |
| 6303-h5 | 178.8 | 401.8 | 0.839 | 0.373 |
| 6306-h2 | 25.9 | 42.3 | 0.927 | 0.567 |
| 6306-h4 | 111.4 | 232.7 | 0.862 | 0.413 |
| 6306-h5 | 174.7 | 392.8 | 0.859 | 0.382 |
| 6306-h6 | 244.5 | 586.7 | 0.884 | 0.368 |
| 6312-h5 | 167.4 | 381.1 | 0.896 | 0.394 |
| 6506-h5 | 179.5 | 407.1 | 0.836 | 0.368 |
| 9106-h5 | 250.6 | 539.6 | 0.898 | 0.417 |
| 9306-h2 | 38.5 | 55.4 | 0.935 | 0.650 |
| 9306-h4 | 168.4 | 335.8 | 0.855 | 0.429 |
| 9306-h5 | 264.0 | 563.3 | 0.852 | 0.399 |
| 9306-h6 | 369.2 | 850.2 | 0.878 | 0.381 |
| 9506-h5 | 269.9 | 578.5 | 0.834 | 0.389 |
| Dataset | ||||
|---|---|---|---|---|
| All data | 0.41 | 0.88 | 17.4% | 3.7% |
| Sets | 0.37 | 0.88 | 2.5% | 1.9% |
| Sets | 0.39 | 0.87 | 4.4% | 3.8% |
| Sets | 0.41 | 0.86 | 4.4% | 0.3% |
| Sets | 0.57 | 0.92 | 12.0% | 1.1% |
| Simulation ID | ||||
|---|---|---|---|---|
| 6306-D175-h250 | 42.7 | 95.5 | 0.88 | 0.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Altstadt, E. An Improved Correlation for the Estimation of the Yield Strength from Small Punch Testing. Metals 2023, 13, 1716. https://doi.org/10.3390/met13101716
Altstadt E. An Improved Correlation for the Estimation of the Yield Strength from Small Punch Testing. Metals. 2023; 13(10):1716. https://doi.org/10.3390/met13101716
Chicago/Turabian StyleAltstadt, Eberhard. 2023. "An Improved Correlation for the Estimation of the Yield Strength from Small Punch Testing" Metals 13, no. 10: 1716. https://doi.org/10.3390/met13101716
APA StyleAltstadt, E. (2023). An Improved Correlation for the Estimation of the Yield Strength from Small Punch Testing. Metals, 13(10), 1716. https://doi.org/10.3390/met13101716






