Artificial Neural Network-Based Critical Conditions for the Dynamic Recrystallization of Medium Carbon Steel and Application
Abstract
1. Introduction
2. Materials and Experiments
2.1. Experimental Procedure and Compression Test Results
2.2. Identification of DRX Model’s Parameters
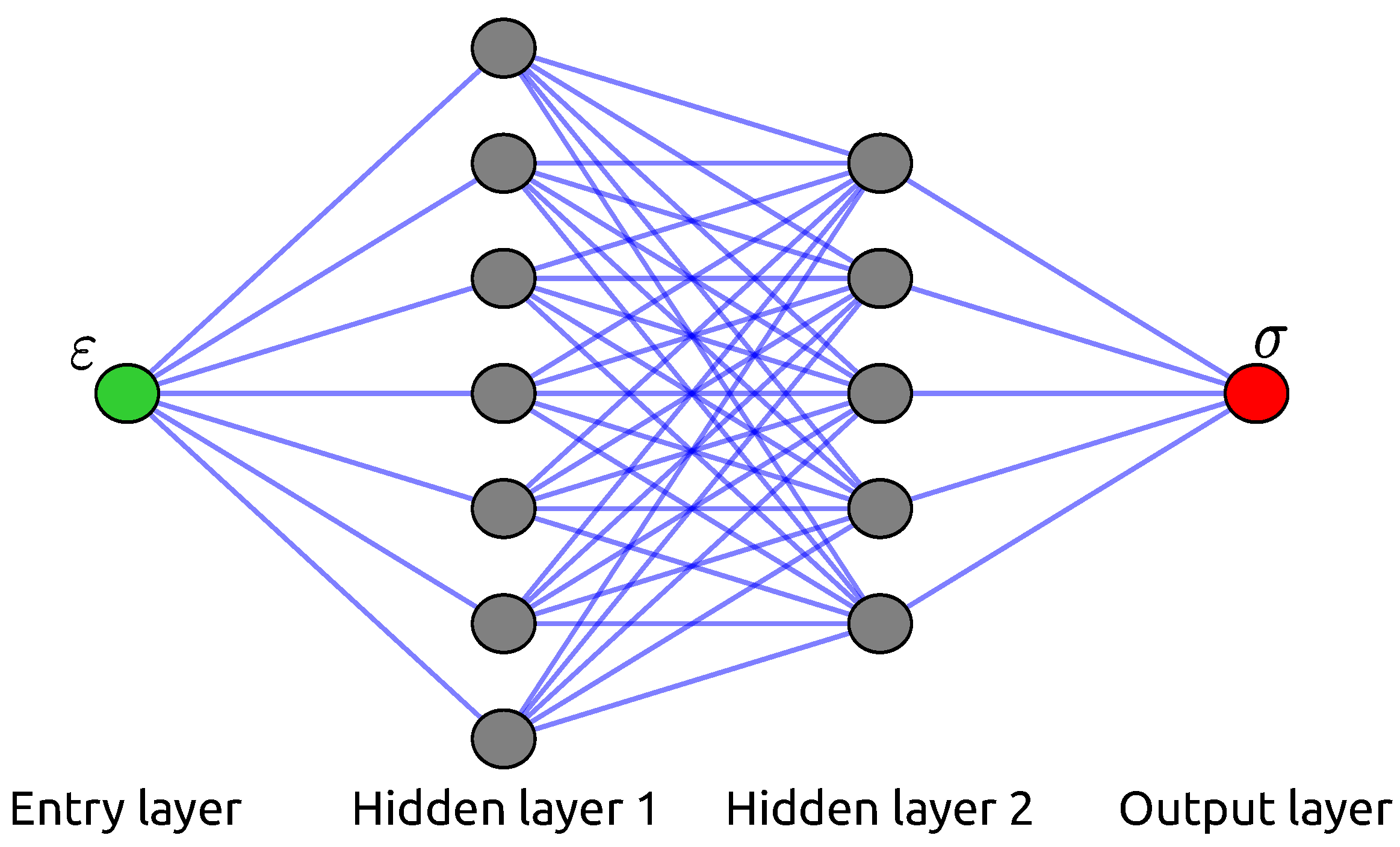
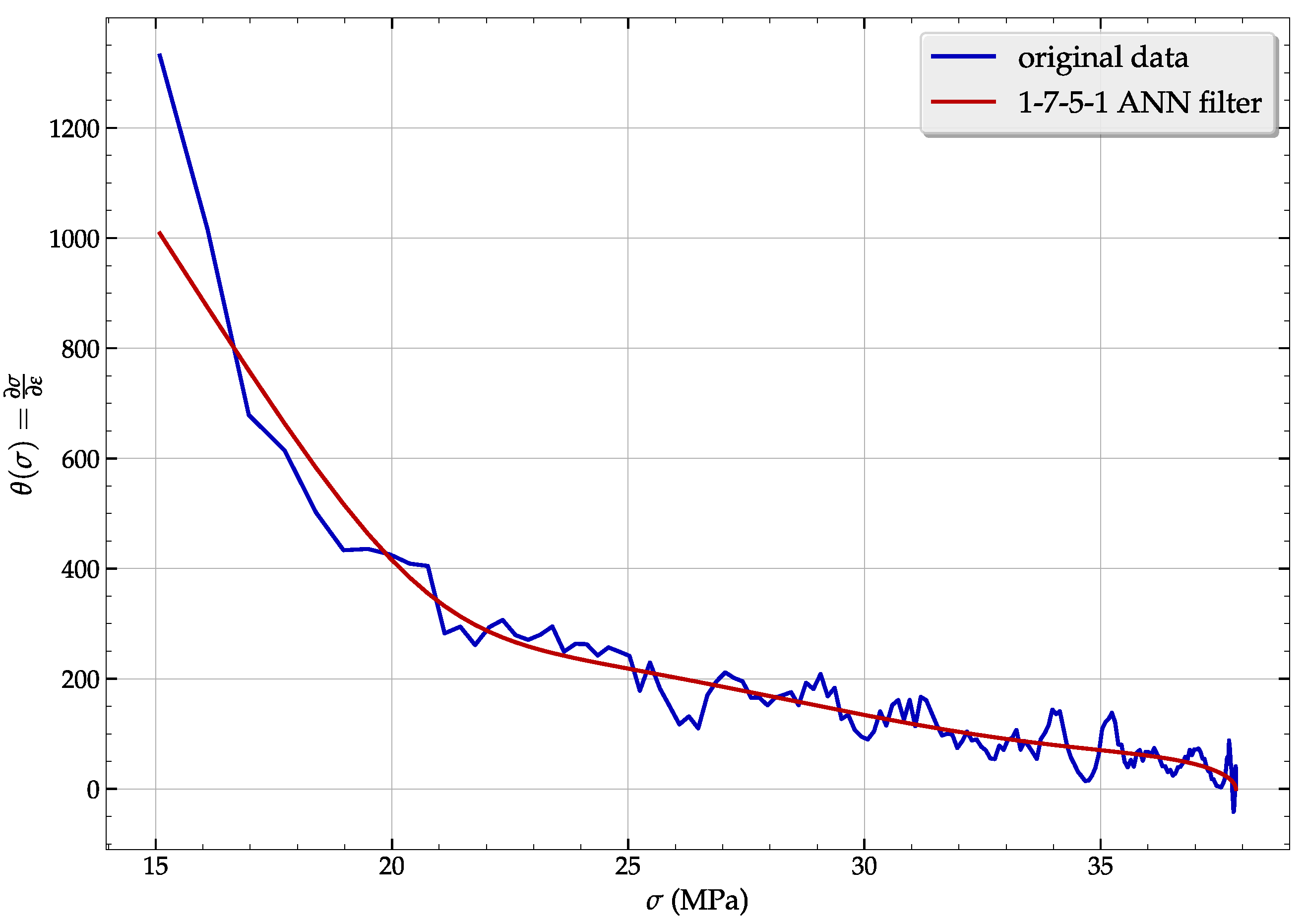
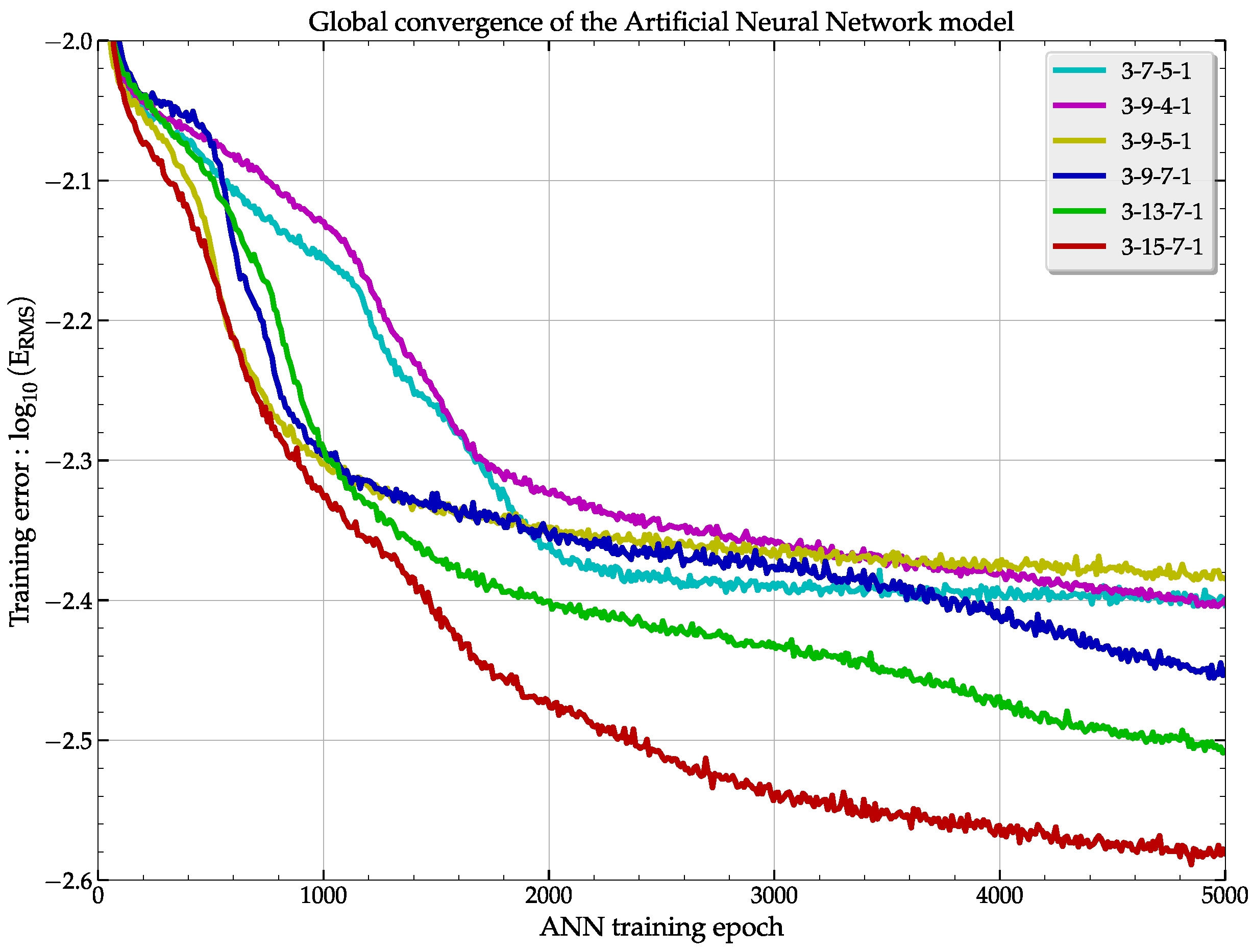
2.2.1. ANN-Based Filtering Model’s Architecture
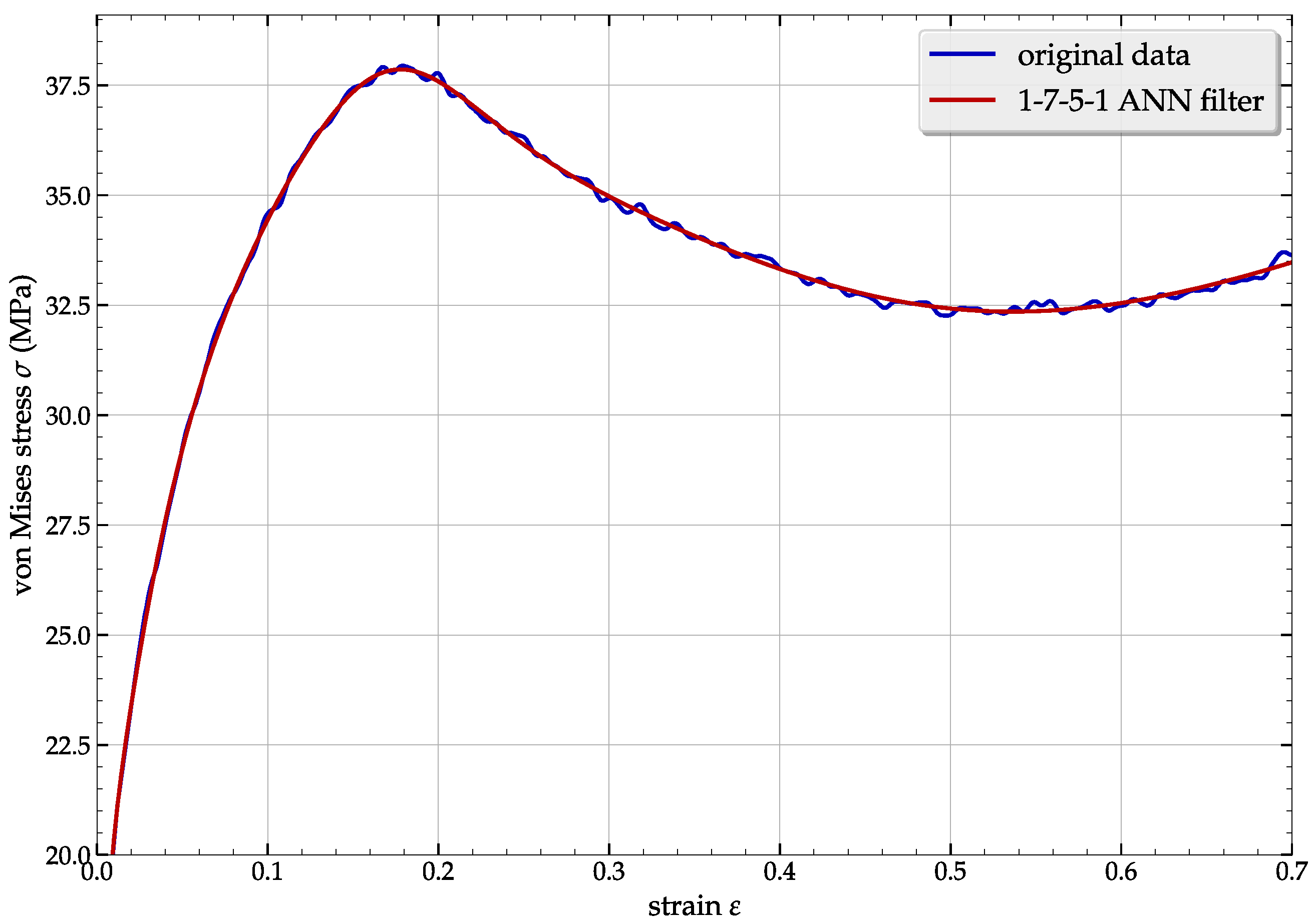
2.2.2. ANN-Based Filtering Model’s Application
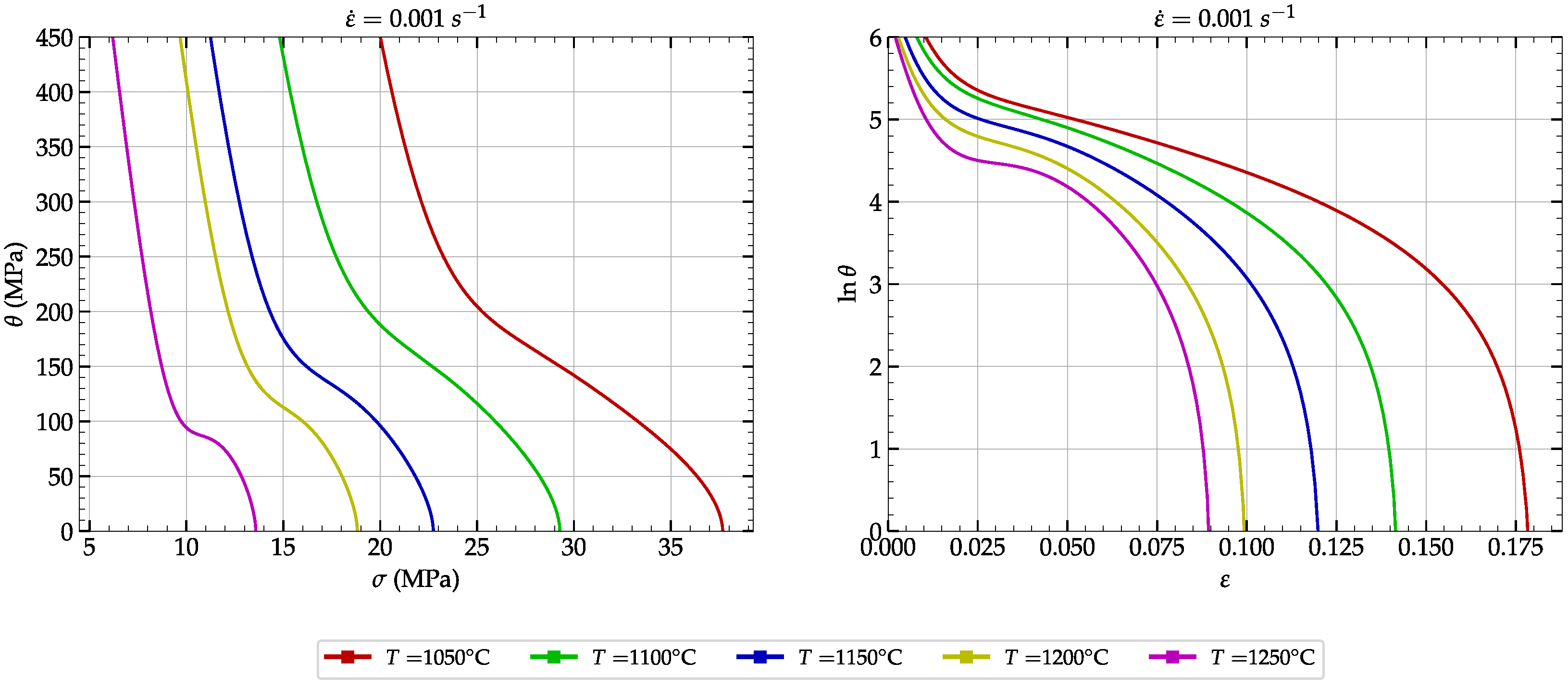
2.2.3. Evaluation of the Critical Conditions
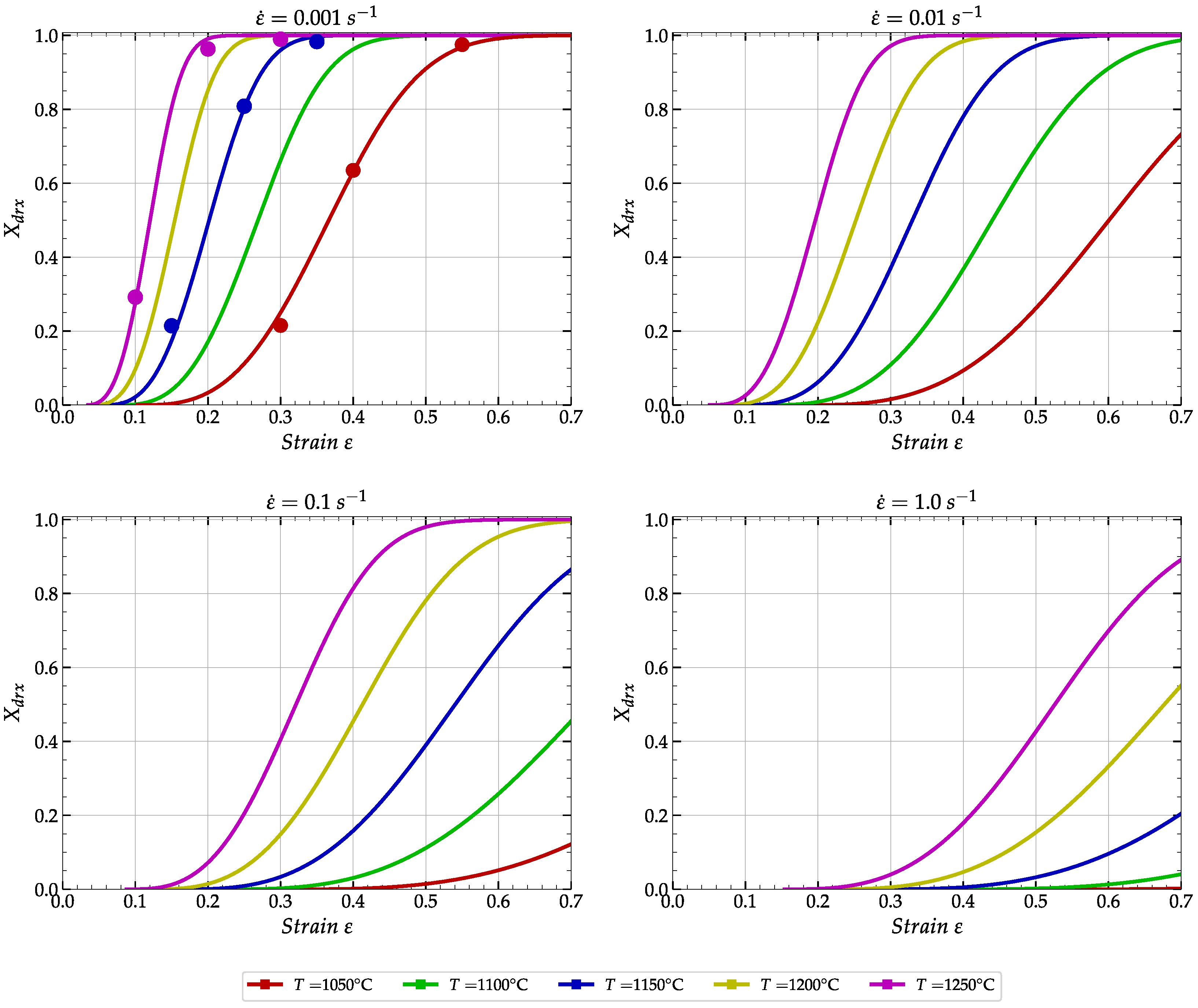
2.3. Evaluation of the DRX Model’s Parameters
3. Numerical Simulation of the Compression
3.1. Identification of the ANN Constitutive Law
3.2. Dynamic Recrystallization Simulation
3.2.1. Temperature and Strain Rate Effects
3.2.2. Comparison with Some Experiments
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial neural network |
| DRX | Dynamic recrystallization |
| DRX’s volume fraction: for experimental and predicted values, respectively | |
| FE | Finite element |
| SRX | Static recrystallization |
| WH | Work hardening |
References
- Javidikia, M.; Sadeghifar, M.; Champliaud, H.; Jahazi, M. Grain size and temperature evolutions during linear friction welding of Ni-base superalloy Waspaloy: Simulations and experimental validations. J. Adv. Join. Process. 2023, 8, 100150. [Google Scholar] [CrossRef]
- Shen, J.; Zhang, L.; Hu, L.; Sun, Y.; Gao, F.; Liu, W.; Yu, H. Effect of subgrain and the associated DRX behaviour on the texture modification of Mg-6.63 Zn-0.56 Zr alloy during hot tensile deformation. Mater. Sci. Eng. A 2021, 823, 141745. [Google Scholar] [CrossRef]
- Babu, K.A.; Mozumder, Y.H.; Athreya, C.N.; Sarma, V.S.; Mandal, S. Implication of initial grain size on DRX mechanism and grain refinement in super-304H SS in a wide range of strain rates during large-strain hot deformation. Mater. Sci. Eng. A 2022, 832, 142269. [Google Scholar] [CrossRef]
- Peng, Y.; Guo, S.; Liu, C.; Barella, S.; Liang, S.; Gruttadauria, A.; Mapelli, C. Dynamic recrystallization behavior of low-carbon steel during hot rolling process: Modeling and simulation. J. Mater. Res. Technol. 2022, 20, 1266–1290. [Google Scholar] [CrossRef]
- Najafizadeh, A.; Jonas, J.J. Predicting the critical stress for initiation of dynamic recrystallization. ISIJ Int. 2006, 46, 1679–1684. [Google Scholar] [CrossRef]
- Gottstein, G.; Frommert, M.; Goerdeler, M.; Schäfer, N. Prediction of the critical conditions for dynamic recrystallization in the austenitic steel 800H. Mater. Sci. Eng. A 2004, 387, 604–608. [Google Scholar] [CrossRef]
- Ryan, N.D.; McQueen, H.J. Dynamic recovery, strain hardening and flow stress in hot working of 316 steel. Czechoslov. J. Phys. B 1989, 39, 458–465. [Google Scholar] [CrossRef]
- Ryan, N.D.; McQueen, H.J. Dynamic softening mechanisms in 304 austenitic stainless steel. Can. Metall. Q. 1990, 29, 147–162. [Google Scholar] [CrossRef]
- Ryan, N.D.; McQueen, H.J. Flow stress, dynamic restoration, strain hardening and ductility in hot working of 316 steel. J. Mater. Process. Technol. 1990, 21, 177–199. [Google Scholar] [CrossRef]
- Poliak, E.I.; Jonas, J.J. A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization. Acta Mater. 1996, 44, 127–136. [Google Scholar] [CrossRef]
- Poliak, E.I.; Jonas, J.J. Initiation of dynamic recrystallization in constant strain rate hot deformation. ISIJ Int. 2003, 43, 684–691. [Google Scholar] [CrossRef]
- Poliak, E.I.; Jonas, J.J. Critical strain for dynamic recrystallization in variable strain rate hot deformation. ISIJ Int. 2003, 43, 692–700. [Google Scholar] [CrossRef]
- Jonas, J.J.; Poliak, E.I. The critical strain for dynamic recrystallization in rolling mills. In Materials Science Forum; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2003; Volume 426, pp. 57–66. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of Phase Change. I General Theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Li, X.; Duan, L.; Li, J.; Wu, X. Experimental study and numerical simulation of dynamic recrystallization behavior of a micro-alloyed plastic mold steel. Mater. Des. 2015, 66, 309–320. [Google Scholar] [CrossRef]
- Estrin, Y.; Mecking, H. A unified phenomenological description of work hardening and creep based on one-parameter models. Acta Metall. 1984, 32, 57–70. [Google Scholar] [CrossRef]
- Mecking, H.; Kocks, U.F. Kinetics of flow and strain-hardening. Acta Metall. 1981, 29, 1865–1875. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, L.; Xu, Q.; Xia, Y.; Shen, W. The kinetics and cellular automaton modeling of dynamic recrystallization behavior of a medium carbon Cr-Ni-Mo alloyed steel in hot working process. Mater. Sci. Eng. A 2016, 678, 33–43. [Google Scholar] [CrossRef]
- Cho, J.R.; Jeong, H.S.; Cha, D.J.; Bae, W.B.; Lee, J.W. Prediction of microstructural evolution and recrystallization behaviors of a hot working die steel by FEM. J. Mater. Process. Technol. 2005, 160, 1–8. [Google Scholar] [CrossRef]
- Razali, M.K.; Joun, M.S. A new approach of predicting dynamic recrystallization using directly a flow stress model and its application to medium Mn steel. J. Mater. Res. Technol. 2021, 11, 1881–1894. [Google Scholar] [CrossRef]
- Wan, Z.; Sun, Y.; Hu, L.; Yu, H. Experimental study and numerical simulation of dynamic recrystallization behavior of TiAl-based alloy. Mater. Des. 2017, 122, 11–20. [Google Scholar] [CrossRef]
- Li, C.; Tan, Y.; Zhao, F. Finite element simulation and process optimization of microstructure evolution in the formation of Inconel 718 alloy bolts. Mater. Res. Express 2018, 6, 026578. [Google Scholar] [CrossRef]
- Cui, N.; Kong, F.; Wang, X.; Chen, Y.; Zhou, H. Hot deformation behavior and dynamic recrystallization of a β-solidifying TiAl alloy. Mater. Sci. Eng. A 2016, 652, 231–238. [Google Scholar] [CrossRef]
- Chen, X.; Sun, J.; Yang, Y.; Liu, B.; Si, Y.; Zhou, J. Finite Element Analysis of Dynamic Recrystallization Model and Microstructural Evolution for GCr15 Bearing Steel Warm–Hot Deformation Process. Materials 2023, 16, 4806. [Google Scholar] [CrossRef]
- Tize Mha, P.; Dhondapure, P.; Jahazi, M.; Tongne, A.; Pantalé, O. Interpolation and Extrapolation Performance Measurement of Analytical and ANN-Based Flow Laws for Hot Deformation Behavior of Medium Carbon Steel. Metals 2023, 13, 633. [Google Scholar] [CrossRef]
- Pantalé, O.; Tize Mha, P.; Tongne, A. Efficient implementation of non-linear flow law using neural network into the Abaqus Explicit FEM code. Finite Elem. Anal. Des. 2022, 198, 103647. [Google Scholar] [CrossRef]
- Galos, J.; Das, R.; Sutcliffe, M.P.; Mouritz, A.P. Review of balsa core sandwich composite structures. Mater. Des. 2022, 221, 111013. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A System for Large-Scale Machine Learning. In Proceedings of the 12th USENIX Conference on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Kingma, D.P.; Lei, J. Adam: A method for stochastic optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, J.; Du, Y.; Wang, G.; Huang, T. Dynamic Recrystallization Simulation for X12 Alloy Steel by CA Method Based on Modified L-J Dislocation Density Model. Metals 2019, 9, 1291. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, J.H. Effect of strain rate upon plastic flow of steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Chen, X.M.; Lin, Y.; Wen, D.X.; Zhang, J.L.; He, M. Dynamic recrystallization behavior of a typical nickel-based superalloy during hot deformation. Mater. Des. 2014, 57, 568–577. [Google Scholar] [CrossRef]
- Li, L.; Wang, Y.; Li, H.; Jiang, W.; Wang, T.; Zhang, C.C.; Wang, F.; Garmestani, H. Effect of the Zener-Hollomon parameter on the dynamic recrystallization kinetics of Mg–Zn–Zr–Yb magnesium alloy. Comput. Mater. Sci. 2019, 166, 221–229. [Google Scholar] [CrossRef]
- Wang, T.; Chen, Y.; Ouyang, B.; Zhou, X.; Hu, J.; Le, Q. Artificial neural network modified constitutive descriptions for hot deformation and kinetic models for dynamic recrystallization of novel AZE311 and AZX311 alloys. Mater. Sci. Eng. A 2021, 816, 141259. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. A constitutive model and data for materials subjected to large strains, high strain rates, and high temperatures. In Proceedings of the 7th International Symposium on Ballistics, Hague, The Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar] [CrossRef][Green Version]
- Zerilli, F.J.; Armstrong, R.W. Dislocation-mechanics-based constitutive relations for material dynamics calculations. J. Appl. Phys. 1987, 61, 1816–1825. [Google Scholar] [CrossRef]
- Hensel, A.; Spittel, T. Kraft- und Arbeitsbedarf Bildsamer Formgebungsverfahren; Deutscher Verlag für Grundstoffindustrie: Leipzig, Germany, 1978. [Google Scholar]
- Sellars, C.M.; McTegart, W.J. On the mechanism of hot deformation. Acta Metall. 1966, 14, 1136–1138. [Google Scholar] [CrossRef]
- Zhang, M.; Sun, X.; Wang, Y. Elevated temperature deformation characteristics of 15Mn7 steels. Procedia Manuf. 2019, 37, 360–366. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, M.; Wang, Y.; Sun, Y.; Wang, Y. Kinetics and numerical simulation of dynamic recrystallization behavior of medium Mn steel in hot working. Steel Res. Int. 2020, 91, 1900675. [Google Scholar] [CrossRef]
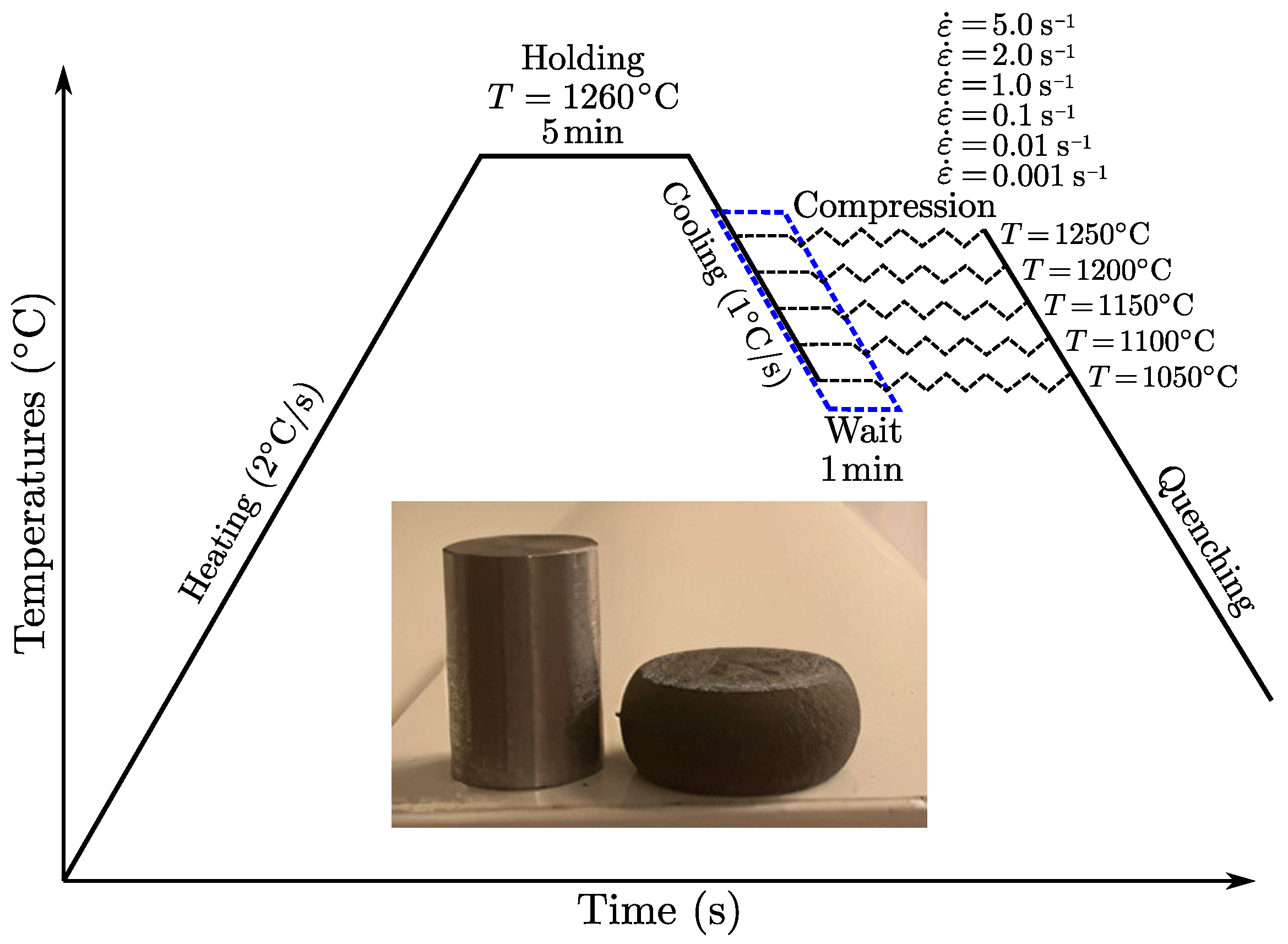
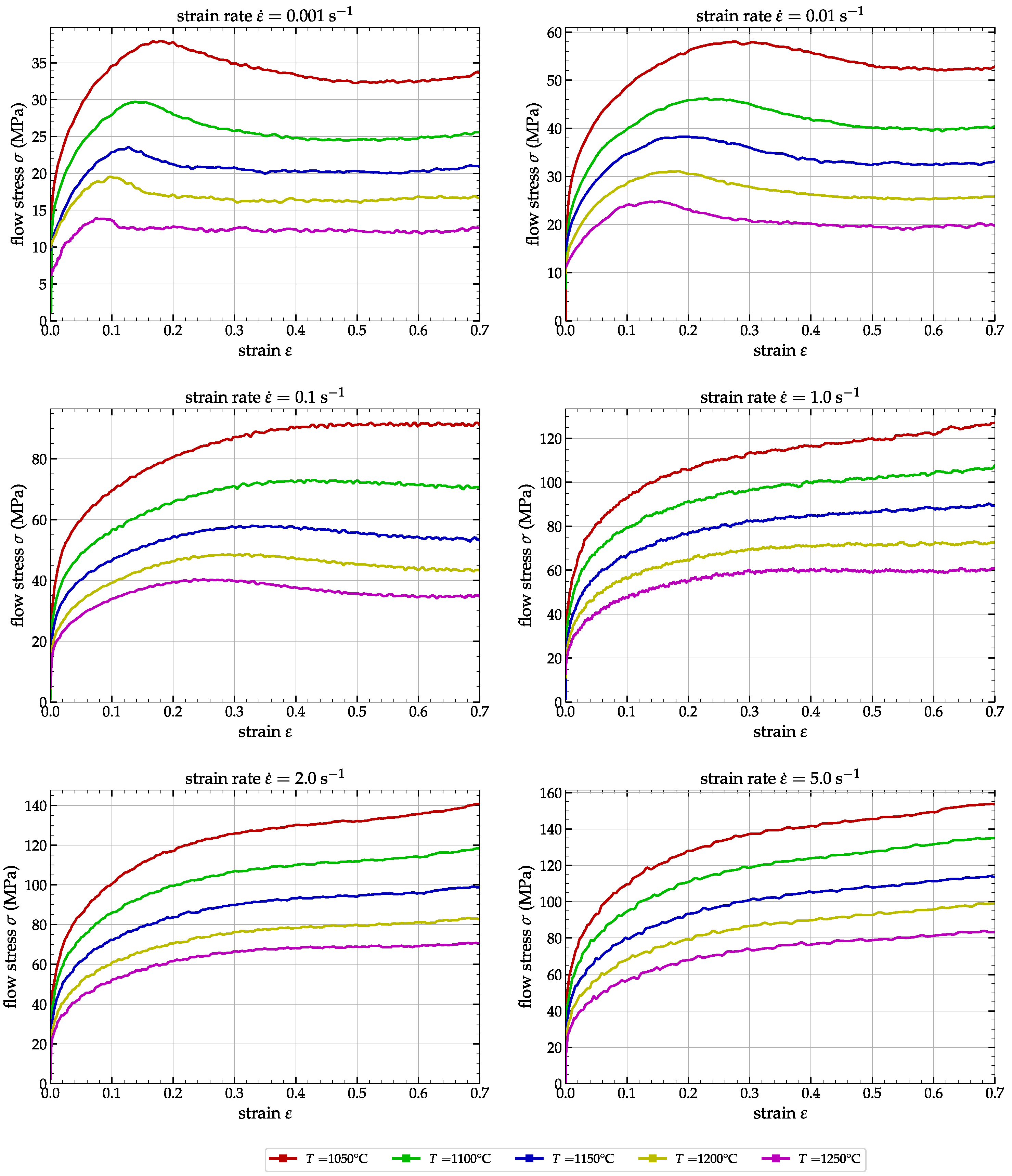


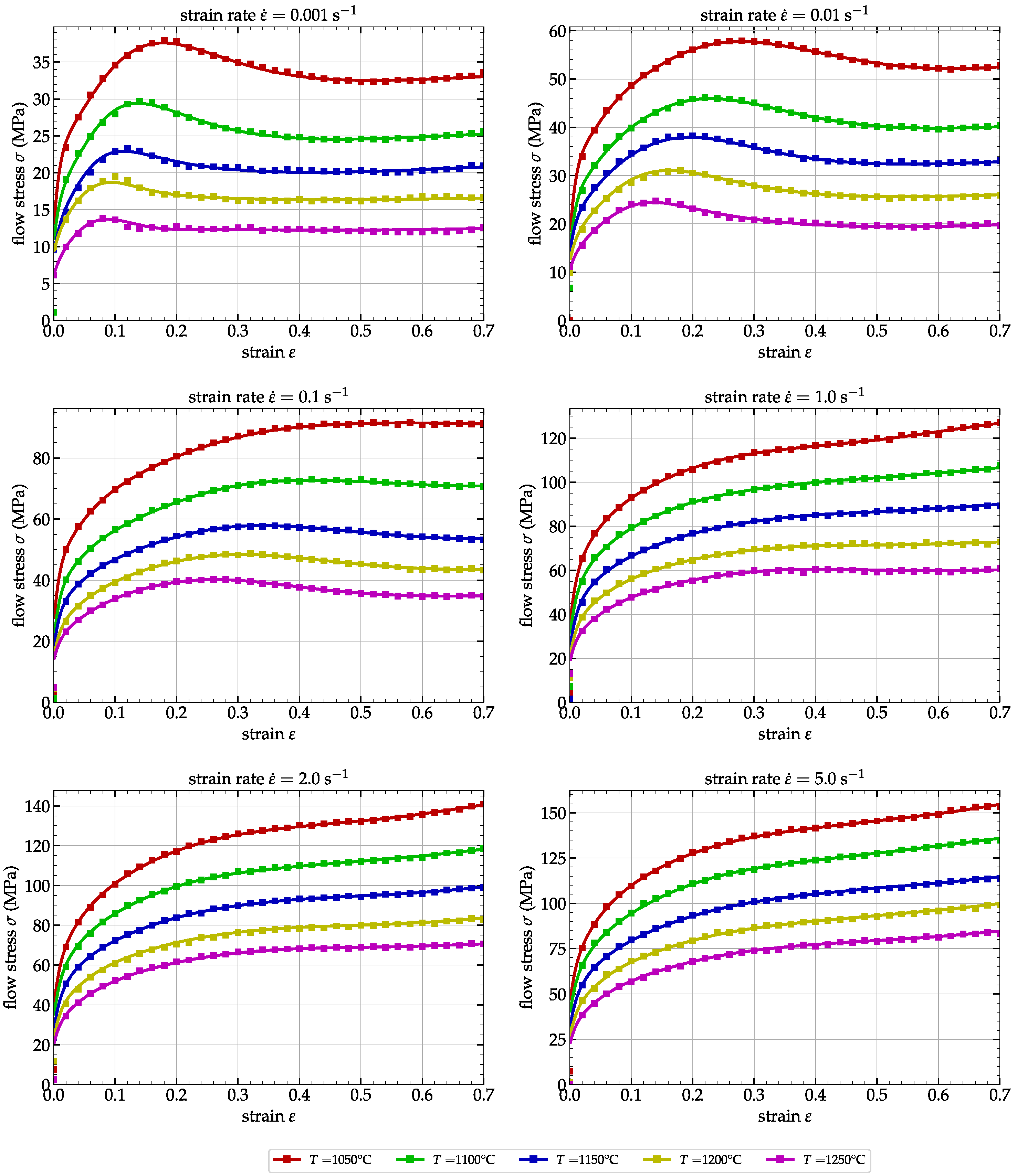
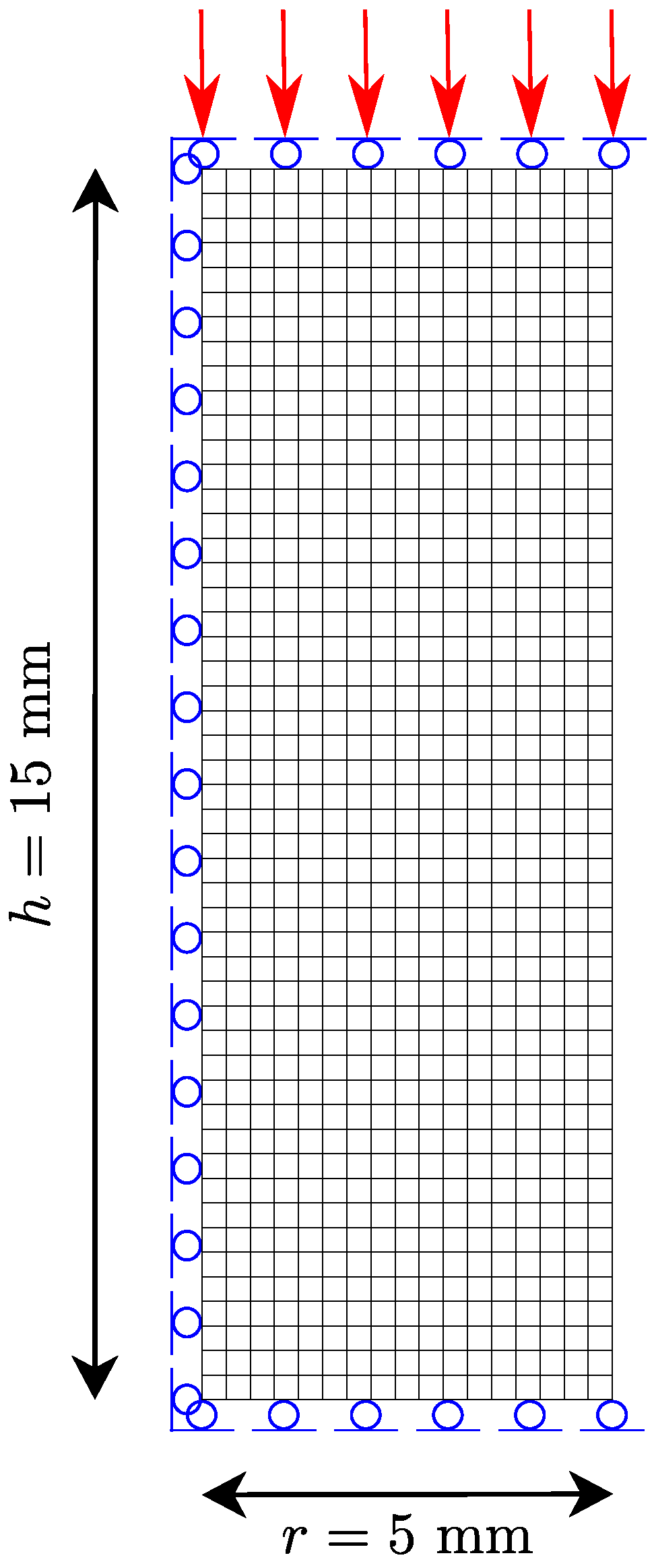
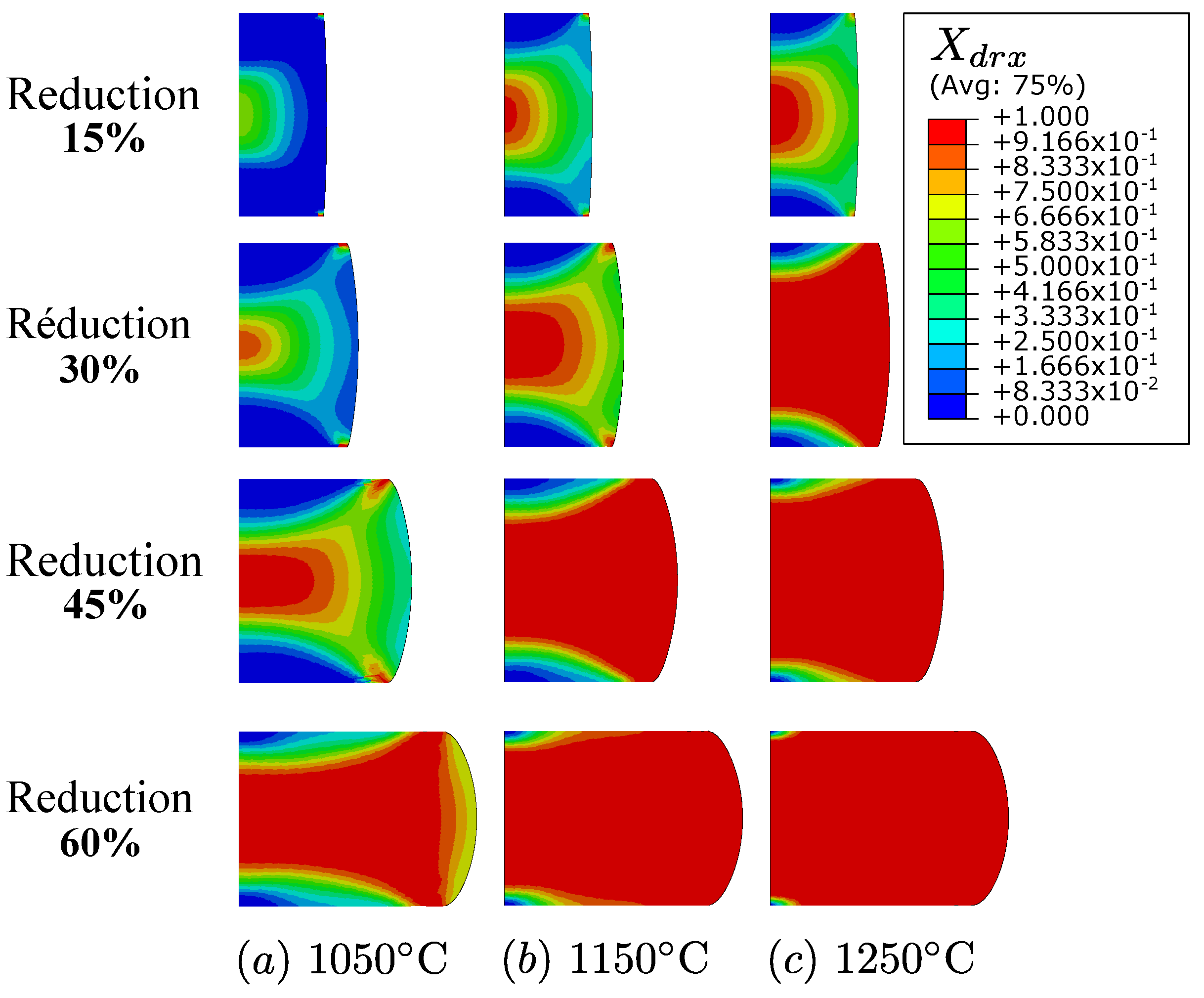
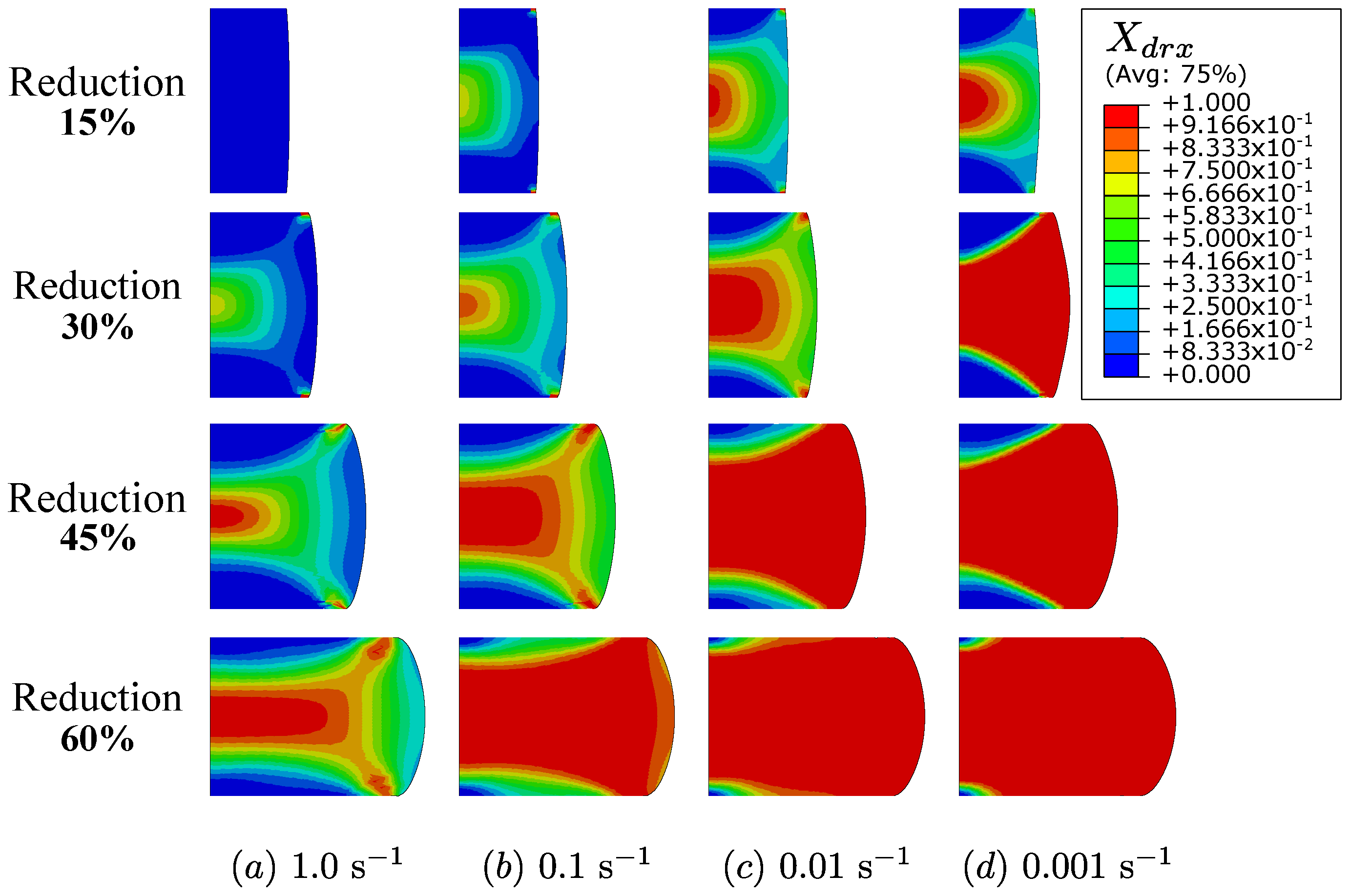


| Element | C | Mn | Mo | Si | Ni | Cr | Cu |
|---|---|---|---|---|---|---|---|
| Wt % |
| () | T (°C) | (MPa) | (MPa) | ||
|---|---|---|---|---|---|
| 1050 | |||||
| 1100 | |||||
| 1150 | |||||
| 1200 | |||||
| 1250 | |||||
| 1050 | |||||
| 1100 | |||||
| 1150 | |||||
| 1200 | |||||
| 1250 | |||||
| 1050 | |||||
| 1100 | |||||
| 1150 | |||||
| 1200 | |||||
| 1250 | |||||
| 1050 | |||||
| 1100 | |||||
| 1 | 1150 | ||||
| 1200 | |||||
| 1250 |
| k | |||||
| Coefficients | 3-7-5-1 | 3-9-4-1 | 3-9-5-1 | 3-9-7-1 | 3-13-7-1 | 3-15-7-1 |
|---|---|---|---|---|---|---|
| 74 | 81 | 92 | 114 | 158 | 180 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tize Mha, P.; Dhondapure, P.; Jahazi, M.; Tongne, A.; Pantalé, O. Artificial Neural Network-Based Critical Conditions for the Dynamic Recrystallization of Medium Carbon Steel and Application. Metals 2023, 13, 1746. https://doi.org/10.3390/met13101746
Tize Mha P, Dhondapure P, Jahazi M, Tongne A, Pantalé O. Artificial Neural Network-Based Critical Conditions for the Dynamic Recrystallization of Medium Carbon Steel and Application. Metals. 2023; 13(10):1746. https://doi.org/10.3390/met13101746
Chicago/Turabian StyleTize Mha, Pierre, Prashant Dhondapure, Mohammad Jahazi, Amèvi Tongne, and Olivier Pantalé. 2023. "Artificial Neural Network-Based Critical Conditions for the Dynamic Recrystallization of Medium Carbon Steel and Application" Metals 13, no. 10: 1746. https://doi.org/10.3390/met13101746
APA StyleTize Mha, P., Dhondapure, P., Jahazi, M., Tongne, A., & Pantalé, O. (2023). Artificial Neural Network-Based Critical Conditions for the Dynamic Recrystallization of Medium Carbon Steel and Application. Metals, 13(10), 1746. https://doi.org/10.3390/met13101746








