Research on Tunnel-Boring Machine Main Bearing Fatigue Damage and Vibration Response
Abstract
1. Introduction
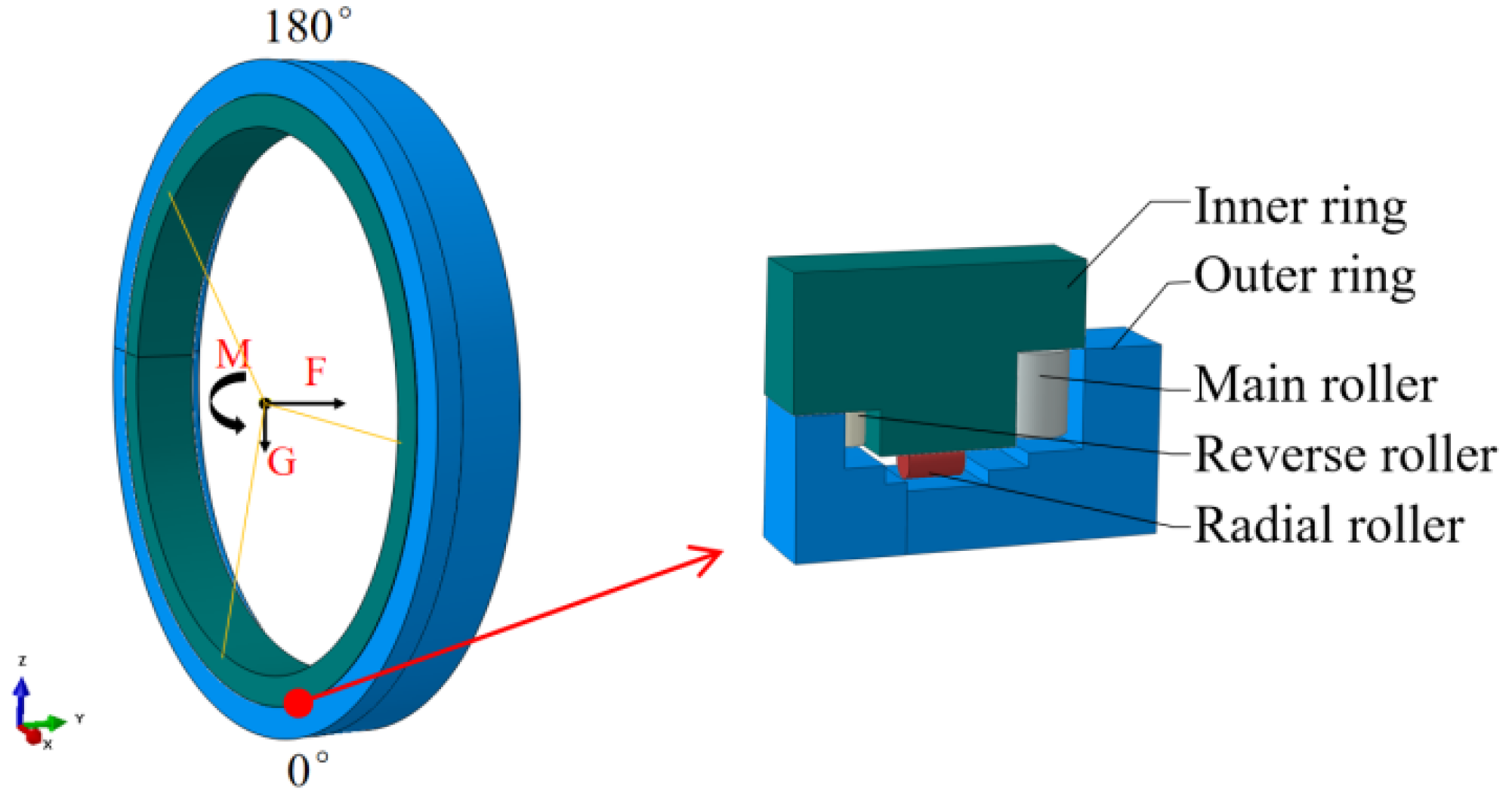
2. Analysis of Main Bearing Fatigue Damage
2.1. Fatigue Damage Model of Main Bearing
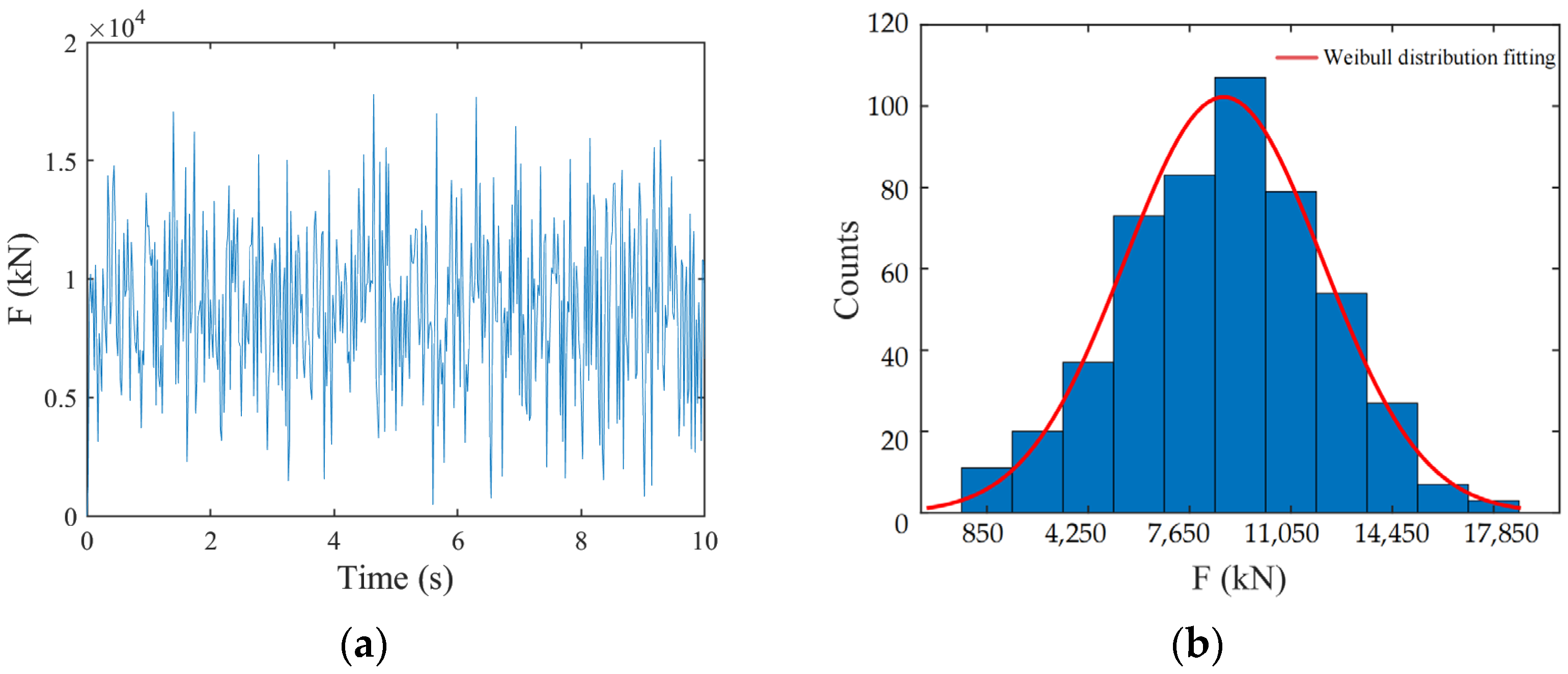
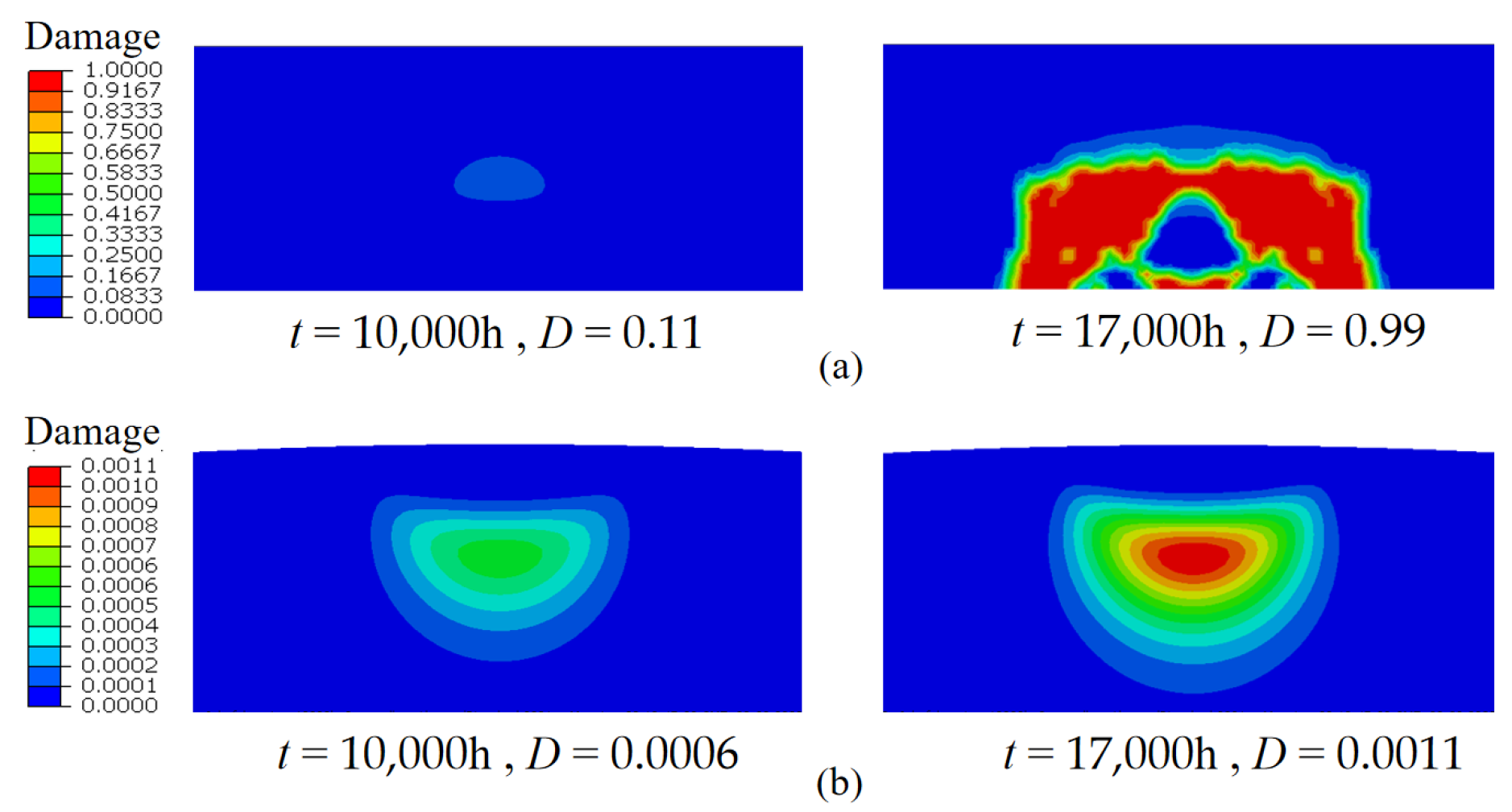
2.2. Fatigue Damage Simulation of Main Bearing
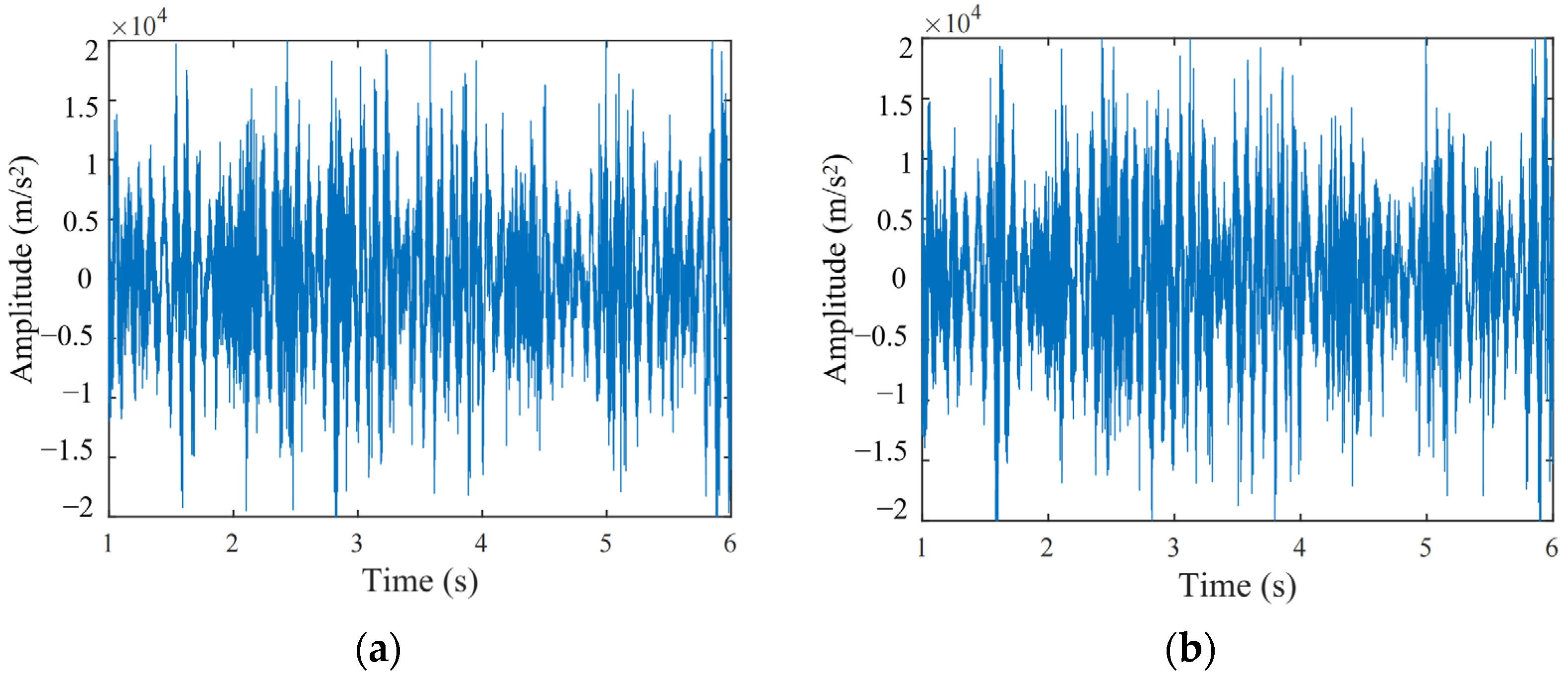
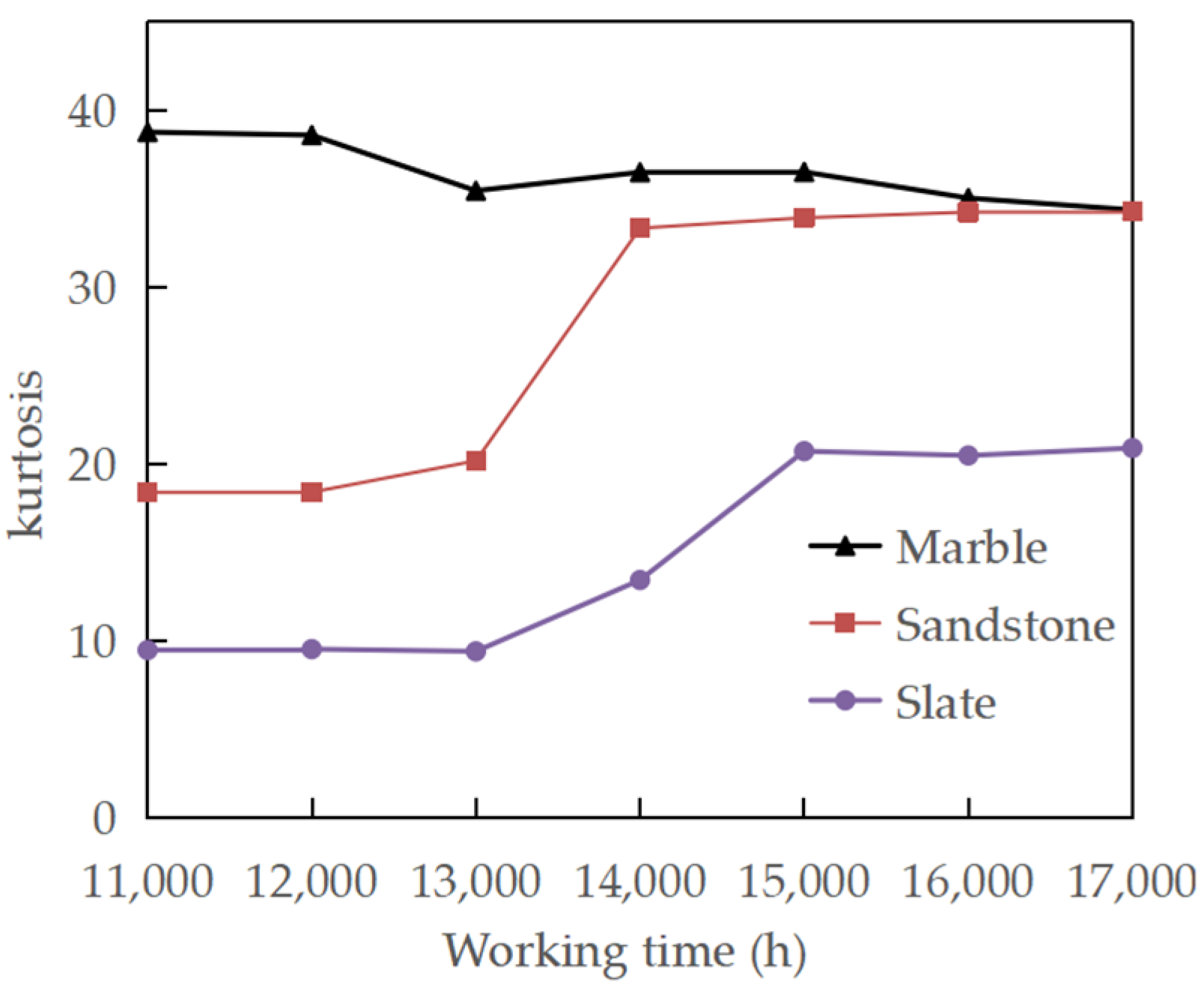
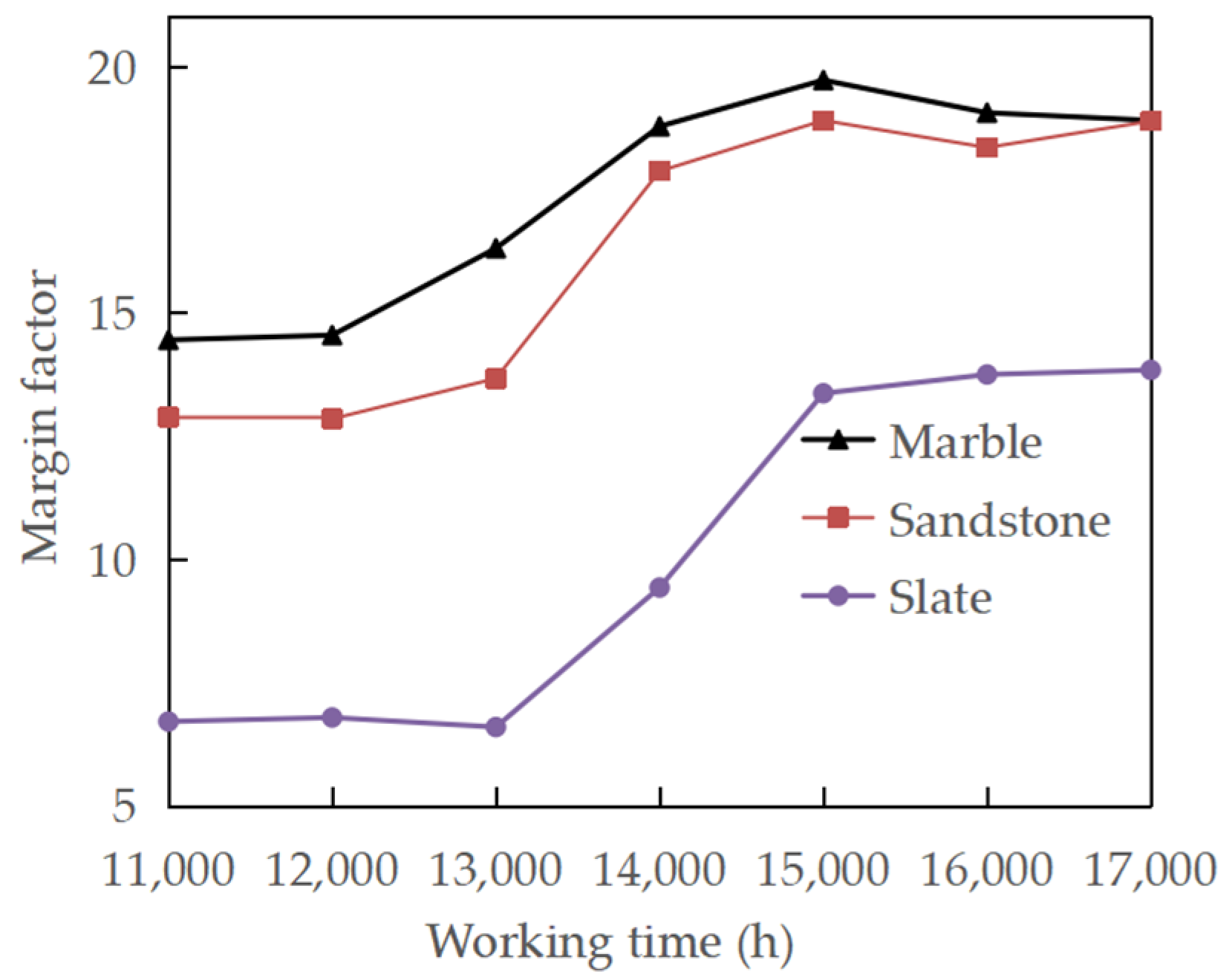
2.3. Variation of TBM Vibration Response
3. Discussion
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Admiraal, H.; Cornaro, A. Why underground space should be included in urban planning policy-And how this will enhance an urban underground future. Tunn. Undergr. Space Technol. 2016, 55, 214–220. [Google Scholar] [CrossRef]
- Li, J.B.; Zhang, Z.G.; Meng, Z.C.; Huo, J.Z.; Xu, Z.H.; Chen, J. Tunnel boring machine cutterhead crack propagation life prediction with time integration method. Adv. Mech. Eng. 2019, 11, 1687814019853451. [Google Scholar] [CrossRef]
- Chen, Y.L.; Chen, Z.L.; Guo, D.J.; Zhao, Z.W.; Lin, T.; Zhang, C.H. Underground space use of urban built-up areas in the central city of Nanjing: Insight based on a dynamic population distribution. Undergr. Space 2022, 7, 748–766. [Google Scholar] [CrossRef]
- Jiang, L.J. Structure design for main bearing of full face rock tunnel boring machine oriented to reliability and vibration behavior. Master’s Thesis, Dalian University of Technology, Dalian, China, 2013. (In Chinese). [Google Scholar]
- Gong, Q.M.; Yin, L.J.; Ma, H.S.; Zhao, J. TBM tunnelling under adverse geological conditions: An overview. Tunn. Undergr. Space Technol. 2016, 57, 4–17. [Google Scholar] [CrossRef]
- Rostami, J.; Chang, S. A closer look at the design of cutterheads for Hard Rock Tunnel-Boring Machines. Engineering 2017, 3, 892–904. [Google Scholar] [CrossRef]
- Li, J.B.; Jing, L.J.; Zheng, X.F.; Li, P.Y.; Yang, C. Application and outlook of information and intelligence technology for safe and efficient TBM construction. Tunn. Undergr. Space Technol. 2019, 93, 103097. [Google Scholar] [CrossRef]
- Pan, Y.; Fu, X.L.; Zhang, L.M. Data-driven multi-output prediction for TBM performance during tunnel excavation: An attention-based graph convolutional network approach. Automat. Constr. 2022, 141, 104386. [Google Scholar] [CrossRef]
- Wang, K.Y.; Wu, X.G.; Zhang, L.M.; Song, X.Q. Data-driven multi-step robust prediction of TBM attitude using a hybrid deep learning approach. Adv. Eng. Inform. 2023, 55, 101854. [Google Scholar] [CrossRef]
- Huang, X.; Liu, Q.S.; Liu, H.; Zhang, P.L.; Pan, S.L.; Zhang, X.P.; Fang, J.N. Development and in-situ application of a real-time monitoring system for the interaction between TBM and surrounding rock. Tunn. Undergr. Space Technol. 2018, 81, 187–208. [Google Scholar] [CrossRef]
- Lan, H.; Xia, Y.M.; Zhu, Z.M.; Ji, Z.Y.; Mao, J.S. Development of on-line rotational speed monitor system of TBM disc cutter. Tunn. Undergr. Space Technol. 2016, 57, 66–75. [Google Scholar] [CrossRef]
- Hu, Y.G.; Li, H.; Liao, X.L. Performance Degradation Model and Prediction Method of Real-time Remaining Life for Wind Turbine Bearings. Proc. CSEE 2016, 36, 1644–1649. (In Chinese) [Google Scholar]
- Wu, C.L. Online Monitoring System of Shield Oil Based on Internet of Things Technology. Tunn. Constr. 2019, 39, 940–945. (In Chinese) [Google Scholar]
- Lungberg, G.; Pamgren, A. Dynamic capacity of rolling bearings. Acta Poly-Tech. Ser. Mech. Eng. 1947, 1, 1–50. [Google Scholar]
- Li, F.K.; Hu, W.P.; Meng, Q.C.; Zhan, Z.X.; Shen, F. A new damage-mechanics-based model for rolling contact fatigue analysis of cylindrical roller bearing. Tribol. Int. 2018, 120, 105–114. [Google Scholar] [CrossRef]
- Göncza, P.; Potočnik, R.; Glodež, S. Fatigue behaviour of 42CrMo4 steel under contact loading. Procedia Eng. 2010, 2, 1991–1999. [Google Scholar] [CrossRef]
- Xu, D.; Xu, Y.C.; Chen, X.; Li, X.L.; Yang, Y.M. Fatigue life prediction of ball bearings by modified Paris law based on critical curved surface. J. Mech. Eng. 2011, 47, 52–57. (In Chinese) [Google Scholar] [CrossRef]
- He, P.Y.; Hong, R.J.; Wang, H.; Ji, X.; Lu, C. Calculation analysis of yaw bearings with a hardened raceway. Int. J. Mech. Sci. 2018, 6, 540–552. [Google Scholar] [CrossRef]
- Zeng, D.F.; Xu, T.; Liu, W.D.; Lu, L.T. Investigation on rolling contact fatigue of railway wheel steel with surface defect. Wear 2020, 446, 203207. [Google Scholar] [CrossRef]
- He, H.F.; Liu, H.J.; Zhu, C.Z.; Wei, P.T.; Sun, Z.D. Study of rolling contact fatigue behavior of a wind turbine gear based on damage-coupled elastic-plastic model. Int. J. Mech. Sci. 2018, 141, 512–519. [Google Scholar] [CrossRef]
- Antonio, G.; Guillermo, E. A model for hybrid bearing life with surface and subsurface survival. Wear 2019, 422–423, 223–234. [Google Scholar]
- Jena, D.; Panigrahi, S. Bearing and gear fault diagnosis using adaptive wavelet transform of vibration signals. Procedia Eng. 2012, 50, 265–274. [Google Scholar]
- Singh, J.; Darpe, A.; Singh, S. Rolling element bearing fault diagnosis based on Over-Complete rational dilation wavelet transform and auto-correlation of analytic energy operator. Mech. Syst. Signal Process. 2018, 100, 662–693. [Google Scholar] [CrossRef]
- Zhang, X.H.; Kang, J.S.; Jin, T.D. Degradation modeling and maintenance decisions based on Bayesian belief networks. IEEE Trans. Reliab. 2014, 63, 620–633. [Google Scholar] [CrossRef]
- Huang, C.J.; Song, H.J.; Qin, N. Fault feature extraction of rolling bearings based on complex envelope spectrum. J. Vib. Shock 2021, 40, 189–195. (In Chinese) [Google Scholar]
- De Godói, L.; De Oliveira, N. Denoising convolutional autoencoder configuration for condition monitoring of rotating machines. J. Braz. Soc. Mech. Sci. 2021, 43, 1–13. [Google Scholar] [CrossRef]
- Liu, X.L.; Liu, H.G.; Yang, J.H.; Litak, G.; Cheng, G.; Han, S. Improving the bearing fault diagnosis efficiency by the adaptive stochastic resonance in a new nonlinear system. Mech. Syst. Signal Process. 2017, 96, 58–76. [Google Scholar] [CrossRef]
- Ambrożkiewicz, B.; Syta, A.; Gassner, A.; Georgiadis, A.; Litak, G.; Meier, N. The influence of the radial internal clearance on the dynamic response of self-aligning ball bearings. Mech. Syst. Signal Process. 2022, 171, 108954. [Google Scholar] [CrossRef]
- Han, M.D. Study on tunnelling loads and structural performance of cutterhead of full face rock tunnel boring machine. Ph.D. Thesis, Tianjin University, Tianjin, China, 2017. (In Chinese). [Google Scholar]
- Bomidi, J.; Weinzapfel, N.; Slack, T.; Mobasher Moghaddam, S.; Sadeghi, F.; Liebel, A.; Weber, J.; Kreis, T. Experimental and numerical investigation of torsion fatigue of bearing steel. J. Tribol. 2013, 135, 031103. [Google Scholar] [CrossRef]
- Xiao, Y.C.; Li, S.; Gao, Z. A continuum damage mechanics model for high cycle fatigue. Int. J. Fatigue 1998, 20, 503–508. [Google Scholar] [CrossRef]
- Roxborough, F.F.; Liu, Z.C. Theoretical considerations on pick shape in rock and coal cutting. In Proceedings of the 6th Underground Operator’s Conference, Kalgoorlie, WA, Australia, 13–14 November 1995. [Google Scholar]










| Density | Yong’s Modulus | Poisson’s Ratio | Yield Strength | Tensile Strength | |
|---|---|---|---|---|---|
| Raceway | 7850 kg·m−3 | 210 GPa | 0.3 | 1047 MPa | 1134 MPa |
| Roller | 7850 kg·m−3 | 209 GPa | 0.28 | 1617 MPa | 2310 MPa |
| t (h) | Main Roller | Main Raceway | Reserve Roller | Reserve Raceway | Radial Roller | Radial Raceway |
|---|---|---|---|---|---|---|
| 1000 | 2.68 × 107 | 3.38 × 107 | 5.46 × 107 | 2.56 × 107 | 5.6 × 107 | 5.76 × 107 |
| t (h) | Main Raceway | Reverse Raceway | Radial Raceway | Main Roller | Reverse Roller | Radial Roller |
|---|---|---|---|---|---|---|
| 10,000 | 0.11 | 0.015 | 9.0 × 10−4 | 6.0 × 10−4 | 1.1 × 10−4 | 5.0 × 10−6 |
| 20,000 | 0.99 | 0.03 | 2.1 × 10−3 | 1.1 × 10−3 | 2.3 × 10−4 | 1.2 × 10−5 |
| Order | Frequency (Hz) | Error (%) | |
|---|---|---|---|
| Experimental Value | Simulated Value | ||
| 1 | 121.2 | 112.7 | 7.1 |
| 2 | 414.8 | 392.2 | 5.5 |
| 3 | 843.4 | 808.1 | 4.2 |
| 4 | 1258.2 | 1350.3 | 7.3 |
| 5 | 1686.8 | 1736.0 | 2.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Qu, C. Research on Tunnel-Boring Machine Main Bearing Fatigue Damage and Vibration Response. Metals 2023, 13, 650. https://doi.org/10.3390/met13040650
Zhang H, Qu C. Research on Tunnel-Boring Machine Main Bearing Fatigue Damage and Vibration Response. Metals. 2023; 13(4):650. https://doi.org/10.3390/met13040650
Chicago/Turabian StyleZhang, Hongliang, and Chuanyong Qu. 2023. "Research on Tunnel-Boring Machine Main Bearing Fatigue Damage and Vibration Response" Metals 13, no. 4: 650. https://doi.org/10.3390/met13040650
APA StyleZhang, H., & Qu, C. (2023). Research on Tunnel-Boring Machine Main Bearing Fatigue Damage and Vibration Response. Metals, 13(4), 650. https://doi.org/10.3390/met13040650








