First-Principles Study of Structural Stability and Mechanical Properties of Ta–W–Hf Alloys
Abstract
:1. Introduction
2. Methods and Details
2.1. Calculation Methods
2.2. Calculation Models
3. Results and Discussion
3.1. Calculation Model and Method Verification
3.2. Crystal Structure Parameters and Structural Ability
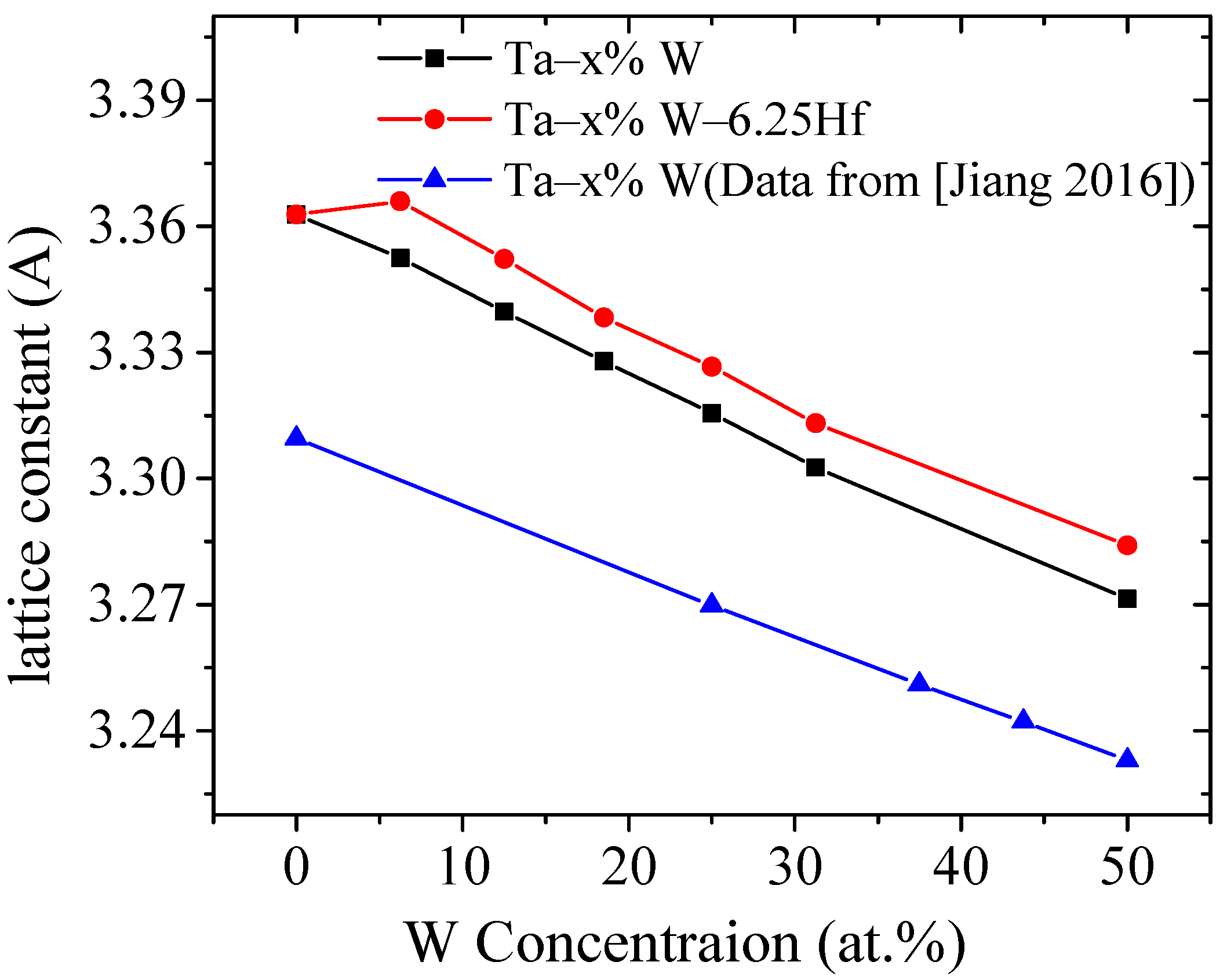
3.2.1. Lattice Constants
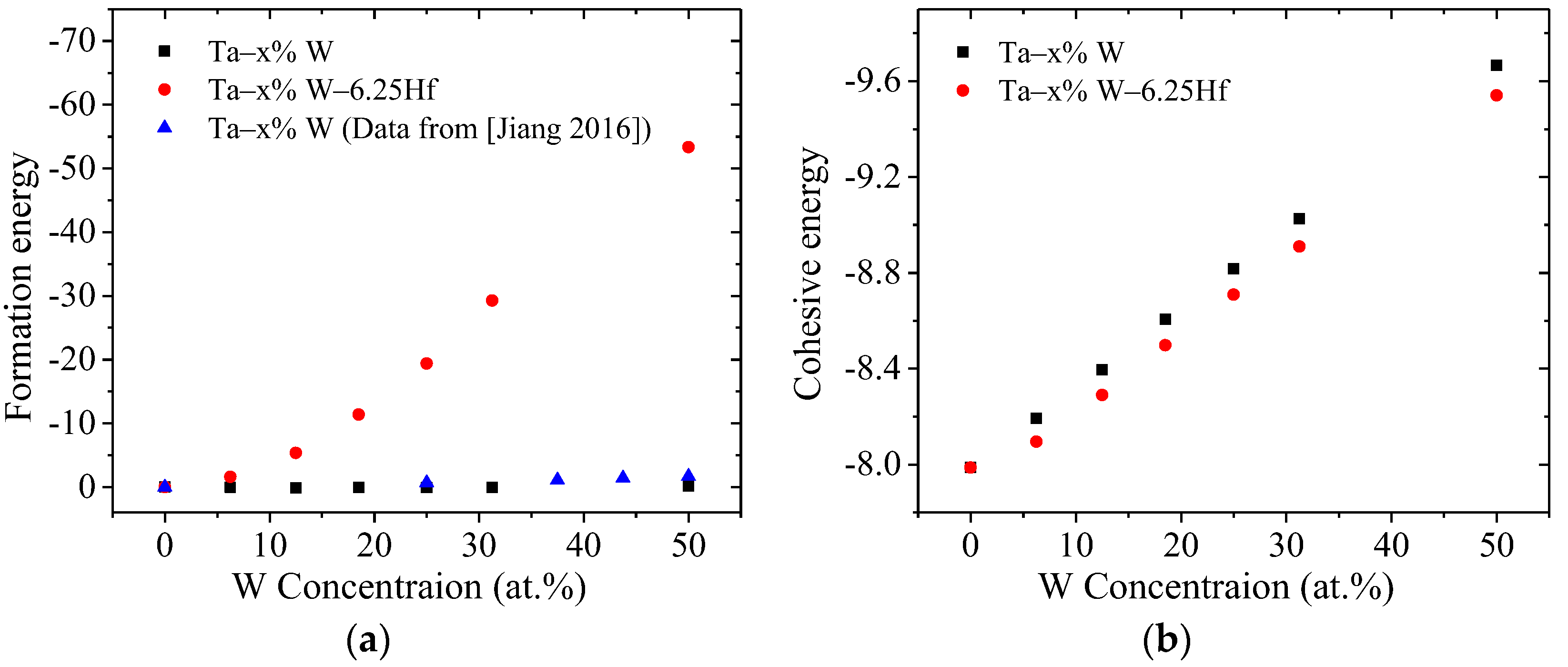
3.2.2. Formation Energy and Cohesive Energy
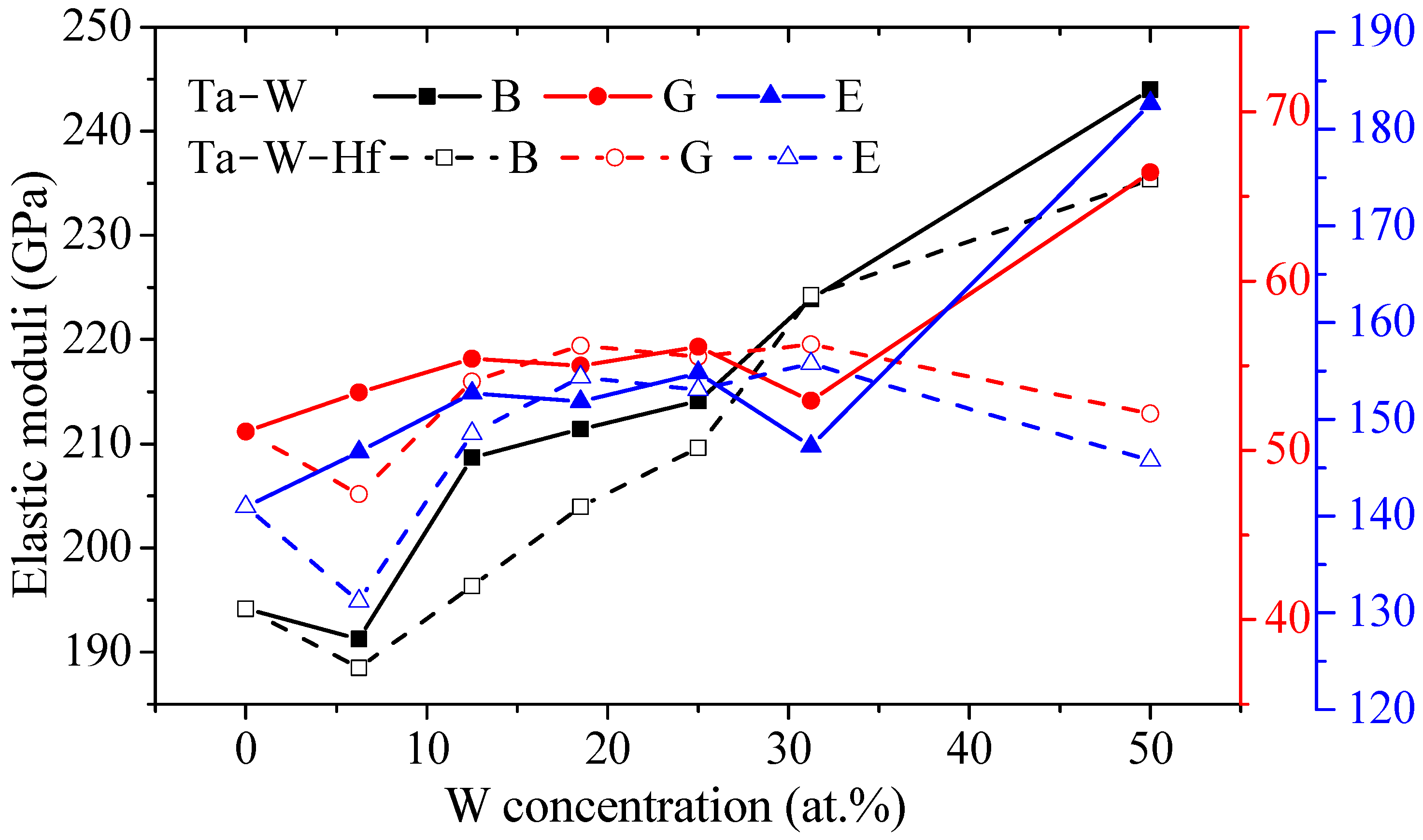
3.3. Mechanical Properties
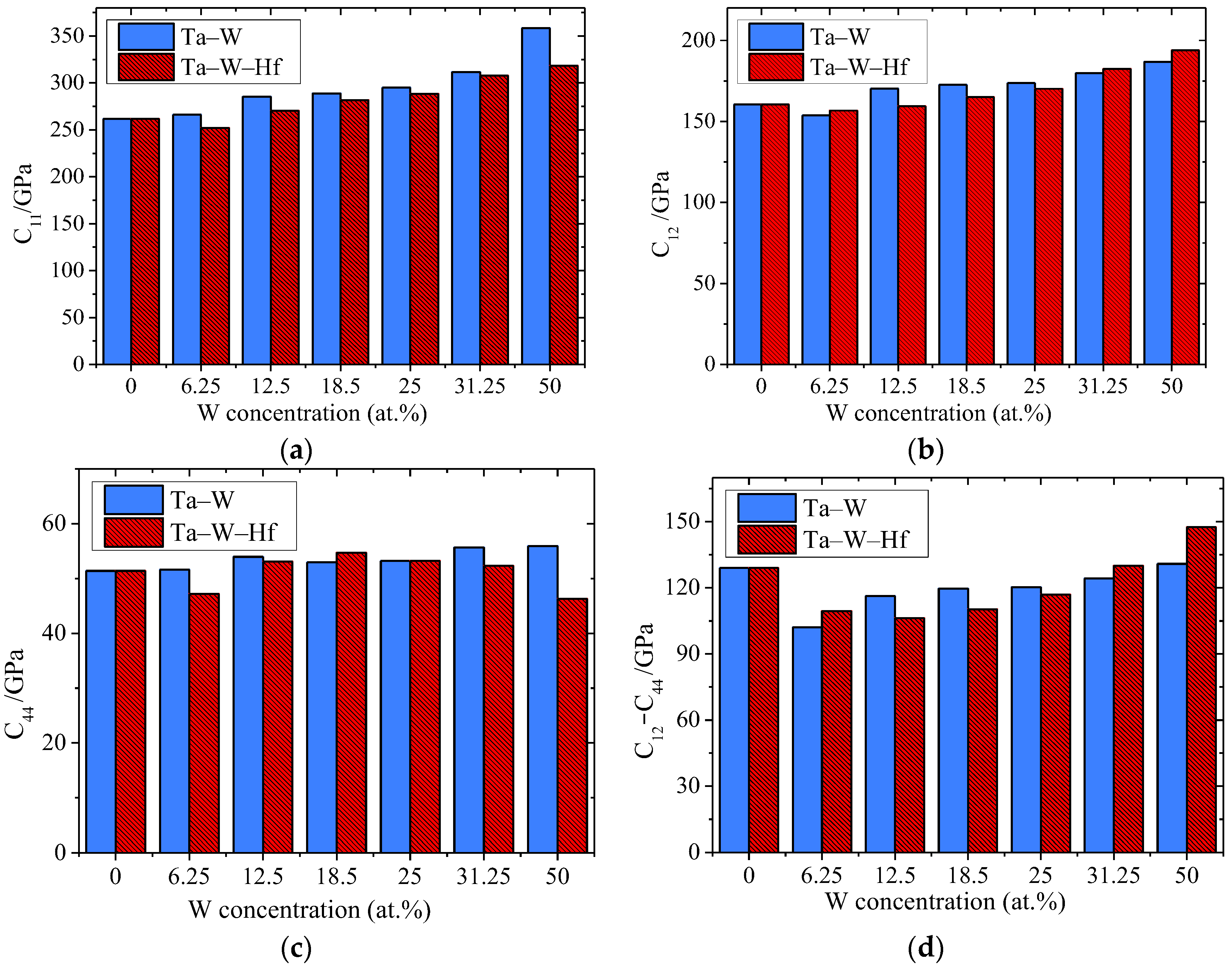
3.3.1. Elastic Properties
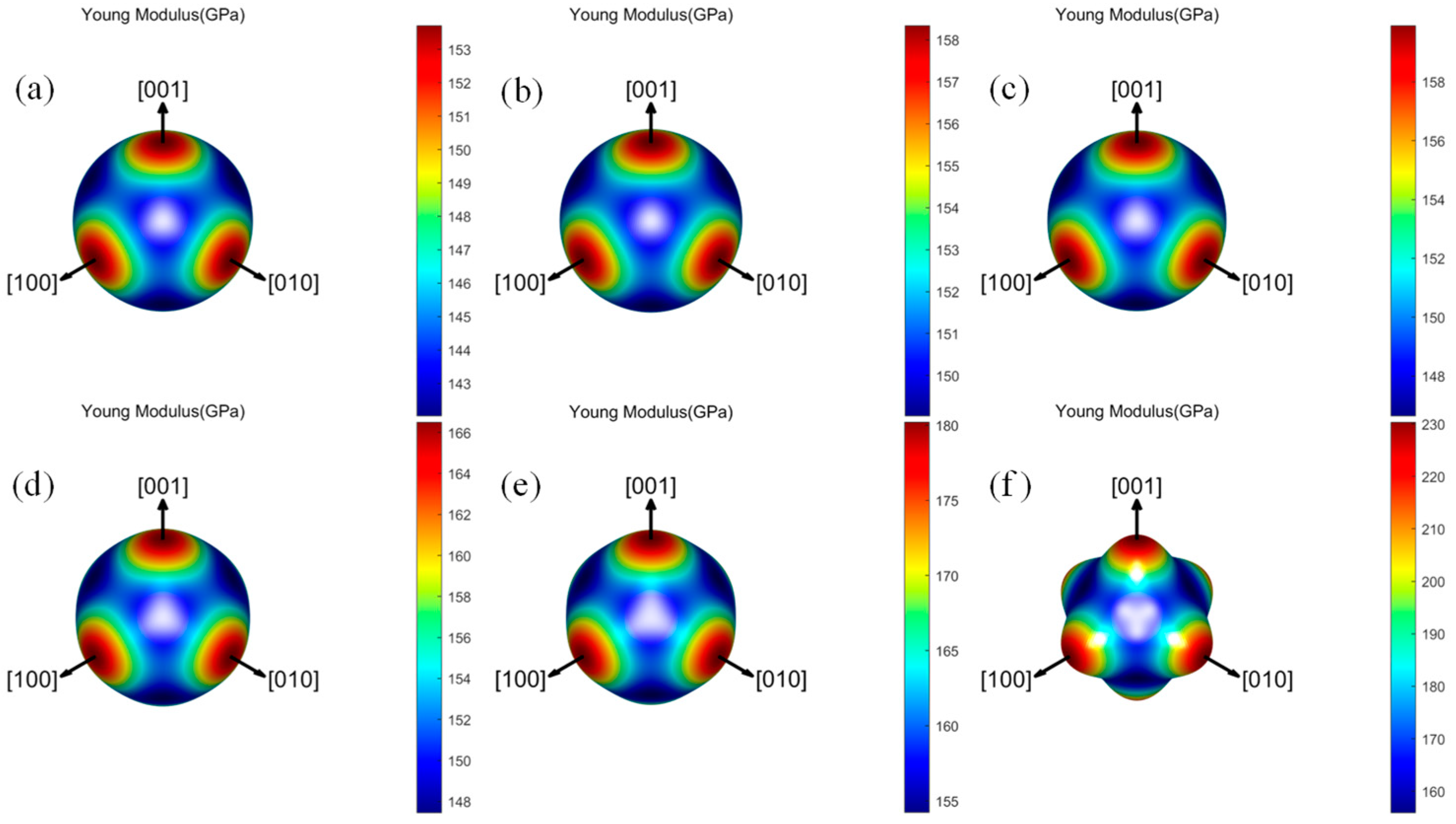
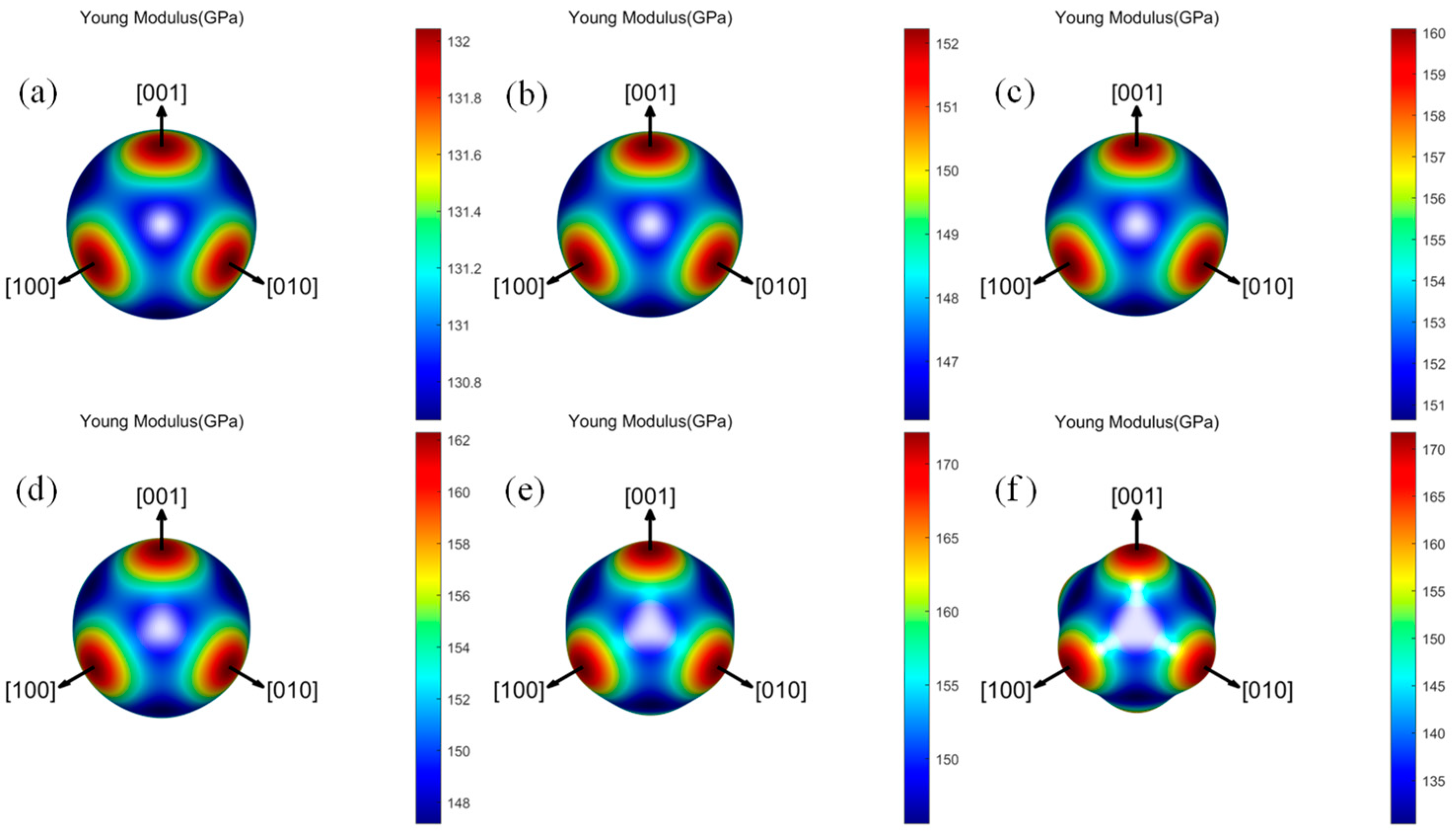
3.3.2. Elastic Anisotropy
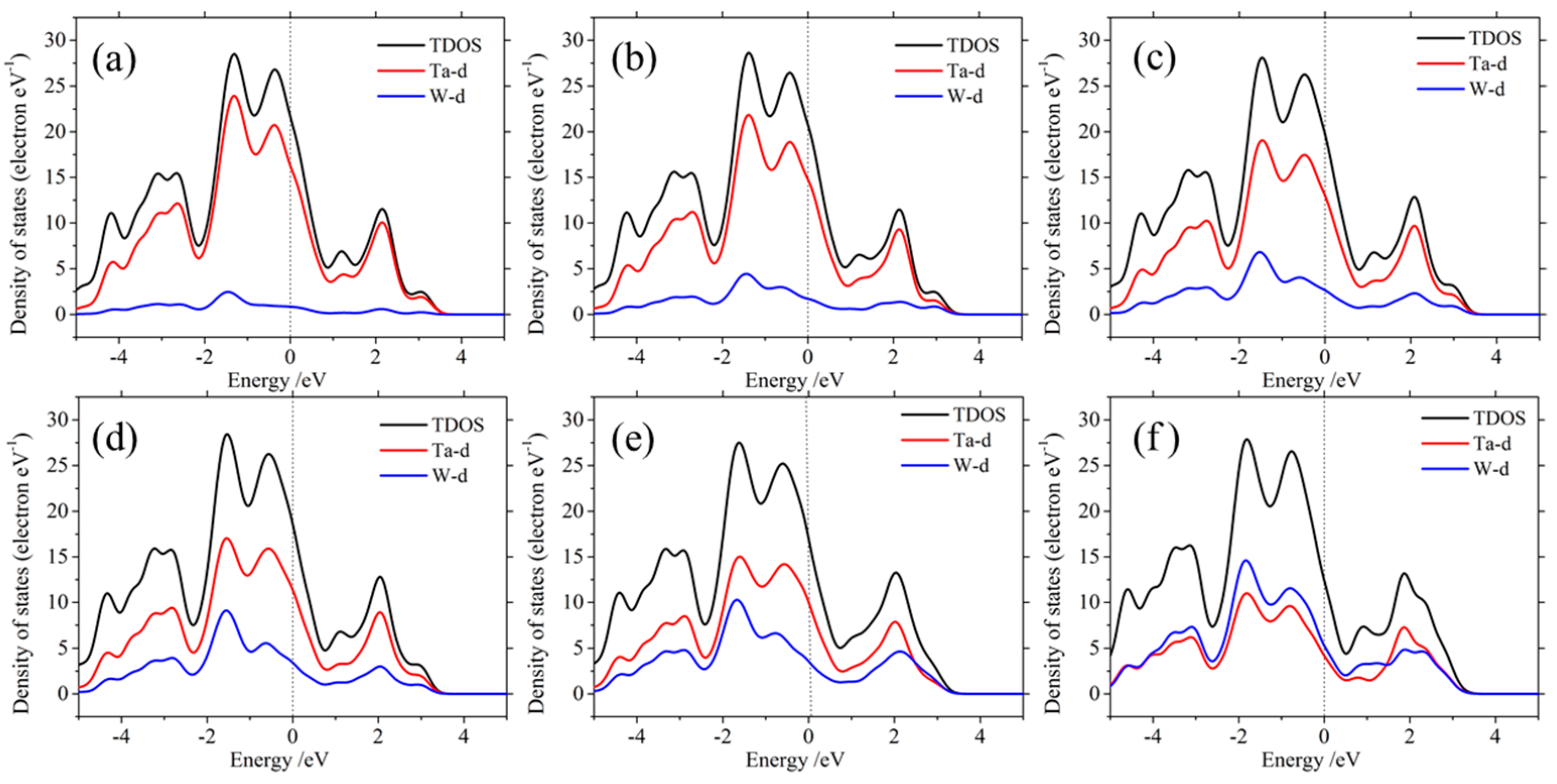
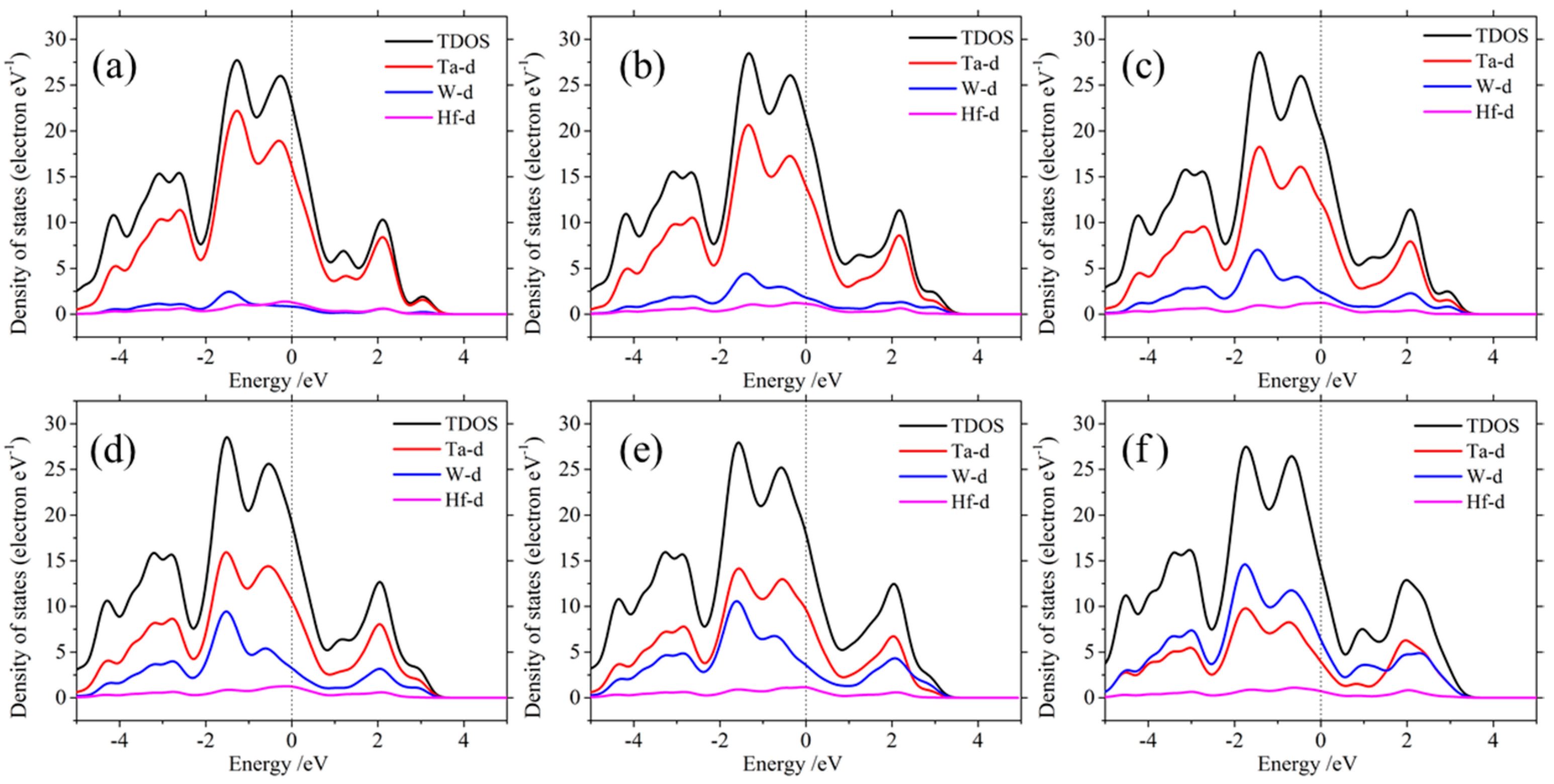
3.4. Electronic Properties
4. Conclusions
- (1)
- All the model are established using the supercell method. It is shown that the stability of the Ta–W–Hf alloy increases with the increase in W content, while the structural stability of the alloys decreases when Hf elements are added to Ta–W alloys;
- (2)
- Both the Ta–W and Ta–W–Hf alloys calculated in this work maintain mechanical stability. For the elastic constants, bulk modulus, shear modulus, Young’s modulus, and anisotropy of the materials, the Ta–W alloy shows a tendency to increase consistently with increasing W content, while the Ta–W–Hf alloy shows a tendency to increase and then decrease. For Young’s modulus and shear modulus of the materials, the highest values are found for Ta–31.25W–6.25Hf;
- (3)
- When the W content is over 25%, the B/G and Poisson’s ratio of the Ta–W–Hf alloy are higher than those of the Ta–W alloy with the same W content, and the addition of Hf increases the ductility of the alloy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rieth, M.; Dudarev, S.L.; de Vicente, S.M.G.; Aktaa, J.; Ahlgren, T.; Autusch, S.; Armstrong, D.E.J.; Balden, M.; Baluc, N.; Barthe, M.F.; et al. Recent progress in research on tungsten materials for nuclear fusion applications in Europe. J. Nucl. Mater. 2013, 432, 482–500. [Google Scholar] [CrossRef] [Green Version]
- Knaster, J.; Moeslang, A.; Muroga, T. Materials research for fusion. Nat. Phys. 2016, 12, 424–434. [Google Scholar] [CrossRef]
- Kaufmann, D.; Monig, R.; Volkert, C.A.; Kraft, O. Size dependent mechanical behaviour of tantalum. Int. J. Plast. 2011, 27, 470–478. [Google Scholar] [CrossRef]
- Novakowski, T.J.; Tripathi, J.K.; Hassanein, A. Effect of high-flux, low-energy He+ ion irradiation on Ta as a plasma-facing material. Sci. Rep. 2016, 6, 1–10. [Google Scholar] [CrossRef]
- Brooks, J.N.; El-Guebaly, L.; Hassanein, A.; Sizyuk, T. Plasma-facing material alternatives to tungsten. Nucl. Fusion 2015, 55, 043002. [Google Scholar] [CrossRef]
- Browning, P.N.; Alagic, S.; Carroll, B.; Kulkarni, A.; Matson, L.; Singh, J. Room and ultrahigh temperature mechanical properties of field assisted sintered tantalum alloys. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2017, 680, 141–151. [Google Scholar] [CrossRef]
- Li, X.B.; Xie, Y.Q. Valence bond structure of Ta-W alloys. Acta Metall. Sin.-Engl. Lett. 2009, 22, 275–283. [Google Scholar] [CrossRef] [Green Version]
- Lv, Y.N.; Hu, K.G.; Huang, Z.; Cao, Z.L.; Wen, S.L.; Zhao, Y.; Pan, M.; Deng, H.Q. Effect of tungsten on the vacancy behaviors in Ta-W alloys from first-principles calculations. Solid State Commun. 2020, 306, 113767. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Wu, Z.H.; Xie, M.Y.; Si, D.H.; Li, L.Y.; Chen, C.; Zhang, Z.; Wu, Y.C. The effect of tungsten content on the rolling texture and microstructure of Ta-W alloys. Mater. Charact. 2020, 159, 110067. [Google Scholar] [CrossRef]
- Zhang, X.; Tian, J.; Xue, M.T.; Jiang, F.; Li, S.Z.; Zhang, B.Z.; Ding, J.; Li, X.P.; Ma, E.; Ding, X.D.; et al. Ta W Refractory Alloys with High Strength at 2000 degrees C. Acta Metall. Sin. 2022, 58, 1253–1260. [Google Scholar] [CrossRef]
- Ma, G.Q.; Zhao, M.; Xiang, S.; Zhu, W.Q.; Wu, G.L.; Mao, X.P. Effect of the Severe Plastic Deformation on the Corrosion Resistance of a Tantalum-Tungsten Alloy. Materials 2022, 15, 7806. [Google Scholar] [CrossRef] [PubMed]
- Zielinski, R.E. Electropolrshing of T111 foils for transmission electron-microscopy. J. Less-Common Met. 1975, 40, 341–343. [Google Scholar] [CrossRef]
- Stecura, S. Dissolution kinetics of small amounts of oxygen in tantalum alloy T-111 and internal oxide displacement reactions during annealing. Oxid. Met. 1976, 10, 291–309. [Google Scholar] [CrossRef]
- Zhang, X.M.; Hu, Z.W.; Liu, J.Y.; Bai, X.F.; Tan, S.B.; Li, Z.K.; Zhang, T.J.; Wang, X.C. Strengthening and grain boundary hardening for Ta–W–Hf alloy. Rare Met. Mater. Eng. 2007, 36, 2156–2159. [Google Scholar]
- Zhang, X.M.; Hu, Z.W.; Tian, F.; Yin, T. Tensile Plastic Deformation of Cell Structure Strengthening Ta–9.2W–0.5Hf Alloy. Rare Met. Mater. Eng. 2008, 37, 1781–1784. [Google Scholar]
- Leonard, K.J.; Busby, J.T.; Zinkle, S.J. Microstructural and mechanical property changes in the Ta-base T-111 alloy following thermal aging. J. Nucl. Mater. 2007, 366, 353–368. [Google Scholar] [CrossRef]
- DiStefano, J.R.; McCoy, H.E. Mechanical properties of T-111 at low to intermediate temperatures. Int. J. Refract. Met. Hard Mater. 2002, 20, 381–387. [Google Scholar] [CrossRef] [Green Version]
- Senkov, O.N.; Daboiku, T.I.; Butler, T.M.; Titus, M.S.; Philips, N.R.; Payton, E.J. High-temperature mechanical properties and oxidation behavior of Hf–27Ta and Hf–21Ta–21X (X is Nb, Mo or W) alloys. Int. J. Refract. Met. Hard Mater. 2021, 96, 105467. [Google Scholar] [CrossRef]
- Senkov, O.N.; Daboiku, T.; Butler, T.M.; Rao, S.I.; Payton, E.J. Microstructure, compression properties, and oxidation behavior of Hf–25Ta–5Me alloys (Me is Mo, Nb, W, 0.5Mo+0.5 W, Cr, or Zr). Int. J. Refract. Met. Hard Mater. 2022, 109, 105968. [Google Scholar] [CrossRef]
- Barklay, C.D.; Howe, J.Y.; Kramer, D.P. Investigation of stress rupture tested neutron irradiated tantalum alloys. In Space Technology and Applications International Forum (STAIF-2008); Univ New Mexico, Inst Space & Nucl Power Studies: Albuquerque, NM, USA, 2008; Volume 969, pp. 439–445. [Google Scholar]
- Barklay, C.D.; Kramer, D.P.; Talnagi, J. Investigation of effects of neutron irradiation on tantalum alloys for radioisotope power system applications. In Space Technology and Applications International Forum (STAIF-2007); Univ New Mexico, Inst Space & Nucl Power Studies: Albuquerque, NM, USA, 2007; Volume 880, pp. 224–228. [Google Scholar]
- Segall, M.D.; Lindan, P.J.D.; Probert, M.J.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717–2744. [Google Scholar] [CrossRef]
- Jiang, D.; Wang, Q.; Hu, W.; Wei, Z.; Tong, J.; Wan, H. The effect of tantalum (Ta) doping on mechanical properties of tungsten (W): A first-principles study. J. Mater. Res. 2016, 31, 3401–3408. [Google Scholar] [CrossRef]
- Featherston, F.H.; Neighbours, J.R. Elastic Constants of Tantalum, Tungsten, and Molybdenum. Phys. Rev. 1963, 130, 1324–1333. [Google Scholar] [CrossRef]
- Pan, R.K.; Ma, L.; Bian, N.; Wang, M.H.; Li, P.B.; Tang, B.Y.; Peng, L.M.; Ding, W.J. First-principles study on the elastic properties of B′ and Q phase in Al–Mg–Si (–Cu) alloys. Phys. Scr. 2013, 87, 015601. [Google Scholar] [CrossRef]
- Wu, Y.N.; Li, L.; Cheng, H.P. First Principles Study on Ta25 Low and High-Temperature Phases. In Proceedings of the APS March Meeting 2010, Portland, OR, USA, 15–19 March 2010. [Google Scholar]
- Voigt, W.B. Lehrbuch der Kristallphysik. Teubner Leipz. 1928. [Google Scholar]
- Watt, J.P.; Davies, G.F.; O’Connell, R.J. The elastic properties of composite materials. Rev. Geophys. 1976, 14, 541–563. [Google Scholar] [CrossRef]
- Born, M.; Huang, K.; Lax, M. Dynamical Theory of Crystal Lattices. Am. J. Phys. USA 1985, 23, 474. [Google Scholar] [CrossRef]
- Xu, W.; Wang, Y.; Wang, C.; Liu, X.; Liu, Z.K. Alloying effects of Ta on the mechanical properties of gamma’ Co-3(Al, W): A first-principles study. Scr. Mater. 2015, 100, 5–8. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.; Xu, Y.; Liu, Q.; Liu, Y. First-principles study on the mechanical properties and thermodynamic properties of Mo–Ta alloys. Plasma Sci. Technol. 2020, 22, 203–210. [Google Scholar] [CrossRef]
- Strachan, A.; Cagin, T.; Gulseren, O.; Mukherjee, S.; Cohen, R.E.; Goddard, W.A. First principles force field for metallic tantalum. Model. Simul. Mater. Sci. Eng. 2004, 12, S445–S459. [Google Scholar] [CrossRef]
- Pugh, S.F. The London, Edinburgh, and Dublin philosophical magazine and journal of science: Series 7. Phil. Mag. 1954, 45, 823–827. [Google Scholar] [CrossRef]
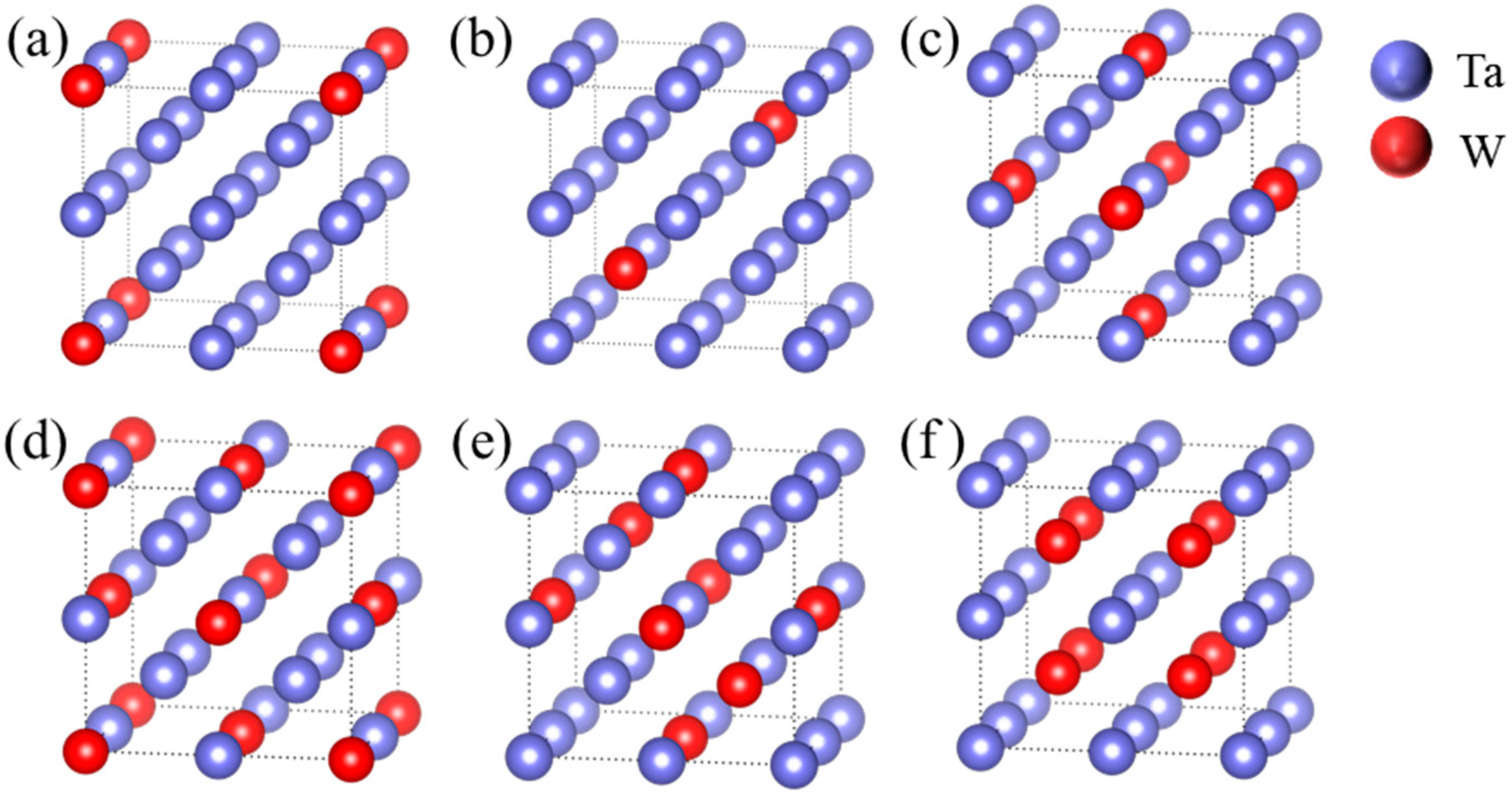


| Strain | Change of Total Energy |
|---|---|
| e = (0,0,0, δ, δ, δ) | |
| e = (δ, δ,0, 0, 0, 0) | |
| e = (δ, δ, δ, 0, 0, 0) |
| Alloys | W (at. %) | Hf (at. %) | W (wt. %) | Ta (wt. %) | a/Å | Note |
|---|---|---|---|---|---|---|
| Ta | 0.000 | 0.000 | 0.000 | - | 3.363 | Present |
| Ta | - | - | - | - | 3.312 | Cal [23] |
| Ta | - | - | - | - | 3.306 | Exp [24] |
| Ta–6.25W | 6.250 | 0.000 | 6.410 | 0.000 | 3.349 | Present |
| Ta–12.50W | 12.50 | 0.000 | 12.680 | 0.000 | 3.335 | Present |
| Ta–18.75W | 18.75 | 0.000 | 21.100 | 0.000 | 3.321 | Present |
| Ta–25.00W | 25.00 | 0.000 | 25.300 | 0.000 | 3.308 | Present |
| Ta–31.25W | 31.25 | 0.000 | 31.590 | 0.000 | 3.296 | Present |
| Ta–50.00W | 50.00 | 0.000 | 50.400 | 0.000 | 3.251 | Present |
| Ta–50.00W | - | 0.000 | - | 0.000 | 3.263 | Cal [23] |
| Ta–6.25W–6.25Hf | 6.250 | 6.250 | 6.410 | - | 3.362 | Present |
| Ta–12.5W–6.25Hf | 12.50 | 6.250 | 12.680 | - | 3.347 | Present |
| Ta–18.75W–6.25Hf | 18.75 | 6.250 | 21.100 | - | 3.332 | Present |
| Ta–25.00W–6.25Hf | 25.00 | 6.250 | 25.300 | - | 3.319 | Present |
| Ta–31.25W–6.25Hf | 31.25 | 6.250 | 31.620 | - | 3.303 | Present |
| Ta–50.00W–6.25Hf | 50.00 | 6.250 | 50.400 | - | 3.269 | Present |
| Alloy | C11 | C12 | C44 | C12–C44 | Note |
|---|---|---|---|---|---|
| Ta | 261.74 | 160.37 | 51.39 | 108.98 | Present |
| Ta | 262.38 | 159.05 | 56.99 | 102.06 | Cal [31] |
| Ta | 277.87 | 167.37 | 62.87 | 104.50 | Cal [23] |
| Ta | 245.18 | 159.8 | 67.58 | 92.22 | Exp [32] |
| Ta–6.25W | 266.25 | 153.73 | 51.60 | 102.13 | Present |
| Ta–12.50W | 285.52 | 170.24 | 53.96 | 116.28 | Present |
| Ta–18.75W | 289.00 | 172.61 | 52.96 | 119.65 | Present |
| Ta–25.00W | 295.10 | 173.60 | 53.22 | 120.38 | Present |
| Ta–25.00W | 320.60 | 180.10 | 60.01 | 120.09 | Cal [23] |
| Ta–31.25W | 311.85 | 179.92 | 55.67 | 124.26 | Present |
| Ta–50.00W | 358.34 | 186.80 | 55.93 | 130.87 | Present |
| Ta–50.00W | 375.72 | 195.85 | 75.48 | 120.37 | Cal [23] |
| Ta–6.25W–6.25Hf | 252.11 | 156.65 | 47.19 | 204.92 | Present |
| Ta–12.5W–6.25Hf | 270.38 | 159.33 | 53.08 | 217.30 | Present |
| Ta–18.75W–6.25Hf | 281.87 | 164.94 | 54.70 | 227.17 | Present |
| Ta–25.00W–6.25Hf | 288.54 | 170.16 | 53.21 | 235.33 | Present |
| Ta–31.25W–6.25Hf | 307.87 | 182.41 | 52.31 | 255.55 | Present |
| Ta–50.00W–6.25Hf | 318.43 | 193.84 | 46.33 | 272.11 | Present |
| Alloy | B | G | E | B/G | σ | A | Note |
|---|---|---|---|---|---|---|---|
| Ta | 194.16 | 51.11 | 140.95 | 3.80 | 0.35 | 1.01 | Present |
| Ta | 193.60 | 54.9 | 150.4 | 3.53 | 0.34 | 1.10 | Cal [31] |
| Ta | 204.20 | 59.82 | 163.50 | 3.42 | 0.34 | 1.14 | Cal [23] |
| Ta | 188.26 | 56.21 | 155.37 | 3.35 | 0.33 | 1.58 | Exp [32] |
| Ta–6.25W | 191.24 | 53.42 | 146.60 | 3.58 | 0.34 | 0.92 | Present |
| Ta–12.50W | 208.66 | 55.40 | 152.70 | 3.77 | 0.35 | 0.94 | Present |
| Ta–18.75W | 211.41 | 55.00 | 151.82 | 3.84 | 0.35 | 0.91 | Present |
| Ta–25.00W | 214.10 | 56.11 | 154.82 | 3.82 | 0.35 | 0.88 | Present |
| Ta–25.00W | 226.94 | 63.92 | 175.29 | 3.55 | 0.34 | 0.85 | Cal [23] |
| Ta–31.25W | 223.90 | 59.58 | 164.18 | 3.76 | 0.35 | 0.84 | Present |
| Ta–50.00W | 243.98 | 66.42 | 182.67 | 3.67 | 0.35 | 0.65 | Present |
| Ta–50.00W | 243.98 | 80.96 | 219.71 | 3.16 | 0.33 | 0.84 | Cal [23] |
| Ta–6.25W–6.25Hf | 188.47 | 47.41 | 131.22 | 3.98 | 0.36 | 0.99 | Present |
| Ta–12.5W–6.25Hf | 196.35 | 54.05 | 148.52 | 3.63 | 0.34 | 0.96 | Present |
| Ta–18.75W–6.25Hf | 203.92 | 56.17 | 154.35 | 3.63 | 0.34 | 0.94 | Present |
| Ta–25.00W–6.25Hf | 209.62 | 55.52 | 153.06 | 3.78 | 0.35 | 0.90 | Present |
| Ta–31.25W–6.25Hf | 224.23 | 56.26 | 155.75 | 3.99 | 0.36 | 0.83 | Present |
| Ta–50.00W–6.25Hf | 235.37 | 52.17 | 145.73 | 4.51 | 0.37 | 0.74 | Present |
| Alloy | |||
|---|---|---|---|
| Ta | 0.0264 | 0 | 0.0026 |
| Ta–6.25W | 0.0090 | 0 | 0.0009 |
| Ta–12.50W | 0.0052 | 0 | 0.0005 |
| Ta–18.75W | 0.0107 | 0 | 0.0011 |
| Ta–25.00W | 0.0211 | 0 | 0.0021 |
| Ta–31.25W | 0.0346 | 0 | 0.0035 |
| Ta–50.00W | 0.2228 | 0 | 0.0218 |
| Ta–6.25W–6.25Hf | 0.0002 | 0 | 0.0000 |
| Ta–12.5W–6.25Hf | 0.0024 | 0 | 0.0002 |
| Ta–18.75W–6.25Hf | 0.0053 | 0 | 0.0005 |
| Ta–25.00W–6.25Hf | 0.0136 | 0 | 0.0014 |
| Ta–31.25W–6.25Hf | 0.0397 | 0 | 0.0040 |
| Ta–50.00W–6.25Hf | 0.1061 | 0 | 0.0105 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ran, X.; Huang, S.; Zhou, S.; Lei, W.; Wu, Y.; Chen, Q. First-Principles Study of Structural Stability and Mechanical Properties of Ta–W–Hf Alloys. Metals 2023, 13, 655. https://doi.org/10.3390/met13040655
Ran X, Huang S, Zhou S, Lei W, Wu Y, Chen Q. First-Principles Study of Structural Stability and Mechanical Properties of Ta–W–Hf Alloys. Metals. 2023; 13(4):655. https://doi.org/10.3390/met13040655
Chicago/Turabian StyleRan, Xudong, Shuhai Huang, Shaolan Zhou, Wei Lei, Yang Wu, and Qiang Chen. 2023. "First-Principles Study of Structural Stability and Mechanical Properties of Ta–W–Hf Alloys" Metals 13, no. 4: 655. https://doi.org/10.3390/met13040655
APA StyleRan, X., Huang, S., Zhou, S., Lei, W., Wu, Y., & Chen, Q. (2023). First-Principles Study of Structural Stability and Mechanical Properties of Ta–W–Hf Alloys. Metals, 13(4), 655. https://doi.org/10.3390/met13040655





