Experimental Study on the Dynamic Behavior of a Cr-Ni-Mo-V Steel under Different Shock Stresses
Abstract
:1. Introduction
2. Experiments
2.1. Materials
2.2. Test Design
3. Results and Discussion
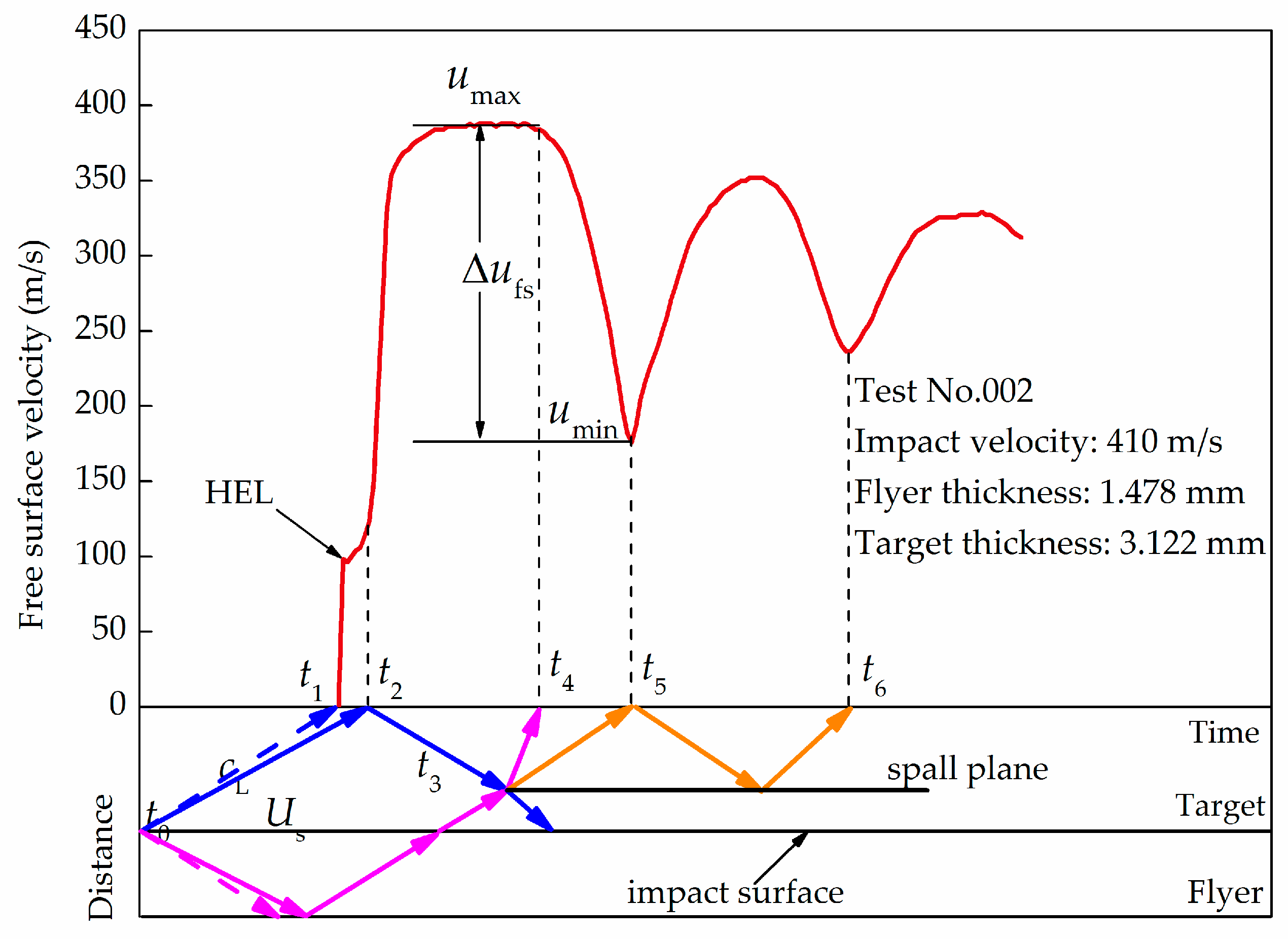
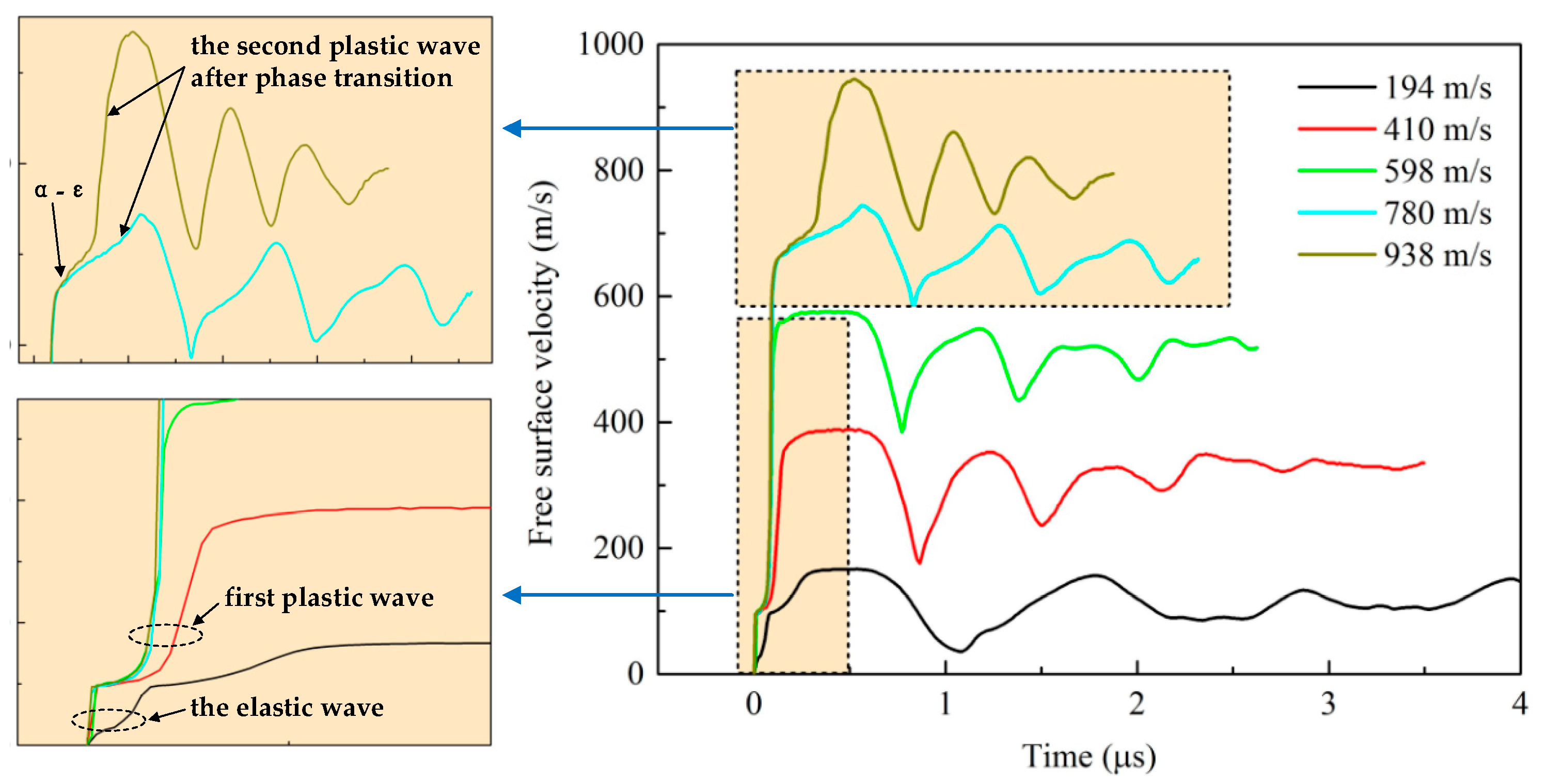
3.1. Gauge Trace Analyses
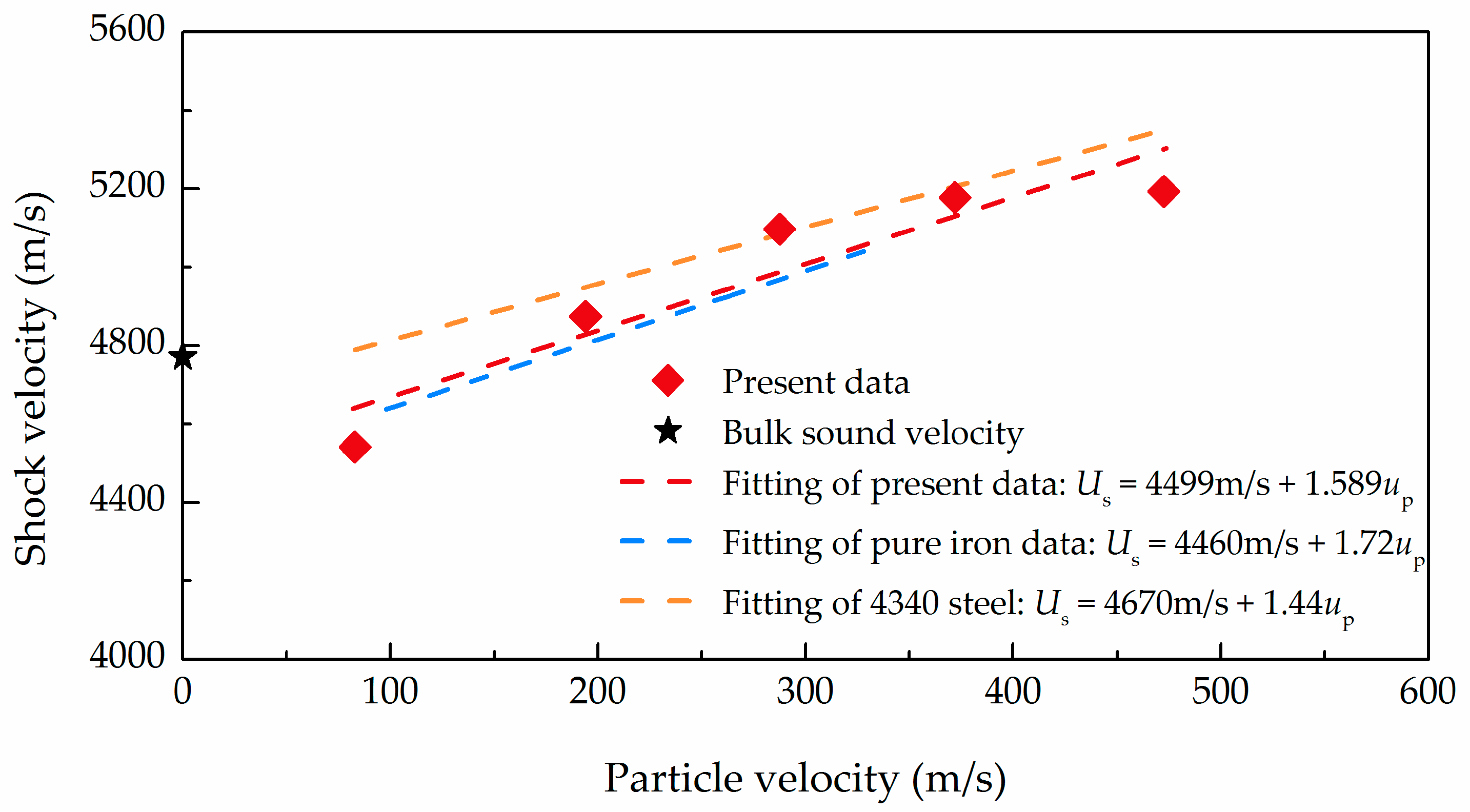
3.2. Hugoniot Relationships
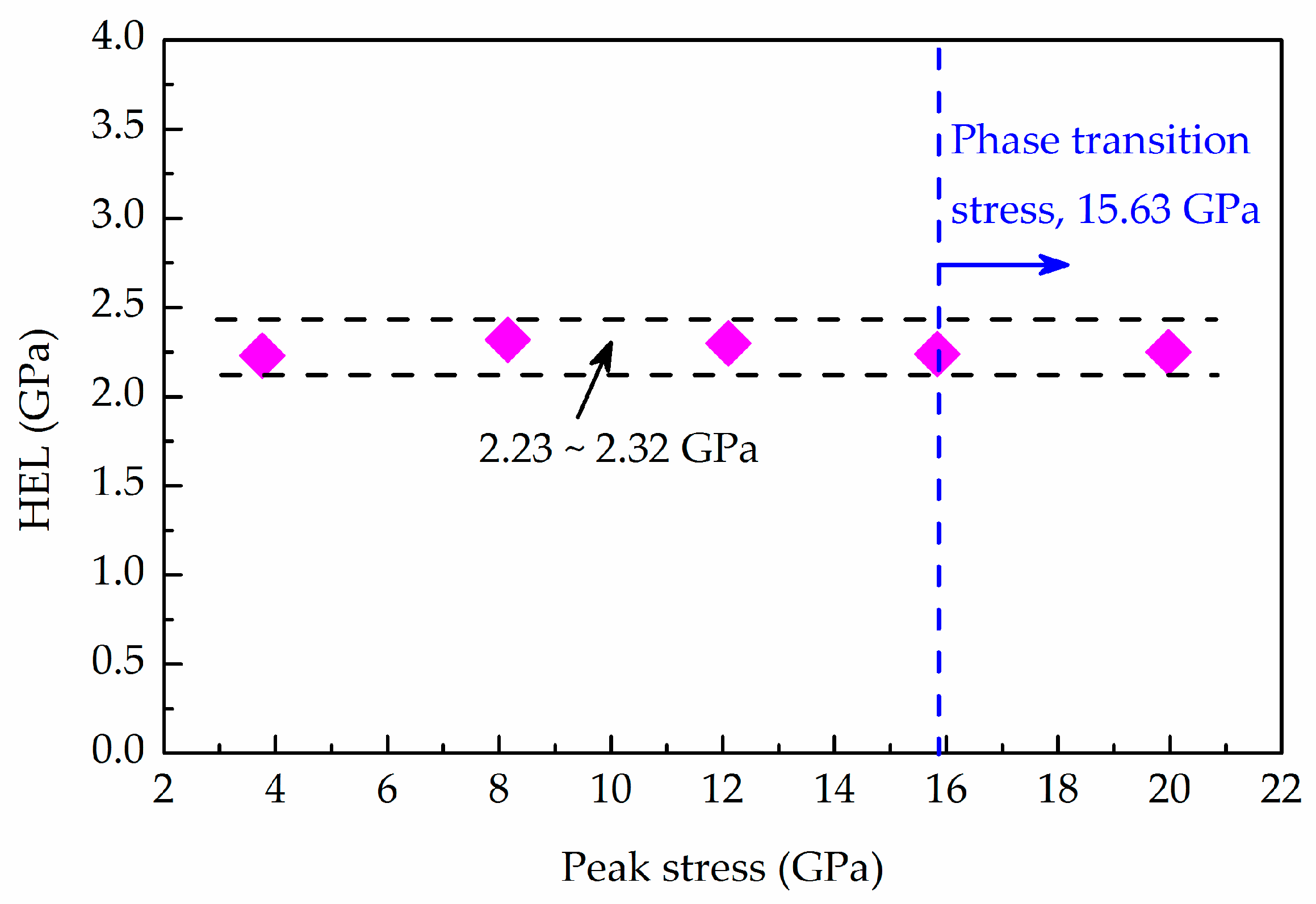
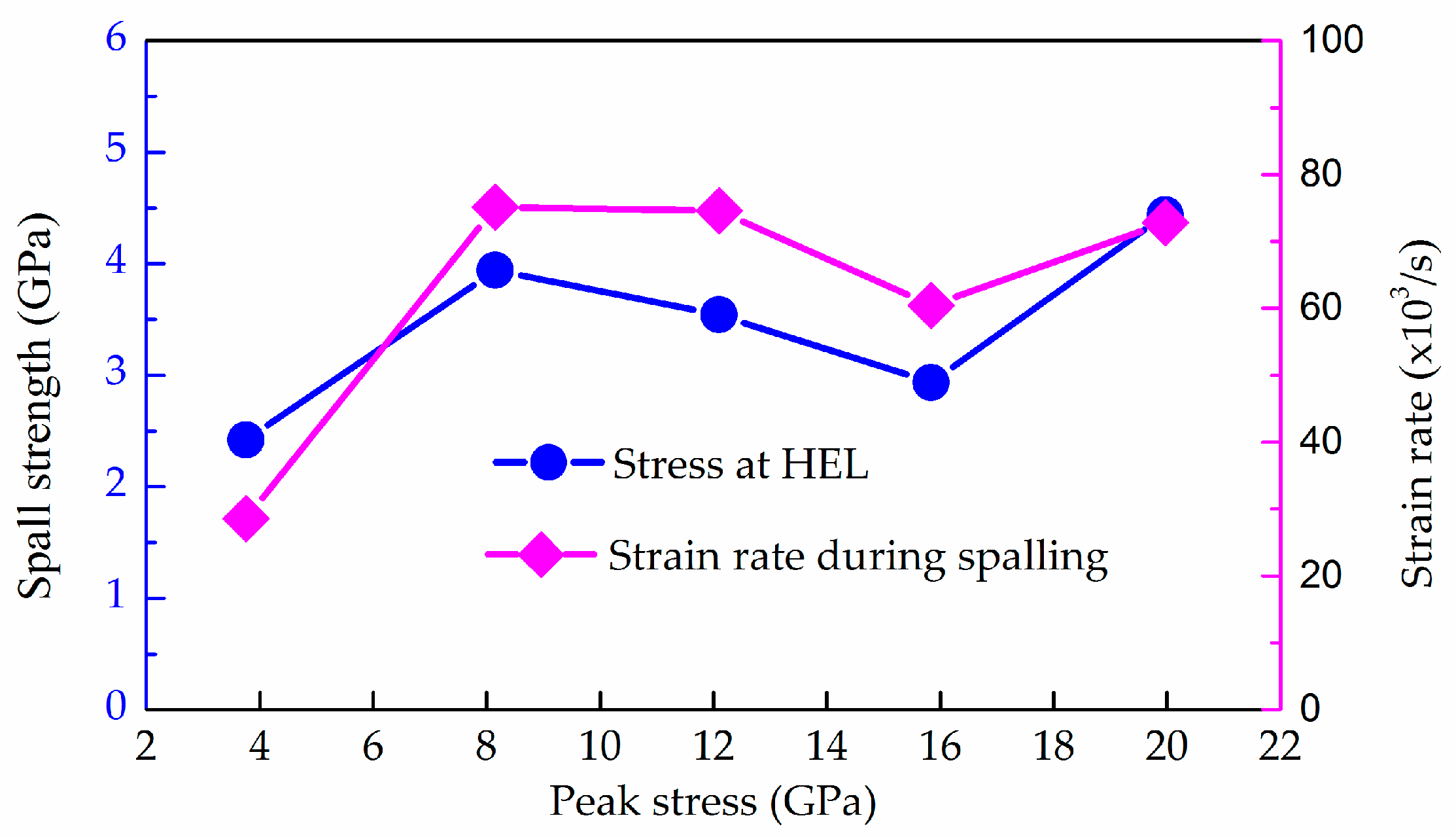
3.3. Hugoniot Elastic Limit and Spall Strength
3.4. Microscopic Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Fan, L.; Xu, C.; Dong, X. Experimental Study of Mechanical Properties of 30SiMn2MoVA Steel Gun Barrel Processed by Cold Radial Forging. J. Press. Vessel. Technol. 2020, 143, 22–29. [Google Scholar] [CrossRef]
- Kuvin, B.F. Advanced High-Strength Steels Application Guidelines Ver. 7.0. Met. Form. 2021, 22, 55. [Google Scholar]
- Matlock, D.K.; Speer, J.G. Third Generation of AHSS: Microstructure Design Concepts. In Microstructure and Texture in Steels; Springer: London, UK, 2009; pp. 185–205. [Google Scholar]
- Perka, A.K.; John, M.; Kuruveri, U.B.; Menezes, P.L. Advanced High-Strength Steels for Automotive Applications: Arc and Laser Welding Process, Properties, and Challenges. Metals 2022, 12, 1051. [Google Scholar] [CrossRef]
- Naylor, D.J. “Microalloyed Forging Steels.” Materials Science Forum; Trans Tech Publications, Ltd.: Zurich, Switzerland, 1998; Volume 284–286, pp. 83–94. [Google Scholar]
- Schino, A.D.; Gaggiotti, M.; Testani, C. Heat treatment effect on microstructure evolution in a 7% Cr steel for forging. Metals 2020, 10, 808. [Google Scholar] [CrossRef]
- Wu, W.; Zhu, M.L.; Liu, X.; Xuan, F.Z. Effect of temperature on high-cycle fatigue and very high cycle fatigue behaviours of a low-strength Cr–Ni–Mo–V steel welded joint. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 45–54. [Google Scholar] [CrossRef]
- Yao, X.; Huang, J.; Qiao, Y.; Sun, M.; Wang, B.; Xu, B. Precipitation Behavior of Carbides and Its Effect on the Microstructure and Mechanical Properties of 15CrNi3MoV Steel. Metals 2022, 12, 1758. [Google Scholar] [CrossRef]
- Du, Y.F.; Lu, H.H.; Shen, X.Q. Coupled effects of banded structure and carbide precipitation on mechanical performance of Cr–Ni–Mo–V steel. Mater. Sci. Eng. A 2022, 832, 142478. [Google Scholar] [CrossRef]
- Pickering, F.B. Physical Metallurgy and the Design of Steels; Applied Science Publishers: Basel, Switzerland, 1978. [Google Scholar]
- Marsh, S.P. LASL Shock Hugoniot Data; University of California Press: Berkeley, CA, USA, 1980. [Google Scholar]
- Thomas, S.A.; Hawkins, M.C.; Matthes, M.K.; Gray, G.T.; Hixson, R.S. Dynamic strength properties and alpha-phase shock Hugoniot of iron and steel. J. Appl. Phys. 2018, 123, 175902. [Google Scholar] [CrossRef] [Green Version]
- Wise, J.L.; Adams, D.P.; Nishida, E.E.; Song, B.; Palmer, T.A. Comparative shock response of additively manufactured versus conventionally wrought 304L stainless steel. APS Shock Compress. Condens. Matter Meet. Abstr. 2015, 1793, 100015. [Google Scholar]
- Czarnota, C.; Jacques, N.; Mercier, S.; Molinari, A. Modelling of dynamic ductile fracture and application to the simulation of plate impact tests on tantalum. J. Mech. Phys. Solids 2008, 56, 1624–1650. [Google Scholar] [CrossRef]
- Hill, R. The Mathematical Theory of Plasticity; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Wu, X.Y. The Dynamic Growth of Voids in Viscoplastic Materials; The Johns Hopkins University: Baltimore, MD, USA, 2003. [Google Scholar]
- Cooper, I.Z.; Rubin, M.B. Modeling damage in silicon carbide due to an impact stress below the HEL. Int. J. Impact Eng. 2014, 65, 174–184. [Google Scholar] [CrossRef]
- Wilkerson, J.W.; Ramesh, K.T. A dynamic void growth model governed by dislocation kinetics. J. Mech. Phys. Solids 2014, 70, 262–280. [Google Scholar] [CrossRef]
- Murr, L.E.; Staudhammer, K.P.; Meyers, M.A. Metallurgical Applications of Shock-Wave and High-Strain-Rate Phenomena; Marcel Dekker: New York, NY, USA, 1986. [Google Scholar]
- Chen, X.; Asay, J.R.; Dwivedi, S.K.; Field, D.P. Spall behavior of aluminum with varying microstructures. J. Appl. Phys. 2006, 99, 023528. [Google Scholar] [CrossRef]
- Jianhong, C.; Rui, C. Microscopic mechanism of cleavage fracture of weld metal. J. Met. 2017, 53, 18. [Google Scholar]
- Satoh, K.; Toyoda, M.; Tsukamoto, M. Mechanism of Fibrous Crack Growth under Constant Loading. Trans. Jpn. Weld. Soc. 1987, 18, 54–60. [Google Scholar]
- Wallin, K. The effect of ductile tearing on cleavage fracture probability in fracture toughness testing. Eng. Fract. Mech. 1989, 32, 523–531. [Google Scholar] [CrossRef]
- Whelchel, R.L.; Kennedy, G.B.; Dwivedi, S.K.; Sanders, T.H. Spall behavior of rolled aluminum 5083-H116 plate. J. Appl. Phys. 2013, 113, 33–482. [Google Scholar] [CrossRef]
- Glam, B.; Moreno, D.; Eliezer, S.; Simca, F.; Bakshi, L. The influence of hydrogen on the dynamic strength and α-ε phase transition of SAE 1020 steel. AIP Conf. Proc. 2020, 2272, 5. [Google Scholar]
- Brar, N.S.; Rosenberg, Z. Shock Hugoniot of 1215 Steel; American Institute of Physics: College Park, ML, USA, 1996. [Google Scholar]
- Dannemann, K.A.; Chalivendra, V.B.; Song, B. Dynamic Behavior of Materials. Exp. Mech. 2012, 52, 117–118. [Google Scholar] [CrossRef] [Green Version]
- Davison, L.; Graham, R.A. Shock compression of solids. Phys. Rep.-Rev. Sect. Phys. Lett. 1979, 55, 255–379. [Google Scholar] [CrossRef]
- Franz, R.E.; Robitaille, J.L. The Hugoniot of 4340 Steel RC 54-55; Army Ballistic Research Lab Aberdeen Proving Ground MD: Clemson, SC, USA, 1979. [Google Scholar]
- Wang, G.Y. Influence of Shock Pre-Compression Stress and Tensile Strain Rate on the Spall Behaviour of Mild Steel. Strain 2011, 47, 398–404. [Google Scholar] [CrossRef]
- Brown, J.M.; Fritz, J.N.; Hixson, R.S. Hugoniot data for iron. J. Appl. Phys. 2000, 88, 5496–5498. [Google Scholar] [CrossRef]
- Ogorodnikov, V.A.; Borovkova, E.Y.; Erunov, S.V. Strength of Some Grades of Steel and Armco Iron under Shock Compression and Rarefaction at Pressures of 2–200 GPa. Combust. Explos. Shock Waves 2004, 40, 597–604. [Google Scholar] [CrossRef]
- Yuan, F.; Prakash, V.; Lewandowski, J.J. Spall strength and Hugoniot elastic limit of a zirconium-based bulk metallic glass under planar shock compression. J. Mater. Res. 2007, 22, 402–411. [Google Scholar] [CrossRef]



| Test Number | Impact Velocity vimp (m/s) | Thickness (mm) | Diameter (mm) | ||
|---|---|---|---|---|---|
| Specimen | OFHC | Specimen | OFHC | ||
| 001 | 194 | 3.058 | 1.497 | 15.00 | 34.97 |
| 002 | 410 | 3.122 | 1.478 | 15.01 | 34.94 |
| 003 | 598 | 3.074 | 1.479 | 15.01 | 35.02 |
| 004 | 780 | 3.083 | 1.487 | 14.99 | 35.01 |
| 005 | 938 | 3.075 | 1.488 | 15.01 | 34.95 |
| Test Number | upfs (m/s) | Us (m/s) | ue (m/s) | σHEL (Gpa) | σpeak (Gpa) | Δufs (m/s) | σspall (Gpa) | (104 s−1) |
|---|---|---|---|---|---|---|---|---|
| 001 | 166 | 4542 | 94.8 | 2.23 | 3.54 | 130.2 | 2.42 | 2.85 |
| 002 | 388 | 4874 | 98.4 | 2.32 | 7.92 | 212.0 | 3.94 | 7.51 |
| 003 | 575 | 5098 | 97.6 | 2.30 | 11.88 | 190.5 | 3.54 | 7.46 |
| 004 | 744 | 5178 | 95.2 | 2.24 | 15.63 | 158.0 | 2.94 | 6.04 |
| 005 | 945 | 5193 | 95.4 | 2.25 | 19.76 | 238.8 | 4.44 | 7.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Li, H. Experimental Study on the Dynamic Behavior of a Cr-Ni-Mo-V Steel under Different Shock Stresses. Metals 2023, 13, 663. https://doi.org/10.3390/met13040663
Zhao X, Li H. Experimental Study on the Dynamic Behavior of a Cr-Ni-Mo-V Steel under Different Shock Stresses. Metals. 2023; 13(4):663. https://doi.org/10.3390/met13040663
Chicago/Turabian StyleZhao, Xinyi, and Hongjun Li. 2023. "Experimental Study on the Dynamic Behavior of a Cr-Ni-Mo-V Steel under Different Shock Stresses" Metals 13, no. 4: 663. https://doi.org/10.3390/met13040663
APA StyleZhao, X., & Li, H. (2023). Experimental Study on the Dynamic Behavior of a Cr-Ni-Mo-V Steel under Different Shock Stresses. Metals, 13(4), 663. https://doi.org/10.3390/met13040663





