Meta-GGA SCAN Functional in the Prediction of Ground State Properties of Magnetic Materials: Review of the Current State
Abstract
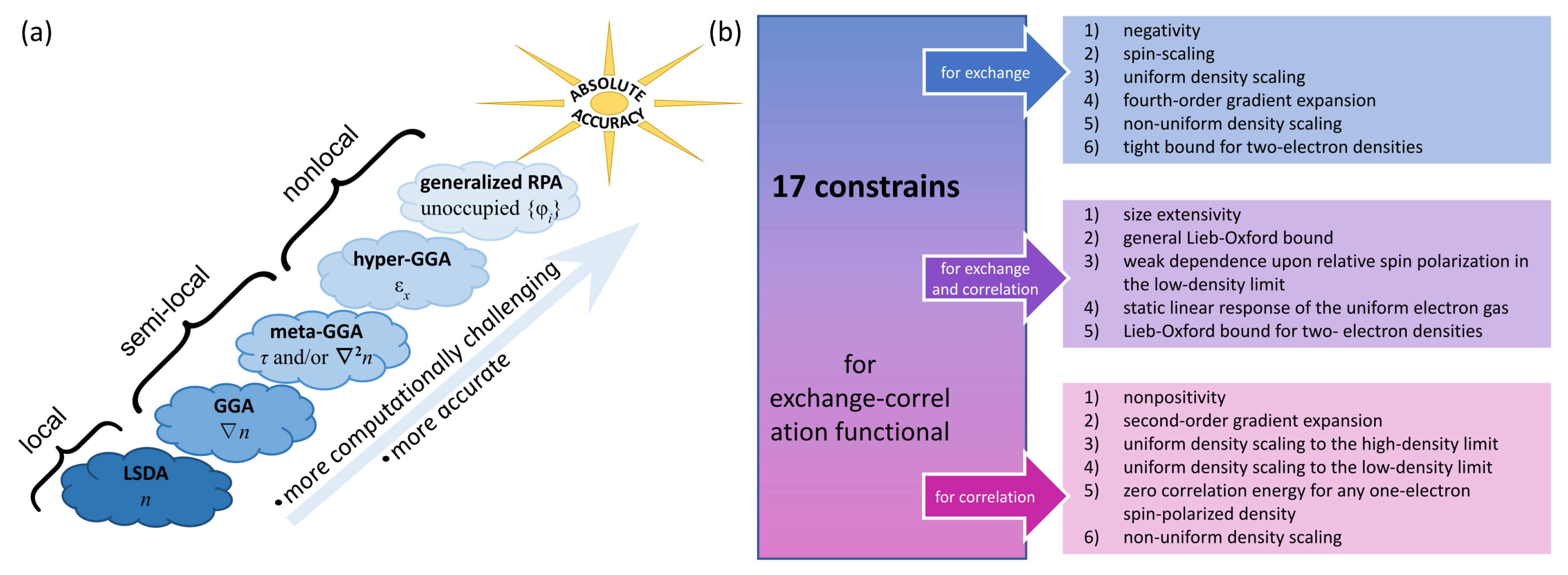
:1. Introduction
2. Pure Metals
3. Binary Intermetallics
3.1. Crystal Structure
3.2. Thermodynamic Stability
- compounds with completely filled d-shells for both TM ions (CF-CF);
- compounds with a completely filled d-shell for one TM ion and a partially filled d-shell for another TM ion (CF-PF);
- compounds with partiallly filled d-shells for both TM ions (PF-PF).
3.3. Magnetic Properties
3.4. Electronic Properties
4. Cuprites and Perovskites
5. Heusler Alloys
5.1. Structural Properties
5.2. Thermodynamic Stability
5.3. Magnetic Properties
5.4. Electronic Properties
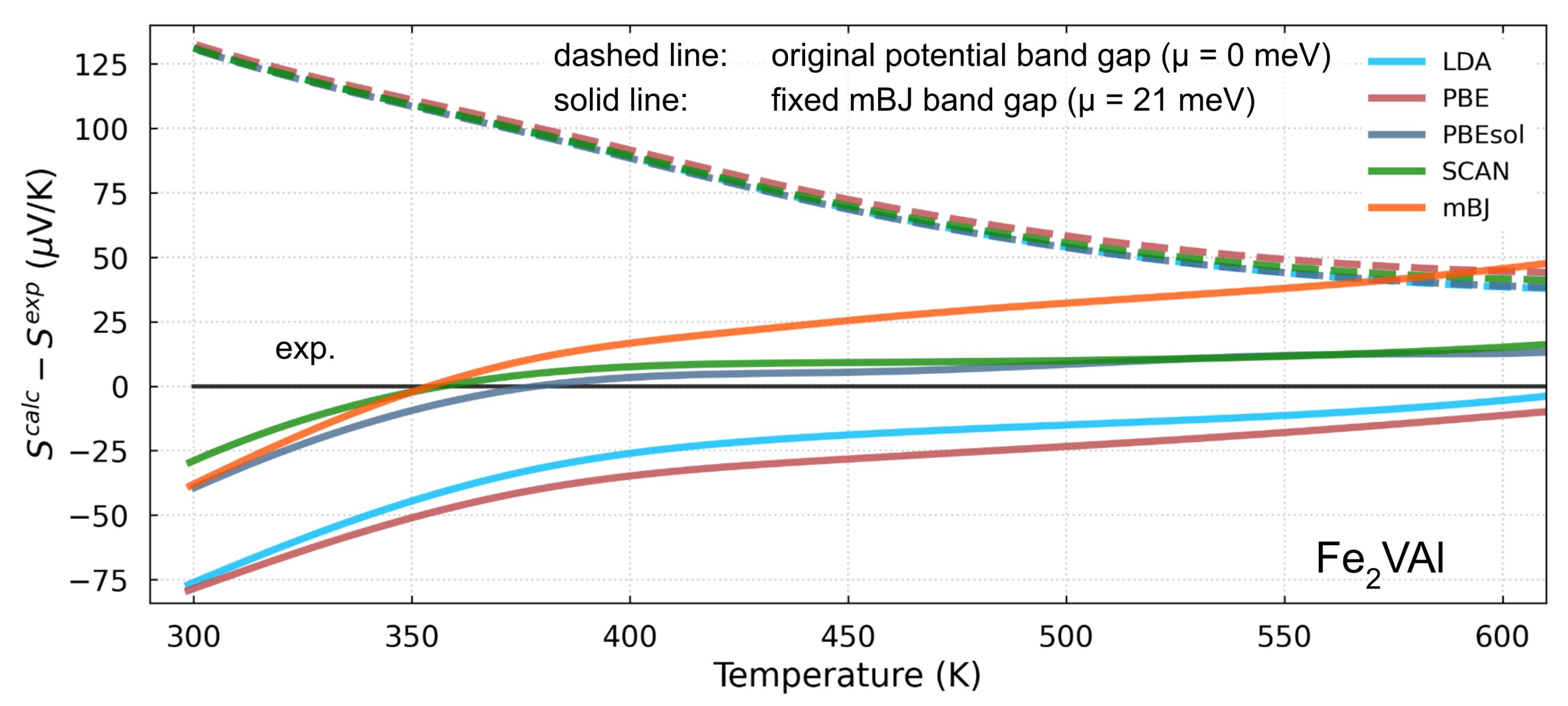
5.5. Transport Properties
- the mBJ functional should explain the thermoelectric properties of these alloys better than SCAN and PBE;
- if is artificially created in band structures derived from other functionalities, then the effective mass calculated from other functionalities can also be used to explain the transport properties.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kohn, W. Nobel Lecture: Electronic structure of matter—wave functions and density functionals. Rev. Mod. Phys. 1999, 71, 1253. [Google Scholar] [CrossRef] [Green Version]
- Martin, R.M. Electronic Structure: Basic Theory and Practical Methods; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Langreth, D.C.; Perdew, J.P. The exchange-correlation energy of a metallic surface. Solid State Commun. 1975, 17, 1425–1429. [Google Scholar] [CrossRef]
- Gunnarsson, O.; Lundqvist, B.I. Exchange and correlation in atoms, molecules, and solids by the spin-density-functional formalism. Phys. Rev. B 1976, 13, 4274. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Yue, W. Accurate and simple density functional for the electronic exchange energy: Generalized gradient approximation. Phys. Rev. B 1986, 33, 8800. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.; Tao, J.; Kümmel, S. Recent Advances in Electron Correlation Methodology; ACS Books: Washington, DC, USA, 2004. [Google Scholar]
- Srivastava, G.; Weaire, D. The theory of the cohesive energies of solids. Adv. Phys. 1987, 36, 463–517. [Google Scholar] [CrossRef]
- Zhang, G.X.; Reilly, A.M.; Tkatchenko, A.; Scheffler, M. Performance of various density-functional approximations for cohesive properties of 64 bulk solids. New J. Phys. 2018, 20, 063020. [Google Scholar] [CrossRef]
- Fuchs, M.; Bockstedte, M.; Pehlke, E.; Scheffler, M. Pseudopotential study of binding properties of solids within generalized gradient approximations: The role of core-valence exchange correlation. Phys. Rev. B 1998, 57, 2134. [Google Scholar] [CrossRef] [Green Version]
- Leung, T.C.; Chan, C.T.; Harmon, B.N. Ground-state properties of Fe, Co, Ni, and their monoxides: Results of the generalized gradient approximation. Phys. Rev. B 1991, 44, 2923. [Google Scholar] [CrossRef] [Green Version]
- Körling, M.; Häglund, J. Cohesive and electronic properties of transition metals: The generalized gradient approximation. Phys. Rev. B 1992, 45, 13293. [Google Scholar] [CrossRef] [PubMed]
- Philipsen, P.; Baerends, E. Cohesive energy of 3d transition metals: Density functional theory atomic and bulk calculations. Phys. Rev. B 1996, 54, 5326. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Godby, R.; Schlüter, M.; Sham, L. Trends in self-energy operators and their corresponding exchange-correlation potentials. Phys. Rev. B 1987, 36, 6497. [Google Scholar] [CrossRef] [PubMed]
- Tran, F.; Blaha, P. Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential. Phys. Rev. Lett. 2009, 102, 226401. [Google Scholar] [CrossRef] [Green Version]
- Stampfl, C.; Mannstadt, W.; Asahi, R.; Freeman, A.J. Electronic structure and physical properties of early transition metal mononitrides: Density-functional theory LDA, GGA, and screened-exchange LDA FLAPW calculations. Phys. Rev. B 2001, 63, 155106. [Google Scholar] [CrossRef] [Green Version]
- Haas, P.; Tran, F.; Blaha, P. Calculation of the lattice constant of solids with semilocal functionals. Phys. Rev. B 2009, 79, 085104. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Kitchaev, D.A.; Yang, J.; Chen, T.; Dacek, S.T.; Sarmiento-Pérez, R.A.; Marques, M.A.; Peng, H.; Ceder, G.; Perdew, J.P.; et al. Efficient first-principles prediction of solid stability: Towards chemical accuracy. NPJ Comput. Mater. 2018, 4, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Jana, S.; Sharma, K.; Samal, P. Assessing the performance of the recent meta-GGA density functionals for describing the lattice constants, bulk moduli, and cohesive energies of alkali, alkaline-earth, and transition metals. Chem. Phys. 2018, 149, 164703. [Google Scholar] [CrossRef]
- Bagno, P.; Jepsen, O.; Gunnarsson, O. Ground-state properties of third-row elements with nonlocal density functionals. Phys. Rev. B 1989, 40, 1997. [Google Scholar] [CrossRef]
- Barbiellini, B.; Moroni, E.; Jarlborg, T. Effects of gradient corrections on electronic structure in metals. J. Phys. Condens. Matter. 1990, 2, 7597. [Google Scholar] [CrossRef]
- Lin, H.; Wray, L.A.; Xia, Y.; Xu, S.; Jia, S.; Cava, R.J.; Bansil, A.; Hasan, M.Z. Half-Heusler ternary compounds as new multifunctional experimental platforms for topological quantum phenomena. Nat. Mater. 2010, 9, 546–549. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Patra, B.; Jana, S.; Constantin, L.A.; Samal, P. Efficient band gap prediction of semiconductors and insulators from a semilocal exchange-correlation functional. Phys. Rev. B 2019, 100, 045147. [Google Scholar] [CrossRef]
- Wen, X.D.; Martin, R.L.; Henderson, T.M.; Scuseria, G.E. Density functional theory studies of the electronic structure of solid state actinide oxides. Chem. Rev. 2013, 113, 1063–1096. [Google Scholar] [CrossRef] [PubMed]
- Sheykhi, S.; Payami, M. Electronic structure properties of UO2 as a Mott insulator. Phys. C Supercond. Appl. 2018, 549, 93–94. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Kurth, S.; Zupan, A.; Blaha, P. Accurate density functional with correct formal properties: A step beyond the generalized gradient approximation. Phys. Rev. Lett. 1999, 82, 2544. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly constrained and appropriately normed semilocal density functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Remsing, R.C.; Zhang, Y.; Sun, Z.; Ruzsinszky, A.; Peng, H.; Yang, Z.; Paul, A.; Waghmare, U.; Wu, X.; et al. Accurate first-principles structures and energies of diversely bonded systems from an efficient density functional. Nat. Chem. 2016, 8, 831–836. [Google Scholar] [CrossRef]
- Pokharel, K.; Furness, J.W.; Yao, Y.; Blum, V.; Irons, T.J.; Teale, A.M.; Sun, J. Exact constraints and appropriate norms in machine-learned exchange-correlation functionals. J. Chem. Phys. 2022, 157, 174106. [Google Scholar] [CrossRef]
- Kaplan, A. Construction of First-Principles Density Functional Approximations and Their Applications to Materials. Ph.D. Thesis, Temple University, Philadelphia, PA, USA, 2022. [Google Scholar]
- Bohm, D.; Pines, D. A collective description of electron interactions. I. Magnetic interactions. Phys. Rev. 1951, 82, 625. [Google Scholar] [CrossRef]
- Becke, A.D. A new mixing of Hartree—Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Albers, R.; Christensen, N.E.; Svane, A. Hubbard-U band-structure methods. J. Phys. Condens. Matter 2009, 21, 343201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aryasetiawan, F.; Biermann, S.; Georges, A. 1 A First-Principles Scheme for Calculating the Electronic Structure of Strongly Correlated Materials: GW+DMFT. In Correlation Spectroscopy of Surfaces, Thin Films, and Nanostructures; Wiley Online Library: Hoboken, NJ, USA, 2004; p. 1. [Google Scholar]
- Kohanoff, J. Electronic Structure Calculations for Solids and Molecules: Theory and Computational Methods; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Cococcioni, M.; De Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA+U method. Phys. Rev. B 2005, 71, 035105. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Levy, M. Physical content of the exact Kohn-Sham orbital energies: Band gaps and derivative discontinuities. Phys. Rev. Lett. 1983, 51, 1884. [Google Scholar] [CrossRef]
- Sham, L.J.; Schlüter, M. Density-functional theory of the energy gap. Phys. Rev. Lett. 1983, 51, 1888. [Google Scholar] [CrossRef]
- Pulkkinen, A.; Barbiellini, B.; Nokelainen, J.; Sokolovskiy, V.; Baigutlin, D.; Miroshkina, O.; Zagrebin, M.; Buchelnikov, V.; Lane, C.; Markiewicz, R.S.; et al. Coulomb correlation in noncollinear antiferromagnetic α-Mn. Phys. Rev. B 2020, 101, 075115. [Google Scholar] [CrossRef] [Green Version]
- Ekholm, M.; Gambino, D.; Jönsson, H.J.M.; Tasnádi, F.; Alling, B.; Abrikosov, I.A. Assessing the SCAN functional for itinerant electron ferromagnets. Phys. Rev. B 2018, 98, 094413. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.; Singh, D.J. Applicability of the strongly constrained and appropriately normed density functional to transition-metal magnetism. Phys. Rev. Lett. 2018, 121, 207201. [Google Scholar] [CrossRef] [Green Version]
- Bai, X.; Li, Y.; Xiao, B.; Rao, Y.; Liang, H.; He, L.; Feng, J. Structural, mechanical, electronic properties of refractory Hf-Al intermetallics from SCAN meta-GGA density functional calculations. Mater. Chem. Phys. 2020, 254, 123423. [Google Scholar] [CrossRef]
- Mahyuddin, M.H.; Staykov, A.; Saputro, A.G.; Agusta, M.K.; Dipojono, H.K.; Yoshizawa, K. Novel mechanistic insights into methane activation over Fe and Cu active sites in zeolites: A comparative DFT study using meta-GGA functionals. J. Phys. Chem. C 2020, 124, 18112–18125. [Google Scholar] [CrossRef]
- Mejía-Rodríguez, D.; Trickey, S. Analysis of over-magnetization of elemental transition metal solids from the SCAN density functional. Phys. Rev. B 2019, 100, 041113. [Google Scholar] [CrossRef] [Green Version]
- Isaacs, E.B.; Wolverton, C. Performance of the strongly constrained and appropriately normed density functional for solid-state materials. Phys. Rev. Mater. 2018, 2, 063801. [Google Scholar] [CrossRef]
- Kübler, J. Theory of Itinerant Electron Magnetism; Oxford University Press: Oxford, UK, 2017; Volume 106. [Google Scholar]
- Endoh, Y.; Ishikawa, Y. Antiferromagnetism of γ iron manganes alloys. J. Phys. Soc. Japan 1971, 30, 1614–1627. [Google Scholar] [CrossRef]
- Dedkov, Y.S.; Voloshina, E.; Richter, M. Preparation and photoemission investigation of bulklike α-Mn films on W (110). Phys. Rev. B 2010, 81, 085404. [Google Scholar] [CrossRef] [Green Version]
- Wexler, R.B.; Gautam, G.S.; Carter, E.A. Exchange-correlation functional challenges in modeling quaternary chalcogenides. Phys. Rev. B 2020, 102, 054101. [Google Scholar] [CrossRef]
- Hennig, R.; Wadehra, A.; Driver, K.; Parker, W.; Umrigar, C.; Wilkins, J. Phase transformation in Si from semiconducting diamond to metallic β-Sn phase in QMC and DFT under hydrostatic and anisotropic stress. Phys. Rev. B 2010, 82, 014101. [Google Scholar] [CrossRef] [Green Version]
- He, B.; Bao, Z.; Zhu, K.; Feng, W.; Sun, H.; Pang, N.; Tsogbadrakh, N.; Odkhuu, D. Itinerant semiconducting antiferromagnetism in metastable V3Ga. Phys. Status Solidi Rapid Res. Lett. 2019, 13, 1900483. [Google Scholar] [CrossRef]
- Jamer, M.E.; Wilfong, B.; Buchelnikov, V.D.; Sokolovskiy, V.V.; Miroshkina, O.N.; Zagrebin, M.A.; Baigutlin, D.R.; Naphy, J.; Assaf, B.A.; Lewis, L.H.; et al. Superconducting and antiferromagnetic properties of dual-phase V3Ga. Appl. Phys. Lett. 2020, 117, 062401. [Google Scholar] [CrossRef]
- Buchelnikov, V.; Sokolovskiy, V.; Miroshkina, O.; Zagrebin, M.; Nokelainen, J.; Pulkkinen, A.; Barbiellini, B.; Lähderanta, E. Correlation effects on ground-state properties of ternary Heusler alloys: First-principles study. Phys. Rev. B 2019, 99, 014426. [Google Scholar] [CrossRef] [Green Version]
- Entel, P.; Dannenberg, A.; Siewert, M.; Herper, H.C.; Gruner, M.E.; Buchelnikov, V.D.; Chernenko, V.A. Composition-Dependent Basics of Smart Heusler Materials from First- Principles Calculations. Mater. Sci. Forum 2011, 684, 1–29. [Google Scholar] [CrossRef]
- Nepal, N.K.; Adhikari, S.; Neupane, B.; Ruzsinszky, A. Formation energy puzzle in intermetallic alloys: Random phase approximation fails to predict accurate formation energies. Phys. Rev. B 2020, 102, 205121. [Google Scholar] [CrossRef]
- Zhang, R.; Singh, B.; Lane, C.; Kidd, J.; Zhang, Y.; Barbiellini, B.; Markiewicz, R.S.; Bansil, A.; Sun, J. Critical role of magnetic moments in heavy-fermion materials: Revisiting SmB6. Phys. Rev. B 2022, 105, 195134. [Google Scholar]
- Devi, A.A.S.; Nokelainen, J.; Barbiellini, B.; Devaraj, M.; Alatalo, M.; Bansil, A. Re-examining the giant magnetization density in α-Fe16N2 with the SCAN+U method. Phys. Chem. Chem. Phys. 2022, 24, 17879–17884. [Google Scholar] [CrossRef] [PubMed]
- Booth, G.H.; Grüneis, A.; Kresse, G.; Alavi, A. Towards an exact description of electronic wavefunctions in real solids. Nature 2013, 493, 365–370. [Google Scholar] [CrossRef] [Green Version]
- Chevrier, V.L.; Ong, S.P.; Armiento, R.; Chan, M.K.; Ceder, G. Hybrid density functional calculations of redox potentials and formation energies of transition metal compounds. Phys. Rev. B 2010, 82, 075122. [Google Scholar] [CrossRef]
- Yang, Z.h.; Peng, H.; Sun, J.; Perdew, J.P. More realistic band gaps from meta-generalized gradient approximations: Only in a generalized Kohn-Sham scheme. Phys. Rev. B 2016, 93, 205205. [Google Scholar] [CrossRef] [Green Version]
- Xiao, H.; Tahir-Kheli, J.; Goddard, W.A., III. Accurate band gaps for semiconductors from density functional theory. J. Phys. Chem. Lett. 2011, 2, 212–217. [Google Scholar] [CrossRef] [Green Version]
- Miroshkina, O.N.; Baigutlin, D.R.; Sokolovskiy, V.V.; Zagrebin, M.A.; Pulkkinen, A.; Barbiellini, B.; Lähderanta, E.; Buchelnikov, V.D. Exchange-correlation corrections for electronic properties of half-metallic Co2FeSi and nonmagnetic semiconductor CoFeTiAl. J. Appl. Phys. 2020, 127, 175108. [Google Scholar] [CrossRef]
- Buchelnikov, V.D.; Sokolovskiy, V.V.; Miroshkina, O.N.; Baigutlin, D.R.; Zagrebin, M.A.; Barbiellini, B.; Singh, B.; Bansil, A.; Lähderanta, E. Design of a stable Heusler alloy with switchable metal-to-half-metal transition at finite temperature. Adv. Theory Simul. 2021, 4, 2100311. [Google Scholar] [CrossRef]
- Godby, R.; Schlüter, M.; Sham, L. Accurate exchange-correlation potential for silicon and its discontinuity on addition of an electron. Phys. Rev. Lett. 1986, 56, 2415. [Google Scholar] [CrossRef]
- Sham, L.; Schlüter, M. Density-functional theory of the band gap. Phys. Rev. B 1985, 32, 3883. [Google Scholar] [CrossRef]
- Heyd, J.; Peralta, J.E.; Scuseria, G.E.; Martin, R.L. Energy band gaps and lattice parameters evaluated with the Heyd-Scuseria-Ernzerhof screened hybrid functional. J. Chem. Phys. 2005, 123, 174101. [Google Scholar] [CrossRef] [PubMed]
- Beeke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648. [Google Scholar] [CrossRef] [Green Version]
- Crowley, J.M.; Tahir-Kheli, J.; Goddard III, W.A. Resolution of the band gap prediction problem for materials design. J. Phys. Chem. Lett. 2016, 7, 1198–1203. [Google Scholar] [CrossRef] [PubMed]
- Ono, S.; Komiya, S.; Ando, Y. Strong charge fluctuations manifested in the high-temperature Hall coefficient of high-Tc cuprates. Phys. Rev. B 2007, 75, 024515. [Google Scholar] [CrossRef] [Green Version]
- Lane, C.; Furness, J.W.; Buda, I.G.; Zhang, Y.; Markiewicz, R.S.; Barbiellini, B.; Sun, J.; Bansil, A. Antiferromagnetic ground state of La2CuO4: A parameter-free ab initio description. Phys. Rev. B 2018, 98, 125140. [Google Scholar] [CrossRef] [Green Version]
- Furness, J.W.; Zhang, Y.; Lane, C.; Buda, I.G.; Barbiellini, B.; Markiewicz, R.S.; Bansil, A.; Sun, J. An accurate first-principles treatment of doping-dependent electronic structure of high-temperature cuprate superconductors. Commun. Phys. 2018, 1, 1–6. [Google Scholar]
- Varignon, J.; Bibes, M.; Zunger, A. Mott gapping in 3d ABO3 perovskites without Mott-Hubbard interelectronic repulsion energy. U. Phys. Rev. B 2019, 100, 035119. [Google Scholar] [CrossRef] [Green Version]
- Zulfiqar, W.; Alay-e Abbas, S.M.; Abbas, G.; Laref, A.; Larsson, J.A.; Shaukat, A. Revisiting the structural, electronic and photocatalytic properties of Ti and Zr based perovskites with meta-GGA functionals of DFT. J. Mater. Chem. C 2021, 9, 4862–4876. [Google Scholar] [CrossRef]
- Zhang, R.; Lane, C.; Singh, B.; Nokelainen, J.; Barbiellini, B.; Markiewicz, R.S.; Bansil, A.; Sun, J. Magnetic and f-electron effects in LaNiO2 and NdNiO2 nickelates with cuprate-like 3dx2 − y2 band. Commun. Phys. 2021, 4, 118. [Google Scholar] [CrossRef]
- Pokharel, K.; Lane, C.; Furness, J.W.; Zhang, R.; Ning, J.; Barbiellini, B.; Markiewicz, R.S.; Zhang, Y.; Bansil, A.; Sun, J. Sensitivity of the electronic and magnetic structures of cuprate superconductors to density functional approximations. NPJ Comput. Mater. 2022, 8, 31. [Google Scholar] [CrossRef]
- Wagner, L.K.; Abbamonte, P. Effect of electron correlation on the electronic structure and spin-lattice coupling of high-Tc cuprates: Quantum Monte Carlo calculations. Phys. Rev. B 2014, 90, 125129. [Google Scholar] [CrossRef] [Green Version]
- Jorgensen, J.; Dabrowski, B.; Pei, S.; Hinks, D.; Soderholm, L.; Morosin, B.; Schirber, J.; Venturini, E.; Ginley, D. Superconducting phase of La2CuO4+δ: A superconducting composition resulting from phase separation. Phys. Rev. B 1988, 38, 11337. [Google Scholar] [CrossRef] [PubMed]
- Uchida, S.; Ido, T.; Takagi, H.; Arima, T.; Tokura, Y.; Tajima, S. Optical spectra of La2−xSrxCuO4: Effect of carrier doping on the electronic structure of the CuO2 plane. Phys. Rev. B 1991, 43, 7942. [Google Scholar] [CrossRef] [PubMed]
- Cox, D.; Zolliker, P.; Axe, J.; Moudden, A.; Moodenbaugh, A.; Xu, Y. Structural studies of La2−xBaxCuO4 between 11–293 K. Mater. Res. Soc. Symp. Proc. 1989, 156, 141. [Google Scholar] [CrossRef]
- Onoda, M.; Shamoto, S.I.; Sato, M.; Hosoya, S. Single Crystal X-Ray Diffraction Study of (La1−xMx)2CuO4−δ (M=Sr and Ba), La2CuO4−δ and LnBa2Cu3O7−δ (Ln=Y, Dy and Ho) Systems. Nov. Superconduct. 1987, 1, 919–920. [Google Scholar]
- Schlipf, M. Heyd-Scuseria-Ernzerhof Screened ExchangeHybrid Functional for Complex Materials: All-Electron Implementation and Application. Ph.D. Thesis, Forschungszentrum Julich, Julich, Germany, 2012. [Google Scholar]
- Dittrich, H.; Karl, N.; Schock, H.; Kuck, S. Ternary Compounds, Organic Semiconductors: Supplement to Vol. III/7h; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Wahl, R.; Vogtenhuber, D.; Kresse, G. SrTiO3 and BaTiO3 revisited using the projector augmented wave method: Performance of hybrid and semilocal functionals. Phys. Rev. B 2008, 78, 104116. [Google Scholar] [CrossRef]
- Verbraeken, M.C.; Suard, E.; Irvine, J.T. Structural and electrical properties of calcium and strontium hydrides. J. Mater. Chem. 2009, 19, 2766–2770. [Google Scholar] [CrossRef]
- Wemple, S. Polarization Fluctuations and the Optical-Absorption Edge in BaTiO3. Phys. Rev. B 1970, 2, 2679. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, J.; Noh, T.; Byun, D.Y.; Yoo, K.S.; Yamaura, K.; Takayama-Muromachi, E. Systematic trends in the electronic structure parameters of the 4d transition-metal oxides SrMO3 (M = Zr, Mo, Ru, and Rh). Phys. Rev. B 2003, 67, 113101. [Google Scholar] [CrossRef] [Green Version]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, B.J.; Howard, C.J.; Chakoumakos, B.C. High-temperature phase transitions in SrHfO3. Phys. Rev. B 1999, 60, 2972. [Google Scholar] [CrossRef]
- Zhang, H.; Qiao, J.; Li, G.; Li, S.; Wang, G.; Wang, J.; Song, Y. Preparation of Ce4+-doped BaZrO3 by hydrothermal method and application in dual-frequent sonocatalytic degradation of norfloxacin in aqueous solution. Ultrason. Sonochem. 2018, 42, 356–367. [Google Scholar] [CrossRef] [PubMed]
- Pies, W.; Weiss, A. Simple Oxocompounds of Zirconium (Oxozirconates). 1976. Available online: https://materials.springer.com/lb/docs/sm_lbs_978-3-540-37567-8_35 (accessed on 2 April 2023).
- Vasilev, A.N.; Buchelnikov, V.D.; Takagi, T.; Khovailo, V.V.; Estrin, E.I. Shape memory ferromagnets. Phys. Usp. 2003, 46, 559–588. [Google Scholar] [CrossRef] [Green Version]
- Buchelnikov, V.D.; Vasiliev, A.N.; Koledov, V.; Taskaev, S.; Khovaylo, V.V.; Shavrov, V.G. Magnetic shape-memory alloys: Phase transitions and functional properties. Phys. Usp. 2006, 49, 871. [Google Scholar] [CrossRef]
- Entel, P.; Buchelnikov, V.D.; Khovailo, V.V.; Zayak, A.T.; Adeagbo, W.A.; Gruner, M.E.; Herper, H.C.; Wassermann, E.F. Modelling the phase diagram of magnetic shape memory Heusler alloys. J. Phys. D Appl. Phys. 2006, 39, 865–889. [Google Scholar] [CrossRef]
- Entel, P.; Buchelnikov, V.D.; Gruner, M.E.; Hucht, A.; Khovailo, V.V.; Nayak, S.K.; Zayak, A.T. Shape memory alloys: A summary of recent achievements. Mater. Sci. Forum 2008, 583, 21–41. [Google Scholar] [CrossRef]
- Planes, A.; Mañosa, L.; Acet, M. Magnetocaloric effect and its relation to shape-memory properties in ferromagnetic Heusler alloys. J. Condens. Matter Phys. 2009, 21, 233201. [Google Scholar] [CrossRef] [Green Version]
- Entel, P.; Gruner, M.E.; Dannenberg, A.; Siewert, M.; Nayak, S.K.; Herper, H.C.; Buchelnikov, V.D. Fundamental aspects of magnetic shape memory alloys: Insights from ab initio and Monte Carlo studies. Mater. Sci. Forum 2010, 635, 3–12. [Google Scholar] [CrossRef] [Green Version]
- Hickel, T.; Uijttewaal, M.; Al-Zubi, A.; Dutta, B.; Grabowski, B.; Neugebauer, J. Ab Initio-Based Prediction of Phase Diagrams: Application to Magnetic Shape Memory Alloys. Adv. Eng. Mater. 2012, 14, 547–561. [Google Scholar] [CrossRef]
- Graf, T.; Felser, C.; Parkin, S.S. Simple rules for the understanding of Heusler compounds. Prog. Solid. State Ch. 2011, 39, 1–50. [Google Scholar] [CrossRef]
- Yu, G.H.; Xu, Y.L.; Liu, Z.H.; Qiu, H.M.; Zhu, Z.Y.; Huang, X.P.; Pan, L.Q. Recent progress in Heusler-type magnetic shape memory alloys. Rare Met. 2015, 34, 527–539. [Google Scholar] [CrossRef]
- Felser, C.; Wollmann, L.; Chadov, S.; Fecher, G.H.; Parkin, S.S. Basics and prospective of magnetic Heusler compounds. APL Mater. 2015, 3, 041518. [Google Scholar] [CrossRef] [Green Version]
- de Paula, V.G.; Reis, M.S. All-d-metal full Heusler alloys: A novel class of functional materials. Chem. Mater. 2021, 33, 5483–5495. [Google Scholar] [CrossRef]
- Tavares, S.; Yang, K.; Meyers, M.A. Heusler alloys: Past, properties, new alloys, and prospects. Prog. Mater. Sci. 2022, 132, 101017. [Google Scholar] [CrossRef]
- He, J.; Rabe, K.M.; Wolverton, C. Computationally accelerated discovery of functional and structural Heusler materials. MRS Bull. 2022, 47, 559–572. [Google Scholar] [CrossRef]
- Baigutlin, D.; Sokolovskiy, V.; Miroshkina, O.; Zagrebin, M.; Nokelainen, J.; Pulkkinen, A.; Barbiellini, B.; Pussi, K.; Lähderanta, E.; Buchelnikov, V.; et al. Electronic structure beyond the generalized gradient approximation for Ni2MnGa. Phys. Rev. B 2020, 102, 045127. [Google Scholar] [CrossRef]
- Barbiellini, B.; Pulkkinen, A.; Nokelainen, J.; Buchelnikov, V.; Sokolovskiy, V.; Miroshkina, O.N.; Zagrebin, M.; Pussi, K.; Lähderanta, E.; Granovsky, A. Correlation effects in the ground state of Ni-(Co)-Mn-Sn Heusler compounds. MRS Adv. 2019, 4, 441–446. [Google Scholar] [CrossRef]
- Buchelnikov, V.; Sokolovskiy, V.; Miroshkina, O.; Baigutlin, D.; Zagrebin, M. Phase transformations in Ni (Co)-Mn (Cr, C)-(In, Sn) Alloys: An ab initio study. Phys. Met. Metallogr. 2020, 121, 202–209. [Google Scholar] [CrossRef]
- Miroshkina, O.N.; Zagrebin, M.A.; Pavlukhina, O.O.; Sokolovskiy, V.V.; Buchelnikov, V.D. The influence of exchange-correlation functionals on the ground state properties of Ni2Mn(Ga, Sn) and Fe2(Ni, V)(Ga, Al) Heusler alloys. Mater. Res. Proc. 2018, 9, 104. [Google Scholar]
- Zelenỳ, M.; Sedlák, P.; Heczko, O.; Seiner, H.; Veřtát, P.; Obata, M.; Kotani, T.; Oda, T.; Straka, L. Effect of electron localization in theoretical design of Ni-Mn-Ga based magnetic shape memory alloys. Mater. Des. 2021, 209, 109917. [Google Scholar] [CrossRef]
- Erager, K.R.; Baigutlin, D.R.; Sokolovskiy, V.V.; Buchelnikov, V.D. Exchange correlation effects in modulated martensitic structures of the Mn2NiGa Alloy. Phys. Met. Metallogr. 2022, 123, 375–380. [Google Scholar] [CrossRef]
- Draganyuk, O.N.; Zhandun, V.S.; Zamkova, N.G. Half-metallicity in Fe2MnSi and Mn2FeSi Heusler compounds: A comparative ab initio study. Mater. Chem. Phys. 2021, 271, 124897. [Google Scholar] [CrossRef]
- Shastri, S.S.; Pandey, S.K. Electronic structure and phonon properties of Fe2ScAs full-Heusler alloy. AIP Conf. Proc. 2019, 2115, 030384. [Google Scholar]
- Abuova, A.; Merali, N.; Abuova, F.; Khovaylo, V.; Sagatov, N.; Inerbaev, T. Electronic properties and chemical bonding in V2FeSi and Fe2VSi Heusler alloys. Crystals 2022, 12, 1546. [Google Scholar] [CrossRef]
- Mellah, D.E.; Demmouche, K. Exchange-correlation and spin-orbit coupling effects in 18-electrons transparent conductors half-Heusler: Ab-initio study. Comput. Condens. Matter 2022, 32, e00690. [Google Scholar] [CrossRef]
- Shastri, S.S.; Pandey, S.K. Thermoelectric properties, efficiency and thermal expansion of ZrNiSn half-Heusler by first-principles calculations. J. Phys. Condens. Matter 2020, 32, 355705. [Google Scholar] [CrossRef]
- Stephen, G.M.; Lane, C.; Buda, G.; Graf, D.; Kaprzyk, S.; Barbiellini, B.; Bansil, A.; Heiman, D. Electrical and magnetic properties of thin films of the spin-filter material CrVTiAl. Phys. Rev. B 2019, 99, 224207. [Google Scholar] [CrossRef] [Green Version]
- Shastri, S.S.; Pandey, S.K. Two functionals approach in DFT for the prediction of thermoelectric properties of Fe2ScX (X= P, As, Sb) full-Heusler compounds. J. Phys. Condens. Matter 2019, 31, 435701. [Google Scholar] [CrossRef] [Green Version]
- Sattar, M.A.; Javed, M.; Al Bouzieh, N.; Benkraouda, M.; Amrane, N. First-principles investigation on the novel half-Heusler VXTe (X = Cr, Mn, Fe, and Co) alloys for spintronic and thermoelectric applications. Mater. Sci. Semicond. Process. 2023, 155, 107233. [Google Scholar] [CrossRef]
- Özdemir Kart, S.; Uludoğan, M.; Karaman, I.; Çağın, T. DFT studies on structure, mechanics and phase behavior of magnetic shape memory alloys: Ni2MnGa. Phys. Status Solidi A 2008, 205, 1026–1035. [Google Scholar] [CrossRef]
- Sozinov, A.; Likhachev, A.; Lanska, N.; Ullakko, K. Giant magnetic-field-induced strain in NiMnGa seven-layered martensitic phase. Appl. Phys. Lett. 2002, 80, 1746–1748. [Google Scholar] [CrossRef]
- Webster, P.; Ziebeck, K.; Town, S.; Peak, M. Magnetic order and phase transformation in Ni2MnGa. Philos. Mag. B 1984, 49, 295–310. [Google Scholar] [CrossRef]
- Çakır, A.; Righi, L.; Albertini, F.; Acet, M.; Farle, M.; Aktürk, S. Extended investigation of intermartensitic transitions in Ni-Mn-Ga magnetic shape memory alloys: A detailed phase diagram determination. J. Appl. Phys. 2013, 114, 183912. [Google Scholar] [CrossRef]
- Straka, L.; Drahokoupil, J.; Pacherová, O.; Fabiánová, K.; Kopeckỳ, V.; Seiner, H.; Hänninen, H.; Heczko, O. The relation between lattice parameters and very low twinning stress in Ni50Mn25+xGa25−x magnetic shape memory alloys. Smart Mater Struct. 2015, 25, 025001. [Google Scholar] [CrossRef] [Green Version]
- Liu, G.; Chen, J.; Liu, Z.; Dai, X.; Wu, G.; Zhang, B.; Zhang, X. Martensitic transformation and shape memory effect in a ferromagnetic shape memory alloy: Mn2NiGa. Appl. Phys. Lett. 2005, 87, 262504. [Google Scholar] [CrossRef]
- Singh, S.; Maniraj, M.; D’Souza, S.; Ranjan, R.; Barman, S. Structural transformations in Mn2NiGa due to residual stress. Appl. Phys. Lett. 2010, 96, 081904. [Google Scholar] [CrossRef]
- Brown, P.; Kanomata, T.; Neumann, K.; Neumann, K.; Ouladdiaf, B.; Sheikh, A.; Ziebeck, K. Atomic and magnetic order in the shape memory alloy Mn2NiGa. J. Phys. Condens. Matter. 2010, 22, 506001. [Google Scholar] [CrossRef]
- Janovec, J.; Zelenỳ, M.; Heczko, O.; Ayuela, A. Localization versus delocalization of d-states within the Ni2MnGa Heusler alloy. Sci. Rep. 2022, 12, 20577. [Google Scholar] [CrossRef]
- Liu, G.; Dai, X.; Yu, S.; Zhu, Z.; Chen, J.; Wu, G.; Zhu, H.; Xiao, J.Q. Physical and electronic structure and magnetism of Mn2NiGa: Experiment and density-functional theory calculations. Phys. Rev. B 2006, 74, 054435. [Google Scholar] [CrossRef] [Green Version]
- Kundu, A.; Gruner, M.E.; Siewert, M.; Hucht, A.; Entel, P.; Ghosh, S. Interplay of phase sequence and electronic structure in the modulated martensites of Mn2NiGa from first-principles calculations. Phys. Rev. B 2017, 96, 064107. [Google Scholar] [CrossRef] [Green Version]
- Miroshkina, O.N.; Eggert, B.; Lill, J.; Beckmann, B.; Koch, D.; Hu, M.Y.; Lojewski, T.; Rauls, S.; Scheibel, F.; Taubel, A.; et al. Impact of magnetic and antisite disorder on the vibrational densities of states in Ni2MnSn Heusler alloys. Phys. Rev. B 2022, 106, 214302. [Google Scholar] [CrossRef]
- Ye, M.; Kimura, A.; Miura, Y.; Shirai, M.; Cui, Y.T.; Shimada, K.; Namatame, H.; Taniguchi, M.; Ueda, S.; Kobayashi, K.; et al. Role of electronic structure in the martensitic phase transition of Ni2Mn1+xSn1−x studied by hard-x-ray photoelectron spectroscopy and ab initio calculation. Phys. Rev. Lett. 2010, 104, 176401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Entel, P.; Gruner, M.E.; Comtesse, D.; Sokolovskiy, V.V.; Buchelnikov, V.D. Interacting magnetic cluster-spin glasses and strain glasses in Ni-Mn based Heusler structured intermetallics. Phys. Status Solidi B 2014, 251, 2135–2148. [Google Scholar] [CrossRef]
- Xiao, H.B.; Yang, C.P.; Wang, R.L.; Marchenkov, V.V.; Bärner, K. Effect of alloying element Al substitution on Ni-Mn-Sn shape memory alloy by first-principle calculations. J. Appl. Phys. 2012, 112, 123723. [Google Scholar] [CrossRef]
- Xiao, H.B.; Yang, C.P.; Wang, R.L.; Marchenkov, V.V.; Luo, X. Martensitic transformation and phase stability of In-doped Ni-Mn-Sn shape memory alloys from first-principles calculations. J. Appl. Phys. 2014, 115, 203703. [Google Scholar] [CrossRef]
- Çakır, A.; Righi, L.; Albertini, F.; Acet, M.; Farle, M. Intermartensitic transitions and phase stability in Ni50Mn50−xSnx Heusler alloys. Acta Mater. 2015, 99, 140–149. [Google Scholar] [CrossRef]
- Baygutlin, D.R.; Sokolovskiy, V.V.; Miroshkina, O.N.; Buchel’nikov, V.D. The half-metallic properties of Heusler alloys Mn2ScZ (Z = Al, Si, P, Ga, Ge, As, In, Sn, Sb): Ab initio study. Fiz. Tverd. Tela. 2021, 63, 1751–1757. [Google Scholar]
- Buchelnikov, V.D.; Sokolovskiy, V.V.; Miroshkina, O.N.; Baigutlin, D.R.; Zagrebin, M.A.; Barbiellini, B.; Lähderanta, E. Prediction of a Heusler alloy with switchable metal-to-half-metal behavior. Phys. Rev. B 2021, 103, 054414. [Google Scholar] [CrossRef]
- Shastri, S.S.; Pandey, S.K. A comparative study of different exchange-correlation functionals in understanding structural, electronic and thermoelectric properties of Fe2VAl and Fe2TiSn compounds. Comput. Mater. Sci. 2018, 143, 316–324. [Google Scholar] [CrossRef] [Green Version]
- Chieda, Y.; Kanomata, T.; Fukushima, K.; Matsubayashi, K.; Uwatoko, Y.; Kainuma, R.; Oikawa, K.; Ishida, K.; Obara, K.; Shishido, T. Magnetic properties of Mn-rich Ni2MnSn Heusler alloys under pressure. J. Alloys Compd. 2009, 486, 51–54. [Google Scholar] [CrossRef]
- Kumar, N.; Saini, H.S.; Singh, M.; Kashyap, M.K. Enhanced thermoelectric properties of Ta-doped Half-Heusler ZrNiSn. Mater. Today Proc. 2020, 26, 3478–3481. [Google Scholar] [CrossRef]
- Oses, C.; Gossett, E.; Hicks, D.; Rose, F.; Mehl, M.J.; Perim, E.; Takeuchi, I.; Sanvito, S.; Scheffler, M.; Lederer, Y.; et al. AFLOW-CHULL: Cloud-oriented platform for autonomous phase stability analysis. J. Chem. Inf. Model. 2018, 58, 2477–2490. [Google Scholar] [CrossRef] [PubMed]
- Planes, A.; Obradó, E.; Gonzalez-Comas, A.; Mañosa, L. Premartensitic transition driven by magnetoelastic interaction in bcc ferromagnetic Ni2MnGa. Phys. Rev. Lett. 1997, 79, 3926. [Google Scholar] [CrossRef] [Green Version]
- Khovailo, V.; Takagi, T.; Bozhko, A.; Matsumoto, M.; Tani, J.; Shavrov, V. Premartensitic transition in Ni2+xMn1−xGa Heusler alloys. J. Phys. Condens. Matter 2001, 13, 9655. [Google Scholar] [CrossRef] [Green Version]
- Zheludev, A.; Shapiro, S.; Wochner, P.; Schwartz, A.; Wall, M.; Tanner, L. Phonon anomaly, central peak, and microstructures in Ni2MnGa. Phys. Rev. B 1995, 51, 11310. [Google Scholar] [CrossRef] [PubMed]
- Zheludev, A.; Shapiro, S.; Wochner, P.; Tanner, L. Precursor effects and premartensitic transformation in Ni2MnGa. Phys. Rev. B 1996, 54, 15045. [Google Scholar] [CrossRef]
- Godlevsky, V.V.; Rabe, K.M. Soft tetragonal distortions in ferromagnetic Ni2MnGa and related materials from first principles. Phys. Rev. B 2001, 63, 134407. [Google Scholar] [CrossRef] [Green Version]
- Zayak, A.; Entel, P.; Enkovaara, J.; Ayuela, A.; Nieminen, R.M. First-principles investigation of phonon softenings and lattice instabilities in the shape-memory system Ni2MnGa. Phys. Rev. B 2003, 68, 132402. [Google Scholar] [CrossRef] [Green Version]
- Haynes, T.; Watts, R.; Laverock, J.; Major, Z.; Alam, M.; Taylor, J.; Duffy, J.; Dugdale, S. Positron annihilation study of the Fermi surface of Ni2MnGa. New J. Phys. 2012, 14, 035020. [Google Scholar] [CrossRef]
- Rogl, G.; Grytsiv, A.; Gürth, M.; Tavassoli, A.; Ebner, C.; Wünschek, A.; Puchegger, S.; Soprunyuk, V.; Schranz, W.; Bauer, E.; et al. Mechanical properties of half-Heusler alloys. Acta Mater. 2016, 107, 178–195. [Google Scholar] [CrossRef]
- Kasuya, T. Exchange mechanisms in Heusler alloys: Virtual double exchange. Solid State Commun. 1974, 15, 1119–1122. [Google Scholar] [CrossRef]
- da Silva, C.E.T.G.; Falicov, L.M. Theory of magnetic properties of rare earth compounds (Localized moments and hybridization effects). J. Phys. C Solid. State Phys. 1972, 5, 63–76. [Google Scholar] [CrossRef]
- Şaşıoğlu, E.; Sandratskii, L.M.; Bruno, P. First-principles calculation of the intersublattice exchange interactions and Curie temperatures of the full Heusler alloys Ni2MnX (X = Ga,In,Sn,Sb). Phys. Rev. B 2004, 70, 024427. [Google Scholar] [CrossRef] [Green Version]
- Cardias, R.; Szilva, A.; Bergman, A.; Di Marco, I.; Katsnelson, M.; Lichtenstein, A.; Nordström, L.; Klautau, A.; Eriksson, O.; Kvashnin, Y.O. The Bethe-Slater curve revisited; new insights from electronic structure theory. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Meinert, M.; Friedrich, C.; Reiss, G.; Blügel, S. GW study of the half-metallic Heusler compounds Co2MnSi and Co2FeSi. Phys. Rev. B 2012, 86, 245115. [Google Scholar] [CrossRef] [Green Version]
- Balke, B.; Fecher, G.H.; Kandpal, H.C.; Felser, C.; Kobayashi, K.; Ikenaga, E.; Kim, J.J.; Ueda, S. Properties of the quaternary half-metal-type Heusler alloy Co2Mn1−xFexSi. Phys. Rev. B 2006, 74, 104405. [Google Scholar] [CrossRef] [Green Version]
- Aryal, A.; Bakkar, S.; Samassekou, H.; Pandey, S.; Dubenko, I.; Stadler, S.; Ali, N.; Mazumdar, D. Mn2FeSi: An antiferromagnetic inverse-Heusler alloy. J. Alloys Compd. 2020, 823, 153770. [Google Scholar] [CrossRef]
- Helmholdt, R.; Buschow, K. Crystallographic and magnetic structure of Ni2MnSn and NiMn2Sn. J. Less-Common Met. 1987, 128, 167–171. [Google Scholar] [CrossRef]
- Nejadsattari, F.; Stadnik, Z.M.; Przewoźnik, J.; Buschow, K.H. Mössbauer spectroscopy, magnetic, and ab initio study of the Heusler compound Fe2NiGa. Phys. B Condens. Matter 2015, 477, 113–122. [Google Scholar] [CrossRef]
- Luo, H.; Zhang, H.; Zhu, Z.; Ma, L.; Xu, S.; Wu, G.; Zhu, X.; Jiang, C.; Xu, H. Half-metallic properties for the Mn2FeZ (Z = Al, Ga, Si, Ge, Sb) Heusler alloys: A first-principles study. J. Appl. Phys. 2008, 103, 083908. [Google Scholar] [CrossRef]
- Tas, M.; Şaşıoğlu, E.; Galanakis, I.; Friedrich, C.; Blügel, S. Quasiparticle band structure of the almost-gapless transition-metal-based Heusler semiconductors. Phys. Rev. B 2016, 93, 195155. [Google Scholar] [CrossRef] [Green Version]
- Sk, S.; Devi, P.; Singh, S.; Pandey, S.K. Exploring the best scenario for understanding the high temperature thermoelectric behaviour of Fe2VAl. Mater. Res. Express 2018, 6, 026302. [Google Scholar] [CrossRef] [Green Version]
- Okamura, H.; Kawahara, J.; Nanba, T.; Kimura, S.; Soda, K.; Mizutani, U.; Nishino, Y.; Kato, M.; Shimoyama, I.; Miura, H.; et al. Pseudogap formation in the intermetallic compounds (Fe1−xVx)3Al. Phys. Rev. Lett. 2000, 84, 3674. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Öğüt, S.; Rabe, K.M. Band gap and stability in the ternary intermetallic compounds NiSnM (M = Ti, Zr, Hf): A first-principles study. Phys. Rev. B 1995, 51, 10443. [Google Scholar] [CrossRef] [Green Version]
- Zou, D.; Xie, S.; Liu, Y.; Lin, J.; Li, J. Electronic structure and thermoelectric properties of half-Heusler Zr0.5Hf0.5NiSn by first-principles calculations. J. Appl. Phys. 2013, 113, 193705. [Google Scholar] [CrossRef]
- Berche, A.; Noutack, M.T.; Doublet, M.L.; Jund, P. Unexpected band gap increase in the Fe2VAl Heusler compound. Mater. Today Phys. 2020, 13, 100203. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Xie, P.; Liu, C.; Li, S.; Lei, X.; Huang, L.; Yuan, G.; Cai, F. Enhanced thermoelectric performance of Hafnium free n-type ZrNiSn half-Heusler alloys by isoelectronic Si substitution. Mater. Today Phys. 2022, 24, 100648. [Google Scholar] [CrossRef]
- Luo, H.; Zhu, Z.; Ma, L.; Xu, S.; Liu, H.; Qu, J.; Li, Y.; Wu, G. Electronic structure and magnetic properties of Fe2YSi (Y = Cr, Mn, Fe, Co, Ni) Heusler alloys: A theoretical and experimental study. J. Phys. D 2007, 40, 7121. [Google Scholar] [CrossRef]
- Galanakis, I.; Özdoğan, K.; Şaşıoglu, E. High-T C fully compensated ferrimagnetic semiconductors as spin-filter materials: The case of CrVXAl (X = Ti, Zr, Hf) Heusler compounds. J. Phys. Condens. Matter 2014, 26, 086003. [Google Scholar] [CrossRef]
- Stephen, G.M.; Buda, G.; Jamer, M.E.; Lane, C.; Kaprzyk, S.; Barbiellini, B.; Graf, D.; Lewis, L.H.; Bansil, A.; Heiman, D. Structural and electronic properties of the spin-filter material CrVTiAl with disorder. J. Appl. Phys. 2019, 125, 123903. [Google Scholar] [CrossRef]
- Do, D.; Lee, M.S.; Mahanti, S.D. Effect of onsite Coulomb repulsion on thermoelectric properties of full-Heusler compounds with pseudogaps. Phys. Rev. B 2011, 84, 125104. [Google Scholar] [CrossRef] [Green Version]
- Sharma, S.; Pandey, S.K. Effect of on-site Coulomb interaction (U) on the electronic and magnetic properties of Fe2MnSi, Fe2MnAl and Co2MnGe. J. Magn. Magn. Mater. 2016, 403, 1–7. [Google Scholar] [CrossRef]
- Hinterleitner, B.; Garmroudi, F.; Reumann, N.; Mori, T.; Bauer, E.; Podloucky, R. The electronic pseudo band gap states and electronic transport of the full-Heusler compound Fe2VAl. J. Mater. Chem. C 2021, 9, 2073–2085. [Google Scholar] [CrossRef]
- Ram, M.; Saxena, A.; Aly, A.E.; Shankar, A. Half-metallicity in new Heusler alloys Mn2ScZ (Z = Si, Ge, Sn). RSC Adv. 2020, 10, 7661–7670. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kandpal, H.C.; Fecher, G.H.; Felser, C. Calculated electronic and magnetic properties of the half-metallic, transition metal based Heusler compounds. J. Phys. D 2007, 40, 1507. [Google Scholar] [CrossRef] [Green Version]
- Gautier, R.; Zhang, X.; Hu, L.; Yu, L.; Lin, Y.; Sunde, T.O.; Chon, D.; Poeppelmeier, K.R.; Zunger, A. Prediction and accelerated laboratory discovery of previously unknown 18-electron ABX compounds. Nat. Chem. 2015, 7, 308–316. [Google Scholar] [CrossRef] [Green Version]
- Aliev, F.; Brandt, N.; Moshchalkov, V.; Kozyrkov, V.; Skolozdra, R.; Belogorokhov, A. Gap at the Fermi level in the intermetallic vacancy system RBiSn (R= Ti, Zr, Hf). Z. Phys. Condens. Matter 1989, 75, 167–171. [Google Scholar] [CrossRef]
- Cui, Y.; Kimura, A.; Miyamoto, K.; Sakamoto, K.; Xie, T.; Qiao, S.; Nakatake, M.; Shimada, K.; Taniguchi, M.; Fujimori, S.I.; et al. Electronic structures of Fe3-x Vx Si probed by photoemission spectroscopy. Phys. Status Solidi (A) 2006, 203, 2765–2768. [Google Scholar] [CrossRef] [Green Version]
- Lue, C.S.; Ross, J.H. Semimetallic behavior in Fe 2 VAl: NMR evidence. Phys. Rev. B 1998, 58, 9763. [Google Scholar] [CrossRef]
- Venkateswara, Y.; Gupta, S.; Samatham, S.S.; Varma, M.R.; Suresh, K.; Alam, A. Competing magnetic and spin-gapless semiconducting behavior in fully compensated ferrimagnetic CrVTiAl: Theory and experiment. Phys. Rev. B 2018, 97, 054407. [Google Scholar] [CrossRef] [Green Version]
- Shen, Q.; Chen, L.; Goto, T.; Hirai, T.; Yang, J.; Meisner, G.; Uher, C. Effects of partial substitution of Ni by Pd on the thermoelectric properties of ZrNiSn-based half-Heusler compounds. Appl. Phys. Lett. 2001, 79, 4165–4167. [Google Scholar] [CrossRef] [Green Version]
- Lejaeghere, K.; Bihlmayer, G.; Björkman, T.; Blaha, P.; Blügel, S.; Blum, V.; Caliste, D.; Castelli, I.E.; Clark, S.J.; Dal Corso, A.; et al. Reproducibility in density functional theory calculations of solids. Science 2016, 351, aad3000. [Google Scholar] [CrossRef] [PubMed] [Green Version]
























| (eV) | (/f.u.) | V (Å) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| PBE | SCAN | exp. | PBE | SCAN | exp. | PBE | SCAN | exp. | |
| LTO | 0.026 [72] | 1.0 [71] | 0.9–1.3 [70] | 0.273 [72] | 0.49 [71] | 0.3–0.6 [77] | 391 [72] | 379.1 [71] | 380.3 [78] |
| 0.979 [72] | 1 [79] | 0.491 [72] | 0.495 [72] | 380.3 [72] | 379.1 [78] | ||||
| LTT | 0 [72] | 1.006 [72] | - | 0.107 [72] | 0.492 [72] | - | 391.4 [72] | 379.8 [72] | 380.3 [80] |
| HTT | 0 [72] | 0.918 [72] | - | 0.262 [72] | 0.479 [72] | - | 384 [72] | 375.4 [72] | 384.2 [81] |
| SrTiO | 2.24 [82] | 2.23 [74] | 3.43 [83] | - | - | - | 61.3 [84] | 59.7 [74] | 58.9 [85] |
| BaTiO | 1.93 [82] | 1.92 [74] | 3.2 [86] | - | - | - | 65.7 [84] | 63.8 [74] | 64.0 [85] |
| SrZrO | 3.68 [82] | 3.65 [74] | 5.6 [87] | - | - | - | 74.0 [88] | 71.4 [74] | 71.7 [89] |
| BaZrO | 3.46 [82] | 3.42 [74] | 5.05 [90] | - | - | - | 77.1 [88] | 74.5 [74] | 73.6 [91] |
| Struc. | XC | NiMnGa | NiMnGa | NiMnGa | NiMnSn | NiMnSn |
|---|---|---|---|---|---|---|
| A | SCAN | −1.583 | −1.100 | −1.158 | −0.832 | −0.686 |
| A | PBE | −0.645 | −0.500 | −0.142 | −0.149 | 0.113 |
| M | SCAN | −1.636 | −1.394 | — | — | −0.708 |
| M | PBE | −0.632 | −0.491 | −0.234 | — | −0.710 |
| FeNiGa | FeNiGa | FeVAl | ||||
| A | SCAN | −1.136 | −0.600 | −1.699 | ||
| A | PBE | −0.426 | 0.124 | −1.691 | ||
| M | SCAN | — | −0.742 | — | ||
| M | PBE | — | 0.001 | — |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sokolovskiy, V.; Baigutlin, D.; Miroshkina, O.; Buchelnikov, V. Meta-GGA SCAN Functional in the Prediction of Ground State Properties of Magnetic Materials: Review of the Current State. Metals 2023, 13, 728. https://doi.org/10.3390/met13040728
Sokolovskiy V, Baigutlin D, Miroshkina O, Buchelnikov V. Meta-GGA SCAN Functional in the Prediction of Ground State Properties of Magnetic Materials: Review of the Current State. Metals. 2023; 13(4):728. https://doi.org/10.3390/met13040728
Chicago/Turabian StyleSokolovskiy, Vladimir, Danil Baigutlin, Olga Miroshkina, and Vasiliy Buchelnikov. 2023. "Meta-GGA SCAN Functional in the Prediction of Ground State Properties of Magnetic Materials: Review of the Current State" Metals 13, no. 4: 728. https://doi.org/10.3390/met13040728
APA StyleSokolovskiy, V., Baigutlin, D., Miroshkina, O., & Buchelnikov, V. (2023). Meta-GGA SCAN Functional in the Prediction of Ground State Properties of Magnetic Materials: Review of the Current State. Metals, 13(4), 728. https://doi.org/10.3390/met13040728








