Analysis of Recrystallization Kinetics Concerning the Experimental, Computational, and Empirical Evaluation of Critical Temperatures for Static Recrystallization in Nb, Ti, and V Microalloyed Steels
Abstract
:1. Introduction
1.1. Non-Recrystallization Temperature
1.1.1. The Role of Process Parameters for TNR
1.1.2. The Impact of Microalloying Elements on TNR
1.1.3. Empirical Equations for TNR
1.2. Static Recrystallization Critical Temperature
1.3. Comparison of TNR and TSRCT
2. Materials and Methods
2.1. Experiments
2.1.1. Double-Hit Compression Tests (DHT)
2.1.2. Hot Torsion Tests (TT)
3. Modeling
3.1. Substructure and Recrystallization Model
3.1.1. Dislocation Density Evolution
3.1.2. Grain Boundary Pinning and Solute Drag
3.1.3. Nucleation of Recrystallized Grains
3.2. Simulation Setup
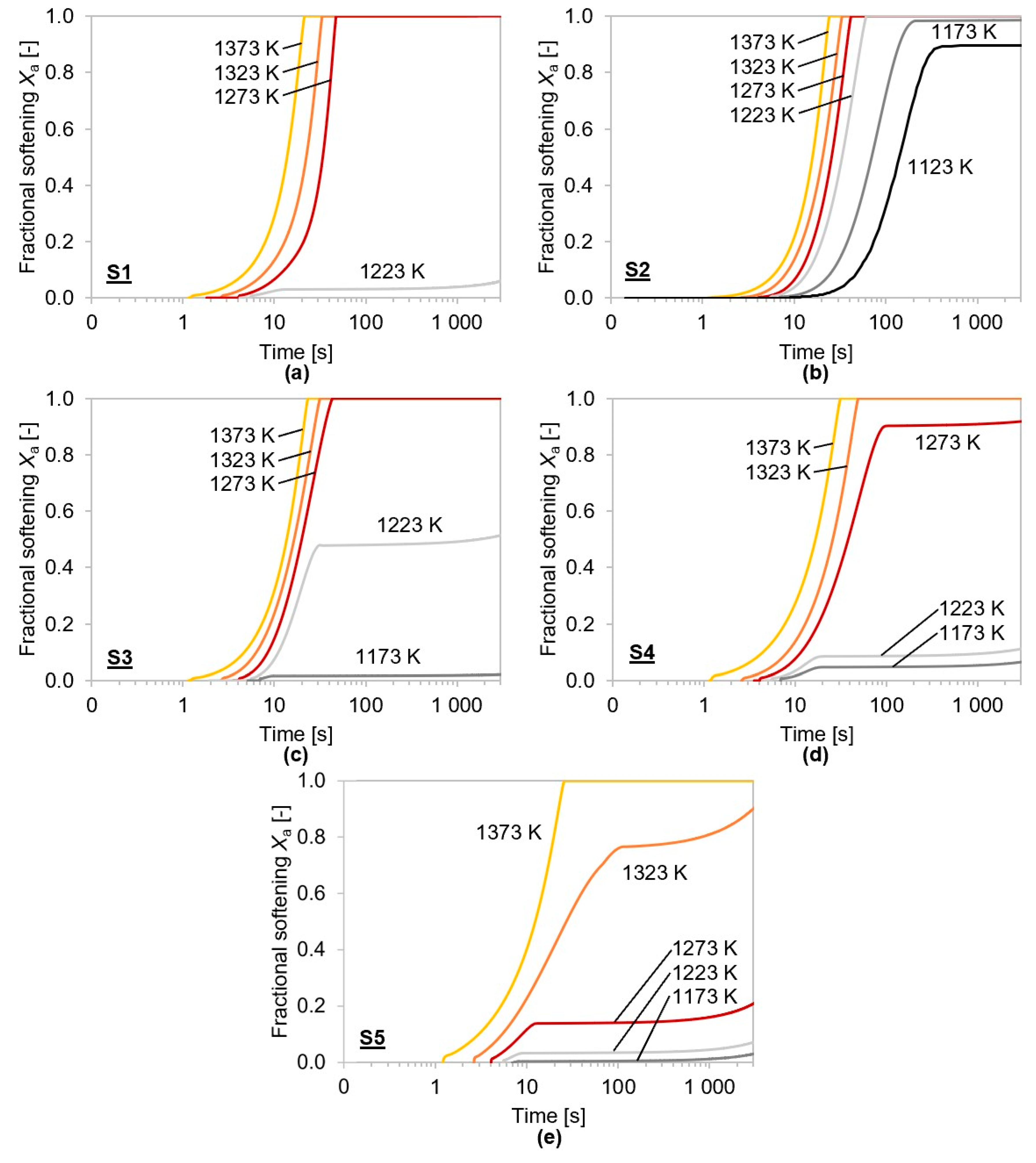
4. Results and Discussion
4.1. Experiments
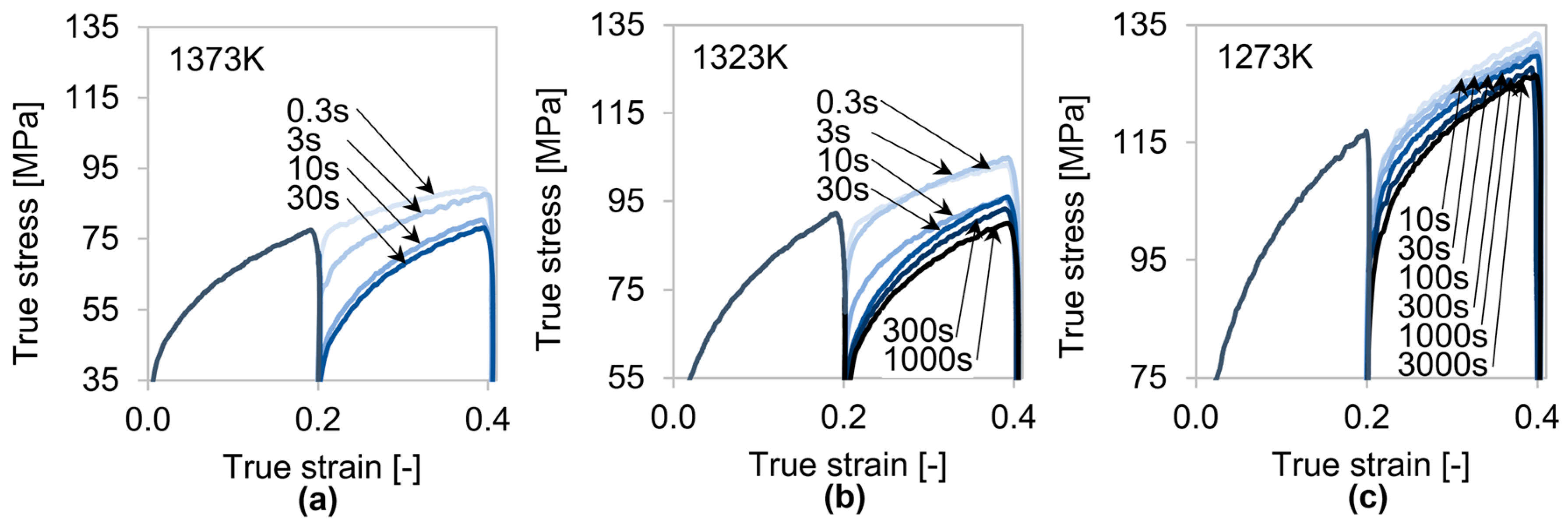
4.1.1. Double-Hit Compression Tests
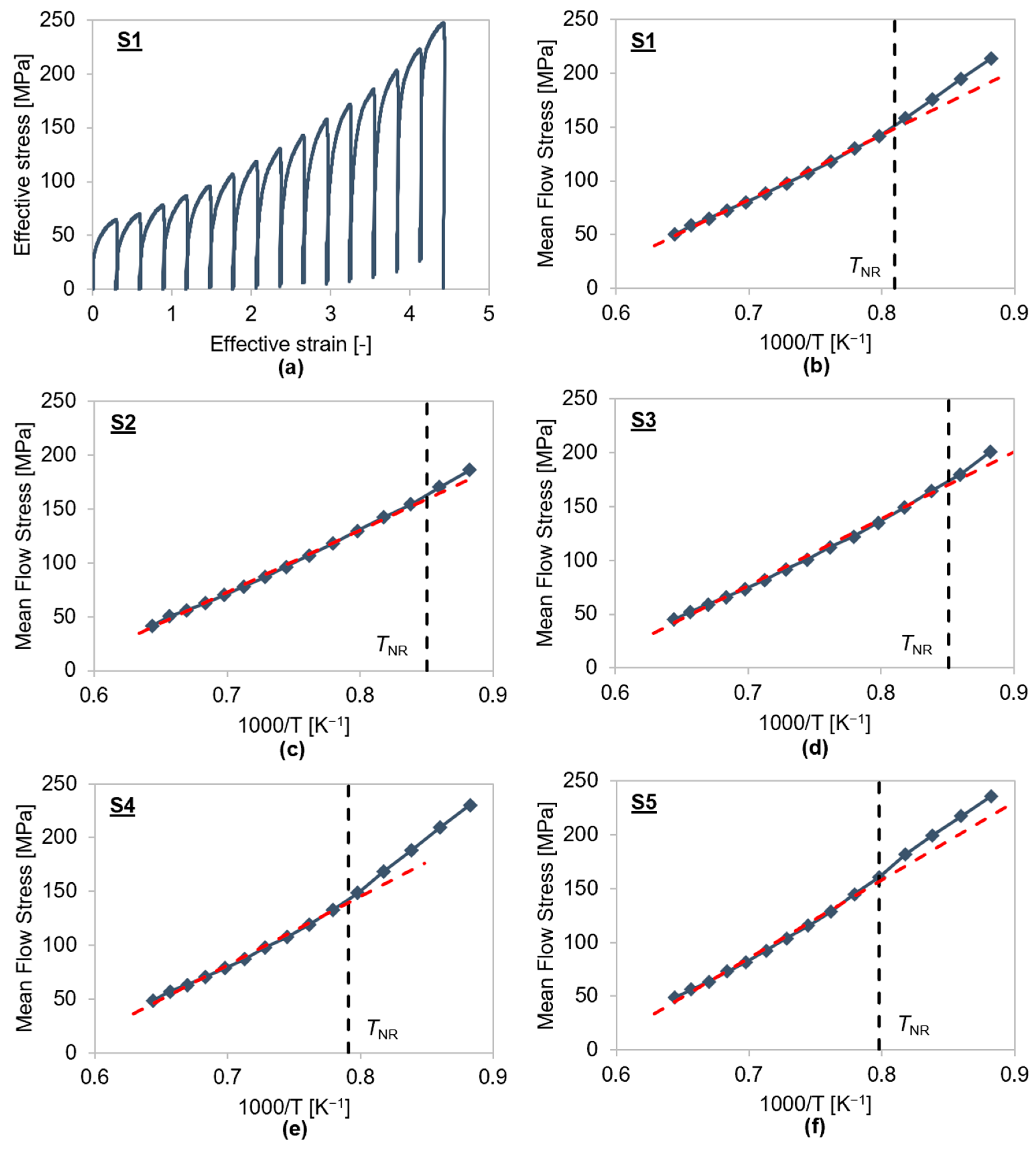
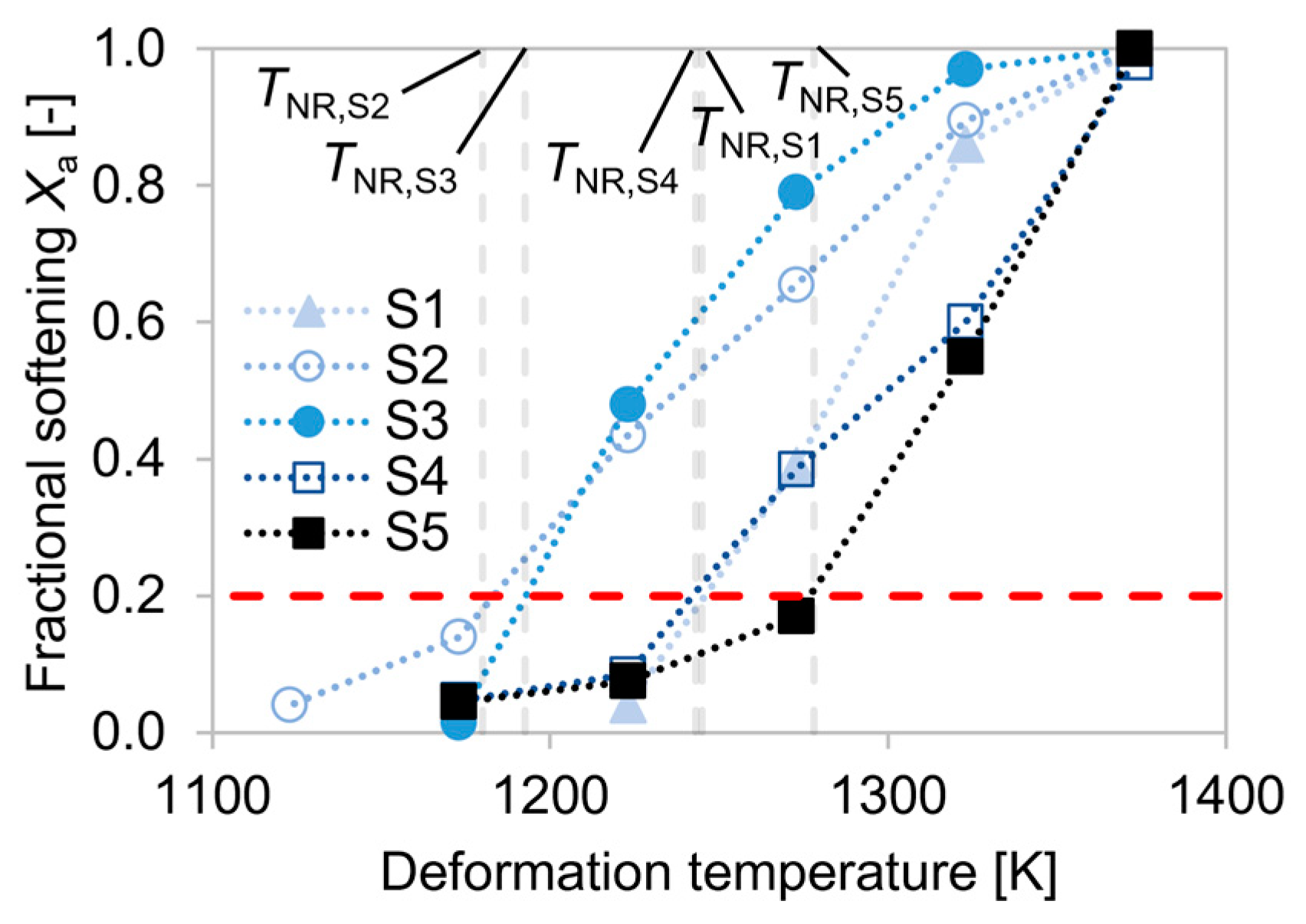
4.1.2. Hot Torsion Tests
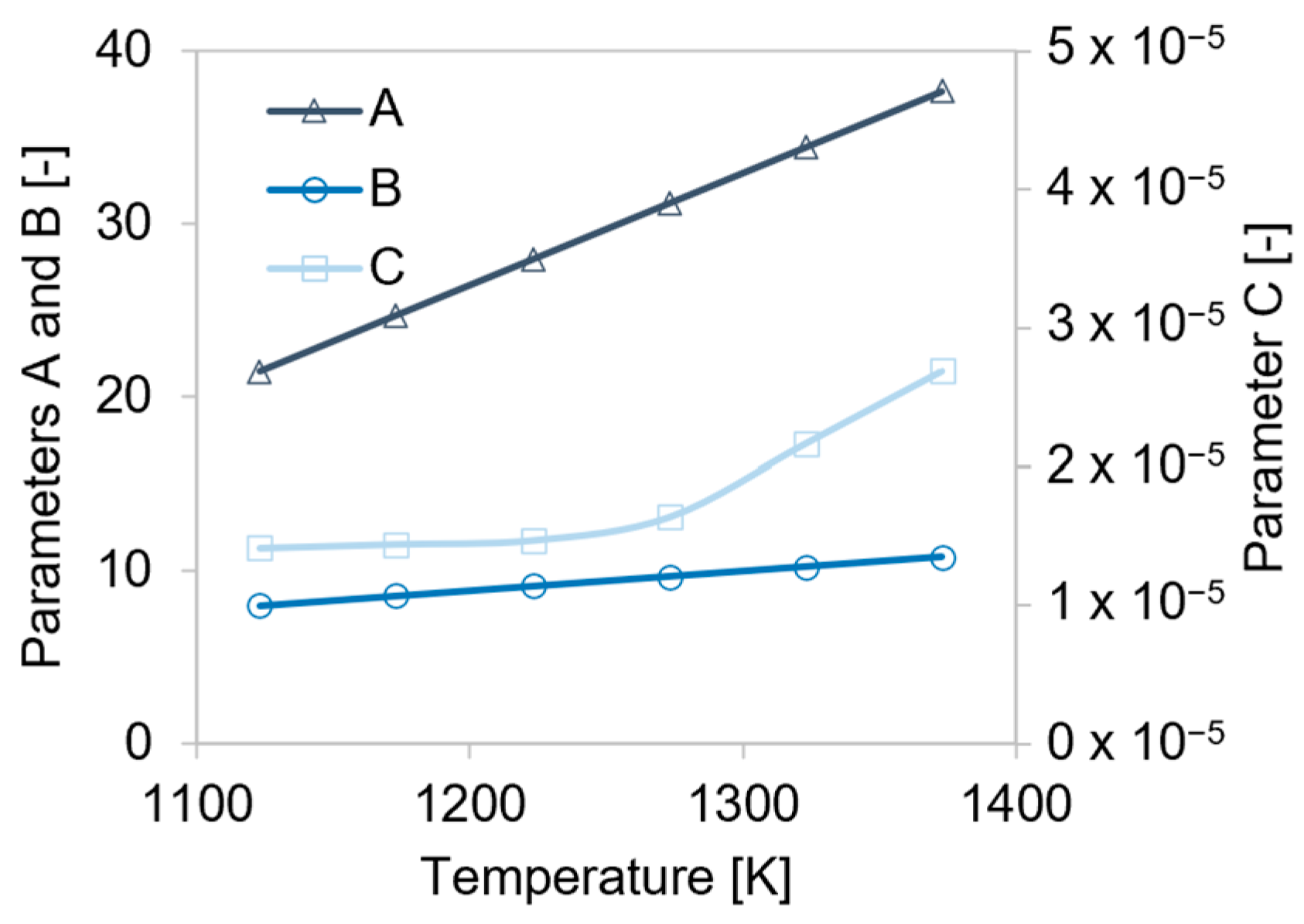
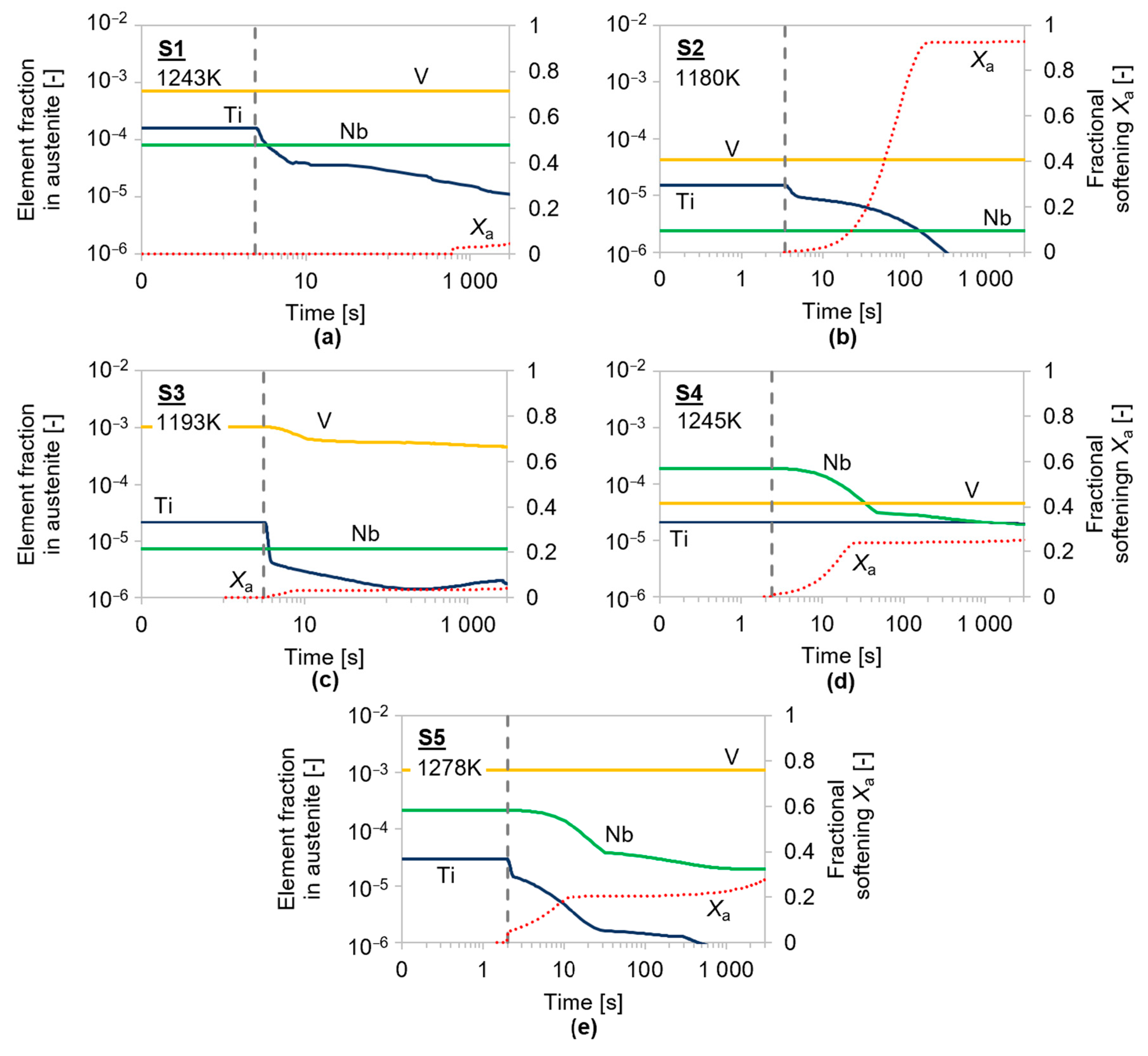
4.2. Simulation
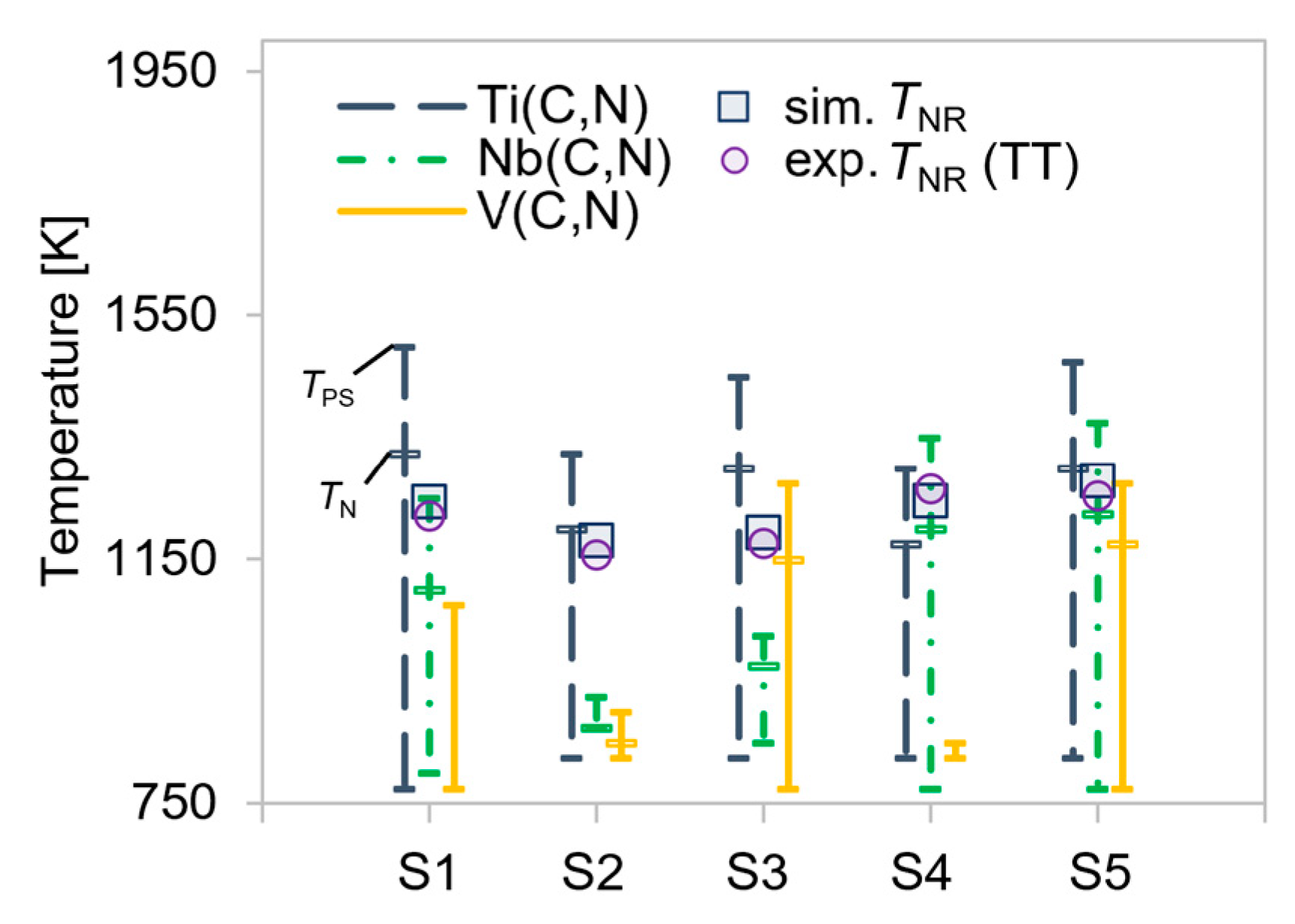
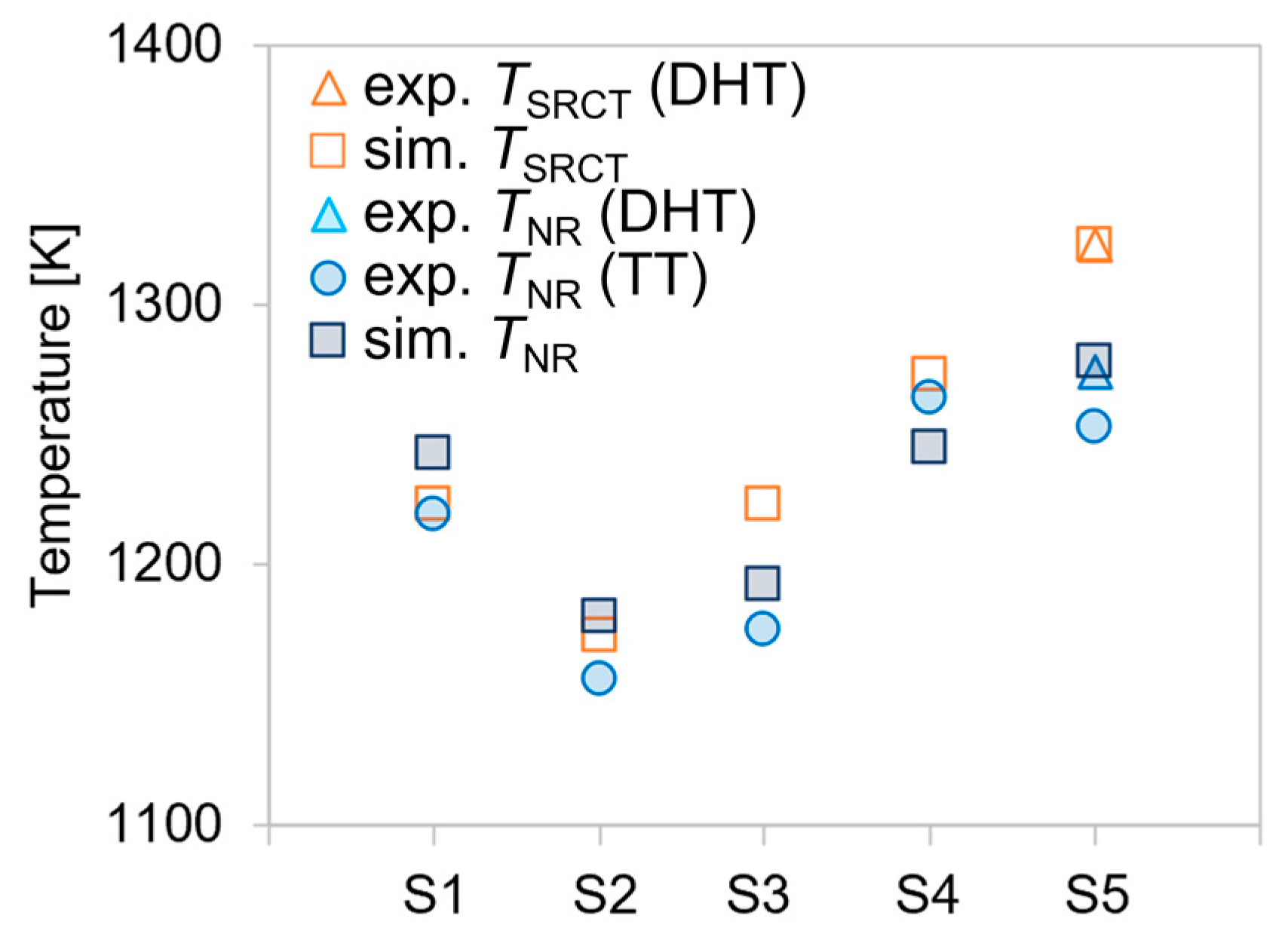
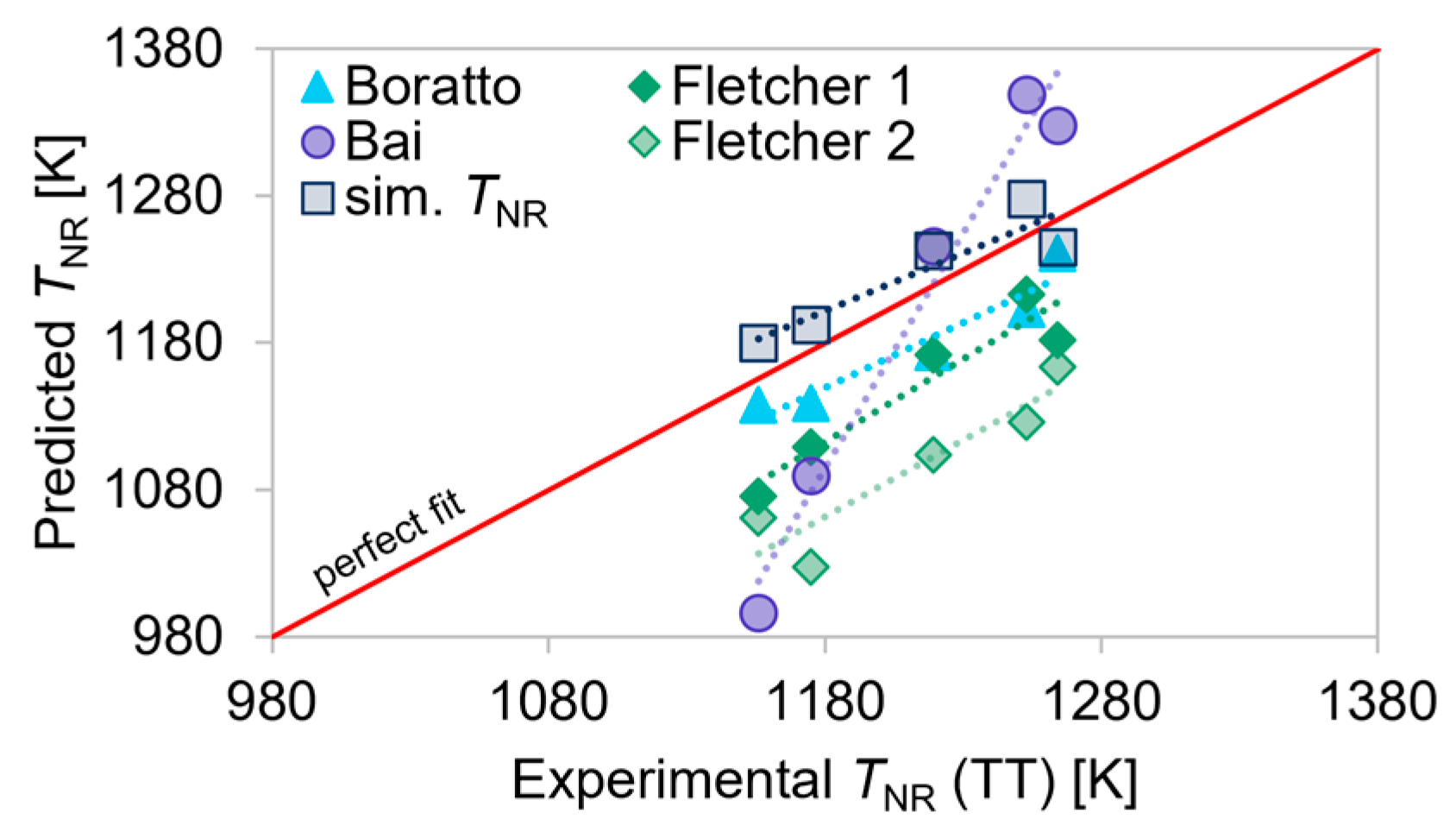
4.3. Comparison of Experimental and Predicted TNR and TSRCT
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Z.G.; Gao, X.H.; Xiong, M.; Li, P.; Misra, R.; Rao, D.Y.; Wang, Y.C. Role of hot rolling procedure and solution treatment process on microstructure, strength and cryogenic toughness of high manganese austenitic steel. Mater. Sci. Eng. A 2021, 807, 140881. [Google Scholar] [CrossRef]
- Sauer, M.; Fabík, R.; Schindler, I.; Kawulok, P.; Opěla, P.; Kawulok, R.; Vodárek, V.; Rusz, S. Analysis of the microstructure development of Nb-microalloyed steel during rolling on a heavy-section mill. Materials 2022, 16, 288. [Google Scholar] [CrossRef]
- Varanasi, R.S.; Gault, B.; Ponge, D. Effect of Nb micro-alloying on austenite nucleation and growth in a medium manganese steel during intercritical annealing. Acta Mater. 2022, 229, 117786. [Google Scholar] [CrossRef]
- Stornelli, G.; Tselikova, A.; Mirabile Gattia, D.; Mortello, M.; Schmidt, R.; Sgambetterra, M.; Testani, C.; Zucca, G.; Di Schino, A. Influence of vanadium micro-alloying on the microstructure of structural high strength steels welded joints. Materials 2023, 16, 2897. [Google Scholar] [CrossRef]
- Yuan, J.; Xiao, Y.; Min, N.; Li, W.; Zhao, S. The influence of precipitate morphology on the growth of austenite grain in Nb-Ti-Al microalloyed steels. Materials 2022, 15, 3176. [Google Scholar] [CrossRef]
- Zhao, Y.; Zheng, J.; Chen, L.; Liu, X. Static recrystallization behavior of low-carbon Nb-V-microalloyed forging steel. Metals 2022, 12, 1745. [Google Scholar] [CrossRef]
- Zhang, Q.; Huo, X.; Li, L.; Chen, S.; Lu, C. Correlation between precipitation and recrystallisation during stress relaxation in titanium microalloyed steel. Metals 2022, 12, 1920. [Google Scholar] [CrossRef]
- Kaikkonen, P.M.; Somani, M.C.; Karjalainen, L.P.; Kömi, J.I. Flow stress behaviour and static recrystallization characteristics of hot deformed austenite in microalloyed medium-carbon bainitic steels. Metals 2021, 11, 138. [Google Scholar] [CrossRef]
- Felker, C.A.; Speer, J.G.; de Moor, E.; Findley, K.O. Hot strip mill processing simulations on a Ti-Mo microalloyed steel using hot torsion testing. Metals 2020, 10, 334. [Google Scholar] [CrossRef]
- Buken, H.; Kozeschnik, E. Modeling static recrystallization in Al-Mg alloys. Metall. Mater. Trans. A 2021, 52, 544–552. [Google Scholar] [CrossRef]
- Kozeschnik, E. Mean-field microstructure kinetics modeling. Encycl. Mater. Met. Alloy. 2022, 4, 521–526. [Google Scholar] [CrossRef]
- CDL-IPE, Inst. of Mat. Sci. and Technol., TU Wien. Thermodynamic Database with Modified Carbo-Nitride Descriptions Based on the Open-License Multi-Component MatCalc Database mc_fe, Version 2.060. Available online: https://www.matcalc.at/images/stories/Download/Database/mc_fe_v2.060.tdb (accessed on 4 April 2023).
- Varela-Castro, G.; Cabrera, J.-M.; Prado, J.-M. Critical Strain for Dynamic Recrystallisation. The Particular Case of Steels. Metals 2020, 10, 135. [Google Scholar] [CrossRef]
- Uranga, P.; Fernández, A.; López, B.; Rodriguez-Ibabe, J. Transition between static and metadynamic recrystallization kinetics in coarse Nb microalloyed austenite. Mater. Sci. Eng., A 2003, 345, 319–327. [Google Scholar] [CrossRef]
- Medina, S.F.; Gómez, M.; Rodríguez, E.; Rancel, L. Influence of accumulated stress in austenite on transformed ferrite grain size by hot rolling for a V-microalloyed steel. ISIJ Int. 2008, 48, 1263–1269. [Google Scholar] [CrossRef]
- Vervynckt, S.; Verbeken, K.; Lopez, B.; Jonas, J.J. Modern HSLA steels and role of non-recrystallisation temperature. Int. Mater. Rev. 2012, 57, 187–207. [Google Scholar] [CrossRef]
- Bai, D.Q.; Yue, S.; Sun, W.P.; Jonas, J.J. Effect of deformation parameters on the. Met. Trans. A 1993, 24, 2151–2159. [Google Scholar] [CrossRef]
- Medina, S.F. Determination of no-recrystallisation temperature in Nb-V-Ti microalloyed steel and discussion of its definition. Mater. Sci. Technol. 1998, 14, 217–221. [Google Scholar] [CrossRef]
- Gómez, M.; Medina, S.F.; Quispe, A.; Valles, P. Static recrystallization and induced precipitation in a low Nb microalloyed steel. ISIJ Int. 2002, 42, 423–431. [Google Scholar] [CrossRef]
- Abad, R.; AI, F.; Lopez, B.; JM, R.-I. Interaction between recrystallization and precipitation during multipass rolling in a low carbon niobium microalloyed steel. ISIJ Int. 2001, 41, 1373–1382. [Google Scholar] [CrossRef]
- Vervynckt, S.; Verbeken, K.; Thibaux, P.; Liebeherr, M.; Houbaert, Y. Austenite recrystallization–precipitation interaction in niobium microalloyed steels. ISIJ Int. 2009, 49, 911–920. [Google Scholar] [CrossRef]
- Gómez, M.; Medina, S.F. Role of microalloying elements in the microstructure of hot rolled steels. Int. J. Mater. Res. 2011, 102, 1197–1207. [Google Scholar] [CrossRef]
- Medina, S.F.; Mancilla, J.E.; Hernandez, C.A. Static recrystallization of hot deformed austenite and induced precipitation kinetics in vanadium microalloyed steels. ISIJ Int. 1994, 34, 689–696. [Google Scholar] [CrossRef]
- Bhargava, G. Grain boundary effects on mechanical properties: Design approaches in steel. In Welding—Modern Topics; Crisóstomo Absi Alfaro, S., Borek, W., Tomiczek, B., Eds.; IntechOpen: London, UK, 2021; pp. 221–234. ISBN 978-1-83881-895-1. [Google Scholar]
- Homsher, C.N. Determination of the Non-Recrystallization Temperature (Tnr) in Multiple Microalloyed Steels. Master’s Thesis, Colorado School of Mines, Golden, CO, USA, 2013. [Google Scholar]
- Akben, M.G.; Weiss, I.; Jonas, J.J. Dynamic precipitation and solute hardening in a V microalloyed steel and two Nb steels containing high levels of Mn. Acta Metall. 1981, 29, 111–121. [Google Scholar] [CrossRef]
- Homsher-Ritosa, C.N. Influence of Processing Parameters and Alloying Additions on the mechanically Determined No-Recrystallization Temperature in Niobium Microalloyed Steels. Ph.D. Thesis, Colorado School of Mines, Golden, CO, USA, 2016. [Google Scholar]
- Boratto, F.; Barbosa, R.; Yue, S.; Jonas, J.J. In Proceedings of the International Conference on Physical Metallurgy of Thermomechanical Processing of Steels and Other Metals, THERMEC-88, Tokyo, Japan, 6–10 June 1988. p. 383. Available online: https://www.worldcat.org/title/thermec-88-international-conference-on-physical-metallurgy-of-thermomechanical-processing-of-steels-and-other-metals-proceedings-june-6-10-1988-keidanren-kaikan-tokyo-japan/oclc/35486134 (accessed on 10 April 2023).
- Maccagno, T.M.; Jonas, J.J.; Yue, S.; McCrady, J.; Slobodian, R.; Deeks, D. Determination of recrystallization stop temperature from rolling mill logs and comparison with laboratory simulation results. ISIJ Int. 1994, 34, 917–922. [Google Scholar] [CrossRef]
- Bai, D.Q.; Bodnar, R.L.; Ward, J.; Dorricott, J.; Sanders, S. Development of discrete X80 line pipe plate at SSAB Americas. Int. Symp. Recent Dev. Plate Steels 2011, 1, 13–22. [Google Scholar]
- Fletcher, F. Meta-analysis of Tnr measurements: Determining new empirical models based on composition and strain. In Proceedings of the Austenite Processing Symposium (Internal Company Presentation), Padua, Italy, 12 September 2008; pp. 1–14. [Google Scholar]
- Medina, S.F.; Mancilla, J.E. Static recrystallization of austenite and strain induced precipitation kinetics in titanium microalloyed steels. Acta Metall. Mater. 1994, 42, 3945–3951. [Google Scholar] [CrossRef]
- Medina, S.F.; Quispe, A. Influence of strain on induced precipitation kinetics in microalloyed steels. ISIJ Int. 1996, 36, 1295–1300. [Google Scholar] [CrossRef]
- Medina, S.F.; Mancilla, J.E. Determination of static recrystallization critical temperature of austenite in microalloyed steels. ISIJ Int. 1993, 33, 1257–1264. [Google Scholar] [CrossRef]
- Medina, S.F.; Quispe, A.; Valles, P.; JL, B. Recrystallization-precipitation interaction study of two medium carbon niobium microalloyed steels. ISIJ Int. 1999, 39, 913–922. [Google Scholar] [CrossRef]
- Sobotka, E.; Kreyca, J.; Poletti, M.C.; Povoden-Karadeniz, E. Analysis and Modeling of Stress-strain Curves in Microalloyed Steels Based on a Dislocation Density Evolution Model. Materials 2022, 15, 6824. [Google Scholar] [CrossRef]
- Facusseh, C.; Salinas, A.; Flores, A.; Altamirano, G. Study of static recrystallization kinetics and the evolution of austenite grain size by dynamic recrystallization refinement of an eutectoid steel. Metals 2019, 9, 1289. [Google Scholar] [CrossRef]
- Perttula, J.S.; Karjalainen, L.P. Recrystallisation rates in austenite measured by double compression and stress relaxation methods. Mater. Sci. Technol. 1998, 14, 626–630. [Google Scholar] [CrossRef]
- Palmiere, E.J.; Garcia, C.I.; DeArdo, A.J. The influence of niobium supersaturation in austenite on the static recrystallization behavior of low carbon microalloyed steels. Metall. Mater. Trans. A 1996, 27, 951–960. [Google Scholar] [CrossRef]
- Khoddam, S.; Hodgson, P.D. Conversion of the hot torsion test results into flow curve with multiple regimes of hardening. J. Mater. Process. Technol. 2004, 153–154, 839–845. [Google Scholar] [CrossRef]
- Ballard, T.J.; Speer, J.G.; Findley, K.O.; de Moor, E. Double twist torsion testing to determine the non recrystallization temperature. Sci. Rep. 2021, 11, 1–19. [Google Scholar] [CrossRef]
- Rešković, S.; Slokar Benić, L.; Lovrenić-Jugović, M. The interdependence of the degree of precipitation and dislocation density during the thermomechanical treatment of microalloyed niobium steel. Metals 2020, 10, 294. [Google Scholar] [CrossRef]
- Kocks, U.F.; Mecking, H. Physics and phenomenology of strain hardening: The FCC case. Prog. Mater. Sci. 2003, 48, 171–273. [Google Scholar] [CrossRef]
- Stechauner, G.; Kozeschnik, E. Assessment of substitutional self-diffusion along short-circuit paths in Al, Fe and Ni. Calphad 2014, 47, 92–99. [Google Scholar] [CrossRef]
- Sherstnev, P.; Lang, P.; Kozeschnik, E. Treatment of simultaneous deformation and solid-state precipitation in thermo-kinetic calculations: (ECCOMAS 2012). In Proceedings of the 6th European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS 2012), Vienna, Austria, 10–14 September 2012; pp. 5331–5338. [Google Scholar]
- Manohar, P.A.; Ferry, M.; Chandra, T. Five Decades of the Zener Equation. ISIJ Int. 1998, 38, 913–924. [Google Scholar] [CrossRef]
- Cahn, J.W. The impurity-drag effect in grain boundary motion. Acta Metall. 1962, 10, 789–798. [Google Scholar] [CrossRef]
- Buken, H.; Zamberger, S.; Kozeschnik, E. A model for the influence of micro-alloying elements on static recrystallization of austenite. In Proceedings of the 6th International Conference on Recrystallization and Grain Growth (ReX&GG 2016); Wiley-VCH: Weinheim, Germany, 2016; pp. 113–118. [Google Scholar]
- Bailey, J.E.; Hirsch, P.B. The recrystallization process in some polycrystalline metals. Proc. R. Soc. A 1962, 267, 11–30. [Google Scholar] [CrossRef]
- Rehman, M.K.; Zurob, H.S. A novel approach to model static recrystallization of austenite during hot rolling of Nb microalloyed steel. Part I: Precipitate-free case. Metall. Mater. Trans. A 2013, 44, 1862–1871. [Google Scholar] [CrossRef]
- Zurob, H.S.; Hutchinson, C.R.; Bréchet, Y.; Purdy, G.R. Modeling recrystallization of microalloyed austenite: Effect of coupling recovery, precipitation and recrystallization. Acta Mater. 2002, 50, 3077–3094. [Google Scholar] [CrossRef]
- Xing, J.; Zhu, G.; Wu, B.; Ding, H.; Pan, H. Effect of Ti Addition on the Precipitation Mechanism and Precipitate Size in Nb-Microalloyed Steels. Metals 2022, 12, 245. [Google Scholar] [CrossRef]
- Tang, S.; Li, X.; Li, J.; Liu, Z.; Wang, G. Role of microalloying elements on recrystallization kinetics of cold-rolled high strength low alloy steels. Metals 2022, 12, 1741. [Google Scholar] [CrossRef]
- Leguen, C. Prior Austenite Grain Size Controlled by Precipitates. Ph.D. Thesis, Université de Lyon, Lyon, France.
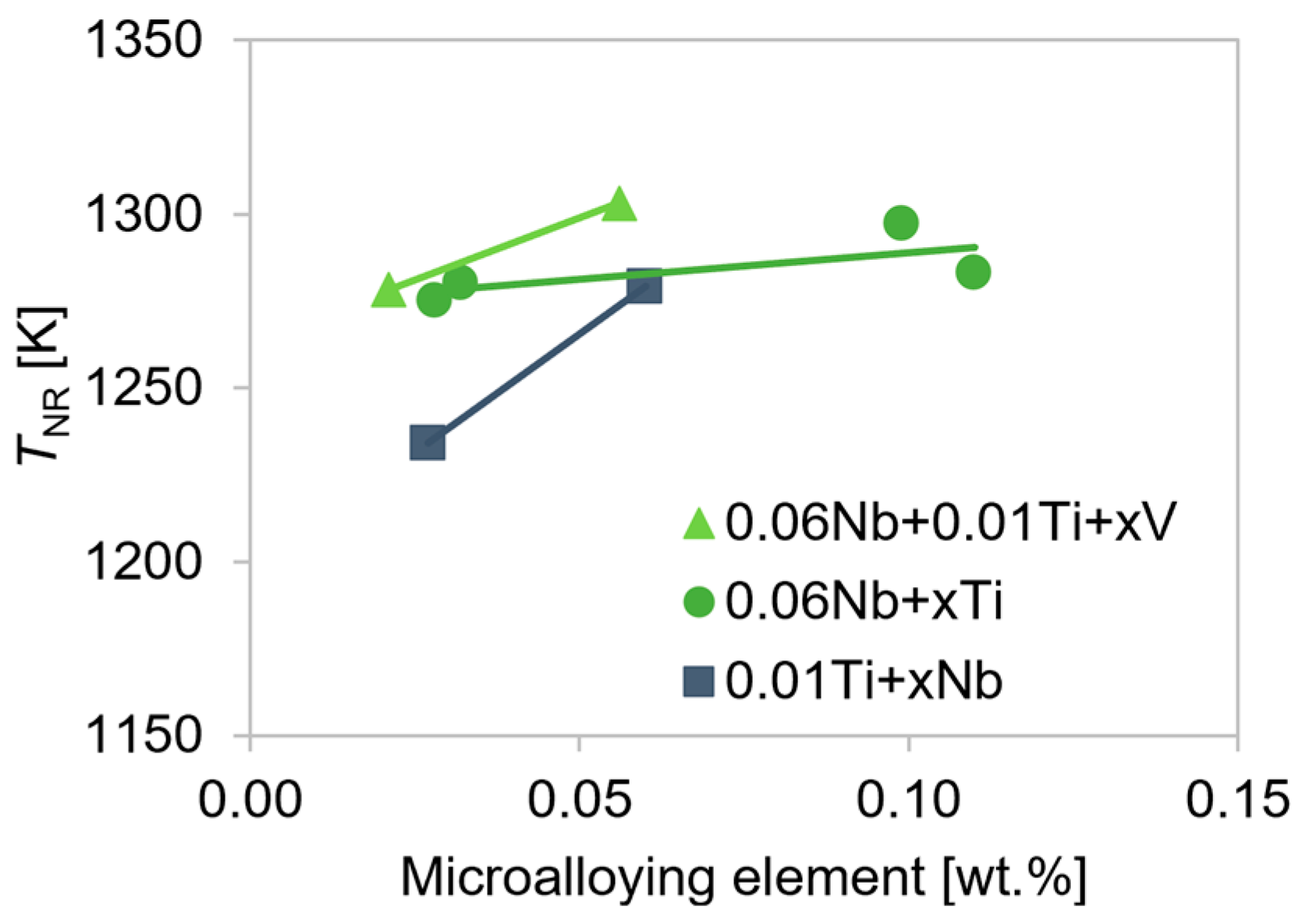

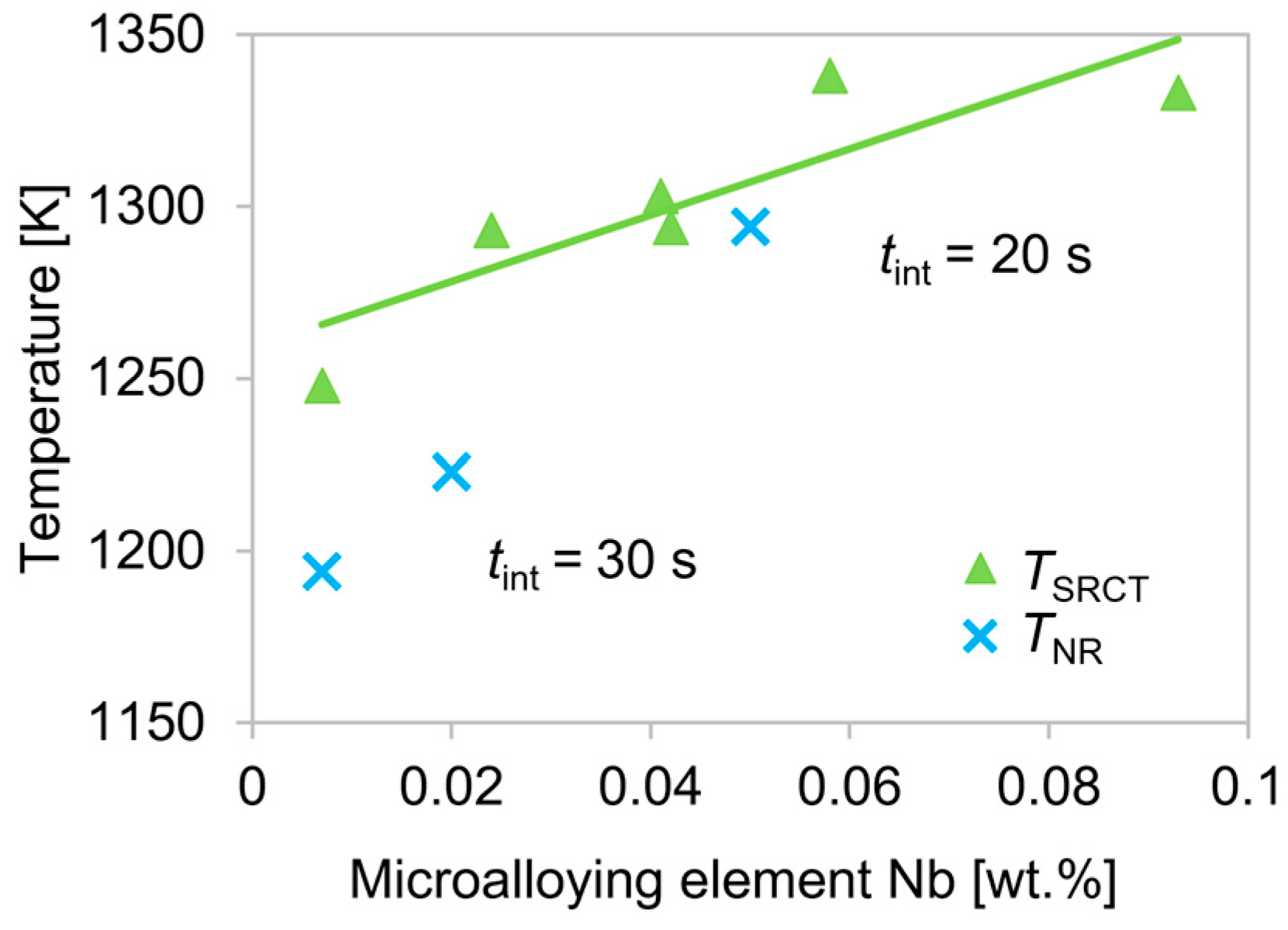
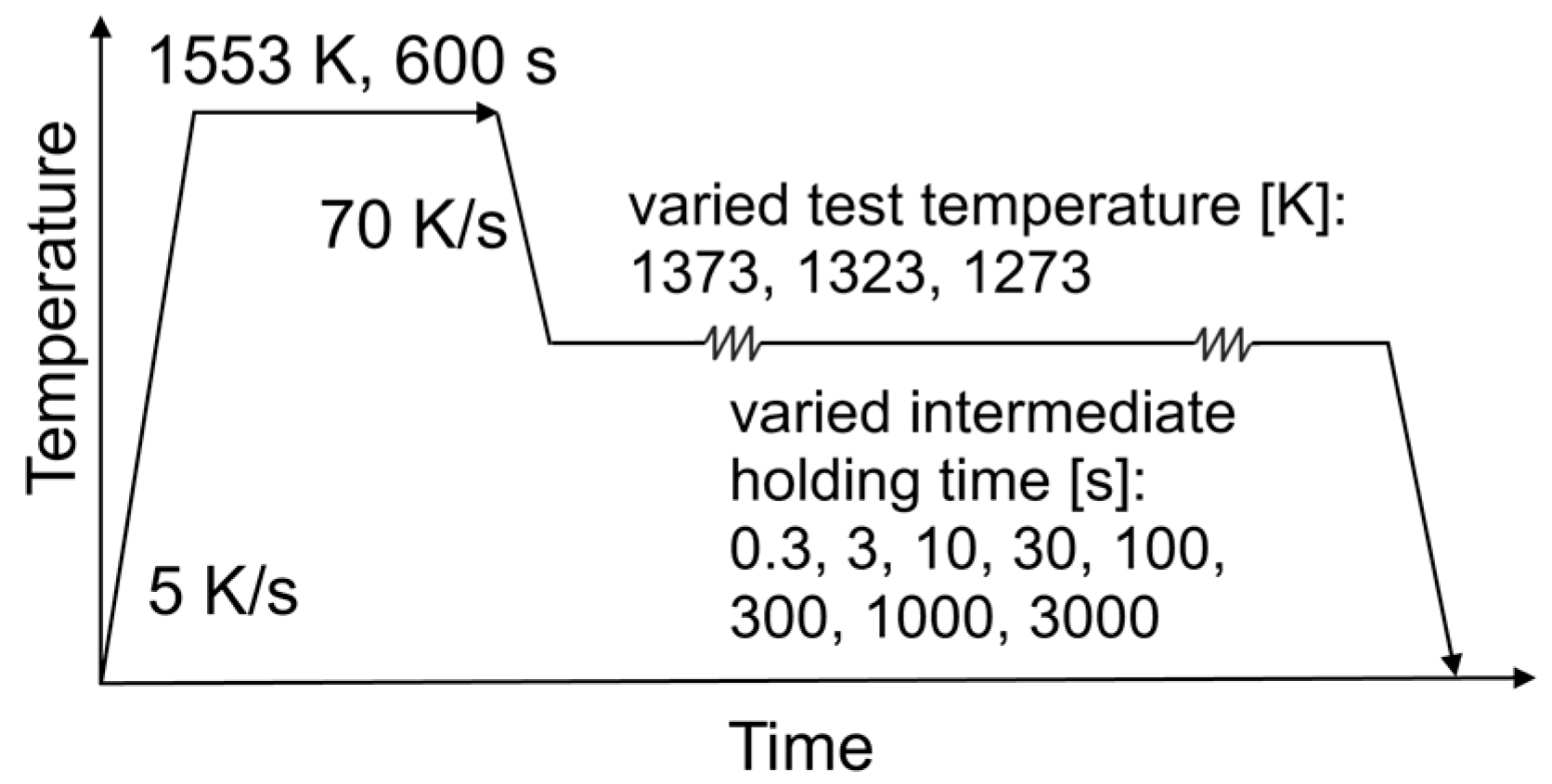
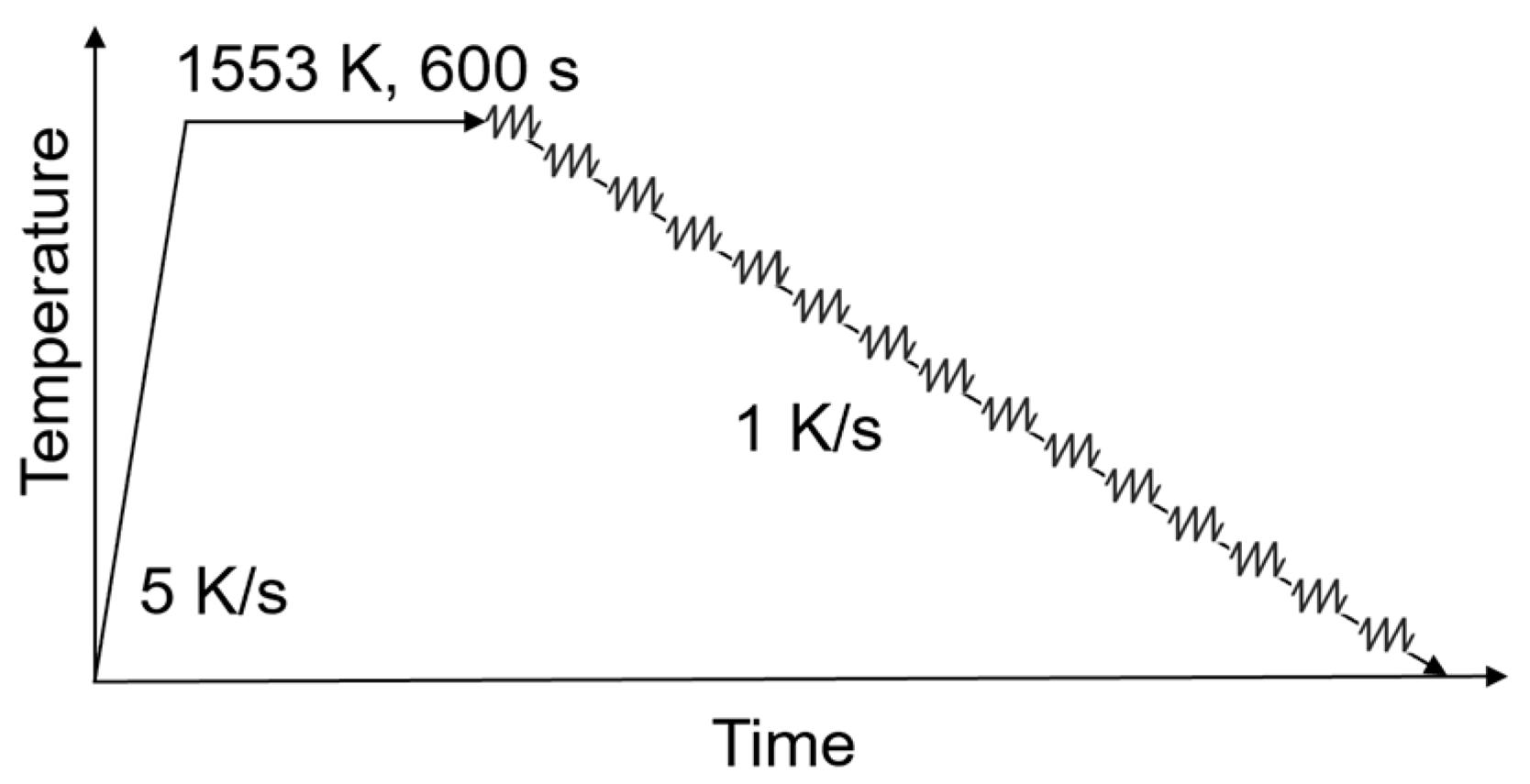


| Steel Grade | C | Mn | Ti | Nb | V | Cr | Al | Si |
|---|---|---|---|---|---|---|---|---|
| S1 | 0.15 | 1.27 | 0.01 | 0.01 | 0.07 | 0.20 | 0.03 | 0.22 |
| S2 | 0.18 | 0.88 | <0.01 | <0.01 | <0.01 | 0.02 | 0.03 | 0.26 |
| S3 | 0.20 | 1.40 | <0.01 | <0.01 | 0.10 | 0.02 | 0.02 | 0.30 |
| S4 | 0.18 | 0.93 | <0.01 | 0.03 | <0.01 | 0.03 | 0.03 | 0.26 |
| S5 | 0.21 | 1.45 | <0.01 | 0.04 | 0.10 | 0.03 | 0.03 | 0.50 |
| Symbol | Name | Value | Unit | Source |
|---|---|---|---|---|
| α | Strengthening coefficient | 0.12 | - | [36] |
| ν | Poisson’s ratio | 0.30 | - | MatCalc default value |
| G | Shear modulus | MPa | MatCalc default value | |
| b | Burgers vector | 2.50 × 10−10 | m | MatCalc default value |
| M | Taylor factor | 3.06 | - | MatCalc default value |
| k | Boltzmann constant | 1.381 × 10−23 | JK−1 | MatCalc default value |
| Deff | Effective diffusion coefficient | m2s−1 | MatCalc default value | |
| DGB | Grain boundary diffusion coeff. | m2s−1 | MatCalc default value | |
| DCB | Cross-boundary diffusion coeff. | 2∙DB | m2s−1 | [50] |
| ρeq,int | Internal equilibrium dislocation density | 1011 | m−2 | MatCalc default value |
| γHAGB | HAGB-energy | 0.5 | Jm−3 | [51] |
| γLAGB | LAGB-energy | 0.3 | Jm−3 | MatCalc default value |
| ω | Grain boundary width | 1 × 10−9 | m | [50] |
| ηHAGB,int | Free HAGB-prefactor | 0.015 | - | [48] |
| ηLAGB,int | Free LAGB-prefactor | 10 | - | MatCalc default value |
| ηHAGB,pin | Pinned HAGB-prefactor | 0.001 | - | This work |
| ηLAGB,pin | Pinned LAGB-prefactor | 0.001 | - | This work |
| kd | Pre-factor for coarsening | 2 | - | This work |
| EB,Ti | Binding energy of Ti | 10,000 | Jmol−1 | [48] |
| EB,Nb | Binding energy of Nb | 11,000 | Jmol−1 | This work |
| EB,V | Binding energy of V | 3000 | Jmol−1 | This work |
| Tcrit,MX | Highest possible solution temperature of (Nb/Ti/V)(C,N) * | 3073/4073/2543 | K | This work |
| λ | Mixing coefficient | (1 − Xav)2 | - | MatCalc default value |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sobotka, E.; Kreyca, J.; Kahlenberg, R.; Jacob, A.; Kozeschnik, E.; Povoden-Karadeniz, E. Analysis of Recrystallization Kinetics Concerning the Experimental, Computational, and Empirical Evaluation of Critical Temperatures for Static Recrystallization in Nb, Ti, and V Microalloyed Steels. Metals 2023, 13, 884. https://doi.org/10.3390/met13050884
Sobotka E, Kreyca J, Kahlenberg R, Jacob A, Kozeschnik E, Povoden-Karadeniz E. Analysis of Recrystallization Kinetics Concerning the Experimental, Computational, and Empirical Evaluation of Critical Temperatures for Static Recrystallization in Nb, Ti, and V Microalloyed Steels. Metals. 2023; 13(5):884. https://doi.org/10.3390/met13050884
Chicago/Turabian StyleSobotka, Evelyn, Johannes Kreyca, Robert Kahlenberg, Aurélie Jacob, Ernst Kozeschnik, and Erwin Povoden-Karadeniz. 2023. "Analysis of Recrystallization Kinetics Concerning the Experimental, Computational, and Empirical Evaluation of Critical Temperatures for Static Recrystallization in Nb, Ti, and V Microalloyed Steels" Metals 13, no. 5: 884. https://doi.org/10.3390/met13050884
APA StyleSobotka, E., Kreyca, J., Kahlenberg, R., Jacob, A., Kozeschnik, E., & Povoden-Karadeniz, E. (2023). Analysis of Recrystallization Kinetics Concerning the Experimental, Computational, and Empirical Evaluation of Critical Temperatures for Static Recrystallization in Nb, Ti, and V Microalloyed Steels. Metals, 13(5), 884. https://doi.org/10.3390/met13050884






