Advanced Statistical Crystal Plasticity Model: Description of Copper Grain Structure Refinement during Equal Channel Angular Pressing
Abstract
:1. Introduction
2. Two-Level Statistical Constitutive Model for Describing the Inelastic Deformation of the FCC Polycrystal
3. Description of the Aspects (Conditions), Original and Modified Relations of the ETMB Model
3.1. Relations of the Original ETMB Model
3.2. Modifications of Some Relations of the ETMB Model Focused on Providing a More Accurate Description of Fragmentation
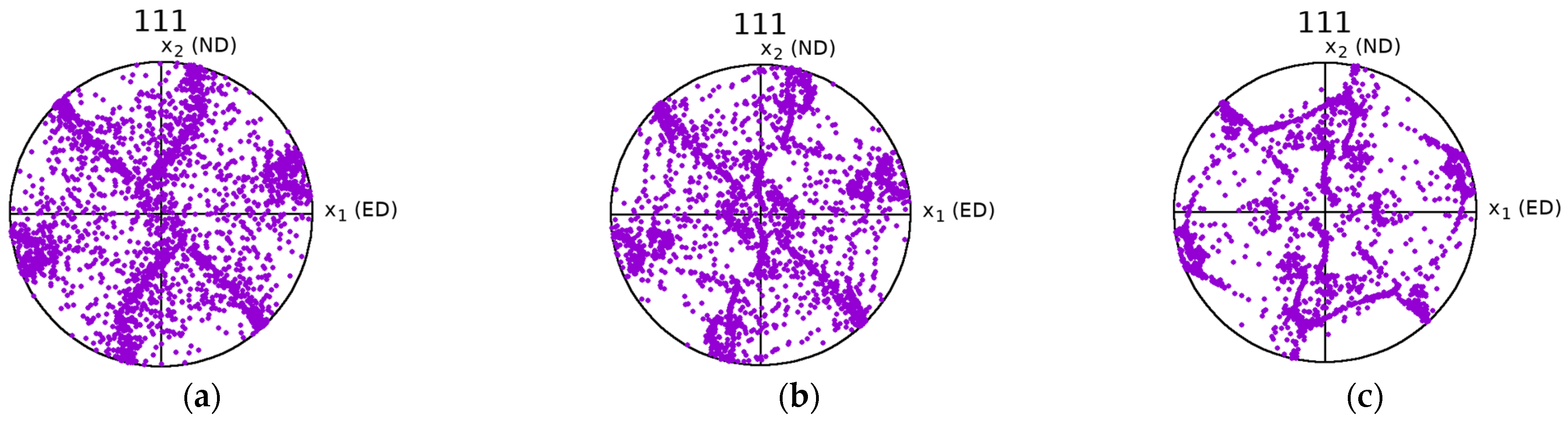
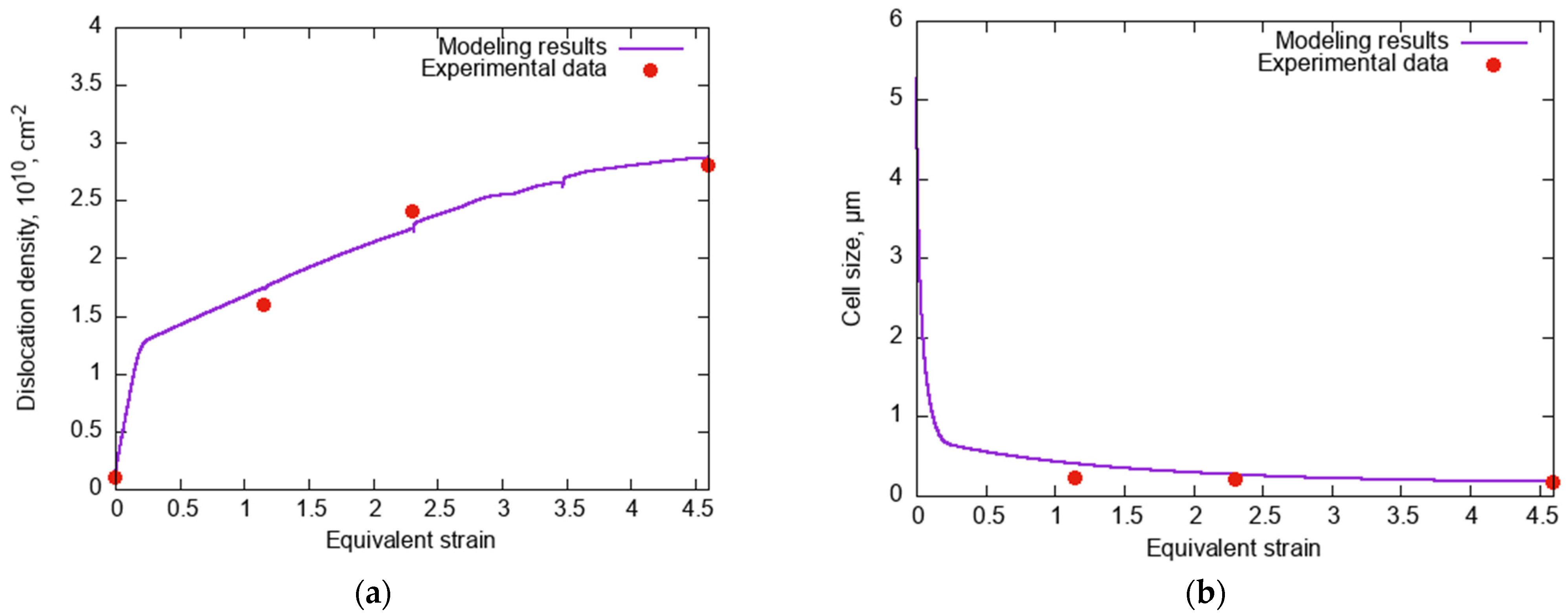
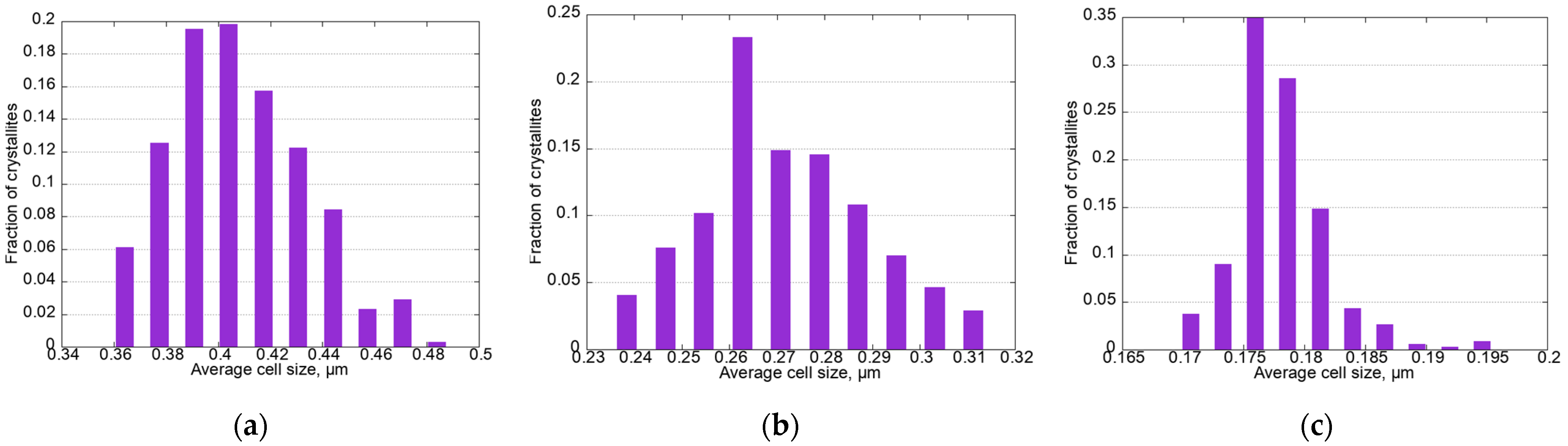
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- McDowell, D.L. A Perspective on Trends in Multiscale Plasticity. Int. J. Plast. 2010, 9, 1280–1309. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.D.; Bieler, T.R.; Raabe, D. Overview of Constitutive Laws, Kinematics, Homogenization and Multiscale Methods in Crystal Plasticity Finite-Element Modeling: Theory, Experiments, Applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Diehl, M. Review and Outlook: Mechanical, Thermodynamic, and Kinetic Continuum Modeling of Metallic Materials at the Grain Scale. MRS Commun. 2017, 7, 735–746. [Google Scholar] [CrossRef]
- Beyerlein, I.J.; Knezevic, M. Review of Microstructure and Micromechanism-Based Constitutive Modeling of Polycrystals with a Low-Symmetry Crystal Structure. J. Mater. Res. 2018, 33, 3711–3738. [Google Scholar] [CrossRef]
- Knezevic, M.; Beyerlein, I.J. Multiscale Modeling of Microstructure-Property Relationships of Polycrystalline Metals during Thermo-Mechanical Deformation. Adv. Eng. Mater. 2018, 20, 1700956. [Google Scholar] [CrossRef]
- Trusov, P.V.; Shveykin, A.I. Multilevel Models of Mono- and Polycrystalline Materials: Theory, Algorithms and Applied Examples; SB RAS Publ.: Novosibirsk, Russia, 2019; p. 605. (In Russian) [Google Scholar]
- Trusov, P.V.; Shveykin, A.I.; Kondratyev, N.S.; Yants, A.Y. Multilevel Models in Physical Mesomechanics of Metals and Alloys: Results and Prospects. Phys. Mesomech. 2021, 24, 391–417. [Google Scholar] [CrossRef]
- Trusov, P.V. Classical and Multi-Level Constitutive Models for Describing the Behavior of Metals and Alloys: Problems and Prospects (as a Matter for Discussion). Mech. Solids 2021, 56, 55–64. [Google Scholar] [CrossRef]
- Zhao, M.; Ji, X.; Feng, Y.; Liang, S.Y. Phase Transformation Prediction Considering Crystallographic Orientation in Microgrinding Multiphase Material. J. Manuf. Sci. Eng. 2020, 142, 104501. [Google Scholar] [CrossRef]
- Zhao, M.; Mao, J.; Ji, X.; Feng, Y.; Liang, S.Y. Effect of Crystallographic Orientation on Residual Stress Induced in Micro-Grinding. Int. J. Adv. Manuf. Technol. 2021, 112, 1271–1284. [Google Scholar] [CrossRef]
- Trusov, P.V.; Shveykin, A.I. Multilevel Crystal Plasticity Models of Single- and Polycrystals. Statistical Models. Phys. Mesomech. 2013, 16, 23–33. [Google Scholar] [CrossRef]
- Trusov, P.V.; Shveykin, A.I. Multilevel Crystal Plasticity Models of Single- and Polycrystals. Direct Models. Phys. Mesomech. 2013, 16, 99–124. [Google Scholar] [CrossRef]
- Rybin, V.V.; Vergazov, A.N.; Likhachev, V.A. Viscous fracture of molybdenum as a consequence of structure fragmentation. Phys. Met. Metallogr. 1974, 37, 620–624. (In Russian) [Google Scholar]
- Rybin, V.V.; Perevezentsev, V.N.; Svirina, Y.V. A Physical Model for the Initial Stages of the Fragmentation of Polycrystals in the Process of Developed Plastic Deformation. Phys. Met. Metallogr. 2017, 118, 1171–1175. [Google Scholar] [CrossRef]
- Horstemeyer, M.F.; McDowell, D.L. Modeling Effects of Dislocation Substructure in Polycrystal Elastoviscoplasticity. Mech. Mater. 1998, 27, 145–163. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Alexandrov, I.V. Nanostructured Materials Obtained by Severe Plastic Deformation; Logos: Moscow, Russia, 2000; p. 272. (In Russian) [Google Scholar]
- Noskova, N.I.; Mulyukov, R.R. Submicrocrystalline and Nanocrystalline Metals and Alloys; UB RAS: Yekaterinburg, Russia, 2003; p. 279. (In Russian) [Google Scholar]
- Kaibyshev, O.A.; Utyashev, F.Z. Superplasticity, Grain Refinement and Machining of Hard-to-Deform Alloys; Nauka: Moscow, Russia, 2002; p. 438. (In Russian) [Google Scholar]
- Mulyukov, R.R.; Imayev, R.M.; Nazarov, A.A.; Imayev, V.M.; Imayev, M.F.; Valitov, V.A.; Galeev, R.M.; Dmitriev, S.V.; Korznikov, A.V.; Kruglov, A.A.; et al. Superplasticity of Ultrafine-Grained Alloys: Experiment, Theory, and Technologies; Nauka: Moscow, Russia, 2014; p. 284. (In Russian) [Google Scholar]
- Sharifullina, E.R.; Shveykin, A.I.; Trusov, P.V. Review of experimental studies on structural superplasticity: Internal structure evolution of material and deformation mechanisms. PNRPU Mech. Bull. 2018, 3, 103–127. (In Russian) [Google Scholar] [CrossRef]
- Trusov, P.V.; Sharifullina, E.R.; Shveykin, A.I. Multilevel Model for the Description of Plastic and Superplastic Deformation of Polycrystalline Materials. Phys. Mesomech. 2019, 22, 402–419. [Google Scholar] [CrossRef]
- Trusov, P.V.; Ostanina, T.V.; Shveykin, A.I. Evolution of the grain structure of metals and alloys under severe plastic deformation: Continuum models. PNRPU Mech. Bull. 2022, 1, 123–155. [Google Scholar] [CrossRef]
- Trusov, P.V.; Ostanina, T.V.; Shveykin, A.I. Evolution of the grain structure of metals and alloys under intense plastic deformation: Multilevel models. PNRPU Mech. Bull. 2022, 2, 114–146. [Google Scholar] [CrossRef]
- Petryk, H.; Stupkiewicz, S. A Quantitative Model of Grain Refinement and Strain Hardening during Severe Plastic Deformation. Mater. Sci. Eng. A 2007, 444, 214–219. [Google Scholar] [CrossRef]
- Glezer, A.M.; Metlov, L.S. Physics of Megaplastic (Severe) Deformation in Solids. Phys. Solid State 2010, 52, 1162–1169. [Google Scholar] [CrossRef]
- Metlov, L.S.; Glezer, A.M.; Varyukhin, V.N. Cyclic Character of the Evolution of the Defect Structure and the Properties of Metallic Materials during Megaplastic Deformation. Russ. Metall. 2015, 2015, 269–273. [Google Scholar] [CrossRef]
- Khomenko, A.V.; Troshchenko, D.S.; Metlov, L.S. Thermodynamics and Kinetics of Solids Fragmentation at Severe Plastic Deformation. Condens. Matter Phys. 2015, 18, 33004. [Google Scholar] [CrossRef]
- Estrin, Y.; Tóth, L.S.; Molinari, A.; Bréchet, Y. A Dislocation-Based Model for All Hardening Stages in Large Strain Deformation. Acta Mater. 1998, 46, 5509–5522. [Google Scholar] [CrossRef]
- Sedláček, R.; Blum, W.; Kratochvíl, J.; Forest, S. Subgrain Formation during Deformation: Physical Origin and Consequences. Met. Mater. Trans. A 2002, 33, 319–327. [Google Scholar] [CrossRef]
- Clayton, J.D.; McDowell, D.L.; Bammann, D.J. Modeling Dislocations and Disclinations with Finite Micropolar Elastoplasticity. Int. J. Plast. 2006, 22, 210–256. [Google Scholar] [CrossRef]
- Romanov, A.E.; Kolesnikova, A.L. Application of Disclination Concept to Solid Structures. Prog. Mater. Sci. 2009, 54, 740–769. [Google Scholar] [CrossRef]
- Fressengeas, C.; Taupin, V.; Capolungo, L. An Elasto-Plastic Theory of Dislocation and Disclination Fields. Int. J. Solids Struct. 2011, 48, 3499–3509. [Google Scholar] [CrossRef]
- Rzhavtsev, E.A.; Gutkin, M.Y. The Dynamics of Dislocation Wall Generation in Metals and Alloys under Shock Loading. Scr. Mater. 2015, 100, 102–105. [Google Scholar] [CrossRef]
- Bobylev, S.V.; Ovid’ko, I.A. Stress-Driven Migration, Convergence and Splitting Transformations of Grain Boundaries in Nanomaterials. Acta Mater. 2017, 124, 333–342. [Google Scholar] [CrossRef]
- Buzolin, R.H.; Canelo-Yubero, D.; Warchomicka, F.; Lasnik, M.; Krumphals, A.; Poletti, M.C. Refinement of the Ti-17 Microstructure after Hot Deformation: Coupled Mesoscale Model. Mater. Sci. Eng. A 2021, 800, 140268. [Google Scholar] [CrossRef]
- Li, S. Dependencies of Grain Refinement on Processing Route and Die Angle in Equal Channel Angular Extrusion of Bcc Materials. Comput. Mater. Sci. 2009, 46, 1044–1050. [Google Scholar] [CrossRef]
- Toth, L.S.; Estrin, Y.; Lapovok, R.; Gu, C. A Model of Grain Fragmentation Based on Lattice Curvature. Acta Mater. 2010, 58, 1782–1794. [Google Scholar] [CrossRef]
- Toth, L.S.; Gu, C.F. Modeling of Disorientation Axis Distribution in Severely Deformed Copper. Scr. Mater. 2013, 69, 183–186. [Google Scholar] [CrossRef]
- Toth, L.S.; Gu, C. Ultrafine-Grain Metals by Severe Plastic Deformation. Mater. Charact. 2014, 92, 1–14. [Google Scholar] [CrossRef]
- Tutcuoglu, A.D.; Hollenweger, Y.; Stoy, A.; Kochmann, D.M. High- vs. Low-Fidelity Models for Dynamic Recrystallization in Copper. Materialia 2019, 7, 100411. [Google Scholar] [CrossRef]
- Vu, V.Q.; Toth, L.S.; Beygelzimer, Y.; Kulagin, R.; Kobaissy, A.H. Modeling of Crystallographic Texture in Plastic Flow Machining. Adv. Eng. Mater. 2020, 22, 1900661. [Google Scholar] [CrossRef]
- Beyerlein, I.J.; Lebensohn, R.A.; Tomé, C.N. Modeling Texture and Microstructural Evolution in the Equal Channel Angular Extrusion Process. Mater. Sci. Eng. A 2003, 345, 122–138. [Google Scholar] [CrossRef]
- Lebensohn, R.A.; Tomé, C.N.; CastaÑeda, P.P. Self-Consistent Modelling of the Mechanical Behaviour of Viscoplastic Polycrystals Incorporating Intragranular Field Fluctuations. Philos. Mag. 2007, 87, 4287–4322. [Google Scholar] [CrossRef]
- Frydrych, K.; Kowalczyk-Gajewska, K. A Three-Scale Crystal Plasticity Model Accounting for Grain Refinement in Fcc Metals Subjected to Severe Plastic Deformations. Mater. Sci. Eng. A 2016, 658, 490–502. [Google Scholar] [CrossRef]
- Lebensohn, R.A.; Zecevic, M.; Knezevic, M.; McCabe, R.J. Average Intragranular Misorientation Trends in Polycrystalline Materials Predicted by a Viscoplastic Self-Consistent Approach. Acta Mater. 2016, 104, 228–236. [Google Scholar] [CrossRef]
- Guo, X.; Seefeldt, M. Modeling Grain Fragmentation and Deformation Textures for Titanium Using a Combined Approach of the Viscoplastic Self-Consistent Model and a Shear Fluctuation Model. J. Mater. Sci. 2017, 52, 8132–8148. [Google Scholar] [CrossRef]
- Zecevic, M.; Pantleon, W.; Lebensohn, R.A.; McCabe, R.J.; Knezevic, M. Predicting Intragranular Misorientation Distributions in Polycrystalline Metals Using the Viscoplastic Self-Consistent Formulation. Acta Mater. 2017, 140, 398–410. [Google Scholar] [CrossRef]
- Raabe, D.; Zhao, Z.; Mao, W. On the Dependence of In-Grain Subdivision and Deformation Texture of Aluminum on Grain Interaction. Acta Mater. 2002, 50, 4379–4394. [Google Scholar] [CrossRef]
- Rezvanian, O.; Zikry, M.A.; Rajendran, A.M. Microstructural Modeling of Grain Subdivision and Large Strain Inhomogeneous Deformation Modes in f.c.c. Crystalline Materials. Mech. Mater. 2006, 38, 1159–1169. [Google Scholar] [CrossRef]
- Ding, H.; Shen, N.; Shin, Y.C. Predictive Modeling of Grain Refinement during Multi-Pass Cold Rolling. J. Mater. Process. Technol. 2012, 212, 1003–1013. [Google Scholar] [CrossRef]
- Tohidlou, E.; Bertram, A. Effect of Strain Hardening on Subgrain Formation during ECAP Process. Mech. Mater. 2019, 137, 103077. [Google Scholar] [CrossRef]
- Gwalani, B.; Fu, W.; Olszta, M.; Silverstein, J.; Yadav, D.R.; Manimunda, P.; Guzman, A.; Xie, K.; Rohatgi, A.; Mathaudhu, S.; et al. Lattice Misorientation Evolution and Grain Refinement in Al-Si Alloys under High-Strain Shear Deformation. Materialia 2021, 18, 101146. [Google Scholar] [CrossRef]
- Wang, H.; Lu, C.; Tieu, K.; Liu, Y. A Crystal Plasticity FE Study of Macro- and Micro-Subdivision in Aluminium Single Crystals {001}<110> Multi-Pass Rolled to a High Reduction. J. Mater. Sci. Technol. 2021, 76, 231–246. [Google Scholar] [CrossRef]
- Liu, J.; Fan, X.; Zheng, W.; Singh, D.J.; Shi, Y. Nanocrystalline Gold with Small Size: Inverse Hall–Petch between Mixed Regime and Super-Soft Regime. Philos. Mag. 2020, 100, 2335–2351. [Google Scholar] [CrossRef]
- Jeon, J.B.; Lee, B.-J.; Chang, Y.W. Molecular Dynamics Simulation Study of the Effect of Grain Size on the Deformation Behavior of Nanocrystalline Body-Centered Cubic Iron. Scr. Mater. 2011, 64, 494–497. [Google Scholar] [CrossRef]
- Zhou, X.; Fu, H.; Zhu, J.-H.; Yang, X.-S. Atomistic Simulations of the Surface Severe Plastic Deformation-Induced Grain Refinement in Polycrystalline Magnesium: The Effect of Processing Parameters. J. Magnes. Alloy. 2022, 10, 1242–1255. [Google Scholar] [CrossRef]
- Syarif, J.; Altoyuri, A.; Mohamed, I.F. Equal Channel Angular Pressing of Single Crystal Aluminum: A Molecular Dynamics Simulation. J. Mater. Res. Technol. 2022, 17, 888–897. [Google Scholar] [CrossRef]
- Shveykin, A.I.; Trusov, P.V.; Romanov, K.A. An approach to numerical estimating the stability of multilevel constitutive models. Comput. Contin. Mech. 2021, 14, 61–76. [Google Scholar] [CrossRef]
- Shveykin, A.I.; Trusov, P.V.; Romanov, K.A. Some results of a numerical estimating of the stability of the FCC metal two-level constitutive model. Comput. Contin. Mech. 2021, 14, 127–143. [Google Scholar] [CrossRef]
- Zhang, C.; Li, H.; Eisenlohr, P.; Liu, W.; Boehlert, C.J.; Crimp, M.A.; Bieler, T.R. Effect of Realistic 3D Microstructure in Crystal Plasticity Finite Element Analysis of Polycrystalline Ti-5Al-2.5Sn. Int. J. Plast. 2015, 69, 21–35. [Google Scholar] [CrossRef]
- Gloaguen, D.; Girault, B.; Fajoui, J.; Klosek, V.; Moya, M.-J. In Situ Lattice Strains Analysis in Titanium during a Uniaxial Tensile Test. Mater. Sci. Eng. A 2016, 662, 395–403. [Google Scholar] [CrossRef]
- Kotha, S.; Ozturk, D.; Ghosh, S. Parametrically Homogenized Constitutive Models (PHCMs) from Micromechanical Crystal Plasticity FE Simulations, Part I: Sensitivity Analysis and Parameter Identification for Titanium Alloys. Int. J. Plast. 2019, 120, 296–319. [Google Scholar] [CrossRef]
- Toth, L.S.; Molinari, A.; Estrin, Y. Strain Hardening at Large Strains as Predicted by Dislocation Based Polycrystal Plasticity Model. J. Eng. Mater. Technol. 2002, 124, 71–77. [Google Scholar] [CrossRef]
- Vinogradov, A.; Estrin, Y. Analytical and Numerical Approaches to Modelling Severe Plastic Deformation. Prog. Mater. Sci. 2018, 95, 172–242. [Google Scholar] [CrossRef]
- Baik, S.C.; Estrin, Y.; Kim, H.S.; Hellmig, R.J. Dislocation Density-Based Modeling of Deformation Behavior of Aluminium under Equal Channel Angular Pressing. Mater. Sci. Eng. A 2003, 351, 86–97. [Google Scholar] [CrossRef]
- Mishra, A.; Kad, B.K.; Gregori, F.; Meyers, M.A. Microstructural Evolution in Copper Subjected to Severe Plastic Deformation: Experiments and Analysis. Acta Mater. 2007, 55, 13–28. [Google Scholar] [CrossRef]
- Esmaeili, F.; Mehri Sofiani, F.; Boroumand, R. A Modified Counterpart of Cyclic Extrusion-Compression: Experimental Study and Dislocation Density-Based Finite Element Modeling. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2016, 232, 465–480. [Google Scholar] [CrossRef]
- Kazeminezhad, M.; Hosseini, E. Modeling of Induced Empirical Constitutive Relations on Materials with FCC, BCC, and HCP Crystalline Structures: Severe Plastic Deformation. Int. J. Adv. Manuf. Technol. 2010, 47, 1033–1039. [Google Scholar] [CrossRef]
- Hosseini, E.; Kazeminezhad, M.; Mani, A.; Rafizadeh, E. On the Evolution of Flow Stress during Constrained Groove Pressing of Pure Copper Sheet. Comput. Mater. Sci. 2009, 45, 855–859. [Google Scholar] [CrossRef]
- Rezaee-Bazzaz, A.; Ahmadian, S.; Reihani, H. Modeling of Microstructure and Mechanical Behavior of Ultra Fine Grained Aluminum Produced by Accumulative Roll-Bonding. Mater. Des. 2011, 32, 4580–4585. [Google Scholar] [CrossRef]
- Parvin, H.; Kazeminezhad, M. Development a Dislocation Density Based Model Considering the Effect of Stacking Fault Energy: Severe Plastic Deformation. Comput. Mater. Sci. 2014, 95, 250–255. [Google Scholar] [CrossRef]
- Liu, F.; Yuan, H.; Yin, J.; Wang, J.T. Influence of Stacking Fault Energy and Temperature on Microstructures and Mechanical Properties of Fcc Pure Metals Processed by Equal-Channel Angular Pressing. Mater. Sci. Eng. A 2016, 662, 578–587. [Google Scholar] [CrossRef]
- Charkhesht, V.; Kazeminezhad, M. Flow Stress Evolution in Further Straining of Severely Deformed Al. Met. Mater. Trans. A 2019, 50, 2371–2380. [Google Scholar] [CrossRef]
- Baik, S.C.; Hellmig, R.J.; Estrin, Y.; Kim, H.S. Modeling of Deformation Behavior of Copper under Equal Channel Angular Pressing. Int. J. Mater. Res. 2003, 94, 754–760. [Google Scholar] [CrossRef]
- Lemiale, V.; Estrin, Y.; Kim, H.S.; O’Donnell, R. Grain Refinement under High Strain Rate Impact: A Numerical Approach. Comput. Mater. Sci. 2010, 48, 124–132. [Google Scholar] [CrossRef]
- Lee, D.J.; Yoon, E.Y.; Ahn, D.-H.; Park, B.H.; Park, H.W.; Park, L.J.; Estrin, Y.; Kim, H.S. Dislocation Density-Based Finite Element Analysis of Large Strain Deformation Behavior of Copper under High-Pressure Torsion. Acta Mater. 2014, 76, 281–293. [Google Scholar] [CrossRef]
- Lugo, N.; Llorca, N.; Cabrera, J.M.; Horita, Z. Microstructures and Mechanical Properties of Pure Copper Deformed Severely by Equal-Channel Angular Pressing and High Pressure Torsion. Mater. Sci. Eng. A 2008, 477, 366–371. [Google Scholar] [CrossRef]
- Beyerlein, I.J.; Tóth, L.S. Texture Evolution in Equal-Channel Angular Extrusion. Prog. Mater. Sci. 2009, 54, 427–510. [Google Scholar] [CrossRef]
- Qu, S.; You, Z.; Gu, R.; Jiang, Y.; Wang, J.T. Fracture Toughness Anisotropy of Ultrafine-Grained Pure Copper Processed by Equal Channel Angular Pressing. Mater. Sci. Eng. A 2020, 782, 139260. [Google Scholar] [CrossRef]
- Alawadhi, M.Y.; Sabbaghianrad, S.; Huang, Y.; Langdon, T.G. Evaluating the Paradox of Strength and Ductility in Ultrafine-Grained Oxygen-Free Copper Processed by ECAP at Room Temperature. Mater. Sci. Eng. A 2021, 802, 140546. [Google Scholar] [CrossRef]
- Habraken, A.M. Modelling the Plastic Anisotropy of Metals. ARCO 2004, 11, 3–96. [Google Scholar] [CrossRef]
- Van Houtte, P.; Li, S.; Seefeldt, M.; Delannay, L. Deformation Texture Prediction: From the Taylor Model to the Advanced Lamel Model. Int. J. Plast. 2005, 21, 589–624. [Google Scholar] [CrossRef]
- Zhang, K.; Holmedal, B.; Hopperstad, O.S.; Dumoulin, S.; Gawad, J.; Van Bael, A.; Van Houtte, P. Multi-Level Modelling of Mechanical Anisotropy of Commercial Pure Aluminium Plate: Crystal Plasticity Models, Advanced Yield Functions and Parameter Identification. Int. J. Plast. 2015, 66, 3–30. [Google Scholar] [CrossRef]
- Trusov, P.V.; Shveykin, A.I.; Kondratev, N.S. Multilevel Metal Models: Formulation for Large Displacement Gradients. NST 2017, 8, 133–166. [Google Scholar] [CrossRef]
- Romanova, V.; Balokhonov, R.; Emelianova, E.; Sinyakova, E.; Kazachenok, M. Early Prediction of Macroscale Plastic Strain Localization in Titanium from Observation of Mesoscale Surface Roughening. Int. J. Mech. Sci. 2019, 161–162, 105047. [Google Scholar] [CrossRef]
- Emelianova, E.S.; Romanova, V.A.; Balokhonov, R.R.; Pisarev, M.; Zinovieva, O.S. A Numerical Study of the Contri-bution of Different Slip Systems to the Deformation Response of Polycrystalline Titanium. Phys. Mesomech. 2021, 24, 166–177. [Google Scholar] [CrossRef]
- Kobaissy, A.H.; Ayoub, G.; Toth, L.S.; Mustapha, S.; Shehadeh, M. Continuum Dislocation Dynamics-Based Grain Fragmentation Modeling. Int. J. Plast. 2019, 114, 252–271. [Google Scholar] [CrossRef]
- Holt, D.L. Dislocation Cell Formation in Metals. J. Appl. Phys. 1970, 41, 3197–3201. [Google Scholar] [CrossRef]
- Rack, H.J.; Cohen, M. Strain Hardening of Iron-Titanium Alloys at Very Large Strains. Mater. Sci. Eng. 1970, 6, 320–326. [Google Scholar] [CrossRef]
- Kuhlmann-Wilsdorf, D.; Van Der Merwe, J.H. Theory of Dislocation Cell Sizes in Deformed Metals. Mater. Sci. Eng. 1982, 55, 79–83. [Google Scholar] [CrossRef]
- Mughrabi, H. A Two-Parameter Description of Heterogeneous Dislocation Distributions in Deformed Metal Crystals. Mater. Sci. Eng. 1987, 85, 15–31. [Google Scholar] [CrossRef]
- Kuhlmann-Wilsdorf, D.; Hansen, N. Geometrically Necessary, Incidental and Subgrain Boundaries. Scr. Metall. Et Mater. 1991, 25, 1557–1562. [Google Scholar] [CrossRef]
- Sil, D.; Varma, S.K. The Combined Effect of Grain Size and Strain Rate on the Dislocation Substructures and Mechanical Properties in Pure Aluminum. Met. Mater. Trans. A 1993, 24, 1153–1161. [Google Scholar] [CrossRef]
- Sauzay, M.; Kubin, L.P. Scaling Laws for Dislocation Microstructures in Monotonic and Cyclic Deformation of Fcc Metals. Prog. Mater. Sci. 2011, 56, 725–784. [Google Scholar] [CrossRef]
- Oudriss, A.; Feaugas, X. Length Scales and Scaling Laws for Dislocation Cells Developed during Monotonic Deformation of (001) Nickel Single Crystal. Int. J. Plast. 2016, 78, 187–202. [Google Scholar] [CrossRef]
- Bailey, J.E.; Hirsch, P.B. The Dislocation Distribution, Flow Stress, and Stored Energy in Cold-Worked Polycrystalline Silver. Philos. Mag. A J. Theor. Exp. Appl. Phys. 1960, 5, 485–497. [Google Scholar] [CrossRef]
- Ohashi, T.; Kawamukai, M.; Zbib, H. A Multiscale Approach for Modeling Scale-Dependent Yield Stress in Polycrystalline Metals. Int. J. Plast. 2007, 23, 897–914. [Google Scholar] [CrossRef]
- Lyu, H.; Ruimi, A.; Zbib, H.M. A Dislocation-Based Model for Deformation and Size Effect in Multi-Phase Steels. Int. J. Plast. 2015, 72, 44–59. [Google Scholar] [CrossRef]
- Amodeo, R.J.; Ghoniem, N.M. A Review of Experimental Observations and Theoretical Models of Dislocation Cells and Subgrains. Res Mech. 1988, 23, 137–160. [Google Scholar]
- Sakai, T.; Belyakov, A.; Kaibyshev, R.; Miura, H.; Jonas, J.J. Dynamic and Post-Dynamic Recrystallization under Hot, Cold and Severe Plastic Deformation Conditions. Prog. Mater. Sci. 2014, 60, 130–207. [Google Scholar] [CrossRef]
- Shveikin, A.I.; Trusov, P.V. Correlation between Geometrically Nonlinear Elastoviscoplastic Constitutive Relations Formulated in Terms of the Actual and Unloaded Configurations for Crystallites. Phys. Mesomech. 2018, 21, 193–202. [Google Scholar] [CrossRef]
- Shveykin, A.I.; Trusov, P.V. Multilevel Models of Polycrystalline Metals: Comparison of Relations Describing the Crystallite Lattice Rotations. NST 2019, 10, 1–20. [Google Scholar] [CrossRef]
- Horstemeyer, M.F.; Potirniche, G.P.; Marin, E.B. Crystal Plasticity. In Handbook of Materials Modeling; Yip, S., Ed.; Springer The Netherlands: Dordrecht, The Netherlands, 2005; pp. 1133–1149. [Google Scholar]
- Anand, L. Single-Crystal Elasto-Viscoplasticity: Application to Texture Evolution in Polycrystalline Metals at Large Strains. Comput. Methods Appl. Mech. Eng. 2004, 193, 5359–5383. [Google Scholar] [CrossRef]
- Khadyko, M.; Dumoulin, S.; Cailletaud, G.; Hopperstad, O.S. Latent Hardening and Plastic Anisotropy Evolution in AA6060 Aluminium Alloy. Int. J. Plast. 2016, 76, 51–74. [Google Scholar] [CrossRef]
- Maresca, F.; Kouznetsova, V.G.; Geers, M.G.D. Reduced Crystal Plasticity for Materials with Constrained Slip Activity. Mech. Mater. 2016, 92, 198–210. [Google Scholar] [CrossRef]
- Grilli, N.; Janssens, K.G.F.; Nellessen, J.; Sandlöbes, S.; Raabe, D. Multiple Slip Dislocation Patterning in a Dislocation-Based Crystal Plasticity Finite Element Method. Int. J. Plast. 2018, 100, 104–121. [Google Scholar] [CrossRef]
- Roters, F.; Diehl, M.; Shanthraj, P.; Eisenlohr, P.; Reuber, C.; Wong, S.L.; Maiti, T.; Ebrahimi, A.; Hochrainer, T.; Fabritius, H.-O.; et al. DAMASK—The Düsseldorf Advanced Material Simulation Kit for Modeling Multi-Physics Crystal Plasticity, Thermal, and Damage Phenomena from the Single Crystal up to the Component Scale. Comput. Mater. Sci. 2019, 158, 420–478. [Google Scholar] [CrossRef]
- Shveykin, A.I. Multilevel Models of Polycrystalline Metals: Comparison of Constitutive Relations for Crystallites. Probl. Strength Plast. 2017, 79, 385–397. [Google Scholar] [CrossRef]
- Trusov, P.; Shveykin, A.; Kondratev, N. Some Issues on Crystal Plasticity Models Formulation: Motion Decomposition and Constitutive Law Variants. Crystals 2021, 11, 1392. [Google Scholar] [CrossRef]
- Trusov, P.V.; Shveykin, A.I. On Motion Decomposition and Constitutive Relations in Geometrically Nonlinear Elastoviscoplasticity of Crystallites. Phys. Mesomech. 2017, 20, 377–391. [Google Scholar] [CrossRef]
- Sheikh, H.; Ebrahimi, R. Modeling the Effect of Strain Reversal on Grain Refinement and Crystallographic Texture during Simple Shear Extrusion. Int. J. Solids Struct. 2017, 126–127, 175–186. [Google Scholar] [CrossRef]
- Ostanina, T.V.; Shveykin, A.I.; Trusov, P.V. The grain structure refinement of metals and alloys under severe plastic deformation: Experimental data and analysis of mechanisms. PNRPU Mech. Bull. 2020, 2, 85–111. [Google Scholar] [CrossRef]
- Hughes, D.A.; Liu, Q.; Chrzan, D.C.; Hansen, N. Scaling of Microstructural Parameters: Misorientations of Deformation Induced Boundaries. Acta Mater. 1997, 45, 105–112. [Google Scholar] [CrossRef]
- Hughes, D.A.; Hansen, N.; Bammann, D.J. Geometrically Necessary Boundaries, Incidental Dislocation Boundaries and Geometrically Necessary Dislocations. Scr. Mater. 2003, 48, 147–153. [Google Scholar] [CrossRef]
- Sarafanov, G.F.; Perevezentsev, V.N. Laws of Deformation Refinement of the Structure of Metals and Alloys: Tutorial Material; Nizhny: Novgorod, Russia, 2007; p. 96. (In Russian) [Google Scholar]
- Mughrabi, H. Dislocation Wall and Cell Structures and Long-Range Internal Stresses in Deformed Metal Crystals. Acta Metall. 1983, 31, 1367–1379. [Google Scholar] [CrossRef]
- Takeuchi, S.; Argon, A.S. Steady-State Creep of Alloys Due to Viscous Motion of Dislocations. Acta Metall. 1976, 24, 883–889. [Google Scholar] [CrossRef]
- Bakó, B.; Groma, I.; Györgyi, G.; Zimányi, G. Dislocation Patterning: The Role of Climb in Meso-Scale Simulations. Comput. Mater. Sci. 2006, 38, 22–28. [Google Scholar] [CrossRef]
- Staker, M.R.; Holt, D.L. The Dislocation Cell Size and Dislocation Density in Copper Deformed at Temperatures between 25 and 700 °C. Acta Metall. 1972, 20, 569–579. [Google Scholar] [CrossRef]
- Koneva, N.A.; Starenchenko, V.A.; Lychagin, D.V.; Trishkina, L.I.; Popova, N.A.; Kozlov, E.V. Formation of Dislocation Cell Substructure in Face-Centred Cubic Metallic Solid Solutions. Mater. Sci. Eng. A 2008, 483–484, 179–183. [Google Scholar] [CrossRef]
- Hosseini, E.; Kazeminezhad, M. ETMB Model Investigation of Flow Softening during Severe Plastic Deformation. Comput. Mater. Sci. 2009, 46, 902–905. [Google Scholar] [CrossRef]
- Argon, A.S.; Moffatt, W.C. Climb of Extended Edge Dislocations. Acta Metall. 1981, 29, 293–299. [Google Scholar] [CrossRef]
- Hosford, W.F. Mechanical Behavior of Materials, 2nd ed.; Cambridge University Press: New York, NY, USA, 2010; p. 419. [Google Scholar]
- Humphreys, F.J.; Hatherly, M. Recrystallization and Related Annealing Phenomena, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2004; p. 658. [Google Scholar]
- An, X.H.; Han, W.Z.; Huang, C.X.; Zhang, P.; Yang, G.; Wu, S.D.; Zhang, Z.F. High Strength and Utilizable Ductility of Bulk Ultrafine-Grained Cu–Al Alloys. Appl. Phys. Lett. 2008, 92, 201915. [Google Scholar] [CrossRef]
- Hegedűs, Z.; Gubicza, J.; Kawasaki, M.; Chinh, N.Q.; Süvegh, K.; Fogarassy, Z.; Langdon, T.G. High Temperature Thermal Stability of Ultrafine-Grained Silver Processed by Equal-Channel Angular Pressing. J. Mater. Sci. 2013, 48, 1675–1684. [Google Scholar] [CrossRef]
- Schafler, E.; Zehetbauer, M.; Ungàr, T. Measurement of Screw and Edge Dislocation Density by Means of X-Ray Bragg Profile Analysis. Mater. Sci. Eng. A 2001, 319–321, 220–223. [Google Scholar] [CrossRef]
- Püschl, W. Models for Dislocation Cross-Slip in Close-Packed Crystal Structures: A Critical Review. Prog. Mater. Sci. 2002, 47, 415–461. [Google Scholar] [CrossRef]
- Hosseini, E.; Kazeminezhad, M. A New Microstructural Model Based on Dislocation Generation and Consumption Mech-anisms through Severe Plastic Deformation. Comput. Mater. Sci. 2011, 50, 1123–1135. [Google Scholar] [CrossRef]
- Bonneville, J.; Escaig, B. Cross-Slipping Process and the Stress-Orientation Dependence in Pure Copper. Acta Metall. 1979, 27, 1477–1486. [Google Scholar] [CrossRef]
- Huang, M.; Rivera-Díaz-del-Castillo, P.E.J.; Bouaziz, O.; van der Zwaag, S. A Constitutive Model for High Strain Rate Deformation in FCC Metals Based on Irreversible Thermodynamics. Mech. Mater. 2009, 41, 982–988. [Google Scholar] [CrossRef]
- Prinz, F.; Argon, A.S.; Moffatt, W.C. Recovery of Dislocation Structures in Plastically Deformed Copper and Nickel Single Crystals. Acta Metall. 1982, 30, 821–830. [Google Scholar] [CrossRef]
- Mohamed, F.A. A Dislocation Model for the Minimum Grain Size Obtainable by Milling. Acta Mater. 2003, 51, 4107–4119. [Google Scholar] [CrossRef]
- Toth, L.S. Modelling of Strain Hardening and Microstructural Evolution in Equal Channel Angular Extrusion. Comput. Mater. Sci. 2005, 32, 568–576. [Google Scholar] [CrossRef]
- Trusov, P.V.; Gribov, D.S. The Three-Level Elastoviscoplastic Model and Its Application to Describing Complex Cyclic Loading of Materials with Different Stacking Fault Energies. Materials 2022, 15, 760. [Google Scholar] [CrossRef]
- Lapovok, R.; Dalla Torre, F.H.; Sandlin, J.; Davies, C.H.J.; Pereloma, E.V.; Thomson, P.F.; Estrin, Y. Gradient Plasticity Constitutive Model Reflecting the Ultrafine Micro-Structure Scale: The Case of Severely Deformed Copper. J. Mech. Phys. Solids 2005, 53, 729–747. [Google Scholar] [CrossRef]
- Kobaissy, A.A.-H.; Ayoub, G.; Nasim, W.; Malik, J.; Karaman, I.; Shehadeh, M. Modeling of the ECAP Induced Strain Hardening Behavior in FCC Metals. Met. Mater. Trans. A 2020, 51, 5453–5474. [Google Scholar] [CrossRef]
- Shveykin, A.; Romanov, K.; Trusov, P. Some Issues with Statistical Crystal Plasticity Models: Description of the Effects Triggered in FCC Crystals by Loading with Strain-Path Changes. Materials 2022, 15, 6586. [Google Scholar] [CrossRef]
- Harder, J. FEM-Simulation of the Hardening Behavior of FCC Single Crystals. Acta Mech. 2001, 150, 197–217. [Google Scholar] [CrossRef]
- Dalla Torre, F.; Lapovok, R.; Sandlin, J.; Thomson, P.F.; Davies, C.H.J.; Pereloma, E.V. Microstructures and Properties of Copper Processed by Equal Channel Angular Extrusion for 1–16 Passes. Acta Mater. 2004, 52, 4819–4832. [Google Scholar] [CrossRef]
- Bronkhorst, C.A.; Kalidindi, S.R.; Anand, L. Polycrystalline Plasticity and the Evolution of Crystallographic Texture in FCC Metals. Phil. Trans. R. Soc. Lond. A 1992, 341, 443–477. [Google Scholar] [CrossRef]
- Estrin, Y.; Tóth, L.S.; Bréchet, Y.; Kim, H.S. Modelling of the Evolution of Dislocation Cell Misorientation under Severe Plastic Deformation. Mater. Sci. Forum 2006, 503–504, 675–680. [Google Scholar] [CrossRef]
- Estrin, Y.; Kim, H.S. Modelling Microstructure Evolution toward Ultrafine Crystallinity Produced by Severe Plastic Deformation. J. Mater. Sci. 2007, 42, 1512–1516. [Google Scholar] [CrossRef]

| Parameter | Definition | Value |
|---|---|---|
| independent components of the elastic property tensor [140] | 168.4 GPa | |
| 121.4 GPa | ||
| 75.4 GPa | ||
| viscoplastic relation (2b) parameter [139] | 0.001 s–1 | |
| m | strain rate sensitivity exponent of the material [139] | 50 |
| initial critical shear stress | 10 MPa | |
| modified Hall–Petch relation (3b) constant | 0.02 | |
| shear modulus [72] | 48 GPa | |
| Burgers vector modulus [63] | 2.56 Å | |
| latent hardening parameter [139] | 2.0 | |
| Bailey–Hirsch parameter | 0.0132 | |
| constant that characterizes the fraction of active sources of dislocation generation [63] | 0.065 | |
| constant that characterizes the fraction of dislocations leaving the cell interiors [63] | 0.012 | |
| initial value of the volume fraction of cell walls [63] | 0.25 | |
| saturation of at large strains [63] | 0.06 | |
| rate of cell walls’ volume fraction decrease [63] | 3.2 | |
| mr | constant | 250 |
| material constant [63] | 0.25 | |
| Debye frequency [72] | 1013 s–1 | |
| number of nearest neighboring sites for vacancy diffusion [72] | 11 | |
| constant [72] | 5 | |
| Poisson’s ratio [72] | 0.31 | |
| stacking fault energy [72] | 45 mJ/m2 | |
| U | self-diffusion activation energy [72] | 203 kJ/mol |
| T | temperature | 300 K |
| R | universal gas constant | 8.31 J/(mol·K) |
| atomic volume [72] | b3 | |
| kB | Boltzmann constant | 1.38·10−23 J/K |
| V | activation volume for cross-slip [72] | 300b3 |
| A | constant | 0.885 |
| numerical constants in (20) | 9.5 | |
| 30 | ||
| 4.0 |
| Pass Number | ||
|---|---|---|
| 0 | 75.4 | 68 ± 6 |
| 1 | 345.6 | 342 ± 5 |
| 2 | 380.0 | 407 ± 22 |
| 4 | 436.4 | 415 ± 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romanov, K.; Shveykin, A.; Trusov, P. Advanced Statistical Crystal Plasticity Model: Description of Copper Grain Structure Refinement during Equal Channel Angular Pressing. Metals 2023, 13, 953. https://doi.org/10.3390/met13050953
Romanov K, Shveykin A, Trusov P. Advanced Statistical Crystal Plasticity Model: Description of Copper Grain Structure Refinement during Equal Channel Angular Pressing. Metals. 2023; 13(5):953. https://doi.org/10.3390/met13050953
Chicago/Turabian StyleRomanov, Kirill, Alexey Shveykin, and Peter Trusov. 2023. "Advanced Statistical Crystal Plasticity Model: Description of Copper Grain Structure Refinement during Equal Channel Angular Pressing" Metals 13, no. 5: 953. https://doi.org/10.3390/met13050953
APA StyleRomanov, K., Shveykin, A., & Trusov, P. (2023). Advanced Statistical Crystal Plasticity Model: Description of Copper Grain Structure Refinement during Equal Channel Angular Pressing. Metals, 13(5), 953. https://doi.org/10.3390/met13050953








