Abstract
Phase equilibria and thermodynamic properties of the Au-Sb-Sn ternary system are important for the design of Au-based alloys as high-temperature lead-free solders to replace high-Pb solders. In this work, phase transition temperatures of five Sb-Sn alloys were measured using differential thermal analysis (DTA), and the temperatures of three invariant reactions were determined. Based on the measured experimental results in this work and the reported results, the Sb-Sn binary system was re-optimized using the CALPHAD method. The calculated results were in good agreement with available phase equilibria and thermodynamic data. This work was further combined with the previous assessments of the Au-Sn and Au-Sb binary systems and the present optimization of the Sb-Sn binary system to calculate the phase equilibria and thermodynamic properties of the Au-Sb-Sn ternary system, according to the reported experimental results, including thermodynamic properties and phase equilibria. The calculated liquidus projection, isothermal sections, vertical sections, as well as enthalpy of mixing and activity of Sn in liquid alloys are consistent well with the reported experimental results. A self-consistent set of thermodynamic parameters was obtained to accurately describe Gibbs energies of various phases in the Au-Sb-Sn ternary system, which would serve as a sound basis for developing a thermodynamic database of multicomponent Au-Sn-based alloy systems.
1. Introduction
High-Pb solders (e.g., 95Pb-5Sn (wt.%)) as high-temperature solders possess excellent soldering properties in electronic packaging and step soldering applications. Lead is harmful to both the environment and human health, and, thus, the use of high-Pb solders has been restricted [,,]. The Au-Sn-based alloys have been proposed as alternative high-temperature Pb-free solders [,]. In particular, the Au-20Sn (wt.%) eutectic alloy is attractive in high-power electronic and optoelectronic devices because of its superior resistance to corrosion and high electrical and thermal conductivity, as well as high mechanical strength [,]. To reduce the costs of Au-based solders, alloying elements, such as Ag, Bi, Cu, Ga, Ge, In, Sb, Si, and Zn, may be added to replace part of the Au []. To understand better the role of alloying elements and to design novel Au-based solders, the knowledge of the reliable phase diagrams and thermodynamic properties of the Au-based alloy systems is indispensable. It was reported that adding Sb to Au-20Sn (wt.%) alloy does not significantly affect its melting temperature []. The phase equilibria of the Au-Sb-Sn ternary system were studied experimentally [,,] and calculated thermodynamically []. However, the thermodynamic properties of liquid Au-Sb-Sn alloys determined recently by Hindler et al. [] and Jendrzejczyk et al. [,] were not considered in the calculation of Kim et al. []. Therefore, the purpose of the present work is to re-optimize the Sb-Sn binary system, based on the measured phase diagram data, and then to obtain a consistent and reliable thermodynamic description of the Au-Sb-Sn ternary system in combination with the previous assessment of the Au-Sb and Au-Sn binary systems using the CALPHAD method [].
2. The Literature Information
2.1. The Au-Sb Binary System
The Au-Sb binary phase diagram has been studied by several researchers [,,,,]. Wang et al. [] assessed the Au-Sb binary system by considering all the available experimental data. The calculations [] are in good agreement with the reported phase equilibria and thermodynamic properties. Therefore, thermodynamic parameters of the Au-Sb binary system obtained by Wang et al. [] were used in this work. The calculated Au-Sb binary phase diagram is shown in Figure 1a.
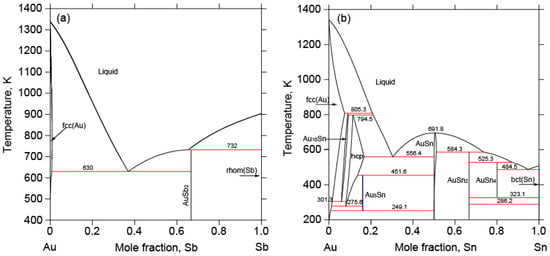
Figure 1.
Calculated (a) Au-Sb and (b) Au-Sn binary phase diagrams by Wang et al. [] with permission from Elsevier, 2011, and Dong et al. [] with permission from Elsevier, 2013.
2.2. The Au-Sn Binary System
Several thermodynamic assessments of the Au-Sn system have been reported [,,,,,]. The calculated results [] show good agreement with most of the experimental data. Therefore, in this work, the assessed results [] were used in the calculation of the Au-Sb-Sn ternary system. Figure 1b shows the calculated Au-Sn binary phase diagram by Dong et al. [].
2.3. The Sb-Sn Binary System
The Sb-Sn binary system was investigated by many researchers [,,,,,,,,]. Schmetterer et al. [,] reported a comprehensive analysis of the experimental study of the Sb-Sn binary system and updated the Sb-Sn binary phase diagram based on the new experimental results. The results [,] show that the intermetallic compound Sb3Sn4 with the Rm space group is a stable phase, rather than Sb2Sn3, which has no clear structural description []. Therefore, Sb3Sn4 is considered, in this work, as a stable intermetallic compound in the Sb-Sn binary system.
On the other hand, Sb3Sn4 in the Sb-Sn binary phase diagram reported by Perdel et al. [] and Ohtani et al. [] decomposes at 515 K to SbSn and bct(Sn) phase, which was accepted by Okamoto []. The assessed results (except for the composition range of SbSn) of Jonsson et al. [] and Kroupa et al. [] are in general agreement with the calculated results of Ohtani et al. []. The experimental Sb-Sn binary phase diagram [,,,] displays a contradiction to the decomposition of Sb3Sn4 at around 515 K. The experimental results determined by Chen et al. [] show that Sb3Sn4 is not decomposed and is stable at room temperature, which was accepted in the new edition of the phase diagram handbook []. Chen et al. [] optimized the Sb-Sn binary system considering the stable intermetallic compound Sb3Sn4 down to room temperature. The stability of Sb3Sn4 was further confirmed by Gierlotka et al. [] through ab initio calculation. Gierlotka et al. [] re-optimized the Sb-Sn binary system, based on the new experimental data []. Borzone et al. [] investigated the phase equilibria in the Sb3Sn4-SbSn composition range experimentally and confirmed the phase transitions related to Sb3Sn4. Lysenko [] calculated the Sb-Sn binary system, including both Sb2Sn3 and Sb3Sn4. Recently, Zhang et al. [] re-assessed the Sb-Sn binary system. According to the experimental results [,,,], Sb3Sn4 is stable at room temperature, which was considered in the present calculation of the Sb-Sn binary system. The experimental data determined in this work and reported in refs. [,,,,] were highly valued in the optimization work.
Thermodynamic properties of the liquid phase in the Sb-Sn binary system were determined experimentally [,,,,,]. The enthalpy of mixing of the liquid Sb-Sn alloys was measured through calorimetry by Witting and Gehring [], Sommer et al. [], and Azzaoui et al. []. The activity of Sn in liquid Sb-Sn alloys was determined by Jendrzejczyk et al. [], Frantic et al. [], and Itoh et al. [] by the electromotive force (EMF) method. The experimental results of thermodynamic properties of the liquid phase in the Sb-Sn binary system [,,,,,] were used in the present calculation of the Sb-Sn binary system.
2.4. The Au-Sb-Sn Ternary System
The phase equilibria of the Au-Sb-Sn ternary system were studied experimentally [,,,]. The reaction scheme of the Au-Sb-Sn ternary system was proposed by Prince et al. [] based on the results of Humpston et al. []. The isothermal section of the Au-Sb-Sn ternary system at 523 K was determined by Schubert et al. [] using X-ray diffraction and metallographic analysis. The solubility of Sn in AuSb2 at 523 K was determined to be 15 at.%. The experimental results [] show no stable ternary intermetallic compound in this ternary system. Kim et al. [] measured phase transitions of two Au-4.8Sb-30.7Sn (at.%) and Au-7.0Sb-28.5Sn (at.%) alloys using differential scanning calorimetry (DSC). Hindler et al. [] determined the liquidus temperature for three vertical sections (: = 2:1, = 1:1, = 1:2) by differential thermal analysis (DTA). The experimental results of phase equilibria and phase transitions [,,,] were used in the present calculation of the Au-Sb-Sn ternary system.
Thermodynamic properties of the Au-Sb-Sn ternary system were investigated experimentally [,,]. Hindler et al. [] measured the enthalpy of mixing of liquid Au-Sb-Sn alloys with different composition ratios (, , = 2:1, 1:1, 1:2) at 873 K and 1073 K using electromotive force (EMF) method. Meanwhile, the activity of Sn in liquid Au-Sb-Sn alloys with different composition ratios ( = 2:1, = 1:1, = 1:2) at 873 K by the EMF method was determined. Jendrzejczyk et al. [] measured the enthalpy of mixing of liquid Au-Sb-Sn alloys with different composition ratios ( = 2:1, = 1:1, = 1:2) at 923 K and 1078 K using a high-temperature calorimeter. Recently, the activity of Sn ( = 2:1, = 1:2) in liquid Au-Sb-Sn alloys at 1273 K was also determined by Jendrzejczyk et al. [] by the EMF method. The determined experimental results [,,] were employed in the present calculation of the Au-Sb-Sn ternary system.
3. Experimental Procedure
Five SbxSn1−x (x = 0.28, 0.32, 0.38, 0.50, 0.55) alloys were prepared by arc-melting using pure metals Sb and Sn (purity, 99.99%). The alloy samples were melted in a 99.99% argon atmosphere. To ensure the uniformity of the composition, the alloy samples were melted more than four times. The thermal analysis measurements of the alloy samples were carried out using a differential scanning calorimeter (DTA, Q–2000 TA instrument, TA Instruments Inc., New Castle, DE, USA) under an argon atmosphere. To ensure the accuracy and reliability of the experimental results, all alloy samples were tested at different heating rates (5 K/min and 10 K/min).
4. Thermodynamic Models
4.1. Solution Phases
In the Au-Sb-Sn ternary system, the molar Gibbs energy of a solution phase Φ (Φ = Liquid, fcc, bct, hcp, rhom, and Au10Sn) is expressed by the substitutional solution model, as follows:
where; represents the molar fraction of element i (i = Au, Sn, Sb), is the Gibbs free energy of pure element i, in the structure of the phase Φ with respect to the standard reference state at 298.15 K and 1 bar, R is the gas constant, and T denotes the absolute temperature in Kelvin. In the present work, the Gibbs energies of the elements Au, Sb, and Sn, as well as , , and , were taken from the SGTE (Scientific Group Thermodata Europe) database [], where the elements Sb and Sn have been updated using the new version of the database. is the excess Gibbs free energy of the Φ phase, which can be expressed as the Redlich–Kister–Muggianu polynomial [,]:
where; j is an integer (j = 0, 1, 2), and are the Au-Sb and Au-Sn interaction parameters taken from the binary systems evaluated by Wang et al. [] and Dong et al. [], and was the parameter to be optimized for the Sb-Sn binary system. The parameters , and were the ternary interaction parameters assessed in this work.
4.2. Binary Compounds
Considering the solubility of Sn in AuSb2, the molar Gibbs energy of AuSb2 is described using the model (Au)0.333333:(Sb, Sn)0.666667, and the formula is given as:
where; and are the site fractions of Sb and Sn in the second sublattice, respectively. and are the Gibbs energies of the pure elements Au and Sb. is the Au-Sb interaction parameter taken from the binary system evaluated by Wang et al. []. and are the lattice stability parameters and the ternary interaction parameters to be optimized. The parameters , , were optimized in this work.
The solubility of the third element in Au5Sn, AuSn2, AuSn4, and Sb3Sn4 was considered negligible in this work due to the lack of available experimental information. Therefore, Au5Sn, AuSn2, AuSn4, and Sb3Sn4 were considered as stoichiometric phases. The Gibbs energies of Au5Sn, AuSn2, and AuSn4 were taken directly from the optimized results of the Au-Sn binary systems by Dong et al. []. Meanwhile, the molar Gibbs energy of Sb3Sn4 was expressed as:
where; and are the Gibbs energies of the pure elements Sb and Sn. The parameters were optimized in this work.
Considering its large composition range, SbSn was described using the model (Sb, Sn)0.5(Sb, Sn)0.5, and the molar Gibbs energy was expressed as:
in which , , and are site fractions of Sb and Sn in the first and second sublattice, respectively. , , , and represent the Gibbs energy of possible end members for SbSn, while the parameters, , , , and represent the interactions within each sublattice.
5. Results and Discussion
Using the experimental data, including phase equilibria and thermodynamic data, the thermodynamic parameters of each phase in the Au-Sb-Sn ternary system were optimized using the PARROT module in Thermo-Calc® software package (Thermo-Calc Software AB Inc., Stockholm, Sweden) developed by Sundman et al. []. Finally, the thermodynamic parameters of the Au-Sb-Sn system were obtained, as shown in Table 1.

Table 1.
Thermodynamic parameters for the Au-Sb-Sn ternary system.
5.1. The Sb-Sn Binary System
The thermal analysis curves of SbxSn1−x (x = 0.28, 0.32, 0.38, 0.50, 0.55) alloys were tested with different heating rates (5 K/min and 10 K/min) under an argon atmosphere. According to the measured thermal analysis curves of the alloys, the onset temperature of the peaks during the heating curve was determined as the temperature of the invariant reactions, while the peak temperature of the last thermal effect was used as the liquidus temperature. The phase transition temperatures of SbxSn1−x (x = 0.28, 0.32, 0.38, 0.50, 0.55) alloys were determined, as shown in Table 2.

Table 2.
Phase transition temperatures of Sb-Sn alloys determined by DTA in this work.
Figure 2 shows the thermal analysis curves of SbxSn1−x (x = 0.28, 0.32, 0.38) alloys at the heating rate of 5 K/min. A slow onset followed by an invariant effect appeared around 510.6–514.4 K with a clear kink before the peak at 516 K. The experimental results were in agreement with the reported data [,,]. The temperatures of two peritectic reactions, L + Sb3Sn4 ↔ bct (Sn) at 516 K and L + SbSn ↔ Sb3Sn4 at 598 K, were determined. Finally, the phase transitions of the liquid phase were at 625.2 K, 640.1 K, and 660.5 K, respectively.
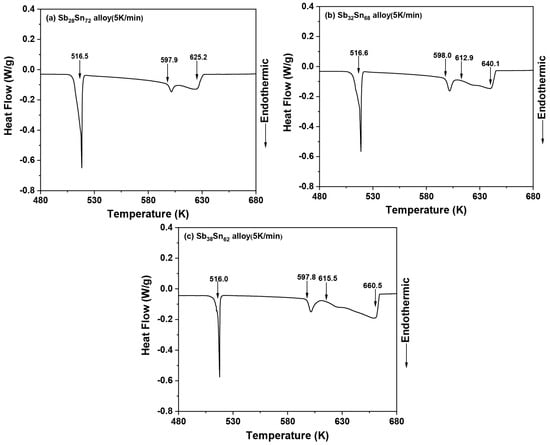
Figure 2.
Thermal analysis curves of SbxSn1−x (x = 0.28, 0.32, 0.38) alloys measured by DTA at 5 K/min.
Figure 3 shows the thermal analysis curves of SbxSn1−x (x = 0.50, 0.55) alloys. As shown in Figure 3a, two weak thermal effects at 514.1 K and 593.3 K were found. The transition from the SbSn single-phase region to the two-phase region with SbSn and liquid phase is visible in the temperature range of 620–693.9 K. The peritectic reaction (L + rhom(Sb) ↔ SbSn at 693.9 K) and the liquidus temperature at 700.2 K were determined. Figure 3b shows endothermic peaks at 510.8 K and 592.4 K, and incomplete peritectic reactions were found in the Sb-Sn binary system, which leads to some spurious effects in the DSC measurements. Four peaks were recorded in the heating curves of these two Sb-Sn alloys, while only two peaks, corresponding to the liquidus and invariant reaction, would be expected. The small thermal effect is related to an excess of the liquid phase due to the incomplete peritectic reaction. The transition from the SbSn single-phase region to the L + SbSn two-phase region was in the temperature range of 620–694 K. The temperature of the peritectic reaction (L + rhom(Sb) ↔ SbSn) and the liquidus temperature were measured as 694.5 K and 727.4 K, respectively.
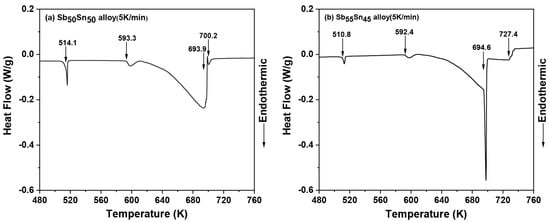
Figure 3.
Thermal analysis curves of SbxSn1−x (x = 0.50, 0.55) alloys measured by DTA at 5 K/min.
Figure 4 displays the calculated Sb-Sn binary phase diagram compared with the experimental data determined in this work and the reported results [,,,,,], as well as the calculated results [,,]. The comparison of the calculated phase diagram in this work with the calculation results [,,] is shown in Figure 4a, while the calculated Sb-Sn binary phase diagram with the experimental data [,,,,,] is given in Figure 4b. In this work, two stable intermetallic compounds, Sb3Sn4 and SbSn, were taken into account, according to the experimental results of Schmetterer et al. [], Gierlotka et al. [], and Borzone et al. []. The calculated results in this work were consistently much better, in accordance with the experimental data [,,,,,] when compared with the calculated results [,,]. In Table 3, the calculated invariant reactions of the Sb-Sn binary phase diagram are compared with the experimental data determined in this work and the reported results [,,,,,], as well as the calculated results [,,,]. The temperatures of three peritectic reactions (L + rhom(Sb) ↔ SbSn, L + SbSn ↔ Sb3Sn4, L + Sb3Sn4 ↔ bct(Sn)) determined experimentally in this work are consistent with the calculated results in this work and the experimental data [,,,,,].
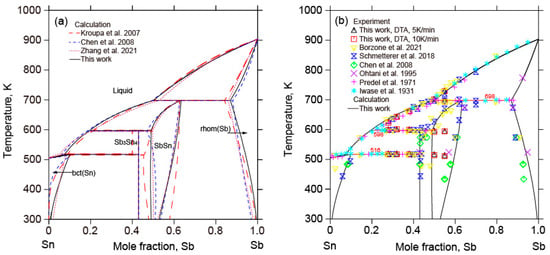
Figure 4.
(a) Calculated Sb-Sn binary phase diagram with the calculated results data from [,,] and (b) the experimental data determined in this work and the reported results data from [,,,,,].

Table 3.
Invariant reactions of the Sb-Sn system.
Figure 5 shows the calculated enthalpy of mixing of the liquid Sb-Sn alloys with the experimental data [,,,] and the calculated results [,,] at 973 K. The calculated enthalpy of mixing of liquid Sb-Sn alloys in this work was consistent with the experimental data [,,,]. Figure 6 presents the calculated activity of Sn in liquid Sb-Sn alloys with the experimental data [,,].
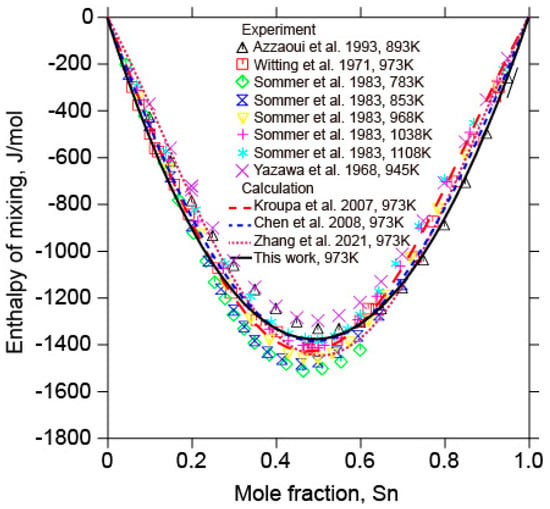
Figure 5.
Calculated enthalpy of mixing of liquid Sb-Sn alloys in relation to the experimental data from [,,,] and the calculated results data from [,,] at 973 K. (Reference states: liquid Sn and liquid Sb).
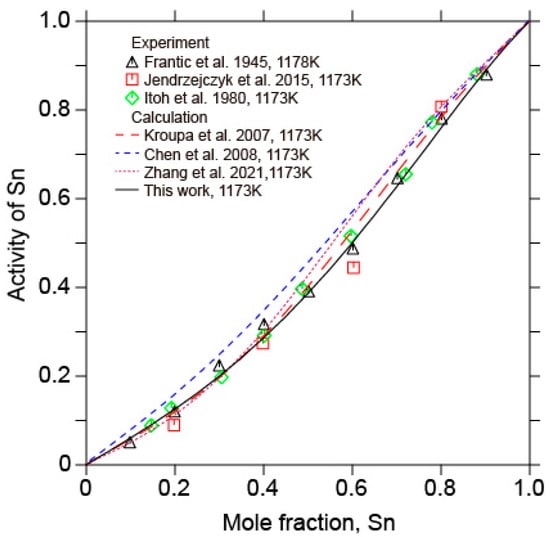
Figure 6.
Calculated activity of Sn in liquid Sb-Sn alloys in relation to the experimental data from [,,] and the calculated results data from [,,] at 1173 K. (Reference state: liquid Sn).
5.2. The Au-Sb-Sn Ternary System
Figure 7 shows the calculated liquidus projection of the Au-Sb-Sn ternary system in this work. The calculated reaction scheme related to the liquid phase is shown in Figure 8. The comparison of the calculated invariant reactions in this work with the literature [] and the calculated results of Kim et al. [] is shown in Table 4. There are eight U-type reactions and one E-type reaction. There were some differences between the calculated invariant reactions in this work and Kim et al. [] due to the liquidus projection of Kim et al. [] not being consistent with the liquidus boundary of the Sb-Sn binary system. The calculated compositions and temperature of the eutectic reaction (L → hcp + AuSn + AuSb2) are in good agreement with the literature [].
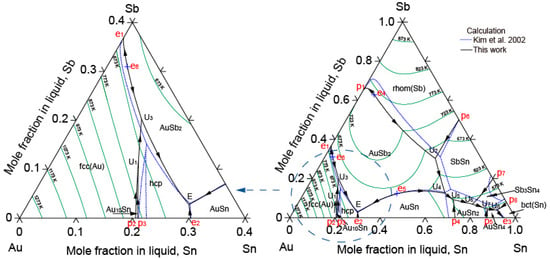
Figure 7.
Calculated liquidus projection of the Au-Sb-Sn ternary system in this work in relation to the calculated results data from [].
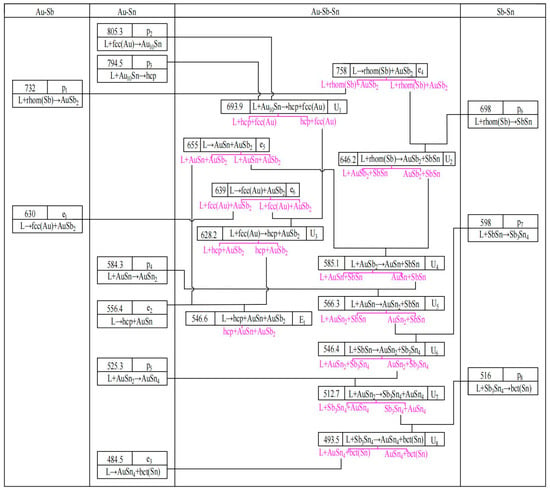
Figure 8.
Reaction scheme in the Au-Sb-Sn ternary system.

Table 4.
Invariant reactions of the Sb-Sn system.
Figure 9 is the calculated isothermal section of the Au-Sb-Sn ternary system at 523 K of this work with the experimental results of Schubert et al. [] and the calculated results of Kim et al. []. Although both Au-Sn and Sb-Sn binary phase diagrams show the liquid phase to be stable at 523 K on the Sn-rich side, the liquid phase and Sb3Sn4 were not observed by Schubert et al. []. Thus, the experimental results of the isothermal section at 523 K measured by Schubert et al. [] were used as a guide for the Au-rich part. The calculated isothermal section at 523 K was in good agreement with the experimental data measured by Schubert et al. [].
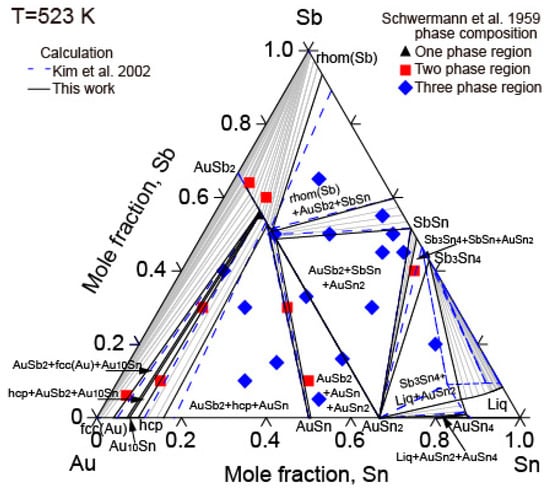
Figure 9.
Calculated isothermal sections of the Au-Sb-Sn ternary system at different temperatures in relation to the experimental data from [] and the calculated results data from [] at 523 K.
Figure 10 shows the calculated vertical section of 64.5 at.% Au with the experimental data [] and the calculated results []. The calculated results in this work were quite close to the assessment by Kim et al. [] and agree reasonably well with the experimental data []. The calculated vertical sections with different molar ratios ( = 2:1, = 1:1, = 1:2) with the experimental data [] and the calculated results [] are depicted in Figure 11. The calculated three vertical sections in this work were consistent with the experimental data [].
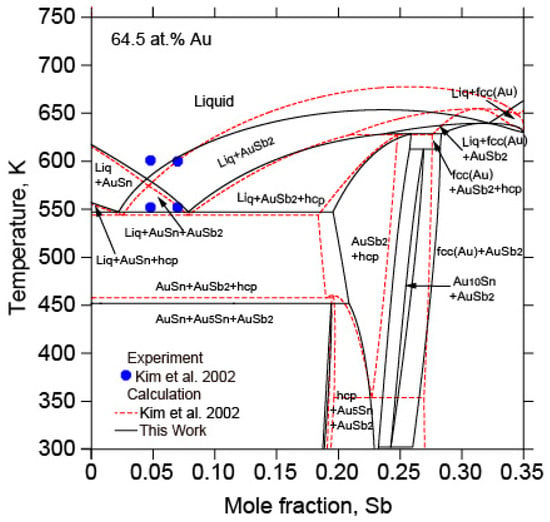
Figure 10.
The calculated vertical section of 64.5 at.% Au in the Au-Sb-Sn ternary system in relation to the experimental data from [] and the calculated results data from [].
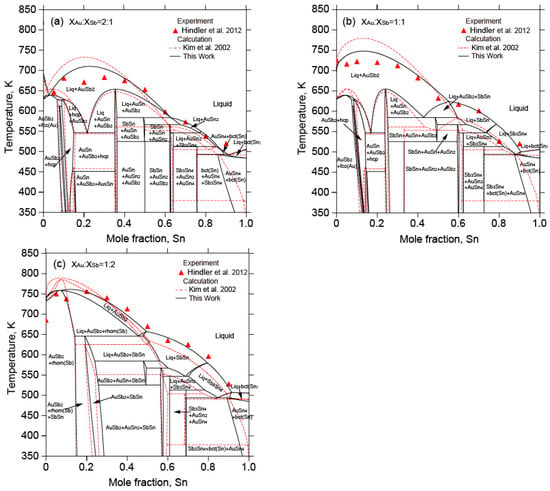
Figure 11.
Calculated vertical sections of the Au-Sb-Sn ternary system in relation to the experimental data from [] and the calculated results data from []. (a)
= 2:1; (b) = 1:1; (c) = 1:2.
Figure 12 is the calculated enthalpy of mixing of the liquid Au-Sb-Sn alloys at 873 K and 1078 K along different sections ( = 2:1, = 1:1, = 1:2) with the experimental data [,] and the calculated results []. It can be seen that the current calculated results were in good agreement with the experimental data [,], while the calculated results of Kim et al. [] were much more negative. Finally, the calculated enthalpies of mixing of liquid Au-Sb-Sn alloys ( = 2:1, = 1:1, = 1:2) with the experimental data [] and the calculated results [] at 873 K are depicted in Figure 13. The calculated results of this work are better in relation to the experimental data []. Figure 14 illustrates the calculated enthalpies of mixing of liquid Au-Sb-Sn alloys along different sections ( = 2:1, = 1:1, = 1:2) in relation to the experimental data [] and the calculated results []. The calculated results in this work are reasonably consistent with the experimental data [] and were better than the calculated results [].
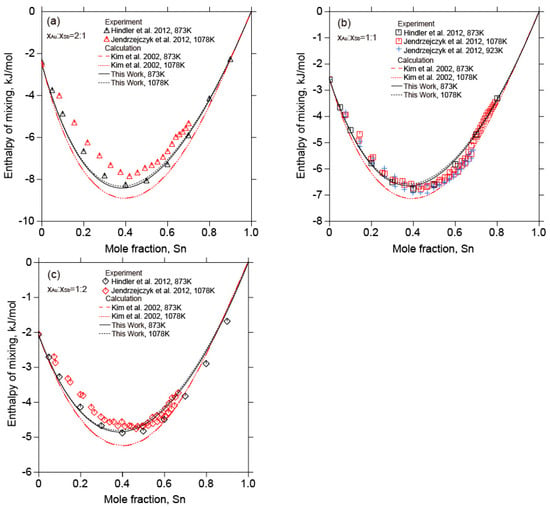
Figure 12.
Calculated enthalpies of mixing of liquid Au-Sb-Sn alloys in relation to the experimental data from [,] and the calculated results [] at 873 K and 1078 K (Reference states: liquid Au, liquid Sb, and liquid Sn). (a)
= 2:1; (b) = 1:1; (c) = 1:2.
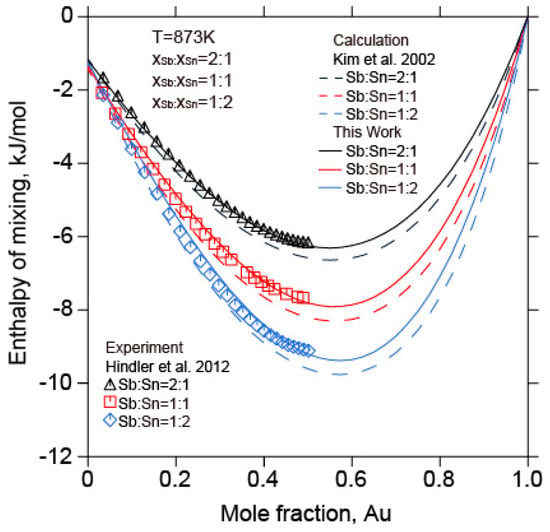
Figure 13.
The calculated enthalpies of mixing of liquid Au-Sb-Sn alloys (
= 2:1, = 1:1, = 1:2) in relation to the experimental data from [] and the calculated results data from [] at 873 K (Reference states: liquid Au, liquid Sb, and liquid Sn).
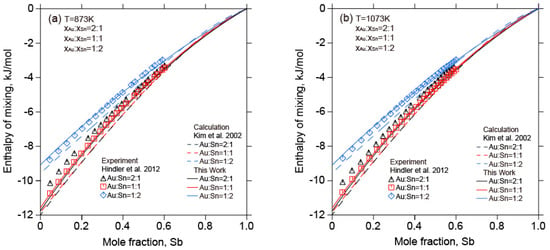
Figure 14.
The calculated enthalpies of mixing of liquid Au-Sb-Sn alloys (
= 2:1, = 1:1, = 1:2) in relation to the experimental data from [] and the calculated results data from [] (Reference states: liquid Au, liquid Sb, and liquid Sn). (a) 873 K; (b) 1073 K.
Figure 15 shows the calculated activity of Sn in liquid Au-Sb-Sn alloys along different sections ( = 2:1, = 1:1, = 1:2) at 873 K and 1273 K in relation to the experimental data [,]. A slight deviation from the experimental data [] at 1273 K was found. Nonetheless, good agreement was still achieved between the calculated activity of Sn in liquid Au-Sb-Sn alloys in this work and the experimental results [,].
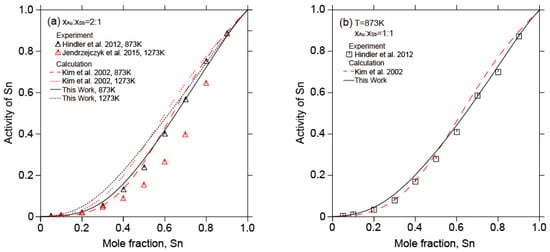
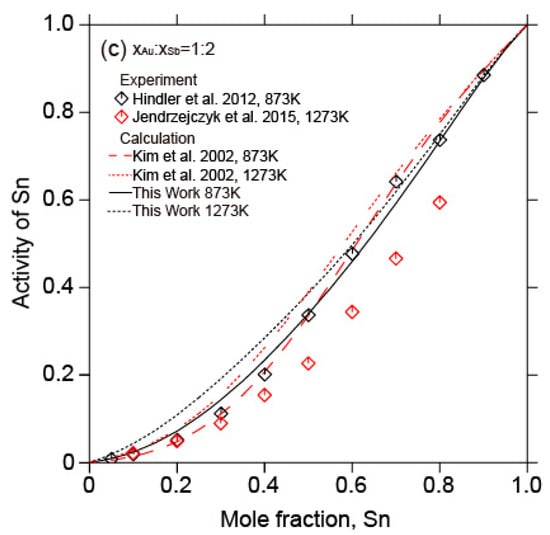
Figure 15.
Calculated activity of Sn in liquid Au-Sb-Sn alloys (
= 2:1, = 1:1, = 1:2) in relation to the experimental data from [,] and the calculated results data from [] at 873 K and 1273 K. (Reference states: liquid Au, liquid Sb, and liquid Sn).
6. Conclusions
In this work, the thermodynamic calculations of the Sb-Sn binary system and Au-Sb-Sn ternary system were performed thermodynamically using the CALPHAD method using experimental phase equilibrium and thermodynamic property data. The following conclusions were drawn:
- The phase transition temperatures of five Sb-Sn alloys were measured using differential thermal analysis (DTA). The temperatures of three invariant reactions (L + Sb3Sn4 ↔ bct(Sn), L + SbSn ↔ Sb3Sn4, and L + rhom(Sb) ↔ SbSn) were determined to be 516 K, 598 K, and 695 K, respectively. Using the experimental results measured in this work and reported results, the Sb-Sn binary system was re-optimized using the CALPHAD method. The calculated results were consistent with the experimental data, including phase equilibria and thermodynamic properties.
- In combination with the previous assessments of the Au-Sn and Au-Sb binary systems and the present optimization of the Sb-Sn binary system, a thermodynamic description of the Au-Sb-Sn ternary system was performed based on the available experimental information on the Au-Sb-Sn ternary system. The calculated liquidus projection, isothermal sections, vertical sections, as well as enthalpy of mixing and activity of Sn in liquid alloys, were consistent with the reported experimental results. A self-consistent set of thermodynamic parameters were obtained to accurately describe Gibbs energies of various phases in the Au-Sb-Sn ternary system, which could serve as a sound basis for developing a thermodynamic database of multicomponent Au-Sn-based alloy systems.
Author Contributions
Conceptualization, J.G.; data curation, J.G., Q.T. and J.W.; investigation, J.G., Q.T., H.Y. and Y.B.; validation, Q.T., H.Y., M.R. and Y.B.; writing—original draft, J.G. and J.W.; software, J.G.; writing—review & editing, J.G. and J.W.; supervision, M.R. and J.W.; funding acquisition, M.R. and J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by China (151009-Z) and Guangxi Undergraduate Training Program for Innovation (S202110595243).
Data Availability Statement
All the data that support the findings of this study are included within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xu, J.; Wu, M.; Pu, J.; Xue, S. Novel Au-Based Solder Alloys: A Potential Answer for Electrical Packaging Problem. Adv. Mater. Sci. Eng. 2020, 2020, 1–16. [Google Scholar] [CrossRef]
- Wang, L.; Xue, S.; Liu, H.; Lin, Y.; Chen, H. Research Progress of Au-20Sn Solder for Electronic Packaging. Cailiao Daobao 2019, 33, 2483–2489. [Google Scholar] [CrossRef]
- Zhang, H.; Minter, J.; Lee, N. A brief review on high-temperature, Pb-free die-attach materials. J. Electron. Mater. 2019, 48, 201–210. [Google Scholar] [CrossRef]
- Rerek, T.; Skowronski, L.; Kobierski, M.; Naparty, M.K.; Derkowska-Zielinska, B. Microstructure and opto-electronic properties of Sn-rich Au-Sn diffusive solders. Appl. Surf. Sci. 2018, 451, 32–39. [Google Scholar] [CrossRef]
- Peng, J.; Wang, M.; Sadeghi, B.; Wang, R.; Liu, H.; Cavaliere, P. Increasing shear strength of Au-Sn bonded joint through nano-grained interfacial reaction products. J. Mater. Sci. 2021, 56, 7050–7062. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, D.; Xiong, J.; Chen, C.; Song, T.; Li, L.; Huang, S. Microstructure evolution and properties of rapidly solidified Au-20Sn eutectic solder prepared by single-roll technology. J. Alloys Compd. 2019, 781, 873–882. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, L.; Li, M. Structure and Properties of Au–Sn Lead-Free Solders in Electronic Packaging. Mater. Trans. 2022, 63, 93–104. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.J.; Tang, C.Y.; Liu, L.B.; Zhou, H.Y.; Jin, Z.P. Thermodynamic description of the Au-Ag-Ge ternary system. Thermochim. Acta 2011, 512, 240–246. [Google Scholar] [CrossRef]
- Kim, J.H.; Jeong, S.W.; Lee, H.M. A thermodynamic study of phase equilibria in the Au-Sb-Sn solder system. J. Electron. Mater. 2002, 31, 557–563. [Google Scholar] [CrossRef]
- Schubert, K.; Breimer, H.; Gohle, R. The structure of the gold-indium, gold-tin, gold-indium-tin, and gold-tin-antimony systems. Z. Fur Met. 1959, 50, 146–153. [Google Scholar]
- Humpston, G. The Constitution of Some Ternary Au-Based Solder Alloys; University of Brunel: London, UK, 1985. [Google Scholar]
- Hindler, M.; Guo, Z.; Mikula, A. Lead-free solder alloys: Thermodynamic properties of the (Au+Sb+Sn) and the (Au+Sb) system. J. Chem. Thermodyn. 2012, 55, 102–109. [Google Scholar] [CrossRef] [PubMed]
- Jendrzejczyk-Handzlik, D.; Fitzner, K. Mixing enthalpies of liquid Au-Sb-Sn alloys. Mon. Für Chem. Chem. Mon. 2012, 143, 1225–1233. [Google Scholar] [CrossRef]
- Jendrzejczyk-Handzlik, D.; Fitzner, K. Thermodynamic properties of liquid (antimony+tin) and (gold+antimony+tin) alloys determined from e.m.f. measurements. J. Chem. Thermodyn. 2015, 85, 86–93. [Google Scholar] [CrossRef]
- Ågren, J. The materials genome and CALPHAD. Chin. Sci. Bull. 2014, 59, 1635–1640. [Google Scholar] [CrossRef]
- Chevalier, P.Y. A thermodynamic evaluation of the Au-Sb and Au-Ti systems. Thermochim. Acta 1989, 155, 211–225. [Google Scholar] [CrossRef]
- Liu, H.S.; Liu, C.L.; Wang, C.; Jin, Z.P.; Ishida, K. Thermodynamic modeling of the Au-ln-Sb system. J. Electron. Mater. 2003, 32, 81–88. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.J.; Liu, L.B.; Zhou, H.Y.; Jin, Z.P. Thermodynamic modeling of the Au-Sb-Si ternary system. J. Alloys Compd. 2011, 509, 3057–3064. [Google Scholar] [CrossRef]
- Gierlotka, W. Thermodynamic description of the binary Au-Sb and ternary Au-In-Sb systems. J. Alloys Compd. 2013, 579, 533–539. [Google Scholar] [CrossRef]
- Dong, H.Q.; Tao, X.M.; Laurila, T.; Vuorinen, V.; Paulasto-Kröckel, M. Thermodynamic modeling of Au-Ce-Sn ternary system. Calphad 2013, 42, 38–50. [Google Scholar] [CrossRef]
- Chevalier, P.Y. A thermodynamic evaluation of the Au-Sn system. Thermochim. Acta 1988, 130, 1–13. [Google Scholar] [CrossRef]
- Liu, H.S.; Liu, C.L.; Ishida, K.; Jin, Z.P. Thermodynamic Modeling of the Au-In-Sn System. J. Electron. Mater. 2003, 32, 1290–1296. [Google Scholar] [CrossRef]
- Dong, H.Q.; Jin, S.; Zhang, L.G.; Wang, J.S.; Tao, X.M.; Liu, H.S.; Jin, Z.P. Thermodynamic Assessment of the Au-Co-Sn Ternary System. J. Electron. Mater. 2009, 38, 2158–2169. [Google Scholar] [CrossRef]
- Grolier, V.; Schmid-Fetzer, R. Thermodynamic evaluation of the Au-Sn system. Int. J. Mater. Res. 2007, 98, 797–806. [Google Scholar] [CrossRef]
- Gao, F.; Wang, C.; Liu, X.; Takaku, Y.; Ohnuma, I.; Ishida, K. Thermodynamic assessment of phase equilibria in the Sn-Au-Bi system with key experimental verification. J. Mater. Res. 2010, 25, 576–586. [Google Scholar] [CrossRef]
- Schmetterer, C.; Polt, J.; Flandorfer, H. The phase equilibria in the Sb-Sn system-Part I: Literature review. J. Alloys Compd. 2017, 728, 497–505. [Google Scholar] [CrossRef]
- Okamoto, H. Sb-Sn (Antimony-Tin). J. Phase Equilib. Diffus. 2012, 33, 347. [Google Scholar] [CrossRef]
- Chen, S.; Chen, C.; Gierlotka, W.; Zi, A.; Chen, P.; Wu, H. Phase equilibria of the Sn-Sb binary system. J. Electron. Mater. 2008, 37, 992–1002. [Google Scholar] [CrossRef]
- Schmetterer, C.; Polt, J.; Flandorfer, H. The phase equilibria in the Sb-Sn system-Part II: Experimental results. J. Alloys Compd. 2018, 743, 523–536. [Google Scholar] [CrossRef]
- Gierlotka, W. On the binary Sb-Sn system: Ab initio calculation and thermodynamic remodeling. J. Mater. Sci. 2019, 55, 347–357. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J.; Yuan, Y. A thermodynamic assessment of the Mg-Sn-Sb ternary system. Calphad 2021, 75, 102361. [Google Scholar] [CrossRef]
- Ohtani, H.; Okuda, K.; Ishida, K. Thermodynamic study of phase equilibria in the Pb-Sn-Sb system. J. Phase Equilib. 1995, 16, 416–429. [Google Scholar] [CrossRef]
- Okamoto, H. Sb-Sn (Antimony-Tin). J. Phase Equilib. Diffus. 1998, 19, 292. [Google Scholar] [CrossRef]
- Predel, B.; Schwermann, W. Constitution and thermodynamics of antimony-tin system. J. Inst. Met. 1971, 99, 169–173. [Google Scholar]
- Jönsson, B.; Ågren, J. Thermodynamic assessment of Sb-Sn system. Mater. Sci. Technol. 1986, 2, 913–916. [Google Scholar] [CrossRef]
- Kroupa, A.; Vízdal, J. The Thermodynamic Database for the Development of Modern Lead-Free Solders. Defect Diffus. Forum 2007, 263, 99–104. [Google Scholar] [CrossRef]
- Borzone, G.; Delsante, S.; Li, D.; Novakovic, R. New Insights into Phase Equilibria of the Sb-Sn System. J. Phase Equilib. Diffus. 2021, 42, 63–76. [Google Scholar] [CrossRef]
- Lysenko, V.A. Thermodynamic reassessment of the Sb-Sn and In-Sb-Sn systems. J. Alloys Compd. 2019, 776, 850–857. [Google Scholar] [CrossRef]
- Wittig, F.E.; Gehring, E. Die Mischungswärmen des Antimons mit B-Metallen: III. Die Systeme mit Zinn und Blei. Ber. Bunsenges. Phys. Chem. 1967, 71, 372–376. [Google Scholar] [CrossRef]
- Sommer, F.; Lück, R.; Rupf-Bolz, N.; Predel, B. Chemical short range order in liquid Sb-Sn alloys proved with the aid of the dependence of the mixing enthalpies on temperature. Mater. Res. Bull. 1983, 18, 621–629. [Google Scholar] [CrossRef]
- Azzaoui, M.; Notin, M.; Hertz, J. Ternary experimental excess functions by means of high-order polynomials: Enthalpy of mixing of liquid Pb-Sn-Sb alloys. Int. J. Mater. Res. 1993, 84, 545–551. [Google Scholar] [CrossRef]
- Frantik, R.O.; Mcdonald, H.J. A Thermodynamic study of the tin-antimony system. Trans. Electrochem. Soc. 1945, 88, 243–251. [Google Scholar] [CrossRef]
- Itoh, K.; Koiko, K.; Narita, Y. Activity measurement of Pb-Sn and Sn-Sb based molten alloys. Nippon Kogo Kaishi 1980, 96, 97–101. [Google Scholar]
- Prince, A.; Raynor, G.V.; Evans, D.S. Phase Diagrams of Ternary Gold Alloys; CRC Press: Boca Raton, FL, USA, 1990; pp. 411–413. [Google Scholar]
- Version 5.0 of Unary Database. Available online: https://www.sgte.net/en/free-pure-substance-database (accessed on 27 April 2023).
- Redlich, O.; Kister, A.T. Thermodynamics of Nonelectrolyte Solutions. Ind. Eng. Chem. 1948, 40, 341–345. [Google Scholar] [CrossRef]
- Muggianu, Y.M.; Gambino, M.; Bros, J.P. Enthalpies of formation of liquid alloys bismuth-gallium-tin at 723k-choice of an analytical representation of integral and partial thermodynamic functions of mixing for this ternary-system. J. Chim. Phys. Phys.-Chim. Biol. 1975, 72, 83–88. [Google Scholar] [CrossRef]
- Sundman, B.; Jansson, B.; Andersson, J. The thermo-calc databank system. Calphad 1985, 9, 153–190. [Google Scholar] [CrossRef]
- Vassiliev, V.; Feutelais, Y.; Sghaier, M.; Legendre, B. Thermodynamic investigation in In-Sb, Sb-Sn and In-Sb-Sn liquid systems. J. Alloys Compd. 2001, 314, 198–205. [Google Scholar] [CrossRef]
- Iwase, K.; Aoki, N.; Osawa, A. DTA measurements in Sb-Sn alloys. Sci. Rep. Tohoku Imp. Univ. 1931, 20, 353. [Google Scholar]
- Loebe, R. Uber die Konstitution der ternaren Lagierungen von Blei, Zinn und Antimon. Metallurgie 1911, 8, 7–15. [Google Scholar]
- Witting, F.E.; Gehring, E. The activity of mixing antimony with tin metals. Ber. Bunsenges. Phys. Chem. 1971, 372–376. [Google Scholar]
- Yazawa, A.; Kawashima, T.; Itagaki, K. Measurements of Heats of Mixing in Liquid Alloys with the Adiabatic Calorimeter. J. Jap. I. Met. 1968, 32, 1281–1287. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).