A Uniformed Calculation Criterion on Heat Band Width of Local PWHT on Welded Joint with Dissimilar Thickness
Abstract
:1. Introduction
2. Finite Element Details
2.1. Geometric Model
2.2. Finite Element Model
2.3. Thermal Analysis
2.4. Stress Analysis
3. Results and Discussion
3.1. Welding Residual Stress Analysis
3.2. Residual Stress and Deformation Analysis by Conventional HB Width
3.3. Effects of Heat Band Width on Residual Stress and Deformation
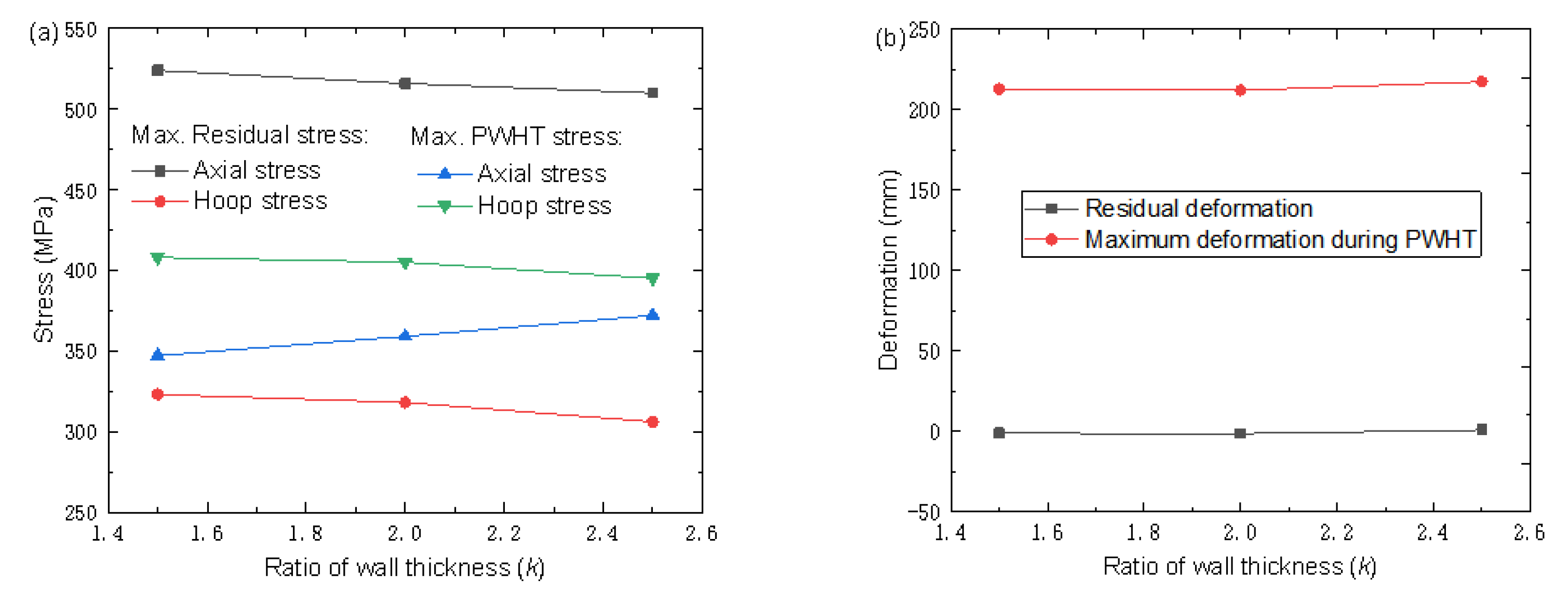
3.4. Optimization of HB Width for Different Thickness Ratios
3.5. Establish Uniformed Calculation Criterion of HB Width
4. Conclusions
- (1)
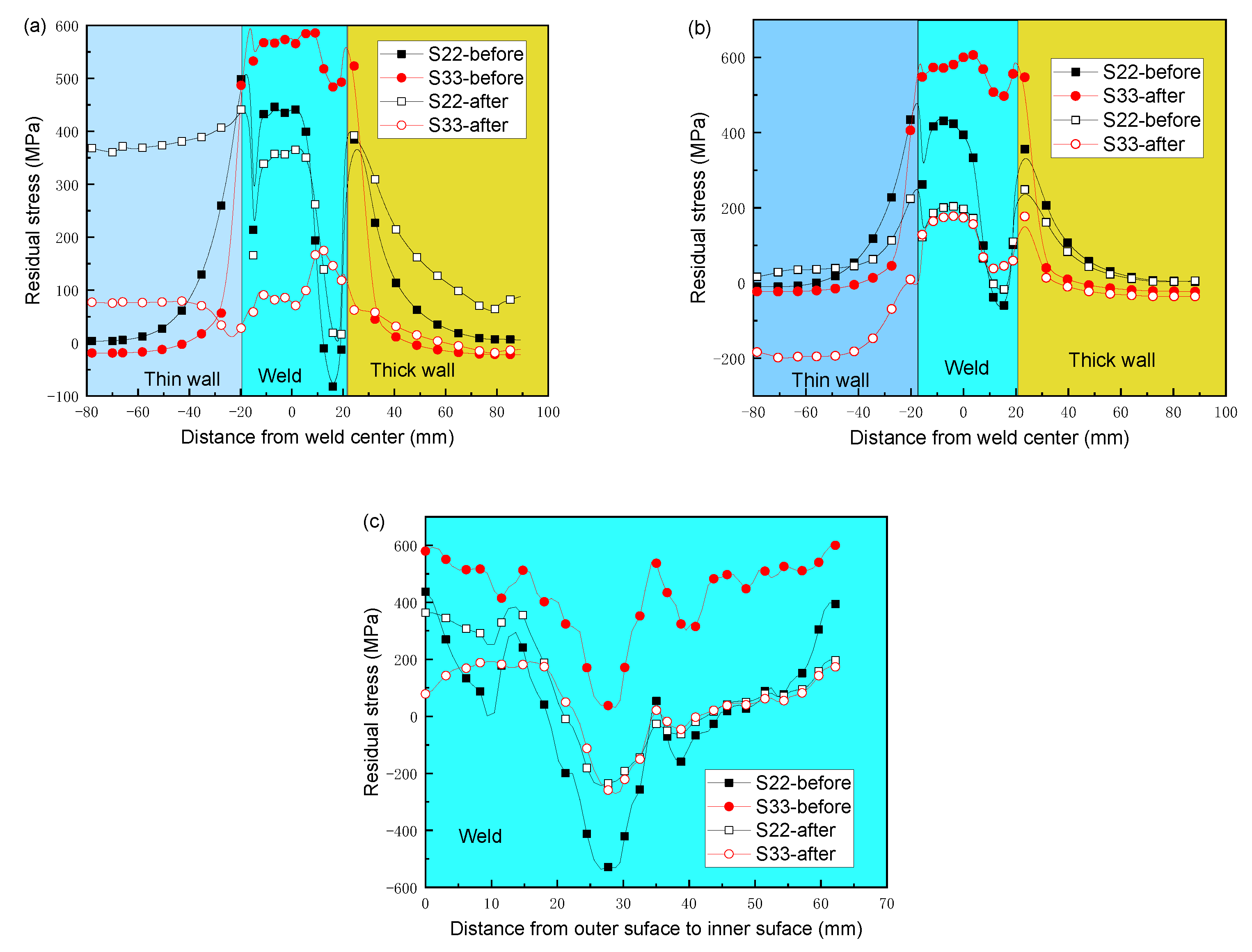
- The maximum axial and circumferential residual stresses are 536 MPa and 793 MPa, respectively, which are located in the weld toes on the outer and inner surfaces. The residual stresses inside the welded joint are relatively small. The hoop residual stresses in the weld of the inner and outer surfaces are larger than the axial residual stresses. From the inner surface to the outer surface, both hoop and axial residual stresses are decreased first and then increased.
- (2)
- The hoop stresses were decreased greatly both on the inner surface and the outer surface, as well as on the inside of the weld joint after PWHT. For the axial stresses, the variation law in the inner wall is different from the outer wall. From the outer surface to the depth of 27 mm, axial stresses were decreased after PWHT. However, the axial stresses from the inner surface to the depth of 35 mm were increased after PWHT. The axial stress in the thin wall is larger than that in the thick wall.
- (3)
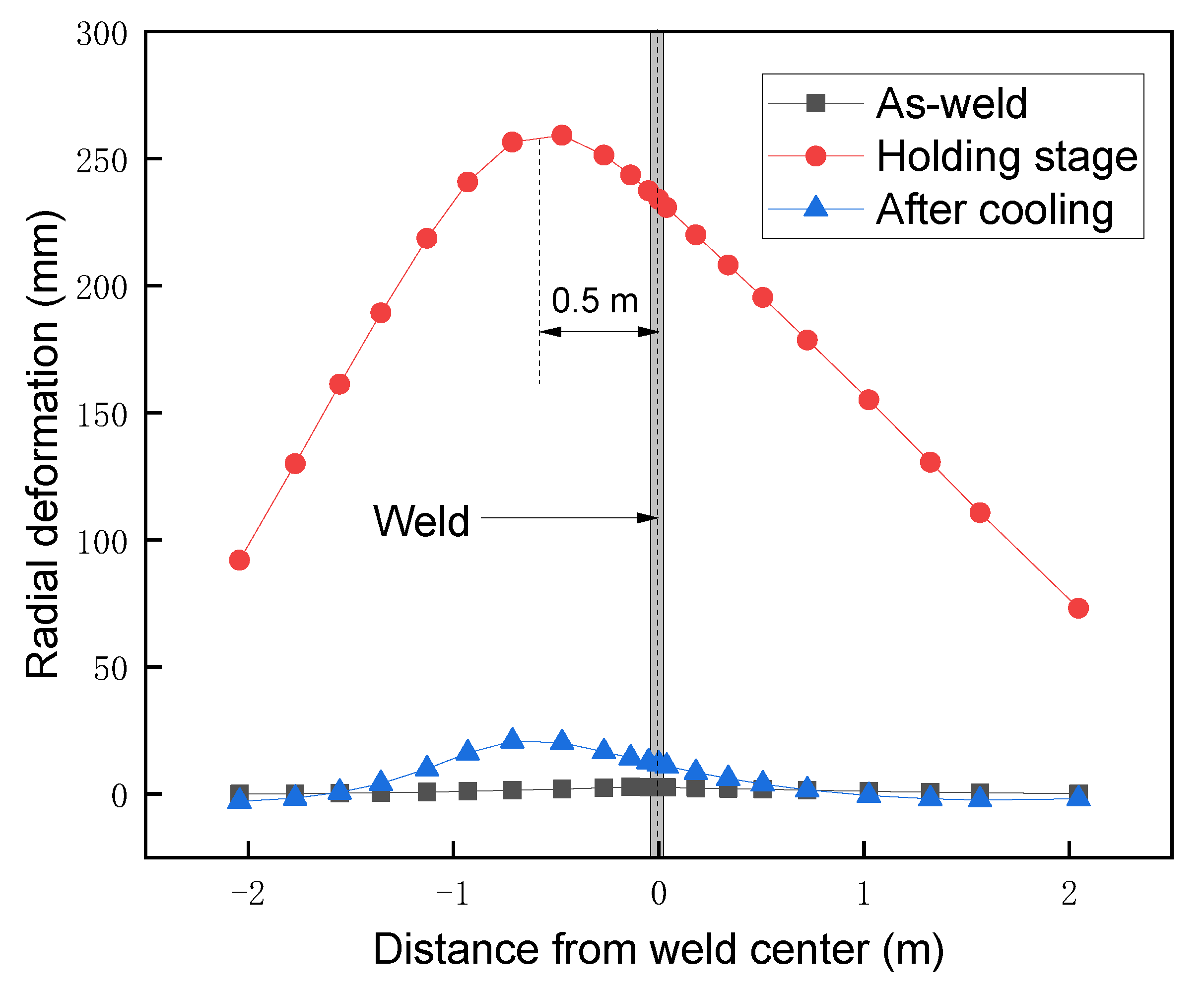
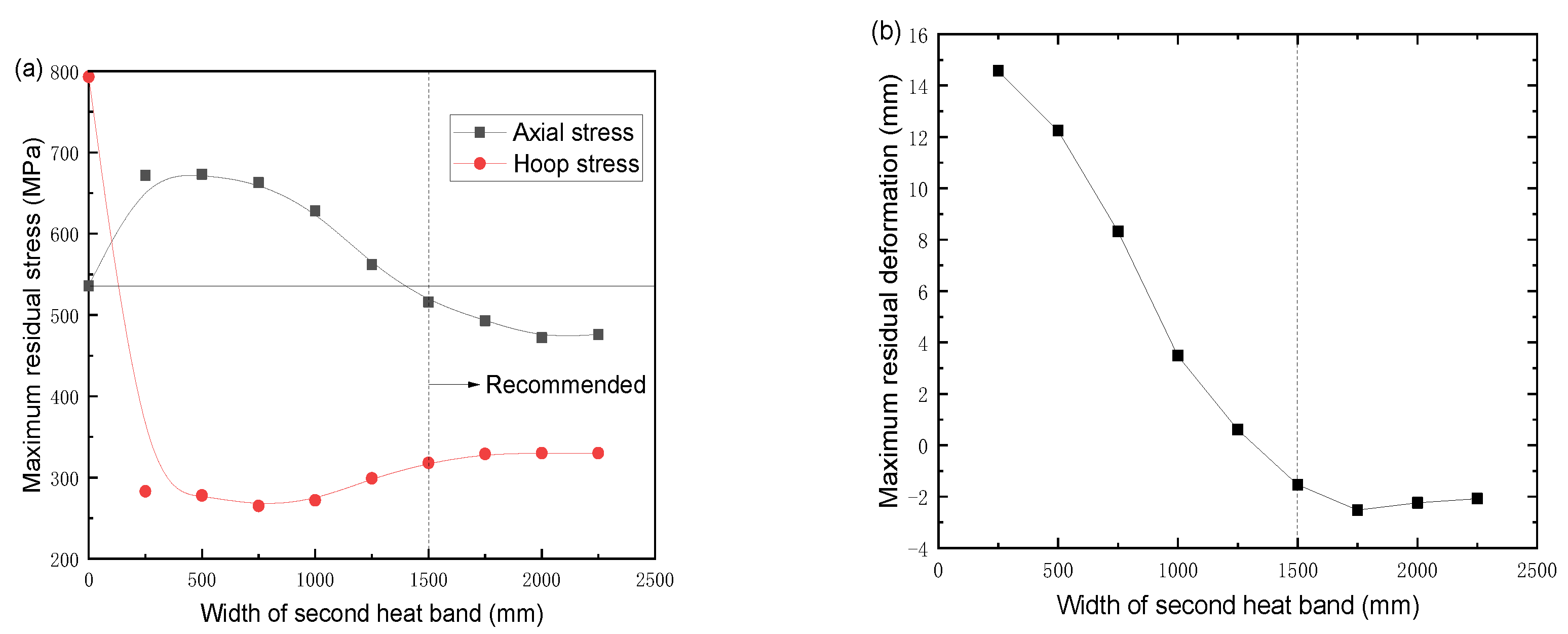
- By comparing the local heat treatment results under the width of the auxiliary heating zone, it is suggested that the width of the auxiliary heating zone of the post-weld heat treatment of the joint with a thickness ratio of 2 is 1500 mm. After heat treatment at the recommended auxiliary heating width, the circumferential stress is reduced by 60% compared with the as-welded state. The radial and axial reductions were 25.2% and 3.7%, respectively. The radial deformation around the welded joint during the holding stage is almost the same. Therefore, the additional bending stress in the weld toe induced by inconsistent deformation is eliminated, enhancing the ability to SCC of the weld joint.
- (4)
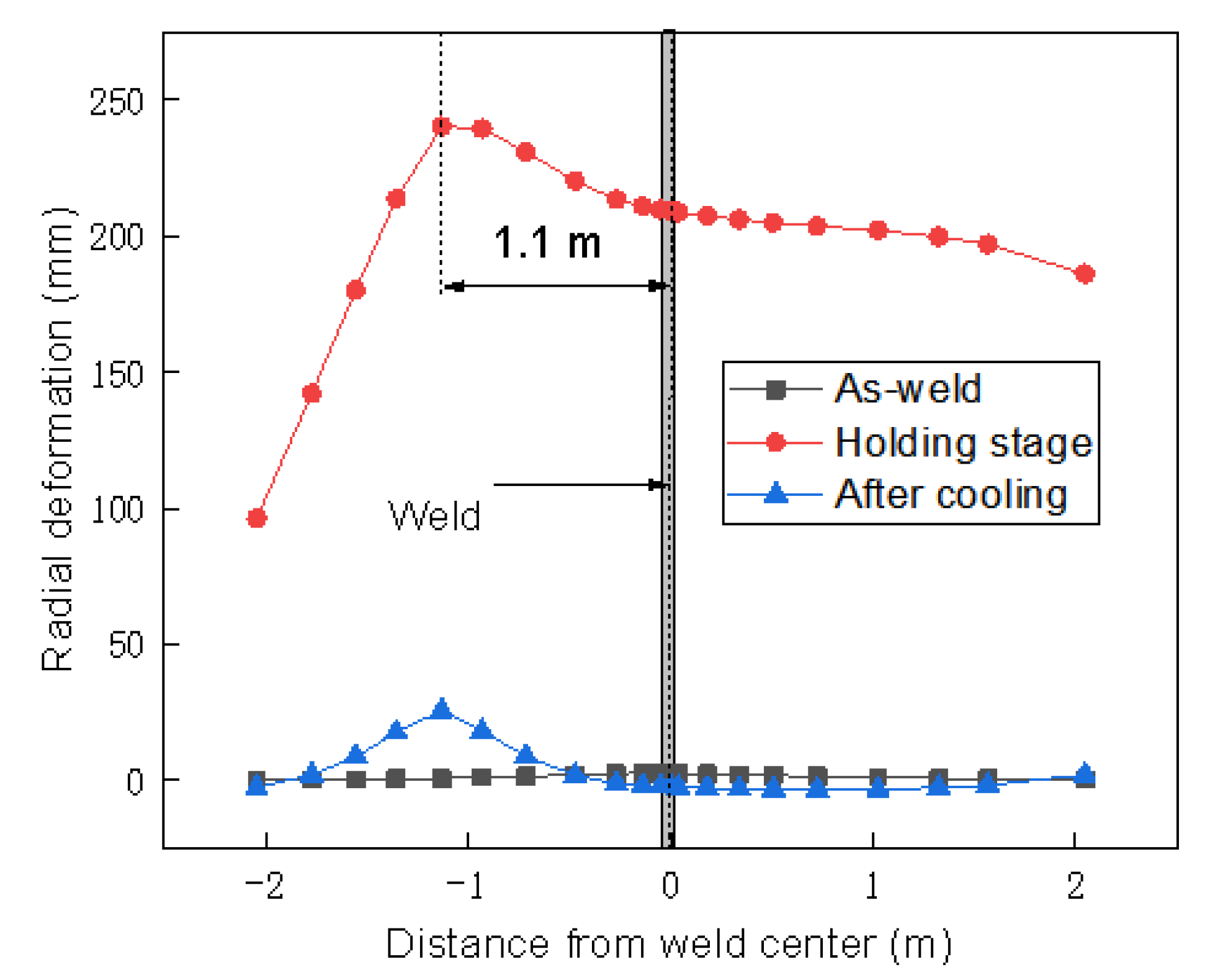
- The optimized auxiliary HB width for the thickness ratio k = 2.5, k = 2, and 1.5 are recommended as 1750 mm, 1500 mm, and 1250 mm. On the whole, the values of stress and deformation in the heat treatment process with different thickness ratios under the optimum heating width are not different. The standard for determining the optimal width of the heating band is consistent.
- (5)
- Comparing the heat treatment results of joints with different thickness ratios under the optimal heating width, it can be seen that the larger the thickness ratio, the larger the auxiliary heating width required to achieve the same heat treatment effect, and the two are positively correlated. The local heat treatment heating formula of unequal-thickness joints based on thickness ratio is further derived: for SA738Gr.B steel.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gain, S.; Das, S.K.; Acharyya, S.K.; Sanyal, D. Friction stir welding of industrial grade AISI 316L and P91 steel pipes: A comparative investigation based on mechanical and metallurgical properties. Int. J. Press. Vessel. Pip. 2023, 201, 104865. [Google Scholar] [CrossRef]
- Mohan Kumar, S.; Rajesh Kannan, A.; Pramod, R.; Siva Shanmugam, N.; Dhinakaran, V. Testing, characterization and numerical prediction (uni-axial tension and bend test) of Double-side TIG welded SS321 plate for pressure vessel application. Int. J. Press. Vessel. Pip. 2022, 197, 104648. [Google Scholar] [CrossRef]
- Huang, T.; Jin, L.; Chen, T.; Qiu, Z. Development and evaluation of welding repair for threaded hole of Reactor Pressure Vessel flange. Int. J. Press. Vessel. Pip. 2021, 197, 104341. [Google Scholar] [CrossRef]
- Zhang, W.; Fang, K.; Hu, Y.; Wang, S.; Wang, X. Effect of machining-induced surface residual stress on initiation of stress corrosion cracking in 316 austenitic stainless steel. Corros. Sci. 2016, 108, 173–184. [Google Scholar] [CrossRef]
- Shen, K.; Zhang, Z.; Jiang, W.; Luo, Y.; Su, H.; Zhang, Y. Generation of compressive residual stress at the root of tube-to-tubesheet welded joints in a heat exchanger. Int. J. Press. Vessel. Pip. 2022, 200, 104848. [Google Scholar] [CrossRef]
- Puliyaneth, M.; Chen, H. Study on the effect of welding residual stress on creep-cyclic plasticity behaviour. Int. J. Press. Vessel. Pip. 2021, 193, 104444. [Google Scholar] [CrossRef]
- Huang, J.; He, Z.; Guo, P.; Lv, S.; Song, J.; Liu, H.; Li, Z.; Fu, Z.; Lv, Y.; Sun, Y.; et al. Experimental investigation on creep strengthening phenomenon of a Ni-based single crystal superalloy under cyclic loading and unloading conditions. J. Alloy. Compd. 2023, 953, 170111. [Google Scholar]
- Fan, K.; Liu, D.; Liu, Y.; Wu, J.; Shi, H.; Zhang, X.; Zhou, K.; Xiang, J.; Magd Abdel Wahab. Competitive effect of residual stress and surface roughness on the fatigue life of shot peened S42200 steel at room and elevated temperature. Tribol. Int. 2023, 183, 108422. [Google Scholar] [CrossRef]
- Samadi, F.; Mourya, J.; Wheatley, G.; Khan, M.N.; Nejad, R.M.; Branco, R.; Macek, W. An investigation on residual stress and fatigue life assessment of T-shape welded joints. Eng. Fail. Anal. 2022, 141, 108422. [Google Scholar] [CrossRef]
- You, S.; Tang, J.; Zhou, W.; Zhao, J.; Chen, H. Research on calculation of contact fatigue life of rough tooth surface considering residual stress. Eng. Fail. Anal. 2022, 140, 106459. [Google Scholar] [CrossRef]
- Yu, B.; Wang, P.; Song, X.; Huo, S. The residual stress relief of post weld heat treatment in SMA490BW welded joints: Simulation and experiment. Int. J. Press. Vessel. Pip. 2022, 200, 104852. [Google Scholar] [CrossRef]
- Kumar, R.; Dey, H.C.; Pradhan, A.K.; Albert, S.K.; Thakre, J.G.; Mahapatra, M.M.; Pandey, C. Numerical and experimental investigation on distribution of residual stress and the influence of heat treatment in multi-pass dissimilar welded rotor joint of alloy 617/10Cr steel. Int. J. Press. Vessel. Pip. 2022, 199, 104715. [Google Scholar] [CrossRef]
- Sekhon, S.S.; Kumar, H.; Sehgal, S. Effect of tool pin profile on performance of friction stir welding of brass-copper-based butt welded joint. Int. J. Mater. Eng. Innov. 2016, 7, 236. [Google Scholar] [CrossRef]
- Luo, Y.; Jiang, W.; Yang, Z.; Wang, C.; Jin, Q.; Gao, T.; Yan, G.; Tu, S.; He, Y. Using reinforce plate to control the residual stresses and deformation during local post-welding heat treatment for ultra-large pressure vessels. Int. J. Press. Vessel. Pip. 2021, 191, 104332. [Google Scholar] [CrossRef]
- Qian, Y.; Zhao, J. Influences of local PWHT from different criteria at home and abroad on the residual stress of the under-matching welded joint. Int. J. Press. Vessel. Pip. 2017, 154, 11–16. [Google Scholar] [CrossRef]
- Citarella, R.; Cricrì, G.; Lepore, M.; Perrella, M. Thermo-mechanical crack propagation in aircraft engine vane by coupled FEM–DBEM approach. Adv. Eng. Softw. 2014, 67, 57–69. [Google Scholar] [CrossRef]
- Rajamurugan, G.; Suresh, S.; Krishnasamy, P. Influence of local post-weld heat treatment and its thermal analysis on thick wall carbon steel pipe. Mater. Today Proc. 2021, 46, 7076–7081. [Google Scholar] [CrossRef]
- Nie, C.; Dong, P. A Thermal stress mitigation technique for local postweld heat treatment of welds in pressure vessels. J. Press. Vessel Technol. 2015, 137, 051404. [Google Scholar] [CrossRef]
- Jin, Q.; Jiang, W.; Gu, W.; Wang, J.; Li, G.; Pan, X.; Song, M.; Zhang, K.; Wu, A.; Tu, S. A primary plus secondary local PWHT method for mitigating weld residual stresses in pressure vessels. Int. J. Press. Vessel. Pip. 2021, 192, 104431. [Google Scholar] [CrossRef]
- Geng, L.; Tu, S.; Gong, J.; Jiang, W.; Zhang, W. On Residual Stress and Relief for an Ultra-Thick Cylinder Weld Joint Based on Mixed Hardening Model: Numerical and Experimental Studies. J. Press. Vessel. Technol. 2018, 140, 041405. [Google Scholar] [CrossRef]
- Ueda, Y.; Yamakawa, T. Analysis of thermal elastic-plastic stress and strain during welding by finite element method. Trans. Jpn. Weld. Soc. 1971, 22, 186–196. [Google Scholar]
- Graßmann, M.; Schleich, F.; Stammler, M. Validation of a finite-element model of a wind turbine blade bearing. Finite Elem. Anal. Des. 2023, 221, 103957. [Google Scholar] [CrossRef]
- Kien, D.N.; Zhuang, X. Radial basis function based finite element method: Formulation and applications. Eng. Anal. Bound. Elem. 2023, 152, 455–472. [Google Scholar] [CrossRef]
- Smith, A.C.; Smith, M. NeT bead on plate round robin: Comparison of transient thermal predictions and measurements. Int. J. Press. Vessel. Pip. 2009, 86, 79–95. [Google Scholar] [CrossRef]
- Goldak, K.; Chakaravarti, A.; Bibby, M. A New Finite Element Model for Welding Heat Sources. Metall. Trans. B 1984, 15, 299–305. [Google Scholar] [CrossRef]
- Boiler and Pressure Vessel Code, Section Ⅲ, Rules for Construction of Nuclear Facility Components, Division 1, Subsection NE-4623. Class MC Components. ASME: New York, NY, USA, 2007; edition with 2008 Addenda. ASME BPVC.Ⅲ.1-2008. Available online: https://www.asme.org/codes-standards/find-codes-standards/bpvc-iii-ncd-bpvc-section-iii-rules-construction-nuclear-facility-components-division-1-subsection-ncd-class-2-class-3-components (accessed on 12 May 2023).
- ASME Boiler and Pressure Vessel Code Section Ⅷ, Division 1 Rules for Construction of Vessels. ASME: New York, NY, USA, 2019. ASME BPVC.Ⅷ.1-2019. Available online: https://www.asme.org/codes-standards/find-codes-standards/bpvc-viii-1-bpvc-section-viii-rules-construction-pressure-vessels-division-1/2023/print-book (accessed on 12 May 2023).
- Peng, W.; Jiang, W.; Sun, G.; Yang, B.; Shao, X.; Tu, S. Biaxial residual stress measurement by indentation energy difference method: Theoretical and experimental study. Int. J. Press. Vessel. Pip. 2022, 195, 104573. [Google Scholar] [CrossRef]
- GB/T 30583.4-2014; Specification for Post Weld Heat Treatment of Pressure Equipment. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China. Standardization Administration: Beijing, China, 2014.


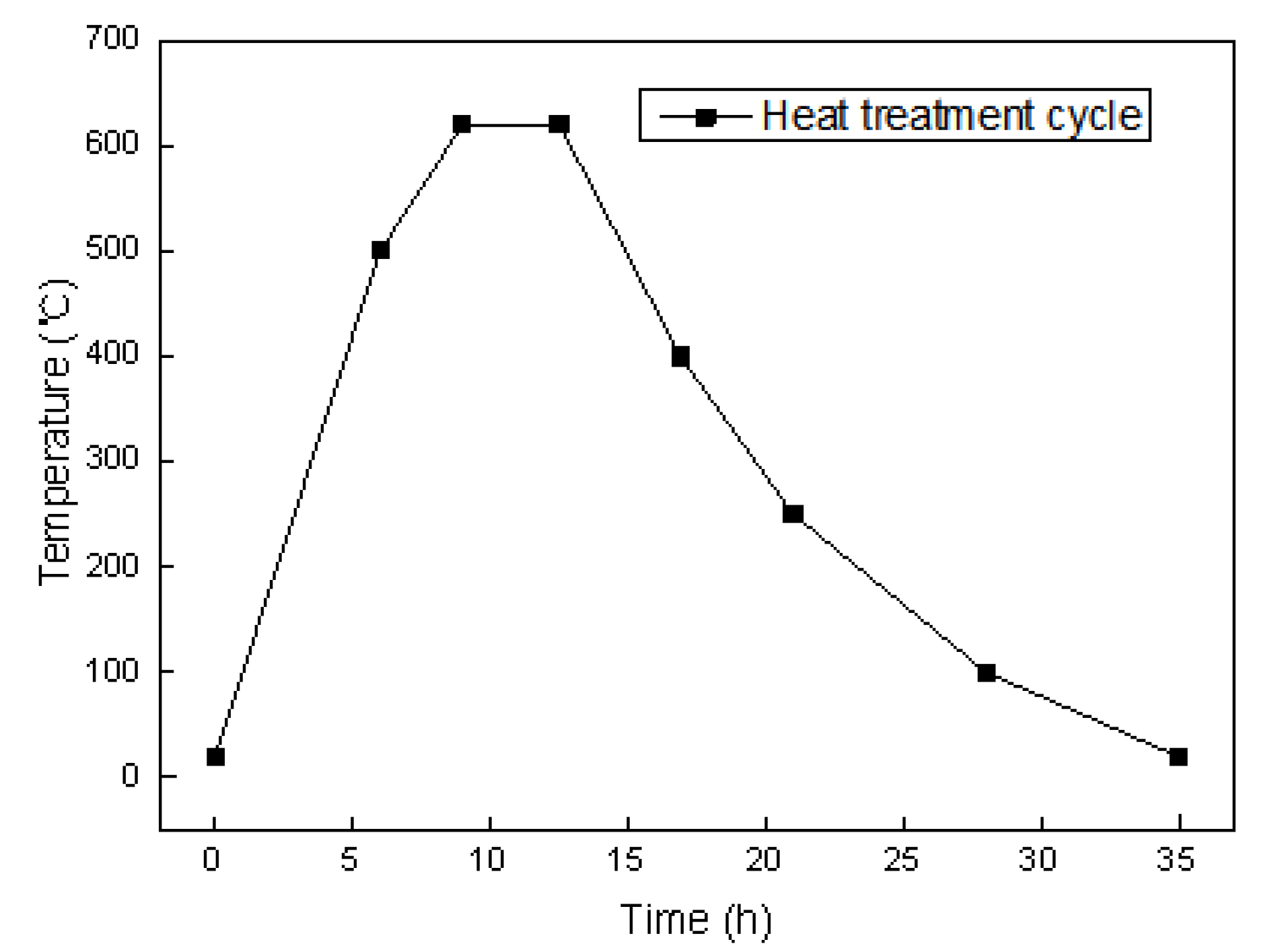

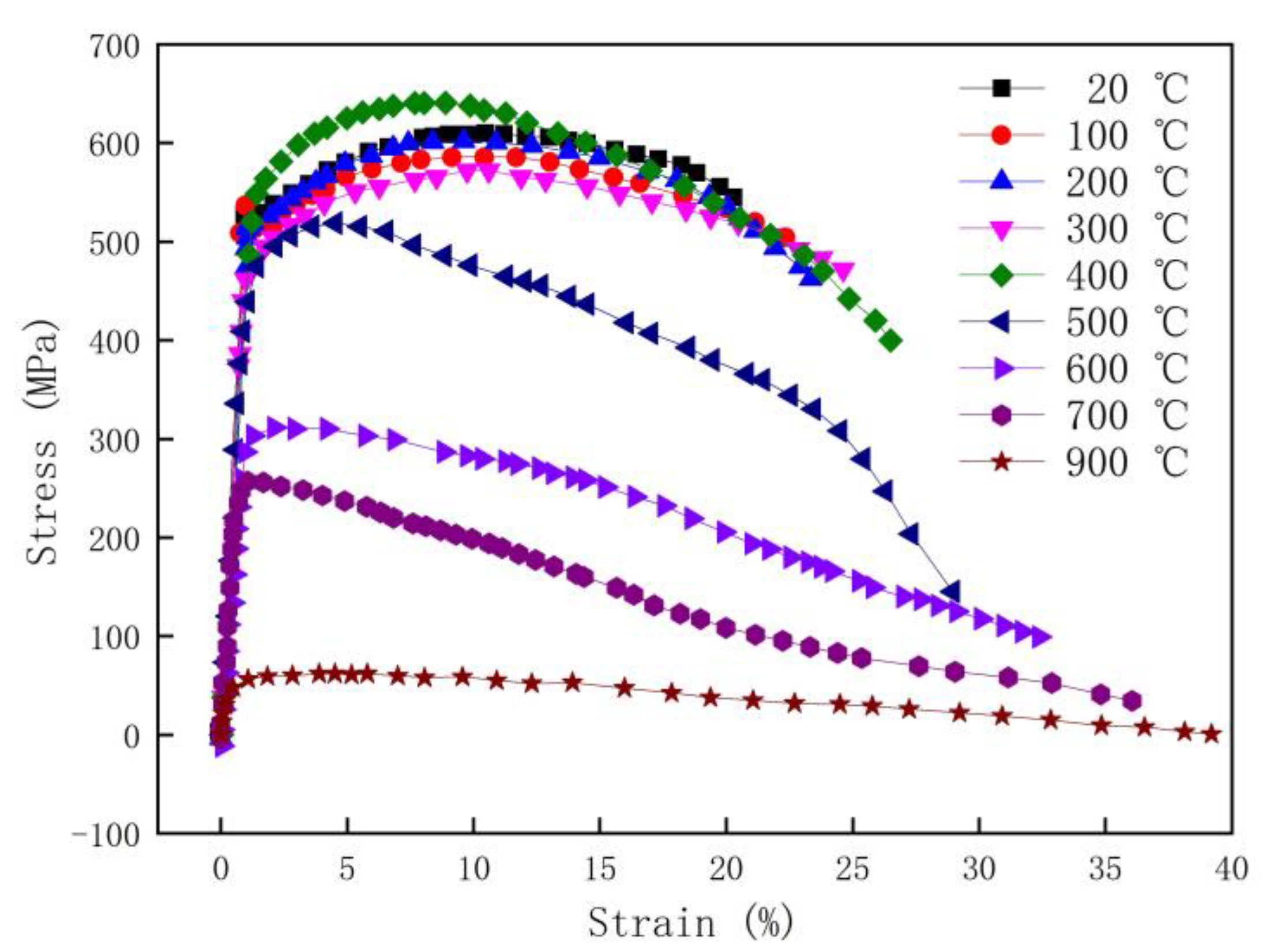

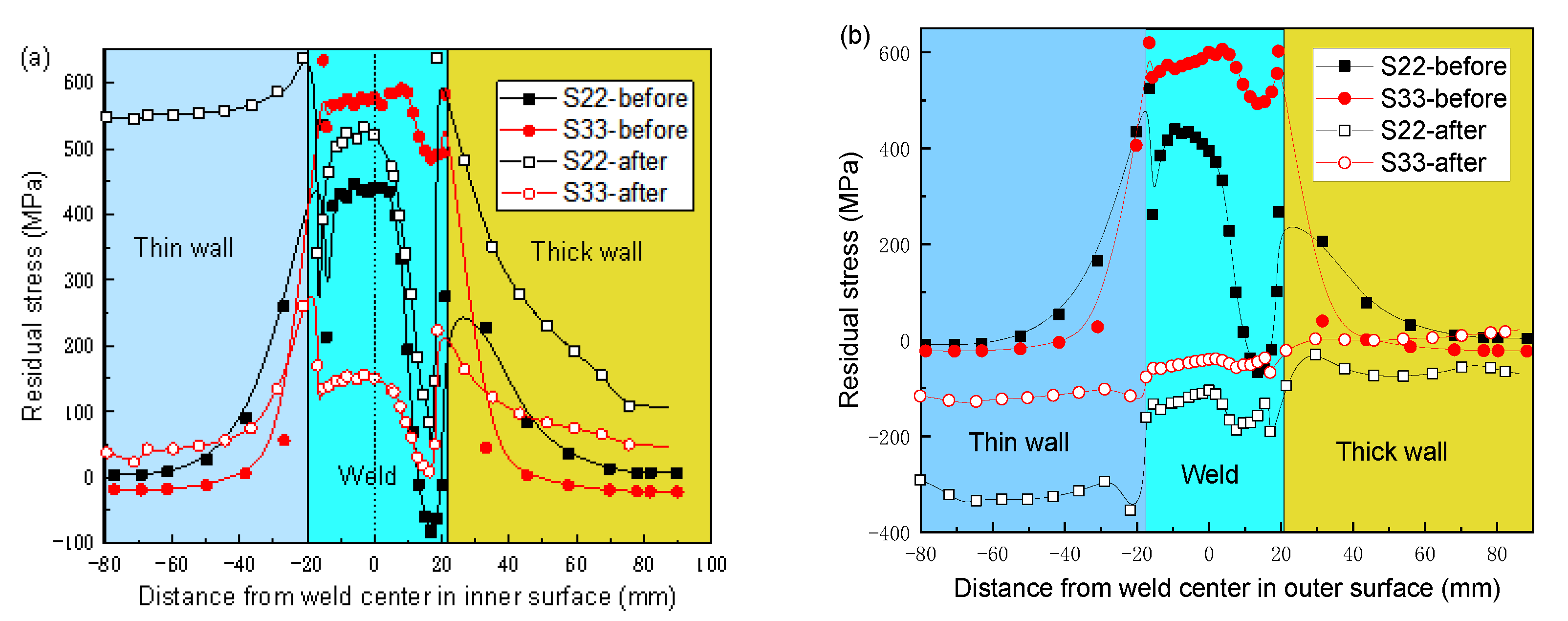
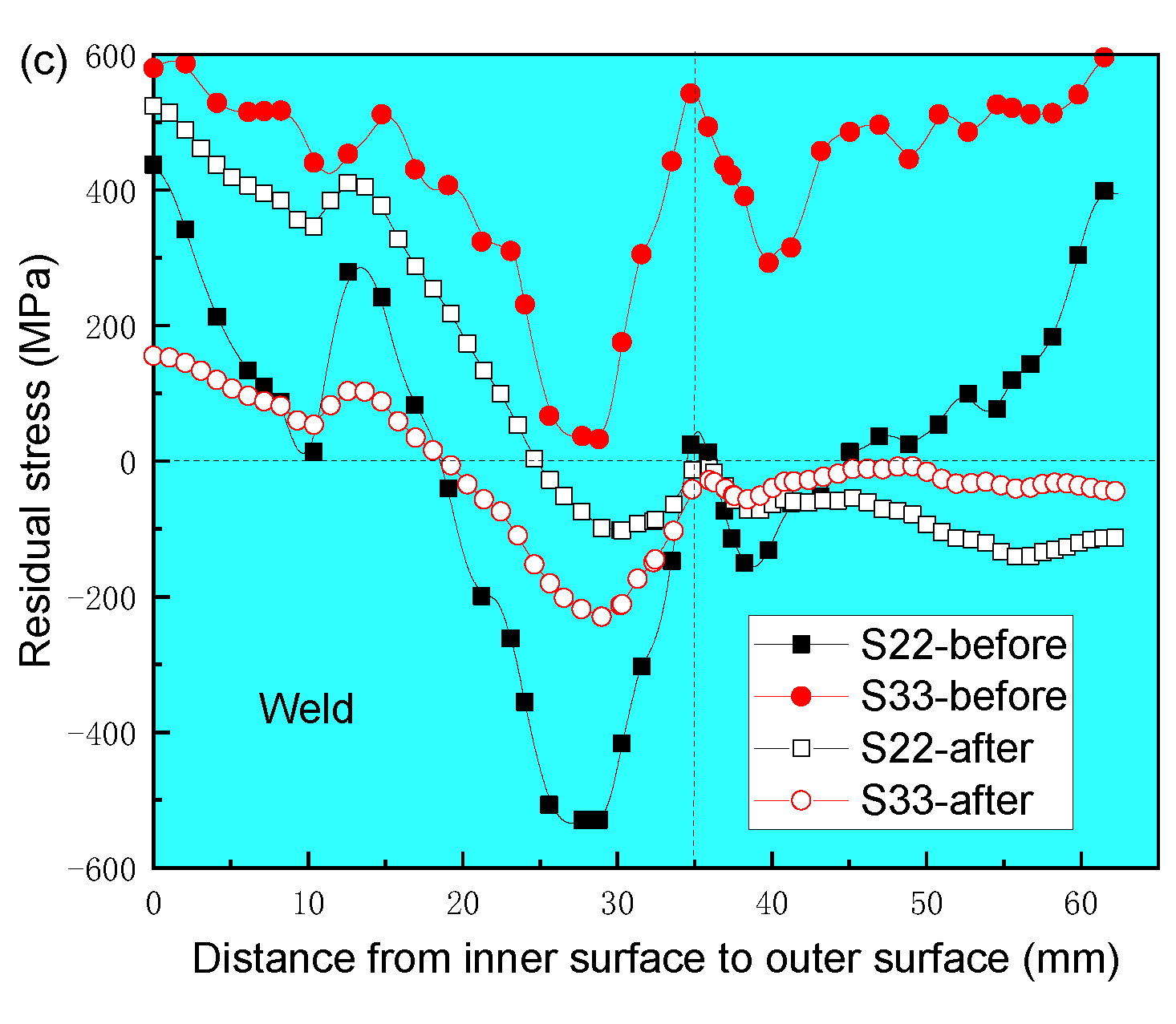



| Material | Fe | Al | Cr | Cu | Mn | Mo | Nb | Ni | Si | V | C | P | S |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Base | 97.143 | 0.028 | 0.18 | 0.02 | 1.44 | 0.2 | 0.51 | 0.3 | 0.3 | 0.04 | 0.11 | 0.0070 | 0.0020 |
| Filler | Bal. | - | ≤0.20 | ≤0.05 | 0.6~1.95 | ≤0.50 | - | 0.8~1.8 | ≤0.80 | ≤0.05 | ≤0.12 | ≤0.03 | ≤0.03 |
| Welding Layer | Welding Passes | Welding Current (A) | Welding Voltage (V) | Welding Speed (cm/min) | Max Heat Input (KJ/mm) |
|---|---|---|---|---|---|
| Backing layer | 1 | 140~155 | 19~30 | 6.6~12 | 38 |
| Filling layer | 2–6/16–24 | 110~120 | 20~25 | 5.5~10 | |
| Filling layer | 7–15/25–35 | 90~130 | 18~29 | 5.3~11 | 37 |
| Covering layer | 36–48 | 140~155 | 19~30 | 6.6~12 | 38 |
| Temperature (°C) | Density ρ × 10−3/(kg/m3) | Thermal Conductivity λ × 10−1/(W/m·°C) | Specific Heat c × 10−2/(J/kg·°C) | Average Expansion Coefficient α × 10−5/°C |
|---|---|---|---|---|
| 20 | 7.846 | 6.30455 | 4.54 | 1.30827 |
| 200 | 7.788 | 5.15221 | 5.28 | 1.36773 |
| 400 | 7.717 | 4.04449 | 6.8 | 1.45132 |
| 600 | 7.643 | 3.41335 | 8.8 | 1.53162 |
| 800 | 7.617 | 2.76772 | 9.99 | 1.19212 |
| 1000 | 7.538 | 2.8706 | 6.26 | 1.39518 |
| 1200 | 7.43 | 3.11267 | 6.56 | 1.58768 |
| 1400 | 7.321 | 3.35538 | 6.88 | 1.73079 |
| Temperature (°C) | 20 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 900 |
|---|---|---|---|---|---|---|---|---|---|
| Elastic modulus (GPa) | 194 | 206 | 180 | 206 | 179 | 186 | 141 | 135 | 123 |
| Tensile strength (MPa) | 674 | 652 | 651 | 654 | 692 | 617 | 318 | 250 | 175 |
| Yield strength (MPa) | 590 | 580 | 536 | 539 | 501 | 495 | 298 | 203 | 153 |
| Young’s modulus (GPa) | 209 | 205 | 196 | 186 | 182 | 175 | 157 | 146 | 38 |
| Poisson’s ratio | 0.29 | 0.29 | 0.29 | 0.30 | 0.30 | 0.31 | 0.31 | 0.32 | 0.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Xie, J.; Luo, Y. A Uniformed Calculation Criterion on Heat Band Width of Local PWHT on Welded Joint with Dissimilar Thickness. Metals 2023, 13, 1100. https://doi.org/10.3390/met13061100
Zhang Y, Xie J, Luo Y. A Uniformed Calculation Criterion on Heat Band Width of Local PWHT on Welded Joint with Dissimilar Thickness. Metals. 2023; 13(6):1100. https://doi.org/10.3390/met13061100
Chicago/Turabian StyleZhang, Yixuan, Jiameng Xie, and Yun Luo. 2023. "A Uniformed Calculation Criterion on Heat Band Width of Local PWHT on Welded Joint with Dissimilar Thickness" Metals 13, no. 6: 1100. https://doi.org/10.3390/met13061100
APA StyleZhang, Y., Xie, J., & Luo, Y. (2023). A Uniformed Calculation Criterion on Heat Band Width of Local PWHT on Welded Joint with Dissimilar Thickness. Metals, 13(6), 1100. https://doi.org/10.3390/met13061100







