Using an Internal State Variable Model Framework to Investigate the Influence of Microstructure and Mechanical Properties on Ballistic Performance of Steel Alloys

Abstract

An internal state variable (ISV)-based constitutive model has been used within a Lagrangian finite element analysis (FEA) framework to simulate ballistic impact of monolithic rolled homogenous armor (RHA) steel plates by RHA steel spheres and cylinders. The ISV model predictions demonstrate good agreement with experimental impact data for spherical projectiles. A simulation-based parametric sensitivity study was performed to determine the influence of a variety of microstructural and mechanical properties on ballistic performance. The sensitivity analysis shows that the lattice hydrogen concentration, material hardness, and initial void volume fraction are dominant factors influencing ballistic performance. Finite element simulations show that variation of microstructure properties could explain the reduced ballistic performance of high hardness materials previously documented in the literature. The FEA framework presented in this work can be used to determine material properties conducive to ballistic-impact resistance.

1. Introduction

1.1. Ballistic Impact Modeling and Experiments

The ballistic impact of ductile metals is a topic of interest for defense and space applications. A summary of seminal experimental impact results and discussions of basic penetration mechanisms is given in [1,2]. These studies characterize a number of plate impact perforation mechanisms as (1) fracture due to stress waves [3,4,5,6,7], (2) radial fracture behind a stress wave [5,8,9,10,11], (3) spallation [9,12,13,14,15,16,17], (4) shear plugging [13,18,19,20,21,22,23,24,25], (5) petaling [19,26,27,28,29,30,31,32], (6) fragmentation [9,33,34,35,36,37,38], and (7) ductile-hole enlargement [39,40,41,42]. The current work primarily focuses on perforation mechanisms of plasticity-induced ruptures related to ductile-hole enlargement and shear plugging.

A wealth of experimental and numerical model data pertaining to material ballistic impact performance exist in the literature. The behavior of a variety of metal plates subjected to normal and oblique impacts by projectiles of varying shapes, sizes, and materials has been discussed [20,43,44,45,46,47,48,49]. Additionally, ref. [50] contains experimental data for hundreds of projectile/target configurations and test conditions. Examples of numerical ballistic penetration models can be found in [51,52,53,54,55,56,57,58,59,60,61,62]. In general, ballistic perforation resistance strongly correlates to the target materials’ strength and hardness values. However, refs. [56,63,64] observed that some steel plates exhibited a decrease in ballistic performance at high hardness values, typically exceeding 400 Brinell hardness number (BHN). Mescall and Rogers [63] attributed this diminishing performance to a change in penetration mechanisms from rupture due to large plastic flow at low hardness values to perforation by localized adiabatic shear-band-driven plugging at high hardness. They surmised that the localized shear banding was driven by an increase in the number of microstructure heterogeneities with increasing hardness resulting from different quench and heat treatment conditions necessary to achieve the desired steel hardness. Recent studies [65,66,67] also attributed the formation of adiabatic shear bands under ballistic impact conditions to rotational dynamic recrystallization and grain growth mechanisms. Mescall and Rogers [63] showed that ballistic performance differences between similar steel alloys is strongly driven by the material’s processing history and subsequent microstructure features, with particular emphasis on the deleterious effect of microstructure impurities and heterogeneities. While the authors theorized that increasing the quantity of microstructure impurities tends to induce localized failure and reduces ballistic performance of target materials, no quantitative correlation between microstructure properties and ballistic performance was established. Throughout the relevant literature, there is an absence of quantitative correlation of material microstructure characteristics and ballistic impact outcomes in steels. Furthermore, commonly used phenomenological constitutive models lacking microstructure property considerations (e.g., the Johnson–Cook model [51]) struggle to capture this microstructure-influenced bifurcation in material behavior during ballistic impact [56].

In this study, the microstructural influences resulting in decreasing ballistic performance at high material hardness [63] are investigated using an internal state variable (ISV)-based constitutive model. Part I of this document pertains to the validation of the combined ISV model and finite element analysis framework for predicting the behavior of materials subjected to ballistic loads. Part II summarizes a simulation-based parametric sensitivity study assessing the influence of select microstructural features and mechanical properties on ballistic performance. Part III presents the effects of variations in microstructural and mechanical properties within a finite element simulation framework on decreased ballistic performance of high hardness steels observed by [63].

1.2. Internal State Variable-Based Constitutive Model for Ductile Materials

A physically motivated viscoplasticity model was developed by Bammann [68] within the ISV thermodynamic framework established by Coleman and Gurtin [69]. Bammann’s ISV plasticity model was revised to account for damage in the form of void volume fraction [70] and later refined to consider damage evolution stemming from the nucleation [71,72], growth, and coalescence of voids [73]. The ISV model presented in [71] incorporates the McClintock [74] void-growth rule for voids growing from secondary-phase particles and the Cocks and Ashby [75] unified growth mechanism model for pre-existing voids. The ISV plasticity–damage model has been used to characterize the structure–property relationships for aluminum [73,76,77] and steel [72,78,79,80,81,82] alloys. The constitutive model has been used within a finite element analysis (FEA) framework to successfully simulate a variety of thermomechanical deformations including forming processes [72,83] and high-velocity impacts [82].

2. Materials and Methods

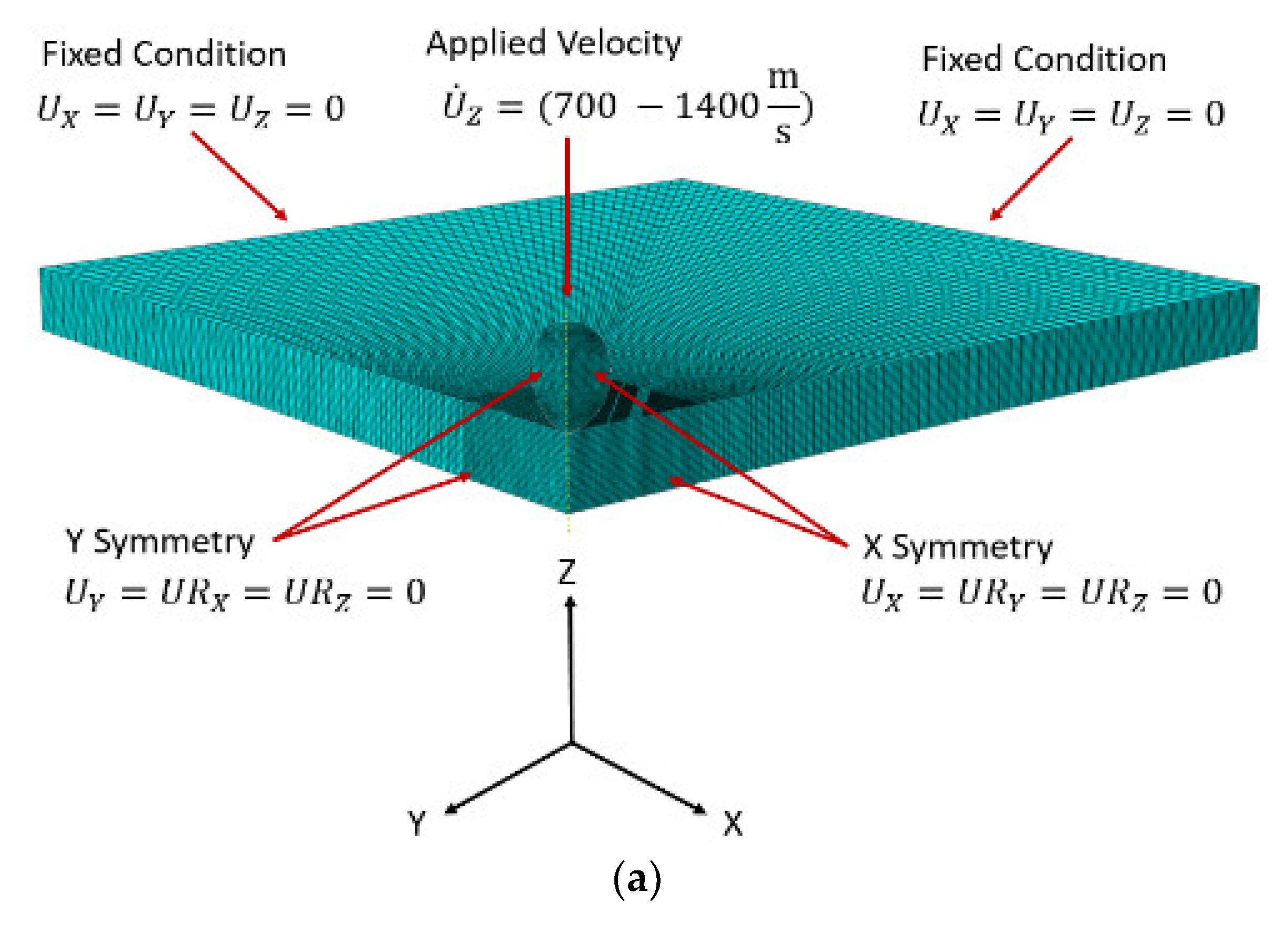
2.1. Part I: Ballistic Impact of Rolled Homogeneous Armor Steel Plates by Spherical Projectiles

Experimental testing of rolled homogeneous armor (RHA) steel spherical projectiles impacting RHA steel plates was performed at the Engineer Research and Development Center (ERDC) in Vicksburg, MS. A number of 457.2 mm wide square RHA steel plates of 9.53 mm and 12.7 mm thickness were experimentally impacted by 12.7 mm diameter RHA steel spheres fired from a .50 caliber rifled barrel at varying velocities to obtain the ballistic limit (perforation) velocity (V50) and residual velocity profiles for each target configuration. The experiments were simulated using an Abaqus-Explicit FEA solver in conjunction with a previously calibrated ISV constitutive model [82] for RHA steel (contained in

Table A1. ISV Model Coefficients for 250 BHN RHA steel alloy used in Part I.

RHA Steel (250 BHN)	Value
Density (tonne/mm3)	7.83 × 10−9
Elastic Modulus (MPa)	205,000
Poisson’s Ratio	0.29
Thermal Conductivity (W·m·K−1)	42.5
Specific Heat (J·kg−1·K−1)	480
Thermal Expansion (K−1)	1.15 × 10−5
Inelastic Heat Fraction	0.3336
Melt Temperature (K)	1803.15
ISV Model Coefficients	-
C01 (MPa)	5
C02 (K)	0
C03 (MPa)	690
C04 (K)	22
C05 (MPa−1)	0.3
C06 (K)	0
C07 (MPa−1)	0.3
C08 (K)	150
C09 (MPa)	4416
C10 (K)	2
C11 (s·MPa−1)	0
C12 (K)	0
C13 (MPa−1)	0.07
C14 (K)	121.5
C15 (MPa)	700
C16 (K)	0
C17 (s*MPa−1)	0
C18 (K)	0
C19	0.006
C20 (K−1)	1100
C21	0
Ca	−0.3
Cb	0
Avoid	0
Bvoid	0
a	32,000
b	10,800
c	36,000
η0 (#/mm2)	200
KIC (MPa·mm½)	2751
d (mm)	0.0035
f	0.00065
NND (mm)	0.16
d0 (mm)	0.002
cd2	1.5
GS0 (mm)	0.01
GS (mm)	0.01
ζ	1
Initial Porosity	0.00065
CTN (K)	300
CTC (K−1)	0.002
McClintock Growth, n	0.3
R0 (mm)	0.001
Cocks-Ashby Growth, m	20

in Appendix A) to validate the ISV model framework for predicting ballistic performance.

2.1.1. Finite Element Simulation Framework

High-velocity quarter-symmetry impact simulations of RHA steel targets by RHA steel spheres and cylinders (Figure 1a,b) were performed using Abaqus-Explicit FEA software (version 6.19, Dassault Systemes Simulia Corporation, Providence, RI, US) in conjunction with ISV constitutive model user material subroutines (VUMAT).

Table 1. Geometric properties of quarter-symmetry projectiles and targets used in Abaqus-Explicit finite element analysis simulations. Here, the quarter-symmetry values for target width are listed.

Case	Object	Shape	Thickness (mm)	Width (mm)	Diameter (mm)	# Elements
1	Projectile	Sphere	-	-	12.70	11,424
	Target	Square	9.53	127.0	-	206,400
2	Projectile	Sphere	-	-	12.70	10,136
	Target	Square	12.70	170.0	-	238,680
3	Projectile	Cylinder	-	12.70	6.35	3840
	Target	Square	6.35	63.50	-	97,344

lists the target/projectile geometric properties and total number of finite elements for each case. Cases 1 and 2 each define spherical impact experiments used to validate the modelling framework. Case 3 simulates the cylindrical projectile impact experiments performed by Mescall and Rogers [63]. Identical RHA steel–mechanical and microstructural properties were used for both the target and projectile in every simulation. In the simulations, the in-plane target plate dimensions were reduced from their actual dimensions to reduce computational expenses. A minimum 10:1 plate-width-to-thickness ratio and 10:1 plate-width-to-projectile-diameter ratio were used to ensure plate edge effects were negligible. An initial velocity was applied to the projectile ranging from 700 to 1400 m/s, where quarter-symmetry boundary conditions were imposed on both the projectile and target plate. Linear hexahedral temperature-displacement-reduced integration elements (C3D8RT) were used to mesh the projectile and target structures. Element erosion of the contact surface between the target and projectile was used to facilitate solution convergence.

2.1.2. Constitutive Model

A theory for ISV plasticity and damage modeling in ductile metals has been developed by Bammann [52,68,70] and Horstemeyer [71,73,78] to predict material-constitutive behavior based on the evolution of microstructure-based internal parameters.

A summary of the ISV plasticity–damage model relations is provided in the following section. A standard tensorial notation is employed. Assume a nominal parameter, (A), bold symbols denote second-rank tensors (A), rate functions are denoted by a dot accent ($\dot{A}$), and frame-indifferent second-rank tensors are denoted by an overbar and dot accent ($\dot{\overline{\mathit{A}}}$).

The relations for objective stress rate, elastic, and inelastic rates of deformation are given by [73] as

$$\dot{\overline{\mathsf{\sigma }}}=\dot{\mathsf{\sigma }}-{\mathit{W}}_e\mathsf{\sigma }+\mathsf{\sigma }{\mathit{W}}_e=\lambda \left(1-\varphi \right)+2\mu \left(1-\varphi \right){\mathit{D}}_{\mathit{e}}-\frac{\dot{\varphi }}{1-\varphi }\mathsf{\sigma },$$

(1)

$${\mathit{D}}_e=\mathit{D}-{\mathit{D}}_{\mathit{i}\mathit{n}},$$

(2)

$${\mathit{D}}_{\mathit{i}\mathit{n}}=\sqrt{\frac{3}{2}}f\left(T\right)\left[\frac{\sqrt{\frac{3}{2}}‖{\mathsf{\sigma }}^{\mathbf{\prime }}-\sqrt{\frac{2}{3}}\mathsf{\alpha }‖-\left(R+Y\left(T\right)\right)\left(1-\varphi \right)}{V\left(T\right)\left(1-\varphi \right)}\right]·\frac{{\mathsf{\sigma }}^{\mathbf{\prime }}-\sqrt{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\mathsf{\alpha }}{‖{\mathsf{\sigma }}^{\mathbf{\prime }}-\sqrt{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\mathsf{\alpha }‖}.$$

(3)

In Equation (1), the objective stress rate, $\dot{\overline{\mathsf{\sigma }}}$, is posed as a function of the Cauchy stress tensor, σ, the Lamé elastic constants, λ and μ, and the elastic spin tensor, W_e. Here, the plastic spin is assumed to be zero. In Equations (2) and (3) D, D_e, and D_in are the total, elastic, and inelastic rates of deformation tensors, respectively. The void volume fraction, $\varphi$, is used to represent damage in Equation (3). Void volume fraction increases compliance (Equation (1)) and inelastic flow rate (Equation (3)). The inelastic flow rate, D_in, is a function of the isotropic hardening, R, kinematic hardening tensor, α, the deviatoric Cauchy stress tensor, σ′, void volume fraction, $\varphi$, and a collection of yield-related parameters, Y(T), V(T), and f(T) described in.

Kinematic and isotropic hardening ISVs (α and R) are used to represent the effects of geometrically necessary and statistically stored dislocation densities, respectively, on the material’s plastic response. The objective kinematic hardening rate, $\dot{\overline{\mathsf{\alpha }}}$, is given through [76] as:

$$\dot{\overline{\mathsf{\alpha }}}=\dot{\mathsf{\alpha }}-{\mathit{W}}_{\mathit{e}}\mathsf{\alpha }+\mathsf{\alpha }{\mathit{W}}_{\mathit{e}}=\left(h\left(T\right){\mathit{D}}_{\mathit{i}\mathit{n}}-\left[\sqrt{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}{r}_d\left(T\right)+r_s\left(T\right)\right]‖\mathsf{\alpha }‖\mathsf{\alpha }\right){\left(\frac{{GS}_0}{GS}\right)}^Z,$$

(4)

where h(T) represents the kinematic hardening modulus, and r_s(T) and r_d(T) represent the temperature-dependent static and dynamic recovery for kinematic hardening [52], GS₀ and GS represent the reference and initial grain size, respectively, and Z is a dimensionless grain-size sensitivity parameter. Similarly, ref. [76] expressed the isotropic hardening rate, $\dot{R}$, as

$$\dot{R}=\left(H\left(T\right)\sqrt{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}{\mathit{D}}_{\mathit{i}\mathit{n}}-\left[\sqrt{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}{R}_d\left(T\right)‖{\mathit{D}}_{\mathit{i}\mathit{n}}‖+R_s\left(T\right)\right]R^2\right){\left(\frac{{GS}_0}{GS}\right)}^Z,$$

(5)

where H(T) represents the isotropic hardening modulus, and R_s(T) and R_d(T) account for the static and dynamic recoveries for isotropic hardening [52].

Horstemeyer [73] posed a microstructure porosity-based damage model as a product of void nucleation, growth, and coalescence terms. The porosity model distinguishes between the void volume fraction contribution from voids nucleated at defects and the expansion of preexisting voids in the following framework:

$$\dot{\varphi }=\left[{\dot{\varphi }}_{particles}+{\dot{\varphi }}_{pores}\right]c+\left[{\varphi }_{particles}+{\varphi }_{pores}\right]\dot{c},$$

(6)

where C is a coalescence parameter, $\dot{C}$ is the rate of void coalescence, ${\varphi }_{particles}$ is the volume fraction of voids nucleated from particles during deformation, and ${\varphi }_{pores}$ is the volume fraction of pre-existing voids. The rate of change in the volume fraction of nucleated and pre-existing voids may be written through [76] as:

$${\dot{\varphi }}_{particles}=\dot{\eta }\nu +\eta \dot{\nu },$$

(7)

and

$${\dot{\varphi }}_{pores}=\left[\frac{1}{{\left(1-{\varphi }_{pore}\right)}^m}-\left(1-{\varphi }_{pore}\right)\right]·\sinh \left[\frac{(2V\left(T\right)/Y\left(T\right))-1}{(2V\left(T\right)/Y\left(T\right))+1}·\frac{I_1}{3\sqrt{J_2}}\right]·‖{\mathit{D}}_{\mathit{i}\mathit{n}}‖.$$

(8)

In Equation (7), ${\dot{\varphi }}_{particles}$ is a function of the average void nucleation (η), void growth (ν), and their respective rates, $\dot{\eta }$ and $\dot{\nu }$. Equation (8) is formulated through Cocks and Ashby [75] to relate the expansion rate of preexisting porosity, ${\dot{\varphi }}_{pores}$, to stress triaxiality, where I₁ is the first stress invariant, and J₂ is the second deviatoric stress invariant. Equation (8) introduces rate sensitivity through the yield terms V(T) and Y(T), and m is the Cocks–Ashby damage coefficient [75].

Horstemeyer [71,73,78] developed a strain rate-, stress state-, temperature-, and microstructure property-dependent expression for the void nucleation rate:

$$\dot{\eta }=\frac{d^{1/2}}{K_{IC}{f}^{1/3}}\eta ·\left(a\left[\frac{4}{27}-\frac{J_3^2}{J_2^3}\right]+b\frac{J_3}{J_2^{\frac{3}{2}}}+c{e}^{m_h{H}_B}‖\frac{I_1}{\sqrt{J_2}}‖\right)‖{\mathit{D}}_{\mathit{i}\mathit{n}}‖exp\left(\raisebox{1ex}{$C_{\eta T}$}\!\left/ \!\raisebox{-1ex}{$T$}\right.\right).$$

(9)

In Equation (9), d is the secondary-phase particle size, f is secondary-phase particle volume fraction, K_IC is the fracture toughness, and J₃ is the third deviatoric stress invariant. Here, invariant ratios containing I₁ correspond to stress triaxiality, while terms containing J₃ capture shear effects. The parameters a, b, and c are used to calibrate void nucleation stress-state sensitivity and, C_ηT is used to capture void nucleation temperature dependence consistent with the findings in [84]. Chandler et al. [85] introduced the parameters H_B and m_h to represent the interfacial hydrogen concentration in atomic parts per million (APPM) and a given material’s fracture sensitivity due to the presence of hydrogen, respectively. Chandler et al. [85] related the lattice hydrogen concentration in stressed regions (H_σ) to the trapped hydrogen concentration at the interfaces of grain and particle boundaries (H_B) using a theoretical approach developed in [86] and [87], i.e.,

$$\frac{H_B}{1-H_B}=\frac{H_{\sigma }}{1-H_{\sigma }}exp\left(\frac{{-W}_B}{RT}\right),$$

(10)

where W_B is the binding energy of hydrogen at trapping sites, R is the universal gas constant, and $H_{\sigma }$ is the hydrogen concentration in stressed regions. The hydrogen concentration in a stressed region (H_σ) is a function of the lattice hydrogen in unstressed regions (H_L) and the hydrostatic pressure (I₁):

$$H_{\sigma }=H_{L}exp\left(\frac{I_{1}V}{3RT}\right)$$

(11)

where V is the hydrogen molar volume.

A model for the growth of voids nucleated from particles was developed in [73], predicated upon the McClintock [74]. Peterson et al. [88] modified the expression to account for shear and temperature sensitivity:

$$\dot{\nu }={\frac{\pi }{6}\left(\left\{A_{void}{D}_0\left[1-{\left(\frac{27J_3}{2{{(3J}_2)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right)}^2\right]\frac{{\mathit{D}}_{\mathit{i}\mathit{j}}^{\mathit{d}}:{{\mathsf{\sigma }}^{\mathbf{\prime }}}_{\mathit{i}\mathit{j}}}{\sqrt{{3J}_2}}+B_{void}{D}_0\frac{J_3}{J_2^{\frac{3}{2}}}‖{\underset{\_}{D}}^{in}‖+\frac{\sqrt{3}{D}_0}{2\left(1-n\right)}\left[\sinh \left(\sqrt{3}\left(1-n\right)\frac{\sqrt{2}{I}_1}{3\sqrt{J_2}}\right)\right]‖{\underset{\_}{D}}^{in}‖\right\}\exp \left(C_{Tv}·T\right)\right)}^3.$$

(12)

where D₀ is the average initial diameter of voids in the material. Stress-invariant ratios are used in conjunction with coefficients A_void, B_void, and n to capture stress-state sensitivity. The coefficient C_Tν controls the void growth ISV’s temperature dependence.

An expression for the void coalescence rate ($\dot{C}$) was developed that accounts for the effects of void nucleation and growth [73], grain size [76], and void nearest-neighbor distance effects [89],

$$\dot{C}=\left[{\left(\raisebox{1ex}{$4D_0$}\!\left/ \!\raisebox{-1ex}{$NND$}\right.\right)}^{\zeta }+{cd}_2\left[\dot{\eta }\nu +\dot{\nu }\eta \right]\right]exp\left(C_{CT}T\right){\left(\raisebox{1ex}{${GS}_0$}\!\left/ \!\raisebox{-1ex}{$GS$}\right.\right)}^Z,$$

(13)

where, NND is the average nearest-neighbor distance between voids, ζ is a dimensionless length-scale calibration parameter, and cd₂ is a void nucleation and growth-sensitivity coefficient.

2.2. Part II: Parameter Sensitivity Study

2.2.1. Second Phase Particle Number Density and Size

Microstructures of crystalline materials are typically heterogeneous, consisting of multiple high-volume fraction phases, small secondary-phase particles, impurities, and voids. Secondary-phase particles are known to serve as nucleation sites for damage in heterogeneous crystalline materials [90,91,92,93,94]. The void nucleation ISV model in [71] (Equation (9)) was predicated on the empirical relationship for void nucleation rate as a function between secondary particle size and volume fraction developed by Gangulee and Gurland [91]. The void nucleation rate was expressed as an exponential function of both particle diameter and number density and is inversely proportional to particle volume fraction. For this study, average particle diameter (d) and average number density (η₀) are treated as independent design variables and average particle area fraction (f) is calculated as the product of particle number density and cross-section area:

$$f={\eta }_0·\pi {\left(\frac{d}{2}\right)}^2.$$

(14)

Several studies [82,95,96,97,98,99,100] have quantified the distribution of second-phase particle number densities for several high-strength steels (

Table 2. Second-phase particle property distributions in high-strength steels from literature sources.

Study	Material	Number Density (#/mm2)	Diameter (μm)	Vol. Fraction
[101]	4340 Steel	800–4000	4.5–9.7	0.060
[102]	0.17-0.44 C Steel	430	14.0	0.066
[103]	HY 180 Steel	2600–6000	0.20–0.32	0.00019–0.00021
[82]	RHA Steel	170	7.0	0.00065

), for second-phase particle number densities in the range of 10²–10³ particles/mm². The nominal upper and lower bounds for η were selected as 250 and 4000 particles/mm², respectively, for the parameter sensitivity study.

The effects of particle size on damage evolution have been noted in the literature [91,100]. Gangulee and Gurland [91] showed that the fraction of fractured particles in a stressed material followed a d^1/2/f^1/3 relationship, thus increasing particle size for a given volume fraction increases void nucleation rates. In steels, secondary-phase particle diameters have been observed to range from the order of 10⁻⁴ to 10⁻² mm (Table 2). The values for particle size, d, correspondingly range from 10⁻⁴ to 10⁻² mm in the parameter sensitivity study.

2.2.2. Grain Size

Grain-size and microstructural morphology effects on the inelastic behavior of crystalline materials have been a cornerstone of metals research for the last century. Hall [104] and Petch [105] observed an inverse square root relationship between grain size and yield stress for various metals. An inverse correlation has also been demonstrated between grain size and hardening rate [95,96,97,106,107,108], although notable exceptions are discussed in [109]. However, grain boundaries serve as preferential nucleation sites for heterogeneities (dislocations, second-phase particles, carbides, and voids) and the correlation between microstructure heterogeneity properties and damage evolution rates is well documented [90,91,92,93,94]. Smaller grain boundaries lead to not only more potential defect precipitation sites (favoring void nucleation) but also shorter distances between defects that can facilitate local stress–field interaction and subsequent void coalescence [93,110,111].

Grain size and morphology influence the damage evolution modes and rates. Void coalescence in Equation (13) is posed as a function of grain size (GS₀, GS) and the grain-size sensitivity exponent (Z). The grain size sensitivity exponent, Z, has been calibrated for a variety of materials, including steel [112]. Grain sizes in steel have been shown to vary from 1 μm in diameter for high-strength steels (and even less than 1 μm in specially designed ultra-fine-grain materials) to greater than a 100 μm size for mild steels [98,105,113]. The bounds for the grain size term, GS, were selected as 1 μm and 100 μm, accordingly. The reference grain size, GS₀, was designated a control variable with a nominal value of 10 μm.

2.2.3. Initial Void Volume Fraction

Porosity in the microstructure of crystalline materials can degrade the material’s mechanical performance. Yamamoto [114] demonstrated that increasing levels of initial porosity significantly reduces the localization to the yield strain ratio. Similarly, Tvergaard [115] used micromechanics-based calculations to show that initial microporosity contributes to large, localized strains and void growth. The initial void volume fraction depends largely on the material’s processing history. Initial void volume fractions can approach 10⁻² to 10⁻¹ for cast steels [116,117,118]. Conversely, wrought steels may exhibit very initial porosities on the order of 10⁻⁴ (cf. [82]). Horstemeyer and Ramaswamy [72] noted that the experimental quantification of void volume fractions lower than 10⁻⁴ is difficult, but numerically demonstrated the significant effects of a microporosity of 10⁻⁶ on void growth rates in aluminum and 304 L stainless steel alloys. For metal alloys, minimal strain is required for failure beyond aggregate void volume fractions of 10⁻¹. Therefore, the upper and lower bounds for initial porosity (ϕ₀) in the parameter sensitivity study were selected as 10⁻² and 10⁻⁶, respectively.

2.2.4. Lattice Hydrogen Concentration

Hydrogen content in steels increases damage evolution rates and amplifies damage effects in a mechanism referred to as ‘hydrogen embrittlement’ [119,120,121,122,123]. Sakamoto and Mantani [124] showed that high-strength steels are particularly susceptible to hydrogen embrittlement because lattice imperfections (dislocations, vacancies, subgrain boundaries, and microvoids) from the martensitic transformation process serve as trapping sites for diffusing hydrogen atoms. Chandler [125] used molecular dynamics (MD) simulations in conjunction with an Ni-H-embedded atom method (EAM) potential [126,127,128] to study the effects of hydrogen concentrations at grain boundaries in a nickel alloy. The local interfacial boundary hydrogen concentration rate from the lattice concentration levels was shown to be strongly correlated to the stress triaxiality in the crystals.

The formalism for the relationship between the void nucleation rate and localized hydrogen concentration was derived for polycrystalline materials [85] and is included in Equations (9)–(11). The effects of lattice hydrogen concentrations between 10⁻⁵ and 10⁻⁴ atomic parts per million (APPM) in 1518 spheroidized steel were studied and showed a significant increase in nucleation rate relative to unhydrogenated materials. Lee and Gangloff [129] observed lattice hydrogen concentrations as high as 10⁻² APPM in hydrogen embrittled steels. In the present study, the upper and lower bounds for lattice hydrogen concentration, H_L, were selected as 10⁻³ and 10⁻⁵ APPM, respectively. Values for the binding energy, W_B = 56 kJ·mol⁻¹, gas constant, R = 8.31 J·mol⁻¹·K⁻¹, molar hydrogen volume, V = 2.0 cm³·mol⁻¹, hydrogen sensitivity, m_h = 3.0, and coefficients used in Equations (10) and (11) were obtained from [85].

2.2.5. Material Hardness

A variety of studies have assessed the effect of hardness and material properties on the ballistic performance of target materials [20,43,44,45,56,62,63,64,130,131]. Theoretically, increasingly hard materials with similar failure strains should perform more favorably under ballistic impact due to higher energy absorption capacity. However, refs. [63,64] and (for blunt projectiles) [56] show the ballistic limit of target materials initially increases with hardness until high Brinell hardness (BHN) levels (greater than 400 BHN), where performance significantly diminished. Mescall and Rogers [63] asserted that variations in microstructure heterogeneity properties for high-hardness materials leads to adiabatic shear-band nucleation, fracture, and subsequent reduced perforation velocities. The sensitivity of residual projectile velocity to mechanical properties affecting hardness has been assessed in this study. The steel hardness values were varied between 250 and 550 BHN to observe the hardness range experimentally studied in [63]. The yield and ultimate tensile strength (UTS) of a previously characterized RHA steel alloy [82] were varied in accordance with known strength–hardness correlations for 4340 steel ([132,133]) to achieve the desired hardness values. The ISV model constants C₀₃, C₀₉, and C₁₅ were varied to achieve the desired mechanical hardness levels and the values of the constants are shown in

Table 3. Mechanical properties and model coefficients for steel alloys of varying Brinell hardness (BHN).

		Brinell Hardness (BHN)
	Description	250	350	450	500	550
Yield (MPa)	-	700	1075	1250	1400	1500
UTS (MPa)	-	870	1150	1392	1600	1740
C03 (MPa)	Model constant affecting yield	690	1003	1203	1300	1403
C09 (MPa)	Kinematic hardening modulus	4416	4416	4416	5216	6016
C15 (MPa)	Isotropic hardening modulus	700	700	700	1000	1300

.

2.2.6. Design of Experiments

A design of experiments (DOE) technique was used to assess the sensitivity of residual projectile velocity to six microstructure and mechanical properties including particle number density (η₀), particle diameter (d), grain diameter (GS), initial void volume fraction (ϕ₀), lattice hydrogen concentration (H_L), and Brinell hardness. Due to the nonlinear relationship between hardness and ballistic merit observed by [63], each parameter was assigned five possible levels, the bounds of which are discussed in previous sections. A finite element simulation of the impact event was simulated for each unique parameter set and, in each instance, the predicted residual velocity was assessed. The corresponding orthogonal array is the L₂₅(5⁶), or L₂₅, array which allows up to six independent parameters with five levels. A full factorial set of calculations would require 5⁶ = 15,625 separate calculations; the L₂₅ array, however, requires only 25. Similar DOE-based computational approaches for studying void growth and nucleation using an ISV constitutive model can be found in [79].

The DOE approach [134] produces a linear system of equations that may be solved to relate the calculation output response vector {R} to the unknown influence vector {A} through the orthogonal array [P]:

$$\left[\mathit{P}\right]\left\{A\right\}=\left\{R\right\}.$$

(15)

The components of [P], {R}, and {A} are described in [134] as:

$$\left[\mathit{P}\right]=\left[\begin{array}{cccccc}+1.0& +1.0& +1.0& +1.0& +1.0& +1.0\\ +1.0& +0.5& +0.5& +0.5& +0.5& +0.5\\ +1.0& 0& 0& 0& 0& 0\\ +1.0& -0.5& -0.5& -0.5& -0.5& -0.5\\ +1.0& -1.0& -1.0& -1.0& -1.0& +1.0\\ +0.5& +1.0& +0.5& 0& -0.5& -1.0\\ +0.5& +0.5& 0& -0.5& -1.0& +1.0\\ +0.5& 0& -0.5& -1.0& +1.0& +0.5\\ +0.5& -0.5& -1.0& +1.0& +0.5& 0\\ +0.5& -1.0& +1.0& +0.5& 0& -0.5\\ 0& +1.0& 0& -1.0& +0.5& -0.5\\ 0& +0.5& -0.5& +1.0& 0& -1.0\\ 0& 0& -1.0& +0.5& -0.5& +1.0\\ 0& -0.5& +1.0& 0& -1.0& +0.5\\ 0& -1.0& +0.5& -0.5& +1.0& 0\\ -0.5& +1.0& -0.5& +0.5& -1.0& +0.5\\ -0.5& +0.5& -1.0& 0& -0.5& 0\\ -0.5& 0& +1.0& -0.5& -1.0& -0.5\\ -0.5& -0.5& +0.5& -1.0& +1.0& -1.0\\ -0.5& -1.0& 0& +1.0& +0.5& +1.0\\ -1.0& +1.0& -1.0& -0.5& 0& +0.5\\ -1.0& +0.5& +1.0& -1.0& -0.5& 0\\ -1.0& 0& +0.5& +1.0& -1.0& -0.5\\ -1.0& -0.5& 0& +0.5& +1.0& -1.0\\ -1.0& -1.0& -0.5& 0& +0.5& +1.0\end{array}\right],\hspace{1em}R=\left[\begin{array}{c}{R}_1\\ R_2\\ R_3\\ R_4\\ R_5\\ R_6\\ R_7\\ R_8\\ R_9\\ R_{10}\\ R_{11}\\ R_{12}\\ R_{13}\\ R_{14}\\ R_{15}\\ R_{16}\\ R_{17}\\ R_{18}\\ R_{19}\\ R_{20}\\ R_{21}\\ R_{22}\\ R_{23}\\ R_{24}\\ R_{25}\end{array}\right],\hspace{1em}A=\left[\begin{array}{c}{A}_1\\ A_2\\ A_3\\ A_4\\ A_5\\ A_6\end{array}\right].$$

(16)

In the orthogonal matrix [P] values of +1, +0.5, 0, −0.5, and −1 represent levels 1, 2, 3, 4, and 5, respectively. The values of each column of [P] are selected such that the inner product between any two columns is zero, satisfying the orthogonality condition. Orthogonality of [P] ensures that each value of {A} uniquely describes test result sensitivity to one test variable (columns of [P]).

Table 4. Levels for microstructure and material properties used in parametric sensitivity study.

	Parameter Levels
Parameter	+1	+0.5	0	−0.5	−1
Particle No. Density (#/mm2)	250	500	1000	2000	4000
Particle Diameter (μm)	0.1	0.5	1.0	5.0	10.0
Grain Diameter (μm)	1.0	5.0	10.0	50.0	100.0
Initial Porosity	10−6	10−5	10−4	10−3	10−2
Lattice Hydrogen (APPM)	10−5	10−4	2.5 × 10−4	5 × 10−4	10−3
Brinell Hardness	250	350	450	500	550

maps each parameter’s respective values to the levels used to populate [P].

To determine the parameter contributions to residual velocity, {A}, the inverse of the level matrix, [P], was multiplied by both sides of Equation (15). Since [P] is a non-square matrix of dimensions m × n = 25 × 6, where m (25) > n (6), the inverse of [P] is formulated as a left inverse matrix, that is,

$${\left[\mathit{P}\right]}_{left}^{-1}={\left({\left[\mathit{P}\right]}^{\mathrm{T}}\left[\mathit{P}\right]\right)}^{-1}{\left[\mathit{P}\right]}^{\mathrm{T}}.$$

(17)

Therefore, the solution for parameter contribution array, {A}, is given as

$$\left\{A\right\}={\left[\mathit{P}\right]}_{left}^{-1}\left\{R\right\}.$$

(18)

2.3. Part III: Modeling the Microstructurally Driven Transition of Penetration Modes for Increasing Material Hardness

In general, a correlation exists between increasing mechanical strength and the ballistic performance of target materials [20,43,44,45,56,62]. However, refs. [56,63,64] observed that the ballistic performance of steel target plates diminished after a certain hardness or strength threshold (usually greater than 400 BHN). Mescall and Rogers [63] attributed the decrease in ballistic performance to a transition in penetration modes from large plasticity-driven rupture in low-hardness steels to plugging [1] driven by localization phenomena (adiabatic shear-band nucleation, propagation, and fracture) in high-hardness steels.

The Abaqus Explicit FEA framework for cylinders impacting semi-infinite plates discussed in Part II was adapted for this study (Part III). The microstructure and mechanical properties of a 4340-steel alloy were varied for hardness values ranging from 250 to 550 BHN. The 4340-steel alloy satisfies RHA steel performance specifications contained in the MIL-A-125060H standard [135]. Figure 2 shows the stress–strain behavior (Figure 2a) and fracture toughness (Figure 2b) of 4340 steel over a 250–550 BHN range using data compiled from [133]. For 4340 steels, both yield and flow strength increase with hardness, However, the material’s fracture toughness drastically decreases above 450 BHN due to changes in the microstructure [132,133].

The microstructure properties selected for variation include initial particle number density, η₀, particle size, d, particle volume fraction, f, and grain size, GS. Sources suggest that lower quench rates and higher tempering temperatures used to achieve softer materials lead to a coarsening of second-phase particles and precipitates accompanied by a reduction in undissolved carbides [133,136,137,138,139]. The rapid quench rates and lower tempering temperatures necessary for achieving and sustaining high volume fraction martensitic grain (high-hardness) steels could plausibly result in finely dispersed, relatively high number density distributions of second-phase particles. Grain size is correlated to thermomechanical processing temperature and time due to recrystallization (cf. [140]). Grain size and hardness are inversely correlated for a given steel alloy, consistent with the findings of [105]. The trends of increasing particle number density and decreasing particle and grain size with increasing hardness were assumed for this study. Particle volume fraction was calculated as a function of size and number density using Equation (14). Specific values for each microstructure property were selected to qualitatively predict the perforation mode and ballistic performance trends discussed in [63]. The ranges of microstructure property values used in this study are bounded by experimentally observed properties for various steel alloys contained in Table 2.

The values of grain diameter, particle diameter, particle volume fraction, and particle number density versus material hardness are included in Figure 3. The range for grain diameter (1–15 μm) was selected based on literature quantifications of high-strength steel microstructures (0.1–1 μm [141]; 12 μm in [82]). Similarly, the range for particle number density (200–4000 particles/mm²) is based on the steel literature findings contained in Table 2. Second-phase particle diameters in steel can vary widely from less than 5 nm [139] to approximately 10 μm [101], which were selected as the particle diameter bounds for this study. These bounds exclude high volume fraction second-phase grains, which can exceed 10 µm. Future studies would benefit from the quantitative microstructural characterization of RHA steel alloys over the 250–550 BHN range to develop physically representative ISV model calibrations for non-idealized materials.

A complete listing of the ISV model constants for each BHN level RHA material is included in

Table A2. ISV Model coefficients for varying hardness RHA steel alloys used in Part III.

RHA Steel	Hardness (BHN)
	250	300	350	400	450	500	550
Density (tonne/mm3)	7.83 × 10−9	7.83 × 10−9	7.83 × 10−9	7.83 × 10−9	7.83 × 10−9	7.83 × 10−9	7.83 × 10−9
Elastic Modulus (MPa)	205,000	205,000	205,000	205,000	205,000	205,000	205,000
Poisson’s Ratio	0.29	0.29	0.29	0.29	0.29	0.29	0.29
Conductivity (W·m·K−1)	42.5	42.5	42.5	42.5	42.5	42.5	42.5
Specific Heat (J·kg−1·K−1)	480	480	480	480	480	480	480
Thermal Expansion (K−1)	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5	1.15 × 10−5
Inelastic Heat Fraction	0.3336	0.3336	0.3336	0.3336	0.3336	0.3336	0.3336
Melt Temperature (K)	1803.15	1803.15	1803.15	1803.15	1803.15	1803.15	1803.15
ISV Model Coefficients	-	-	-	-	-	-	-
C01 (MPa)	5	5	5	5	5	5	5
C02 (K)	0	0	0	0	0	0	0
C03 (MPa)	690	803	1003	1113	1203	1300	1400
C04 (K)	22	22	22	22	22	22	22
C05 (MPa−1)	0.3	0.3	0.3	0.3	0.3	0.3	0.3
C06 (K)	0	0	0	0	0	0	0
C07 (MPa−1)	0.3	0.3	0.3	0.3	0.3	0.3	0.3
C08 (K)	150	150	150	150	150	150	150
C09 (MPa)	4416	4416	4416	4416	4416	5216	6016
C10 (K)	2	2	2	2	2	2	2
C11 (s·MPa−1)	0	0	0	0	0	0	0
C12 (K)	0	0	0	0	0	0	0
C13 (MPa−1)	0.07	0.07	0.07	0.07	0.07	0.07	0.07
C14 (K)	121.5	121.5	121.5	121.5	121.5	121.5	121.5
C15 (MPa)	700	700	700	700	700	1000	1300
C16 (K)	0	0	0	0	0	0	0
C17 (s·MPa−1)	0	0	0	0	0	0	0
C18 (K)	0	0	0	0	0	0	0
C19	0.006	0.006	0.006	0.006	0.006	0.006	0.006
C20 (K−1)	1100	1100	1100	1100	1100	1100	1100
C21	0	0	0	0	0	0	0
Ca	−0.3	−0.3	−0.3	−0.3	−0.3	−0.3	−0.3
Cb	0	0	0	0	0	0	0
Avoid	0	0	0	0	0	0	0
Bvoid	0	0	0	0	0	0	0
a	32,000	32,000	32,000	32,000	32,000	32,000	32,000
b	10,800	10,800	10,800	10,800	10,800	10,800	10,800
c	360	360	360	360	360	360	360
η0 (#/mm2)	200	200	200	200	250	2000	4000
KIC (MPa·mm½)	2846	2800	2751	2625	2530	1802	1500
d (mm)	0.007	0.00525	0.0035	0.002625	0.0015	0.000035	0.0000035
f	0.00245	0.001378	0.00065	0.000517	0.000375	1.23 × 10−8	6.13 × 10−7
NND (mm)	0.08	0.08	0.08	0.08	0.08	0.08	0.08
d0 (mm)	0.002	0.002	0.002	0.002	0.002	0.002	0.002
cd2	1.5	1.5	1.5	1.5	1.5	1.5	1.5
GS0 (mm)	0.01	0.01	0.01	0.01	0.01	0.01	0.01
GS (mm)	0.015	0.0125	0.01	0.0075	0.005	0.0025	0.001
ζ	1.3	1.3	1.3	1.3	1.3	1.3	1.3
Initial Porosity	0.00065	0.00065	0.00065	0.00065	0.00065	0.00065	0.00065
CTN (K)	300	300	300	300	300	300	300
CTC (K−1)	0.002	0.002	0.002	0.002	0.002	0.002	0.002
McClintock Growth, n	0.3	0.3	0.3	0.3	0.3	0.3	0.3
D0 (mm)	0.001	0.001	0.001	0.001	0.001	0.001	0.001
Cocks-Ashby Growth, m	20	20	20	20	20	20	20

in Appendix A. The complete perforation velocity of each material system was determined as used as a metric for evaluating ballistic performance:

$$M=\raisebox{1ex}{$V_p$}\!\left/ \!\raisebox{-1ex}{$V_{p0}$}\right.,$$

(19)

where M represents ballistic merit, V_p is the perforation velocity of the current material system and is normalized by a nominal perforation velocity (taken to be V_p at 250 BHN), V_p0.

3. Results and Discussion

3.1. Part I: Validation of Internal State Variable Finite Element Framework

Finite element simulations of ballistic impact of RHA steel plates of varying thickness by 12.7 mm diameter RHA steel spheres were performed to demonstrate the usefulness of ISV-based constitutive models for predicting ballistic performance of materials. The ISV model coefficients for the 250 BHN RHA steel alloy used in the study are contained in Table A1 in Appendix A. Residual velocities from simulations are compared to experimental residual velocity data generated by ERDC in Figure 4. Figure 4 demonstrates the agreement between simulation and experimental data for complete perforation and residual projectile velocities. In Figure 4, both experimental and numerical residual velocity data appear to follow a parabolic shape with increasing initial projectile velocity consistent with literature findings [21,45,50,53,54,55,56]. The FEA model prediction strongly agrees with experimentally determined perforation velocity of the 9.53 mm thick plate (750 m/s predicted; 754 m/s observed). The model underpredicts the perforation velocity of the 12.7 mm thick plate by 5.7 percent (1150 m/s predicted; 1218.6 m/s observed) and tends to overpredict projectile residual velocity (Figure 4). The shapes of the predicted residual velocity curves generally agree with experimental residual velocity data. Therefore, the ISV constitutive model can be confidently used within a Lagrangian FEA framework to predict behaviors of materials during high velocity impacts.

3.2. Part II: Parameter Sensitivity Study

Twenty-five simulations of 6.35 mm diameter, 12.7 mm long RHA cylinders impacting 6.35 mm thick RHA steel target plates were performed to assess the effect of (1) particle number density, (2) particle size, (3) grain size, (4) initial void volume fraction, (5) lattice hydrogen concentration, and (6) mechanical hardness on projectile residual velocity. The residual velocity results for 25 simulations included in Figure 5 were used to populate the {R} array. The data in Figure 5 were used in conjunction with the parameter level matrix [P] to solve Equation (18) and determine the sensitivity of residual velocity to parameters (1)–(6). The results of the parameter sensitivity array {A} were normalized by the maximum value of {A} and are shown in Figure 6.

Figure 6 shows that for the parameter ranges studied, lattice hydrogen concentration is the dominant factor affecting projectile residual velocity while mechanical hardness plays a substantial secondary role (0.78 normalized contribution). Sufficiently high levels of lattice hydrogen concentration approaching 0.001 APPM result in significant void nucleation rate in materials experiencing tensile pressure. The initial compressive pressure wave is reflected from the target’s rear surface as a high-amplitude tensile pressure wave. According to Equations (9)–(11), sufficiently hydrogenated materials undergo significant hydrogen segregation to trapping sites at interfaces (dislocation, void, grain, subgrain, and inclusion boundaries) and experience high void nucleation rates that weaken the target’s structural integrity in a manner consistent with hydrogen embrittlement [119,120,121,122].

The influence of mechanical hardness on projectile residual velocity is understandable given proper context. Consider materials of differing mechanical strengths but identical failure strains; the stronger material will be able to dissipate the most energy as mechanical energy absorption corresponds to the integral of the stress–strain product (${\int }_0^{\mathsf{\epsilon }}\mathsf{\sigma }d\mathsf{\epsilon }$). In the DOE, no specifications were made as to the relationship of hardness, strength, failure strain, and damage evolution rates; these properties were assumed to be uncorrelated (a required assumption from Taguchi, 1987) for the sake of establishing the orthogonal matrix [P]. Under these assumptions, the normalized sensitivity of residual velocity to material hardness (A₆) was determined to be 0.78. Thus, material hardness is a strong secondary influence on the ballistic performance of metal targets. Future studies would benefit from considering the correlation between mechanical strength and ductility.

Initial void volume fraction, grain size, and particle number density all play secondary roles with normalized sensitivity contributions of 0.38, 0.33, and 0.24, respectively. Particle size had negligible effects on residual velocity.

Table 5. Select test levels and resultant residual velocity values from parameter sensitivity study.

Test	Particle No. Density (μm)	Particle Diameter (μm)	Grain Diameter (μm)	Initial Porosity	Lattice Hydrogen (APPM)	Brinell Hardness (BHN)	Residual Velocity (m/s)
7	500	0.5	10	10−3	10−3	250	589.60
8	500	1.0	50	10−2	10−5	350	518.94
13	1000	1.0	100	10−5	5 × 10−4	250	559.44
19	2000	5.0	5	10−2	2.5 × 10−4	250	521.16
25	4000	10.0	50	10−4	10−4	250	560.12
9	500	5.0	100	10−6	10−4	450	0
10	500	10.0	1	10−5	2.5 × 10−4	500	0
15	1000	10.0	5	10−3	10−5	450	0
18	2000	1.0	1	10−3	10−4	550	0
24	4000	5.0	10	10−6	10−5	550	0

was generated to provide additional context for the parameter contributions to residual velocity. Specifically, Table 5 displays the parameter sets resulting in residual velocities over 500 m/s (representing residual of greater than 50% of initial projectile velocity) and residual velocities of 0 m/s (projectile fully arrested). Significant initial porosity (ϕ_pore = 0.01) in test 8 (see Table 5) could have played a dominant role in the test’s high residual velocity (518.94 m/s) because of the otherwise low lattice hydrogen concentration (10⁻⁵ APPM) and moderate target and projectile hardness (350 BHN). However, high residual projectile velocities only occurred at initial porosities under 10⁻² in the presence of either significant lattice hydrogen concentrations (10⁻³ and 5·10⁻⁴ APPM in tests 7 and 13, respectively) or low material hardness (250 BHN in tests 7, 13, 18, and 19). Table 5 shows no conclusive correlation between particle number density, particle diameter, and grain diameter for tests resulting in the highest and lowest projectile residual velocities.

3.3. Part III: Modeling the Microstructurally Driven Transition of Penetration Modes for Increasing Target Material Hardness

Abaqus Explicit finite element simulations were performed using an ISV constitutive model for RHA steel alloys of varying mechanical and microstructure properties to demonstrate a microstructurally driven transition in target perforation modes from plastic rupture to shear plugging initially discussed in [63]. Figure 7 shows images of the cross sectional and rear target surface during perforation for 300, 400, and 500 BHN steels. In Figure 6, the contours represent plastic equivalent strain (ε_p) and grey hues denote regions of material experiencing ε_p > 0.5.

The figures show a decrease in the cross-sectional area experiencing large strains as BHN levels increase from 300 to 500. Figure 7a shows that, for soft targets (in this case 300 BHN, grain diameter = 12.5 μm, d = 5.0 μm, η₀ = 200 particles/mm², K_IC = 2800 MPa·mm^1/2) impacted at a ballistic limit velocity of 850 m/s, perforation tends to occur due to rupture resulting from large bending deformation, consistent with [63]. Figure 7b shows that perforation of the 400 BHN plate (grain diameter = 7.5 μm, d = 3.5 μm, f = 0.0011, η₀ = 200 particles/mm², K_IC = 2625 MPa·mm^1/2) due to impact at 1000 m/s ballistic limit velocity occurs via combined bending and shear petaling perforation modes. Figure 8 shows that for these theoretical materials, the targets sustain large plastic deformation that facilitates impact energy dissipation resulting in a domain of increasing Ballistic Merit (BM = 1.0625 at 300 BHN and BM = 1.25 at 400 BHN—Figure 8). These materials can sustain relatively large plastic strain fields due to the low initial particle density distributions and high fracture toughness, which contribute to low initial void nucleation rates and delayed onset of strain localization and fracture.

Conversely, the 500 BHN plate (grain diameter = 2.5 μm, d = 0.035 μm, η₀ = 2000 particles/mm², K_IC = 1800 MPa·mm^1/2) impacted at a ballistic limit velocity of 950 m/s shows perforation via localized shear plugging (Figure 7c). The increase in second-phase particle number density and decrease in fracture toughness (Figure 3) contribute to the increased nucleation rates under plastic strain relative to softer target materials. Through Figure 6, we infer that the increase initial particle number density and decreasing grain size have a compounding contribution to the total damage accumulation rate (thus adversely affecting ballistic performance) through the void nucleation and void coalescence rates, respectively. Logically, increasing second-phase particle number density (2000 particles/mm² at 500 BHN, 200 particles/mm² at 400 and 300 BHN) increases the number of potential void nucleation sites, while decreasing the material grain size (2.5 μm at 500 BHN, 12.5 and 7.5 μm at 300 and 400 BHN, respectively) and decreasing the distance between defects (particles, subgrains, and high-angle grain boundaries) and thus stimulates more rapid onset of void interaction and instability. While the property distributions for these simulation materials are theoretical, each value selected is representative of documented microstructure characteristics in steels shown through Table 2.

The substantially higher void nucleation and coalescence rates for the 500 BHN material facilitates strain localization phenomena (described by the inverse relationship of inelastic rate of deformation, D_in, and damage, $\varphi$, in Equation (3)) and ultimately produces localized shear fracture modes (plugging). The localized fracture dissipates less energy than the large plastic-ductility perforation modes, and the target shows perforation at lower velocities (950 m/s at 500 BHN) than softer targets (1000 m/s at 400 BHN). This tendency reflects non-monotonic ballistic performance with the material hardness trend documented in [63].

The ballistic merit of each hardness RHA alloy was calculated using the minimum perforation velocity data from simulations in part III in conjunction with Equation (19). In this case, the perforation velocity for each material was normalized by the perforation velocity of the 250 BHN material (800 m/s). In Figure 8, the predicted ballistic merit behavior for increasing target hardness is compared to ballistic merit data experimentally generated by [63] for vacuum-induction-melted (VIM) and electroslag-remelted (ESR) 6.35 mm 4340 steel plates impacted by 6.35 mm diameter, 12.7 mm long 4340 steel cylinders. Figure 7 demonstrates the ISV model’s ability to predict the trend of decreasing ballistic performance at elevated material hardness given sufficient variation of microstructure properties.

Figure 2b and Figure 3 show that fracture toughness, grain size, particle size, and particle volume fraction decrease with BHN, while particle number density increases. Each of the mechanical and microstructure properties vary in such a way that the ISV model predictions for the void nucleation rate in Equation (9) and void coalescence rate in Equation (13) increase with increasing BHN. The increasing rate of damage evolution by Equations (6) and (7) leads to strain localization in damage-affected elements by the inelastic flow rule in Equation (3). The coupled localization of strain and damage is responsible for the change in predicted perforation modes in Figure 7 from rupture due to large plasticity at low BHN values (BHN < 450) to shear plugging at high BHN values (BHN > 450). The microstructure and material-property-driven transition to highly localized straining and damage evolution diminishes the high BHN material’s ability to effectively dissipate impact energy through large regions of plastic strain. The ultimate result is a decrease in ballistic performance of high hardness plates consistent with the results of [63]. This trend is a result of an ISV model framework predicated upon idealized property assumptions for varying hardness materials. A true validation of this framework requires thorough microstructure and mechanical property characterizations of several hardness classes of steels and subsequent calibration of high-fidelity ISV constitutive models. Such efforts would enable the assessment of the ISV model’s ability to accurately predict the transition in penetration mechanism and ballistic performance of real materials. If validated, the model framework could be used to design materials with microstructures optimized for resistance to dynamic impacts.

Parts II and III of this study focused on the influence of microstructure and mechanical properties on the ballistic perforation behavior of steel alloys. The following summary may be drawn from these findings:

• Increasing lattice hydrogen concentration (from 10⁻⁵ to 10⁻³ APPM) exponentially increases void nucleation rates (Equation (9)) in materials subjected to greater than zero stress triaxiality through [85]. As the material expands under tension, hydrogen is freer to migrate through the lattice to preferential trapping sites near grain or inclusion boundaries. The hydrogen reduces the local fracture toughness contributing to increasing void nucleation rates. Macroscopically, this corresponds to more localized fracture and perforation modes in high-tensile pressure regions, less energy absorption through global plastic strain accumulation, and reduced perforation velocities.
• Perforation velocity is strongly sensitive to target material hardness. Increasing hardness (and corresponding yield and rate hardening characteristics) from 250 BHN to 550 BHN increases the mechanical work for a given strain, thus reducing greater energy from the impact event, and subsequently increasing the velocity required to perforate the material.
• Perforation velocity shows finite normalized sensitivity to initial void volume fraction (0.38), grain size (0.33), and particle number density (0.25) in descending order. These sensitivities are relatively smaller than the lattice hydrogen concentration (1.0) and hardness sensitivities (0.78) but are still significant. Increasing levels of initial porosity from 10⁻⁶ to 10⁻² increases material compliance (Equation (3)) and reduces the void nearest-neighbor distance, thus accelerating the onset of void coalescence and unstable fracture (consider the coupled effects of Equations (6) and (13)). Reducing the grain size exponentially increases void coalescence rate (GS in Equation (13)) through reduction in defect nearest-neighbor distances, contributing to the earlier onset of coalescence with strain once voids have nucleated. Increasing the second-phase particle number density from 250 to 4000 voids/mm² increases the number of initial points of localized stress concentration and void nucleation in the microstructure. Physically, increasing the particle number density reduces the neighbor distance once voids have begun to nucleate, contributing to earlier material instability.
• Perforation velocity shows negligible sensitivity to particle size. Mathematically, nucleation rate, $\dot{\eta }$ is correlated to particle diameter, d, through a square root relationship $\dot{\eta }$ ∝ d^1/2, while the nucleation rate’s relationship to lattice hydrogen concentration and particle number density is exponential and linear, respectively. Physically, the fracture of larger particles would produce conditions conducive to void growth (Equation (12)), However, ballistic penetration is a high strain rate event that favors a large quantity of nucleation events leading to final rupture through coalescence rather than the growth of large voids.
• Diminished ballistic performance trends in high hardness (>450 BHN) targets experimentally observed by [63] can be qualitatively predicted using an ISV based framework featuring decreasing grain size, particle size, particle volume fraction, and fracture toughness and increasing particle number density with increasing material hardness in accord with qualitative trends documented in the relevant literature. A single order of magnitude increase in particle number density (250 to 2000 particles/mm²) and corresponding reduction in grain size (5 to 2.5 μm) from 450 to 500 BHN hardness degrades the Ballistic Merit from 1.24 to 1.13, despite the increase in yield and flow strength of the material. The reduction in ballistic resistivity is caused by a transition from large ductility perforation modes to localized shear plugging (Figure 7).
• Traditional constitutive modeling approaches can struggle to successfully predict changes in perforation behavior for alloys of similar element composition and varying processing history [56,63,64]. This work demonstrates that a deformation history- and microstructure property-dependent ISV constitutive model can predict changes in ballistic perforation modes and nonmonotonic trends in ballistic limit for increasing target strength.

4. Conclusions

Simulations of ballistic impact of spherical- and cylindrical-shaped rolled homogeneous armor steel (RHA) projectiles against semi-infinite RHA target plates have been performed within an Abaqus Explicit finite element analysis (FEA) framework using internal state variable (ISV)-based constitutive models. The effects of varying microstructure and mechanical properties on projectile residual velocity have been assessed in a parametric sensitivity study and show that target material performance strongly degraded due to the increasing lattice hydrogen concentration and improved because of the increasing material hardness in the absence of microstructure considerations. Increasing levels of initial porosity and particle number density with decreasing grain size contributed to the decreased ballistic performance of target materials. The tendency for high-hardness steel targets to exhibit reduced ballistic performance has been predicted by FEA simulations through sufficient variation in microstructure and material properties, specifically increasing defect number density coupled with reduced grain size and fracture toughness. The ISV material model demonstrates the ability to capture non-monotonic ballistic performance trends for increasing target material hardness while traditional constitutive models struggle to replicate these tendencies.