Internal Elastic Strains of AZ31B Plate during Unloading at Twinning-Active Region
Abstract
:1. Introduction
2. The Crystal Plasticity Model
3. Experiment Procedure
4. Results and Discussion
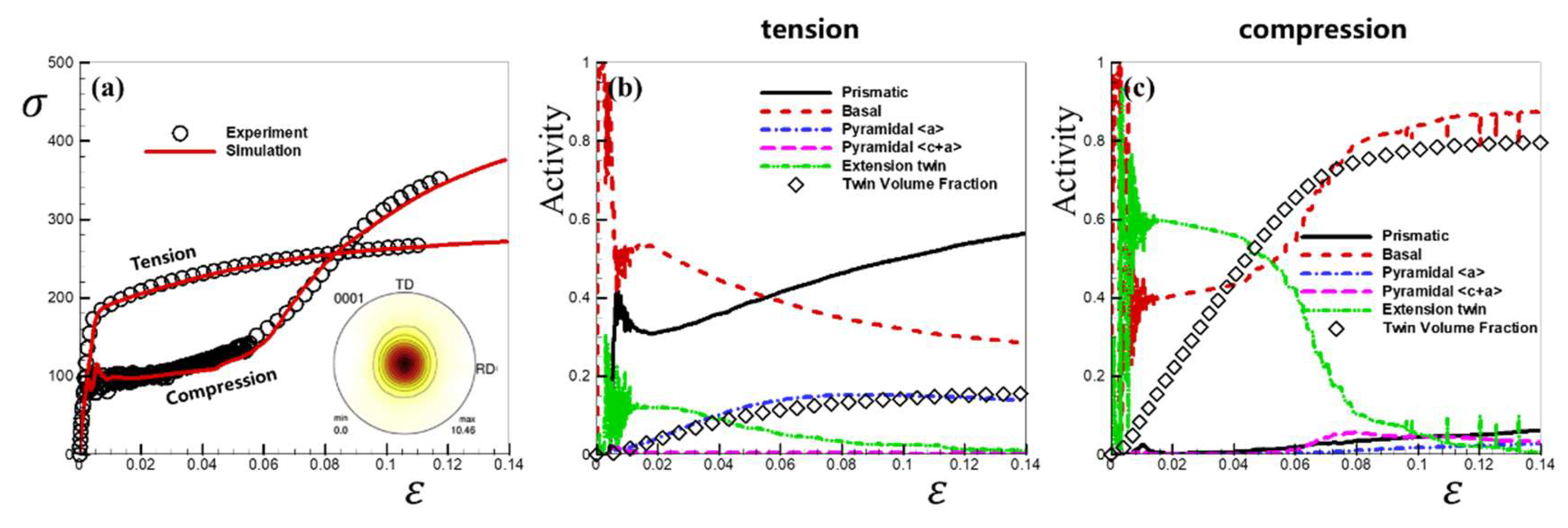
4.1. Parameter Calibration
4.2. Mechanical Behaviors during Cyclic Loading-Unloading
5. Concluding Remarks
- Magnesium alloys exhibit significant inelastic behavior during the unloading, and this phenomenon was observed consistently in both modeling and experimental studies.
- In situ neutron diffraction experiments have captured the decrease in {00.2} diffraction intensity and the evolution of lattice strains during stress relaxation. The residual lattice elastic strain can be released spontaneously by detwinning behavior if the twins are sufficient. Prior to the stress unloading reaching zero, the internal elastic strains of the {00.2} and {10.3} planes have already decreased to zero and exhibited strains with opposite signs due to twin-induced back stress. This leads to the development of internal stresses within the material, triggering the activation of detwinning processes. The quantity of twins has a significant impact on the effectiveness of back stress; as the twin volume fraction increases, the impact of back stress becomes more pronounced.
- The EVPSC-TDT model, incorporating back stresses, exhibits excellent predictive capabilities for the macroscopic stress–strain response and evolution of diffraction intensities, demonstrating excellent agreement with experimental measurements. Given that the magnitude of the vertical axis is in the order of 10−3, the deviation between the simulation and experimental data is less than 20% when the unloading reached 0.4. The model effectively captures the reduction in twin volume fraction with a deviation less than 2% and provides a reasonable explanation for the discrepancies observed in simulated microscale lattice elastic strains. Furthermore, the model elucidates that the inelastic behavior of magnesium alloys is closely associated with significant detwinning and basal slip activities.
- Under tensile loading, the predominant deformation mechanisms in magnesium alloys are basal slip and prismatic slip. Conversely, under compression, twinning is prominently activated and becomes a dominant deformation mechanism alongside basal slip. In addition to detwinning, basal slip is also a responsible deformation mechanism for inelastic behavior, and prismatic slip complements the inelastic behavior.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Song, J.; Chen, J.; Xiong, X.; Peng, X.; Chen, D.; Pan, F. Research Advances of Magnesium and Magnesium Alloys Worldwide in 2021. J. Magnes. Alloy 2022, 10, 863–898. [Google Scholar] [CrossRef]
- Prasad, S.V.S.; Prasad, S.B.; Verma, K.; Mishra, R.K.; Kumar, V.; Singh, S. The Role and Significance of Magnesium in Modern Day Research-A Review. J. Magnes. Alloy 2022, 10, 1–61. [Google Scholar] [CrossRef]
- Zhu, G.; Yang, C.; Shen, G.; Peng, Y.; Shi, B. The Asymmetric Pre-Yielding Behaviour during Tension and Compression for a Rolled AZ31 Mg Alloy. Int. J. Mater. Form. 2022, 15, 26. [Google Scholar] [CrossRef]
- Bong, H.J.; Lee, J.; Lee, M.-G. Modeling Crystal Plasticity with an Enhanced Twinning–Detwinning Model to Simulate Cyclic Behavior of AZ31B Magnesium Alloy at Various Temperatures. Int. J. Plast. 2022, 150, 103190. [Google Scholar] [CrossRef]
- Muránsky, O.; Carr, D.G.; Šittner, P.; Oliver, E.C. In situ neutron diffraction investigation of deformation twinning and pseudoelastic-like behaviour of extruded AZ31 magnesium alloy. Int. J. Plast. 2009, 25, 1107–1127. [Google Scholar] [CrossRef]
- Tang, W.; Lee, J.Y.; Wang, H.; Steglich, D.; Li, D.; Peng, Y.; Wu, P. Unloading Behaviors of the Rare-Earth Magnesium Alloy ZE10 Sheet. J. Magnes. Alloy 2021, 9, 927–936. [Google Scholar] [CrossRef]
- Wagoner, R.H.; Lim, H.; Lee, M.-G. Advanced issues in springback. Int. J. Plast. 2013, 45, 3–20. [Google Scholar] [CrossRef]
- Ling, Y.; Roostaei, A.A.; Glinka, G.; Jahed, H. Fatigue of ZEK100-F magnesium alloy: Characterisation and modelling. Int. J. Fatigue 2019, 125, 179–186. [Google Scholar] [CrossRef]
- Lou, X.Y.; Li, M.; Boger, R.K.; Agnew, S.R.; Wagoner, R.H. Hardening evolution of AZ31B Mg sheet. Int. J. Plast. 2007, 23, 44–86. [Google Scholar] [CrossRef]
- Wang, H.; Wu, P.D.; Wang, J. Modeling inelastic behavior of magnesium alloys during cyclic loading–unloading. Int. J. Plast. 2013, 47, 49–64. [Google Scholar] [CrossRef]
- Gharghouri, M.A.; Weatherly, G.C.; Embury, J.D.; Root, J. Study of the mechanical properties of Mg-7.7at.% Al by in-situ neutron diffraction. Philos. Mag. A 1999, 79, 1671–1695. [Google Scholar] [CrossRef]
- Li, Y.; Enoki, M. Recovery behaviour of pure magnesium in cyclic compression–quick unloading-recovery process at room temperature investigated by AE. Mater. Trans. 2008, 49, 1800–1805. [Google Scholar] [CrossRef] [Green Version]
- Hama, T.; Takuda, H. Crystal-plasticity finite-element analysis of inelastic behavior during unloading in a magnesium alloy sheet. Int. J. Plast. 2011, 27, 1072–1092. [Google Scholar] [CrossRef] [Green Version]
- Hama, T.; Kitamura, N.; Takuda, H. Effect of twinning and detwinning on inelastic behavior during unloading in a magnesium alloy sheet. Mater. Sci. Eng. A 2013, 583, 232–241. [Google Scholar] [CrossRef] [Green Version]
- Yaghoobi, M.; Chen, Z.; Murphy-Leonard, A.D.; Sundararaghavan, V.; Daly, S.; Allison, J.E. Deformation Twinning and Detwinning in Extruded Mg-4Al: In-Situ Experiment and Crystal Plasticity Simulation. Int. J. Plast. 2022, 155, 103345. [Google Scholar] [CrossRef]
- Huang, W.; Chen, J.; Zhang, R.; Yang, X.; Jiang, L.; Xiao, Z.; Liu, Y. Effect of deformation modes on continuous dynamic recrystallization of extruded AZ31 Mg alloy. J. Alloy Compd. 2022, 897, 163086. [Google Scholar] [CrossRef]
- Frydrych, K.; Libura, T.; Kowalewski, Z.; Maj, M.; Kowalczyk-Gajewska, K. On the Role of Slip, Twinning and Detwinning in Magnesium Alloy AZ31B Sheet. Mater. Sci. Eng. A 2021, 813, 141152. [Google Scholar] [CrossRef]
- Bong, H.J.; Hu, X.; Sun, X.; Ren, Y. Temperature-Dependent Constitutive Modeling of a Magnesium Alloy ZEK100 Sheet Using Crystal Plasticity Models Combined with in Situ High-Energy X-Ray Diffraction Experiment. J. Magnes. Alloy 2022, 10, 2801–2816. [Google Scholar] [CrossRef]
- Chang, Y.; Lloyd, J.T.; Becker, R.; Kochmann, D.M. Modeling microstructure evolution in magnesium: Comparison of detailed and reduced-order kinematic models. Mech. Mater. 2017, 108, 40–57. [Google Scholar] [CrossRef]
- Wang, H.; Wu, P.D.; Tomé, C.N.; Huang, Y. A finite strain elastic–viscoplastic self-consistent model for polycrystalline materials. J. Mech. Phys. Solids 2010, 58, 594–612. [Google Scholar] [CrossRef]
- Wang, F.H.; Qiao, H.; Wang, Y.Q.; Dong, J.; Jiang, Y.Y.; Wu, P.D. Numerical Study of Deformation Behavior of Rolled AZ31B Plate under Cyclic Loading in Different Material Orientations Based on the EVPSC-TDT Model. Int. J. Plast. 2021, 147, 103109. [Google Scholar] [CrossRef]
- Tang, D.; Zhou, K.; Tang, W.; Wu, P.; Wang, H. On the Inhomogeneous Deformation Behavior of Magnesium Alloy Beam Subjected to Bending. Int. J. Plast. 2022, 150, 103180. [Google Scholar] [CrossRef]
- Zhang, X.; Li, S.; Guo, X.; Wang, H.; Yu, Q.; Wu, P. Effects of Texture and Twinning on the Torsional Behavior of Magnesium Alloy Solid Rod: A Crystal Plasticity Approach in Comparison with Uniaxial Tension/Compression. Int. J. Mech. Sci. 2021, 191, 106062. [Google Scholar] [CrossRef]
- Wang, H.; Wu, P.D.; Wang, J.; Tomé, C.N. A crystal plasticity model for hexagonal close packed (HCP) crystals including twinning and de-twinning mechanisms. Int. J. Plast. 2013, 49, 36–52. [Google Scholar] [CrossRef]
- Wang, H.; Wu, P.D.; Wang, J. Modelling the role of slips and twins in magnesium alloys under cyclic shear. Comp. Mater. Sci. 2015, 96, 214–218. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Wu, P.; Kurukuri, S.; Worswick, M.J.; Peng, Y.; Tang, D.; Li, D. Strain rate sensitivities of deformation mechanisms in magnesium alloys. Int. J. Plast. 2018, 107, 207–222. [Google Scholar] [CrossRef]
- Wang, H.; Tang, D.; Li, D.Y.; Peng, Y.H.; Wu, P.D. Effects of detwinning on the inelasticity of AZ31B sheets during cyclic loading and unloading. Int. J. Appl. Mech. 2018, 10, 1850095. [Google Scholar] [CrossRef]
- Wang, H.; Li, D.; Peng, Y.; Wu, P.D. Numerical study of inelastic behavior of magnesium alloy sheets during cyclic loading-unloading. J. Phys. Conf. Ser. 2018, 1063, 012050. [Google Scholar] [CrossRef]
- Cheng, J.; Jong Bong, H.; Qiao, H.; Hu, X.; Sun, X.; Ghosh, S.; Wu, P. Comparison of Three State-of-the-Art Crystal Plasticity Based Deformation Twinning Models for Magnesium Alloys. Comput. Mater. Sci. 2022, 210, 111480. [Google Scholar] [CrossRef]
- Beyerlein, I.J.; Tomé, C.N. A dislocation-based constitutive law for pure Zr including temperature effects. Int. J. Plast. 2008, 24, 867–895. [Google Scholar] [CrossRef]
- Capolungo, L.; Marshall, P.E.; McCabe, R.J.; Beyerlein, I.J.; Tomé, C.N. Nucleation and growth of twins in Zr: A statistical study. Acta Mater. 2009, 57, 6047–6056. [Google Scholar] [CrossRef]
- Wang, H.; Clausen, B.; Capolungo, L.; Beyerlein, I.J.; Wang, J.; Tomé, C.N. Stress and strain relaxation in magnesium AZ31 rolled plate: In-situ neutron measurement and elastic viscoplastic polycrystal modeling. Int. J. Plast. 2016, 79, 275–292. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Clausen, B.; Tomé, C.N.; Wu, P.D. Studying the effect of stress relaxation and creep on lattice strain evolution of stainless steel under tension. Acta Mater. 2013, 61, 1179–1188. [Google Scholar] [CrossRef]
- Wang, H.; Wu, P.; Wang, J. Numerical assessment of the role of slip and twinning in magnesium alloy AZ31B during loading path reversal. Metall. Mater. Trans. A 2015, 46, 3079–3090. [Google Scholar] [CrossRef]
- Proust, G.; Tomé, C.N.; Jain, A.; Agnew, S.R. Modeling the effect of twinning and detwinning during strain-path changes of magnesium alloy AZ31. Int. J. Plast. 2009, 25, 861–880. [Google Scholar] [CrossRef]
- Wu, L.; Agnew, S.R.; Ren, Y.; Brown, D.W.; Clausen, B.; Stoica, G.M.; Wenk, H.R.; Liaw, P.K. The effects of texture and extension twinning on the low-cycle fatigue behavior of a rolled magnesium alloy, AZ31B. Mater. Sci. Eng. A 2010, 527, 7057–7067. [Google Scholar] [CrossRef]
- Agnew, S.R.; Duygulu, Ö. Plastic anisotropy and the role of non-basal slip in magnesium alloy AZ31B. Int. J. Plast. 2005, 21, 1161–1193. [Google Scholar] [CrossRef]
- Jain, A.; Agnew, S.R. Modeling the temperature dependent effect of twinning on the behavior of magnesium alloy AZ31B sheet. Mater. Sci. Eng. A 2007, 462, 29–36. [Google Scholar] [CrossRef]
- Simmons, G.; Wang, H. Single Crystal Elastic Constants and Calculated Aggregate Properties: A Handbook, 2nd ed.; M.I.T. Press: Cambridge, MA, USA, 1971; ISBN 978-0-262-19092-3. [Google Scholar]



| Mode | (MPa) | (MPa) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Basal | 98 | 1 × 107 | 3.21 | 8 × 109 | 0.033 | 80 | 1 | 0.2 | 13 |
| Prismatic | 25 | 1 × 107 | 3.21 | 4 × 108 | 0.033 | 80 | 1 | 0.2 | 13 |
| Pyramidal | 315 | 1 × 107 | 6.12 | 1.2 × 108 | 0.033 | 80 | 1 | 0.2 | 13 |
| Twinning | 35 | NA * | 0.492 | NA | NA | NA | NA | NA | 13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Q.; Zhou, X.; Zhang, X.; Liu, C.; Wang, H. Internal Elastic Strains of AZ31B Plate during Unloading at Twinning-Active Region. Metals 2023, 13, 1388. https://doi.org/10.3390/met13081388
He Q, Zhou X, Zhang X, Liu C, Wang H. Internal Elastic Strains of AZ31B Plate during Unloading at Twinning-Active Region. Metals. 2023; 13(8):1388. https://doi.org/10.3390/met13081388
Chicago/Turabian StyleHe, Qichang, Xiangyu Zhou, Xiaodan Zhang, Chuhao Liu, and Huamiao Wang. 2023. "Internal Elastic Strains of AZ31B Plate during Unloading at Twinning-Active Region" Metals 13, no. 8: 1388. https://doi.org/10.3390/met13081388
APA StyleHe, Q., Zhou, X., Zhang, X., Liu, C., & Wang, H. (2023). Internal Elastic Strains of AZ31B Plate during Unloading at Twinning-Active Region. Metals, 13(8), 1388. https://doi.org/10.3390/met13081388







